Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.
Calculus
Application of derivativesSketch the graph and the rectangles y 3 2 O 3 2 y 3 2 mal places 1 2 y 3 2 1 1 2 X

Calculus
Application of derivativessquare is inscribed in a circle such that each corner touches the circle A Find a function that gives the area of the square as a function of the radius of the circle Simplify the function as much as possible and describe any symmetry in the function Make certain to show all the steps you use to come up with the function as well as describe your reasoning B State the domain and range of the function you came up with in part A keeping in mind all practical considerations
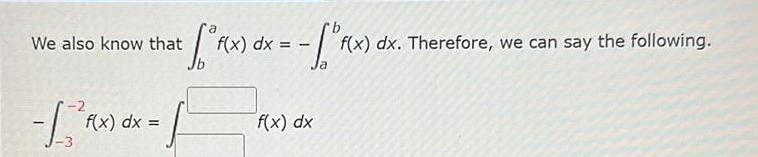
Calculus
Application of derivativesWe also know that I Rx it f x f x dx f x dx F F x f x dx f x dx Therefore we can say the following

Calculus
Vector Calculusnot be able to come back to the skipped part Tutorial Exercise Express the number as a ratio of integers 0 82 0 82828282
Calculus
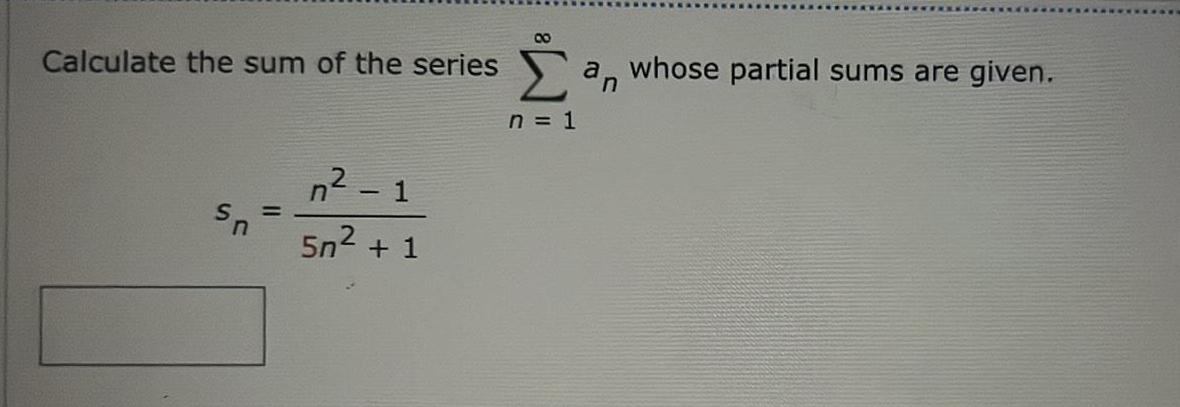
Limits & ContinuityCalculate the sum of the series sn n 1 5n 1 00 a whose partial sums are given n 1
Calculus
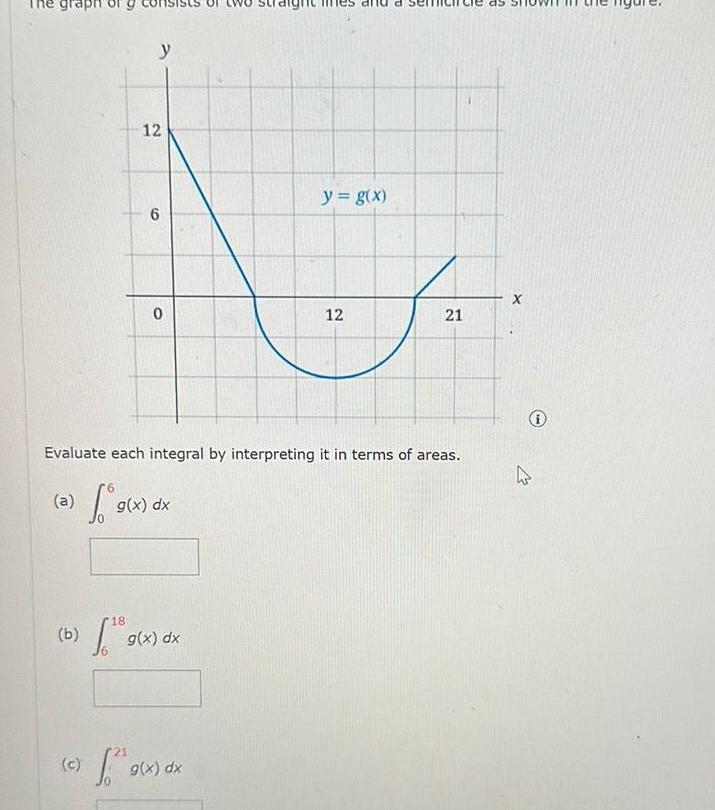
Application of derivativesgrap a b 18 g c y 12 6 1 9 0 Evaluate each integral by interpreting it in terms of areas g x dx g x dx y g x g x dx 12 21 X 4
Calculus
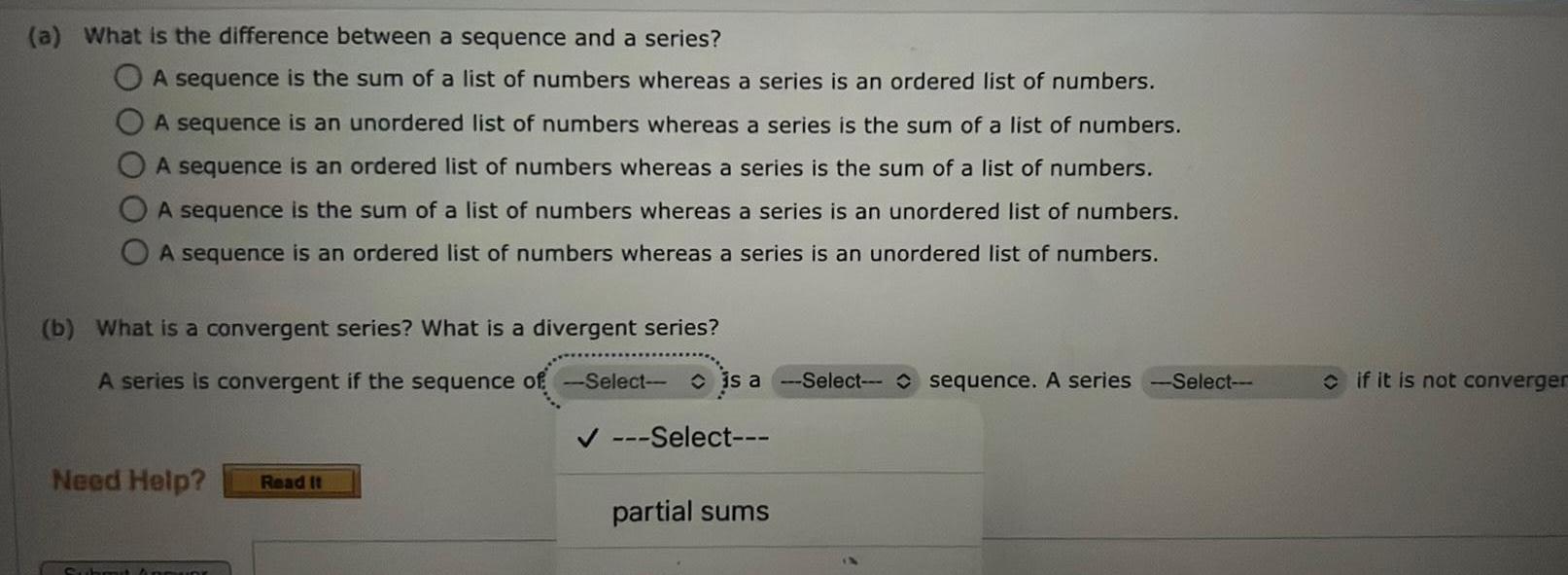
Vector Calculusa What is the difference between a sequence and a series A sequence is the sum of a list of numbers whereas a series is an ordered list of numbers A sequence is an unordered list of numbers whereas a series is the sum of a list of numbers A sequence is an ordered list of numbers whereas a series is the sum of a list of numbers A sequence is the sum of a list of numbers whereas a series is an unordered list of numbers A sequence is an ordered list of numbers whereas a series is an unordered list of numbers b What is a convergent series What is a divergent series A series is convergent if the sequence of Select is a Select sequence A series Need Help Read It Sub Select partial sums Select if it is not converger
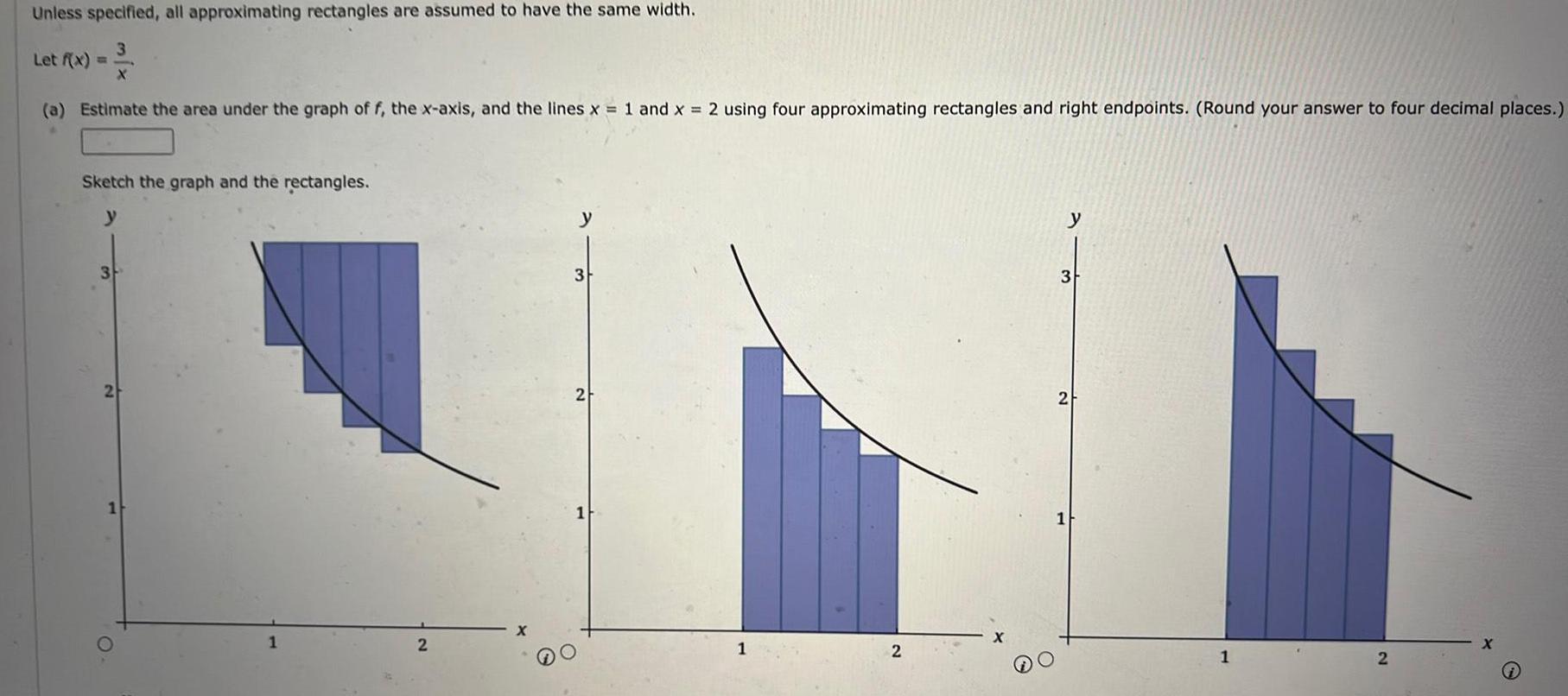
Calculus
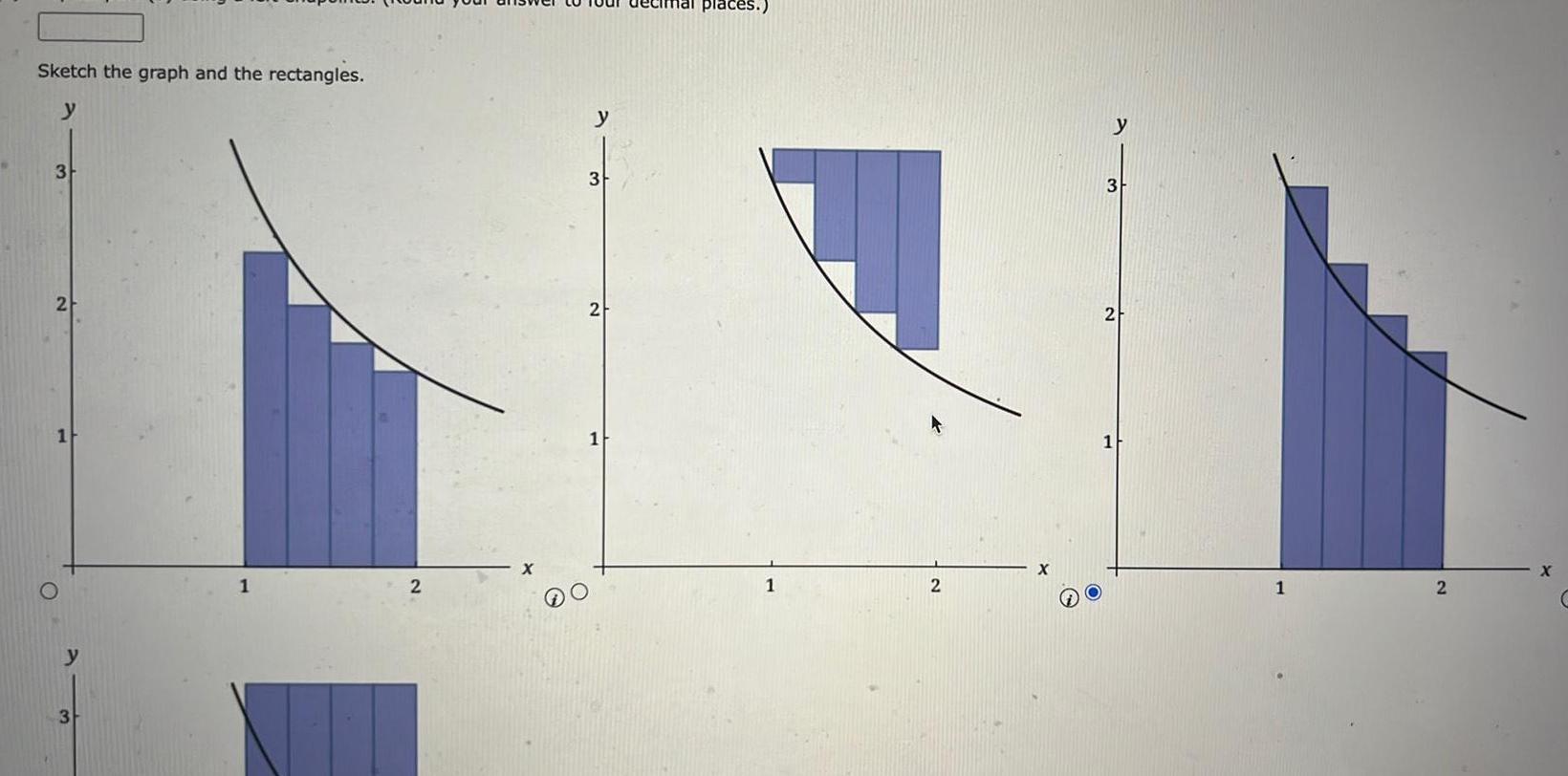
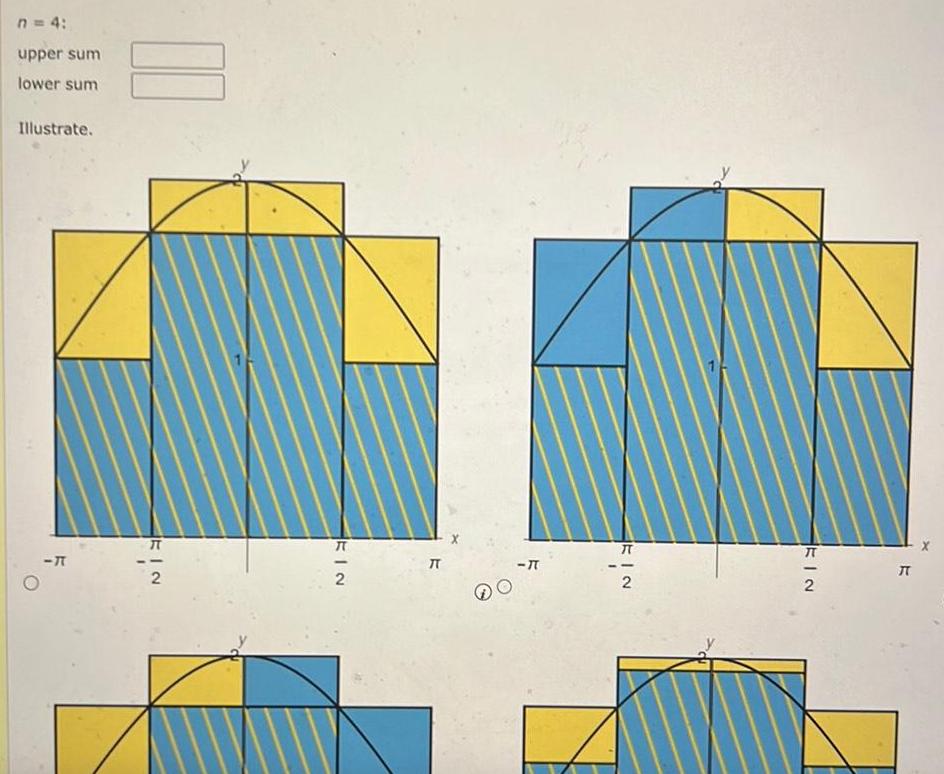
Application of derivativesUnless specified all approximating rectangles are assumed to have the same width Let f x X a Estimate the area under the graph of f the x axis and the lines x 1 and x 2 using four approximating rectangles and right endpoints Round your answer to four decimal places Sketch the graph and the rectangles y 3 2 O 2 3 2 1 1 2 y 3 2 1 2 X
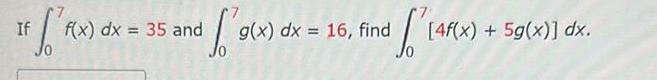

Calculus
Definite IntegralsWrite the following expression as a single definite integral of the form m F x f x dx F x dx f x dx f x dx Step 1 f x dx f x dx f x dx Using the first and second integrals since we have 3 1 4 f x dx F x We know that for a b c f x dx f x dx
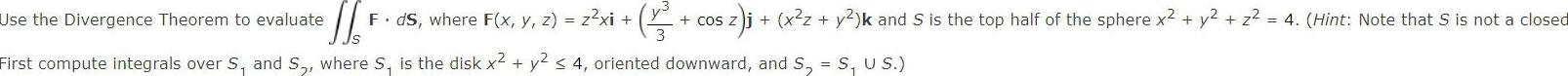
Calculus
Definite Integrals1 3 Use the Divergence Theorem to evaluate F ds where F x y z z xi First compute integrals over S and S where S is the disk x y2 4 oriented downward and S S U S cos Z sz j x z y k and S is the top half of the sphere x y z 4 Hint Note that S is not a closed
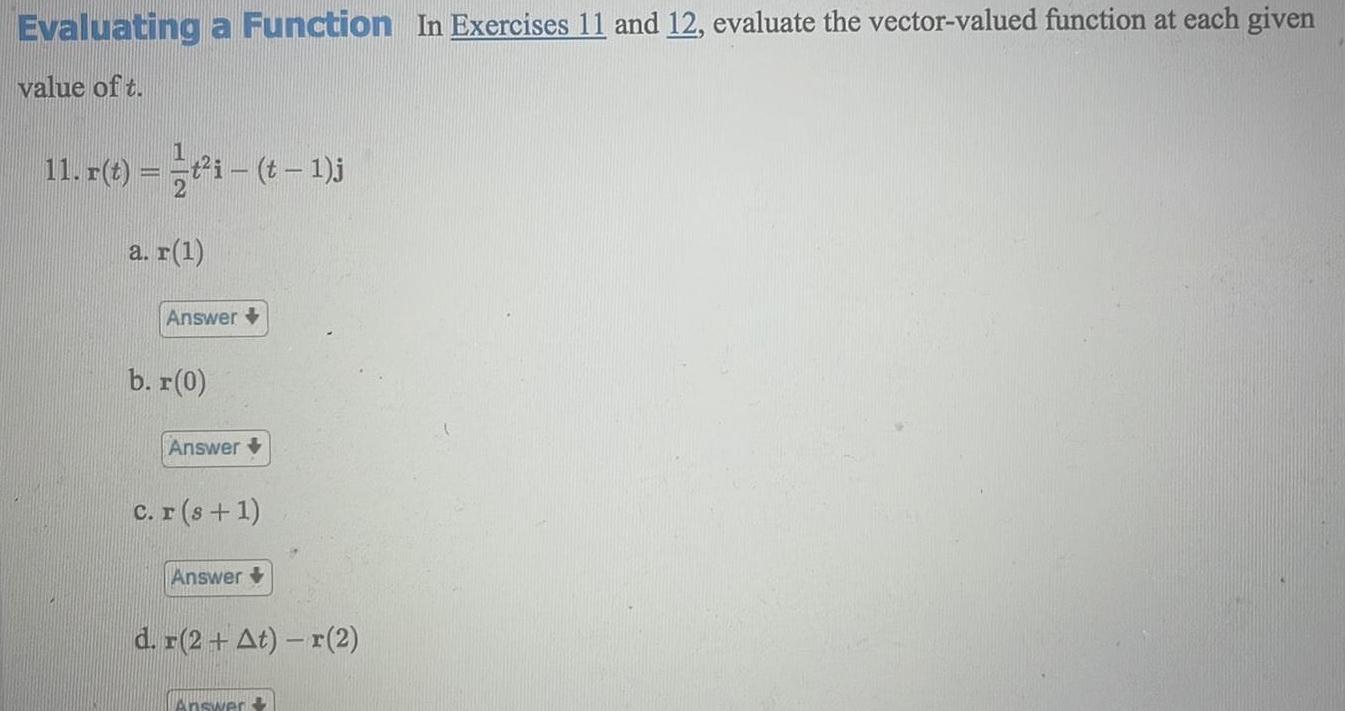
Calculus
Vector CalculusEvaluating a Function In Exercises 11 and 12 evaluate the vector valued function at each given value of t 11 r t i t 1 j a r 1 Answer b r 0 Answer c r s 1 Answer d r 2 At r 2 Answer
Calculus
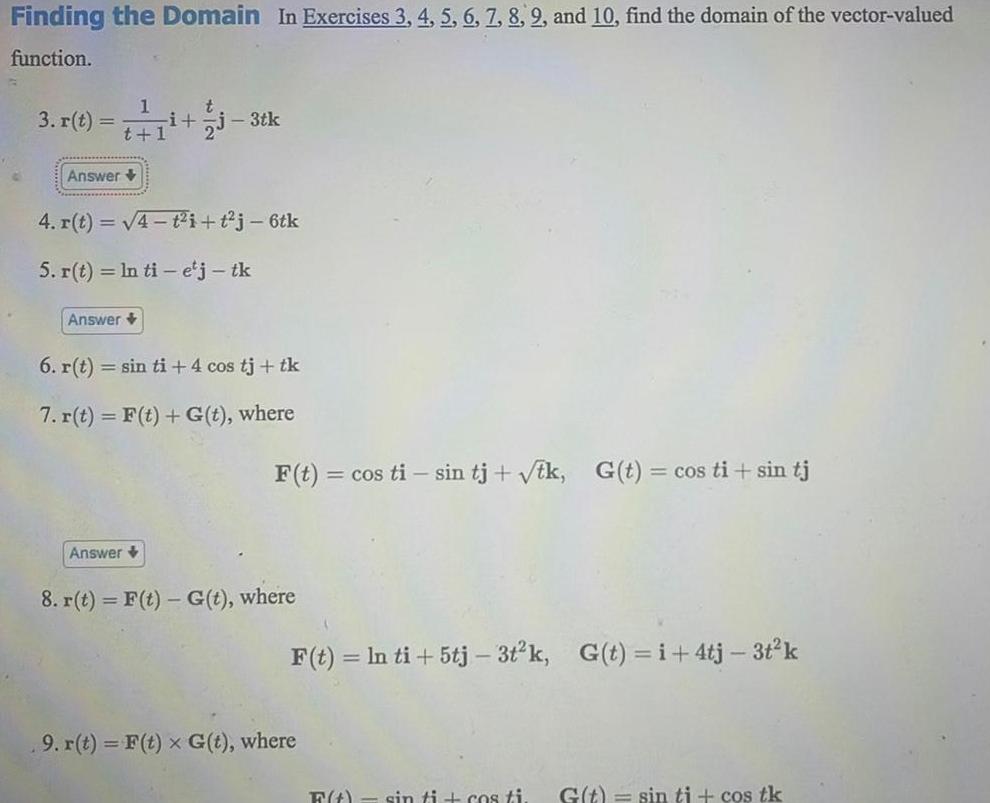
Vector CalculusFinding the Domain In Exercises 3 4 5 6 7 8 92 and 10 find the domain of the vector valued function 3 r t i j3tk Answer 4 r t 4 t i t j 6tk 5 r t ln ti e j tk Answer 6 r t sin ti 4 cos tj tk 7 r t F t G t where Answer F t cos ti sin tj tk G t cos ti sin tj 8 r t F t G t where F t ln ti 5tj 3t k G t i 4tj 3t k 9 r t F t x G t where F t sin ti cos ti G t sin ti cos tk

Calculus
DifferentiationHigher Order Differentiation In Exercises 19 20 21 and 22 find a r t b r t and c r t r t 19 r t t i t j 2 Answer 20 r t t i t t j 1

Calculus
Application of derivativesFinding the Domain In Exercises 3 4 5 6 7 8 9 and 10 find the domain of the vector valued function 1 t 3 r t i j 3tk t 1 Answer 4 r t 4 t i t j 6tk 5 r t In ti e j tk

Calculus
Application of derivativesFinding the Domain In Exercises 3 4 5 6 7 8 2 and 10 find the domain of the vector valued function 3 r t i j3tk

Calculus
DifferentiationFinding a Derivative In Exercises 11 12 13 14 15 16 17 and 18 find r t 11 r t t i 5tj Answer 12 r t ti 1 j 13 r t 3 cos ti 2 sin tj k

Calculus
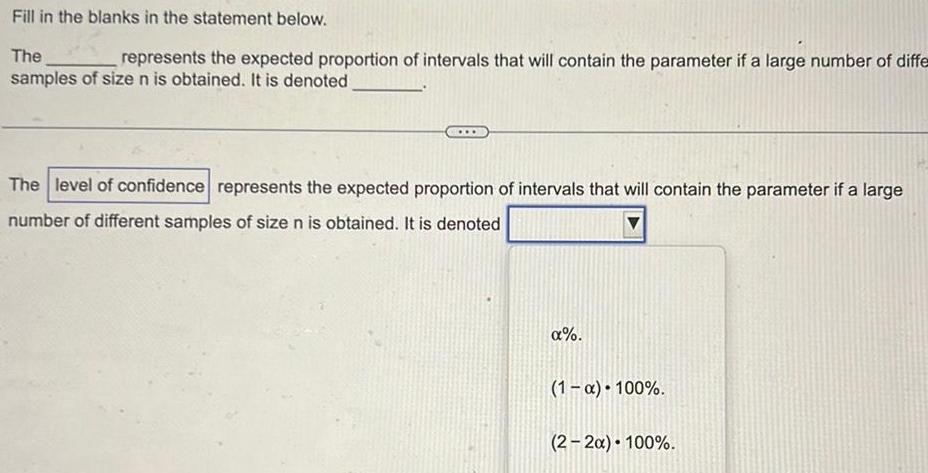
Limits & ContinuityFill in the blanks in the statement below The represents the expected proportion of intervals that will contain the parameter if a large number of diffe samples of size n is obtained It is denoted The level of confidence represents the expected proportion of intervals that will contain the parameter if a large number of different samples of size n is obtained It is denoted 1 x 100 2 2x 100

Calculus
Vector CalculusDifferentiation of Vector Valued Functions In Exercises 3 4 5 6 7 8 9 and 10 find r t to and r to for the given value of to Then sketch the curve represented by the vector valued function and sketch the vectors r to and r to to 3 3 r t 1 t2 i tj Answer 4 r t 1 t i t j 5 r t cos ti sin tj Answer to 1 to 6 r t 3 sin ti 4 cos tj 7 r t e e t to 0 to

Calculus
Vector Calculusfferentiation of Vector Valued Functions In Exercises 3 4 5 6 7 8 2 and 10 find r t and r to for the given value of to Then sketch the curve represented by the vector valued function and etch the vectors r to and r to 3 r t 1 i tj to
Calculus
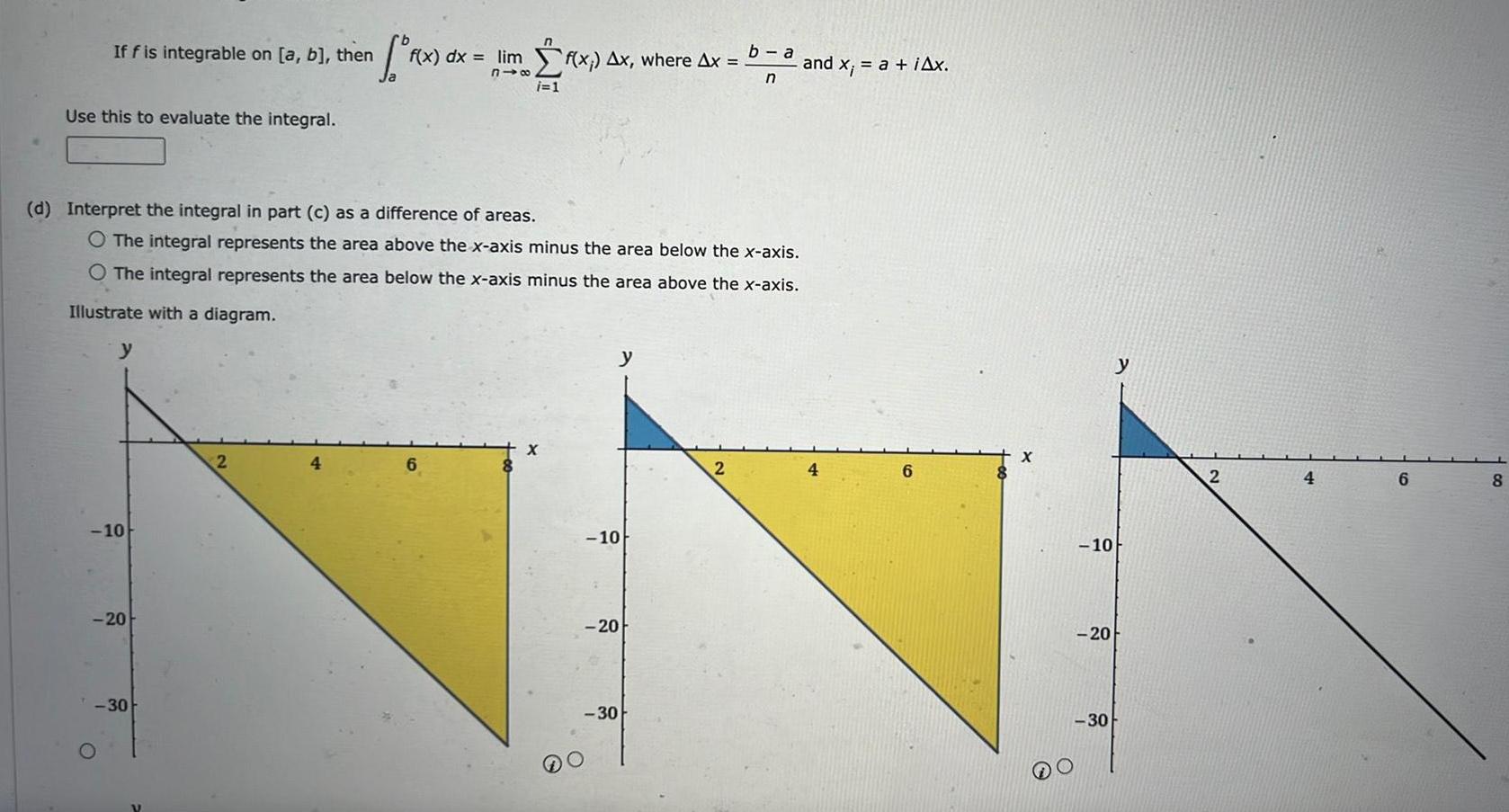
Definite IntegralsIf f is integrable on a b then Use this to evaluate the integral y d Interpret the integral in part c as a difference of areas O The integral represents the area above the x axis minus the area below the x axis O The integral represents the area below the x axis minus the area above the x axis Illustrate with a diagram 10 20 30 n f r x dx 11 dx limf x Ax where Ax n i 1 2 10 20 30 b a 2 and x a iAx 10 20 30 2 4 6 co 8

Calculus
Vector CalculusFinding a Unit Vector In Exercises 15 16 17 and 18 find a unit vector that is orthogonal to both u and v 15 u 4 3 1 v 2 5 3 Answer 16 u 8 6 4 v 10 12 2 17 u 3i 2j 5k v i j 4k
Calculus
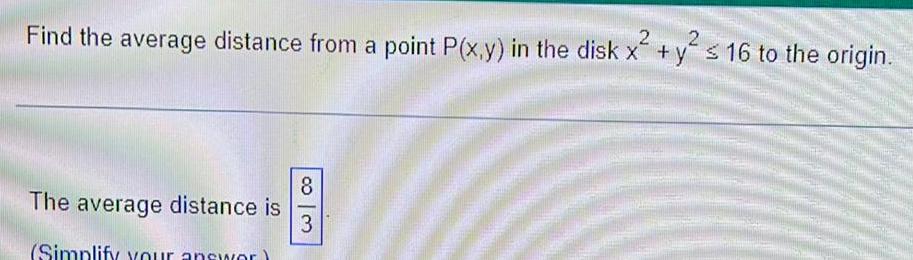
Application of derivatives2 2 Find the average distance from a point P x y in the disk x y 16 to the origin The average distance is Simplify your answer 8 1 3

Calculus
Vector CalculusArea In Exercises 19 20 21 and 22 find the area of the parallelogram that has the given vectors adjacent sides Use a computer algebra system or a graphing utility to verify your result 19 u j v j k Answer 20 u i j k v j k 21 u 3 2 1 v 1 2 3
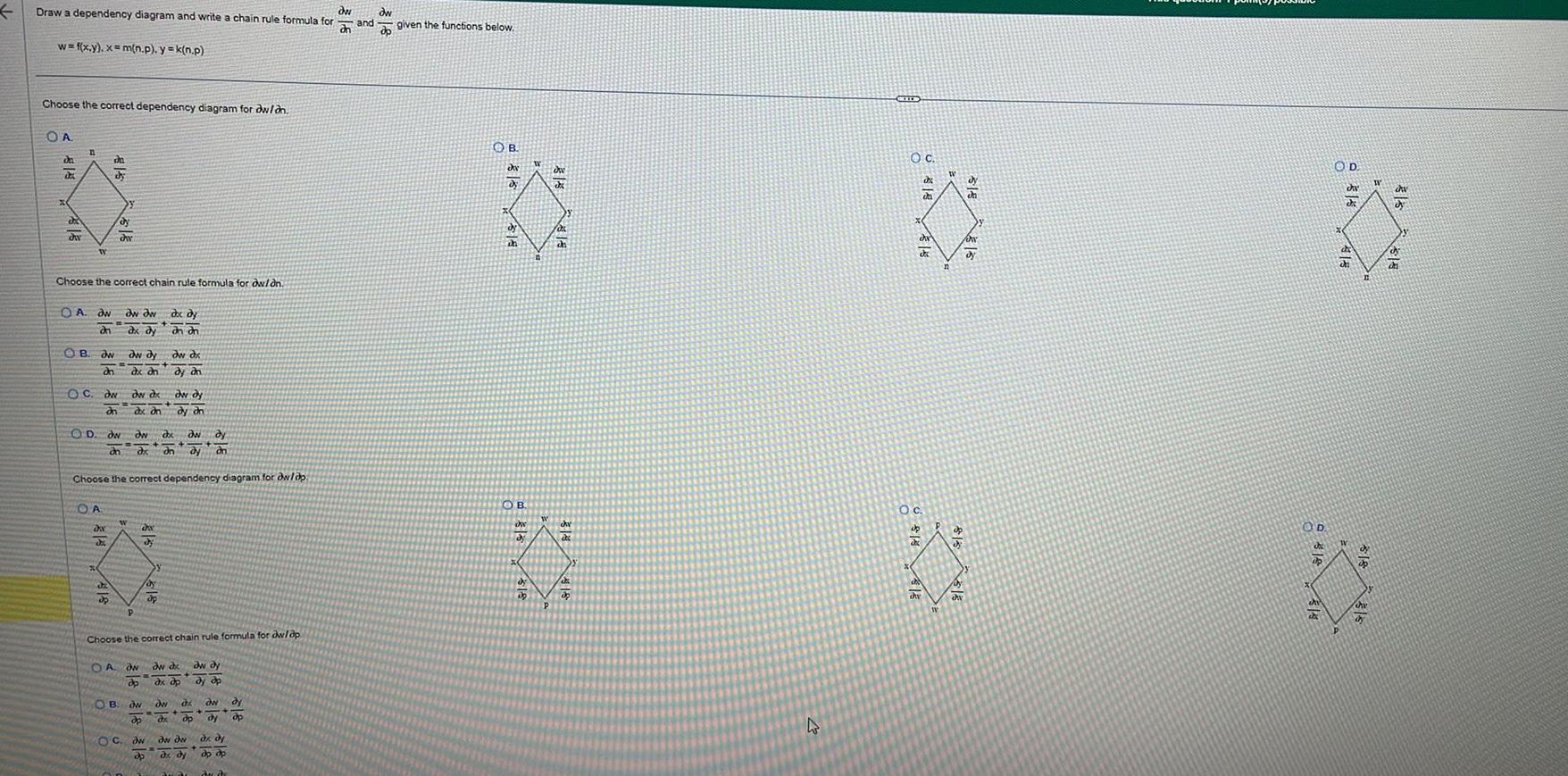
Calculus
Definite IntegralsDraw a dependency diagram and write a chain rule formula for w f x y x m n p y k n p Choose the correct dependency diagram for dw on OA da da du dw n W OA dw Choose the correct chain rule formula for dw dn 316 du dy OB aw dh OC dw dn dy d OD dw an OA ON dw dw ax dy OB dw dy dw dx de dn dy dh dw dx dx an Choose the correct dependency diagram for dwlop OC dw dx Ow dy dx dn dy an da di dx dy an an Choose the correct chain rule formula for dw ap dw dy dy dn dy Op OA ON aw dx do dx dp ow op dw ap ow d de op aw dy dy op dw dw de dy ON dy dx dy ap op Y du ch dy op 316 and 318 given the functions below OB dy ch OB ch 4 CIDE da da Oc du dy OD 316 314 OD dar di di Up W Jav

Calculus
Application of derivativesFinding a Cross Product In Exercises 11 12 13 and 14 find u v and show that it is orthogonal to both u and v 11 u 4 1 0 v 6 3 0

Calculus
Limits & ContinuityFinding Cross Products In Exercises 7 8 2 and 10 find a u x v b v x u and C V X V 7 u 2i 4j v 3i 2j 5k
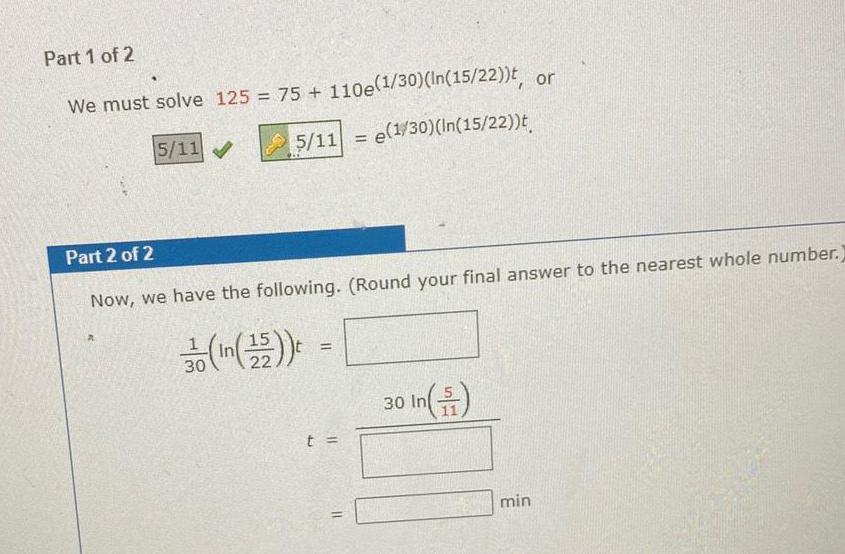
Calculus
Application of derivativesPart 1 of 2 We must solve 125 75 110e 1 30 In 15 22 t or 5 11 e 1 30 In 15 22 t 5 11 Part 2 of 2 Now we have the following Round your final answer to the nearest whole number 1 30 In 15 t t 11 30 In min
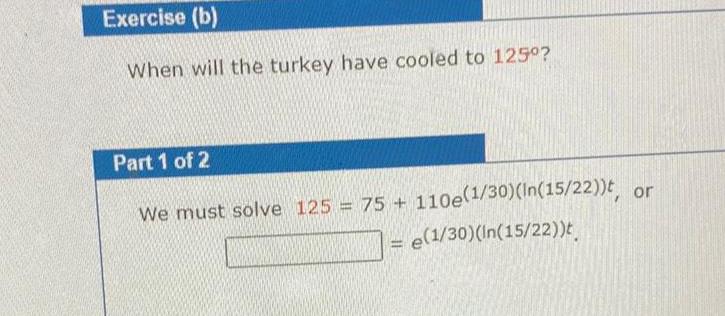
Calculus
Application of derivativesExercise b When will the turkey have cooled to 125 Part 1 of 2 We must solve 125 75 110e 1 30 In 15 22 t or e 1 30 In 15 22 t
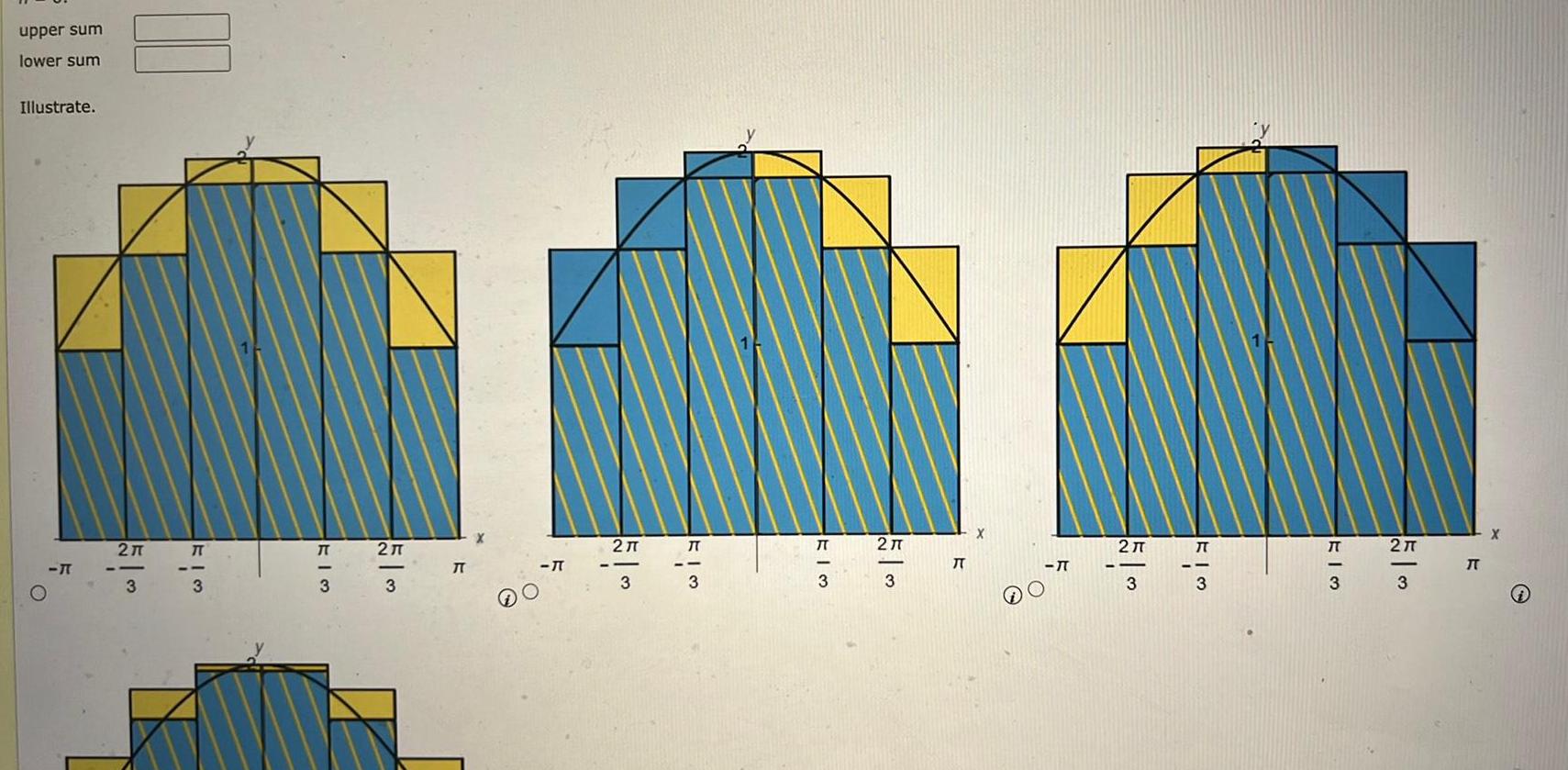
Calculus
Definite Integralsupper sum lower sum Illustrate 11 FIS 7 3 T DO T 2T FIM KI3 5 3 K 7 O 510 2 T 1 KI3 FI3 5 K IT
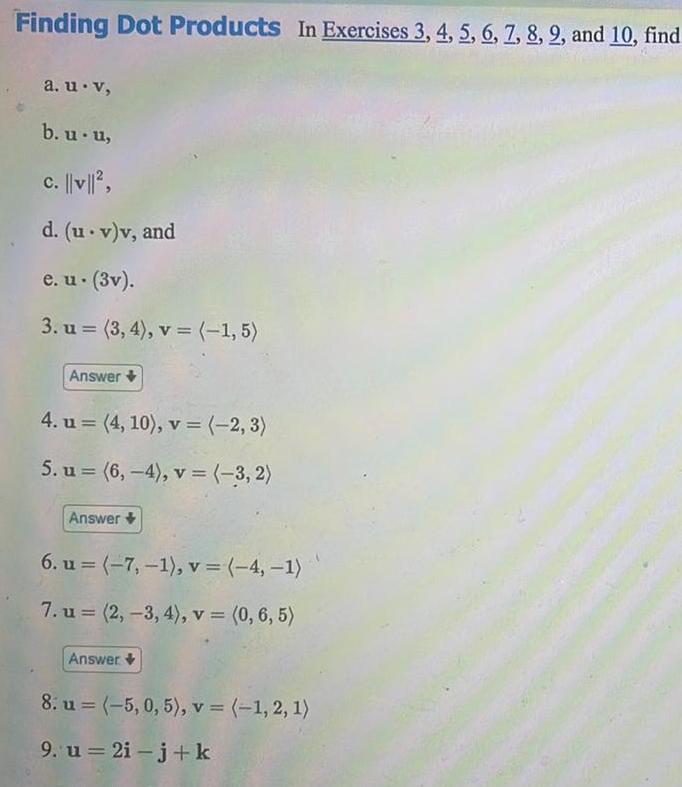
Calculus
Vector CalculusFinding Dot Products In Exercises 3 4 5 6 7 8 9 and 10 find a u v b u u c v d u v v and e u 3v 3 u 3 4 v 1 5 Answer 4 u 4 10 v 2 3 5 u 6 4 v 3 2 Answer 6 u 7 1 v 4 1 7 u 2 3 4 v 0 6 5 Answer 8 u 5 0 5 v 1 2 1 9 u 2i j k
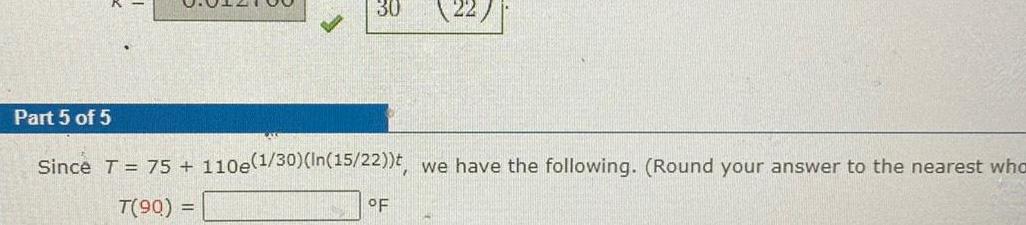
Calculus
Application of derivatives30 Part 5 of 5 Since T 75 110e 1 30 In 15 22 t we have the following Round your answer to the nearest who T 90 F

Calculus
Definite IntegralsWith a programmable calculator or a computer it is possible to evaluate the expressions for the sums of areas of approximating rectangles even for large values of n using looping On a TI u Is command or a For EndFor loop on a Casio use Isz on an HP or in BASIC use a FOR NEXT loop Compute the sum of the areas of approximating rectangles using equal subintervals and righ endpoints for n 10 30 50 and 100 n 10 30 50 100 the region under y 4 cos x the x axis and the lines x 0 and x T 2 Sum of Areas Use these estimates to guess the value of the exact area
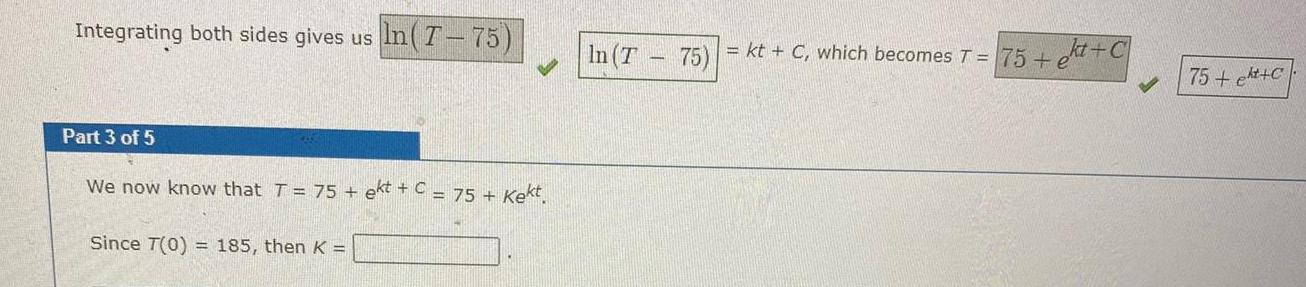
Calculus
DifferentiationIntegrating both sides gives us In 7 75 Part 3 of 5 We now know that T 75 ekt C 75 Kekt Since T 0 185 then K In T 75 kt C which becomes T 75 kt C 75 kt C

Calculus
Definite IntegralsExpress the integral as a limit of Riemann sums using right endpoints Do not evaluate the limit r6 5 x dx Find the width of each subinterval in terms of n Find the ith endpoint in terms of n x Evaluate f x 5 x at the ith endpoint f x units Express the integral as the limit of Riemann sums using right endpoints lim 318 n i 1
Calculus
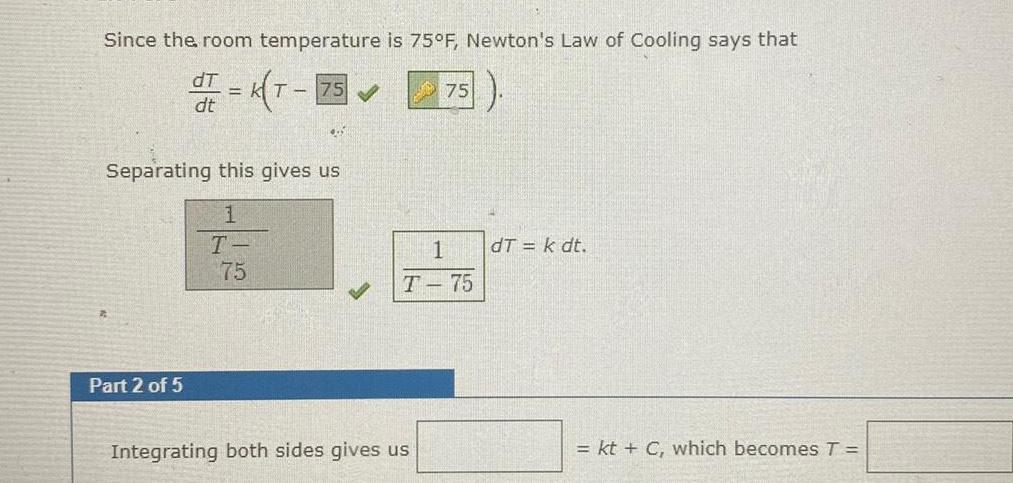
Application of derivativesSince the room temperature is 75 F Newton s Law of Cooling says that dT dr K T 75 dt 455 Separating this gives us 1 T 75 Part 2 of 5 75 1 T 75 Integrating both sides gives us dT k dt kt C which becomes T
Calculus
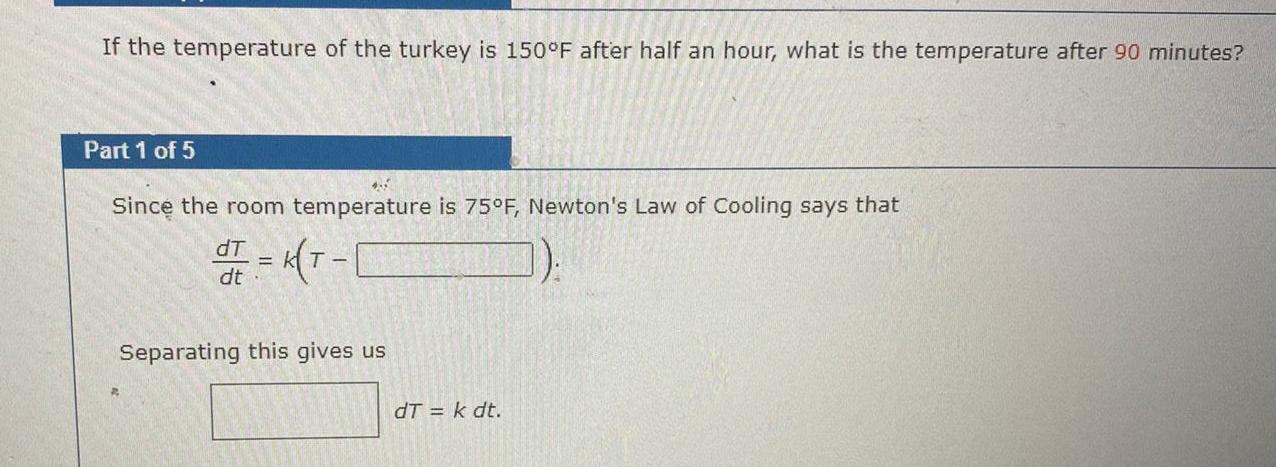
Application of derivativesIf the temperature of the turkey is 150 F after half an hour what is the temperature after 90 minutes Part 1 of 5 Since the room temperature is 75 F Newton s Law of Cooling says that dT d K T 1 dt Separating this gives us dT k dt
Calculus
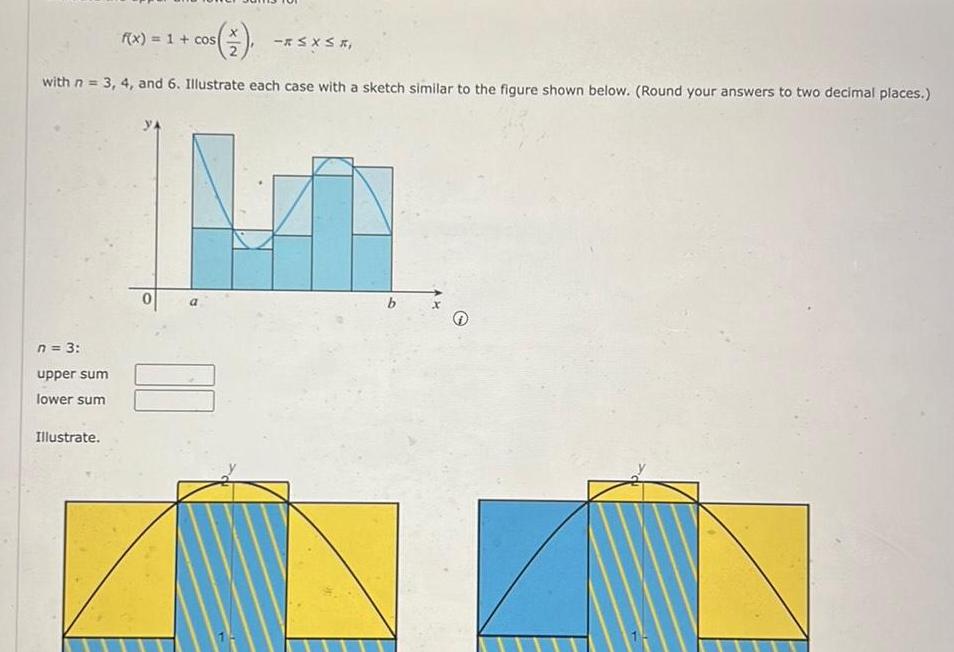
Definite Integralsf x 1 cos with n 3 4 and 6 Illustrate each case with a sketch similar to the figure shown below Round your answers to two decimal places n 3 upper sum lower sum Illustrate RS XS b
Calculus
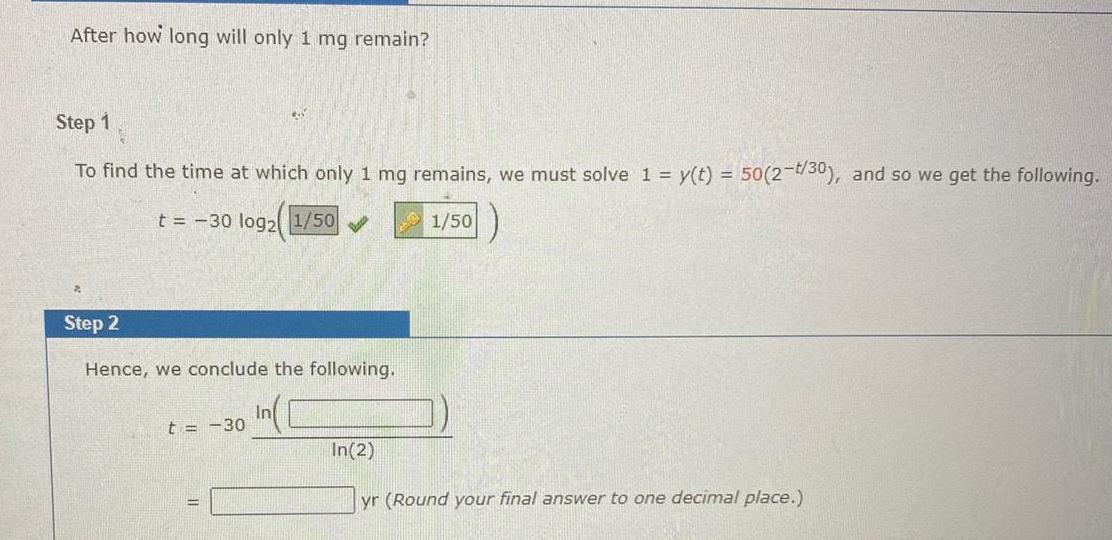
Limits & ContinuityAfter how long will only 1 mg remain Step 1 To find the time at which only 1 mg remains we must solve 1 y t 50 2 t 30 and so we get the following t 30 log2 1 50 1 50 Step 2 Hence we conclude the following t 30 In In 2 yr Round your final answer to one decimal place
Calculus
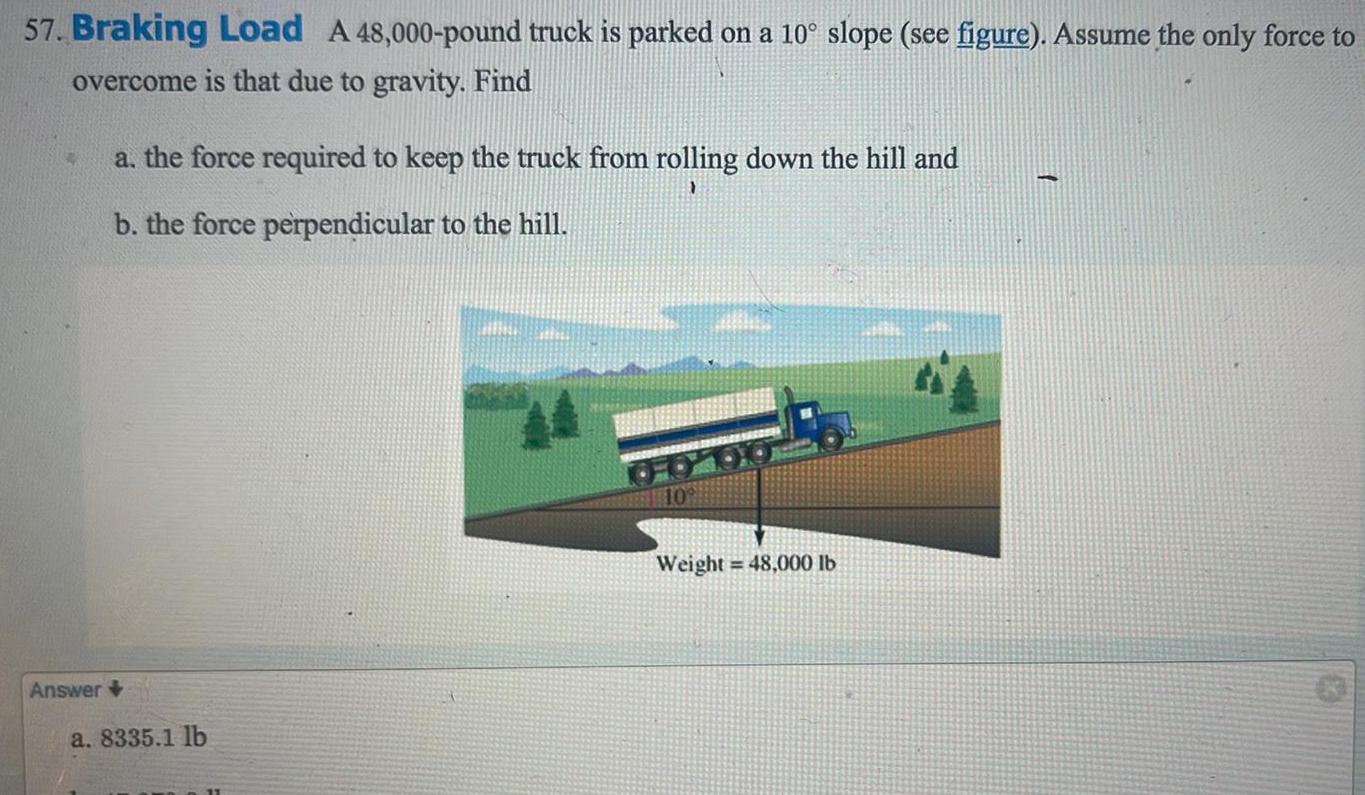
Limits & Continuity57 Braking Load A 48 000 pound truck is parked on a 10 slope see figure Assume the only force to overcome is that due to gravity Find Answer a the force required to keep the truck from rolling down the hill and b the force perpendicular to the hill a 8335 1 lb Weight 48 000 lb
Calculus
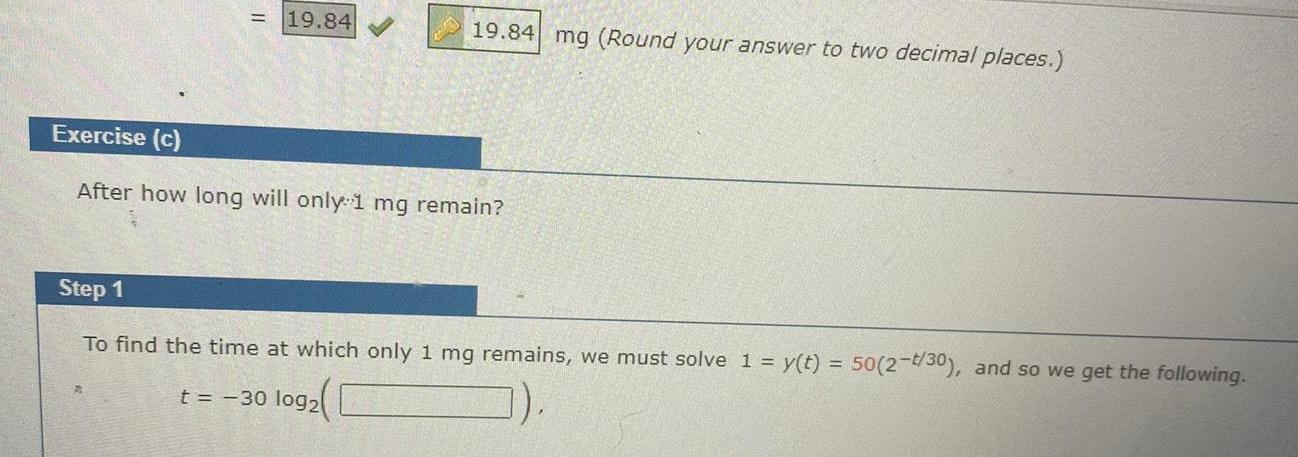
Application of derivatives19 84 19 84 mg Round your answer to two decimal places Exercise c After how long will only 1 mg remain Step 1 To find the time at which only 1 mg remains we must solve 1 y t 50 2 t 30 and so we get the following t 30 log2
Calculus
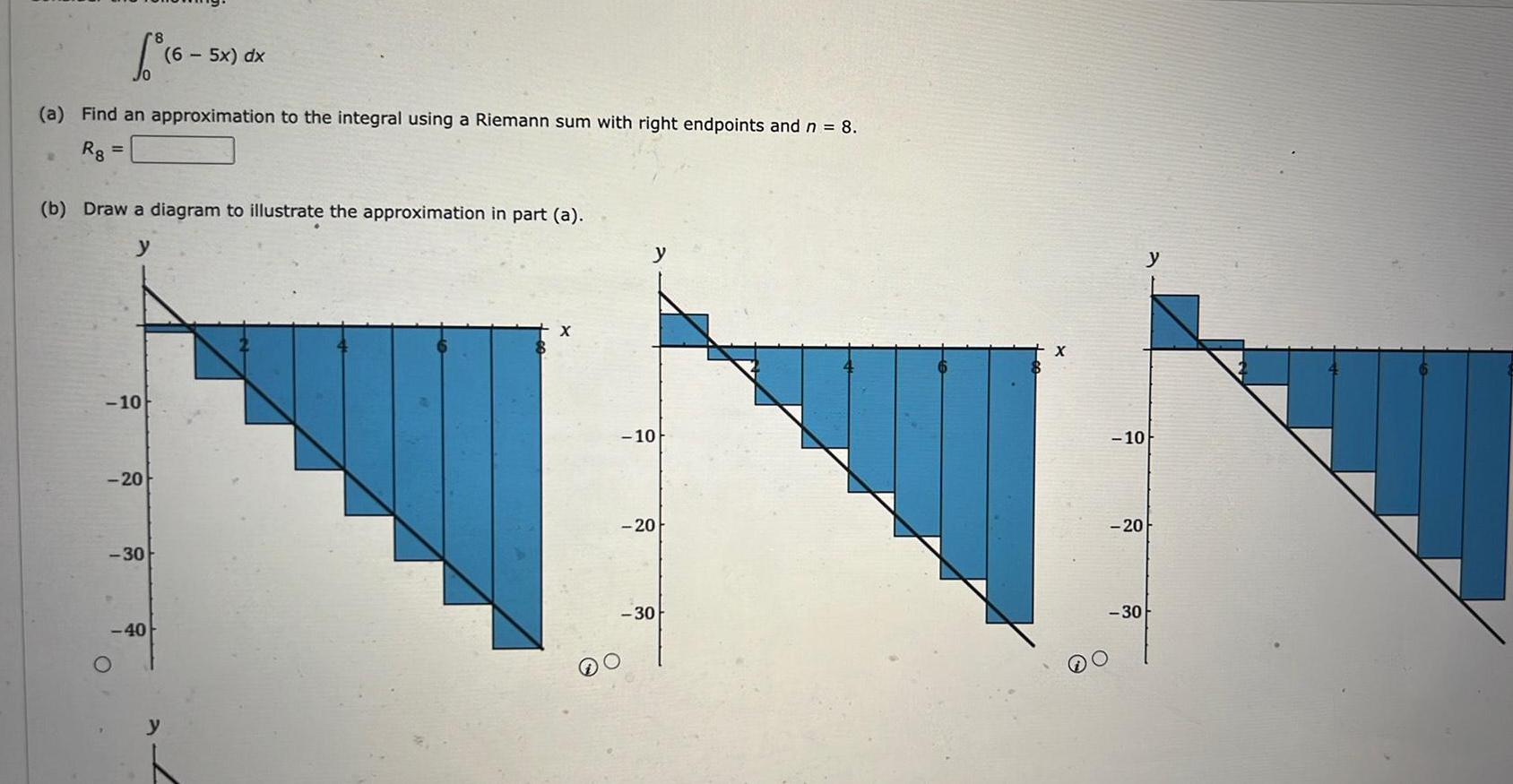
Application of derivatives6 16 5 a Find an approximation to the integral using a Riemann sum with right endpoints and n 8 Rg b Draw a diagram to illustrate the approximation in part a y 10 20 6 5x dx 30 40 10 20 30 10 20 30 y
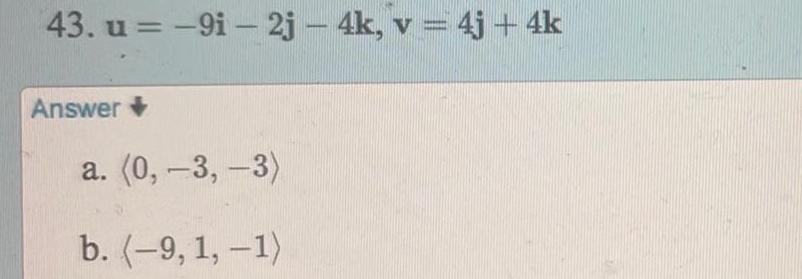
Calculus
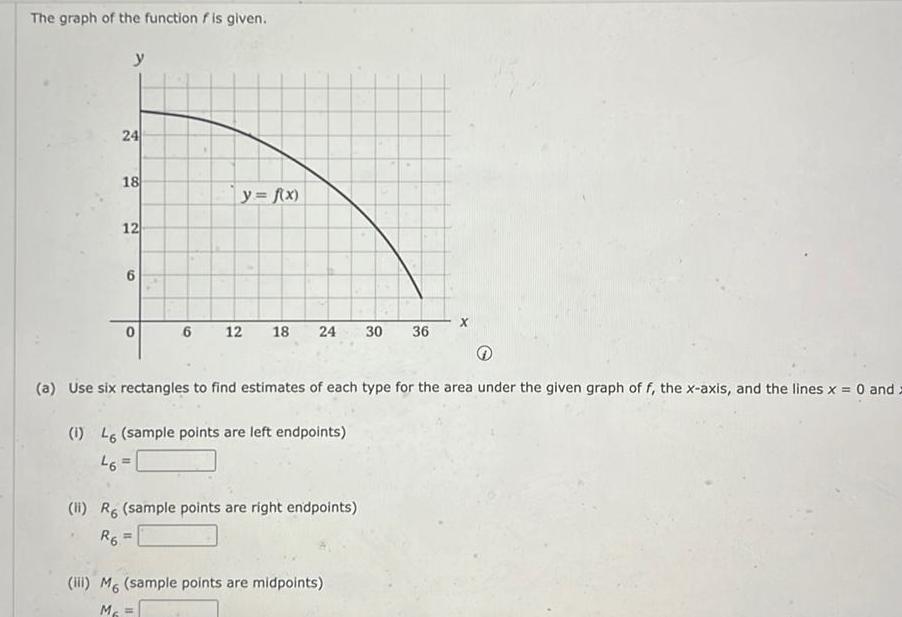
Definite IntegralsThe graph of the function f is given y 24 18 12 9 0 6 y f x 12 18 24 30 36 a Use six rectangles to find estimates of each type for the area under the given graph of f the x axis and the lines x 0 and 1 L sample points are left endpoints 46 li R sample points are right endpoints R6 X iii M6 sample points are midpoints M