Vectors Questions and Answers



Geometry
Vectors4 Let 0 A B and C be the vertices of a tetrahedron and 2 1 2 is the centroid of OABC by ratio 3 1 Vertex O is the origin If G is a centroid of AABC for the tetrahedron evaluate the value of 1OG 1

Geometry
Vectors8 Using vectors explain how to determine the volume of the following parallelepiped Determine its volume B 6 3 5 A 4 0 0 x O C 2 3 5 D 6 5 3

Geometry
Vectors1 Consider the vectors a 2i k b 4i j 3k and c i 4j 3k determine the following fully simplified b 3b 2c a a b c c 1 e exb 2 g Vector projection of bonto c 2 d x 1 f b c

Geometry
Vectors9 Explain why it is not possible to determine a vector that is mutually perpendicular to vectors 2 1 and b 2 2


Geometry
Vectors16 3 eesees A 9 3 If AB has length 9 3 and AC has length 16 3 find The length of BC The measure of angle B in degrees The measure of angle C in degrees B If you use a calculator to find a decimal approximation your answer must be accurate to at least 3 decimal places

Geometry
Vectors13 9 A AC has length 13 9 and BC has length 16 1 find The length of AB The measure of angle B in degrees The measure of angle C in degrees 16 1 B you use a calculator to find a decimal approximation your answer must be accurate to at least 3 ecimal places

Geometry
Vectorsfind x 1 2t the an d for the plane parallel to the line and that contains z 1 2 t x 3y 77 2 an equation for y 2 3 t line of intersection of the planes 3x 1ly 172 2


Geometry
VectorsThe likelihood of falling into an alcohol induced coma is highest when consuming Group of answer choices 5 alcoholic drinks in 2 hours a whole 750 mL bottle of whisky in 2 hours a whole 750 mL bottle of beer in 2 hours enough alcohol to raise blood alcohol levels above 0 55

Geometry
VectorsFind the exact values of the trigonometric functions sin O sinn 0 5 sin 1 0 5 sin 2 1 and sin 6 O sin x 0 5 sin x 0 5 sin 2 0 5 sin 0 5 1 6

Geometry
Vectors10 15 Use the Laplace transform to solve the initial value problem y y 8 t 2n y 0 1 y 0 0 No credit for any other method


Geometry
Vectorsangle Your Turn Apply the tangent ratio to find unknown lengths 1 A ladder needs to reach the second story window which is 10 feet above the ground and make an angle with the ground at 70 How far out from the building does the base of the ladder need to be positioned Round your answer to the nearest tenth EXPLAIN 3 Finding an Angle Measure Using Tangent Read Explain 3 and complete Your Turn 1 2 adapted from Lesson 13 1 Show all your work The inverse tangent function tan x takes a tangent ratio x and returns the angle If ratio the length of the two legs of a right triangle are nown then the inverse tangent function can be used to find the unknown measure of an angle of that right triangle You can use a scientific calculator to determine the value of this angle for any given ratio Again when using a calculator to evaluate an inverse trigonometric function you will need to make sure it is in degree mode not radian mode see explain 2 above Inverse of the Tangent Function Words Symbols Let ZA be an acute angle of right triangle A ABC and let x be the tangent ratio of ZA The inverse tangent of x is the measure of ZA tan 1 If tan A x then tan x mLA Y CA m A 70 X 10 ft Z tan x angle

Geometry
VectorsENGAGE Simplifying Radical Expressions Complete the following activity with your teacher in order to start your learning on trigonometry Simplifying Radicals a 49 c 175 Multiplying Radicals e 5 10 Ge B 3 12 6 b 18 d 5 45 f 6 6 h 4 20 5 80 A 8 10 4 Matic factor free Circle pairs Pull one number from each pair and marply 2 x 2 455 4 The number the branch at the end ot circled is left inside the radical Answer 455 5 2 5 10 Combine into one radical Then simplify what s inside 2 5 73 2 7 5 3 14 15 Multiply the regular numbers together and multipy the radicals together
Geometry
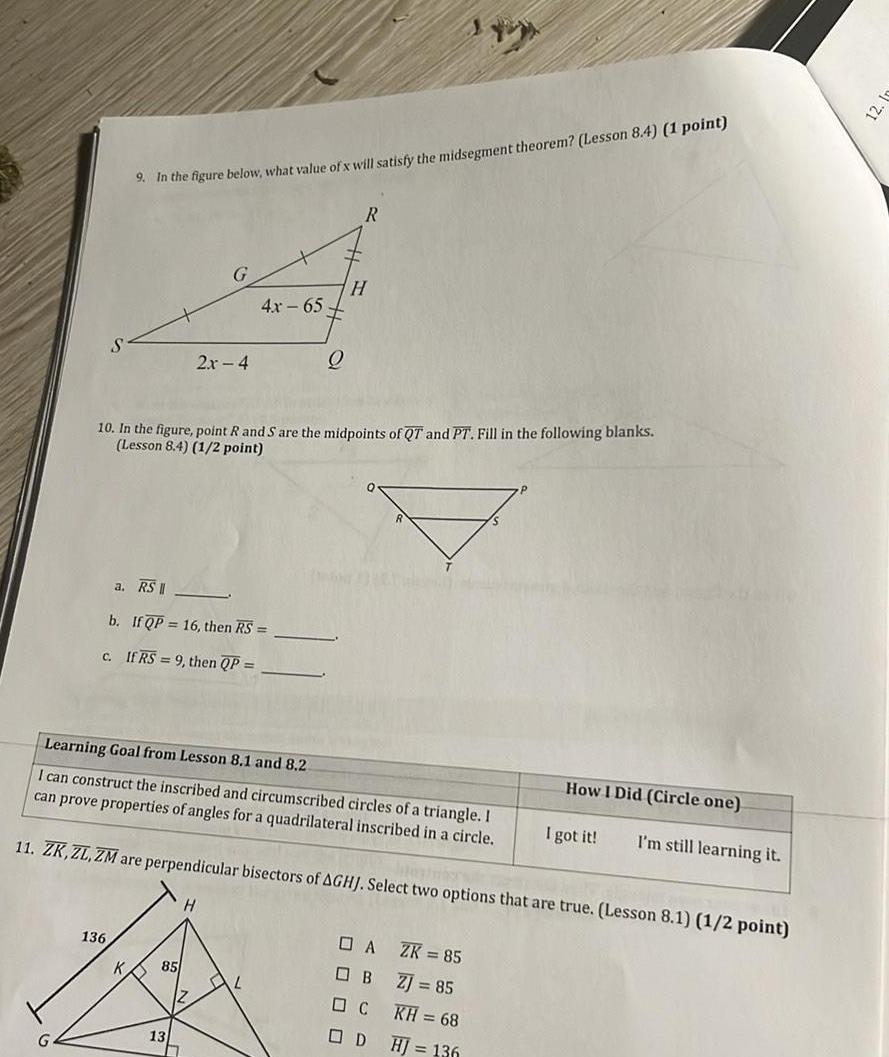
Vectors9 In the figure below what value of x will satisfy the midsegment theorem Lesson 8 4 1 point 136 G a RS II b If QP 16 then RS C If RS 9 then QP 2x 4 85 10 In the figure point R and S are the midpoints of QT and PT Fill in the following blanks Lesson 8 4 1 2 point 13 4x 65 Learning Goal from Lesson 8 1 and 8 2 I can construct the inscribed and circumscribed circles of a triangle I can prove properties of angles for a quadrilateral inscribed in a circle 11 ZK ZL ZM are perpendicular bisectors of AGHJ Select two options that are true Lesson 8 1 1 2 point Q AL R H A OB C D ZK 85 ZJ 85 KH 68 HJ 136 How I Did Circle one I got it I m still learning it 12 1

Geometry
VectorsFind the area of the triangle having the indicated angle and sides Round your answer to one decimal place C 128 a 3 b 5

Geometry
VectorsHan invests 13 000 into a fund that combines stocks and bonds The return varies from year to year The balance at 5 year intervals is given in the table below The goal of this exercise is to find constants a and b such that the model y ae best fits the data In order to do that we apply the natural logarithm to both sides of the model This yields In y In ae and using properties of logarithms In y In a Ine In y In a bt If we let Y In y c In a and c b the problem now reduces to finding the linear fit Y q c the set of dats point and A the problem now reduces to ending the linear 1 Yar 0 5 10 15 201 25 481 b 16 in 182 n 1992231 Part b art a The sectos 1 andy have already been created for you Compute a veckor by evaluating the natur ogerim of yote tut the natural lopapeis entered aning in MATLAB Create the marrix X for the near Create the vector t 0 5 10 15 20 25 y Balance 1 000 13 14 5 16 18 2 19 9 22 3 Create the mass Find the dolasky decomposition of S and store EU Solve the angular system Sobe the tangular system cw using the backslash Compute le the best fit use in the backslash command Computea varabies a undb spectively Et figure mena new u Pantal upper case Use o to plot point fit togethe original data points Use Linviath 2 and axis tight your polise style and color the Ine black Rheum by ting told off T dwhen and e are the values you found in part o w the authe

Geometry
VectorsAlthough there are clear benefits to free trade governments impose quotas to pre quantity of products that can be imported into a country The figure below illustrates the effects of a quota placed on shoes Without trade the equilibrium domestic price of a pair of shoes is 140 With free trade the domestic price of a pair of shoes falls to the world price of 100 If the government imposes an import quota the domestic price increases to 120 Use the information in the figure to answer the questions that follow 1st attempt Part 1 1 point When there is no quota Part 2 1 point With the quota Part 3 1 point Price Po 140 Pa 120 Pw 100 H C D 350 20 150 B 200 pairs of shoes are imported pairs of shoes are imported Soomestic only 400 Domestic S Stree trade Quantity shoes See Hint See Hint See Hint

Geometry
VectorsFind the magnitude and positive direction angle of the The magnitude of the vector is 8 Simplify your answer The direction angle is Simplify your answer Use angle measures greater than or equal to 0 and less than 360


Geometry
VectorsUse the parallelogram rule to find the magnitude of the resultant for the two forces shown in the figure 15 lb 45 7 lb The magnitude of the resultant force is lb Round to the nearest tenth as needed

Geometry
VectorsFind the parametrization for the line segment joining the points P 0 1 9 and Q 0 1 9 Draw coordinate axes and sketch the segment indicating the direction of increasing t for th parametrization COB Find the parametrization for the line segment joining the two points Use P 0 1 9 as the base point and PQ as the vector Let y 1 2t X y z 0sts Type expressions using t as the variable

Geometry
VectorsA water main is to be constructed with a 25 grade in the north direction and a 10 grade in the east direction Determine the angle 8 required in the water main for the tum from north to east 0 radians Type your answer in radians Round to the nearest hundredth as needed JELEN Points 0 of 2 North East not drawn to scale

Geometry
VectorsThe distance D between a point Q and a line in space is given by PQ x u D X where u is a direction vector for the line and P is a point on the line a Find the shortest distance between the point Q 9 0 0 and the line passing through the points P 0 0 8 and P 0 1 9 b Find the shortest distance between the point Q 9 0 0 and the line segment from P 0 0 8 to P 0 1 9

Geometry
VectorsThe lines represented by the equations 2y 3x Answer Attempt 1 out of 5 O parallel neither parallel nor perpendicular O the same line O perpendicular 18 and y x 4 are Submit Answer

Geometry
VectorsB HW R When you are finished check the solutions with your teacher 1 In the figure below PU 12 VT 5 and VQ 6 Which of the following is FALSE Complete problems 1 2 below for independent practice T H H C 2 In the figure below FE 8 EH 8 and HD 18 Which of the following is FALSE F S H Q E ARU 12 OBUV 3 CPR 17 D PV 10 D A FD BE B BH FD CEH ED OD BE 24 Optional Complete problems 5 7 11 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the forth

Geometry
VectorsA manufacturer sells backpacks and tents The profit function for the manufacturer is a function z f x y where x is the quantity in thousands of backpacks that is sold y is the quantity in thousands of tents that is sold and z is in thousands of dollars Suppose that f 10 14 23 and fx 10 14 4 and fy 10 14 3 Estimate the profit obtained if the manufacturer sells 12 000 backpacks and 14 000 tents O a 3 000 b 4 000 O c 26 000 O d 27 000 O e 29 000 O f 31 000 O g 49 000 O h 50 000

Geometry
VectorsWy 3 Dilate line with a scale factor of 2 The image is line g Which labeled point could be the center of this dilation A A B B C C D D A B D 8 4 Quadrilateral A B C E is the image of quadrilateral ABCE after a dilation centered at F What is the scale factor of this dilation 3 A B 1 5 A B 6 3 Mathematics F E C C 2 5 5 E

Geometry
VectorsDetermine the aplitude midline period and an equation involving the sine function for the graph shown below S 5 4 3 2 1 10 8 6 4 2 2 4 6 8 y c 1 2 3 X 5

Geometry
Vectors8 cm 9 a Given the square based prism shown where AB 3 cm and AE state whether each statement is true or false Explain i AB GH GH b Calculate the magnitude of BD BE and BH H E F CG iii AD DC iv AH BG ii EA ii EA CG G

Geometry
Vectors4 Vectors a b and care as shown a Construct a b 7 b Construct a b 2 c Compare your results from parts a and b

Geometry
Vectors3 Given the vectors a b and 2 construct vectors equivalent to each of the following b 1 7 fo to

Geometry
Vectors2 Given AABC draw appropriate arrows on the sides of the triangle and give a single vector equivalent for each of the following a BC CA b AB BC CA C AB AC d BC BA

Geometry
Vectors1 The vectors and are drawn as shown below Draw a vector equivalent to each of the following X

Geometry
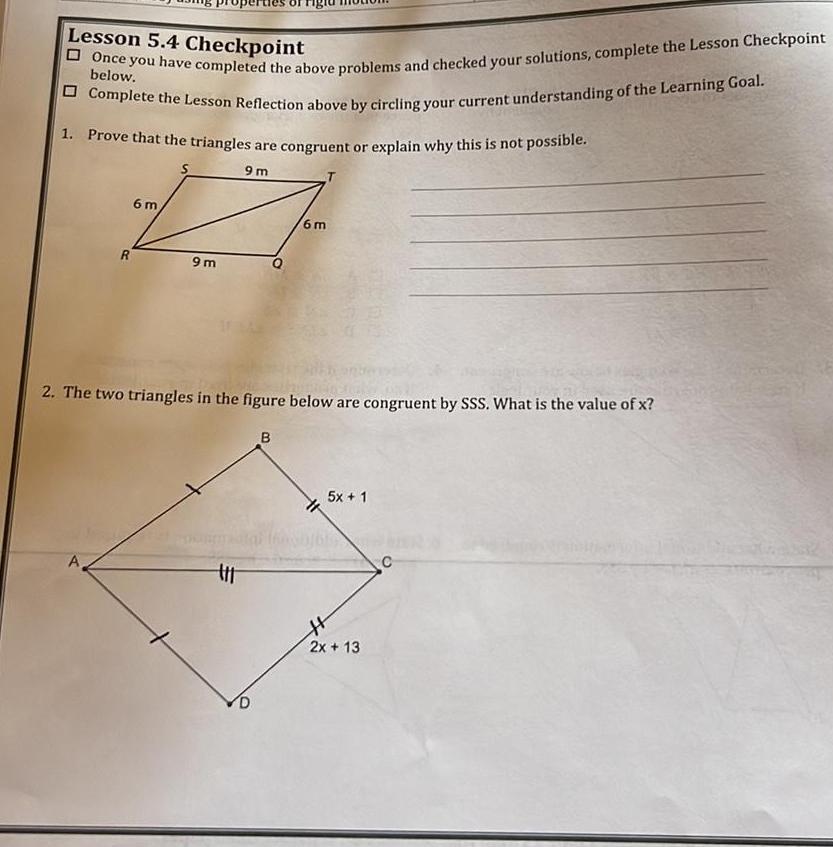
VectorsLesson 5 4 Checkpoint below Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Prove that the triangles are congruent or explain why this is not possible 9m R A 6 m 9m 2 The two triangles in the figure below are congruent by SSS What is the value of x t D 6m B 5x 1 H 2x 13 C

Geometry
VectorsIn the universal set U a b c h define subsets of cars with the characteristics shown to the right Describe the following set in words and then find the set Pnc Define the set Pn C in words Choose the correct answer below Click on the icon to view the table of new car features DU 000 OA The set is the set of cars that cost more than 20 000 and are not compact B The set is the set of cars that both cost more than 20 000 and are compact OC The set is the set of cars that either cost more than 20 000 or are compact OD The set is the set of cars that cost 20 000 or less and are not compact Identify the elements of the set Pn C Select all that apply A g C h E d G e P price is above 20 000 C is compact G has a good safety rating has antitheft package A W 1 PnC is the empty set warranty is at least three years B b D C F f H a Data table Car a b C d e f 9 h Cost 23 000 16 500 21 600 21 000 20 400 18 900 18 100 23 800 Size midrange subcompact compact compact compact subcompact subcompact midrange Print Warranty years 3 2 3 3 2 3 4 4 Done

Geometry
VectorsSuppose that A and B are angles in standard position Use the given information to find a SIA A 3x 8 17 cos A 3x 13 A 2 B 2 and sin B a sin A B Simplify your answer including any radicals Use integers or fractions for any numbers in the expression

Geometry
VectorsCOS 22 0 12 Simplify your answer including any radicals Use integers or fractions for any numbers in the expression COS

Geometry
VectorsFemales 7 1 inches 5th percentile 10 1 inches 95th percentile Conclusion Males The 10th to 90th percentile of males will fit this workstation Females The 5th to 95th percentile of females will fit this workstation Additional Notes The above assumes that the J key is 0 5 inches above the desk If the J key is at a different height then the percentile range will need to be adjusted accordingly The above also assumes that a footrest is provided for workers with shorter legs If a footrest is not provided then the percentile range will need to be adjusted to exclude workers whose seated elbow position is below 7 5 inches

Geometry
VectorsGiven T R 2 1 2 1 15 4 t and sin t 1 15 4 00 1 15 4 None of the above 1 4 find the value of sin t 28 cos t 28

Geometry
VectorsA cricket striker hits the ball with an angle of 0 46 and an initial speed of Vo 105 feet per second There is a helping wind blowing with an angle of elevation of a 9 and a speed of w 8 feet per second The speed represents the length of the wind vector 0 y y t b Determine the time for the ball to hit the ground Ground time a Determine the parametric representations for x and y as functions of time where t is in seconds Note If entering exact values your angles must be in radians not degrees x x t seconds c Determine the downrange distance Downrange Distance W foot a Wx W
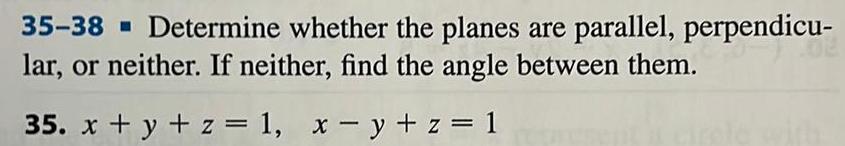
Geometry
Vectors35 38 Determine whether the planes are parallel perpendicu lar or neither If neither find the angle between them 35 x y z 1 x y z 1

Geometry
Vectors21 32 Find an equation of the plane 21 The plane through the point 1 1 3 and with normal vector i 4j k

Geometry
VectorsDetermine whether the function is one to one If so a write an equation for the inverse function in the form y f x b graph fand f on the same axes and c give the domain and the range of f and f1 If the function is not one to one say so f x a Write an equation for the inverse function in the form y f x Select the correct choice below and if necessary fill in any answer boxes to complete your choice A The function f x is one to one and f x Simplify your answer OB The function is not one to one b Choose the correct graph for f and r below The graph of f is shown in solid blue The graph off is shown in dashed red OA OB O C O D The function f x is not one to one Q Q

Geometry
VectorsLevi is standing at 16 feet from a grain silo The distance from Levi to a point o tangency on the tank is 25 feet How far is Levi from the center of the silo Q P O 10 feet 24 feet 02754 feet 25 ft 16 ft R

Geometry
VectorsQuestion 9 A ray that divides an angle into two angles that are congruent A B C D E F Vertex Distance Formula Segment Addition Postulate Plane Linear Pair Angle Bisector