Calculus Questions
The best high school and college tutors are just a click away, 24×7! Pick a subject, ask a question, and get a detailed, handwritten solution personalized for you in minutes. We cover Math, Physics, Chemistry & Biology.

Calculus
Differentiationdw dt For the given functions a express as a function of t both by using the Chain Rule and by expressing w in terms of t and differentiating directly with respect to t Then b evaluate w 6ye Inz x In 1 y tant z 1 1 dw at the given value of t dt by dw dt


Calculus
Application of derivativesA fence must be built to enclose a rectangular area of 5000 ft2 Fencing material costs 1 per foot for the two sides facing north and south and 2 per foot for the other two sides Fin the cost of the least expensive fence The cost of the least expensive fence is

Calculus
Application of derivativesA fence must be built to enclose a rectangular area of 5000 ft Fencing material costs 3 per foot for the two sides facing north and south and 6 per foot for the other two sides Find the cost of the least expensive fence The cost of the least expensive fence is Simplify your answer

Calculus
Differential equationsA yeast culture is growing at the rate of W t 0 5e0 1t grams per hour If the starting culture weighs 5 grams what I will be the weight of the culture W t after t hours After 3 hours The weight of the culture after t hours will be W t


Calculus
Indefinite IntegrationFind the slope of the graph of the function at the given point Use the derivative feature of a graphing utility to confirm your results Function Point 0 0 f 0 8 sin 0 0 f 0


Calculus
Application of derivativesA baseball diamond has the shape of a square with sides 90 feet long see figure A player running from second base to third base at a speed of 27 feet per second is 24 feet from third base At what rate in ft sec is player s distance from home plate changing Round your answer to two decimal places 3rd ft sec Home


Calculus
Limits & Continuityuestion z 6 5 4 3 2 1 3 y 4 5 46 3 6 Write an equation for the function graphed above



Calculus
Definite IntegralsCompute the following derivative using the method of your choi cos x5 sin 5x dx cos x5 sin 5x

Calculus
Definite IntegralsFind the arc length of the curve below on the given interval y In x x 1 for 1 x 65 Hint Integrate with respect to y The length of the curve is Simplify your answer

Calculus
Application of derivativesUse a calculator to make a table to approximate the following limit Confirm your result with l H pital s Rule lim 1 3h h 0 Complete the table below Round to four decimal places as needed h 10 1 10 2 1 h 10 10 4 1 3h h h 10 1 2 10 10 10 4 3 1 1 3h

Calculus
Limits & ContinuityUse a calculator to make a table to approximate the following limit Confirm your result with l H pital s Rule 17 1 X lim X 0 Complete the table below Do not round until the final answer Then round to six decimal places as needed 17 1 17 X 10 1 10 2 10 3 X h 10 1 10 2 10 3 X

Calculus
Definite IntegralsUse the inverse relations between In x and e exp x and the properties of In x to prove the following properties a exp 0 1 b exp x y exp x exp y c exp x exp xy y rational a How can exp 0 be calculated Choose the correct answer below OA Find In exp 0 B Calculate exp 0 as the product of a constant and 0 c Find a value a for which In a 0 and substitute In a for 0 D Calculate the limit of exp x as x approaches 0 X S dt Recall that Inx X dt For what value is Type an exac answer X S dt 0

Calculus
Definite IntegralsFind the volume of the solid generated when R shaded region is revolved about the given line 1 x y 1 x 1 about y 1 The volume of the solid obtained by revolving the region about 1 i 5x

Calculus
Vector CalculusDetermine whether the following statements are true and give an explanation or counterexample Assume x 0 and y 0 a In xy Inx Iny b In 0 1 c In x y Inx Iny d 2 2Inx 1 e The area under the curve y and above the x axis on the interval 1 e is 1 a Choose the correct answer below OA The statement is false because In 35 In 5 In 7 OB The statement is true For x 0 and y 0 In xy Inx In y by the Product Rule of Logarithms OC The statement is false because In 5 In 7 In 5 7 OD The statement is true For x 0 and y 0 In xy Inx In y by the Quotient Rule of Logarithms

Calculus
DifferentiationCompute the following derivative using the method of your choice d cos x4 sin x dx d cos x4 sin x

Calculus
Definite IntegralsDetermine the following indefinite integral Check your work by differentiation S5 dr dr



Calculus
Limits & ContinuityShow all necessary work in your solutions Problem 1 Find the arc length of the graph of y x 2 3 2 from x 0 to x





Calculus
Limits & ContinuityConstruct a table of values to find the value of the limit from both sides for lim x 2 x 8 2 x

Calculus
Limits & ContinuityEvaluate the following limits a b NOTE If needed enter INF for o and INF for o HINT Look at where the exponential fuction is going in the f 4 lim 200 ex 7 4 lim 2 0 e 7

Calculus
Indefinite IntegrationFind the following integral Note that you can check your answer by differentiation S 6e4 3 3 dy

Calculus
DifferentiationFind the following integral Note that you can check your answer by differentiatio S 6e4 y Vy dy


Calculus
Definite IntegralsFind the following integral Note that you can check your answer by differentiation S 7 e2z dx




Calculus
Limits & ContinuityThe expression e7 9 6 can be written as ef a where f x is a function of x Find f x f x

Calculus
Application of derivativesSolve each equation for A Solve In 11x 1 5 for x 0 B Solve e 8 1 3 for x x 3
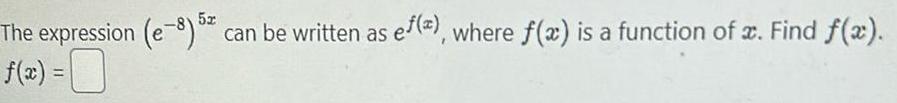
Calculus
Application of derivativesThe expression e 8 52 can be written as ef 2 where f a is a function of x Find f x f x 0

Calculus
Application of derivativesGiven functions Find 3x g x x 6 h x h x a hog x b State the domain in interval notation x

Calculus
Application of derivatives5 4 M 2 3 2 3 The minimum degree of the polynomial is 2 The minimum degree of the polynomial is 3 The minimum degree of the polynomial is 4 The minimum degree of the polynomial is 5 The minimum degree of the polynomial is 6 The leading coefficient is positive The leading coefficient is negative Based on the end behavior the polynomial is odd Based on the end behavior the polynomial is even


Calculus
DifferentiationA fireworks mortar is launched straight upward from a pool deck platform 10 m off the ground at an initial velocity of 62 m sec The height of the mortar can be modeled by h t 4 9t 2 62t 10 where h t is the height in meters and t is the time in seconds after launch What is the maximum height Round to the nearest meter do not include units in your answer

Calculus
Definite IntegralsFactor completely using synthetic division 3x 5x 4x 4 given that 2 is a root x intercept value Write the answer in linear factor form You must show work to receive credit

Calculus
Limits & ContinuityA salesperson makes a base salary of 1100 per month Once he reaches 38 000 in total sales he earns an additional 6 commission on the amount of sales over 38 000 Write a piecewise defined function to model the salesperson s total monthly salary in as a function of the amount in sales x

Calculus
Application of derivativesThe monthly profit for a company that makes picture frames depends on the price per frame The company determines that the profit is approximated by P x 50x 80 000x 2500 where x is the price per frame and P x is the monthly profit based on that price Find the price that generates the maximum profit

Calculus
Definite IntegralsProblem 5 Use the method of cylindrical shells to find the volume when the region bounded above by x y and x 2 y and below by the x axis and rotated around the x axis

Calculus
Limits & ContinuityWhat is the angle measure 52 48 51 equivalent to in decimal degrees Enter your answer rounded to the nearest thousandth of a degree in the box