2D Geometry Questions and Answers

Geometry
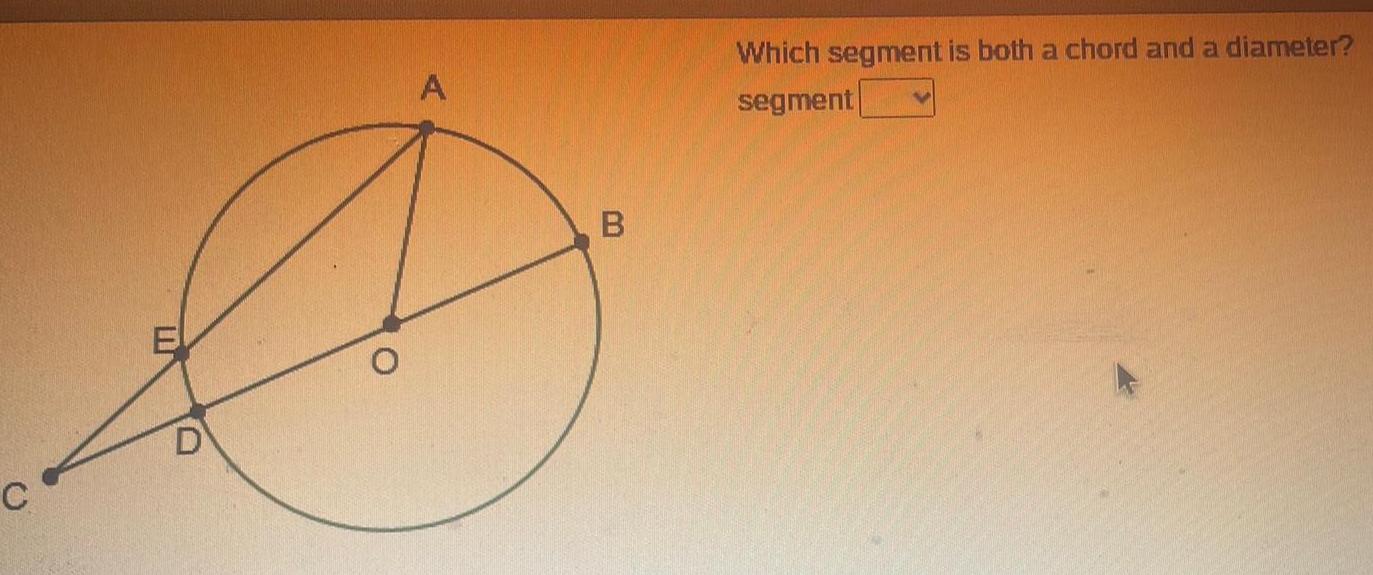
2D GeometryWords to Know Write the letter of the definition next to the matching word as you work through the lesson You may use the glossary to help you A arc chord inscribed angle intercepted arc tangent to a circle Central Angles anangle whose vertex is on a circle and whose sides are chords B an arc in the interior of an angle that has its endpoints on the angle C a part of a circle between two given endpoints D a line line segment or ray that intersects a circle at exactly one point and contains no points inside the circle E a segment with both endpoints on a circle

Geometry
2D GeometryDirections Determine whether a permutation or combination can be used Then solve 19 Three cards from a standard deck of 52 cards are chosen at random What is the probability that all three cards chosen are hearts 21 If the 3 digit security code on the back of a credit card using the digits 0 9 has no repeating digits what is the probability that the code does not contain any numbers less than 52 20 Marissa has a 50 20 10 5 and 1 bill in her wallet She takes the bills out and randomly line them up What is the probability that the first bill is greater than 5 22 There are twelve seniors and eight juniors on the prom committee If two students are chosen at random to decide on decorations what is the probability that one is a senior and one is a junior
Geometry
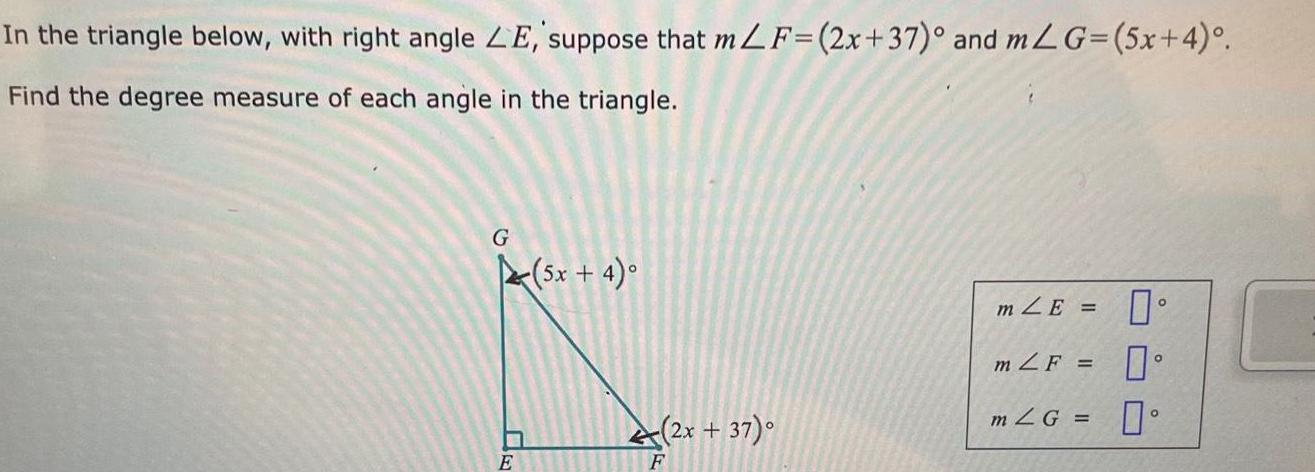
2D GeometryIn the triangle below with right angle LE suppose that mLF 2x 37 and mL G 5x 4 Find the degree measure of each angle in the triangle G E 5x 4 2x 37 F m ZE m LF m LG 0 0 0

Geometry
2D Geometry5 The center of a circle is 1 15 and one point on the circle s circumference is 4 15 What is the length of the diameter 2 points a 5 b 10 c 25 d O O O 100 A OB O C
Geometry
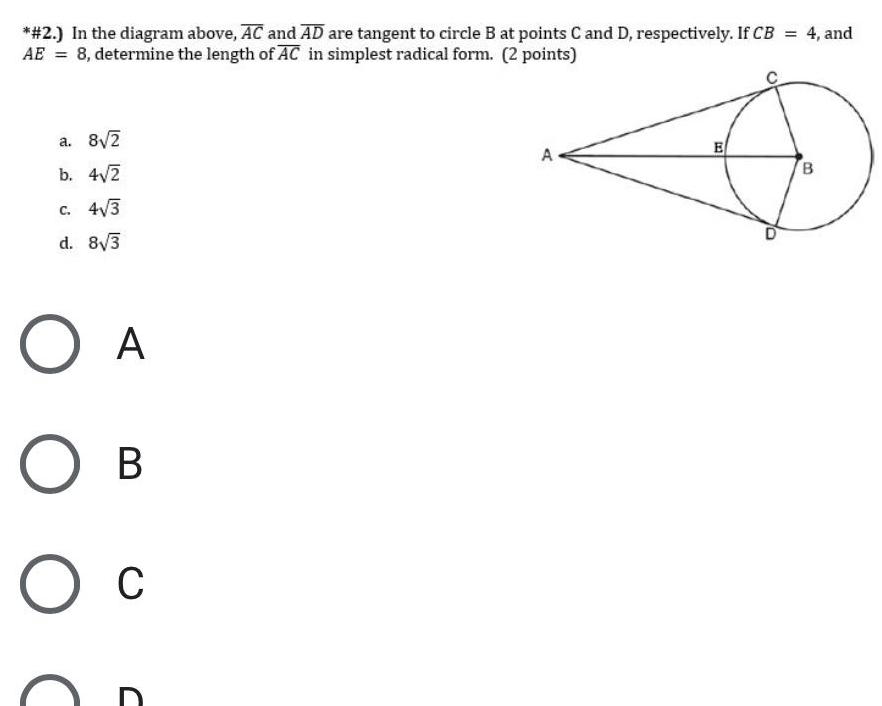
2D Geometry2 In the diagram above AC and AD are tangent to circle B at points C and D respectively If CB 4 and AE 8 determine the length of AC in simplest radical form 2 points a 8 2 b 4 2 c 4 3 d 8 3 O A O B O C A E B
Geometry
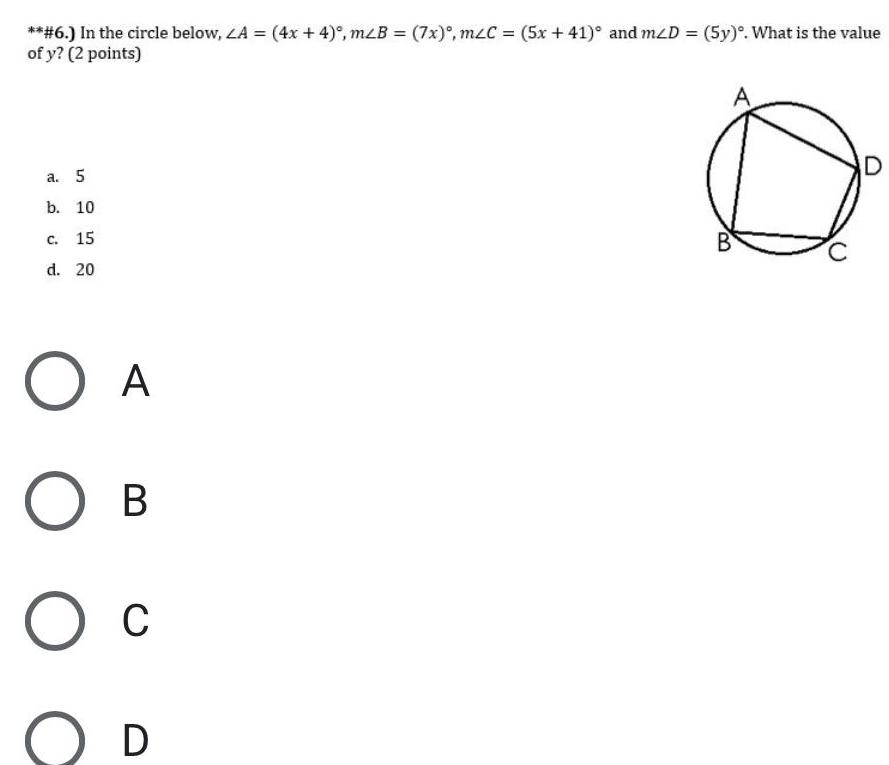
2D Geometry6 In the circle below LA 4x 4 mzB 7x mzC 5x 41 and m D 5y What is the value of y 2 points a 5 b 10 C 15 d 20 O A O O B C D B D
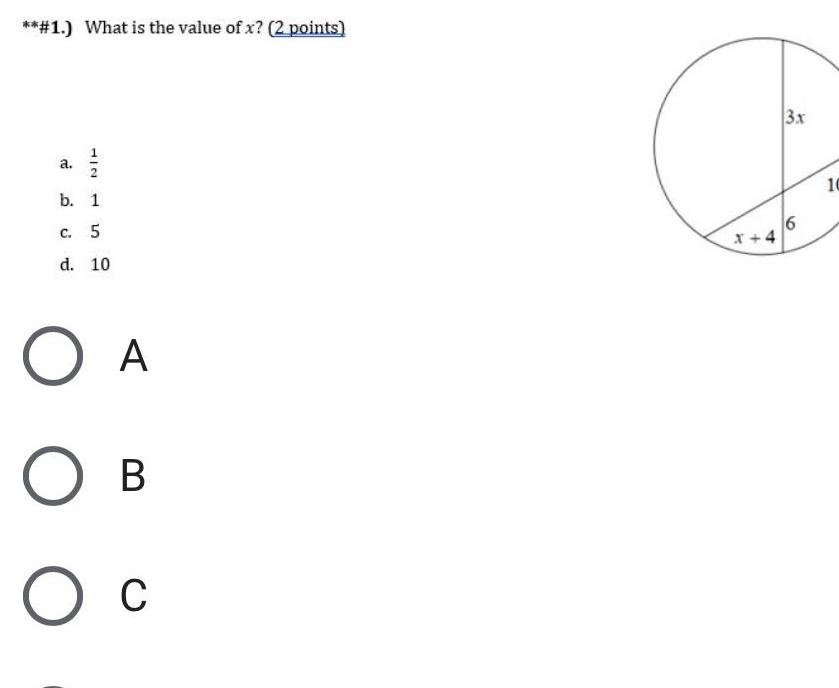
Geometry
2D Geometry3 1 1 point What is the measure of ZY 136 b X 68 Z Type your answer 1 point What is the measure of FGH 101 H
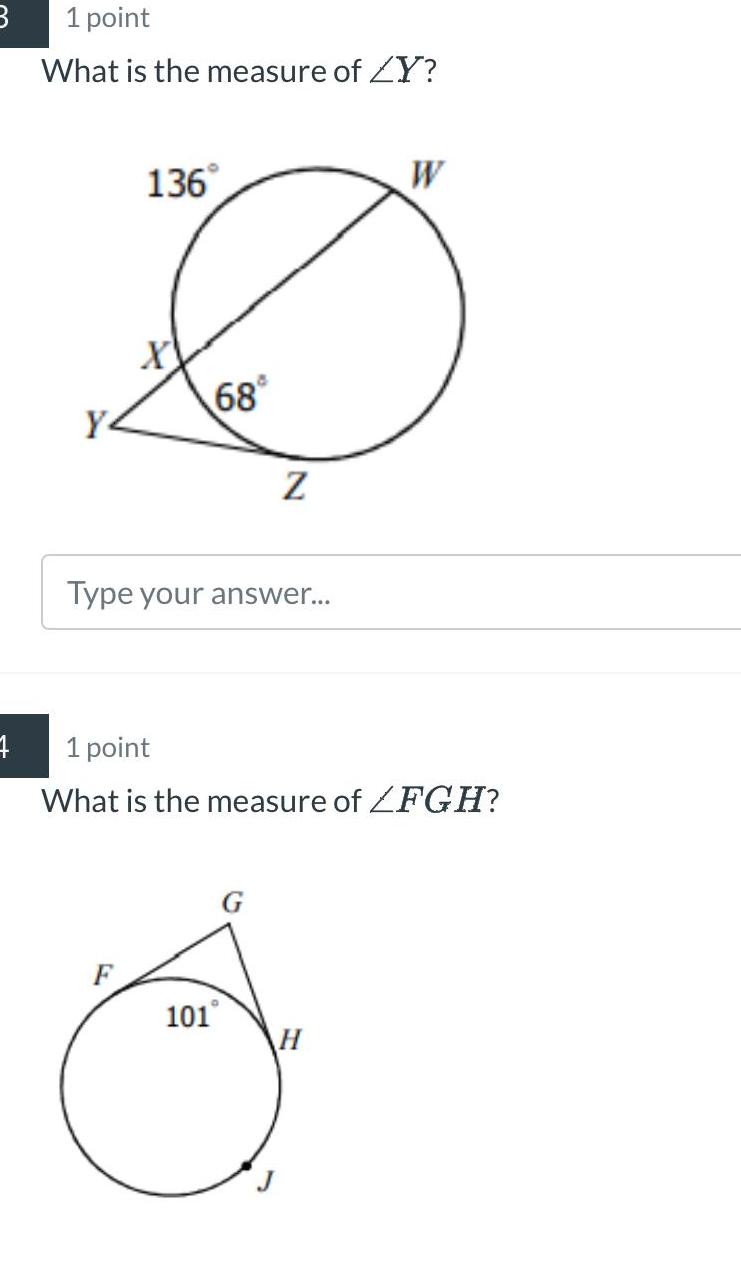
Geometry
2D GeometryWhat is the measure of the arc RU R S 88 30 V 35 Type your answer U x 1 point What is the measure of x 27 T 18
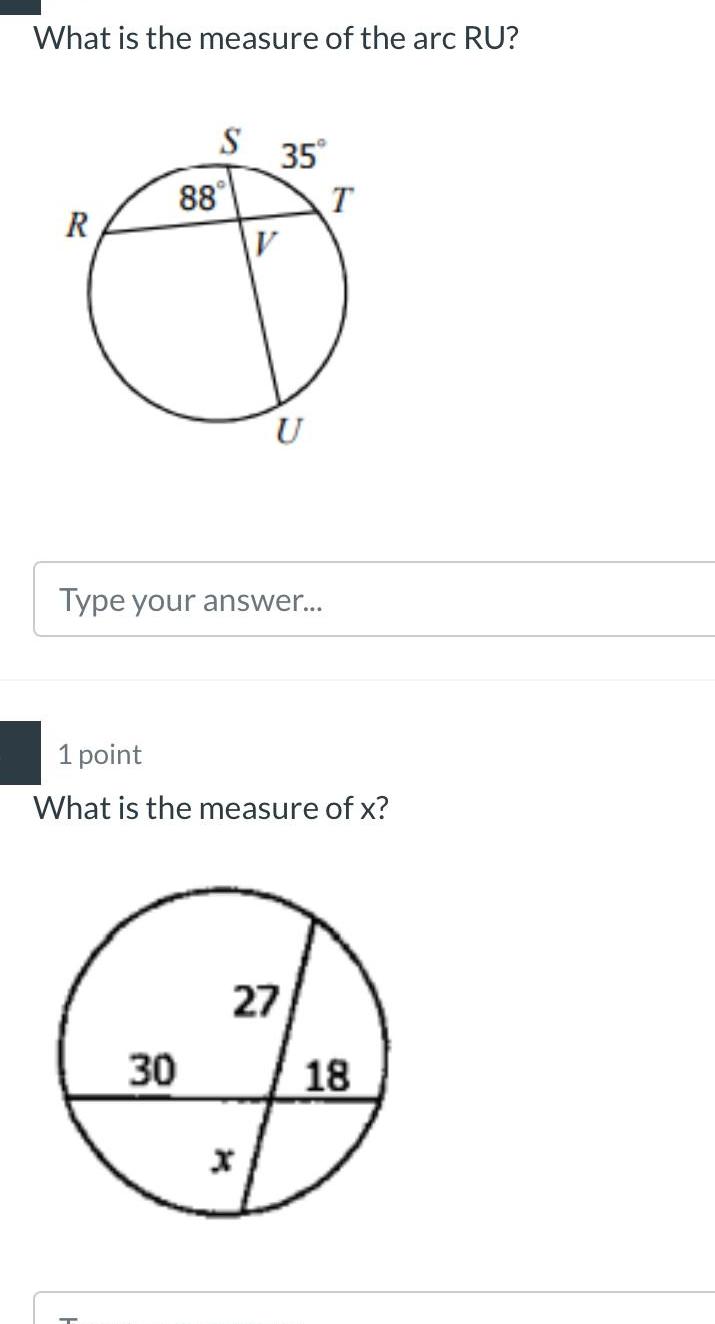
Geometry
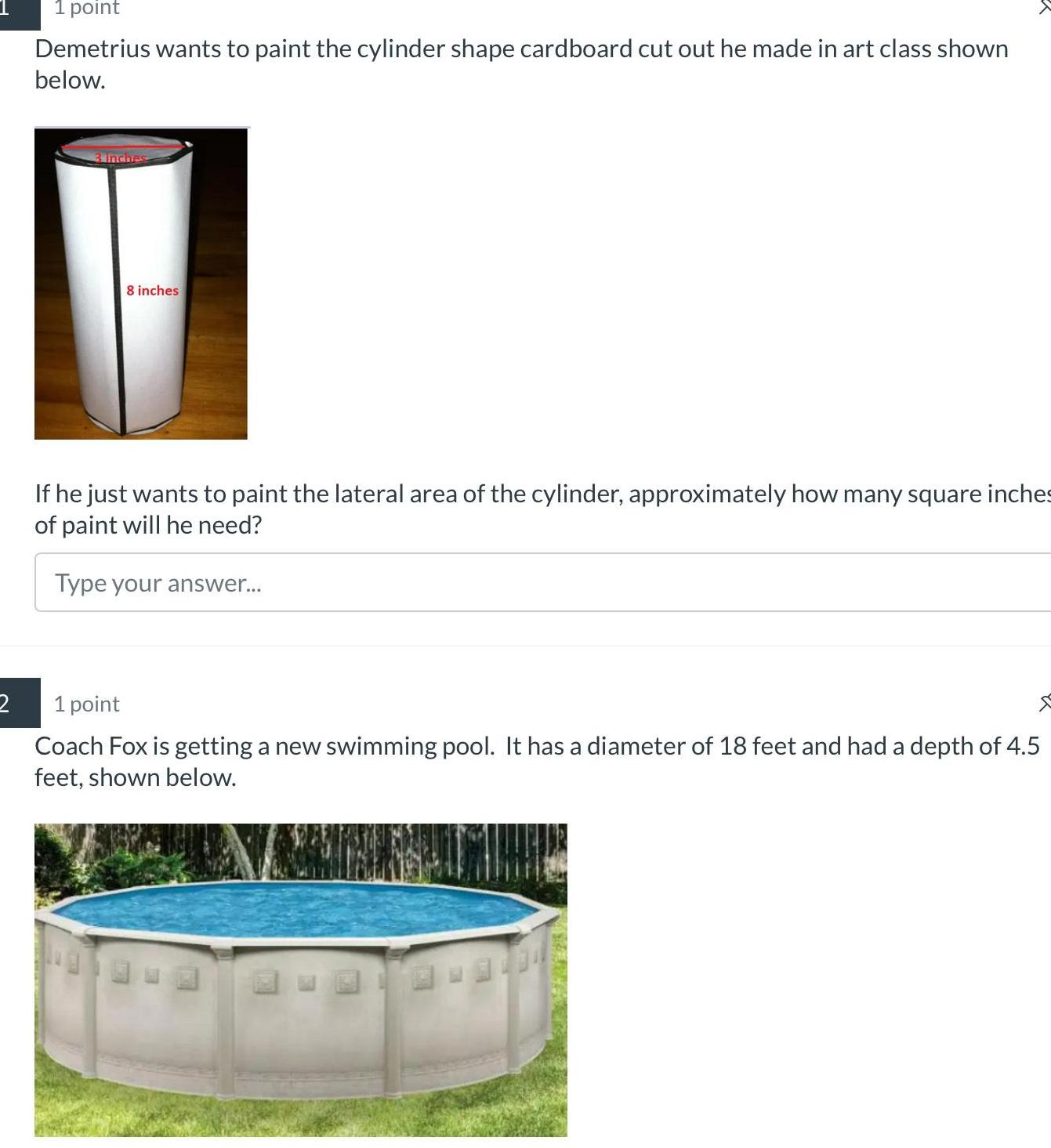
2D Geometry2 1 point Demetrius wants to paint the cylinder shape cardboard cut out he made in art class shown below 3 inches 8 inches If he just wants to paint the lateral area of the cylinder approximately how many square inches of paint will he need Type your answer 1 point Coach Fox is getting a new swimming pool It has a diameter of 18 feet and had a depth of 4 5 feet shown below 1204
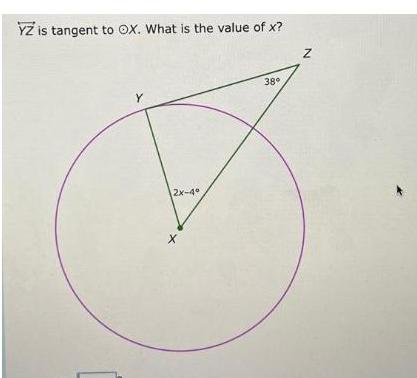

Geometry
2D Geometry5 Let ABCD be a square of area 1 Let X Y Z W be random points on AB BC CD DA taken uniformly and independently of each other Let S be the area of the quadrangle XYZW D C We A Z a Find the expression of S in terms of X Y Z W Y B
Geometry
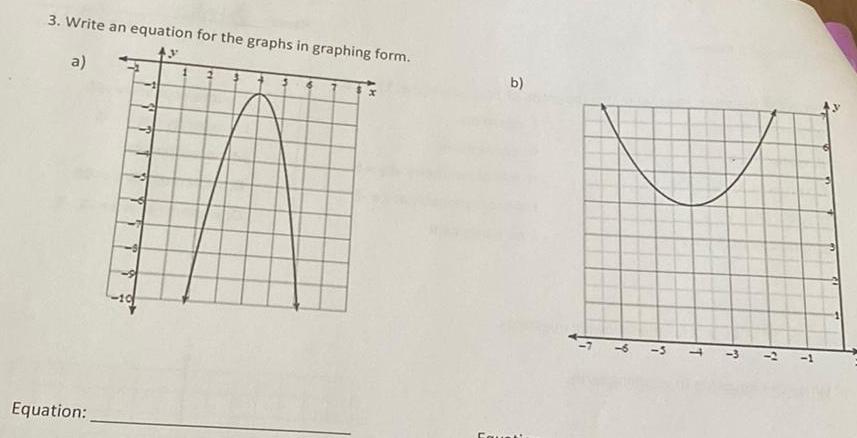
2D Geometry3 Write an equation for the graphs in graphing form y a Equation 1 2 3 3 6 b NU d T 7 7 7
Geometry
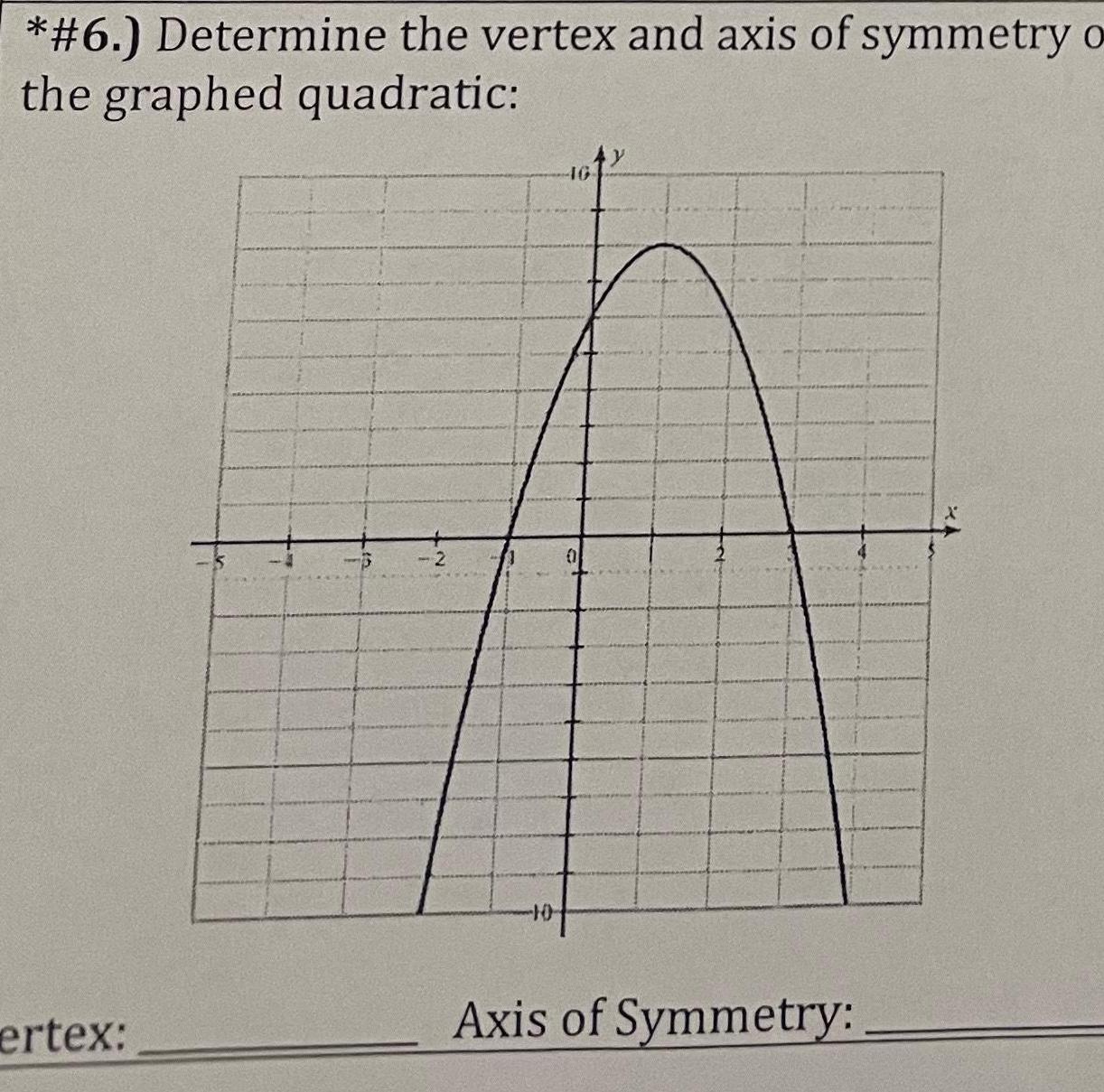
2D Geometry6 Determine the vertex and axis of symmetry o the graphed quadratic ertex 4y Axis of Symmetry
Geometry
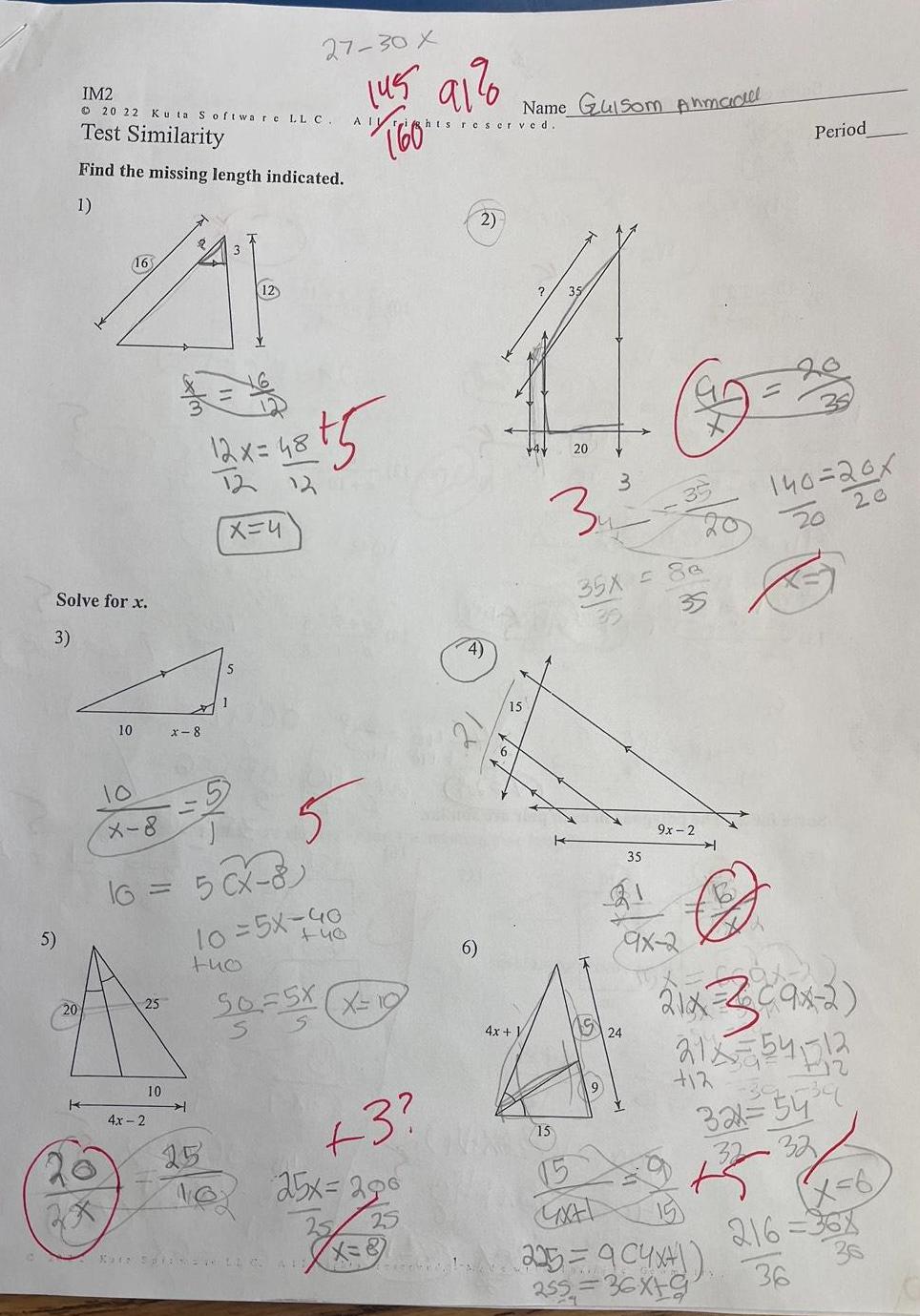
2D Geometry3 Solve for x 5 20 IM2 20 22 Kuta Software LL C Test Similarity Find the missing length indicated 1 K X 16 10 25 4x 2 x 8 10 5 X 8 16 5 CX 8 12x 48 12 12 x 4 1 25 12 tho 10 5X 40 16 27 30 X 4875 145 91 40 Kate Spia 120 AT Ale 50F5X XE S rights reserved 3 SASCH 2 4 6 Name Guisom Ahmadal 4x y V 4 20 34 15 15 GX 35X 8e 35 21 9x 2 20 9x 2 12 25x 296 25 25 X 8 225 904x41 255 36X19 15 Period 20 21x3c9x 2 21 54 12 321 54 32 X 6 216 36x 36 36 35 140 20x 20 20
Geometry
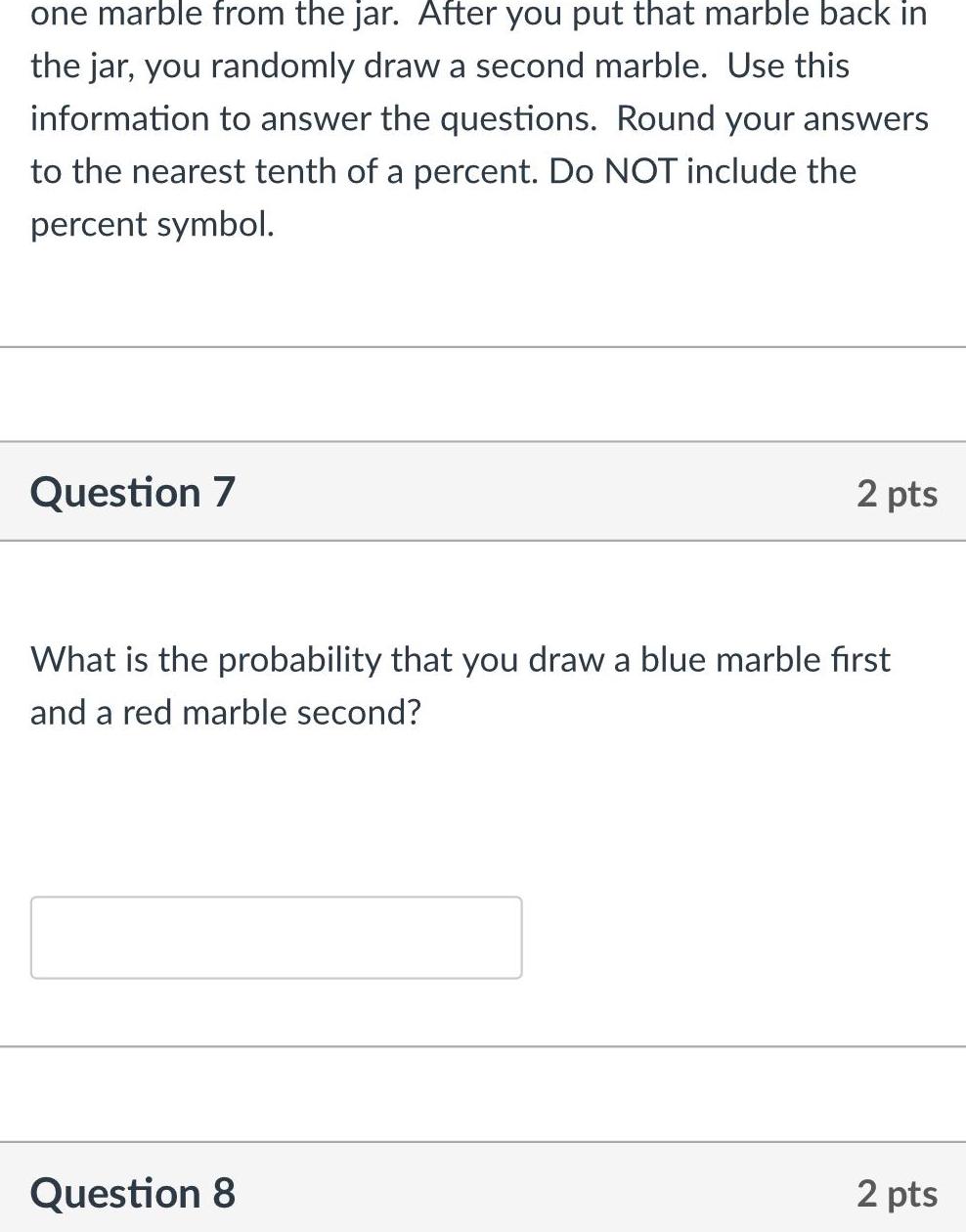
2D Geometryone marble from the jar After you put that marble back in the jar you randomly draw a second marble Use this information to answer the questions Round your answers to the nearest tenth of a percent Do NOT include the percent symbol Question 7 2 pts What is the probability that you draw a blue marble first and a red marble second Question 8 2 pts
Geometry
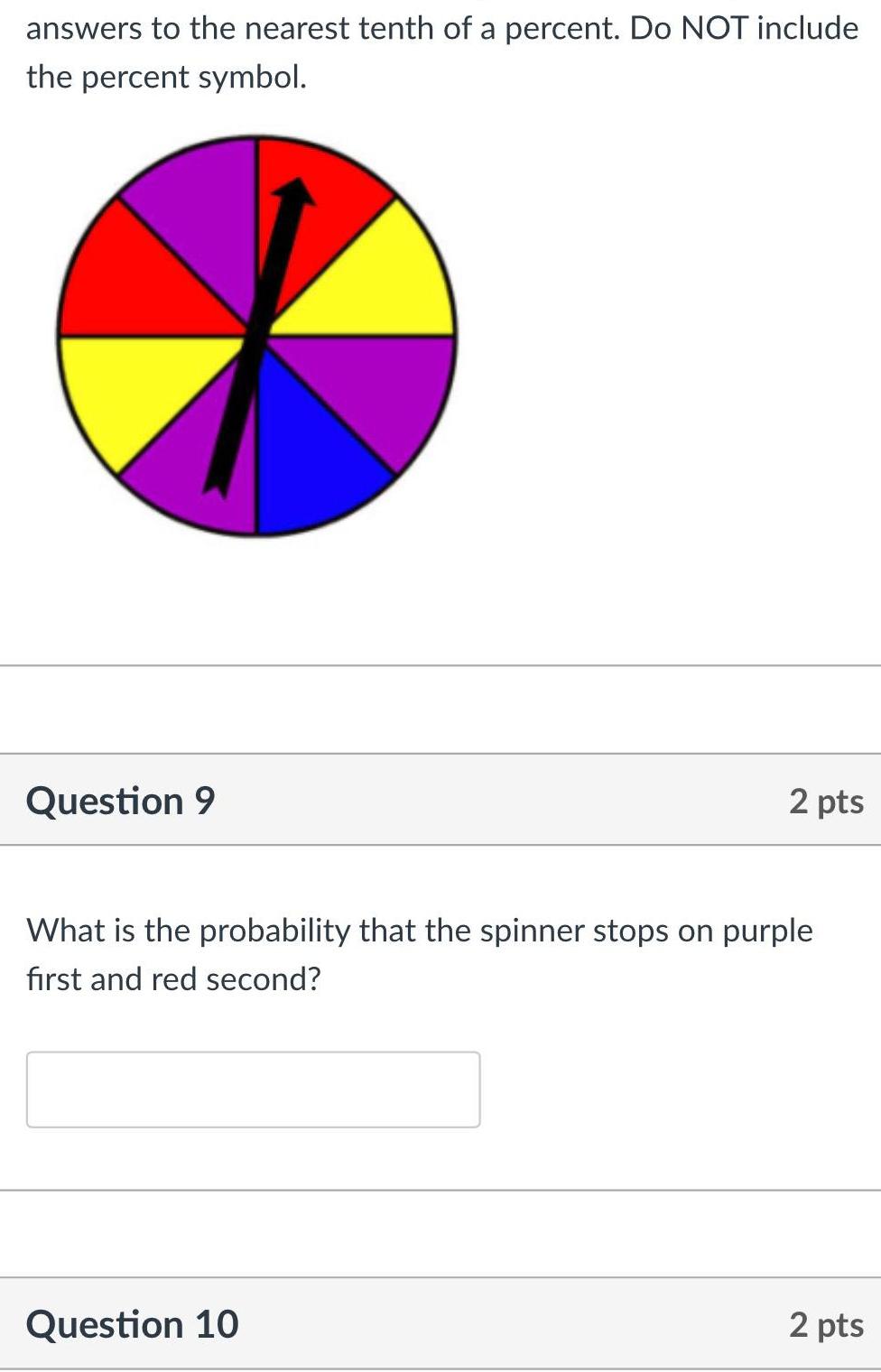
2D Geometryanswers to the nearest tenth of a percent Do NOT include the percent symbol Question 9 2 pts What is the probability that the spinner stops on purple first and red second Question 10 2 pts

Geometry
2D GeometryThere are 4 green 10 red and 6 yellow marbles in a bag You choose a marble without looking put it aside and choose another marble without looking Find the probability that you choose a red marble followed by a yellow marble Express all probabilities as simplified fractions

Geometry
2D GeometryA bag holds 4 white marbles and 2 blue marbles You choose a marble without looking put it aside and choose another marble without looking Find the probability that you choose a white marble followed by a blue marble Express all probabilities as simplified fractions

Geometry
2D GeometryA die has the numbers 3 5 6 8 10 and 12 on its faces You roll the die twice What is the probability that you roll an odd number on both rolls Enter your answer as a simplified fraction
Geometry
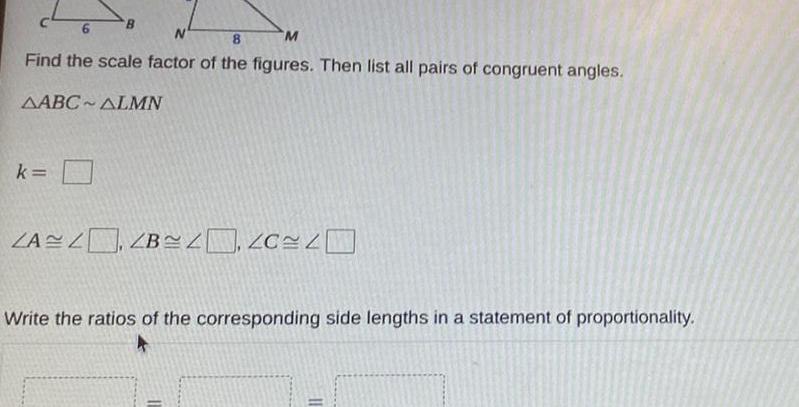
2D Geometryc46 N 8 M Find the scale factor of the figures Then list all pairs of congruent angles AABC ALMN k B ZAZ ZB Write the ratios of the corresponding side lengths in a statement of proportionality
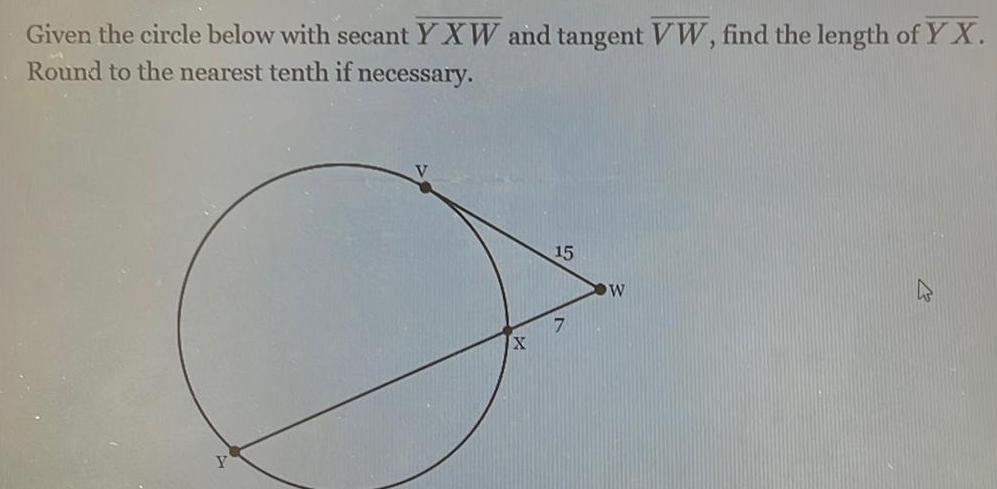
Geometry
2D GeometryGiven the circle below with secant YXW and tangent VW find the length of YX Round to the nearest tenth if necessary Y X 15 7 W

Geometry
2D Geometry2 Find the solutions to the quadratic below using completing the square x 10x 4 0

Geometry
2D GeometryProving the First Case of the Inscribed Angle Theorem Given AB is the diameter of a circle and is one side of the angle that intercepts AC Prove mzABC is half the measure of AC 180 2x B You can draw line segment CD by the unique Since the triangle isl x D Triangle BCD is isosceles since BD and CD are both circle and all radii of a given circle are congruent EFO x A postulate of the its base angles are congruent

Geometry
2D Geometry4 ERROR ANALYSIS Describe and correct the error in solving x 8x 10 by completing the square X x 8x 10 x 8x 16 10 x 4 10 x 4 10 x 4 V 10
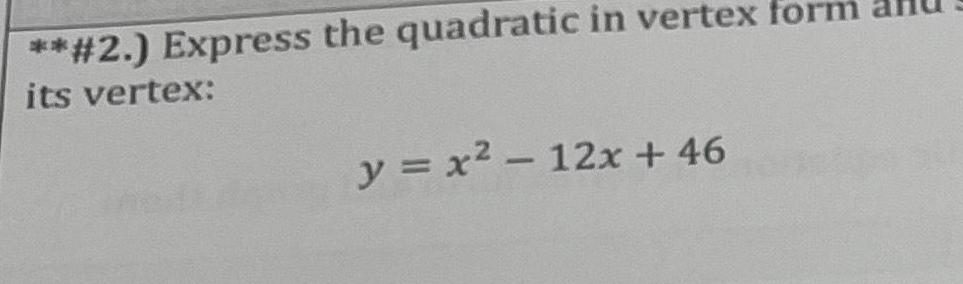
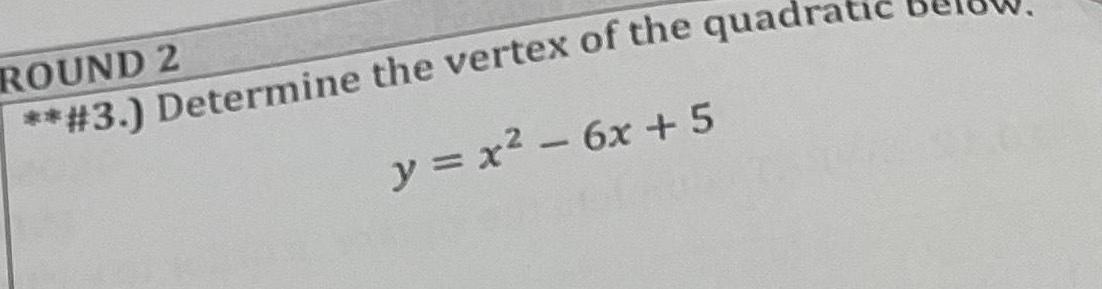
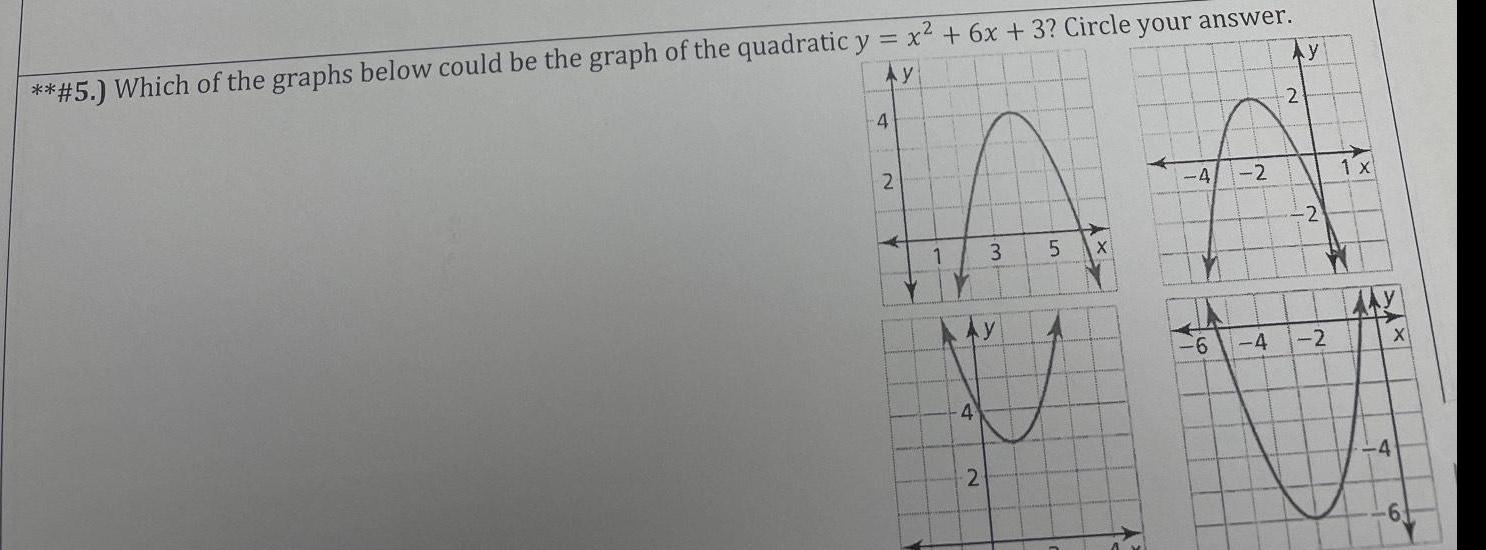
Geometry
2D Geometry5 Which of the graphs below could be the graph of the quadratic y x 6x 3 Circle your answer Ay 4 2 Ay 4 3 2 5 XY 4 IA 6 3 2 Ay 4 2 2 2 1 x X YA Ex 4 6
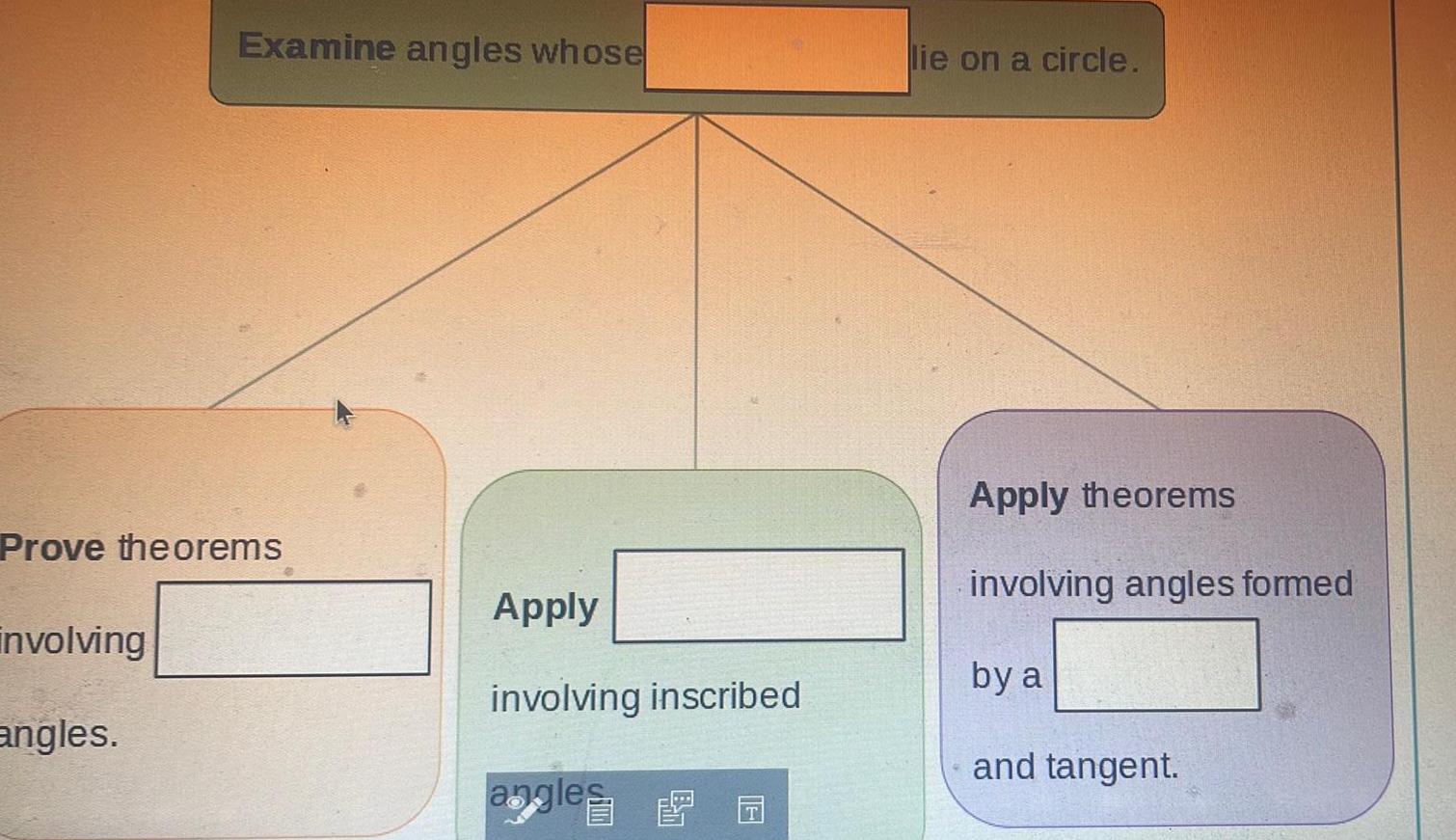
Geometry
2D GeometryExamine angles whose Prove theorems involving angles Apply involving inscribed angles G lie on a circle Apply theorems involving angles formed by a and tangent

Geometry
2D Geometryside of the angle that intercepts AC Prove The measure of ZABC is half the measure of AC ZADC and ZBDC are supplementary since they form a The measure of ZADC 180 180 2x which simplifies to or twice the measure of angle ABC Since ZADC is a central that of AC FLL LLL LLLL 180 2x D B thlebblebi bla bla kbEWERBLETT Since the measure of ZABC is x the measure of AC is 2x pair The sum of their measures is 180 xo its measure 2x is equal to that C
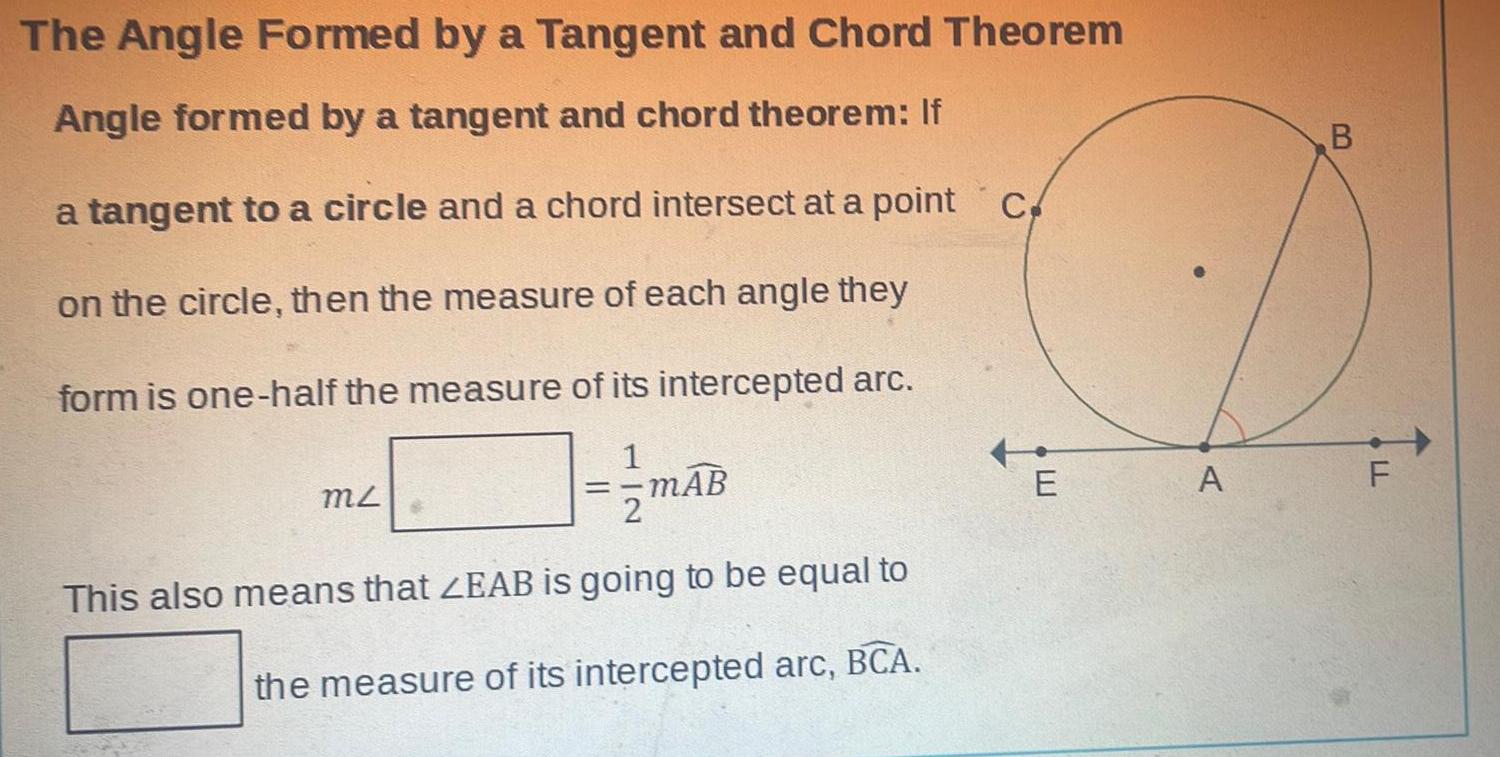
Geometry
2D GeometryThe Angle Formed by a Tangent and Chord Theorem Angle formed by a tangent and chord theorem If a tangent to a circle and a chord intersect at a point c on the circle then the measure of each angle they form is one half the measure of its intercepted arc MZ mAB This also means that ZEAB is going to be equal to the measure of its intercepted arc BCA E A B LL F
Geometry
2D GeometryThe trinket store is open for 14 hours per day They sell an average of 5 trinkets per hour The back storeroom currently has 560 trinkets in it 1 Write an equation that estimates the number of trinkets T that will be in the storeroom after H hours 2 How many days will it take to run out of trinkets

Geometry
2D GeometryFind the volume of each object 1 the rectangular prism part of the milk container 2 the cylinder part of the measuring cup 6 3 cm 7 cm 10 cm 7 cm 7 cm
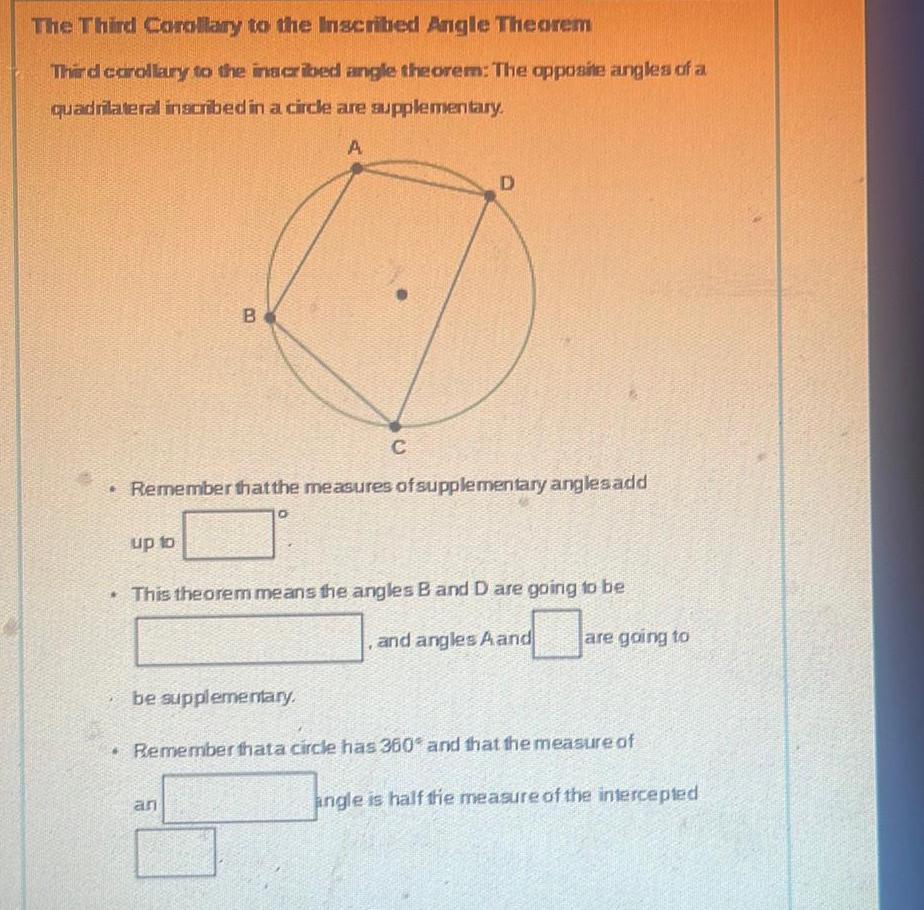
Geometry
2D GeometryThe Third Corollary to the Inscribed Angle Theorem Third corollary to the inscribed angle theorem The opposite angles of a quadrilateral inscribed in a circle are supplementary A B up to C Remember that the measures of supplementary anglesadd O D This theorem means the angles B and D are going to be and angles A and be supplementary are going to Remember thata circle has 360 and that the measure of angle is half the measure of the intercepted
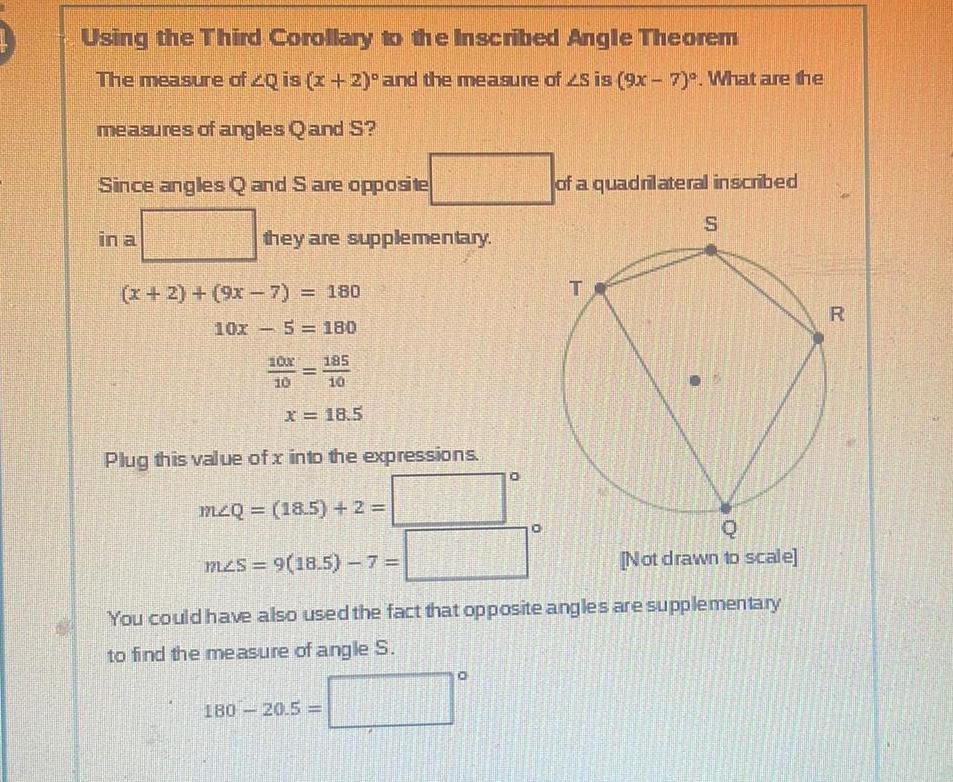
Geometry
2D GeometryUsing the Third Corollary to the Inscribed Angle Theorem The measure of 20 is x 2 and the measure of 2S is 9x 7 What are the measures of angles Q and S Since angles Q and S are opposite in a they are supplementary x 2 9x 7 180 10x5 180 Our 185 10 10 x 18 5 Plug this value of x into the expressions m20 18 5 2 180 20 5 0 0 of a quadrilateral inscribed T S m s 9 18 5 7 You could have also used the fact that opposite angles are supplementary to find the measure of angle S Q Not drawn to scale R
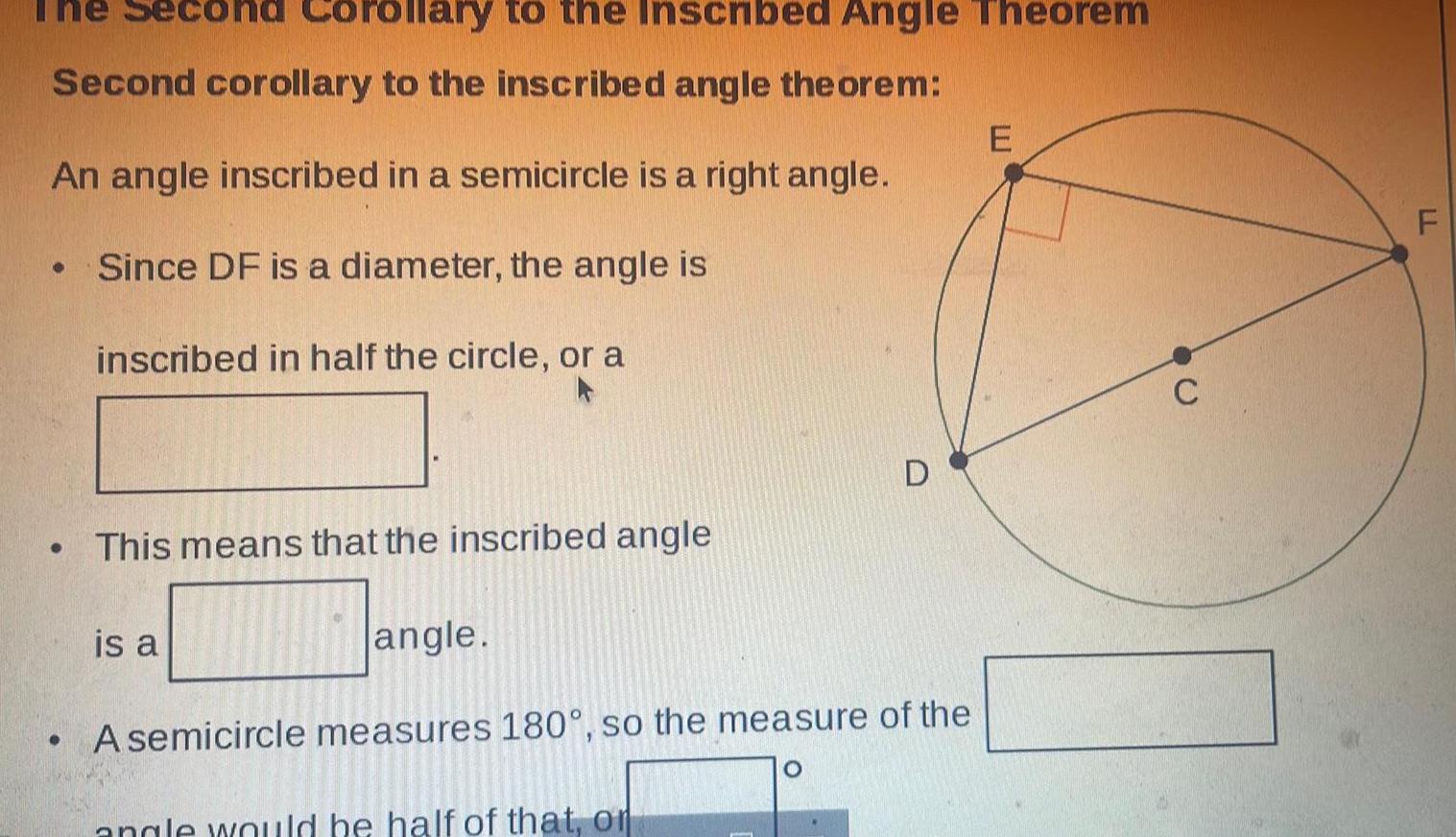
Geometry
2D GeometrySecond corollary to the inscribed angle theorem An angle inscribed in a semicircle is a right angle Since DF is a diameter the angle is inscribed in half the circle or a Coroll ry to the Inscribed Angle Theorem This means that the inscribed angle is a angle A semicircle measures 180 so the measure of the angle would be half of that or E C LL
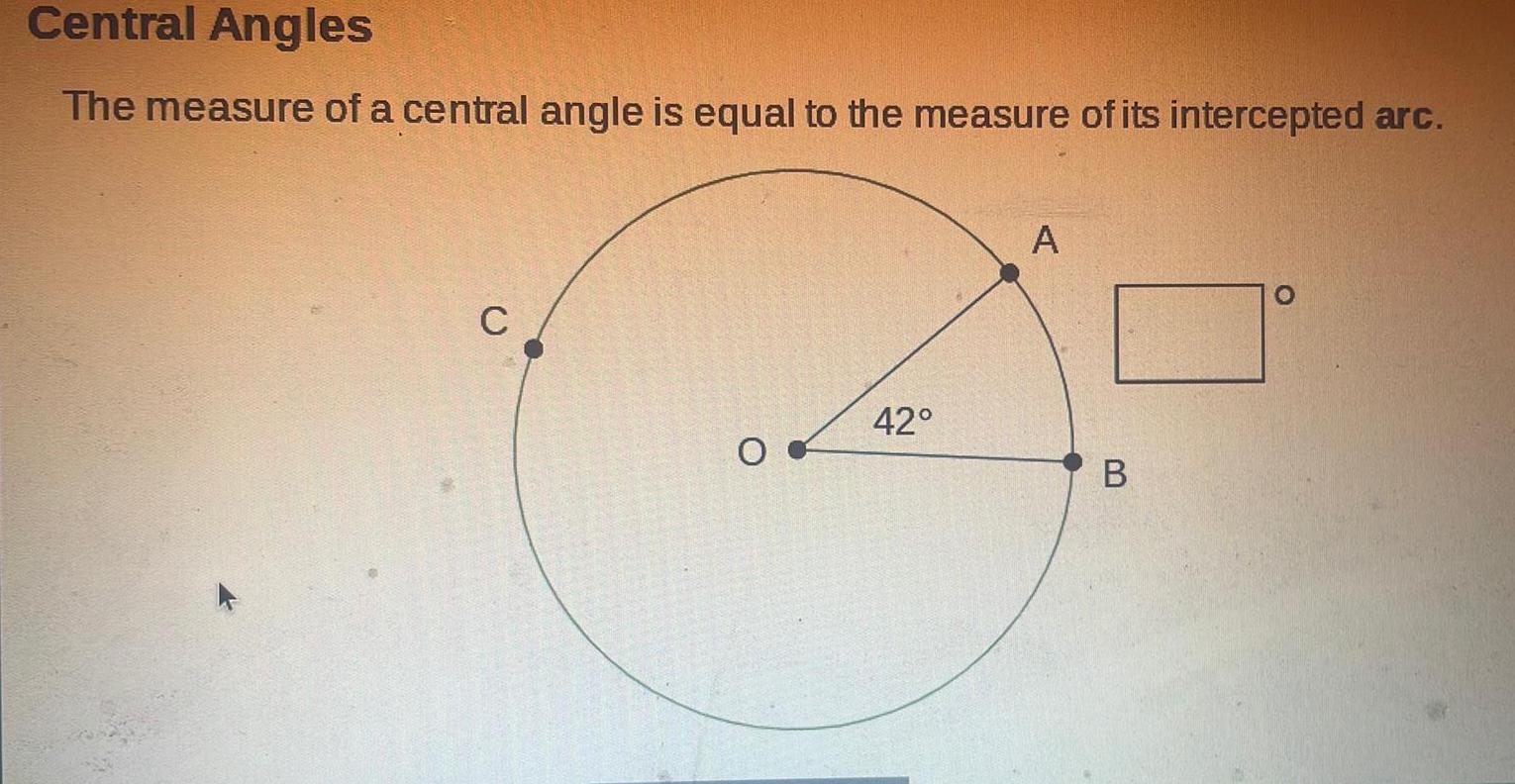
Geometry
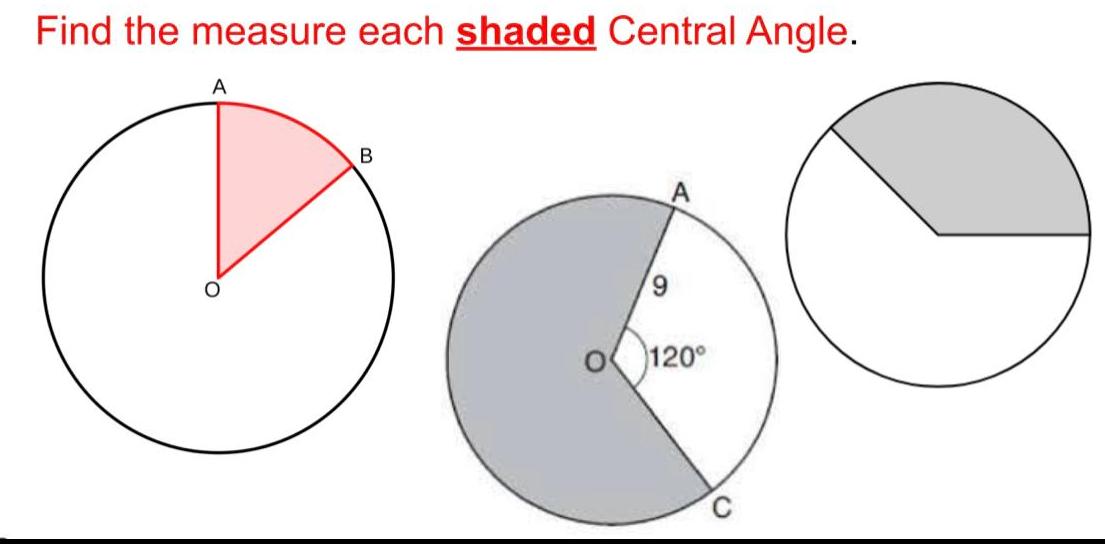
2D GeometryCentral Angles The measure of a central angle is equal to the measure of its intercepted arc C 42 A B
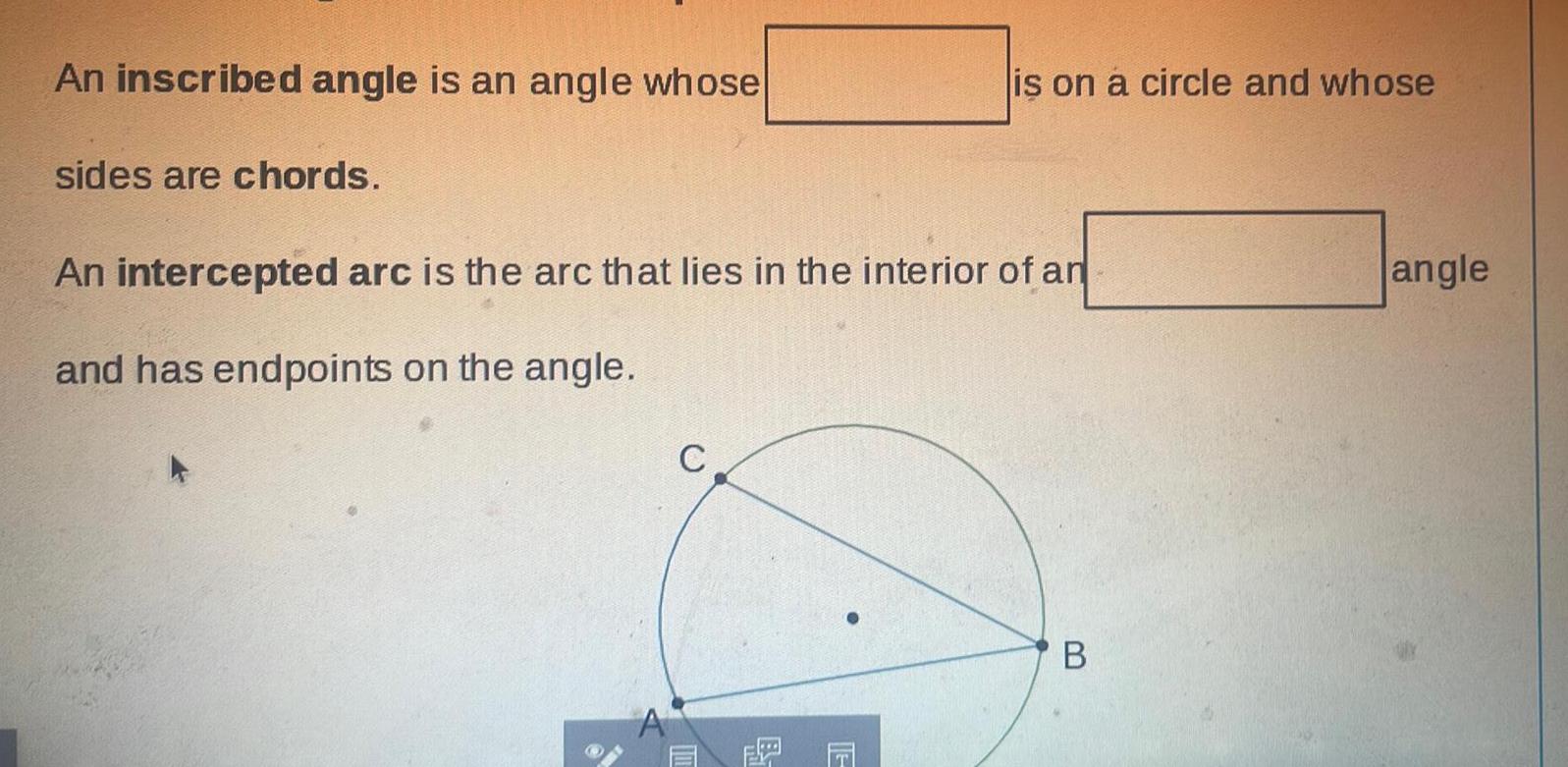
Geometry
2D GeometryAn inscribed angle is an angle whose sides are chords is on a circle and whose An intercepted arc is the arc that lies in the interior of an and has endpoints on the angle C B angle
Geometry
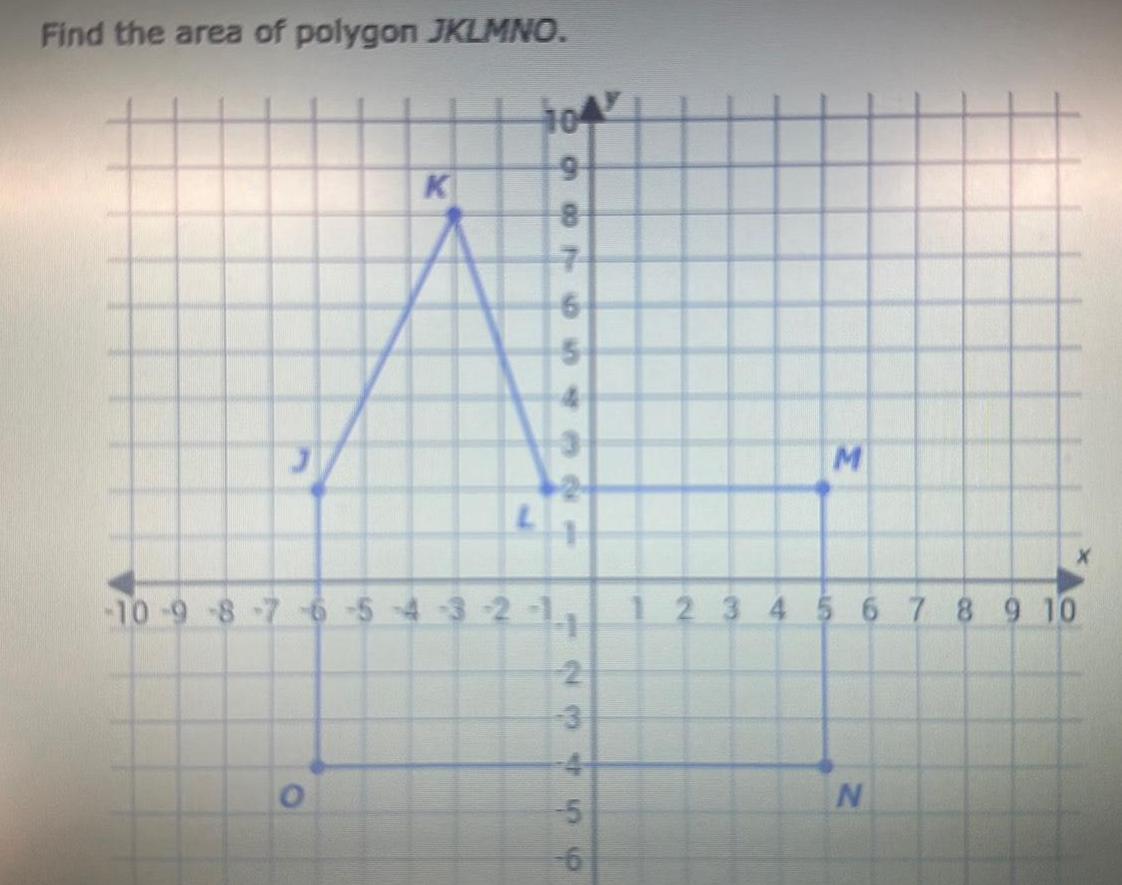
2D GeometryFind the area of polygon JKLMNO K 104 886 9 7 bl 2 10 9 8 7 6 5 4 3 2 11 123 2 456 M 1 2 3 4 5 6 7 8 9 10 N
Geometry
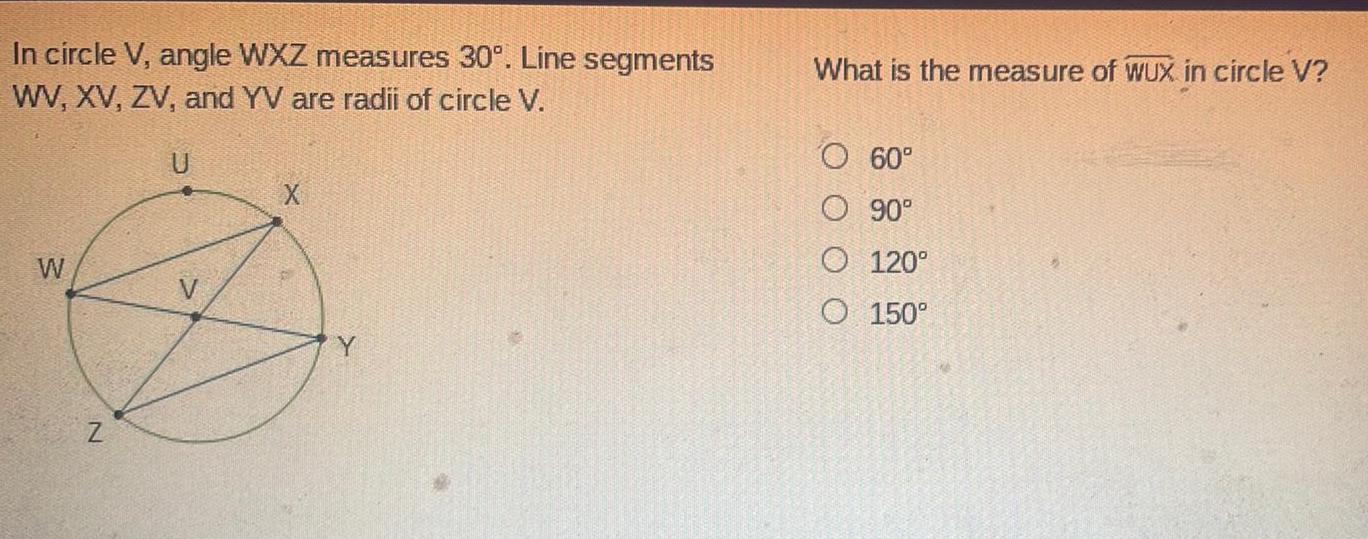
2D GeometryIn circle V angle WXZ measures 30 Line segments WV XV ZV and YV are radii of circle V W U X Y What is the measure of WUX in circle V O 60 O 90 O 120 O 150

Geometry
2D GeometryLine segment GJ is a diameter of circle L Angle K measures 4x 6 H K What is the value of x O 21 24 O 32 044

Geometry
2D GeometryLine segment XY is tangent to circle Z at point U X T U W Y 12 If the measure of UV is 84 what is the measure of ZYUV A O O O O 42 84 96 168

Geometry
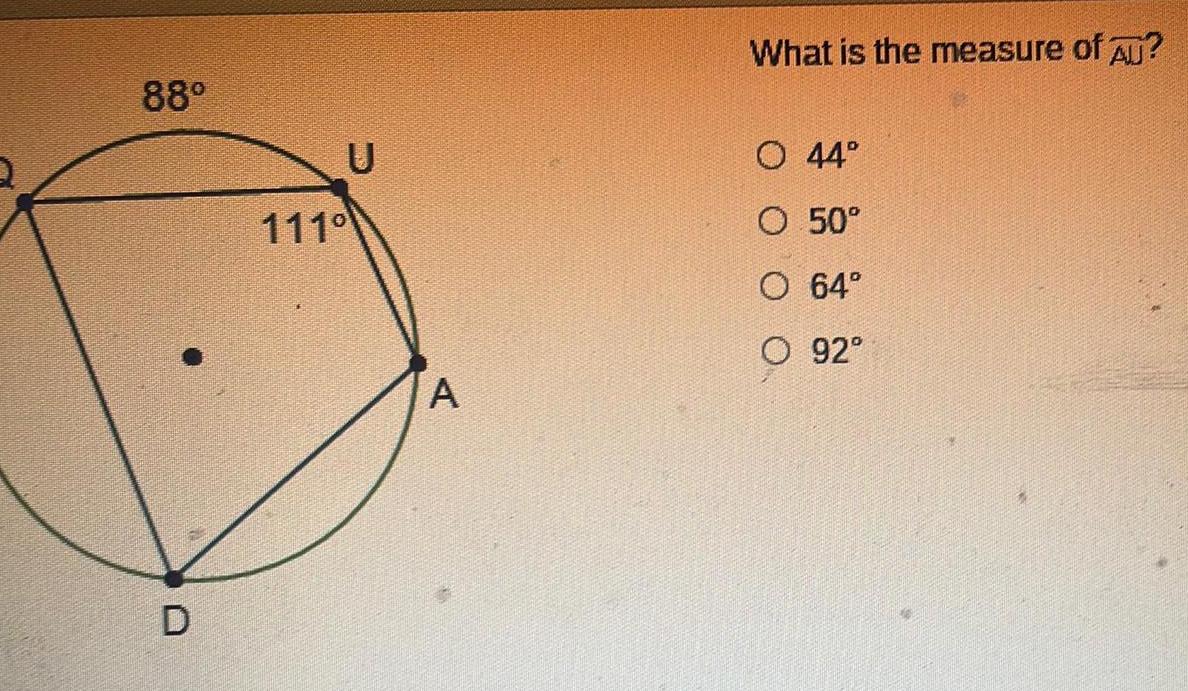
2D GeometryIn circle D angle ADC measures 7x 2 Arc AC measures 8x 8 A B C What is the measure of ZABE O 36 O 43 O 72 O 144
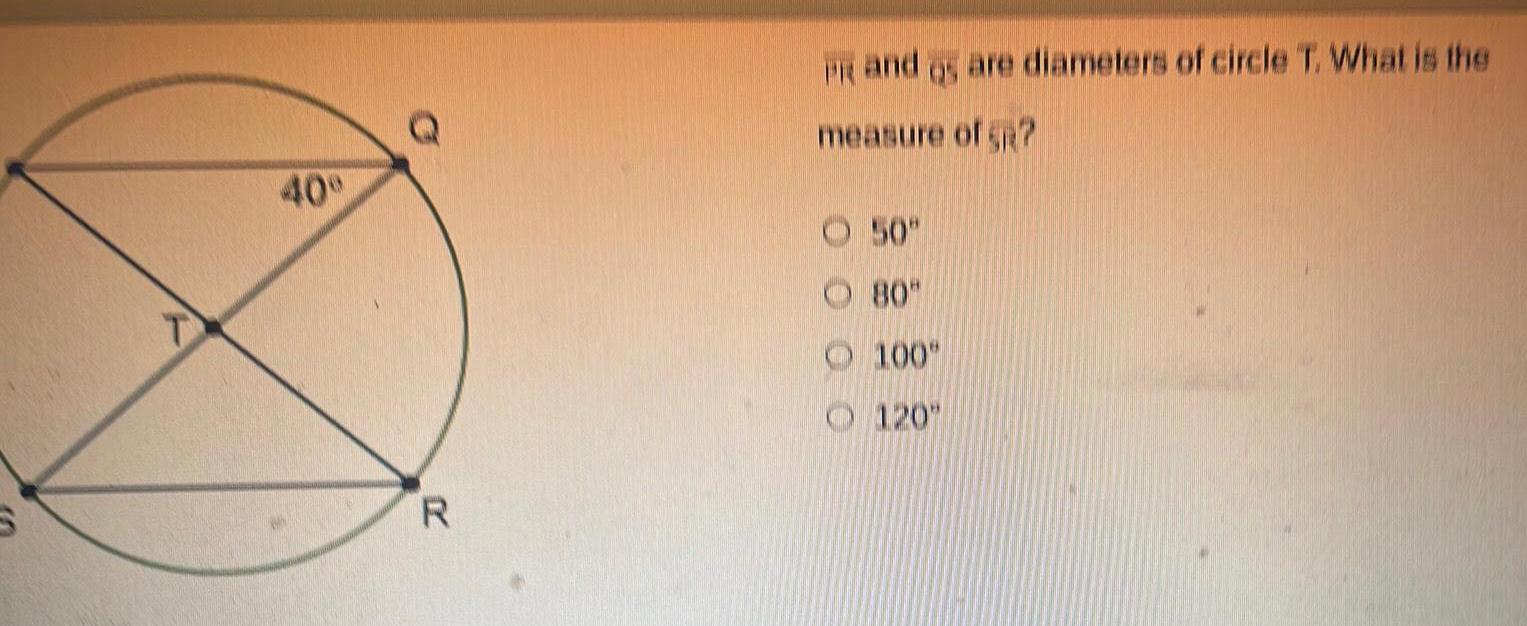
Geometry
2D Geometry40 Q R PR and gs are diameters of circle T What is the measure of SR 50 80 100 120

Geometry
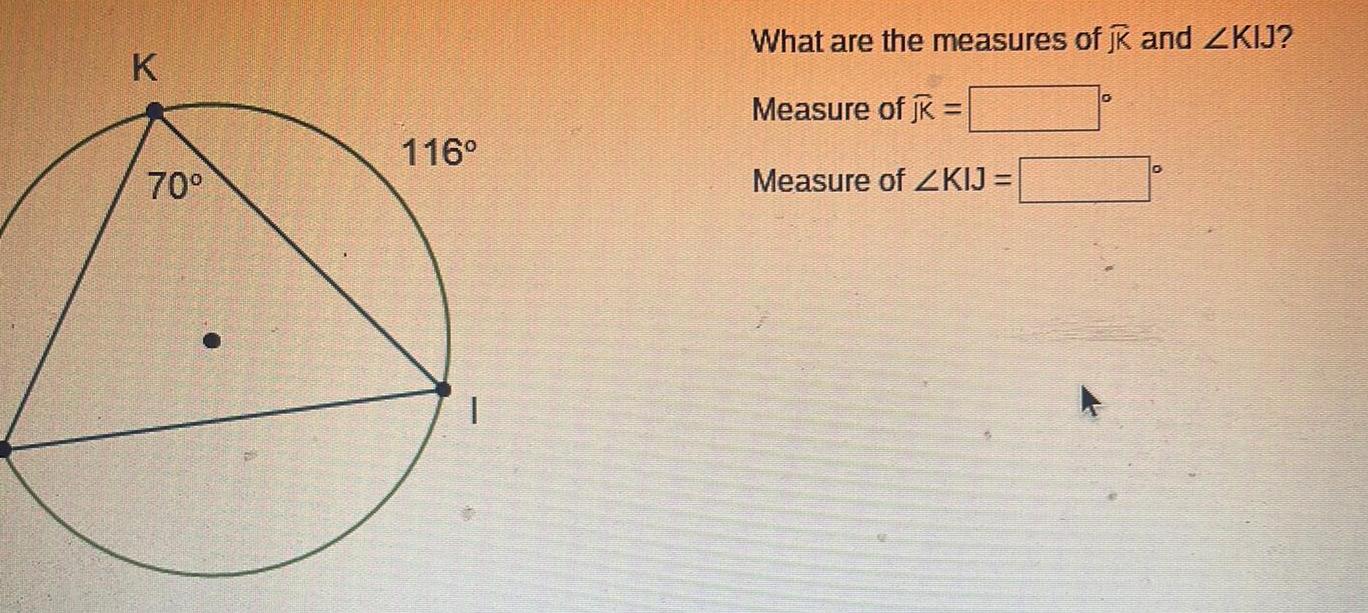
2D Geometry4 11 Given ZKJL and ZKML intercept arc KL Prove m2KJL mZKML 19 11 rst Co 11 orollary to the Inscribed Angle Theorem K M L Statements 1 ZKJL intercepts KL 2 ZKML intercepts KL 3 mZKJL mKL 4 mZKML mKL 5 mZKJL m KML 1 given 2 given 3 4 5 Reasons

Geometry
2D GeometryA C B The measure of ZB is 3x 4 and the measure of ZD is 2x 6 What are the measures of angles B and D m2B mZD