Area Questions and Answers

Geometry
AreaA rectangular pyramid fits exactly on
top of a rectangular prism. The prism
has a length of 15 cm, a width of 5
cm, and a height of 7 cm. The
pyramid has a height of 13 cm. Find
the volume of the composite space
figure.
850 cm³
2275 cm3
1500 cm²
500 cm³

Geometry
Areaper has a range of 5 meters as shown. The Jet of water from the sprinkler sweeps out at an angle of 85° as the nozzie turns. What is the area watered by the sprinkler? Use the value = 3.14, and round your answer to one decimal place.
A. 15.6 square meters
B. 17.8 square meters
C. 18.5 square meters
D. 19.2 square meters
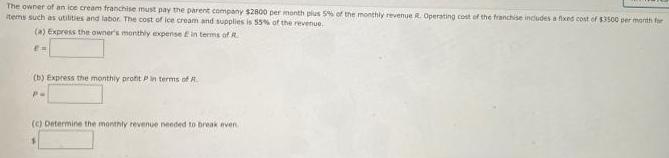
Geometry
AreaThe owner of an ice cream franchise must pay the parent company $2800 per month plus 5% of the monthly revenue R. Operating cost of the franchise includes a fixed cost of $3500 per month for
items such as utilities and labor. The cost of ice cream and supplies is 55% of the revenue.
(a) Express the owner's monthly expense E in terms of R.
(b) Express the monthly profit in terms of R
(c) Determine the monthly revenue needed to break even
Geometry
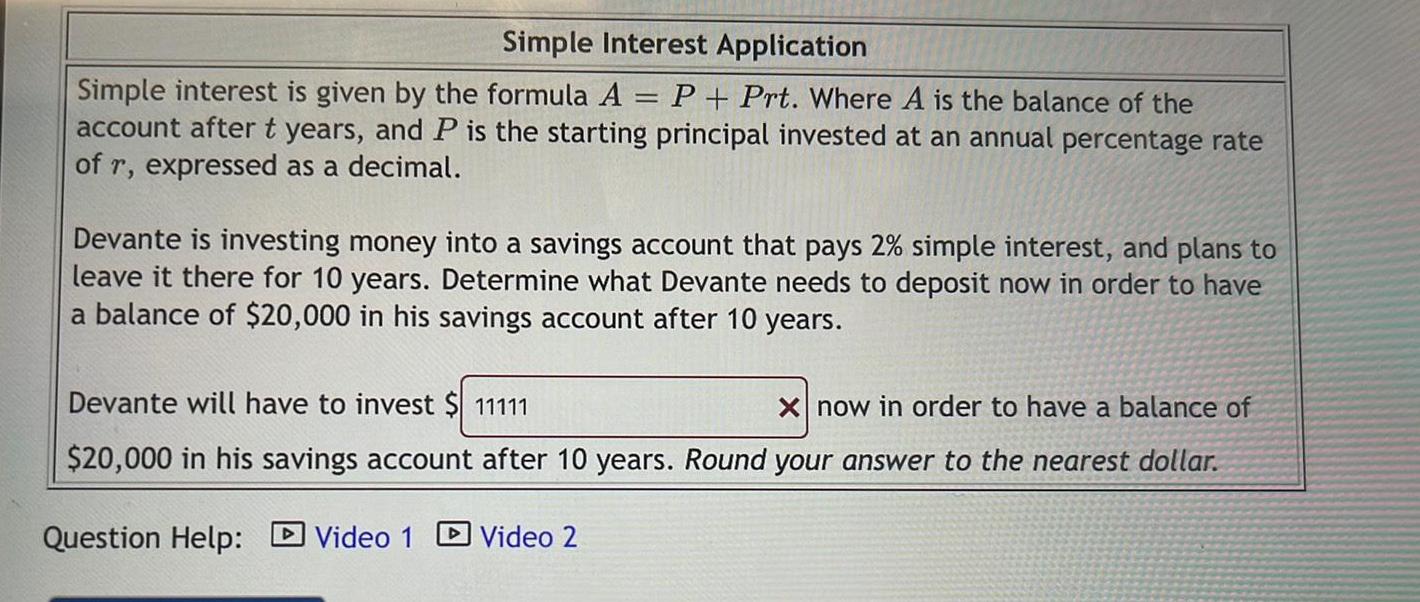
AreaSimple interest is given by the formula A P+Prt. Where A is the balance of the account after t years, and P is the starting principal invested at an annual percentage rate of r, expressed as a decimal.
Devante is investing money into a savings account that pays 2% simple interest, and plans to leave it there for 10 years. Determine what Devante needs to deposit now in order to have a balance of $20,000 in his savings account after 10 years.
Devante will have to invest $ now in order to have a balance of $20,000 in his savings account after 10 years. Round your answer to the nearest dollar.

Geometry
AreaThe area of a square garden is 98m². How long is the diagonal?
07√6 m
O 196 m
○ 14 m
O 49 m

Geometry
AreaFind the cost of carpeting the following rectangular rooms.
a. Dimensions: 6.5 m x 4.5 m; cost = $13.85 persquare meter
b. Dimensions: 15 ft x 11 ft; cost = $30 per square yard

Geometry
AreaA cylinder has a base radius of 3m and a height of 17m. What is its volume in cubic m,
to the nearest tenths place?

Geometry
Area6. Fill in the missing terms of the arithmetic sequences.
a) __________, 11,_______,7_____
b) _________, -3, _______,3______
c) 5,____ ,_____ ,11,_____

Geometry
AreaThe volume of a triangular pyramid is 224 units³. If the base and height of the triangle that forms its base are 12 units and 8 units respectively, find the height of the pyramid.
Geometry
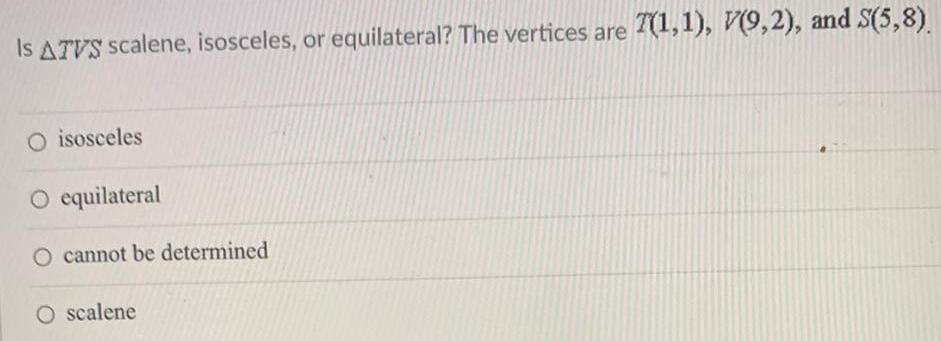
AreaIS ATVS scalene, isosceles, or equilateral? The vertices are 7(1,1), V(9,2), and S(5,8)
O isosceles
O equilateral
cannot be determined
O scalene

Geometry
AreaA recipe for blueberry muffins states that it yields 12 muffins, with 280 calories per muffin. You instead decide to make mini-muffins, and the recipe yields 20 mini-muffins. If you eat 6 mini-muffins, how many calories will you consume?

Geometry
AreaPizzas are measured by diameter.
Determine the area of a 6-inch personal pizza. Round your answer to the nearest hundredth.
square inches
Determine the area of a 16-inch personal pizza. Round your answer to the nearest hundredth.
of square inches
A 6-inch personal pizza has 570 calories. Determine the number of calories in the 16-inch pizza. Round your answer to the nearest calorie.
There are 1520 x calories in the 16-inch pizza.
A 16-inch pizza is cut into 8 slices. Estimate the number of calories in one slice of a 16-inch pizza.
Round your answer to the nearest calorie.
There are calories in one slice of the 16-inch pizza.
Geometry
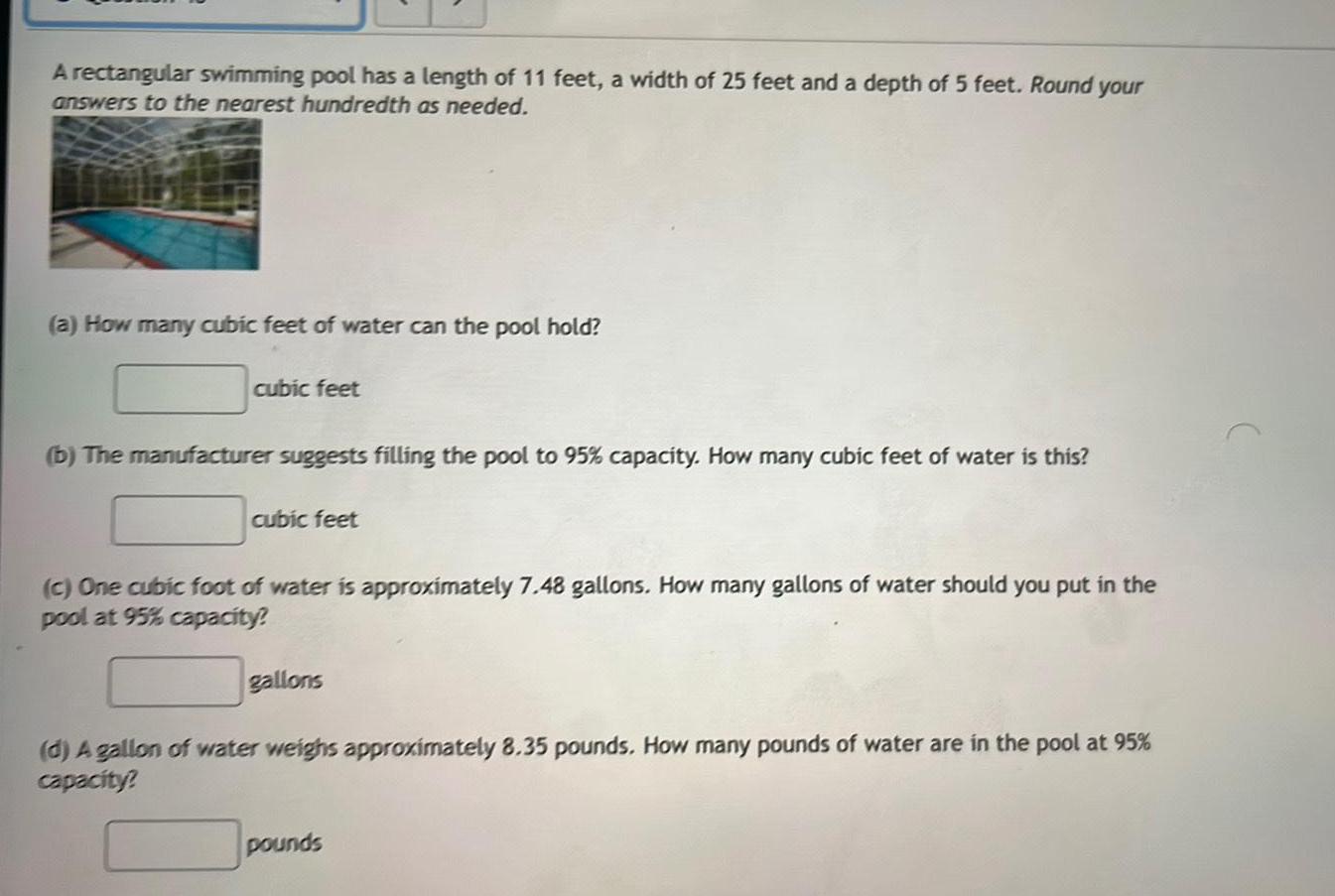
AreaA rectangular swimming pool has a length of 11 feet, a width of 25 feet and a depth of 5 feet. Round your
answers to the nearest hundredth as needed.
(a) How many cubic feet of water can the pool hold?
cubic feet
(b) The manufacturer suggests filling the pool to 95% capacity. How many cubic feet of water is this?
cubic feet
(c) One cubic foot of water is approximately 7.48 gallons. How many gallons of water should you put in the
pool at 95% capacity?
gallons
(d) A gallon of water weighs approximately 8.35 pounds. How many pounds of water are in the pool at 95%
capacity?
pounds

Geometry
AreaA box has length 6 feet, width feet, and height 7 inches. Find the volume of the box in cubic feet and in cubic inches.
_____cubic inches______cubic feet
Round your answers to the nearest tenth as needed.

Geometry
AreaIs the statement a good definition? If not, find a counterexample. A square is a figure with two pairs of parallel sides and four right angles.
No; a parallelogram is a counte rexample.
No; a rectangle is a counterexample.
No; a rhombus is a counterexample.
The statement is a good definition.
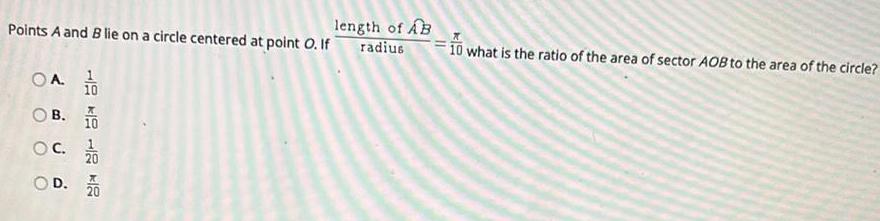
Geometry
AreaPoints A and B lie on a circle centered at point O. If length of AB/ radius = π/10 what is the ratio of the area of sector AOB to the area of the circle?
A.1/10
B. π/10
C. 1/10
D. π/20

Geometry
AreaJake volunteers to help out his younger brother's basketball team in his free time. One of his tasks is to ensure that all the basketballs have enough air in them. Given that a properly inflated basketball measures 8.8 inches across, what is the total volume of air inside six of Jake's basketballs? Assume that the wall of each ball is infinitely thin.
A. 681.47 π cubic inches
B. 1,651.32 π cubic inches.
C. 3,775.23 π cubic inches
D. 5,451.78 π cubic inches

Geometry
AreaFind the area of a triangle with base 1-2/3 inches and height 5 inches?
Write your answer as a proper fraction or mixed number in reduced form.
Area = square inches

Geometry
AreaA solid machine part is to be manufactured as shown in the figure. The part is made by cutting a small cone off the top of a larger cone. The small cone has a base radius of 3 inches and a height of 5 inches. The larger cone has a base radius of 9 inches and had a height of 15 inches prior to being cut. What is the volume of the resulting part illustrated in the figure?
A. 15π cubic inches
B. 155π cubic inches
C. 390π cubic inches
D. 405π cubic inches
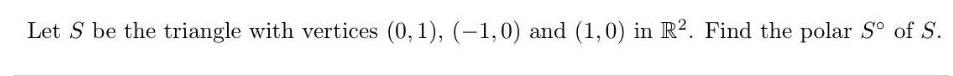
Geometry
AreaLet S be the triangle with vertices (0,1), (-1,0) and (1,0) in R2. Find the polar Sº of S.

Geometry
AreaDiego says, "To find arc length, divide the measure of the central angle by 360. Then multiply that by the area of the circle." Do you agree with Diego?
Show or explain your reasoning.

Geometry
AreaSolid metal support poles in the form of right cylinders are made out of metal with a density of 4.5 g/cm³. This metal can be purchased for $0.33 per kilogram. Calculate the cost of a utility pole with a radius of 10.4 cm and a height of 660 cm. Round your answer to the nearest cent. (Note: the diagram is not drawn to scale)

Geometry
Area3. What is the area of a circle with a diameter of 18 cm?
18π cm²
81π cm²
324π cm²
1296π cm²

Geometry
AreaThe steeple of a building is in the shape of a regular pyramid with a triangular base. Each of the 3 base sides is 4.6 meters long, and the steeple is 7 meters high. Compute the number of cubic meters of airspace contained in the steeple. Round the answer to the nearest cubic meter.
The steeple of a building is in the shape of a regular pyramid with a triangular base. Each of the 3 base sides is 4.6 meters long, and the steeple is 7 meters high. Compute the number of cubic meters of airspace contained in the steeple. Round the answer to the nearest cubic meter.

Geometry
AreaThe surface area of a cylinder is 1927 square feet, and its height is 10 feet. Find its diameter.

Geometry
AreaTriangle ABC has vertices at (-4, 0), (-1, 6) and (3, -1). What is the perimeter of triangle ABC, rounded to the nearest tenth?

Geometry
AreaDetermine the distance of the centroid from the x - axis of the solid formed by revolving the
bounded region by the curve x²=4y and the line x = 4 about the line x = 4.
A 3/5
B 7/10
C) 5/9
D 4/5

Geometry
Areathe length of a rectangle is 5 times the width if the perimeter of the rectangle is 60m find its length and width

Geometry
AreaA sector of a circle has an arc length of 7 cm and a central angle of π 6 radians. What is the area of the sector?
A. 2π cm²
B. 3π cm²
C. π cm²
D. 5π cm²
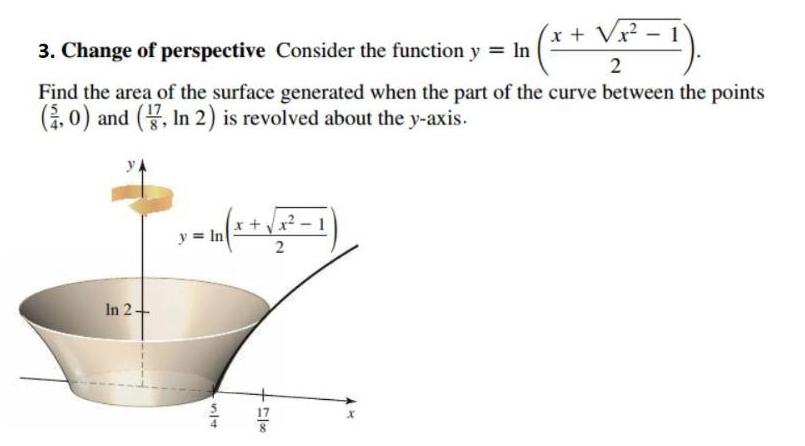
Geometry
AreaChange of perspective Consider the function y = ln( x + √x²-1 / 2). Find the area of the surface generated when the part of the curve between the points (5/4,0) and (17/8, In 2) is revolved about the y-axis.

Geometry
AreaThe total surface area, in square units, of a cylinder with a radius of r units and a height of h units can be represented by the formula
SA = 2πr² + 2πrh.
The first term of the expression represents the total area of the 2 circular bases of the cylinder, and the second term represents the lateral area of the cylinder.
In a certain cylinder, the radius is related to the height as shown in the
expression 2πx² + 2x (x + 3).
Which of the following statements could be true? Select all that apply.
A)The lateral area of a cylinder can be represented by the expression 2πx².
B)The height of a cylinder is 3 times the length of its radius.
C)The radius of a cylinder is equal to x units, and the height of a cylinder is equal to x + 3 units.
D)The area of one of the bases of a cylinder can be represented by the expression πX²
E)The radius of a cylinder is 3 units less than its height.
Geometry
AreaThere is a smaller circle inside of a larger circle. The smaller circle's radius is 2 and the larger circle's radius is 21. What is the difference between the area of the larger circle and the area of the smaller circle? Round to the nearest tenth.
Geometry
AreaA tank in the shape of a hemisphere has a radius of 13 feet. If the liquid that fills the tank has a density of 69 pounds per cubic foot, what is the total weight of the liquid in the tank, to the nearest full pound?

Geometry
AreaCalculate the surface area of a cylindrical water tank that is 4m high and has a diameter of 12m.
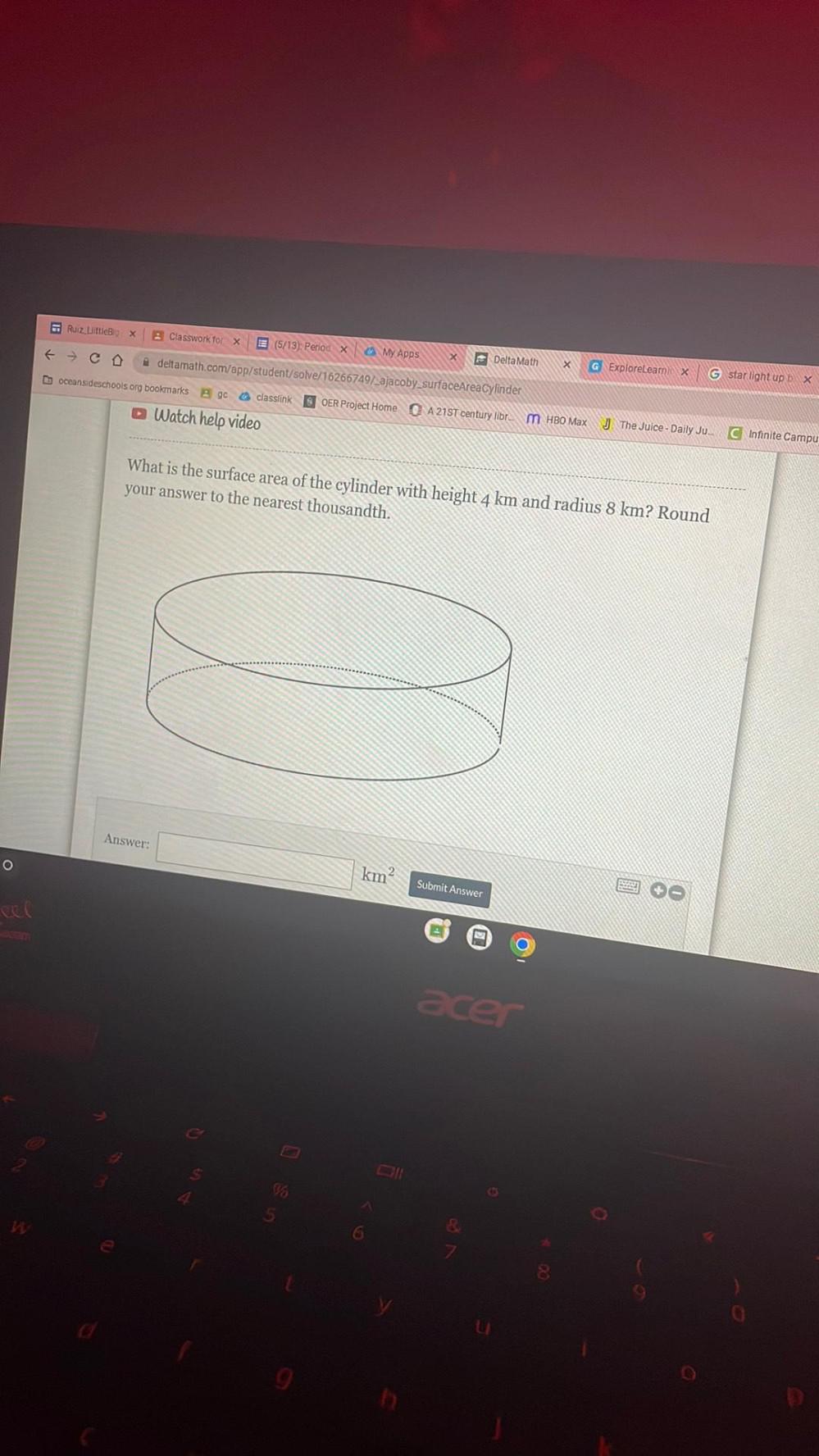
Geometry
AreaWhat is the surface area of the cylinder with height 4 km and radius 8 km? Round your answer to the nearest thousandth.


Geometry
AreaThe ratio of the heights of two similar cones is 4:5.
If the base area of the large cone is 2251 cm, find the base area of the small
cone. Give an exact answer, typing pi to represent the letter π
The base area of the small cone is ______ cm^2

Geometry
AreaThe height of a certain prism is 35mm. A second prism that is similar to the first one has a height of 25mm. Determine the volume ratio of the larger prism to the smaller prism.
Reduce your answer completely.
The volume ratio of the larger prism to the smaller prism is __________ : ____________

Geometry
AreaA right square pyramid has a base edge length of 4 inches and a height of 7 inches. The pyramid is sliced by a plane that passes through the vertex of the pyramid and two of the midpoints of opposite sides of the base of the pyramid. Determine the area of the cross section formed by the intersection of the plane and the pyramid.
The area of the cross section is _____________ in².

Geometry
AreaThere is a sphere P with radius 5 units at center (10, 9 ,11). Another object Q is
defined by the vertices (-9,1, -2), (-5,1,-1), (1, -2, 1), (3,-6, -1), (3, 2, 1). Find the AABB of each of P and Q. Do the AABBs of P and Q collide each other?
Geometry
AreaA tree has circumference of 86 inches. Find the area of a circle with that circumference.
The area of the circle is _______
(Simplify your answer. Round to two decimal places as needed.)

Geometry
Area1-15. The area of a square plot of land 21.34 ch. by 17.89 ch. is
a. 381.774 ac.
b. 381.761 ac.
c. 38.176 ac.
d. 38.177 ac.
1-16. Convert 32,567.78 Standard Feet to U.S. Survey feet.
a. 32,567.45 ft.
b. 32,567.95 ft.
c. 32,568.71 ft.
d. 32,568.53 ft.
1-17. 21.61892 grads converted to D/M/S equals
a. 19° 27' 25"
b. 24° 01' 16"
c. 24° 02' 10"
d. 19° 27' 44"
1-18. Round oft 21° 36' 24.6" to the nearest second.
a. 21° 36' 25"
b. 21° 36' 24"
c. 21. 36' 23"
d. 21° 36' 26"
1-19. Round off 3.49562 acres to 3 decimal places.
a. 3.497 acres
b. 3.496 acres
c. 3.495 acres
d. 3.494 acres
1-20. Round off 1,724.6753 ft to 2 decimal places.
a. 1,724.67 ft
b. 1,724.66 ft
c. 1,724.69 ft
d. 1,724.68 ft

Geometry
AreaAn irrigation system waters in circular patterns. Each irrigated section is a circle with a diameter of 40 feet. What is the area of an irrigated section?
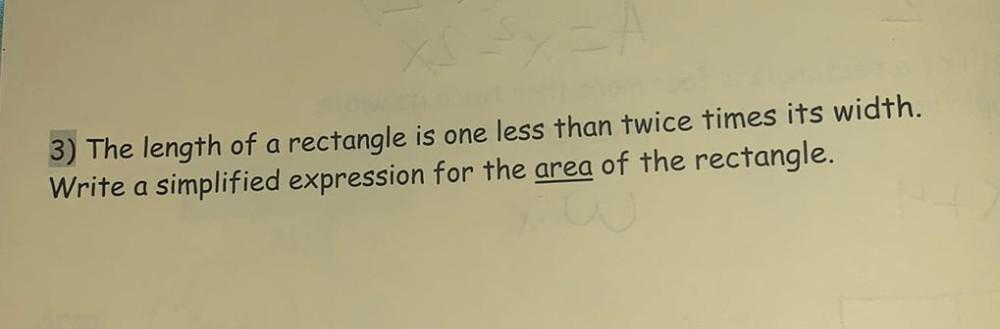
Geometry
AreaThe length of a rectangle is one less than twice times its width. Write a simplified expression for the area of the rectangle.
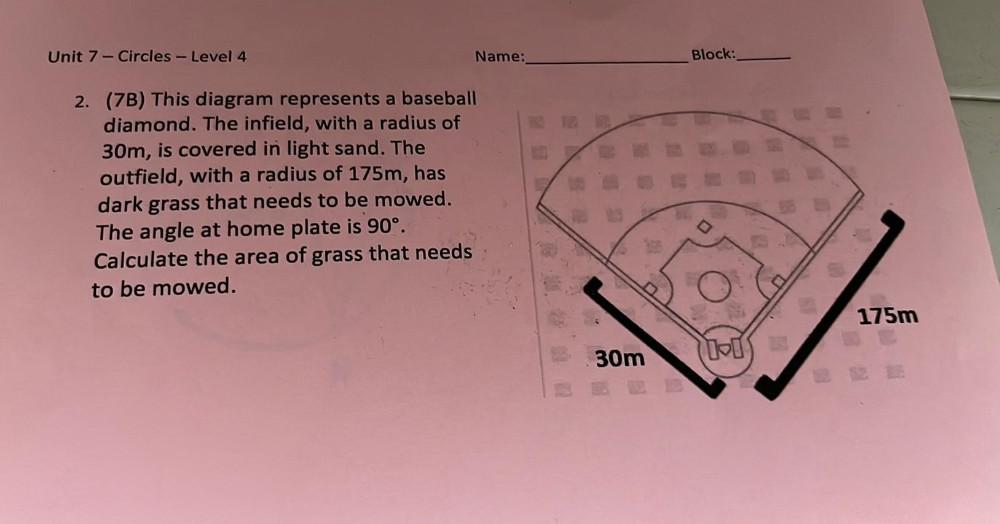
Geometry
AreaThis diagram represents a baseball diamond. The infield, with a radius of 30m, is covered in light sand. The outfield, with a radius of 175m, has dark grass that needs to be mowed. The angle at home plate is 90°. Calculate the area of grass that needs to be mowed.
Geometry
Areaa. Use the Factor-Label Method to determine the number of feet in 2(1/2) miles.
b. A fence company is measuring a rectangular area in order to install a fence around its perimeter. If the length of the rectangular area is 130 yards and the width is 75 feet, what is the total length of the distance to be fenced?
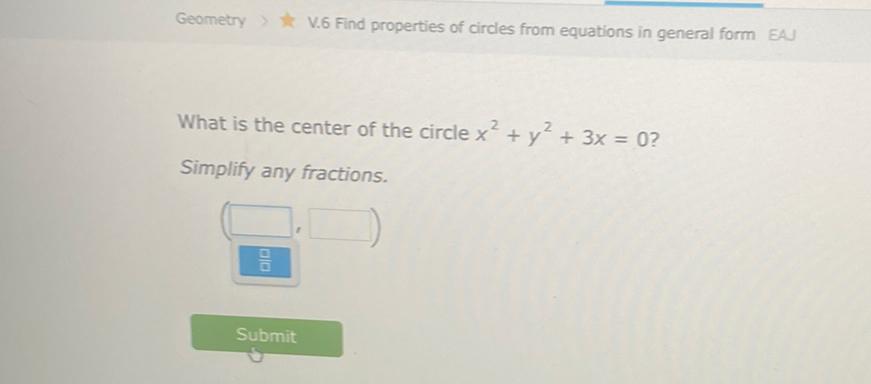
Geometry
AreaA rectangular swimming pool has a length of 37 feet, a width of 17 feet and a depth of 5 feet. Round answers to the nearest hundredth as needed.
(a) How many cubic feet of water can the pool hold? _____ cubic feet
(b) The manufacturer suggests filling the pool to 95% capacity. How many cubic feet of water is this? ______ cubic feet
Geometry
AreaThe volume of a cone with radius r and height h is
given by the formula V=1/3(πr² h).
A cone-shaped pile of sawdust has a base diameter of 26 feet, and is 10 feet tall.
The volume of the sawdust pile is____ft³.

Geometry
AreaDetermine the area of the parallelogram with vertices (2.7, 6), (5, 6, 5), (-7, 12. 12), and (-4, 11, 11). Use the square root symbol '' where needed to give an exact value for your answer.
Area =