Coordinate system Questions and Answers
Geometry
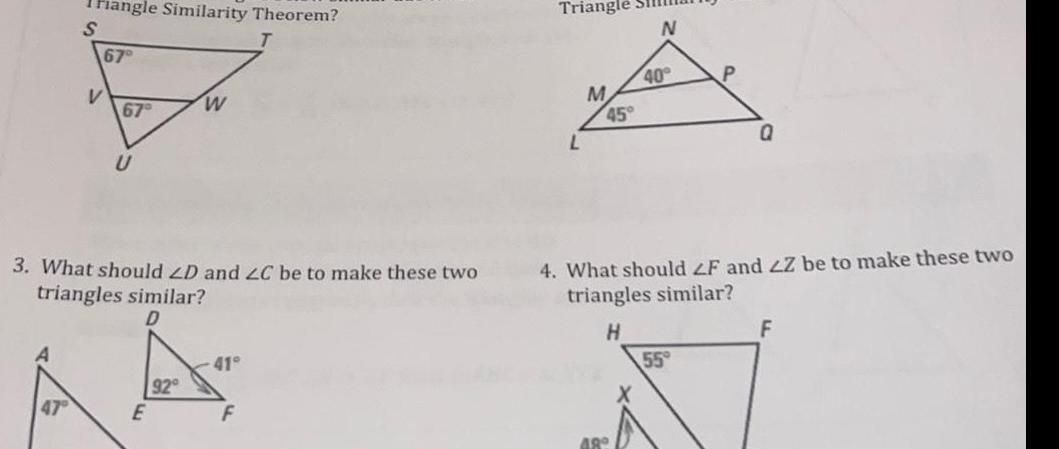
Coordinate systemTriangle Similarity Theorem S 67 V 67 U 3 What should ZD and ZC be to make these two triangles similar E W 92 41 F Triangle L M 45 N 48 40 P 4 What should ZF and Z be to make these two triangles similar H 55 Q F
Geometry
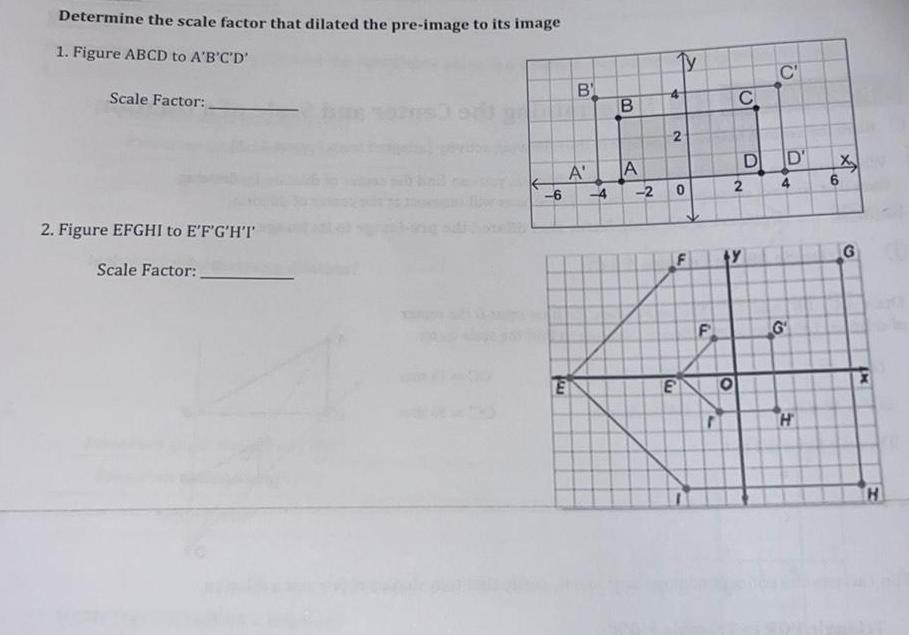
Coordinate systemDetermine the scale factor that dilated the pre image to its image 1 Figure ABCD to A B C D Scale Factor 2 Figure EFGHI to E F G H T Scale Factor B E B A A 6 4 2 Ty 4 2 0 F E F C O Y D 2 O D 4 G H X 6 G L M H
Geometry
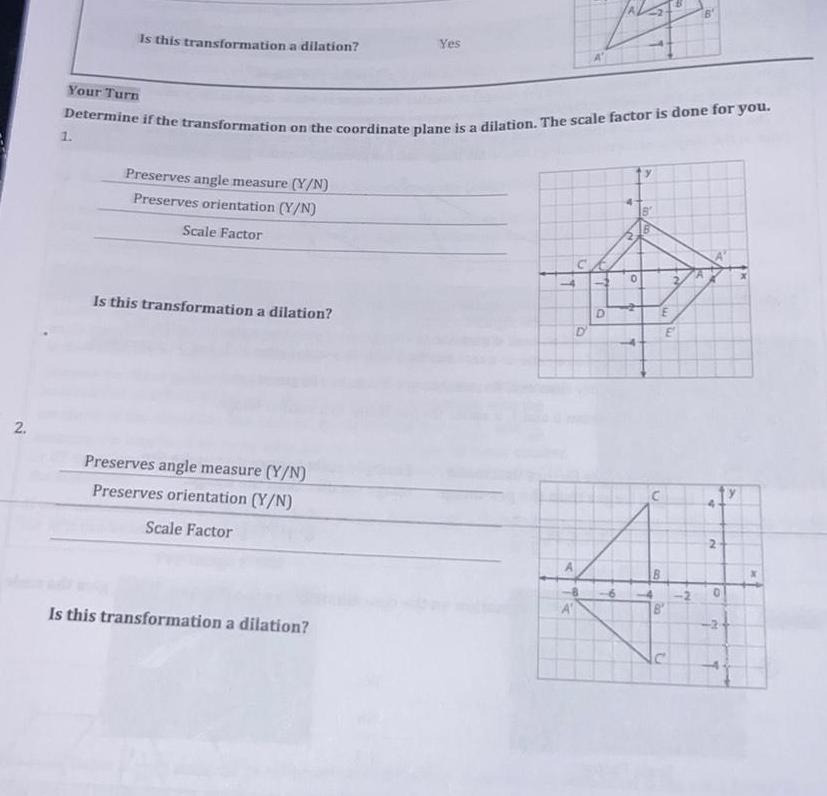
Coordinate system2 Your Turn Is this transformation a dilation 1 Determine if the transformation on the coordinate plane is a dilation The scale factor is done for you Preserves angle measure Y N Preserves orientation Y N Scale Factor Is this transformation a dilation Preserves angle measure Y N Preserves orientation Y N Scale Factor Yes Is this transformation a dilation 16 J J D 4 N 0 A aya B n E B 00 U B 421 12 2 0 A T
Geometry
Coordinate system7 Quadrilateral MATH has vertices M 6 4 A 4 2 T 0 1 H 1 8 What are the vertices of the image 5 after a dilation with a scale factor of using the origin as the center of dilation 2
Geometry
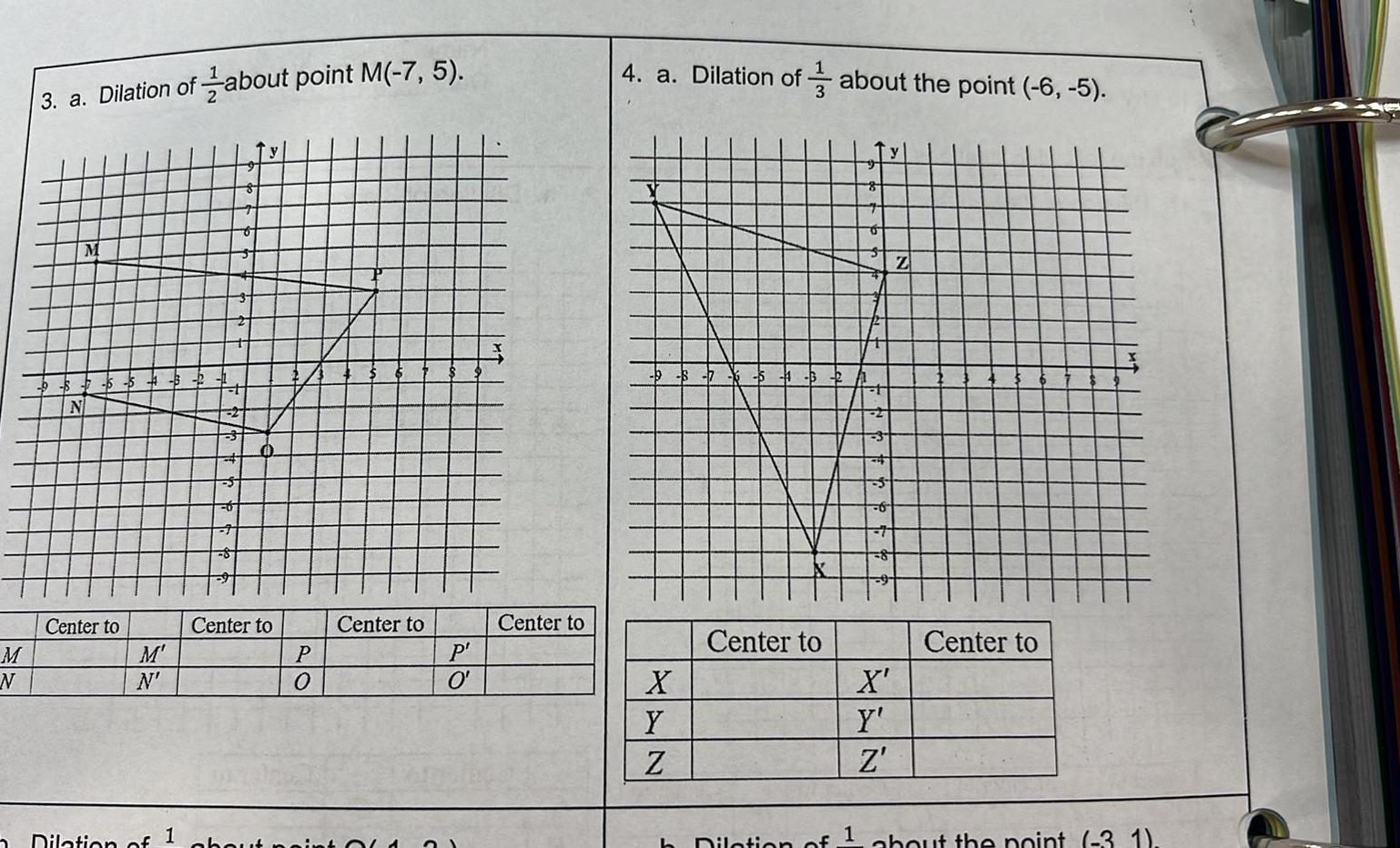
Coordinate systemM N 2 3 a Dilation of about point M 7 5 M Center to M N Dilation of 1 A Center to P O Center to about noint OLA P O Center to 4 a Dilation of about the point 6 5 B X Y Z 6 Center to h Dilation of t 1 3 5 6 7 8 X Y Z Z Center to about the point 3 1
Geometry
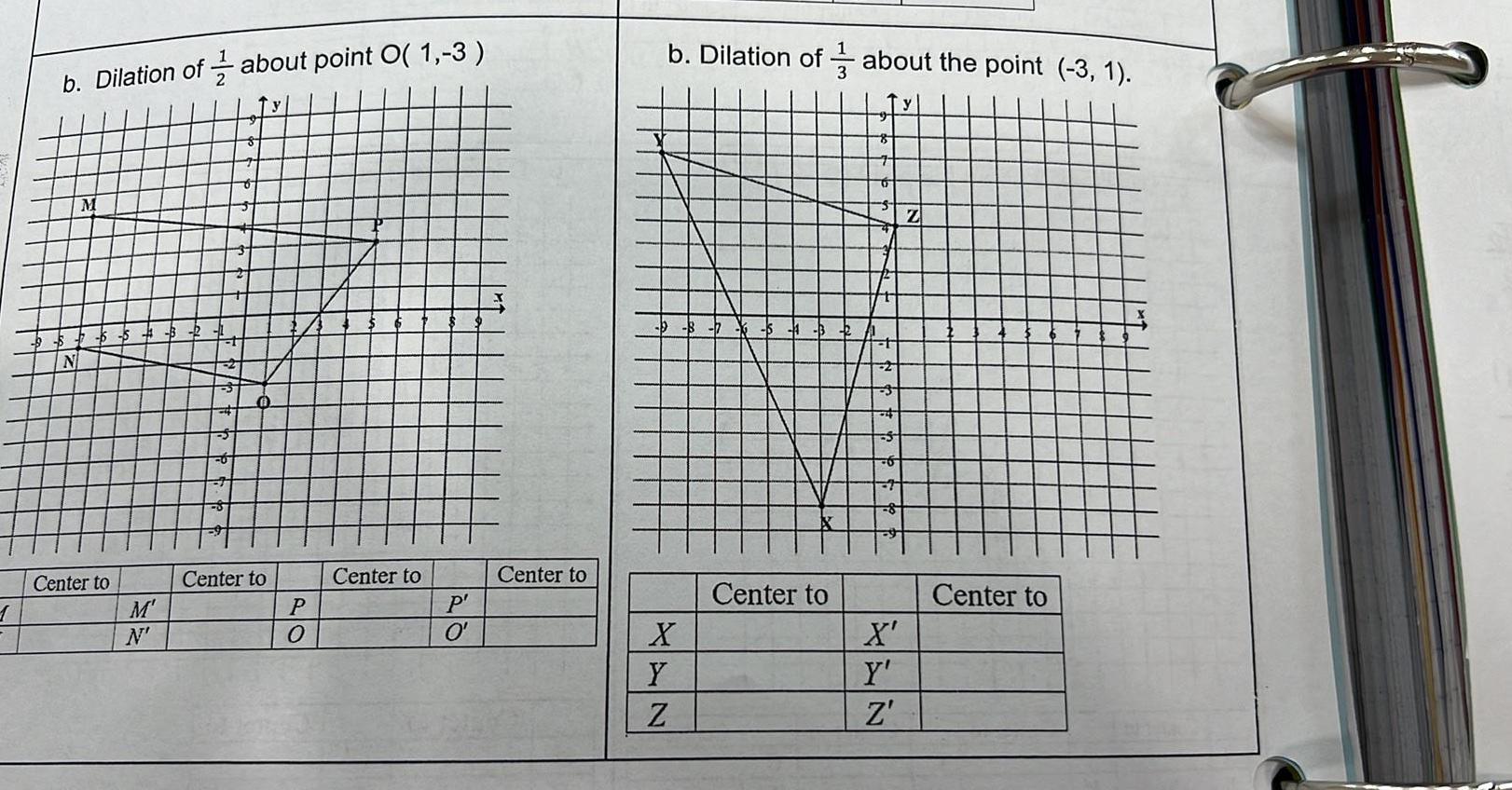
Coordinate system1 b Dilation of about point O 1 3 Center to M N Center to P Center to P O Center to b Dilation of about the point 3 1 3 X Y Z Center to 8 S 6 8 X Y Z Z Center to
Geometry
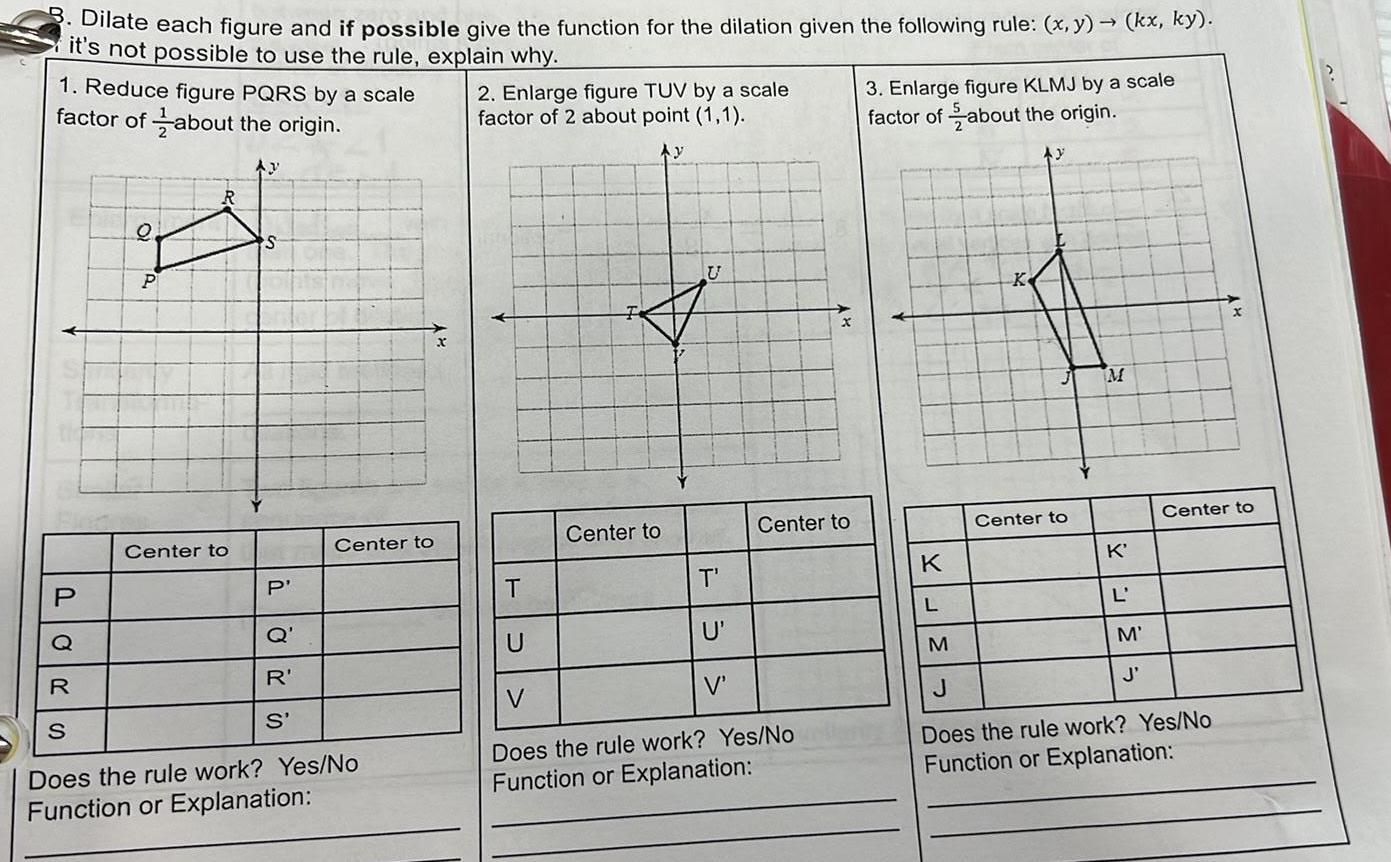
Coordinate systemDilate each figure and if possible give the function for the dilation given the following rule x y it s not possible to use the rule explain why 1 Reduce figure PQRS by a scale factor of about the origin Ay P O P Center to S P Q R S Center to R S Does the rule work Yes No Function or Explanation 2 Enlarge figure TUV by a scale factor of 2 about point 1 1 Ay Center to U T Center to T U V Does the rule work Yes No Function or Explanation U V 3 Enlarge figure KLMJ by a scale factor of about the origin K L K J kx ky Center to M K L M J Center to M J Does the rule work Yes No Function or Explanation
Geometry
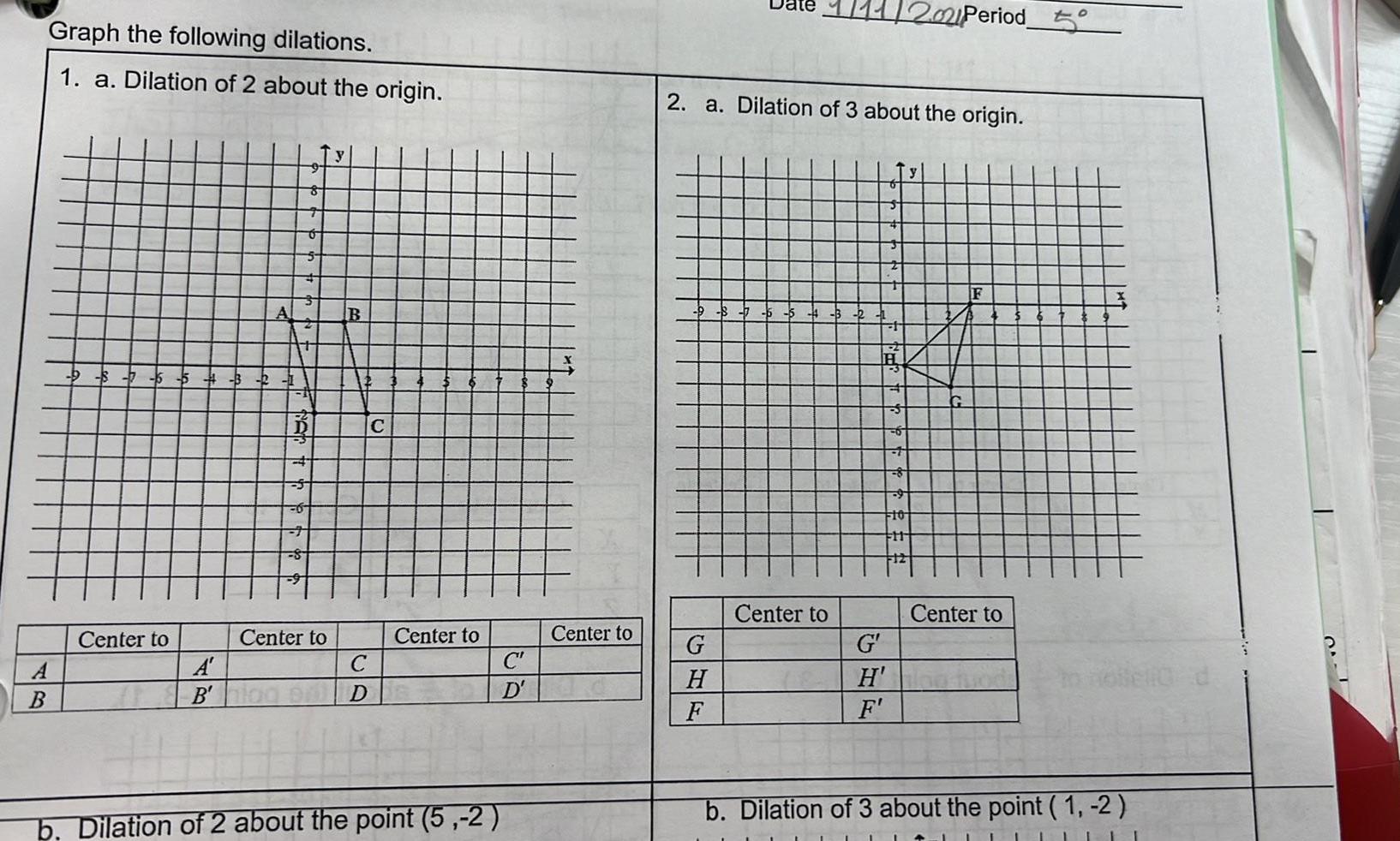
Coordinate systemGraph the following dilations 1 a Dilation of 2 about the origin A B 5 5 3 2 1 Center to 0 S 8 Center to B 12 A C B hiad on D C Center to C D Dilation of 2 about the point 5 2 Center to 2 a Dilation of 3 about the origin G H F Center to G H F 2021 Period 10 FH1 12 Center to b Dilation of 3 about the point 1 2 40
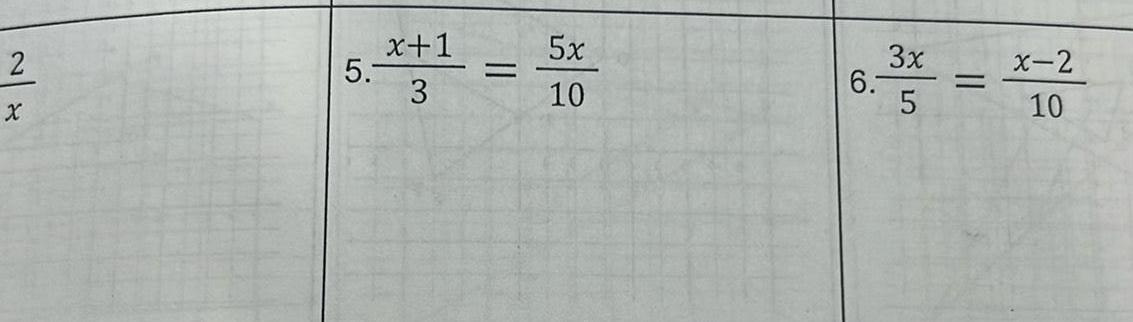
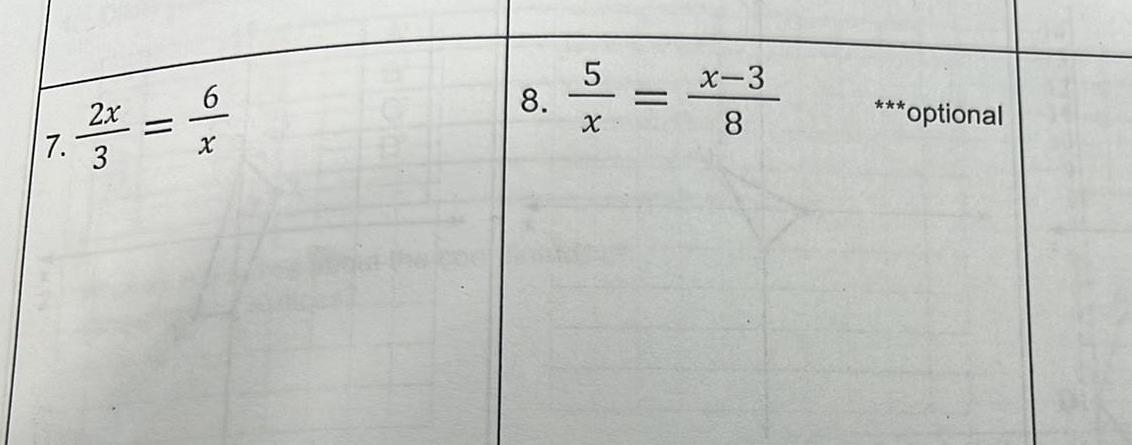
Geometry
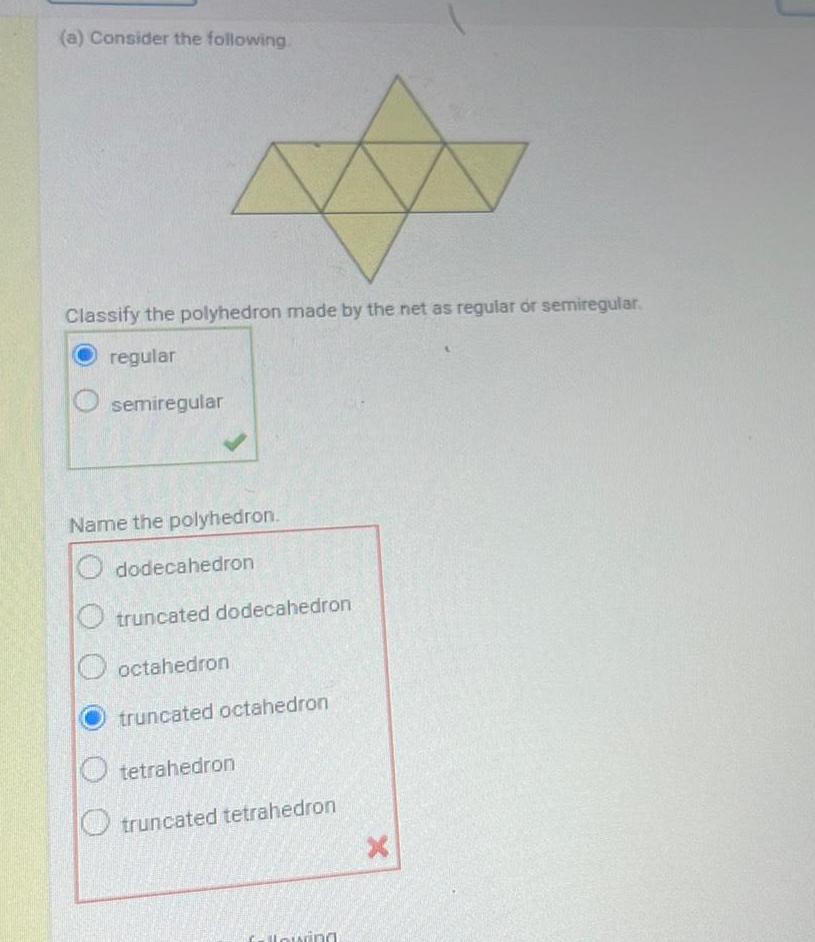
Coordinate systema Consider the following Classify the polyhedron made by the net as regular or semiregular regular semiregular Name the polyhedron dodecahedron truncated dodecahedron octahedron truncated octahedron Otetrahedron truncated tetrahedron following X
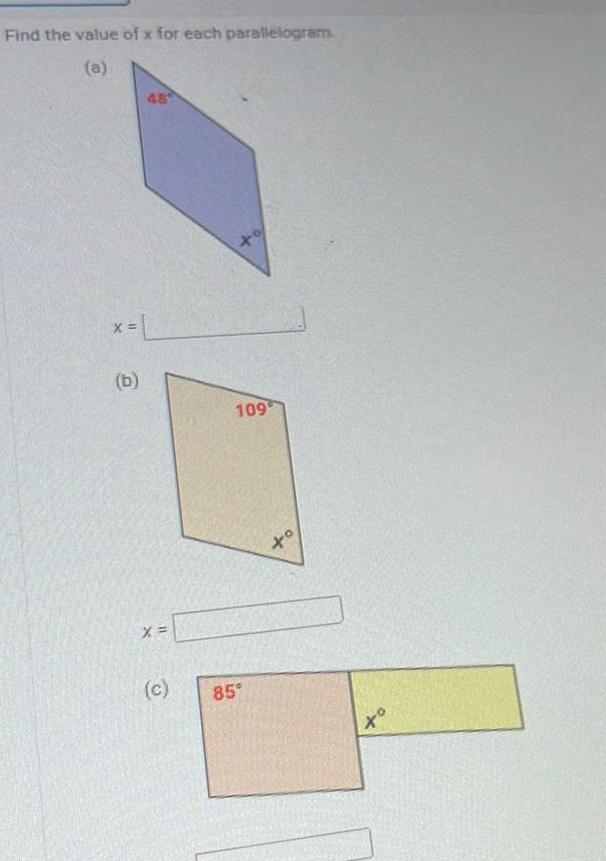
Geometry
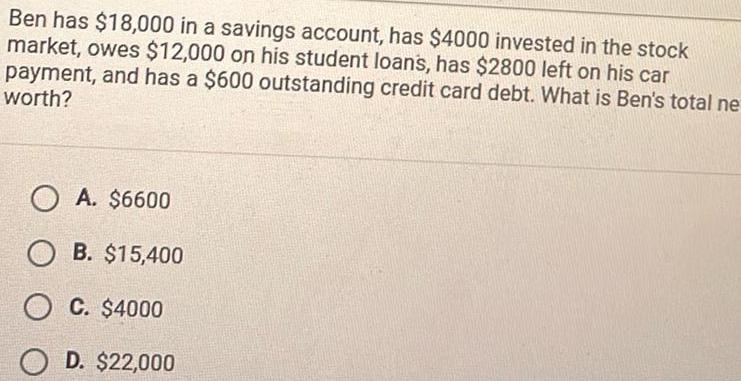
Coordinate systemBen has 18 000 in a savings account has 4000 invested in the stock market owes 12 000 on his student loans has 2800 left on his car payment and has a 600 outstanding credit card debt What is Ben s total ne worth OA 6600 OB 15 400 OC 4000 D 22 000

Geometry
Coordinate systemWhich describes the measure of a person s financial worth determined by adding everything that a person owns and subtracting everything that the person owes OA Liability capital OB Owner s equity C Net worth

Geometry
Coordinate systemb c d Yes the polygon is regular It is both equilateral and equiangular No the polygon is not regular It is equilateral but it is not equiangular O No the polygon is not regular It is equiangular but it is not equilateral No the polygon is not regular It is neither equilateral nor equiangular Yes the polygon is regular It is both equilateral and equiangular No the polygon is not regular It is equilateral but it is not equiangular No the polygon is not regular It is equiangular but it is not equilateral O No the polygon is not regular It is neither equilateral nor equiangular 7m 7m 8 m 8 m 94 7m Yes the polygon is regular It is both equilateral and equiangular No the polygon is not regular It is equilateral but it is not equiangular No the polygon is not regular It is equiangular but it is not equilateral No the polygon is not regular It is neither equilateral nor equiangular 94 7 m Yes the polygon is regular It is both equilateral and equiangular No the polygon is not regular It is equilateral but it is not equiangular No the polygon is not regular It is equiangular but it is not equilateral No the polygon is not regular It is neither equilateral nor equiangular

Geometry
Coordinate systemChris has 8000 in a savings account 5000 invested in the stock markel owns a new laptop computer worth 1500 he has 12 000 left to pay on his student loans and he has 700 outstanding credit card debt What is Chris s total net worth OA 12 700 B 8000 C 1800 OD 14 500
Geometry
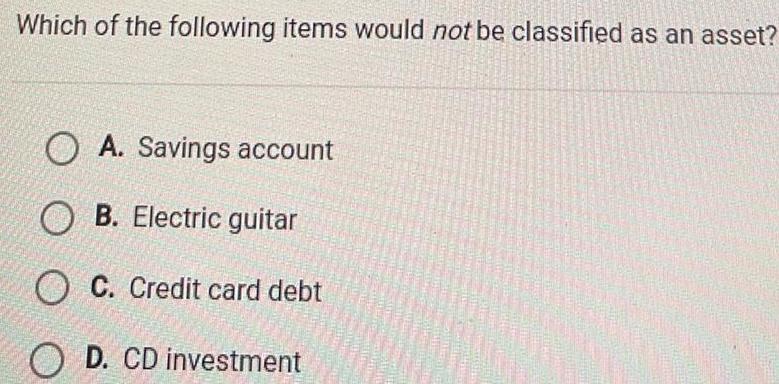
Coordinate systemWhich of the following items would not be classified as an asset OA Savings account OB Electric guitar OC Credit card debt OD CD investment

Geometry
Coordinate systemShawn saw an advertisement for a loan that offered no financing charges for 12 months If he takes the loan which of these scenarios is most likely to occur OA Shawn won t be charged interest for the first 12 months of the loan but he will have to make payments for the first 12 months OB Shawn will be charged interest for the first 12 months of the loan but he won t have to make payments for the first 12 months OC Shawn won t be charged interest for the first 12 months of the loan nor will he have to make payments for the first 12 months O D Shawn will be charged interest for the first 12 months of the loan and he will also have to make payments for the first 12 months

Geometry
Coordinate systemWhich of these statements describes a sale A The shopper receives a discount later and pays sales tax on the full price of the item B The shopper receives a discount now and pays sales tax on the discounted price of the item C The shopper receives a discount later and pays sales tax on the discounted price of the item D The shopper receives a discount now and pays sales tax on the full price of the item
Geometry
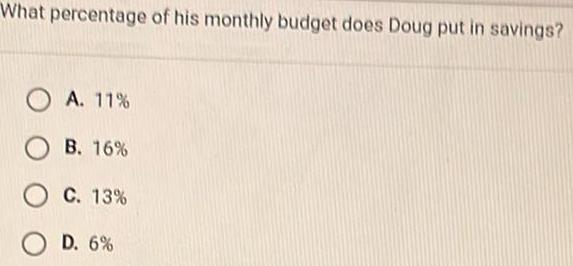
Coordinate systemWhat percentage of his monthly budget does Doug put in savings A 11 B 16 C 13 O D 6

Geometry
Coordinate systemMilena s take home pay is 1200 a month 12 of her take home pay is spent on her cable bill How much is Milena s monthly cable bill OA 104 OB 120 OC 144 OD 144
Geometry
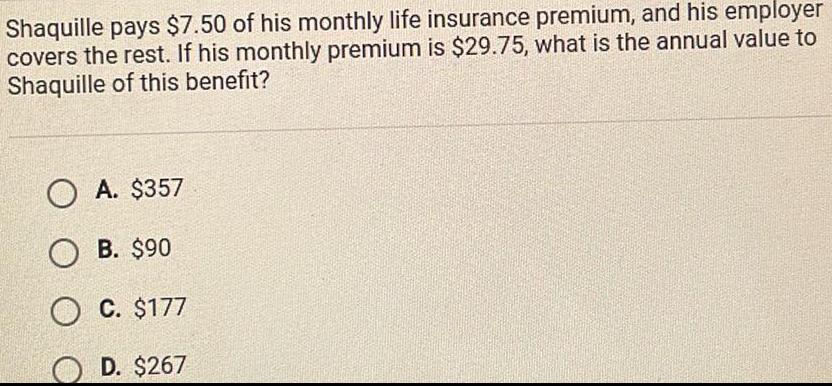
Coordinate systemShaquille pays 7 50 of his monthly life insurance premium and his employer covers the rest If his monthly premium is 29 75 what is the annual value to Shaquille of this benefit OA 357 B 90 O C 177 D 267

Geometry
Coordinate systemA sales manager has weekends off and has 20 paid vacation days per yea including holidays that fall on weekdays If her salary is 93 600 per year what is her pay per workday OA 345 OB 360 C 365 OD 390

Geometry
Coordinate systemBartholomew just got a new credit card that offers both an introductory AP and a standard APR If the standard APR is 19 8 which of the following rates would most likely be the introductory APR A 39 8 OB 19 8 OC 9 8 D 29 8
Geometry
Coordinate systemadie is considering getting a credit card and using it instead of cash Whicll f these is a good reason for her to do so OA Sadie definitely won t have to pay any fees or charges with a credit card B Sadie won t be able to buy anything she can t pay for with a credit card O C Sadie may be able to participate in a rewards program with a credit card D There is less of a chance that Sadie s identity will get stolen with a credit card
Geometry
Coordinate systemWhat is the name of the investment strategy in which a person invests equa mounts in different CDs with different maturity dates OA Liquidity strategy OB CD ladder C Money market account

Geometry
Coordinate systemVanessa wants to buy a CD for 500 that earns 3 APR and is compounded quarterly The CD matures in 2 years She will be paid the interest she earns each quarter How much interest will Vanessa have earned on this CD after the first quarter OA 2 50 O B 3 75 O C 1 25 OD 15 00
Geometry
Coordinate systemThomas wants to buy a CD for 500 that earns 3 APR and is compounded quarterly The CD matures in 3 years and the early redemption fee is 3 months interest If Thomas were to take his money out 3 months before the CD matures how much money would he get back after the early redemption fee OA 507 58 OB 511 33 OC 539 08 OD 542 43

Geometry
Coordinate systemCecil has a credit card that uses the adjusted balance method For the days of one of his 30 day billing cycles his balance was 340 He then made a purchase for 290 so his balance jumped to 630 and it remained that amount for the next 10 days Cecil then made a payment of 150 so his balance for the last 10 days of the billing cycle was 480 If his credit card s APR is 19 which of these expressions could be used to calculate the amount Cecil was charged in interest for the billing cycle O A 0 15 30 340 O B 0 19 365 30 10 340 10 630 10 150 C 0 19 30 lis190 30

Geometry
Coordinate systemWalter has a credit card that uses the average daily balance method For the first 15 days of a 31 day billing cycle his balance was 1440 but then he paid off his entire balance and didn t make any new purchases If his credit card s APR is 22 how much was Walter charged in interest for the billing cycle OA 26 91 OB 0 OC 13 89 D 13 02
Geometry
Coordinate systemWhat is the name of the monetary value that is printed on the front of the bond O A Liquidity value O B Bond value C Face value
Geometry
Coordinate systemSuppose you purchase a 1000 bond with a 4 coupon What is the periodic interest rate of this bond O A 1 B 4 O C 0 2 D 2
Geometry
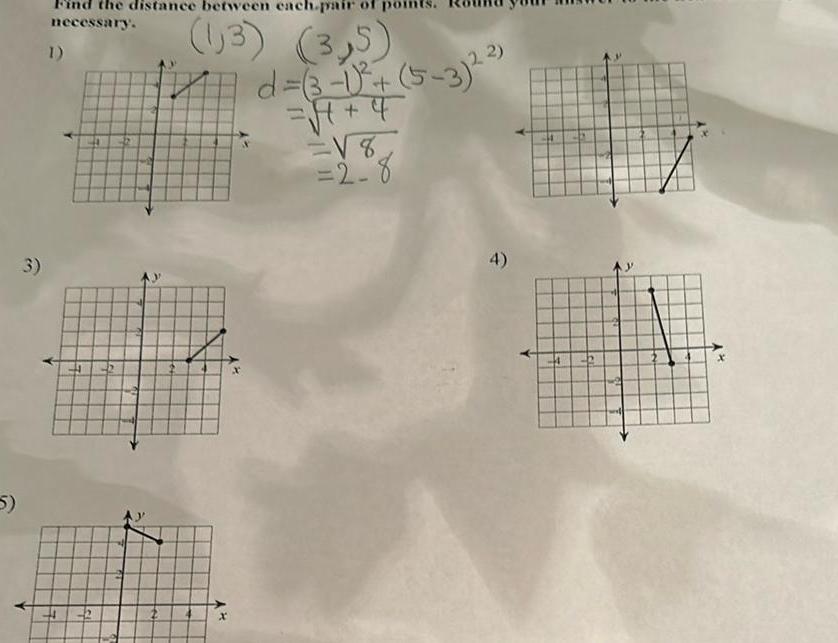
Coordinate system5 3 Find the distance between each pair points necessary 1 4 4 4 4 2 2 13 3 5 d 3 1 5 3 4 4 8 2 8 4

Geometry
Coordinate systemSolve by completing the square p 10p 1 Write your answers as integers proper or improper fractions in simplest form or decimal rounded to the nearest hundredth or p
Geometry
Coordinate systemWhat type of solutions does this equation have s 27 two imaginary solutions no solutions two real solutions

Geometry
Coordinate systemEXPLAIN 2 Proving Opposite Angles Are Congruent Read the section below and complete the following activity adapted from Lesson 9 1 Example Prove that the opposite angles of a parallelogram are congruent Given ABCD is a parallelogram Prove ZA ZC A similar proof shows that ZB ZD 5 Theorem 2 If a quadrilateral is a parallelogram then its opposite angles are congruent The gure WXYZ is a parallelogram 2ZWX 2XYZ and ZWZY ZWXY 1 ABCD is a parallelogram 2 Draw DB 6 3 AB DC AD BC 4 7 Statements Statement Reason Bank 1 2 6 3 1 Given D Reasons 4 Alternate Interior Angles Theorem 5 Reflexive Property of Congruence 6 ASA Triangle Congruence Theorem 7 A ABD A CDB 2 Through any two 7R CPCTC points there is exactly one line W 7S LA LC B 4 LADB LCBD LABD LCDB 5 DB DB 3 Definition of parallelogram

Geometry
Coordinate systemChloe filed for Chapter 13 bankruptcy in 2008 Even if she planned to take the maximum time allowed under Chapter 13 to repay her debts she must have planned to repay them by no later than what year OA 2016 OB 2015 OC 2013 OD 2014

Geometry
Coordinate systemCindy lives in Connecticut and makes 59 000 a year If the median annual income is 68 595 in Connecticut and 50 233 in the United States as a whole is Cindy likely to qualify for Chapter 7 bankruptcy A No Cindy is not likely to qualify because her yearly income is below the median annual income of Connecticut O B Yes Cindy is likely to qualify because her yearly income is above the median annual income of the United States as a whole C Yes Cindy is likely to qualify because her yearly income is below the median annual income of Connecticut OD No Cindy is not likely to qualify because her yearly income is above the median annual income of the United States as a whole
Geometry
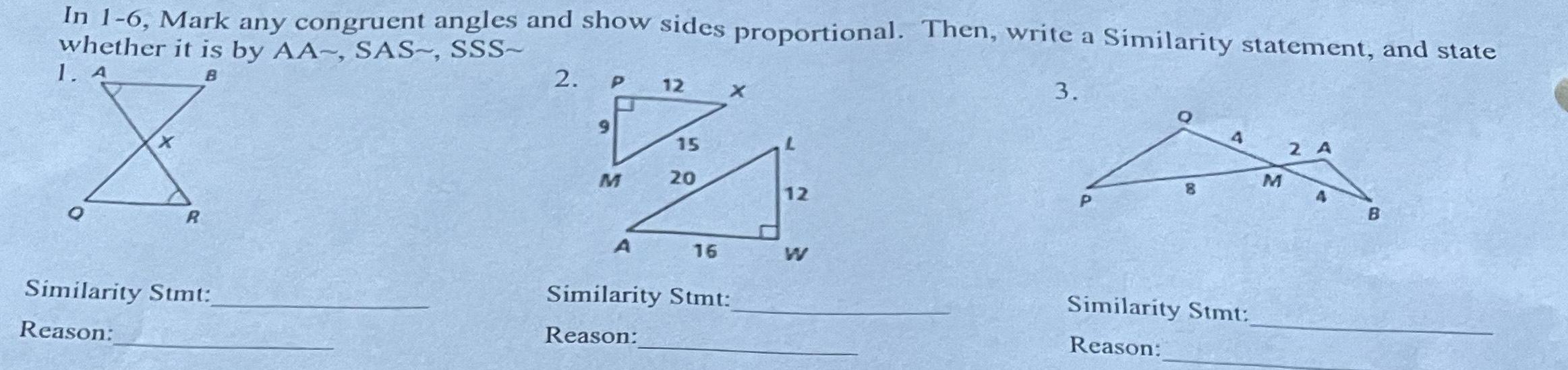
Coordinate systemIn 1 6 Mark any congruent angles and show sides proportional Then write a Similarity statement and state whether it is by AA SAS SSS 1 A B 3 O R Similarity Stmt Reason 2 9 P M A 12 15 20 16 Similarity Stmt Reason 12 W P 8 4 Similarity Stmt Reason M 2 A B
Geometry
Coordinate systemWhich type of bankruptcy is available to all businesses but I corporations to put a stay on creditors while allowing the company to reorganize with the company sometimes continuing to run or being put up for sale while it is bankrupt O A Chapter 7 OB Chapter 9 O C Chapter 11 OD Chapter 13

Geometry
Coordinate systemShelby s annual take home pay is 51 000 What is the maximum amount that she can spend per month paying off credit cards and loans and not be in danger of credit overload O A 4250 00 OB 850 00 O C 1062 50 OD 3400 00
Geometry
Coordinate systemXYZ Insurance offers an annuity with 5 9 APR for the next ten years You decide to invest 100 each quarter into this account What type of annuity is this OA Recurring payment fixed annuity OB Single payment variable annuity C Recurring payment variable annuity D Single payment fixed annuity
Geometry
Coordinate systemDanielle invests 50 a month in an annuity that earns 4 APR and is compounded monthly What is the future value of Danielle s account in 3 years O A 1909 06 OB 2082 39 OC 2153 85 D 1843 29

Geometry
Coordinate systemCarson wants to use a sheet of fiberboard 29 inches long to create a skateboard ramp with a 19 angle of elevation from the ground How high will the ramp rise from the ground at its highest end Round your answer to the nearest tenth of an inch if necessary


Geometry
Coordinate systemDora took out an 8 year loan for 83 000 at an APR of 10 7 compounded monthly while Edith took out an 8 year loan for 93 000 at an APR of 10 7 compounded monthly Who would save more by paying off her loan 6 years early OA Edith would save more because she borrowed 10 000 more in principal O B Edith would save more because she borrowed 10 000 less in principal O C Dora would save more because she borrowed 10 000 less in principal D Dora would save more because she borrowed 10 000 more in
Geometry
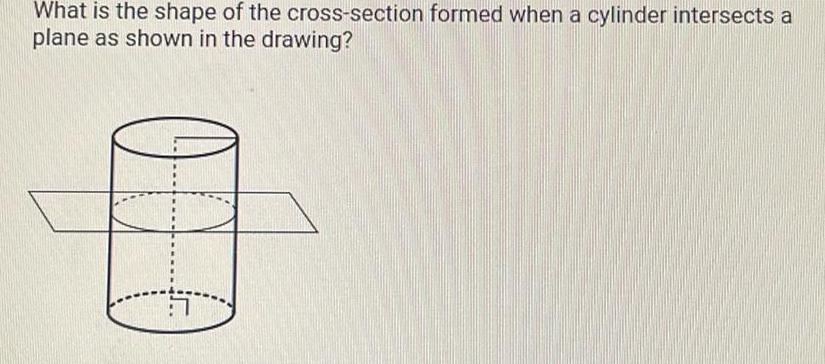
Coordinate systemWhat is the shape of the cross section formed when a cylinder intersects a plane as shown in the drawing

Geometry
Coordinate system17 Denklemi e im kesi im bi iminde yaz n Ard ndan e imi ve y kesi im noktas n belirleyin 5x 2y 6 E im kesi im formu

Geometry
Coordinate systemT6 Prove trigonometric identities using reciprocal identities quotient identities Pythagorean identities sum or difference identities restricted to sine cosine and tangent double angle identities restricted to sine cosine and tangent 1 15 pts Prove 3 of the following identities for all permissible values of the variable Clearly indicate the selected identity and the chosen side State any non permissible values sinx A C 1 cos x cos 8 cote sec8 tan 8 B cot 8 1 sin 0 tan 8 1 cos 0 1 60s sinx tan x cos x CSCX 1 cos x D cot 0

Geometry
Coordinate systemE im ve y kesi im noktas n kullanarak her denklemin grafigl 3 15 y x 1 4 yama y int 7 6 5 4 3 2 1 2 3 4 5 8 3 4 5 16 8y 16x 24 E im kesi im formu yama y int 7 5 6 4 3 2 6 5 3 24 2 2 3 5