Logarithms Questions and Answers

Math - Others
LogarithmsThe intensity levels / of two earthquakes measured on a seismograph can be compared by the formula log(I₁/I₂)= M₁ - M₂ where M is the magnitude given by the Richter Scale. In August 2009, an earthquake of magnitude 6.1 hit Honshu, Japan. In March 2011, that same region experienced yet another, more devastating earthquake, this time with a magnitude of 9.0. How many times greater was the intensity of the 2011 earthquake? Round to the nearest whole number.


Math - Others
LogarithmsThe difference of magnitudes of earthquakes, according to the Richter scale, is given by M₁ - M₂ = log(I₁ / I₂). If Earthquake 1 has magnitude 6.5 and Earthquake 2 has magnitude 5.0, determine how many times greater the intensity of Earthquake 1 is than that of Earthquake 2.

Math - Others
LogarithmsThe binary entropy function describes the expected amount of information provided by each flip of
a coin when the probability of the "heads" face showing is p. It is given by
H(p) = -plog₂ (p) - (1 - p) log₂ (1 - p).
Compute the value of H(0.1), and round your answer to four decimal places.
Math - Others
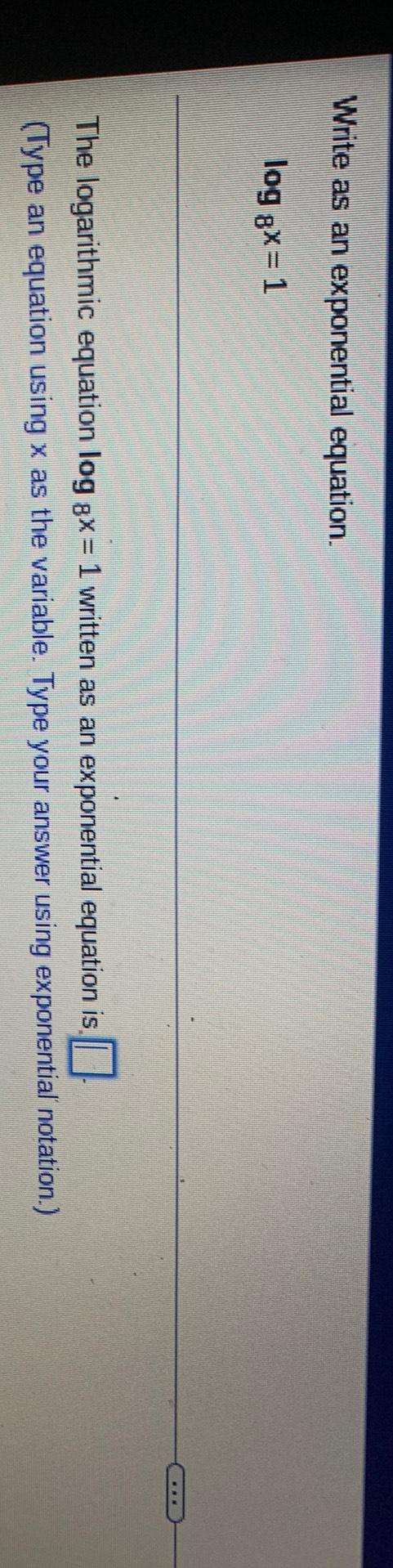
LogarithmsWrite as an exponential equation.
log 8x = 1
The logarithmic equation log gx = 1 written as an exponential equation is
Math - Others
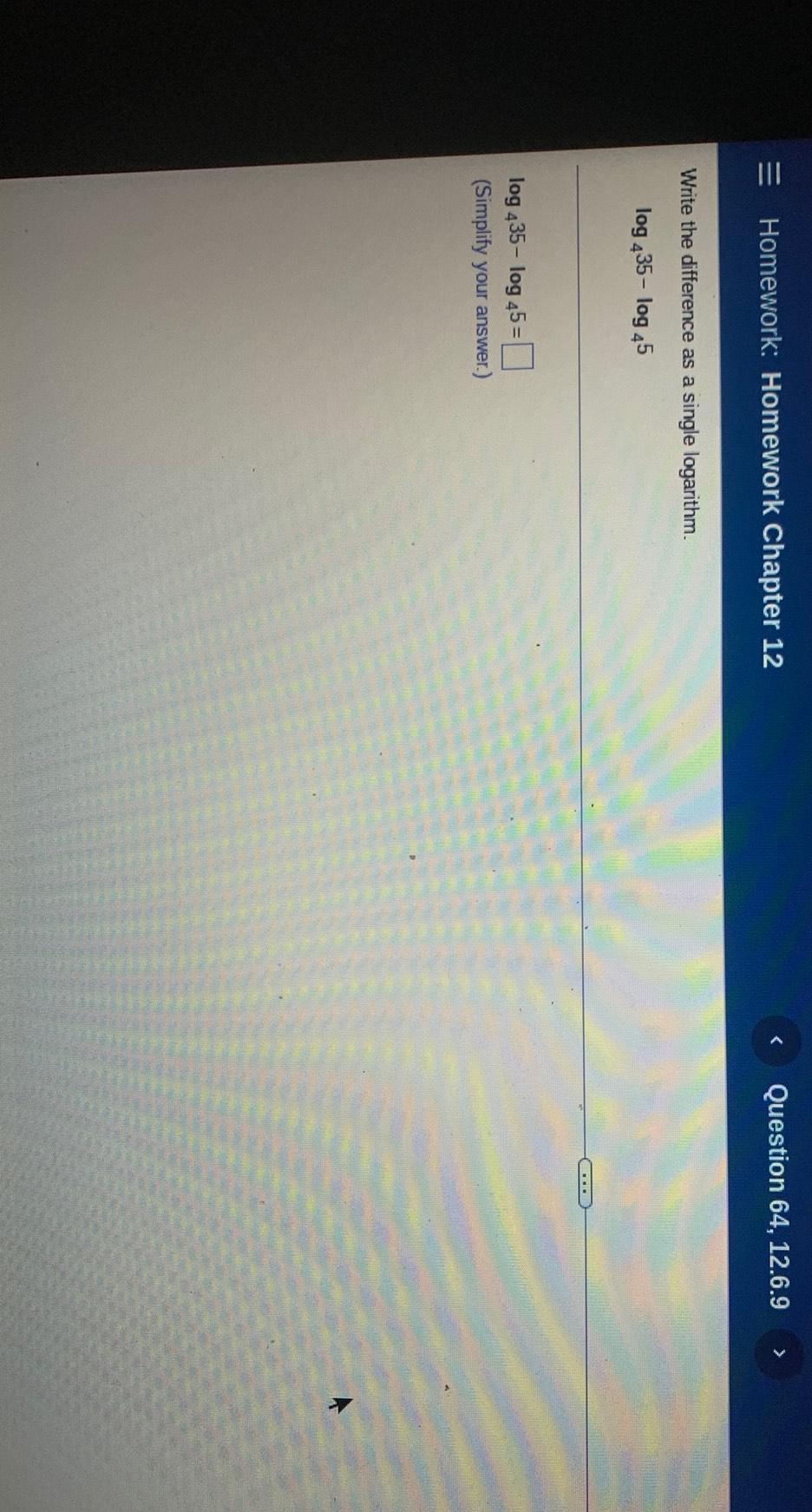
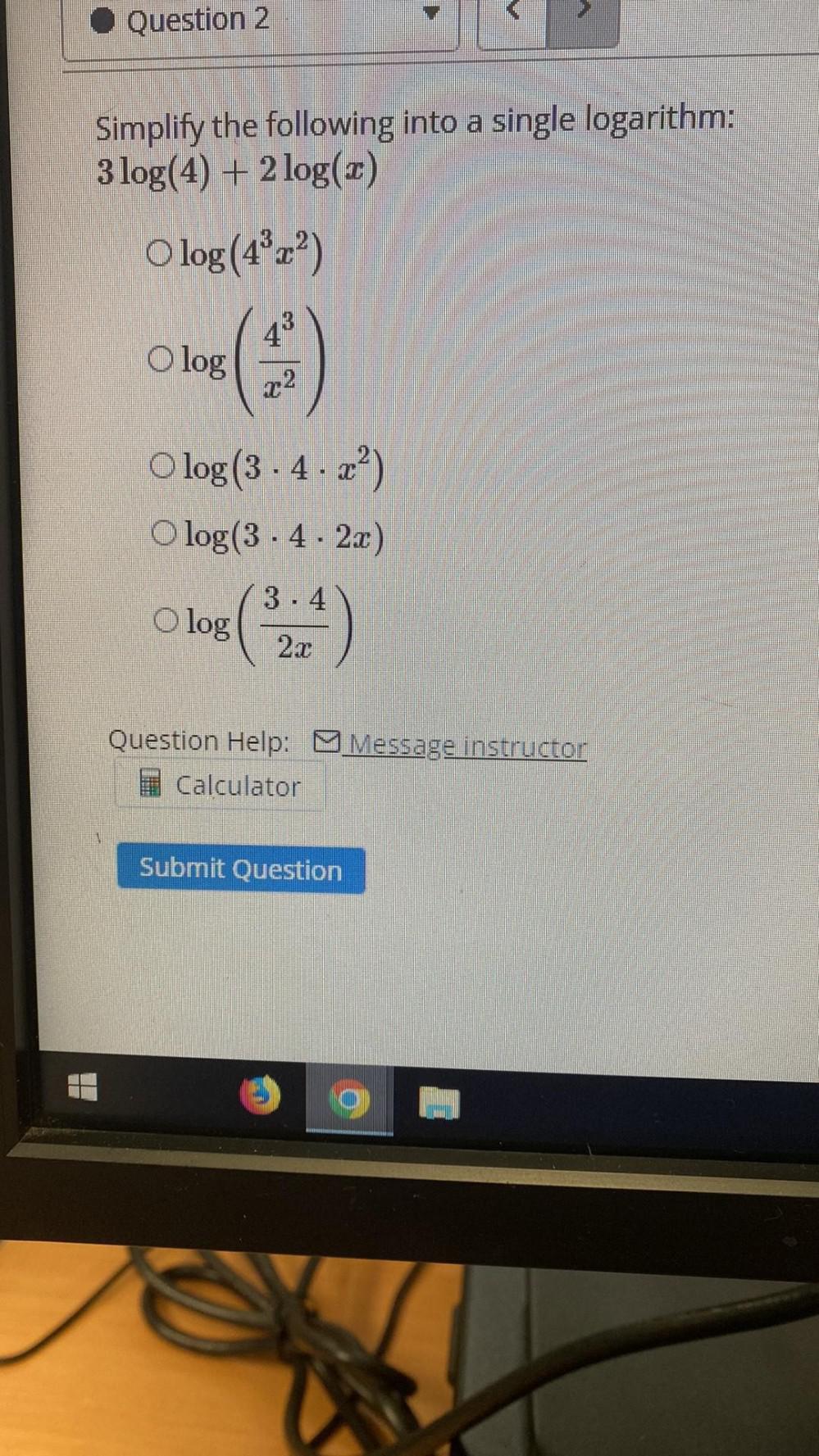
LogarithmsSimplify the following into a single logarithm: 3 log(4) + 2 log(x)
log (4³x²)
log(4³/x²)
log (3.4.x²)
log (3.4.2x)
log (3.4/2x)
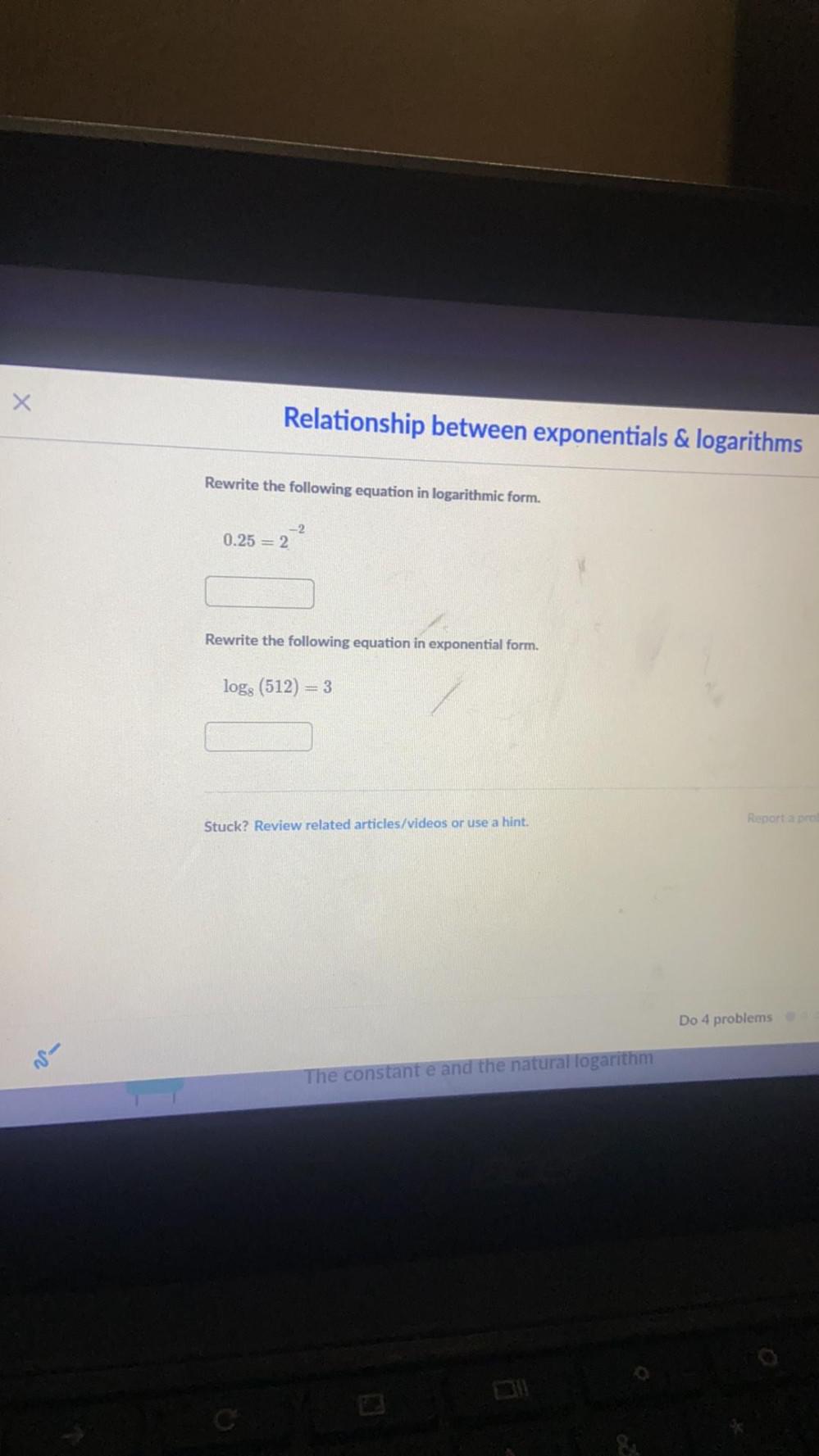
Math - Others
LogarithmsRewrite the following equation in logarithmic form.
0.25 = 2-²
Rewrite the following equation in exponential form.
log₈ (512) = 3
![What is the effect in the time required to solve a problem when you double the size of the input from n to 2n, assuming that the number of milliseconds the algorithm uses to solve the problem with input size n is each of these function? [Express your answer in the simplest form possible, either as a ratio or a difference. Your answer may be a function of n or a constant.]
a) log log n
b) log n
c) 100n
d) n log n
e) n²
f) n³
g) 2ⁿ](https://media.kunduz.com/media/sug-question/raw/78482082-1659646663.199819.jpeg?w=256)
Math - Others
LogarithmsWhat is the effect in the time required to solve a problem when you double the size of the input from n to 2n, assuming that the number of milliseconds the algorithm uses to solve the problem with input size n is each of these function? [Express your answer in the simplest form possible, either as a ratio or a difference. Your answer may be a function of n or a constant.]
a) log log n
b) log n
c) 100n
d) n log n
e) n²
f) n³
g) 2ⁿ
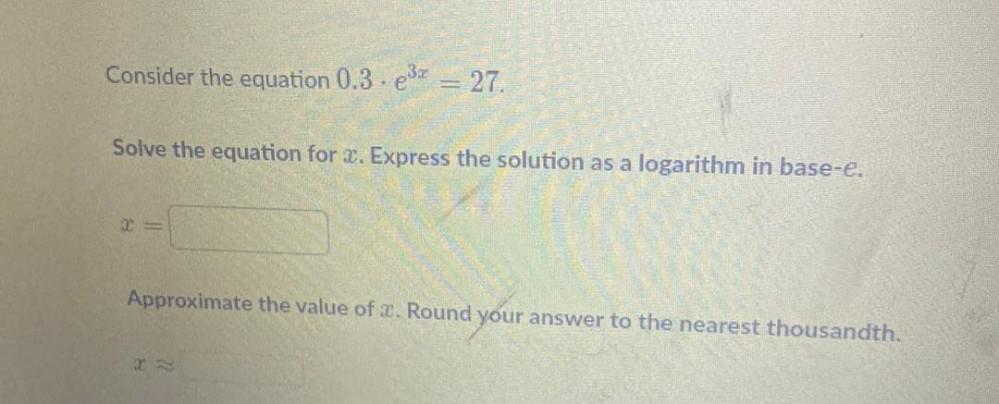
Math - Others
LogarithmsConsider the equation 0.3 . e³ˣ = 27.
Solve the equation for x. Express the solution as a logarithm in base-e.
x = __________
Approximate the value of x. Round your answer to the nearest thousandth.
x ≈ _____

Math - Others
LogarithmsEvaluate the logarithm.
Round your answer to the nearest thousandth.
2 log₃ (1/52) ≈ _______


Math - Others
LogarithmsAtmospheric pressure P in pounds per square inch is represented by the formula P=14.7e^-0.21x, where x is the number of miles above sea level. To the nearest foot, how high is the peak of a mountain with an atmospheric pressure of 8.131 pounds per square inch? (Hint: there are 5,280 feet in a mile)
The mountain is Number ___ feet high.

Math - Others
Logarithms0.6 0.4 0.3
p= 0.2 0.3 0.3
0.2 0.3 0.4
The weather in Columbus is either good, indifferent, or bad on any given day. If the weather is good today, there is a 60% chance it will be good tomorrow, a 20% chance it will be indifferent, and a 20% chance it will be P = bad. If the weather is indifferent today, there is a 40% chance it will be good tomorrow, and a 30% chance it will be indifferent. Finally, if the weather is bad today, there is a 30% chance it will be good tomorrow and a 30% chance it will be indifferent. The stochastic matrix for this situation is shown to the right. In the long run, how likely is it for the weather in Columbus to be indifferent on a given day?
In the long run, how likely is it for the weather in Columbus to be indifferent on a given day?
_______________% (Round to the nearest integer as needed.)
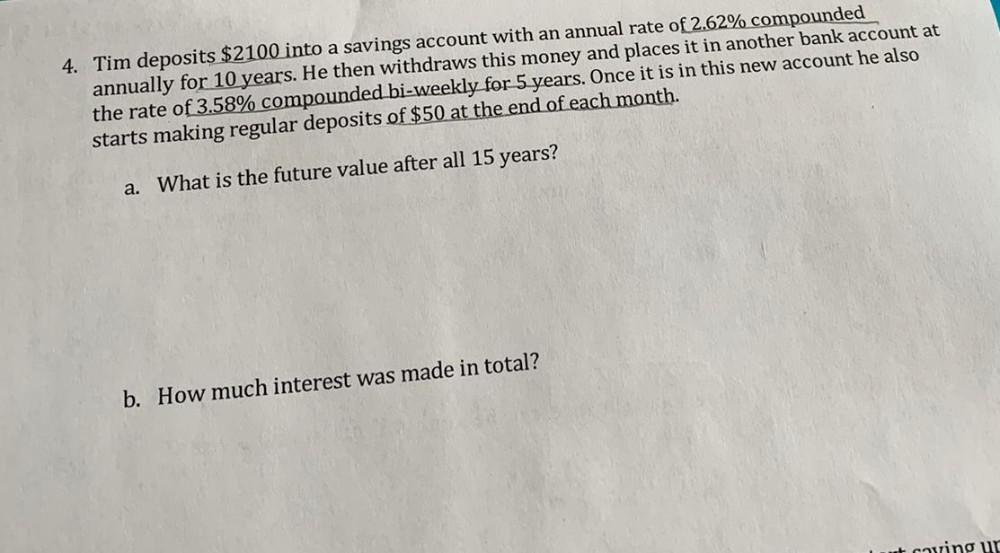
Math - Others
LogarithmsTim deposits $2100 into a savings account with an annual rate of 2.62% compounded annually for 10 years. He then withdraws this money and places it in another bank account at the rate of 3.58% compounded bi-weekly for 5 years. Once it is in this new account he also starts making regular deposits of $50 at the end of each month.
a. What is the future value after all 15 years?
b. How much interest was made in total?

Math - Others
Logarithms2. Consider a five-node element in one dimension. The element
length is 4, with node 1 at x₁ = 2, X₂=3, x3 = 4, x4 = 5, x5 = 6.
2-1) Construct the shape functions for the element.
2-2) The temperatures at the nodes are given by
3
Te = 1
0
-1
2
.find the temperature field at x-3.5 using shape functions
constructed in (2-1).
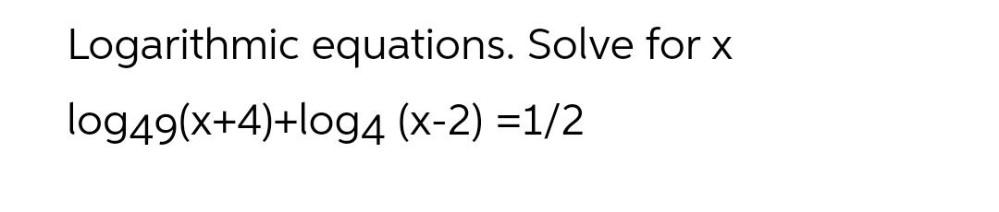
Math - Others
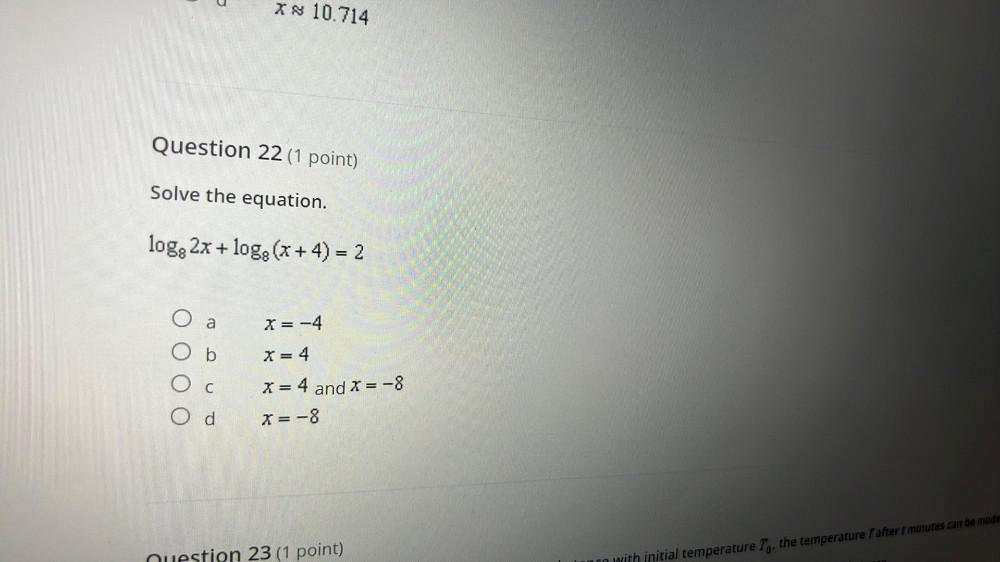
LogarithmsSolve the equation.
log₈2x + log₈(x + 4) = 2
x = -4
x = 4
x = 4 and x = -8
x = -8
Math - Others
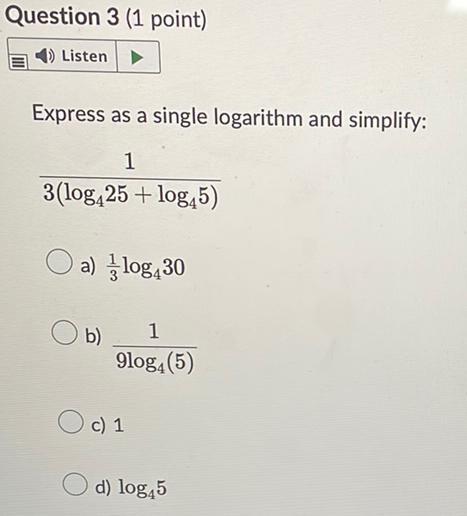
LogarithmsExpress as a single logarithm and simplify:
1/3(log₄25+ log₄5)
a)(1/3) log₄30
b)1/9log₄(5)
c) 1
d) log₄5
Math - Others
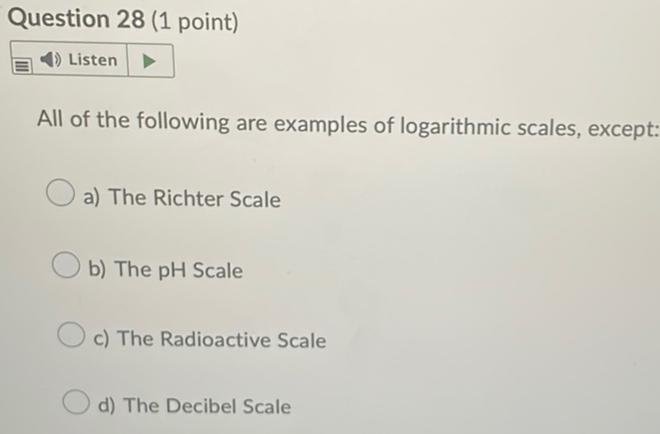
LogarithmsAll of the following are examples of logarithmic scales, except:
a) The Richter Scale
b) The pH Scale
c) The Radioactive Scale
d) The Decibel Scale

Math - Others
LogarithmsRewrite the equation log₈₀ 100 = z in exponential form.
a) 100 = 80 ᶻ
b) z =80¹⁰⁰
c) z⁸⁰= 100
d) 80 = 100ᶻ

Math - Others
LogarithmsTo three decimal places, the slope of the tangent to the curve f(x) = log₁₀x, at x=1 is:
a) 0.868
b) 0.251
c) 1.000
d) 0.434

Math - Others
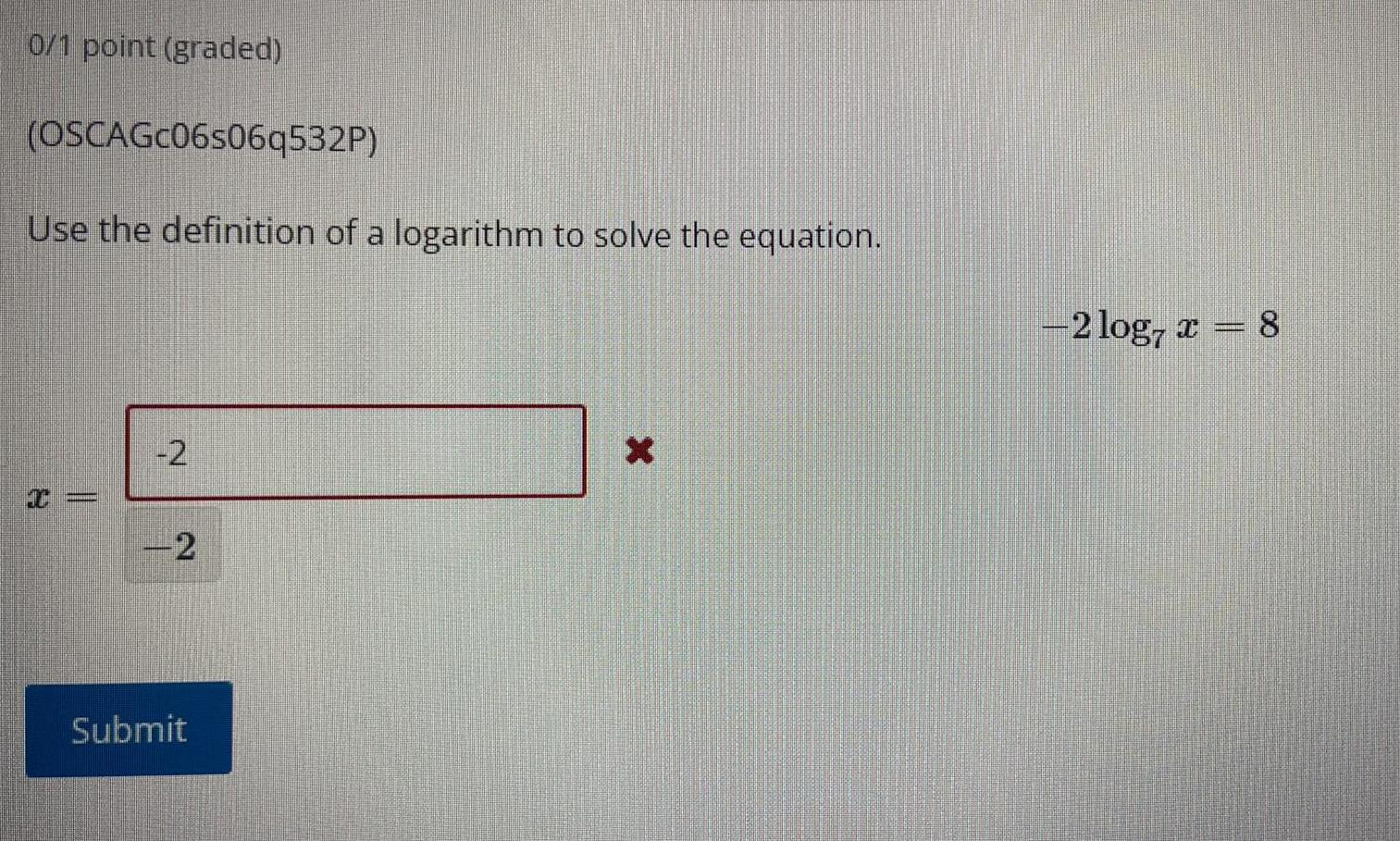
LogarithmsUse the one-to-one property of logarithms to solve the equation.
log5(2n² - 10n) = log5 (-24+n²)

Math - Others
LogarithmsGraph each logarithmic function. Find the domain
and range.
24. y = log5 (x - 1)
25. y = 4 log x+5

Math - Others
LogarithmsA quotient function. The two functions that you must divide are...
Logarithmic Functions: y= 25 log9 (x+11)
Exponential Function: y=60^x
State the Domain, Range and vertical or horizontal Asymptotes. Justify your answer with reference to your equation and graph. Provide a sketch of your function.
Math - Others
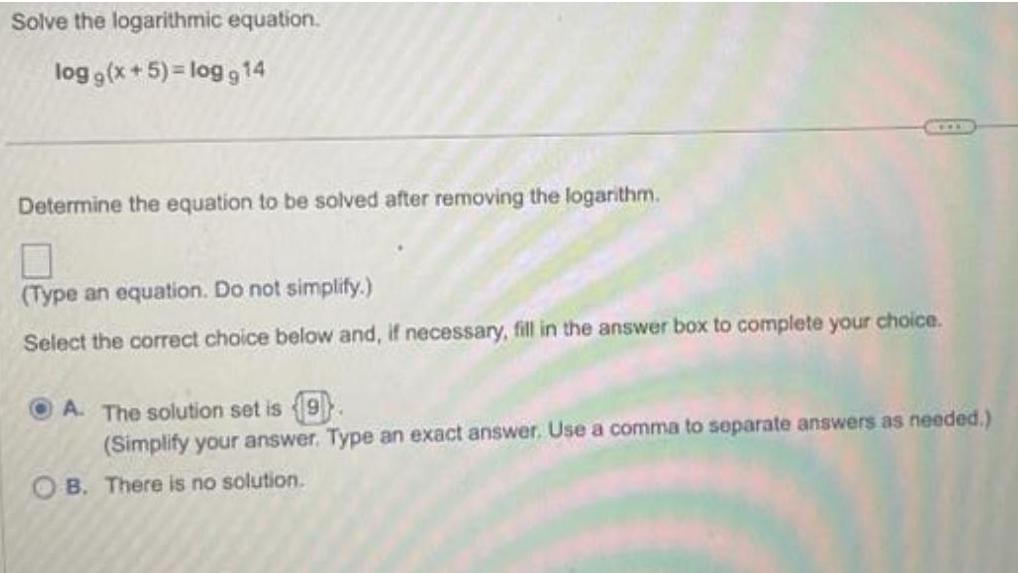
LogarithmsSolve the logarithmic equation.
log 9(x+5)= log914
Determine the equation to be solved after removing the logarithm.
(Type an equation. Do not simplify.)
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is
(Simplify your answer. Type an exact answer. Use a comma to separate answers as needed.)
B. There is no solution.

Math - Others
LogarithmsExercise 2.6. Determine the fractional Taylor expansions for the following cases:
(a) f(x)= x³, a = 0, and n = 2.8,
(b) f(x) = sinx, a = 0, and n = 1.2.
![Condense the expression to the logarithm of a single quantity.
1/2[9 In(x + 7) + In(x) - In(x⁹ – 5)]](https://media.kunduz.com/media/sug-question/raw/84622433-1658606934.9299908.jpeg?w=256)
Math - Others
LogarithmsCondense the expression to the logarithm of a single quantity.
1/2[9 In(x + 7) + In(x) - In(x⁹ – 5)]
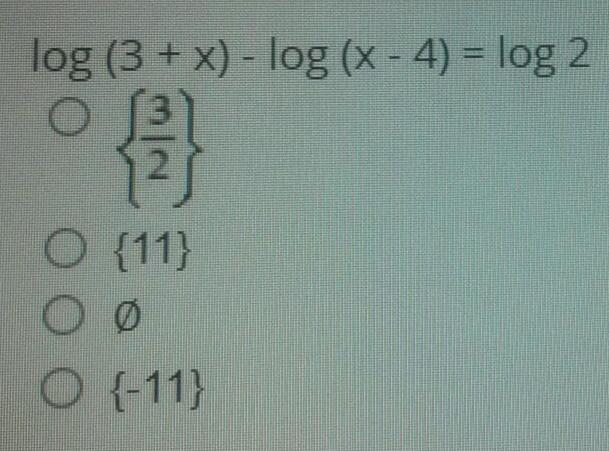
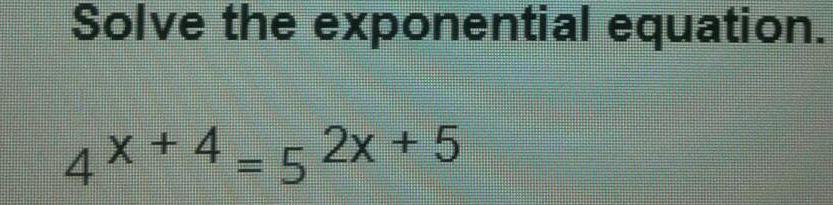

Math - Others
LogarithmsWrite in logarithmic form.
1/9=3^-2
The logarithmic form is.
(Use integers or fractions for any numbers in the expression.)


Math - Others
LogarithmsFind the solution of the exponential equation 5e^x-4=12
The exact solution (using natural logarithms) is: x =
The approximate solution, rounded to 4 decimal places is: x =
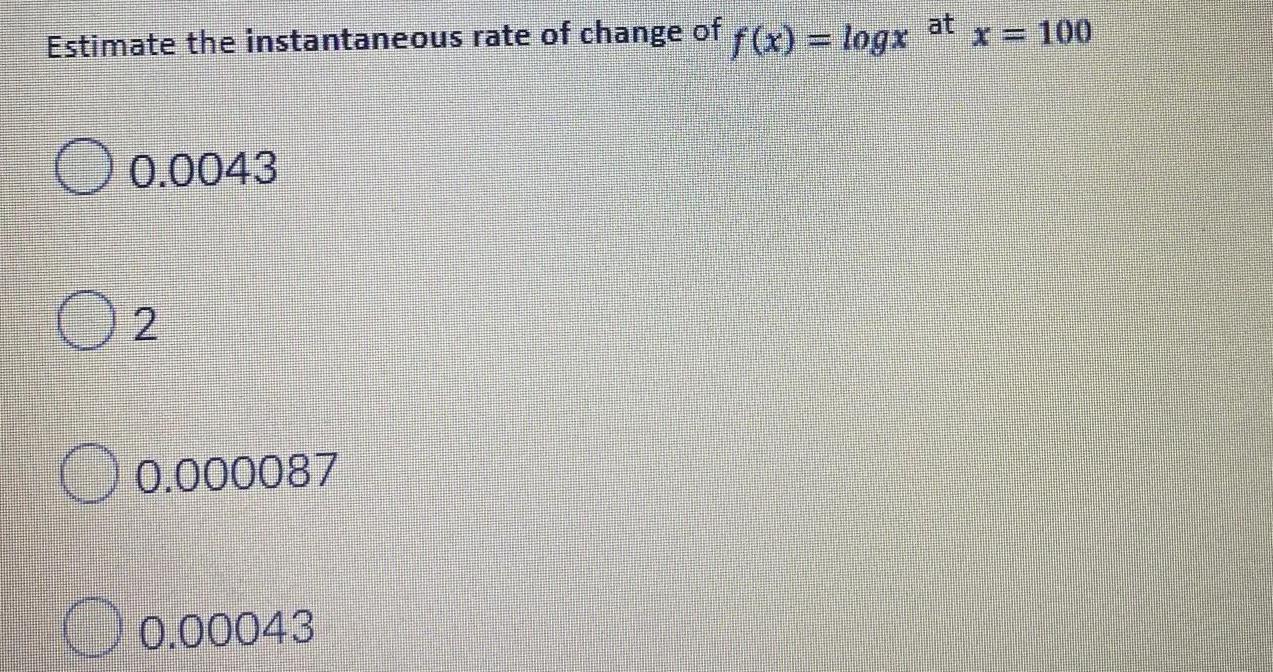
Math - Others
LogarithmsEstimate the instantaneous rate of change of f(x) = logx at x=100
0.0043
2
0.000087
0.00043

Math - Others
LogarithmsWrite the equation in equivalent logarithmic form.
6=36^1/2
What is the equivalent logarithmic form?

Math - Others
LogarithmsUse the exponential decay model, A = Ao e^kt, to solve the following.
The half-life of a certain substance is 19 years. How long will it take for a sample of this substance to decay to 88% of its original amount?
It will take approximately___for the sample of the substance to decay to 88% of its original amount.
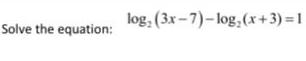

Math - Others
LogarithmsSolve log 4x + log 13 = 0. Round to the nearest thousandth if necessary.
3.25
0.019
0.311
52
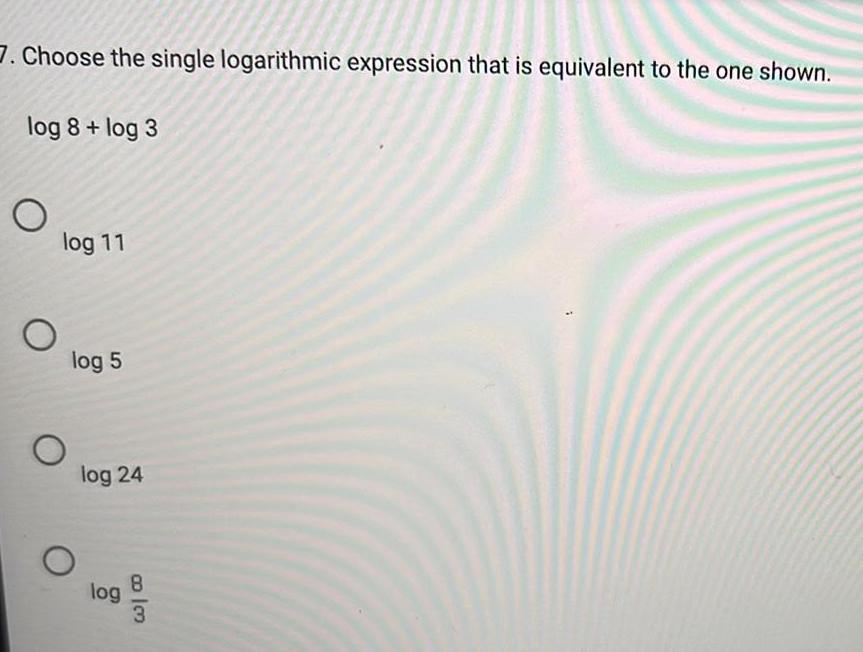
Math - Others
LogarithmsChoose the single logarithmic expression that is equivalent to the one shown.
log 8+ log 3
log 11
log 5
log 24
log 8/3

Math - Others
LogarithmsHow is the graph of log x + 6 translated from the graph of log x?
shifted left 6 units
shifted up 6 units
shifted down 6 units
shifted right 6 units
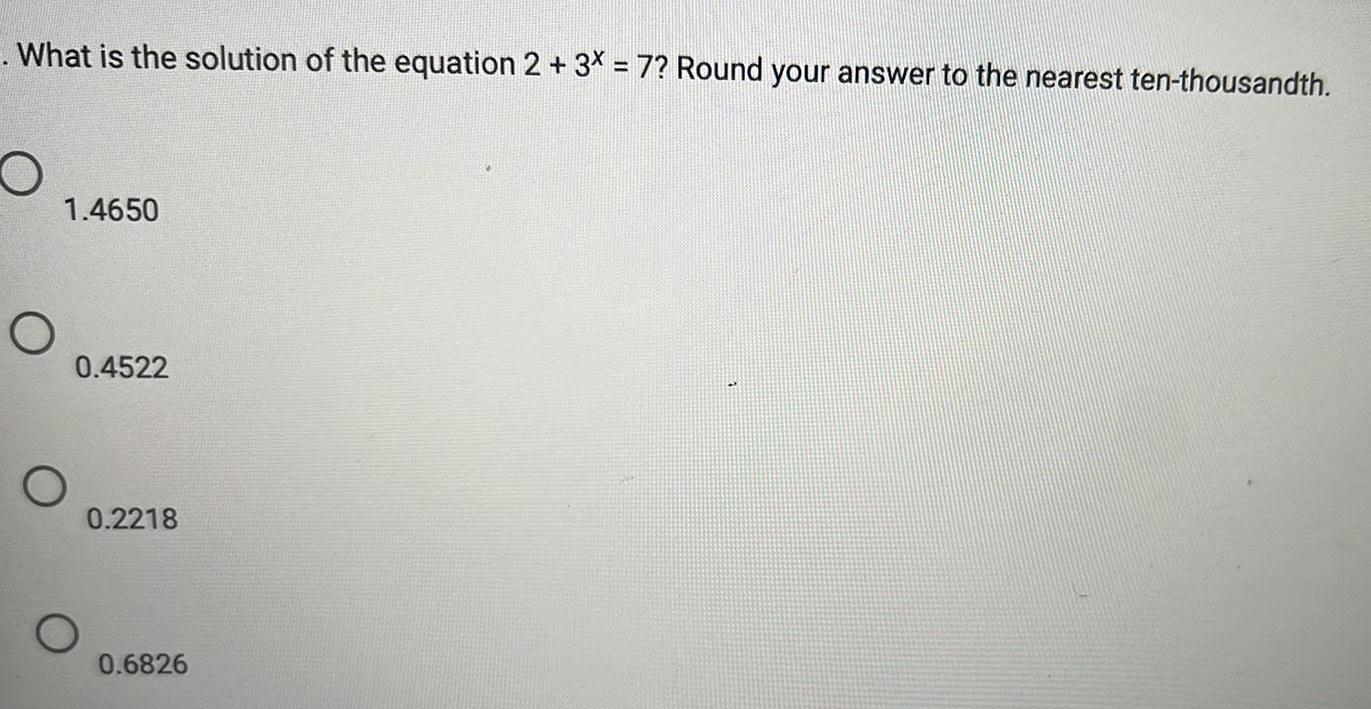
Math - Others
LogarithmsWhat is the solution of the equation 2 + 3x = 7? Round your answer to the nearest ten-thousandth.
1.4650
0.4522
0.2218
0.6826

Math - Others
LogarithmsExpand the logarithm.
log 5x/4y
log 5 + log x - log 4 - log y
log 5 + log x - log 4 + log y
log5/4 + log x - log y
log 5x - log 4y

Math - Others
Logarithms3. Complete the following table by converting from exponential form to logarithmic form or from logarithmic form to exponential form.
Exponential Form Logarithmic Form
(1/3)^-4
log25 5 =1/2
2^m =n
logb 4 =a

Math - Others
Logarithms7. Solve the exponential equations. Round to 4 decimal places when necessary.
a)81^2x=27^2x-5
b) 4000 = 200e^8x
c) 5^x = 35
Math - Others
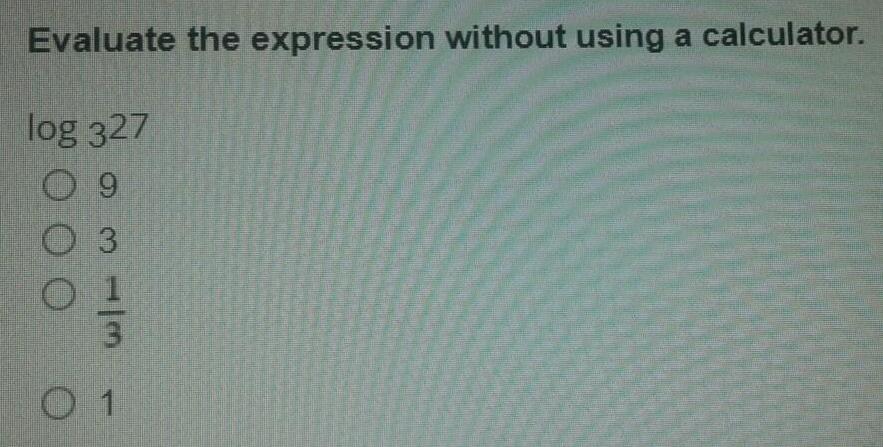
LogarithmsWhich is the logarithmic form of 64 = 1296?
log6 1296 = 4
log 1296 = 4.6
log 1296 = 4
log4 1296 = 6

Math - Others
LogarithmsSolve log 3x - log 13 = 2. Round to the nearest thousandth if necessary.
29
433.333
6.527
10.914

Math - Others
LogarithmsHow is the graph of log x - 4 translated from the graph of log x?
shifted down 4 units
shifted left 4 units
shifted right 4 units
shifted up 4 units