Trigonometry Questions and Answers
![Find sin θ and tan θ if cos θ = 7/25, assuming that 0≤θ < π /2.
sinθ = []
tanθ=[]](https://media.kunduz.com/media/sug-question/raw/79074443-1659644643.6276298.jpeg?w=256)
Math - Others
TrigonometryFind sin θ and tan θ if cos θ = 7/25, assuming that 0≤θ < π /2.
sinθ = []
tanθ=[]
Math - Others
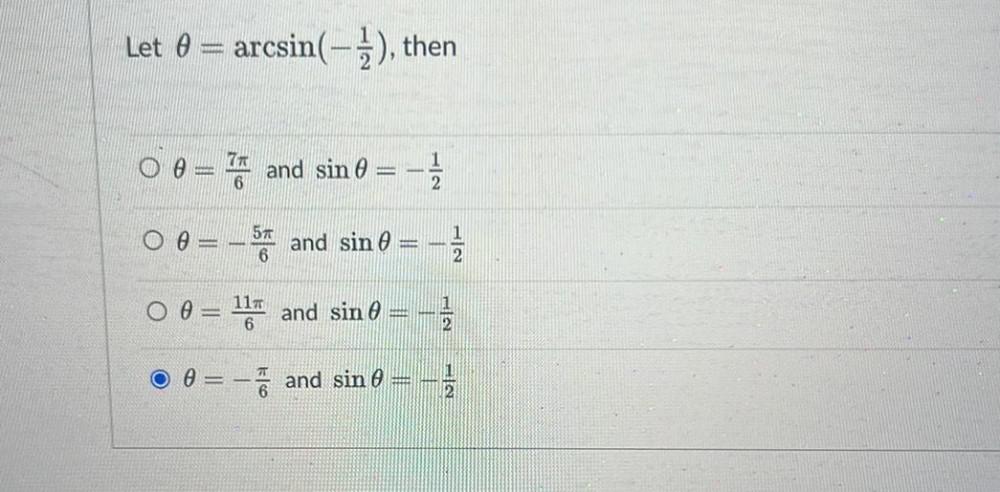
TrigonometryLet θ= arcsin(-1/2), then
θ=7π/6 and sinθ = -1/2
θ=-5π/6 and sinθ = -1/2
θ= 11π/6 and sinθ = =1/2
θ = -π/6 and sinθ = -1/2

Math - Others
TrigonometryLet θ = arccos (-1/2), then
θ = -4π/3 and cosθ = -1/2
θ = 2π/3 and cosθ = -1/2
θ = 4π/3 and cosθ = -(1/2)
θ = -(2π/3) and cosθ = -1/2
![Find the vertical translation of y = 5+2sin[6x + π/6]
A) Up 5
B) Down 5
C) Up 1/6
D) Down π/6](https://media.kunduz.com/media/sug-question/raw/79296603-1659644009.4023545.jpeg?w=256)
Math - Others
TrigonometryFind the vertical translation of y = 5+2sin[6x + π/6]
A) Up 5
B) Down 5
C) Up 1/6
D) Down π/6

Math - Others
TrigonometryVerify the following identity.
sin ²x + cos2x = 1 - sin ² x
To transform the left side into the right side, should be changed to and the left side simplified.
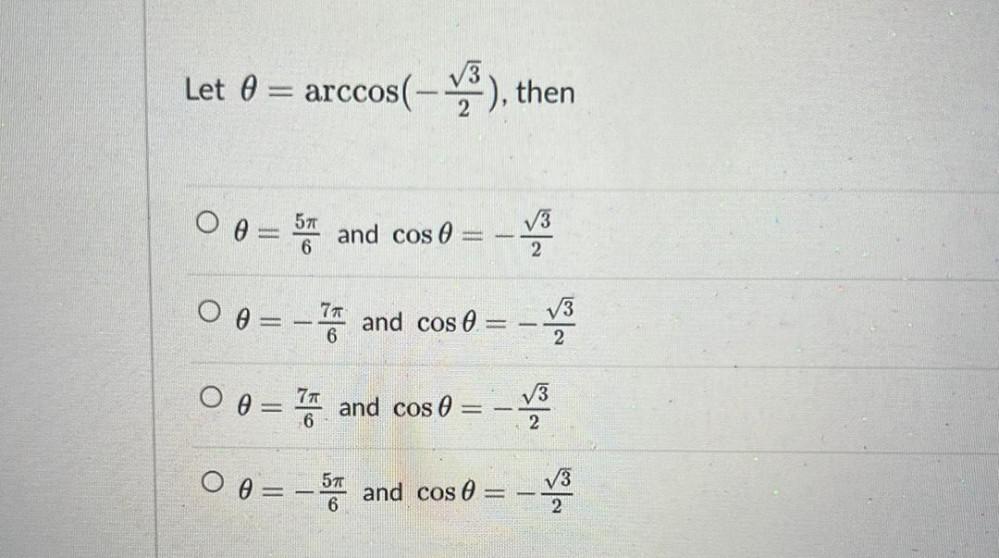
Math - Others
TrigonometryLet θ = arccos(-√3/2), then
A) θ = 5π/6 and cos θ = -(√3/2)
B) θ = -(7π/6) and cos θ = -(√3/2)
C) θ = 7π/6 and cos θ = -(√3/2)
D) θ = -5π/6 and cos θ = -(√3/2)

Math - Others
TrigonometryLet θ = arctan(-√3/3), then
A) θ = 5π/6 and tan θ = -√3/3
B) θ = 11π/6 and tanθ = -√3/3
C) θ = -π/6 and tan θ = -√3/3
D) θ = -7π/6 and tanθ = -√3/3

Math - Others
TrigonometryLet θ = arcsin (3^-2)/2, then
a)θ=π/3 and sinθ=(3^-2)/2
b)θ=-5π/3 and sinθ=(3^-2)/2
c)θ=2π/3 and sinθ=(3^-2)/2
d0θ=-4π/3 and sinθ=(3^-2)/2
Math - Others
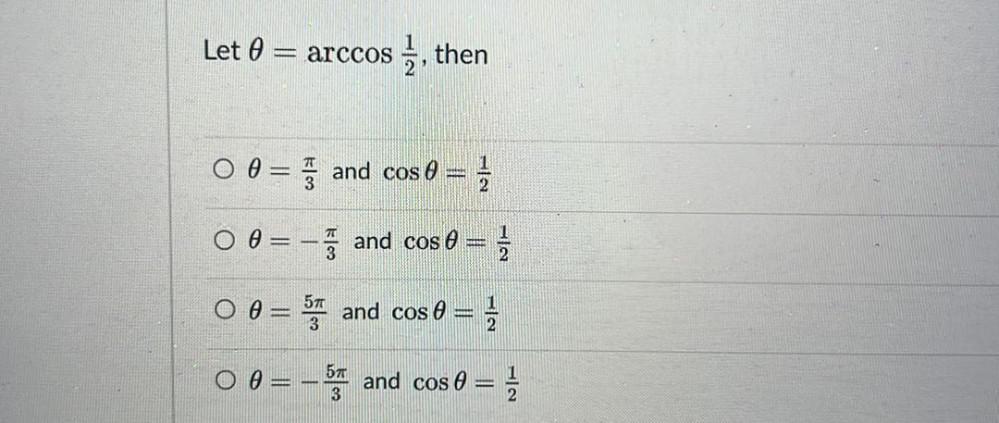
TrigonometryLet θ = arccos(1/2), then
A) θ = π/3 and cos θ =1/2
B) θ = -(π/3) and cos θ = 1/2
C) θ = 5π/3 and cos θ = 1/2
D) θ = -5π/3 and cos θ = 1/2

Math - Others
TrigonometryLet θ = arctan(√3), then
A) θ = π/3 and tan θ = √3
B) θ = 4π/3 and tan θ = √3
C) θ = -(2π/3) and tan θ = √3
D) θ = -(5π/3) and tan θ = √3

Math - Others
TrigonometryLet θ = arctan(-1), then
A) θ = 3π/4 and tanθ =-1
B) θ = -(π/4) and tanθ =-1
C) θ = -(5π/4) and tanθ =-1
D) θ = 7π/4 and tanθ =-1

Math - Others
TrigonometryIF θ = arctan x, then
(a) tanθ = x and -π/2 < θ < π/2
(b)tanθ = x and 0 < θ ≤ 2 π
(c)tanθ = x and -π/2 ≤ θ < π/2
(d)) tanθ = x and θ ≠ (2k+1) π/2,k:integer

Math - Others
TrigonometryIF θ = arctan 12/5,then
tanθ =12/5 and π <θ < 3π/2
tanθ =12/5 and 0 <θ < π/2
tanθ = 12/5 and -2π < θ < − 3π/2
tanθ= 12/5 and -π< θ < -π/2

Math - Others
TrigonometryIF = arccos x,-1 ≤ x ≤ 1, then
(a)cos θ = x and ≤ θ ≤ π/2
(b)cos θ = x and θ ∈ (-∞, ∞)
(c)cos θ = x and 0≤ θ ≤ 2π
(d)cos θ =x and 0 ≤ θ ≤ π

Math - Others
TrigonometryLet x E Z. Prove that for all nEN,
(x + 5) (3") = x(3") + 5 (mod 15).
Cite any theorems or propositions you use.

Math - Others
TrigonometryIF θ = arctan(-4/3), then
a. tan θ = -4/3 and -π < θ < -π/2
b. tan θ = -4/3 and 3π/2 < θ < 2π
c. tan θ = -4/3 and -π/2 < θ < 0
d. tan θ = -4/3 and π/2 < θ < π

Math - Others
TrigonometryFind the vertical translation of y=5+2 sin(6x + π/6)
A) Up 5
B) Down 5
C) Up 1/6
D) Down π/6

Math - Others
TrigonometryIF θ = arcsin 4/5, then
(a)sinθ=4/5 and -3π/2 < θ < -π
(b)sinθ=4/5 and 0 < θ < π/2
(c)sinθ=4/5 and -2π< θ < -3π/2
(d)sinθ=4/5 and π/2 < θ < π
![IF θ= arcsin x, -1 ≤ x ≤ 1, then
(a)sin θ= x and x ∈[0, 2π]
(b)sin θ = x and x ∈ (-∞, ∞)
(c)sin θ = x and -π/2 ≤ θ ≤ π/2
(d)sin θ = x and -π/2 < θ < π/2](https://media.kunduz.com/media/sug-question/raw/79237002-1659642971.1331813.jpeg?w=256)
Math - Others
TrigonometryIF θ= arcsin x, -1 ≤ x ≤ 1, then
(a)sin θ= x and x ∈[0, 2π]
(b)sin θ = x and x ∈ (-∞, ∞)
(c)sin θ = x and -π/2 ≤ θ ≤ π/2
(d)sin θ = x and -π/2 < θ < π/2
Math - Others
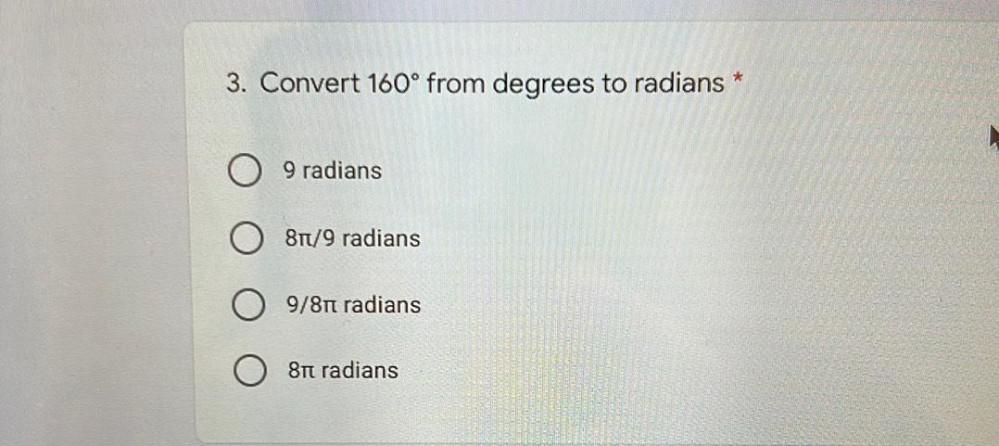
TrigonometryConvert 160° from degrees to radians
9 radians
8π/9 radians
9/8π radians
8π radians

Math - Others
TrigonometryA Ferris wheel has a radius of 42.4 feet. The bottom of the Ferris wheel sits 0.6 feet above the ground. You board the Ferris wheel at the 6 o'clock position and rotate counter-clockwise,
a). Write a function f that determines your height above the ground (in feet) in terms of the number of radians you have swept out from the 6 o'clock position, a.
f(a)=
b. Write a function g, that determines your height above the ground (in feet) in terms of the number of feet you have traveled since you started rotating.
g(s) =
![Use a Double- or Half-Angle Formula to solve the equation in the interval [0, 2π). (Enter your answers as a comma-separated list.)
tan(θ/2) -sin(θ)=0 .
θ=[?]](https://media.kunduz.com/media/sug-question/raw/79532035-1659642164.5717316.jpeg?w=256)
Math - Others
TrigonometryUse a Double- or Half-Angle Formula to solve the equation in the interval [0, 2π). (Enter your answers as a comma-separated list.)
tan(θ/2) -sin(θ)=0 .
θ=[?]

Math - Others
TrigonometryFind the angle of least positive measure(in degrees, not equal to the given measure) that is coterminal with A.
A=517°
The measure is ______ °

Math - Others
TrigonometryFind the measure (in degrees, not equal to the given measure) of the least positive angle that is coterminal with A.
A= 27 °
The measure of the least positive coterminal angle is ____ °.
(Simplify your answer.)

Math - Others
TrigonometryA tire is rotating 360 times per min. Through how many degrees does a point on the edge of the tire move in 1/2 sec.
The point on the edge of the tire rotates ____ in 1/2 sec.
(Type an integer or a simplified fraction.)
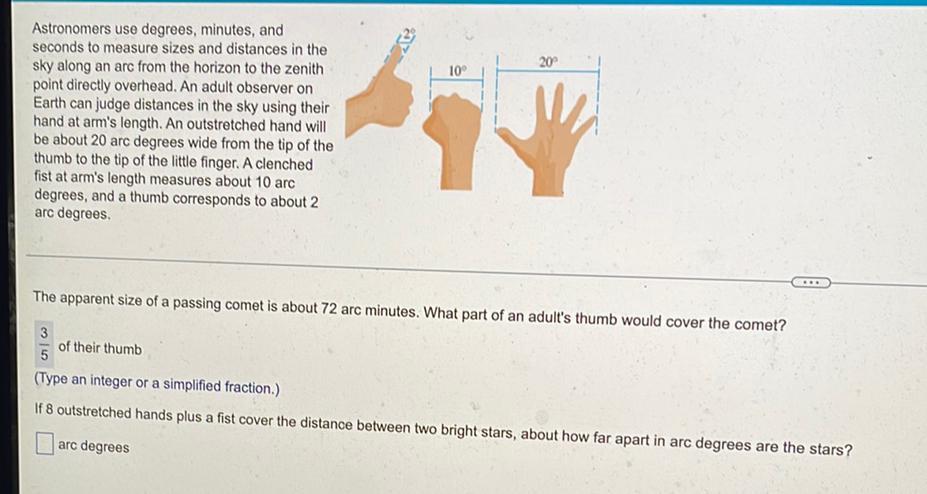
Math - Others
TrigonometryAstronomers use degrees, minutes, and seconds to measure sizes and distances in the sky along an arc from the horizon to the zenith point directly overhead. An adult observer on Earth can judge distances in the sky using their hand at arm's length. An outstretched hand will be about 20 arc degrees wide from the tip of the thumb to the tip of the little finger. A clenched fist at arm's length measures about 10 arc degrees, and a thumb corresponds to about 2 arc degrees.
The apparent size of a passing comet is about 72 arc minutes. What part of an adult's thumb would cover the comet?
_______ of their thumb
(Type an integer or a simplified fraction.)
If 8 outstretched hands plus a fist cover the distance between two bright stars, about how far apart in arc degrees are the stars?
_______ arc degrees
![Use the trigonometric function values of quadrantal angles to evaluate the expression below.
[cos (-90°)]²+ [sin (-90°)]²
[cos (-90°)]²+ [sin (-90°)]²=_____________](https://media.kunduz.com/media/sug-question/raw/80089492-1659639613.1230319.jpeg?w=256)
Math - Others
TrigonometryUse the trigonometric function values of quadrantal angles to evaluate the expression below.
[cos (-90°)]²+ [sin (-90°)]²
[cos (-90°)]²+ [sin (-90°)]²=_____________

Math - Others
TrigonometryDetermine the domain and range of the function:
y = 4 cos 3(x + 1) - 3
Domain:_______________________
Range:______________________

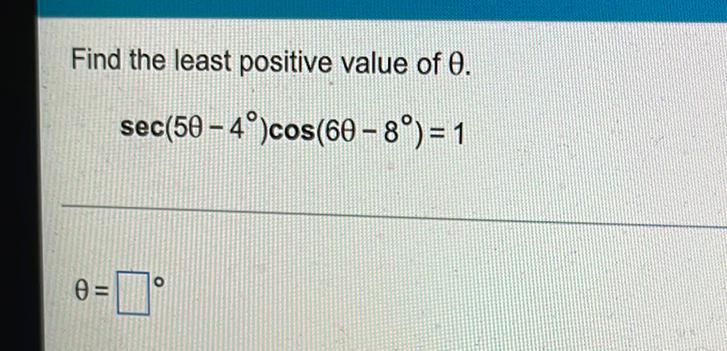
Math - Others
TrigonometryFind the least positive value of θ.
sec(5θ - 4°)cos(6θ – 8°) = 1
θ=______________________⁰
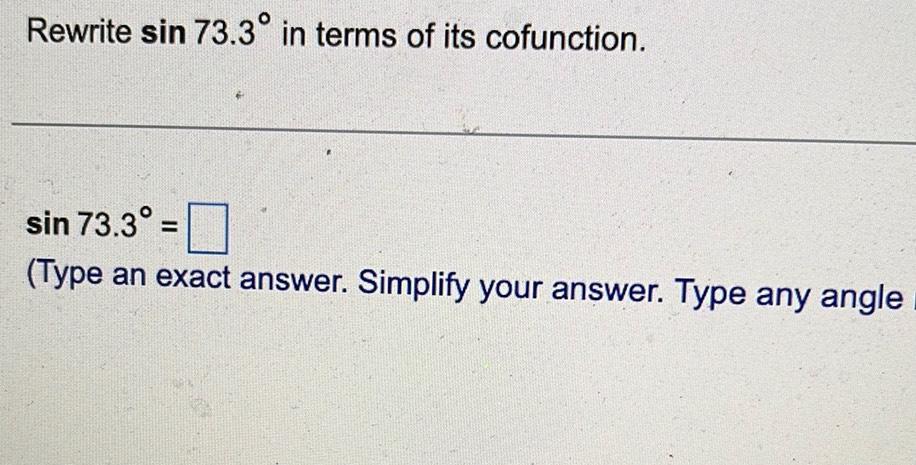
Math - Others
TrigonometryRewrite sin 73.3° in terms of its cofunction.
sin 73.3° =
(Type an exact answer. Simplify your answer. )
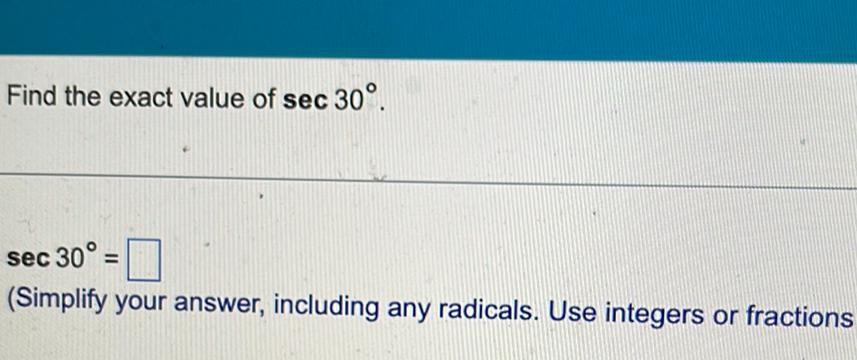
Math - Others
TrigonometryFind the exact value of sec 30°.
sec 30°=
(Simplify your answer, including any radicals. Use integers or fractions)
Math - Others
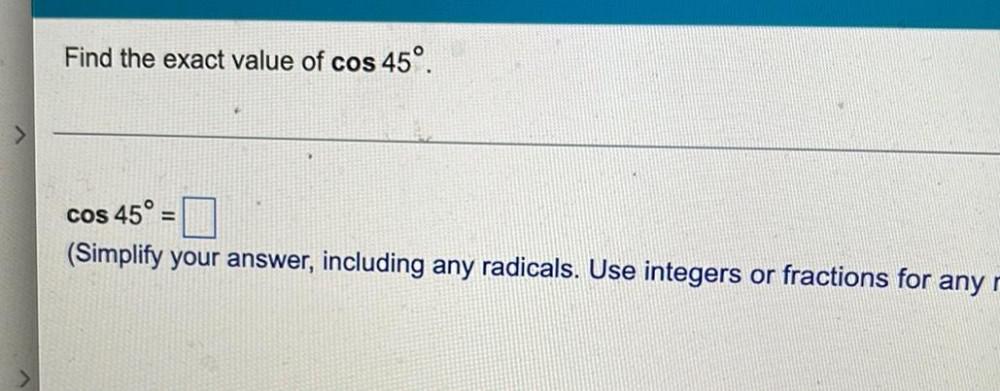
TrigonometryFind the exact value of cos 45°.
cos 45° =
(Simplify your answer, including any radicals. )

Math - Others
TrigonometryThe equation, with a restriction on x, is the terminal side of an angle θ in standard position. −2x+y=0, x≥0.
(I)Give the exact values of the six trigonometric functions of θ.
(II)Select the correct choice below and, if necessary, fill in the answer box to
complete your choice.
(A.) sin θ=
(Simplify your answer. Use integers or fractions for any numbers in the expression. Type an exact answer, using radicals as needed. Ratio
(B.) The function is undefined.
Math - Others
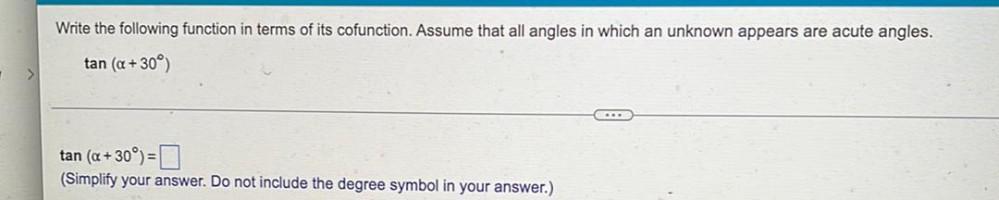
TrigonometryWrite the following function in terms of its cofunction. Assume that all angles in which an unknown appears are acute angles.
tan (α +30°)
tan (α+30°) =
(Simplify your answer. Do not include the degree symbol in your answer.)
Math - Others
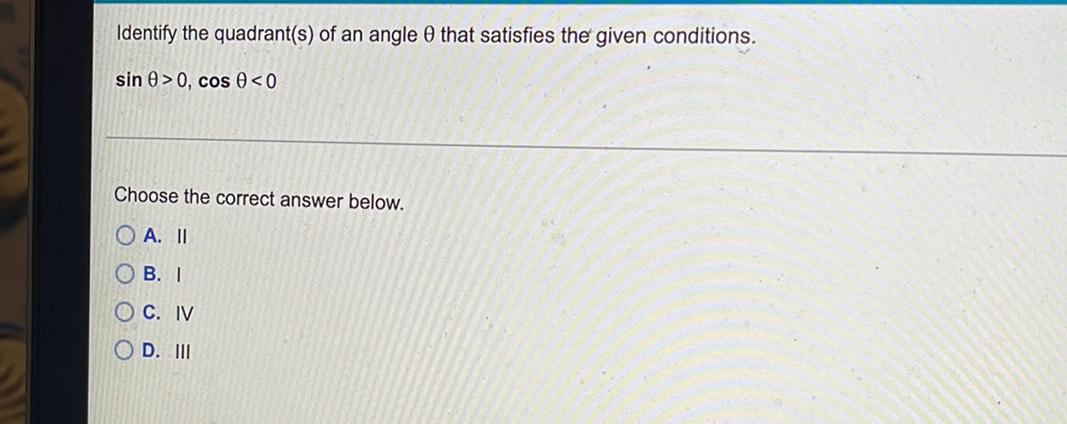
TrigonometryIdentify the quadrant(s) of an angle θ that satisfies the given conditions.
sin θ>0, cos θ<0
Choose the correct answer below.
A. II
B. I
C. IV
D. III

Math - Others
TrigonometryFind the indicated function value. If it is undefined say so.
cos 1800°
Select the correct choice below and fill in any answer boxes in your choice.
(A). cos 1800° =______
(B). The solution is undefined.
Math - Others
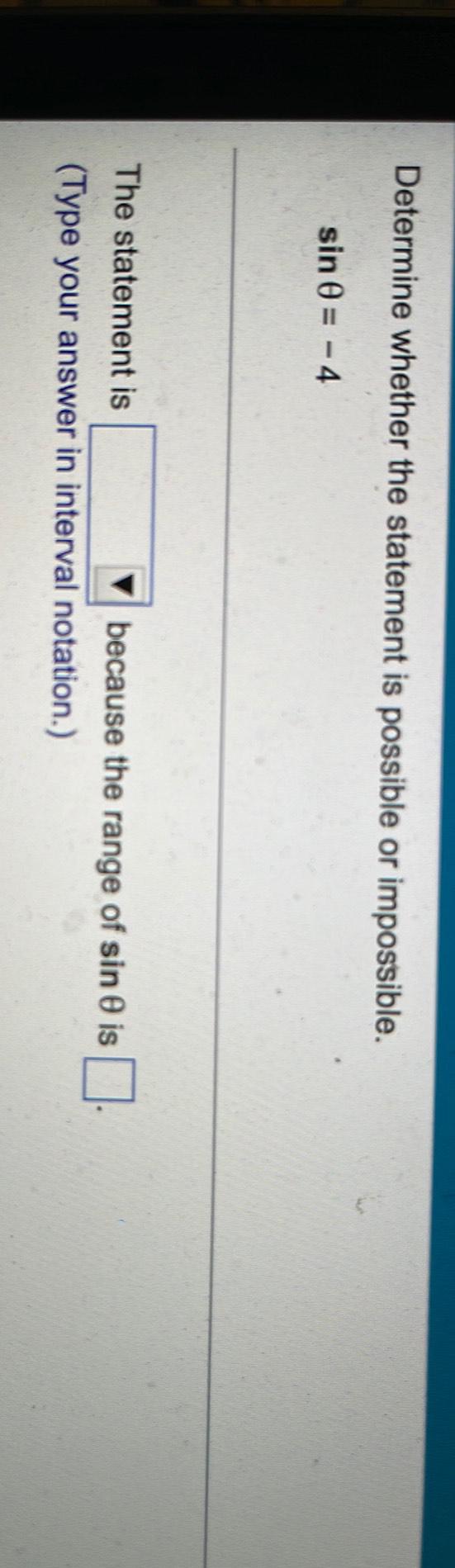
TrigonometryDetermine whether the statement is possible or impossible.
sin θ= -4
The statement is______ because the range of sine is._______
Math - Others
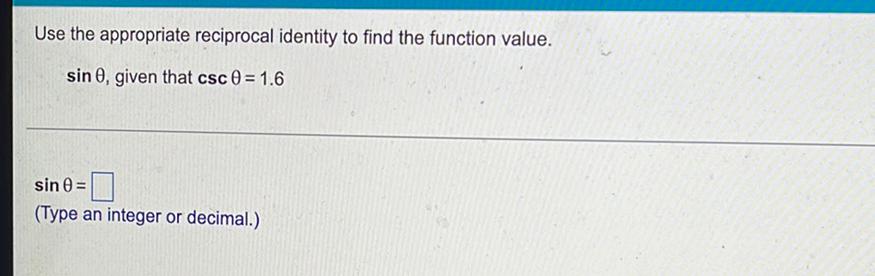
TrigonometryUse the appropriate reciprocal identity to find the function value.
sin θ, given that csc θ = 1.6
sin θ= ___
(Type an integer or decimal.)

Math - Others
TrigonometryFind the exact value of csc θ , given that cot θ =-1/4 and is in quadrant IV. Rationalize denominators when applicable.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A.) csc θ= ____(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)
B.) The function is undefined.
Math - Others
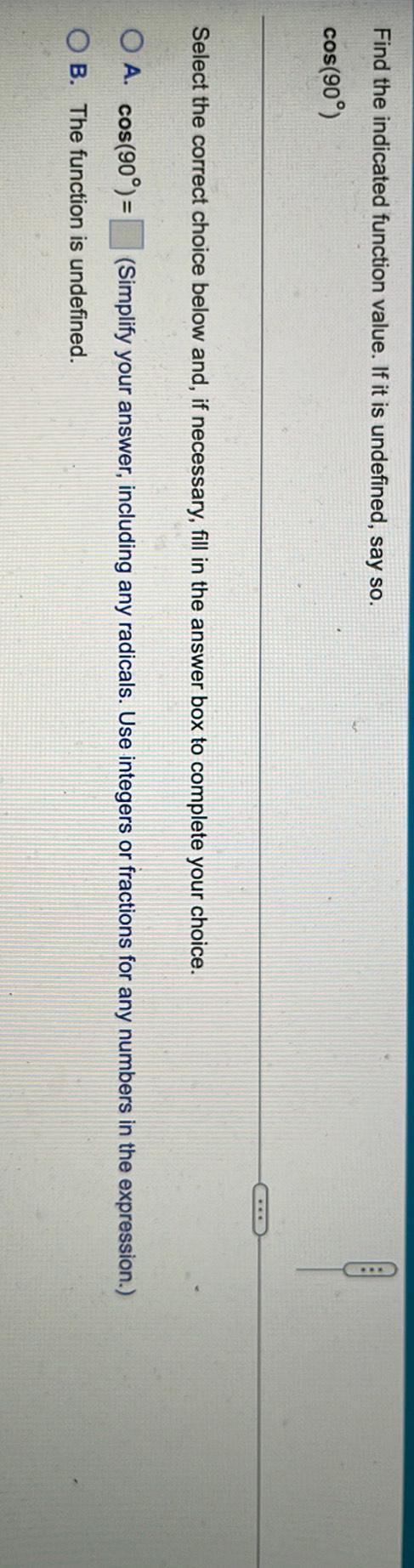
TrigonometryFind the indicated function value. If it is undefined, say so.
cos(90°)
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
(A). cos(90°) =
(B). The function is undefined.
Math - Others
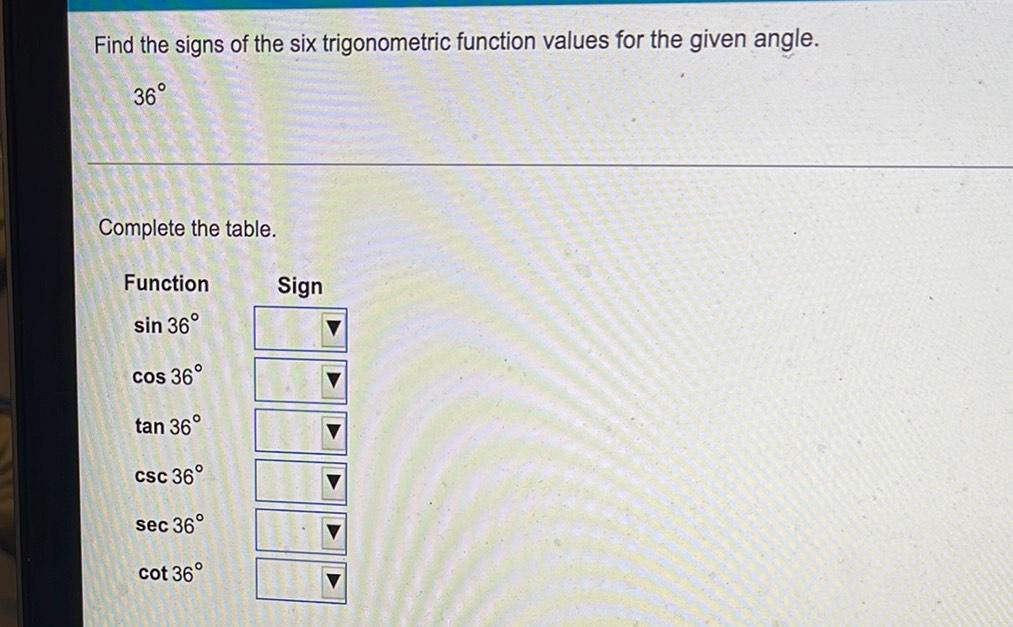
TrigonometryFind the signs of the six trigonometric function values for the given angle.
36°
Complete the table.
Function. Sign
sin 36° ---
cos 36° ---
tan 36 ---
csc 36° ---
sec 36° ---
cot 36° ---

Math - Others
TrigonometryFind a solution for the equation. Assume that all angles in which an unknown appears are acute angles.
csc α = sec(α + 10°)
α=
(Simplify your answer. Type an integer or a decimal.)
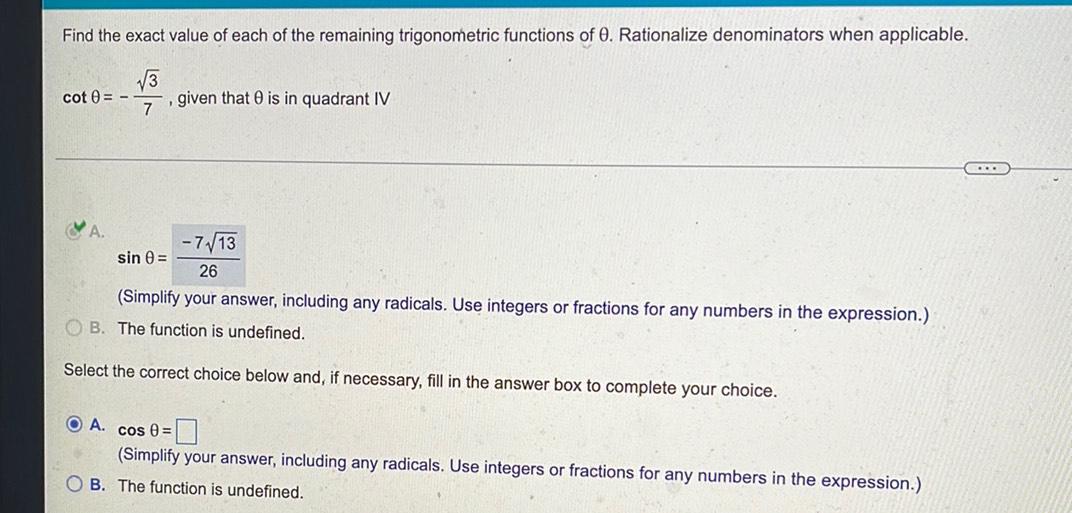
Math - Others
TrigonometryFind the exact value of each of the remaining trigonometric functions of θ. Rationalize denominators when applicable.
cot θ = - √3/7 , given that θ is in quadrant IV
A ) Sin θ=
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)
B.) The function is undefined.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A.) cos θ= ____
(Simplify your answer, including any radicals. Use integers or fractions for any numbers in the expression.)
B. )The function is undefined.
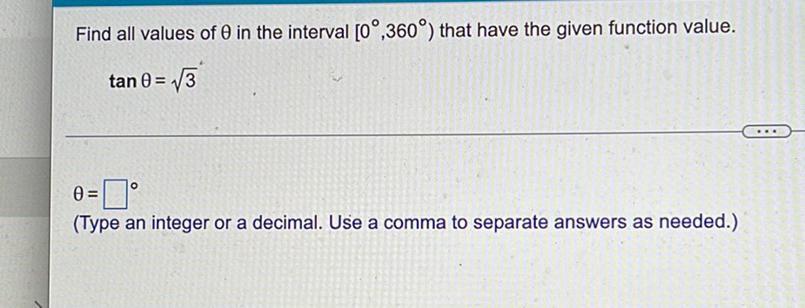
Math - Others
TrigonometryFind all values of θ in the interval [0°,360°) that have the given function value . tanθ= √3
θ=___°
(Type an integer or a decimal. Use a comma to separate answers as needed.)

Math - Others
TrigonometryFind one solution for the equation. Assume that all angles involved are acute angles.
sin (θ+25°) = cos (2θ+5°)
θ= ⁰
(Simplify your answer.)
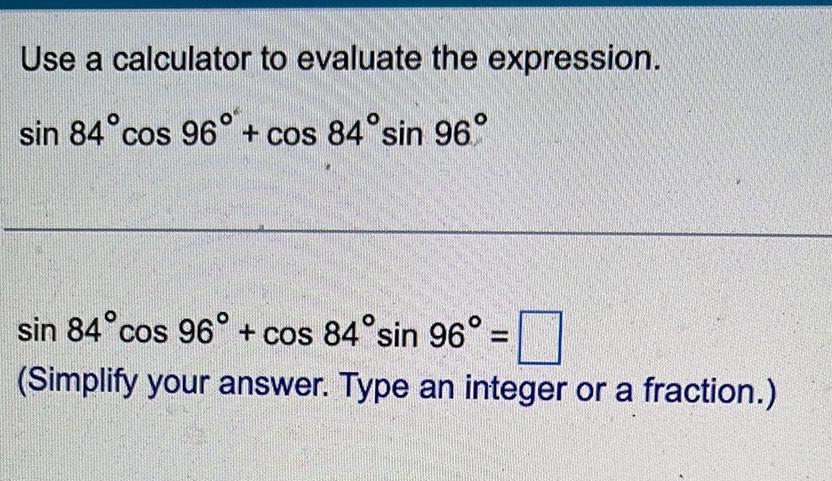
Math - Others
TrigonometryUse a calculator to evaluate the expression.
sin 84° cos 96° + cos 84°sin 96.
sin 84°cos 96° + cos 84°sin 96° = _______________
![Find all values of θ, if θ is in the interval [0°, 360°)and has the given function value.
csc θ =2√3/(3)
θ=[?]°
(Type an integer or a decimal. Use a comma to separate answers as needed.)](https://media.kunduz.com/media/sug-question/raw/80260509-1659638368.5345182.jpeg?w=256)
Math - Others
TrigonometryFind all values of θ, if θ is in the interval [0°, 360°)and has the given function value.
csc θ =2√3/(3)
θ=[?]°
(Type an integer or a decimal. Use a comma to separate answers as needed.)
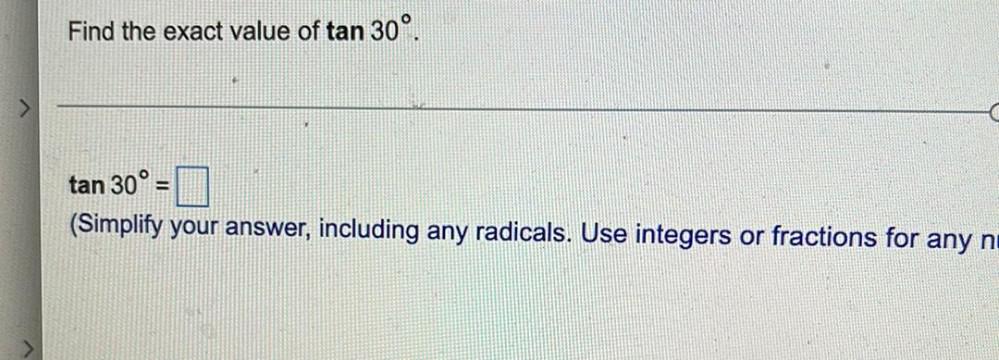
Math - Others
TrigonometryFind the exact value of tan 30°.
tan 30º =
(Simplify your answer, including any radicals. )