Probability Questions and Answers
Statistics
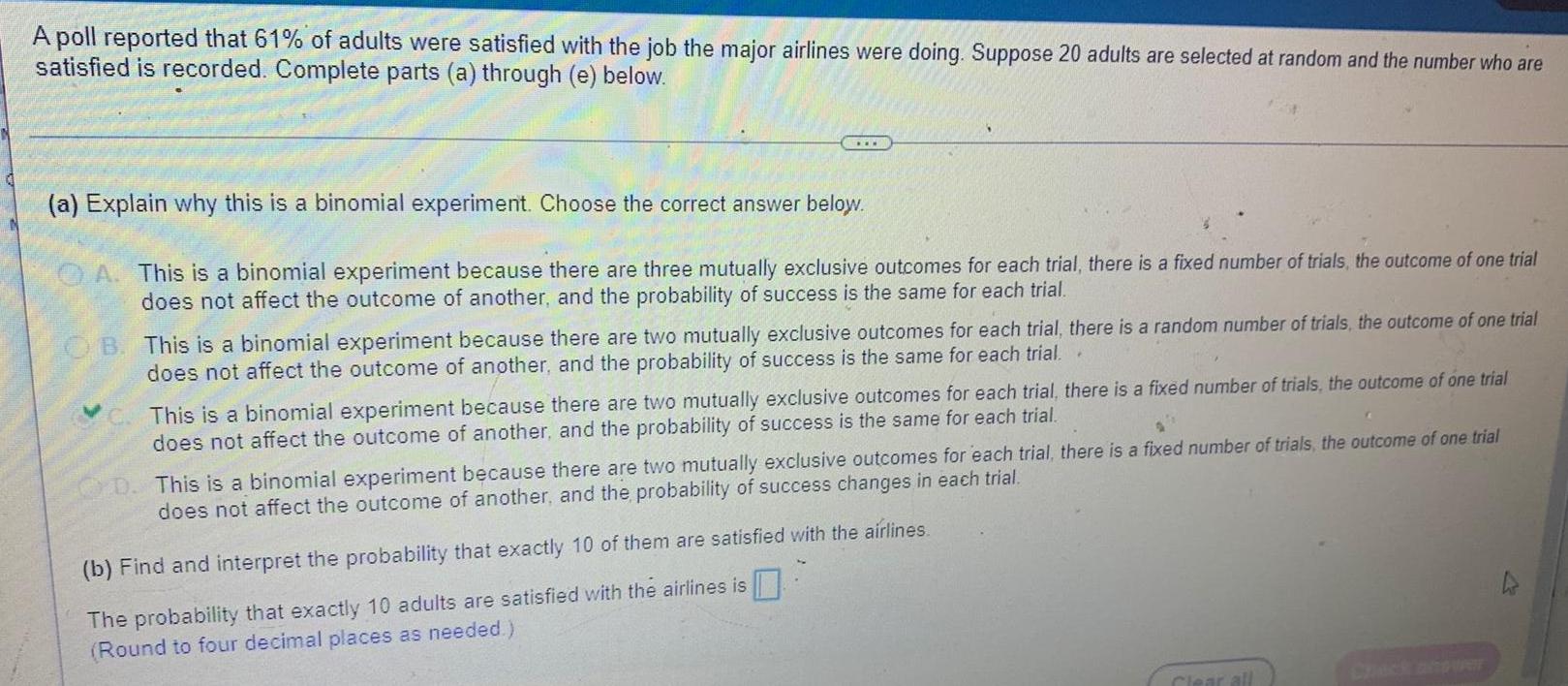
ProbabilityA poll reported that 61% of adults were satisfied with the job the major airlines were doing. Suppose 20 adults are selected at random and the number who are satisfied is recorded. Complete parts (a) through (e) below.
(a) Explain why this is a binomial experiment. Choose the correct answer below.
A. This is a binomial experiment because there are three mutually exclusive outcomes for each trial, there is a fixed number of trials, the outcome of one trial does not affect the outcome of another, and the probability of success is the same for each trial.
B. This is a binomial experiment because there are two mutually exclusive outcomes for each trial, there is a random number of trials, the outcome of one trial does not affect the outcome of another, and the probability of success is the same for each trial..
This is a binomial experiment because there are two mutually exclusive outcomes for each trial, there is a fixed number of trials, the outcome of one trial does not affect the outcome of another, and the probability of success is the same for each trial.
D. This is a binomial experiment because there are two mutually exclusive outcomes for each trial, there is a does not affect the outcome of another, and the probability of success changes in each trial.
(b) Find and interpret the probability that exactly 10 of them are satisfied with the airlines.
The probability that exactly 10 adults are satisfied with the airlines is
(Round to four decimal places as needed.)

Statistics
ProbabilityAccording to an almanac, 70% of adult smokers started smoking before turning 18 years old.
(a) If 200 adult smokers are randomly selected, how many would we expect to have started smoking before turning 18 years old?
(b) Would it be unusual to observe 180 smokers who started smoking before turning 18 years old in a random sample of 200 adult smokers? Why?

Statistics
ProbabilityNews reports indicate that nationally, 45% of Americans are planning
"staycations" at home this year instead of a vacation trip. Suppose we take a
random sample of 200 people in our city and find that 113 of them are planning
"staycations."
Let p = the proportion in our city who are planning staycations this year. A 98%
confidence interval for P is
a) (0.496, 0.634)
b) (0.483, 0.646)
c) No confidence interval is necessary, since we know p = 45%.
d) (0.480, 0.648)

Statistics
ProbabilityDetermine whether the following probability experiment represents a binomial experiment and explain the reason for your answer. An experimental drug is administered to 110 randomly selected individuals, with the number of individuals responding favorably recorded. Does the probability experiment represent a binomial experiment?
A. Yes, because the experiment satisfies all the criteria for a binomial experiment.
B. No, because there are more than two mutually exclusive outcomes for each trial.
C. No, because the probability of success differs from trial to trial.
D. No, because the trials of the experiment are not independent.
Statistics
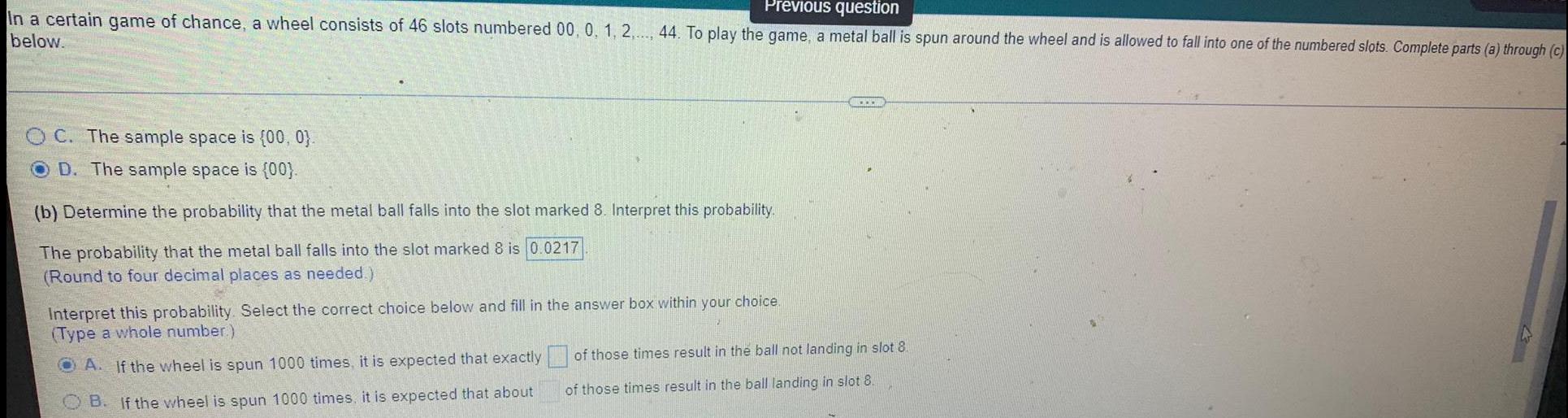
ProbabilityIn a certain game of chance, a wheel consists of 46 slots numbered 00, 0, 1, 2,..., 44. To play the game, a metal ball is spun around the wheel and is allowed to fall into one of the numbered slots. Complete parts
(a) through (c) below.
C. The sample space is (00, 0).
D. The sample space is (00).
(b) Determine the probability that the metal ball falls into the slot marked 8. Interpret this probability.The probability that the metal ball falls into the slot marked 8 is 0.0217
(Round to four decimal places as needed.) Interpret this probability. Select the correct choice below and fill in the answer box within your choice.
(Type a whole number)
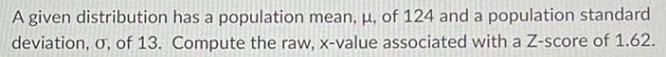
Statistics
ProbabilityA given distribution has a population mean, μ, of 124 and a population standard deviation, o, of 13. Compute the raw, x-value associated with a Z-score of 1.62.

Statistics
ProbabilitySuppose that a single card is selected from a standard 52-card deck. What is the probability that the card drawn is a club? Now suppose that a single card is drawn from a standard 52-card deck, but it is told that the card is black What is the probability that the card drawn is a club?

Statistics
ProbabilityThe probability that a randomly selected 4-year-old male feral cat will live to be 5 years old is 0.99301.
(a) What is the probability that two randomly selected 4-year-old male feral cats will live to be 5 years old?
(b) What is the probability that six randomly selected 4-year-old male feral cats will live to be 5 years old?
(c) What is the probability that at least one of six randomly selected 4-year-old male feral cats will not live to be 5 years old? Would it be unusual if at least one of six randomly selected 4-year-old male feral cats did not live to be 5 years old?

Statistics
ProbabilityDue to a manufacturing error, five cans of regular soda were accidentally filled with diet soda and placed into a 18-pack. Suppose that two cans are randomly selected from the 18-pack. Complete parts (a) through (c).
(a) Determine the probability that both contain diet soda.
P(both diet)= (Round to four decimal places as needed.)
(b) Determine the probability that both contain regular soda.
P(both regular) = (Round to four decimal places as needed.)
Would this be unusual?
No
Yes
(c) Determine the probability that exactly one is diet and exactly one is regular.
P(one diet and one regular) = (Round to four decimal places as needed.)
Statistics
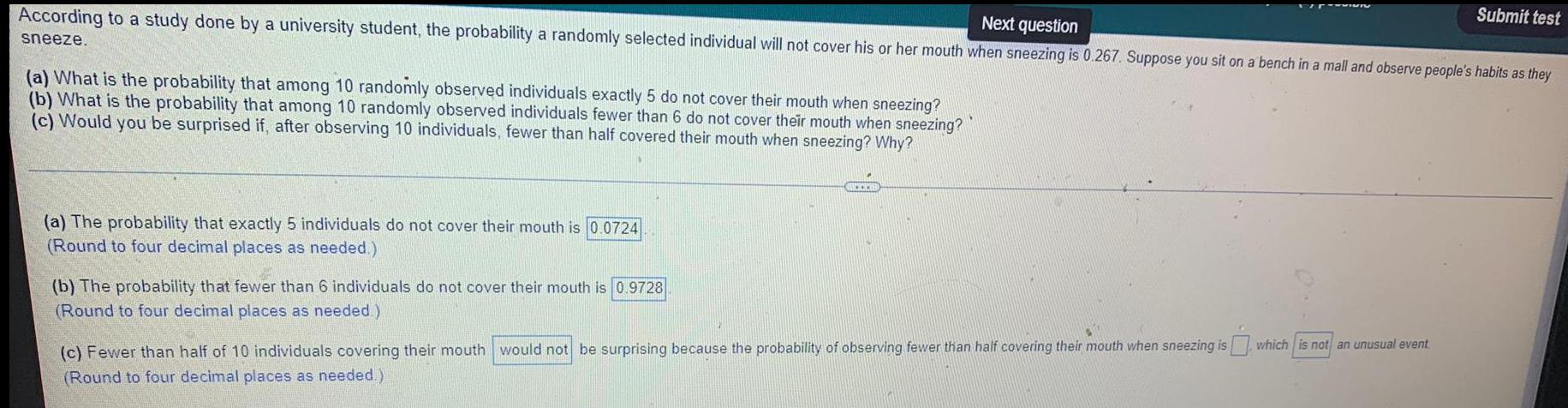
ProbabilityAccording to a study done by a university student, the probability a randomly selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a mall and observe people's habits as they sneeze.
(a) What is the probability that among 10 randomly observed individuals exactly 5 do not cover their mouth when sneezing?
(b) What is the probability that among 10 randomly observed individuals fewer than 6 do not cover their mouth when sneezing?
(c) Would you be surprised if, after observing 10 individuals, fewer than half covered their mouth when sneezing? Why?
(a) The probability that exactly 5 individuals do not cover their mouth is
(Round to four decimal places as needed.)
(b) The probability that fewer than 6 individuals do not cover their mouth is
(Round to four decimal places as needed.)
(c) Fewer than half of 10 individuals covering their mouth would not be surprising because the probability of observing fewer than half covering their mouth when sneezing is which is not an unusual event
(Round to four decimal places as needed.)

Statistics
ProbabilityA bag of 31 tulip bulbs contains 11 red tulip bulbs, 12 yellow tulip bulbs, and 8 purple tulip bulbs. Suppose two tulip bulbs are randomly selected without replacement from the bag
(a) What is the probability that the two randomly selected tulip bulbs are both red?
(b) What is the probability that the first bulb selected is red and the second yellow?
(c) What is the probability that the first bulb selected is yellow and the second red?
(d) What is the probability that one bulb is red and the other yellow?
(a) The probability that both bulbs are red is.
(Round to three decimal places as needed.)
(b) The probability that the first bulb is red and the second is yellow is
(Round to three decimal places as needed.)
(c) The probability that the first bulb is yellow and the second is red is
(Round to three decimal places as needed.)
(d) The probability that one bulb is red and one is yellow is
(Round to three decimal places as needed.)
Statistics
ProbabilityIn a certain game of chance, a wheel consists of 38 slots numbered 00, 0, 1, 2,..., 36. To play the game, a metal ball is spun around the wheel and is allowed to fall into one of the numbered slots. Complete parts (a) through (c) below.
(a) Determine the sample space. Choose the correct answer below.
A. The sample space is (00, 0, 1, 2,..., 36).
B. The sample space is (00, 0).
C. The sample space is {1, 2...., 36).
D. The sample space is (00).
(b) Determine the probability that the metal ball falls into the slot marked 3. Interpret this probability.
The probability that the metal ball falls into the slot marked 3 is.
(Round to four decimal places as needed.)
Interpret this probability. Select the correct choice below and fill in the answer box within your choice.
(Type a whole number)
A. If the wheel is spun 1000 times, it is expected that about of those times result in the ball landing in slot 3.
B. If the wheel is spun 1000 times, it is expected that exactly of those times result in the ball landing in slot 3.
Statistics
ProbabilityThe probability that a randomly selected 3-year-old male feral cat will live to be 4 years old is 0.98533.
(a) What is the probability that two randomly selected 3-year-old male feral cats will live to be 4 years old?
(b) What is the probability that nine randomly selected 3-year-old male feral cats will live to be 4 years old?
(c) What is the probability that at least one of nine randomly selected 3-year-old male feral cats will not live to be 4 years old? Would it be unusual if at least one of nine randomly selected 3-year-old male feral cats did not live to
be 4 years old?
(a) The probability that two randomly selected 3-year-old male feral cats will live to be 4 years old is
(Round to five decimal places as needed.)
(b) The probability that nine randomly selected 3-year-old male feral cats will live to be 4 years old is
(Round to five decimal places as needed.)
(c) The probability that at least one of nine randomly selected 3-year-old male feral cats will not live to be 4 years old is
(Round to five decimal places as needed.)
Would it be unusual if at least one of nine randomly selected 3-year-old male feral cats did not live to be 4 years old?
because the probability of this happening is 0.05
Statistics
ProbabilityA bag of 100 tulip bulbs purchased from a nursery contains 40 red tulip bulbs, 40 yellow tulip bulbs, and 20 purple tulip bulbs.
(a) What is the probability that a randomly selected tulip bulb is red?
(b) What is the probability that a randomly selected tulip bulb is purple?
(c) Interpret these two probabilities.
(a) The probability that a randomly selected tulip is red is
(Type an integer or a decimal. Do not round.)
(b) The probability that a randomly selected tulip bulb is purple is.
(Type an integer or a decimal. Do not round.)
(c) Select the correct choice below and fill in the answer boxes within your choice.
(Type whole numbers.)
A. If 100 tulip bulbs were sampled with replacement, one would expect about______of the bulbs to be red and about_______of the bulbs to be purple.
B. If 100 tulip bulbs were sampled with replacement.. one would expect exactly ________of the bulbs to be red and exactly_______of the bulbs to be purple.

Statistics
ProbabilityA computer can be classified as either cutting-edge or ancient. Suppose that 92% of computers are classified as ancient.
(a) Two computers are chosen at random. What is the probability that both computers are ancient?
(b) Four computers are chosen at random. What is the probability that all four computers are ancient?
(c) What is the probability that at least one of four randomly selected computers is cutting-edge? Would it be unusual that at least one of four randomly selected computers is cutting-edge?
(a) Two computers are chosen at random. What is the probability that both computers are ancient?
The probability is
(b) Four computers are chosen at random. What is the probability that all four computers are ancient?
The probability is
(Round to four decimal places as needed.)
(c) What is the probability that at least one of four randomly selected computers is cutting-edge?
Statistics
ProbabilityDue to a manufacturing error, three cans of regular soda were accidentally filled with diet soda and placed into a 24-pack. Suppose that two cans are randomly selected from the 24-pack. Complete parts (a) through (c).
(a) Determine the probability that both contain diet soda. P(both diet)=(Round to four decimal places as needed.)
(b) Determine the probability that both contain regular soda. P(both regular) = (Round to four decimal places as needed.)
Would this be unusual?
Yes
No
(c) Determine the probability that exactly one is diet and exactly one is regular. P(one diet and one regular) = (Round to four decimal places as needed.)

Statistics
ProbabilityA set has 10 outliers. If every value of this set is increased by 5 percent, how many outliers will there now be?
(A) Fewer than 10
(B) 10
(C) 11
(D) More than 11
(E) It is impossible to determine without further information.

Statistics
ProbabilityThe mean length of human pregnancies is 266 days with a standard deviation of 16 days. Which of the following is the best description of the standard deviation?
(A) Approximately the median time between the lengths of individual pregnancies and 266 days
(B) Approximately the mean time between the lengths of individual pregnancies and 266 days
(C) Approximately the square root of the mean time between the lengths of individual pregnancies and 266 days
(D) One-third the time between the maximum individual length of pregnancies and 266 (E) One-sixth the time between the maximum and minimum individual lengths of pregnancies

Statistics
ProbabilityWhat is the probability that a randomly selected orange will have less than 660 IU of vitamin C?

Statistics
ProbabilityA new surgery is successful 75% of the time. If the results of 7 such surgeries are randomly sampled, what is the probability that more than 5 of them are successful? Carry your intermediate computations to at least four decimal places, and round your answer to two decimal places.
Statistics
ProbabilitySuppose Emerson wins 34% of all checker games.
(a) What is the probability that Emerson wins two checker games in a row?
(b) What is the probability that Emerson wins five checker games in a row?
(c) When events are independent, their complements are independent as well. Use this result to determine the probability that Emerson wins five checker games in
a row, but does not win six in a row.
(a) The probability that Emerson wins two checker games in a row is
(Round to four decimal places as needed.)
Statistics
ProbabilityAbout 8% of the population of a large country is nervous around strangers. If two people are randomly selected, what is the probability both are nervous around strangers? What is the probability at least one is nervous around strangers? Assume the events are independent.
(a) The probability that both will be nervous around strangers is
(Round to four decimal places as needed.)
(b) The probability that at least one person is nervous around strangers is
(Round to four decimal places as needed.)
Statistics
ProbabilitySuppose that a computer chip company has just shipped 10,000 computer chips to a computer company. Unfortunately, 60 of the chips are defective.
(a) Compute the probability that two randomly selected chips are defective using conditional probability.
(b) The probability that the first randomly selected chip is defective is 60/ 10000=0.006 =0.6%. Compute the probability that two randomly selected chips are defective
under the assumption of independent events.
(Round to eight decimal places as needed.)
(b) The probability is
(Round to eight decimal places as needed.)
When small samples are taken from large populations without replacement, the assumption of independence does not significantly affect the probability. Based
on the results, what does this mean?
A. The probabilities are very different, but the probability found assuming independent events is smaller, so it does not matter.
B. The probabilities are exactly the same.
C. The probabilities are nearly the same.
D. The probabilities are very different, but the probability found assuming independent events is larger, so it does not matter.
Statistics
ProbabilityAccording to a center for disease control, the probability that a randomly selected person has hearing problems is 0.157. The probability that a randomly selected person has vision problems is 0.082. Can we compute the probability of randomly selecting a person who has hearing problems or vision problems by adding these probabilities? Why or why not?
Choose the correct answer below.
A. Yes, because this is an application of the Addition Rule for Disjoint Events.
B. Yes, because hearing and vision are two different senses, and therefore, they are two unique problems.
C. No, because hearing and vision problems are not mutually exclusive. So, some people have both hearing and visi problems. These people would be included twice in the probability.
D. No, because hearing problems and vision problems are events that are too similar to one another.

Statistics
ProbabilityA probability experiment is conducted in which the sample space of the experiment is S={1,2,3,4,5,6,7,8,9,10,11,12). Let event E={1,2,3,4,5,6,7,8,9). Assume each outcome is equally likely. List the outcomes in E^c. Find P (E^c).
List the outcomes in E^c. Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. E^c=
B. E ^c= { }

Statistics
ProbabilityThe spinner for a child's board game has five equally-sized colored regions, one of which is green. If we spin the spinner 50 times, construct a box model for the percentage of times the spinner lands on green.
a. The number of draws is
b. The average of the tickets in the box is
c. The SD of the tickets in the box is

Statistics
ProbabilityAccording to a survey, 45% of teenagers could recognize a picture of legendary film star John Wayne. What is the probability that a randomly-selected teenager could recognize John Wayne?
0.55
0.45
0.01
0.82

Statistics
ProbabilityA population has μ = 50. Which value of σ would make X = 55 an extreme value out in the tail of the population
distribution?
σ =1
σ = 6
σ = 10
This is impossible to determine based on the information provided.
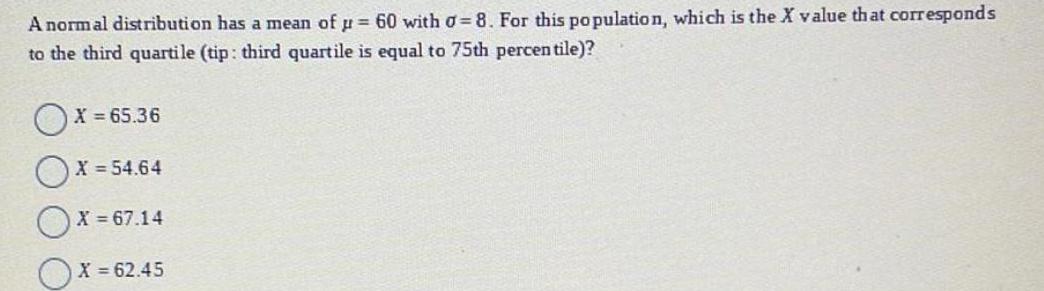
Statistics
ProbabilityA normal distribution has a mean of µ = 60 with σ=8. For this population, which is the X value that corresponds to the third quartile (tip: third quartile is equal to 75th percentile)?
X = 65.36
X = 54.64
X = 67.14
X = 62.45
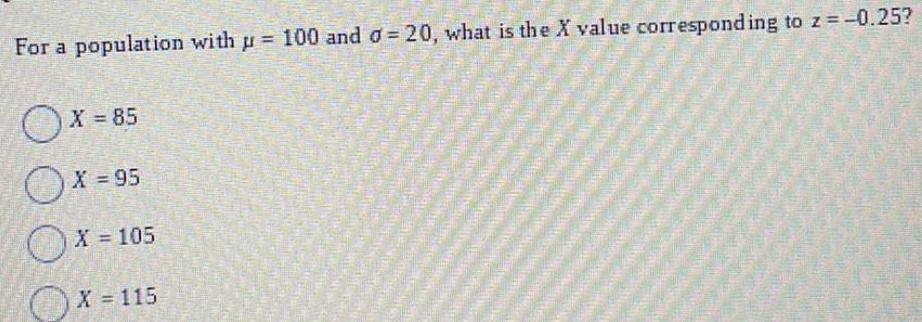
Statistics
ProbabilityFor a population with µ = 100 and σ = 20, what is the X value corresponding to z = -0.25?
X = 85
X = 95
X = 105
X = 115

Statistics
ProbabilityScores on a standard IQ test are normally distributed with mean 100 and standard deviation 15. Use the Empirical Rule and make a sketch for each problem. What percent of the population have IQS
a) below 70?
b) between 70 and 115?
c) above 145?

Statistics
ProbabilityWhich statement accurately describes the proportions in the tails of a normal distribution?
The proportion in the left-hand tail is smaller than the proportion in the right-hand tail.
Proportions in both the left-hand and right-hand tails tend to be relatively large.
Proportions in both tails are the same.
Proportions in both tails are negative.

Statistics
ProbabilityA normal distribution has a mean of µ = 40 with σ = 10. If a vertical line is drawn through the distribution at X = 34, which proportion of the scores are on the left side of the line?
0.7257
0.2743
0.0668
0.1976

Statistics
ProbabilityMarty is a principal who needs to contact the highest performing 15% of students in his school's current graduating class about an opportunity to join the school's academic honor society. At his school, students' grade point averages is a normally distributed variable. Marty should contact students who have a grade point average that correspond with a z-score greater than or equal to _____
z = +1.04.
z = +0.25.
z = -1.04.
z = -0.25.
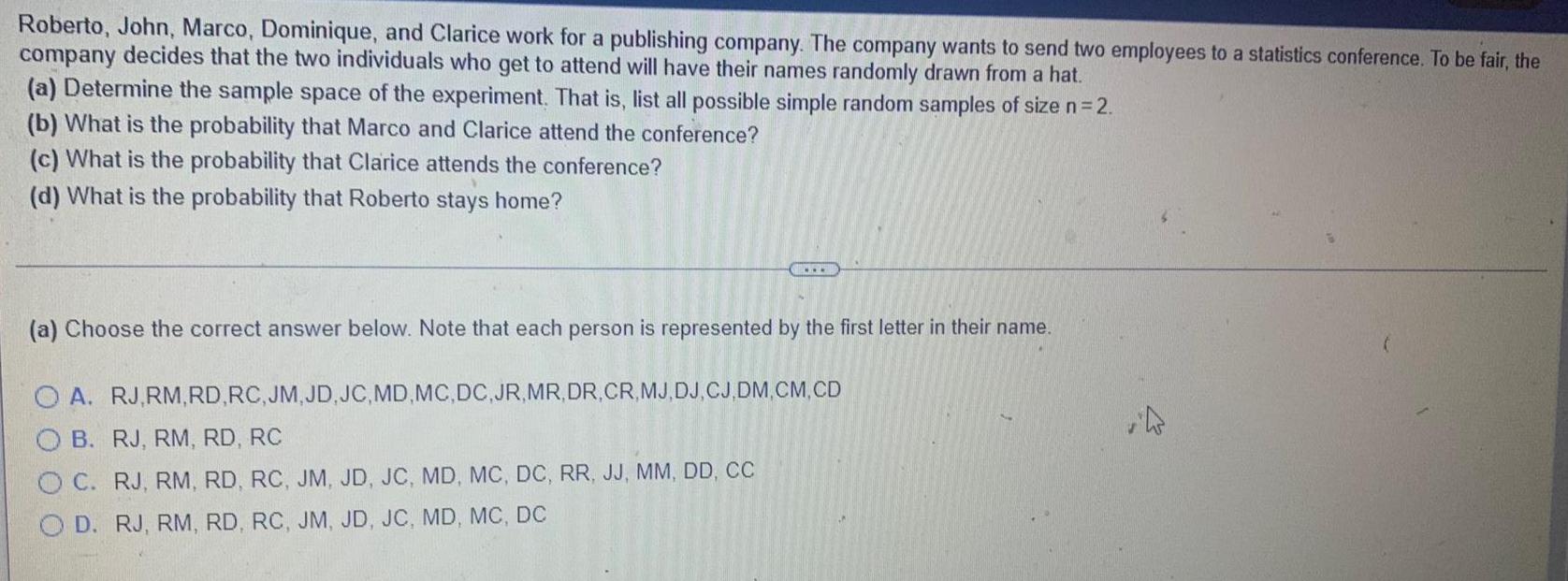
Statistics
ProbabilityRoberto, John, Marco, Dominique, and Clarice work for a publishing company. The company wants to send two employees to a statistics conference. To be fair, the company decides that the two individuals who get to attend will have their names randomly drawn from a hat.
(a) Determine the sample space of the experiment. That is, list all possible simple random samples of size n = 2.
(b) What is the probability that Marco and Clarice attend the conference?
(c) What is the probability that Clarice attends the conference?
(d) What is the probability that Roberto stays home?
(a) Choose the correct answer below. Note that each person is represented by the first letter in their name.
A. RJ,RM, RD, RC, JM, JD, JC,MD,MC, DC, JR,MR, DR, CR, MJ, DJ, CJ, DM,CM, CD
B. RJ, RM, RD, RC
C. RJ, RM, RD, RC, JM, JD, JC, MD, MC, DC, RR, JJ, MM, DD, CC
D. RJ, RM, RD, RC, JM, JD, JC, MD, MC, DC

Statistics
ProbabilityA baseball player hit 57 home runs in a season. Of the 57 home runs, 18 went to right field, 20 went to right center field, 9 went to center field, 8 went to left center
field, and 2 went to left field.
(a) What is the probability that a randomly selected home run was hit to right field?
(b) What is the probability that a randomly selected home run was hit to left field?
(c) Was it unusual for this player to hit a home run to left field? Explain.
......
(a) The probability that a randomly selected home run was hit to right field is 0.316.
(Round to three decimal places as needed.)
(b) The probability that a randomly selected home run was hit to left field is
(Round to three decimal places as needed.)

Statistics
ProbabilityAirline passengers arrive randomly and independently at the passenger-screening facility at a major international airport. The mean arrival rate is 10 passengers per minute. Compute the probability of at least one arrival in a 15-second period.

Statistics
ProbabilityWhich statement about the Nicki Minaj sample is true compared to the Kendrick Lamar sample?
The Nicki Minaj sample has a larger mean and a larger standard deviation than the Kendrick Lamar
sample.
The Nicki Minaj sample has a larger mean and a smaller standard deviation than the Kendrick Lamar
sample.
The Nicki Minaj sample has the same mean and a larger standard deviation than the Kendrick Lamar
sample.
The Nicki Minaj sample has the same mean and a smaller standard deviation than the Kendrick
Lamar sample.
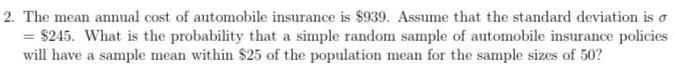
Statistics
ProbabilityThe mean annual cost of automobile insurance is $939. Assume that the standard deviation is o $245. What is the probability that a simple random sample of automobile insurance policies will have a sample mean within $25 of the population mean for the sample sizes of 50?

Statistics
ProbabilityCalculate the relative probability of photoelectric absorption for annihilation photons in lead versus aluminum shielding.

Statistics
ProbabilityTo avoid having her hours cut back at work, Bridgett must avoid performing in the lowest 40% of the
distribution of workers at her job. Specifically, typical amount of items manufactured at her job form a normal distribution with y = 100 and o= 4. Bridgett needs to manufacture more than items in order to avoid having her hours cut back at work.
X = 99
X = -101
X = 103
X = 97

Statistics
ProbabilityA vertical line drawn through a normal distribution at z = -0.72 separates the distribution into two sections. The proportion in the smaller section is 0.2358.
True
False
Statistics
ProbabilityIf one score is randomly selected from a normal distribution with = 100 and d = 20, the probability of
obtaining a score greater than X = 73 is p = 0.4115.
True
False

Statistics
ProbabilityFor a normal distribution with = 100 and d=10, the score that separates the top 60% of the distribution from the rest of the distribution is X = 105.
True
False

Statistics
ProbabilityA party host gives a door prize to one guest chosen at random. There are 48 men and 42 women at the party. What is the probability that the prize goes to a woman?
a) 88%
b) 42/90
c) 47%
d) 42/48

Statistics
ProbabilityI toss a penny and observe whether it lands heads up or tails up. Suppose the penny is fair, that is, the probability of heads is 1/2 and the probability of tails is 1/2. This means
a) every occurrence of a head must be balanced by a tail in one of the next two or three tosses.
b) if I flip the coin many, many times, the proportion of heads will be approximately 1/2, and this proportion will tend to get closer and closer to 1/2 as the number of tosses increases.
c) regardless of the number of flips, half will be heads and half will be tails.
d) all of the above.

Statistics
ProbabilityIn many settings, the "rules of probability" are just basic facts about percents. A company that offers courses to prepare students for the Graduate Management Admission Test (GMAT) has the following information about its customers: 20% are undergraduate students in business; 15% are undergraduate students in other fields of study; 60% are college graduates who are currently employed, and 5% are college graduates who are not employed. If we pick a customer at random, what is the probability that we get a customer that is an undergraduate?

Statistics
ProbabilityA bell shaped distribution has u = 40 and a = 8. Using the Empirical Rule Find the proportion of scores that are: (Make a sketch for each problem)
a) x > 48
b) 24 <x< 48
c) x < 24

Statistics
ProbabilityLet the sample space be S= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10). Suppose the outcomes are equally likely. Compute the probability of the event E= "an even number less than 9."
P(E)=
(Type an integer or a decimal. Do not round.)

Statistics
ProbabilityA survey of 400 randomly selected high school students determined that 254 play organized sports.
(a) What is the probability that a randomly selected high school student plays organized sports?
(b) Interpret this probability.
(a) The probability that a randomly selected high school student plays organized sports is