Probability Questions and Answers
Statistics
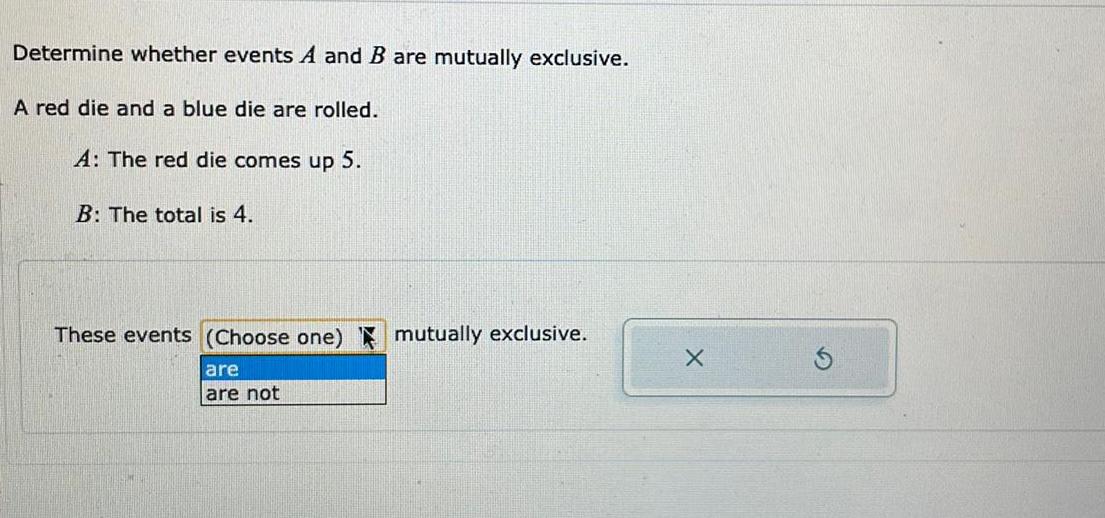
ProbabilityDetermine whether events A and B are mutually exclusive.
A red die and a blue die are rolled.
A: The red die comes up 5.
B: The total is 4.
These events (Choose one) mutually exclusive.

Statistics
ProbabilitySampling and Sampling Distributions (CTL): The College Board reported the following mean scores for the three parts of the Scholastic Aptitude Test (SAT) (The World Almanac): Critical Reading 502; Mathematics 515; Writing 494. Assume that the population standard deviation on each part of the test is sigma = 100. What is the probability that a random sample of 90 test takers will provide a sample mean test score within 10 points of the population mean of 502 on the Critical Reading part of the test?
Statistics
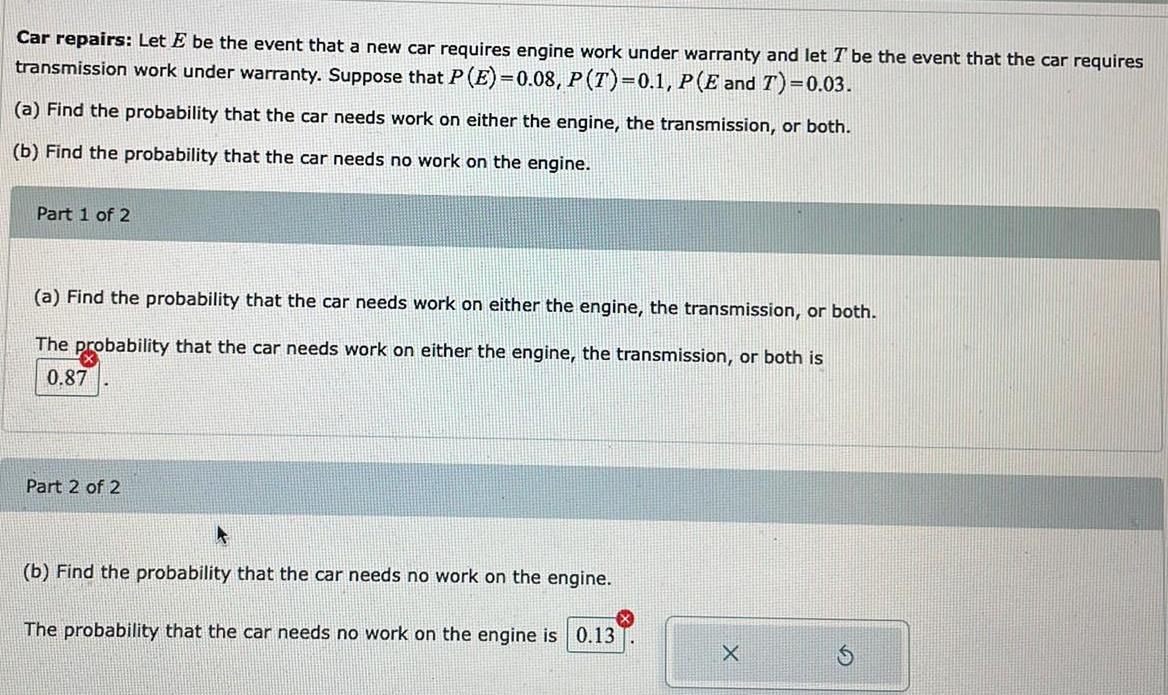
ProbabilityLet E be the event that a new car requires engine work under warranty and let T be the event that the car requires transmission work under warranty. Suppose that P (E)=0.08, P (T)=0.1, P(E and T)=0.03.
(a) Find the probability that the car needs work on either the engine, the transmission, or both.
(b) Find the probability that the car needs no work on the engine.

Statistics
ProbabilityFind the probability of an event and identify whether it is experimental or theoretical.
1. When a fair dice is rolled once, what is the probability of a number less than 7?
2. A standard deck of 52 cards consists of 13 black spades, 13 black clubs, 13 red hearts, and 13 red diamonds. Each suit has an ace, a king, a queen, a jack and the numbers from 2 to 10. A card is drawn from a well-shuffled deck of 52 cards. What is the probability of drawing a queen?
3. A thumbtack was tossed 50 times. It landed "point up" 35 times and "point down" 15 times. What is the probability that on the next toss, it will land "point up"?
Statistics
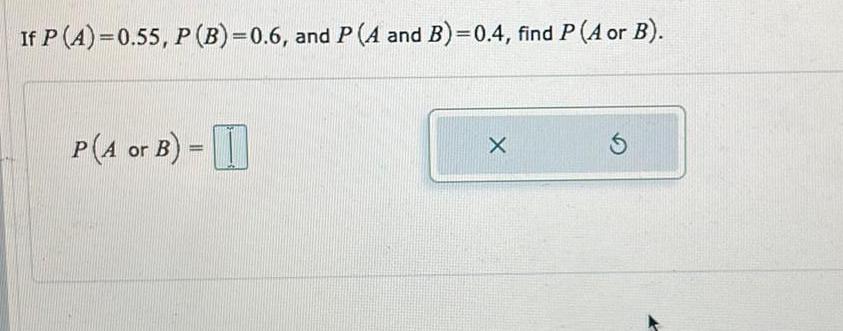
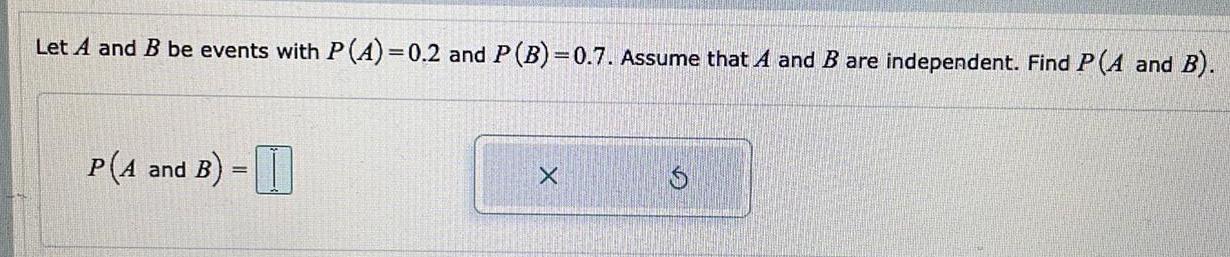
ProbabilityLet A and B be events with P(A)=0.2 and P (B)=0.7. Assume that A and B are independent. Find P(A and B).

Statistics
ProbabilityAt a certain car dealership, the probability that a customer purchases an SUV is 0.18. Given that a customer purchases an SUV, the probability that it is black is 0.21. What is the probability that a customer purchases a black SUV? Round your answer to four decimal places, if necessary.
The probability that a customer purchases a black SUV is
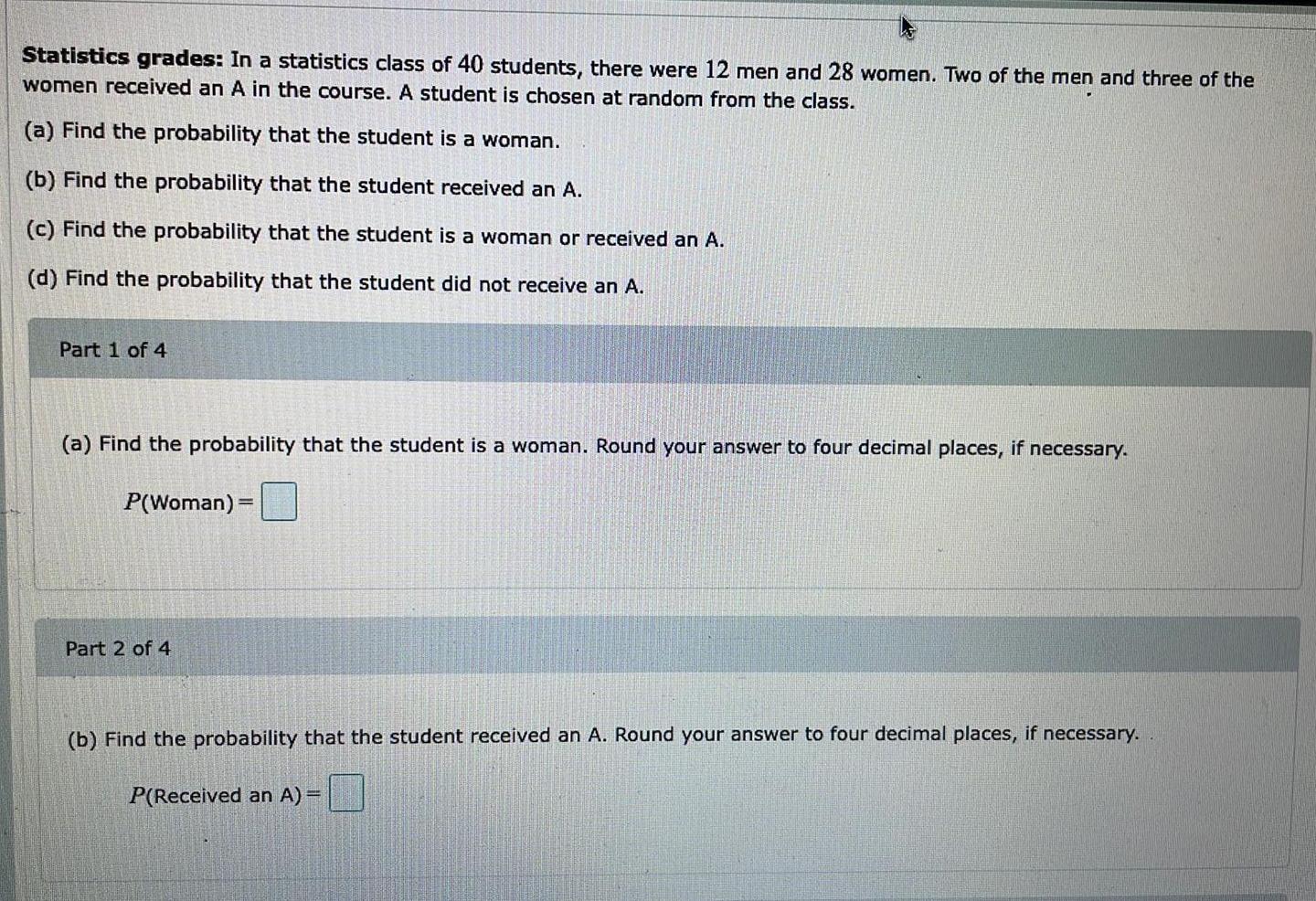
Statistics
ProbabilityIn a statistics class of 40 students, there were 12 men and 28 women. Two of the men and three of the women received an A in the course. A student is chosen at random from the class.
(a) Find the probability that the student is a woman.
(b) Find the probability that the student received an A.
(c) Find the probability that the student is a woman or received an A.
(d) Find the probability that the student did not receive an A.
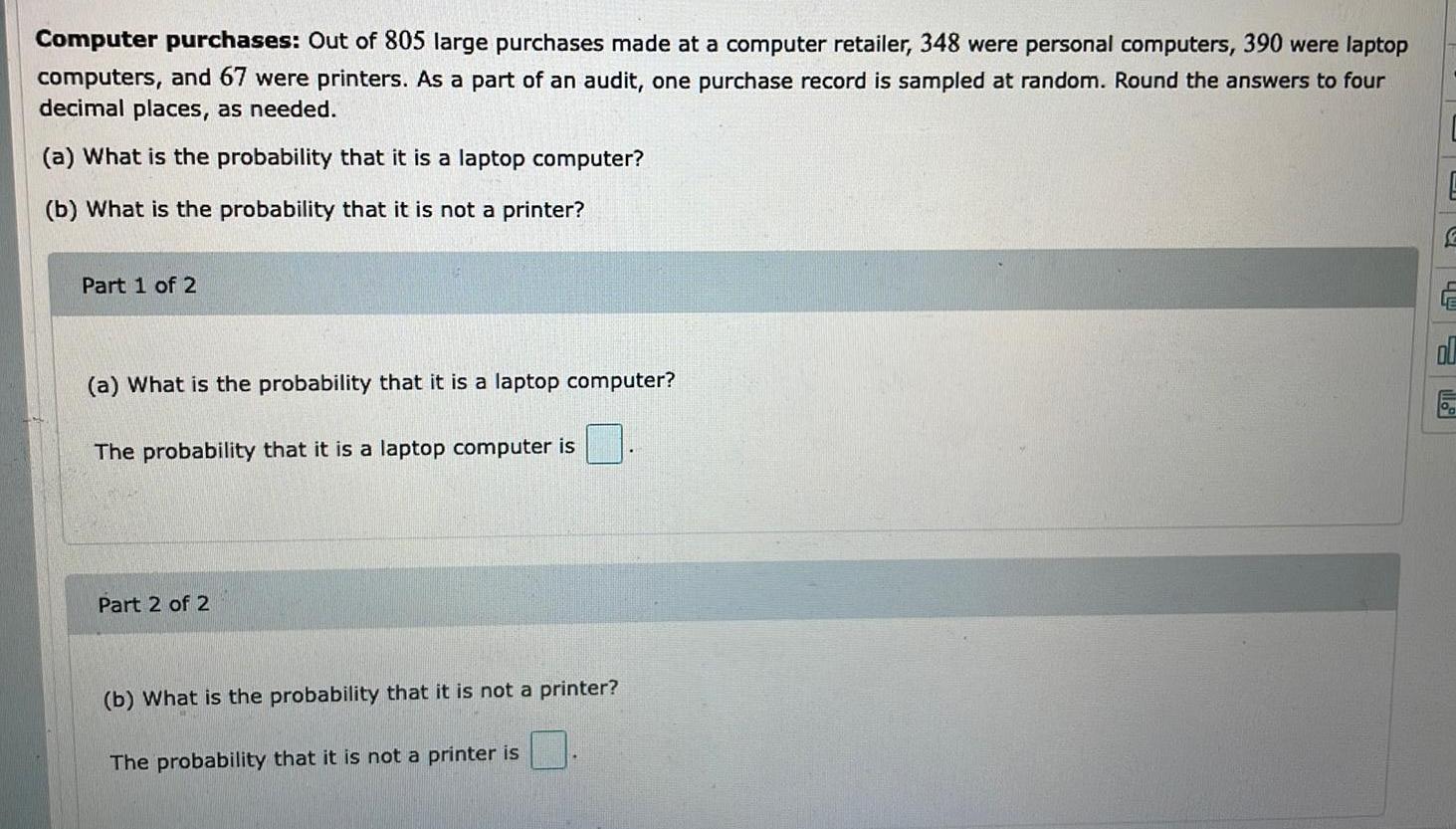
Statistics
ProbabilityComputer purchases: Out of 805 large purchases made at a computer retailer, 348 were personal computers, 390 were laptop computers, and 67 were printers. As a part of an audit, one purchase record is sampled at random. Round the answers to four decimal places, as needed.
(a) What is the probability that it is a laptop computer?
(b) What is the probability that it is not a printer?
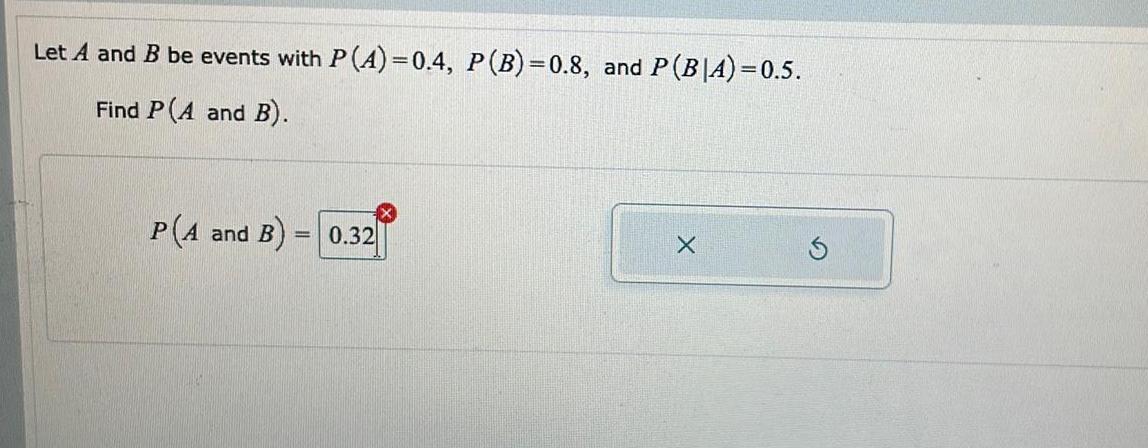
Statistics
ProbabilityLet A and B be events with P(A)=0.4, P (B)=0.8, and P(B|A)=0.5.
Find P(A and B).

Statistics
ProbabilityConsider the experiment where you toss two coins and roll a six-faced die at the same time.
5. What is the probability of getting a head, tail, and a five?
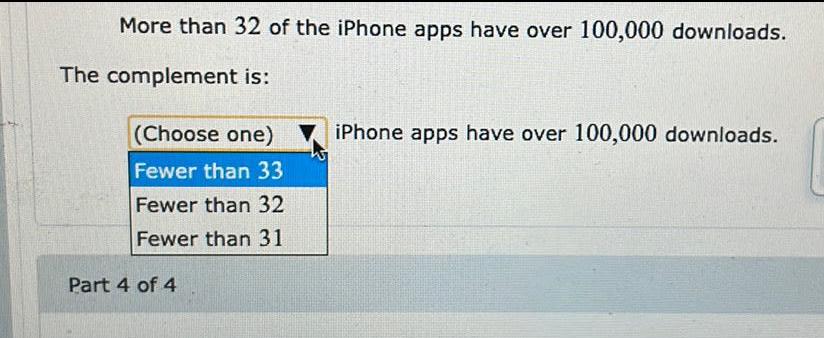
Statistics
ProbabilityMore than 32 of the iPhone apps have over 100,000 downloads.
The complement is:

Statistics
ProbabilityA fair coin is tossed four times. What is the probability that all four tosses are heads? Write your answer as a fraction or a decimal, rounded to four decimal places.
The probability that all four tosses are heads is

Statistics
ProbabilityInterest centers around the life of an electronic component. Suppose it is known that the probability that the component survives for more than 7000 hours is 0.35. Suppose also that the probability that the component survives no longer than 6000 hours is 0.15.
(a) What is the probability that the life of the component is less than or equal to 7000 hours?
(b) What is the probability that the life is greater than 6000 hours?
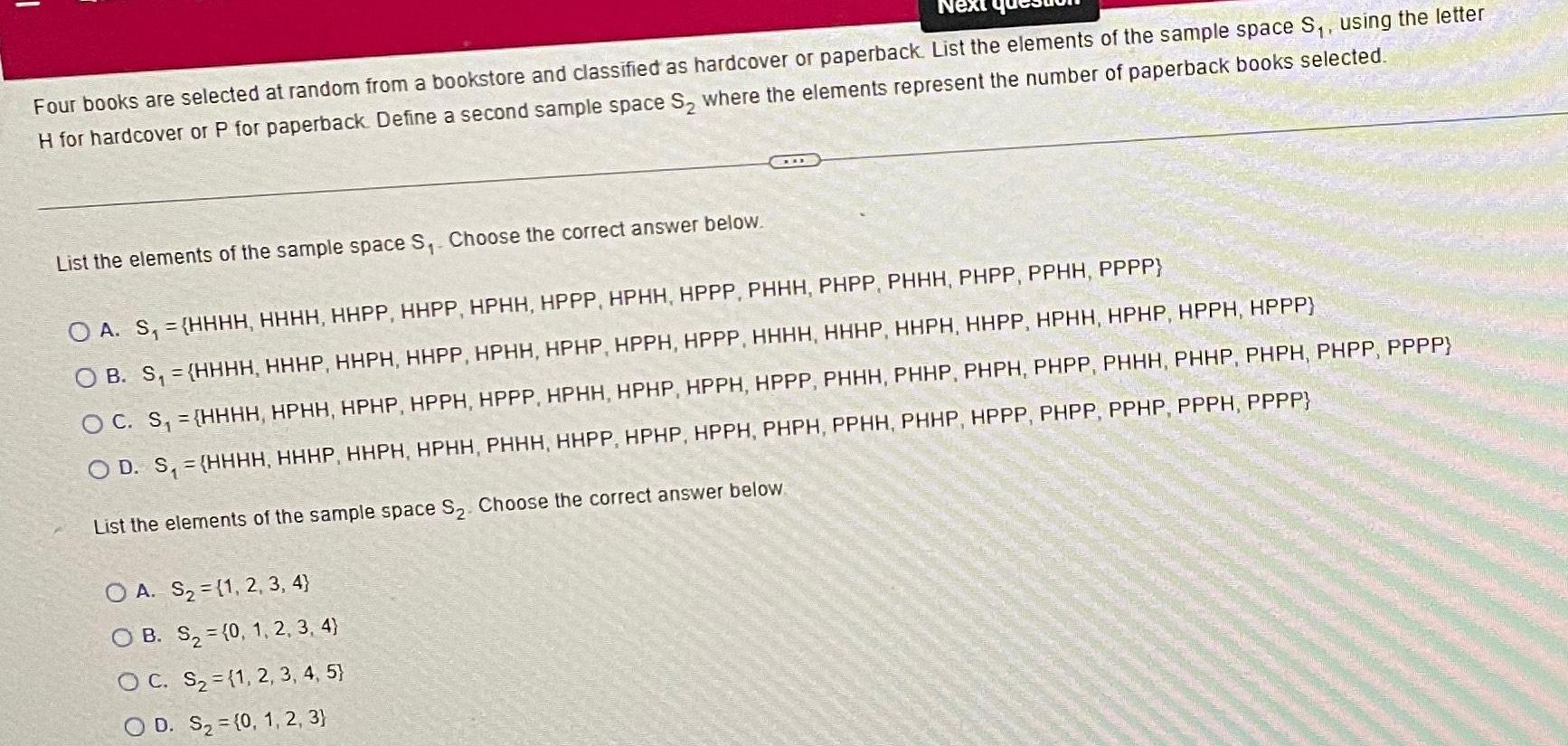
Statistics
ProbabilityFour books are selected at random from a bookstore and classified as hardcover or paperback. List the elements of the sample space S₁, using the letter H for hardcover or P for paperback. Define a second sample space S₂ where the elements represent the number of paperback books selected.
List the elements of the sample space S₁. Choose the correct answer below.
A. S1 = {HHHH, HHHH, HHPP, HHPP, HPHH, HPPP, HPHH, HPPP, PHHH, PHPP, PHHH, PHPP, PPHH, PPPP}
B. S1 = {HHHH, HHHP, HHPH, HHPP, HPHH, HPHP, HPPH, HPPP, HHHH, HHHP, HHPH, HHPP, HPHH, HPHP, HPPH, HPPP)
C. S1 = {HHHH, HPHH, HPHP, HPPH, HPPP, HPHH, HPHP, HPPH, HPPP, PHHH, PHHP, PHPH, PHPP, PHHH, PHHP, PHPH, PHPP, PPPP}
D. S1 = (HHHH, HHHP, HHPH, HPHH, PHHH, HHPP, HPHP, HPPH, PHPH, PPHH, PHHP, HPPP, PHPP, PPHP, PPPH, PPPP)
List the elements of the sample space S₂. Choose the correct answer below.
A. S₂ = {1, 2, 3, 4)
B. S₂ = (0, 1, 2, 3, 4)
C. S₂ = {1, 2, 3, 4, 5)
D. S₂ = {0, 1, 2, 3)
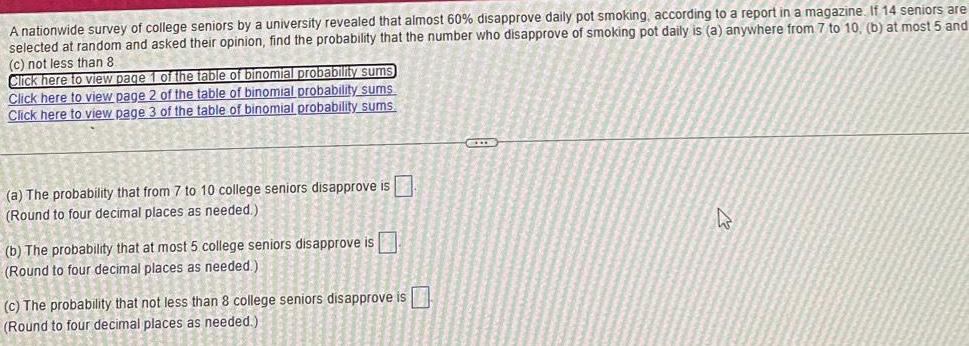
Statistics
ProbabilityA nationwide survey of college seniors by a university revealed that almost 60% disapprove daily pot smoking, according to a report in a magazine. If 14 seniors are selected at random and asked their opinion, find the probability that the number who disapprove of smoking pot daily is (a) anywhere from 7 to 10, (b) at most 5 and (c) not less than 8.
(a) The probability that from 7 to 10 college seniors disapprove is
(Round to four decimal places as needed.)
(b) The probability that at most 5 college seniors disapprove is
(Round to four decimal places as needed.)
(c) The probability that not less than 8 college seniors disapprove is
(Round to four decimal places as needed.).
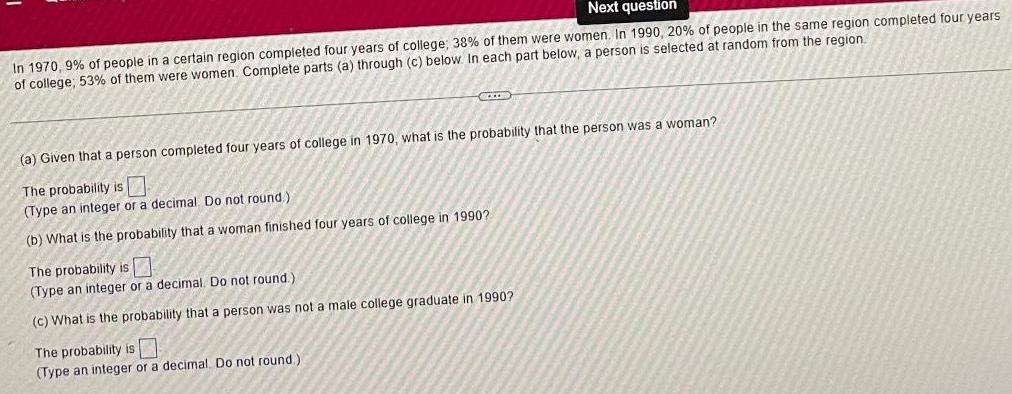
Statistics
ProbabilityIn 1970, 9% of people in a certain region completed four years of college, 38% of them were women. In 1990, 20% of people in the same region completed four years of college; 53% of them were women. Complete parts (a) through (c) below. In each part below, a person is selected at random from the region.
(a) Given that a person completed four years of college in 1970, what is the probability that the person was a woman?
The probability is
(Type an integer or a decimal. Do not round)
(b) What is the probability that a woman finished four years of college in 1990?
The probability is
(Type an integer or a decimal. Do not round.)
(c) What is the probability that a person was not a male college graduate in 1990?
The probability is
(Type an integer or a decimal. Do not round)

Statistics
ProbabilityA$150,000 mortgage amortized by monthly payments over 25 years is renewable after five years.
(a) If interest is 6.04% compounded semi-annually, what is the size of each monthly payment?
(b) Find the total interest paid during the first year.
(c) Compute the interest included in the 39th payment.
(d) If the mortgage is renewed after five years at 7.52% compounded semi-annually, what is the size of the month
payment for the renewal period?
(e) Construct a partial amortization schedule showing details of the first three payments for each of the two terms
(a) The size of each monthly payment is $ 963.28
(Round the final answer to the nearest cent as needed. Round all intermediate values to six decimal places as
needed.)
(b) The total interest paid is $ 8,875.46
(Round the final answer to the nearest cent as needed. Round all intermediate values to six decimal places as
needed.)
(c) The interest included in the 39th payment is $1757/37
(Round the final answer to the nearest cent as needed Round all intermediate values to six decimal places as
needed.)

Statistics
ProbabilityThe combined scores of the almost 1.7 million high school seniors taking the SAT in 2013 were approximately Normal with mean 1011 and standard deviation 216. According to the 68-95-99.7 Rule, what percent of high school seniors had SAT scores between
1011 - 216 = 795
and
1011 + 216 = 1227?
99.7%
95%
68%
all of them.

Statistics
ProbabilityAccording to the 68-95-99.7 Rule, what percent of high school seniors had SAT scores between
579 and 1443?
68%
95%
99.7%
impossible to tell.

Statistics
ProbabilityAccording to the 68-95-99.7 Rule, 99.7% of high school seniors had SAT scores between
what and what?

Statistics
ProbabilityThe upper arm length of females over 20 years old in the United States is approximately Normal with mean 35.8 cm and standard deviation 2.1 cm.
According to the 68-95-99.7 Rule, what percent of women over 20 have upper arm length less than 40 cm?

Statistics
ProbabilityFor 14-year-old boys, the distribution of blood cholesterol is approximately Normal with mean µ=170 milligrams of cholesterol per deciliter of blood (mg/dL) and standard deviation o = 30 mg/dL. According to the 68-95-99.7 Rule, what percent of 14-year-old boys have cholesterol between 110 and 140?
13.5%
27%
95%
68%

Statistics
ProbabilitySelect ALL of the CORRECT answers.
Standard deviation s for a data set can be equal to 0...
only if the data values are all 0.
impossible.
or positive, but never negative.
every time that the data values are all the same.

Statistics
ProbabilityA fair coin is flipped 100 times. Let X be the number of heads. What normal distribution best approximates X? Provide your answer below:
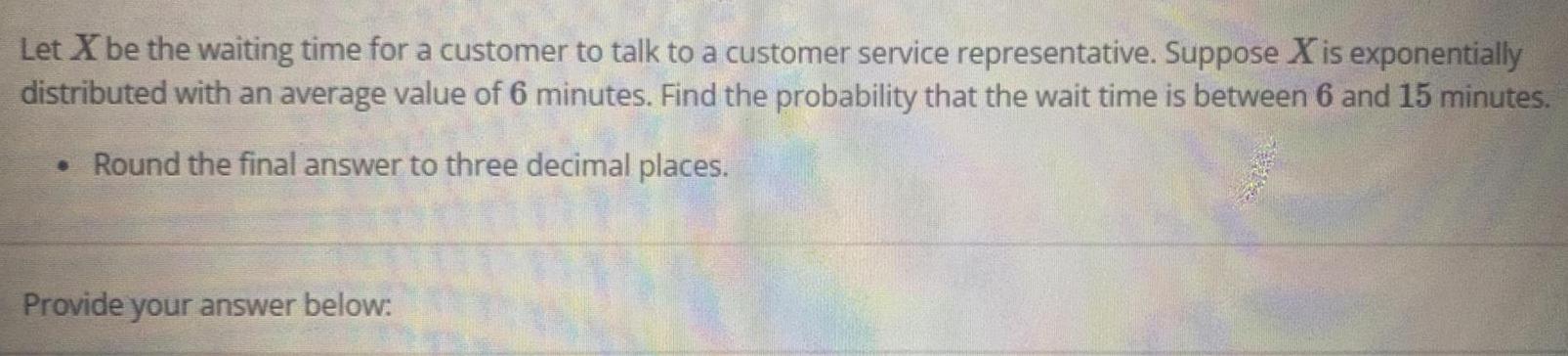
Statistics
ProbabilityLet X be the waiting time for a customer to talk to a customer service representative. Suppose X is exponentially distributed with an average value of 6 minutes. Find the probability that the wait time is between 6 and 15 minutes.
• Round the final answer to three decimal places.
Provide your answer below:
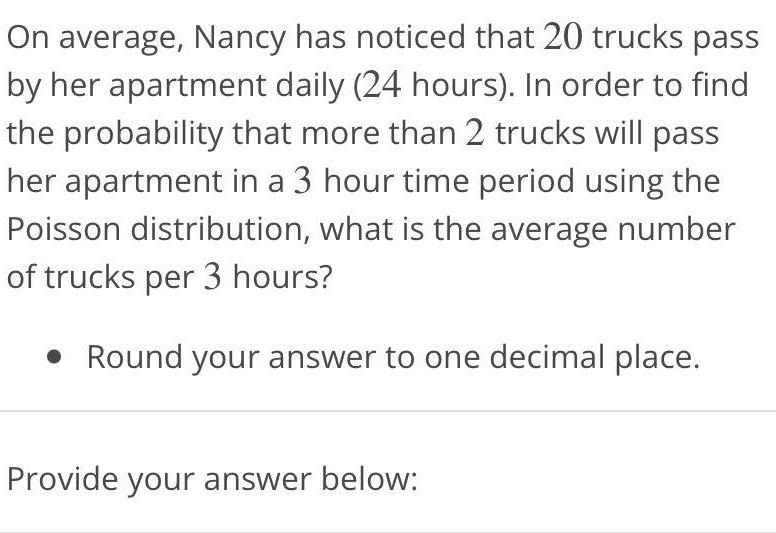
Statistics
ProbabilityOn average, Nancy has noticed that 20 trucks pass by her apartment daily (24 hours). In order to find the probability that more than 2 trucks will pass her apartment in a 3 hour time period using the Poisson distribution, what is the average number of trucks per 3 hours?
• Round your answer to one decimal place. Provide your answer below:

Statistics
ProbabilityA tire company finds the lifespan for one brand of its tires is normally distributed with a mean of 47,500 miles and a standard deviation of 3,000 miles. What mileage would correspond to the the highest 3% of the tires?
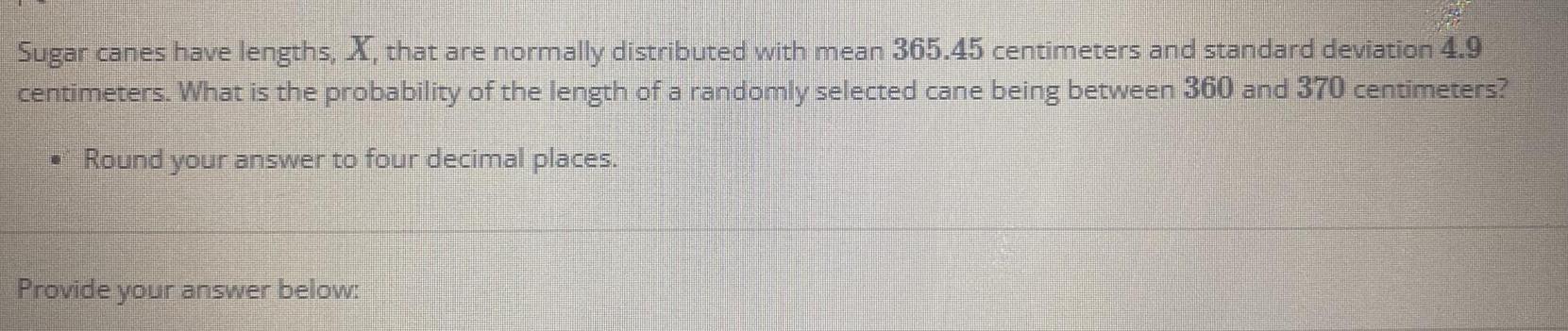
Statistics
ProbabilitySugar canes have lengths, X, that are normally distributed with mean 365.45 centimeters and standard deviation 4.9 centimeters. What is the probability of the length of a randomly selected cane being between 360 and 370 centimeters?
Round your answer to four decimal places.
Provide your answer below:
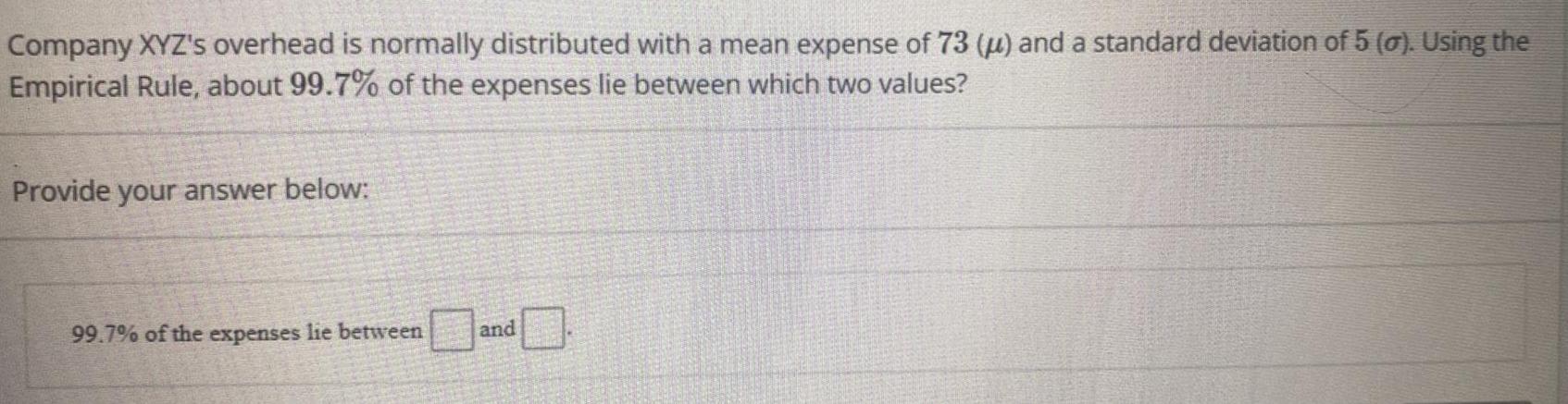
Statistics
ProbabilityCompany XYZ's overhead is normally distributed with a mean expense of 73 (μ) and a standard deviation of 5(σ). Using the Empirical Rule, about 99.7% of the expenses lie between which two values?
Provide your answer below:
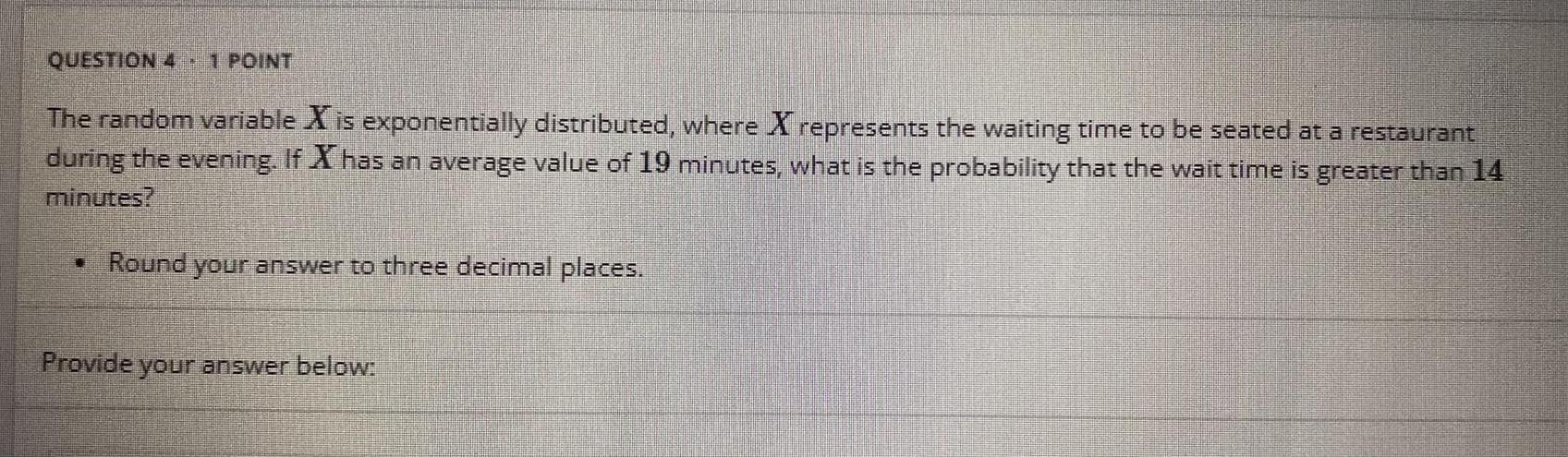
Statistics
ProbabilityThe random variable X is exponentially distributed, where X represents the waiting time to be seated at a restaurant during the evening. If X has an average value of 19 minutes, what is the probability that the wait time is greater than 14 minutes?
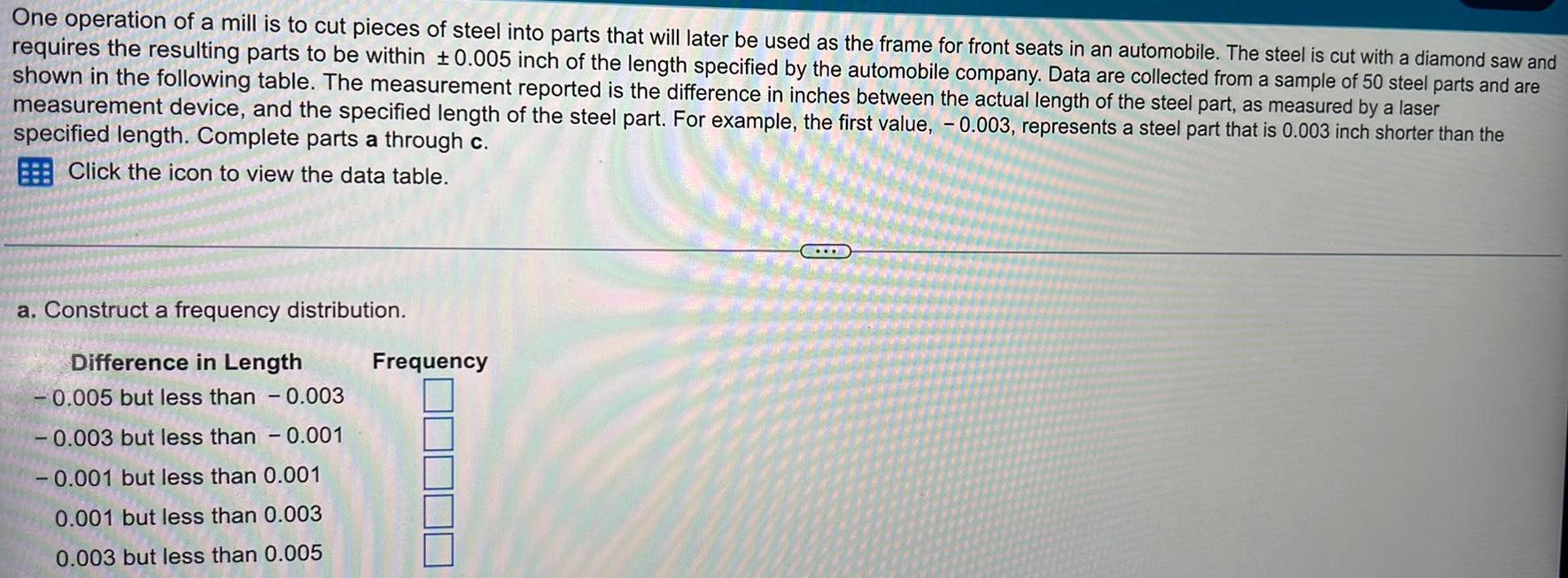
Statistics
ProbabilityOne operation of a mill is to cut pieces of steel into parts that will later be used as the frame for front seats in an automobile. The steel is cut with a diamond saw and requires the resulting parts to be within ±0.005 inch of the length specified by the automobile company. Data are collected from a sample of 50 steel parts and are shown in the following table. The measurement reported is the difference in inches between the actual length of the steel part, as measured by a laser measurement device, and the specified length of the steel part. For example, the first value, -0.003, represents a steel part that is 0.003 inch shorter than the specified length. Complete parts a through c.
a. Construct a frequency distribution.
-0.005 but less than 0.003
-0.003 but less than 0.001
-0.001 but less than 0.001
0.001 but less than 0.003
0.003 but less than 0.005

Statistics
ProbabilityA county office gets an average of 10 calls in a 2 hour time period. What is the probability that the county office will get more than 0 calls in a 15 minute period?

Statistics
ProbabilityThe probability of buying a movie ticket with a popcorn coupon is 0.608. If you buy 10 movie tickets, what is the probability that 3 or more of the tickets have popcorn coupons? (Round your answer to 3 decimal places if necessary.)
Provide your answer below:
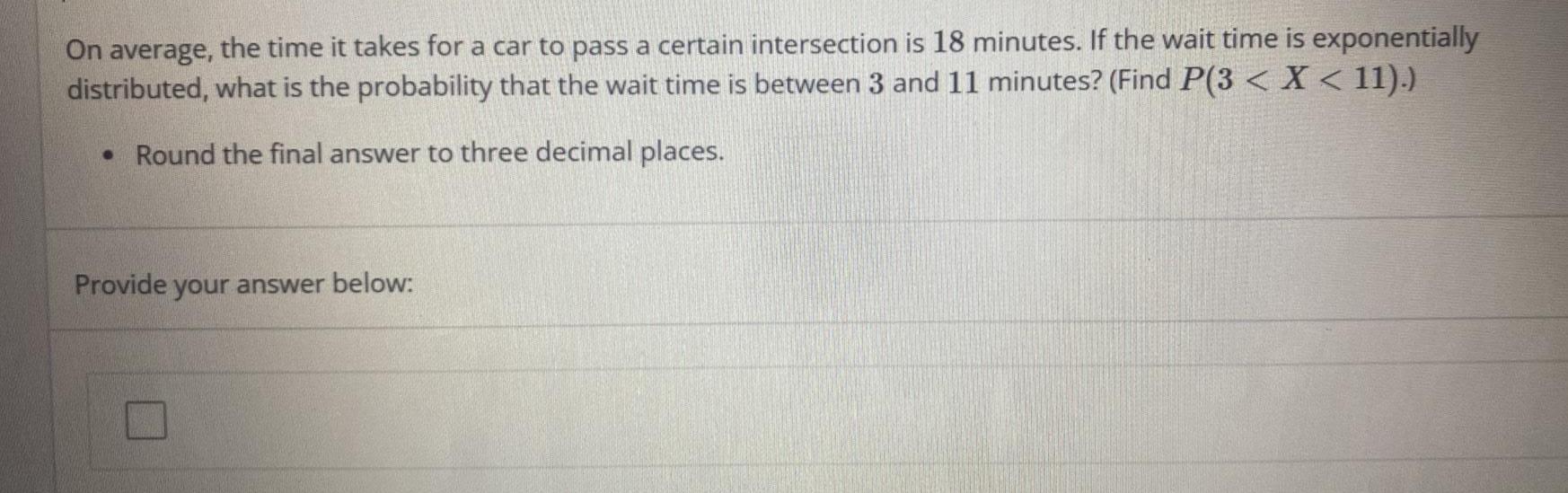
Statistics
ProbabilityOn average, the time it takes for a car to pass a certain intersection is 18 minutes. If the wait time is exponentially distributed, what is the probability that the wait time is between 3 and 11 minutes? (Find P(3 < X < 11).)
• Round the final answer to three decimal places.
Provide your answer below:

Statistics
ProbabilityA multiple-choice test consists of 160 questions with possible answers of A, B, C, and D. Estimate the probability that with random guessing, the number of correct answers is between 50 and 55, inclusive. Use Excel to find the probability. • Round your answer to four decimal places.

Statistics
ProbabilityA softball pitcher has a 0.675 probability of throwing a strike for each pitch and a 0.325 probability of throwing a ball. If the softball pitcher throws 29 pitches, we want to know the probability that exactly 19 of them are strikes. Consider strikes as successes in the binomial distribution.

Statistics
ProbabilityLet X be the waiting time for a fire department to get called to a house fire, where X has an average value of 32 hours. If the random variable X is known to be exponentially distributed, what are the parameters of this exponential distribution?
• Enter your answer for A as a fraction.

Statistics
ProbabilityThe amount of time it takes Tom to make breakfast is continuous and uniformly distributed between 4 minutes and 11 minutes. What is the probability that it takes Tom between 5 and 6 minutes given that it takes less than 9 minutes for him to make breakfast?
• Provide the final answer as a fraction.

Statistics
ProbabilityOn average, Stephanie has noticed that 19 trucks pass by her apartment daily (24 hours). In order to find the probability that exactly 6 trucks will pass her apartment in a 9 hour time period using the Poisson distribution, what is the time interva of interest?
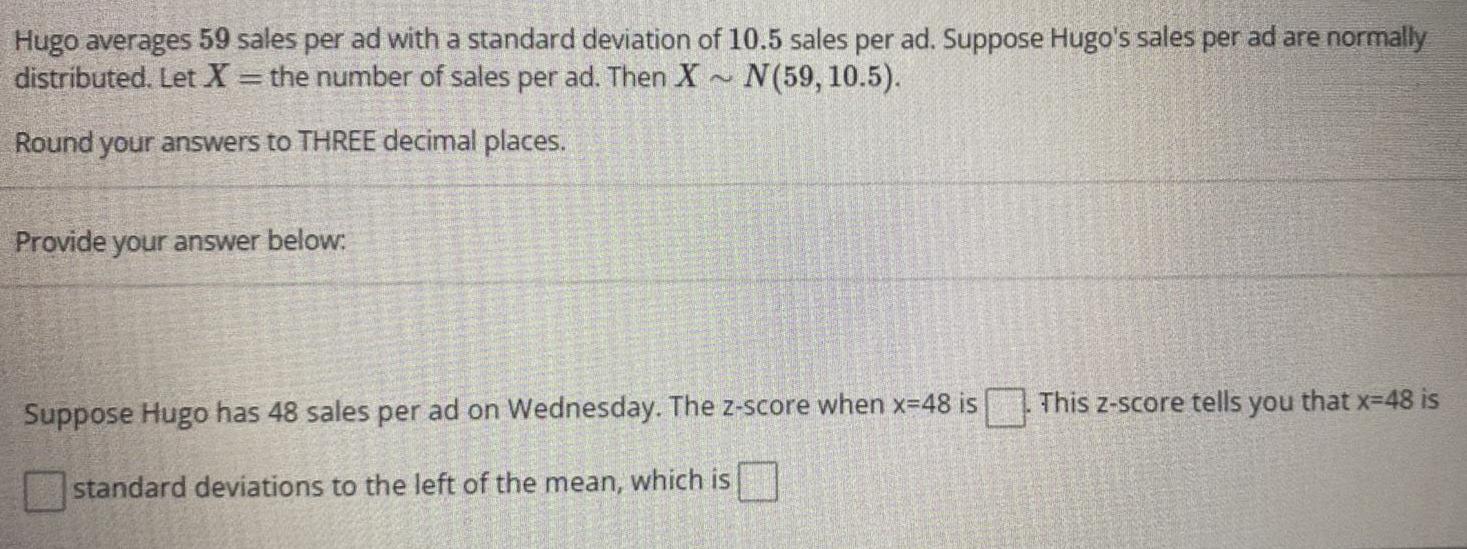
Statistics
ProbabilityHugo averages 59 sales per ad with a standard deviation of 10.5 sales per ad. Suppose Hugo's sales per ad are normally distributed. Let X = the number of sales per ad. Then X ~N(59, 10.5). Round your answers to THREE decimal places. Provide your answer below:
Suppose Hugo has 48 sales per ad on Wednesday. The z-score when x=48 is This z-score tells you that x-48 is __ standard deviations to the left of the mean, which is __
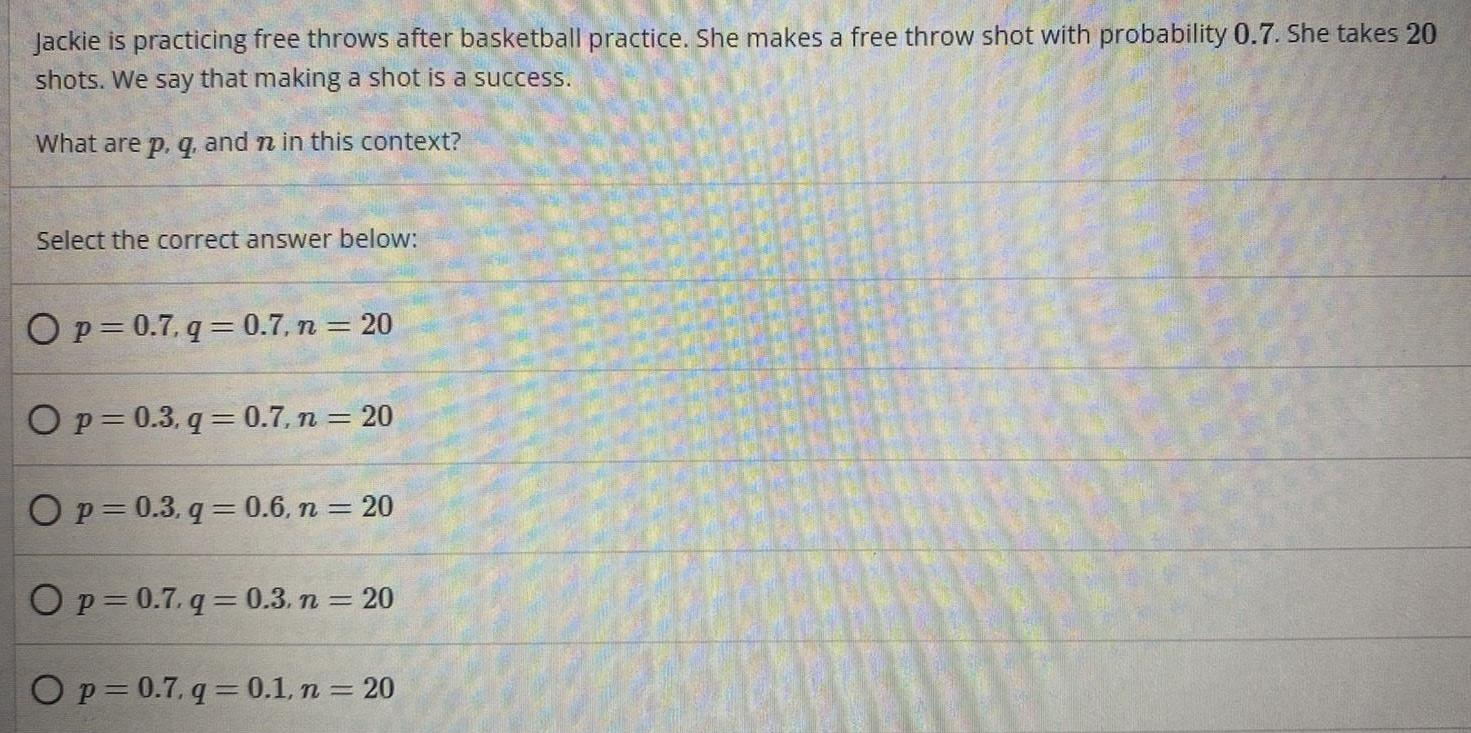
Statistics
ProbabilityJackie is practicing free throws after basketball practice. She makes a free throw shot with probability 0.7. She takes 20 shots. We say that making a shot is a success.
What are p, q, and n in this context?
Select the correct answer below:
p=0.7.q=0.7, n = 20
p=0.3, q=0.7, n = 20
p=0.3.q=0.6, n = 20
p=0.7.q=0.3. n = 20
p=0.7.q=0.1, n = 20
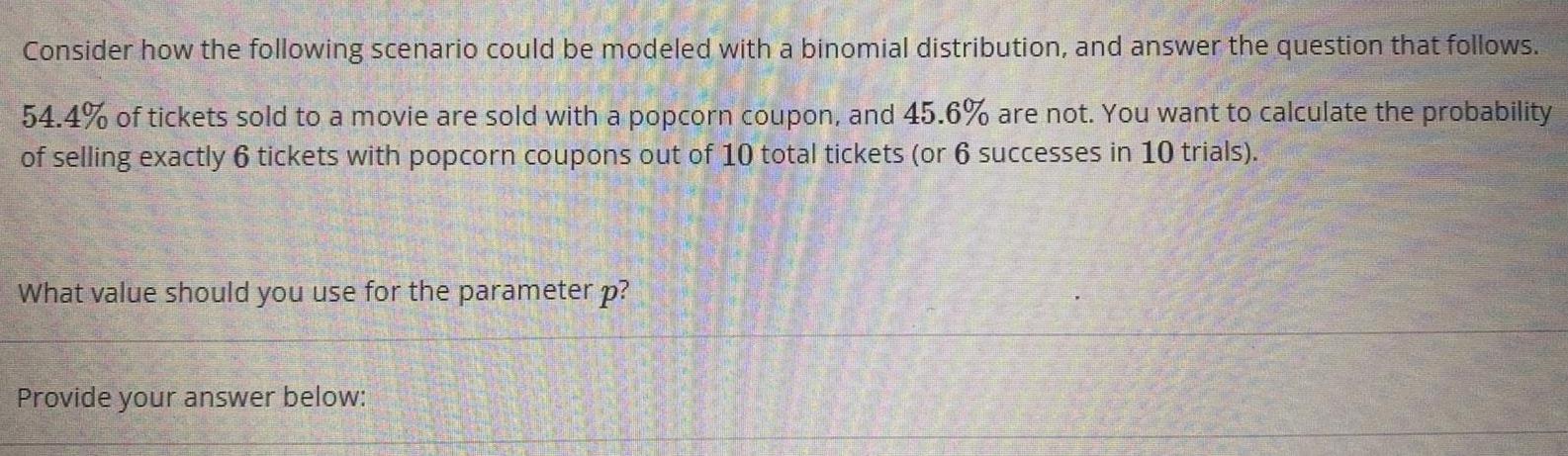
Statistics
ProbabilityConsider how the following scenario could be modeled with a binomial distribution, and answer the question that follows. 54.4% of tickets sold to a movie are sold with a popcorn coupon, and 45.6% are not. You want to calculate the probability of selling exactly 6 tickets with popcorn coupons out of 10 total tickets (or 6 successes in 10 trials). What value should you use for the parameter p? Provide your answer below:
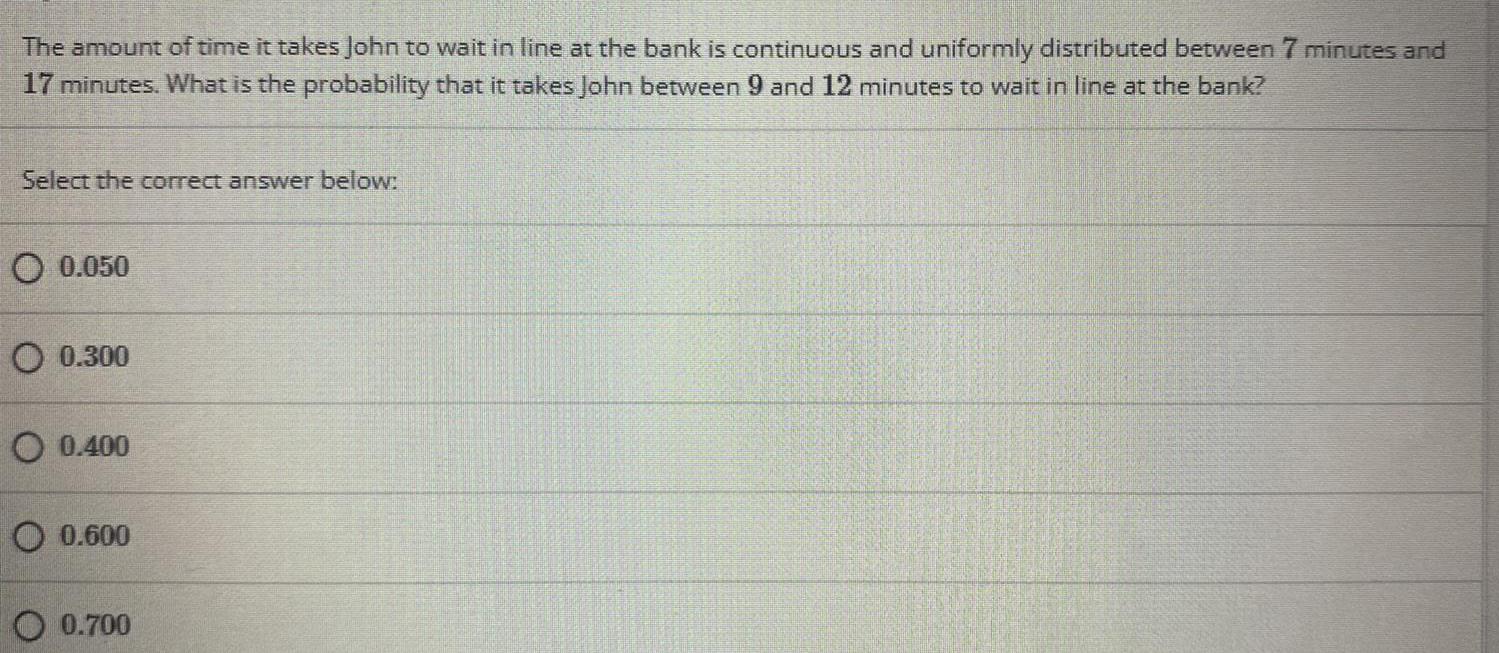
Statistics
ProbabilityThe amount of time it takes John to wait in line at the bank is continuous and uniformly distributed between 7 minutes and 17 minutes. What is the probability that it takes John between 9 and 12 minutes to wait in line at the bank?
Select the correct answer below:
0.050
0.300
0.400
0.600
0.700

Statistics
ProbabilityJustin has a bird feeder which gets visited by an average of 18 birds every 2 hours during daylight hours. What is the probability that the bird feeder will be visited by more than 5 birds in a 40 minute period during daylight hours? (Round your answer to three decimal places.)

Statistics
ProbabilityGiven that P(A AND B) = 0.37 and P(A/B) = 0.68, what is P(B)? | Round your answer to three decimal places.

Statistics
ProbabilityThe amount of time it takes Hugo to solve a Rubik's cube is continuous and uniformly distributed between 4 minutes and 11 minutes. What is the probability that it takes Hugo less than 5 minutes given that it takes less than 6 minutes for him to solve a Rubik's cube?
• Provide the final answer as a fraction.

Statistics
ProbabilityWhich of the following scenarios contain biased samples? Select all that apply.
Select all that apply.
To estimate the mean number of sales that coworkers take at his company, Benjamin collects data from a randomly selected proportionate number of coworkers from each company site.
Howard wants to estimate the mean cost of waste in his company. He collects data by recording waste from the first process step.
To estimate the political party distribution of residents in his state, Sean collects data from a large group of randomly selected residents of his city.
Teresa wants to estimate the mean amount of money spent on clothes per week by mall shoppers. She collects data from every 10th person entering a clothing store at the mall.

Statistics
ProbabilityIf the probability that a randomly chosen college student uses a ride sharing app is 0.27, then what is the probability that a randomly chosen college student does not use a ride sharing app?
Give your answer as a decimal.
Provide your answer below:

Statistics
ProbabilityA softball pitcher has a 0.507 probability of throwing a strike for each pitch. If the softball pitcher throws 15 pitches, what is the probability that exactly 8 of them are strikes?
Insert the correct symbol to represent this probability.