2D Geometry Questions and Answers

Geometry
2D Geometry4 Draw 2 lines that could be the image of line m by a dilation Label the lines n and P 0 MATH m

Geometry
2D Geometryram shores A BDF its medians centroid H and the lengths of of the subsegments Apply the Centroid theorem to find other lengths Given Bl 18 find EH 2 Given BH 18 find BE 3 Given CH 4 find CF 4 Given BD 30 find BC 4 is done for you BD BC CD Segment Addition Postulate 30 BC BC Definition of Midpoint 30 2BC 15 BC Simplify Division Property of Equality 5 Given BG 11 find BF B 18 H E D

Geometry
2D GeometryComplete the Two Column Proof of the Converse of the Angle Bisector Theorem Given VX1YX and VZ 1 YZ and VX VZ Prove YV bisects ZXYZ Two Column Proof of the Converse of the Angle Bisector Theorem Statements 1 VX 1 YX and VZ 1 YZ 2 VX VZ 3 ZVXY and ZVZY are right angles 4 YV YV 5 AVXY A VZY 6 LXYV LZYV 7 YV bisects ZXYZ Reason Bank Given Reasons Reflexive Property of Congruence Definition of Perpendicular Lines
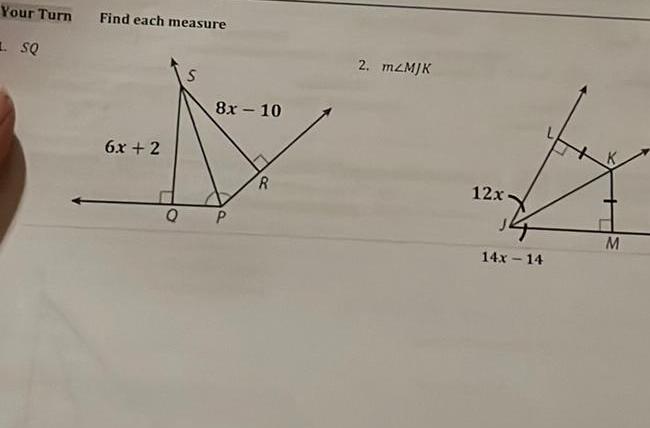
Geometry
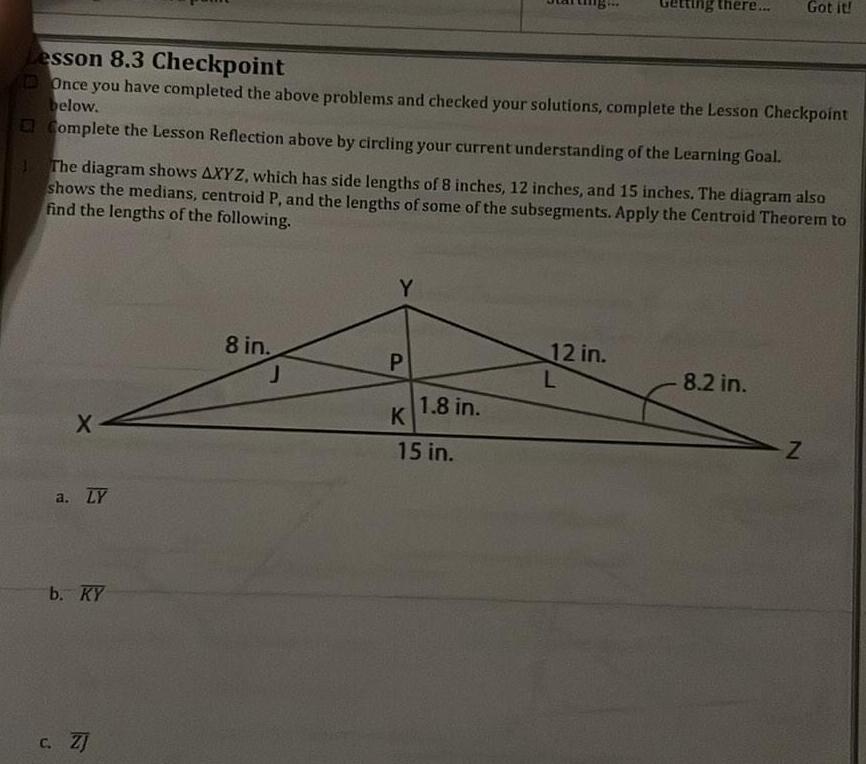
2D GeometryLesson 8 3 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal X The diagram shows AXYZ which has side lengths of 8 inches 12 inches and 15 inches The diagram also shows the medians centroid P and the lengths of some of the subsegments Apply the Centroid Theorem to find the lengths of the following a LY b KY c ZJ 8 in J Y P K 1 8 in 15 in ng there 12 in L Got it 8 2 in Z

Geometry
2D GeometryLesson 7 3 Homework HW Independent Practice 100 6 1 Order the sides from shortest to longest Complete problems 1 8 below for independent practice 12 When you are finished check the solutions with your teacher 3 Order the angles from least to greatest M e 2 Order the sides from shortest to longest L K 97 55 4 Order the angles from least to greatest 17 16 R 5 State if the following measures can be the sides 6 State if the following measures can be the sides of a triangle of a triangle 12 6 13 9 18 9 7 State if the following measures can be the sides 8 State if the following measures can be the sides of a triangle of a triangle 8 3 6 11 7 20 Optional Complete problems 5 7 13 14 17 19 21 23 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Geometry
2D GeometryLesson 7 2 Homework A HW 12 Complete problems 1 6 below for independent practice 1 Find the value of x in the figure below 45 When you are finished check the solutions with your teacher 3 Find the value of x in the figure below 5 Find the value of x in the isosceles triangle shown below Then find the measure of Z A B 2r 4 3r Optional Complete problems 4 5 7 9 16 2 Find the value of x in the figure below x 4 Find the value of x in the figure below 2x 8 X 10 55 6 In the figure below 2WXZ and ZWYZ are bisected forming isosceles triangle WXY and ZXY What is the value of W W 25
Geometry
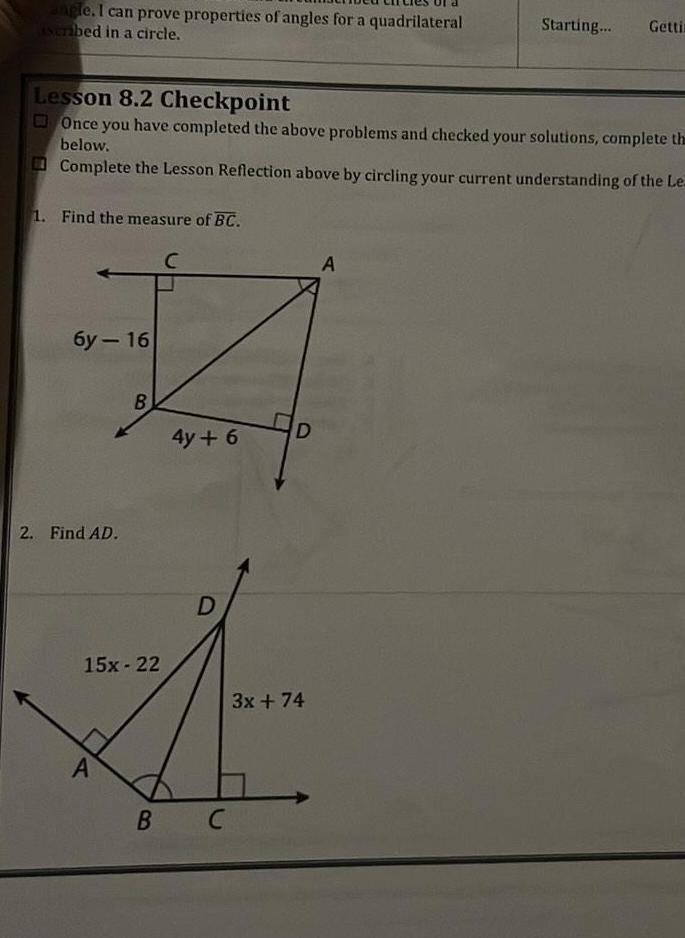
2D Geometryangle I can prove properties of angles for a quadrilateral ascribed in a circle Lesson 8 2 Checkpoint Once you have completed the above problems and checked your solutions complete the below Complete the Lesson Reflection above by circling your current understanding of the Le 1 Find the measure of BC C 6y 16 2 Find AD B 15x 22 A B 4y 6 D C D 3x 74 Starting Gettin A
Geometry
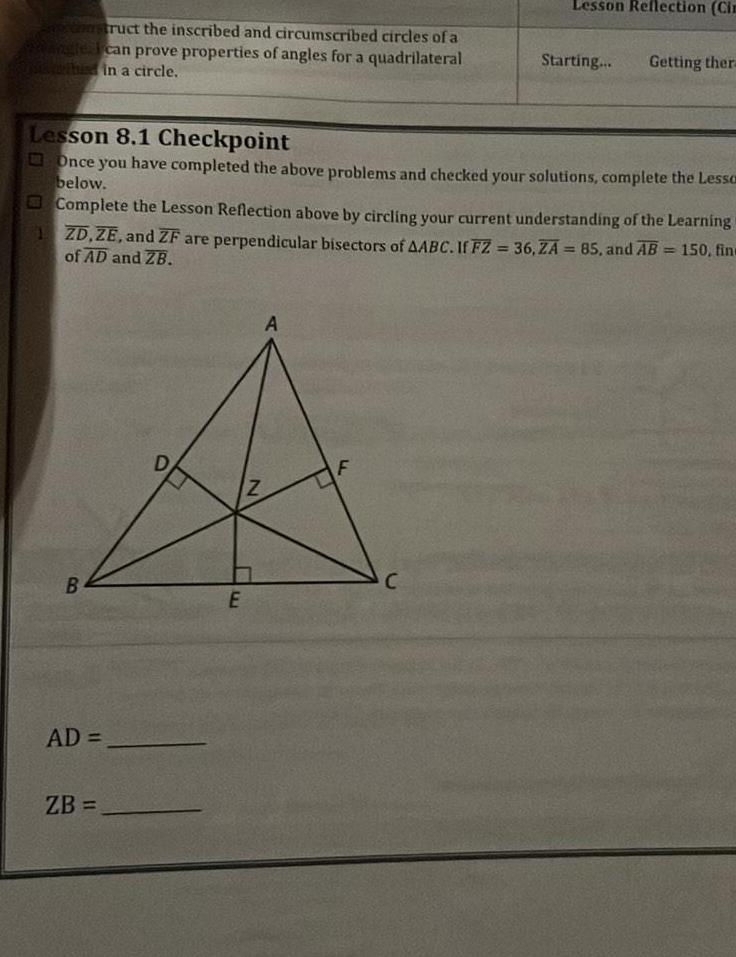
2D Geometrystruct the inscribed and circumscribed circles of a angle I can prove properties of angles for a quadrilateral mithid in a circle B Lesson 8 1 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesso below AD Complete the Lesson Reflection above by circling your current understanding of the Learning ZD ZE and ZF are perpendicular bisectors of AABC If FZ 36 ZA 85 and AB 150 fine of AD and ZB ZB E N A Lesson Reflection Cim F Starting C Getting thera

Geometry
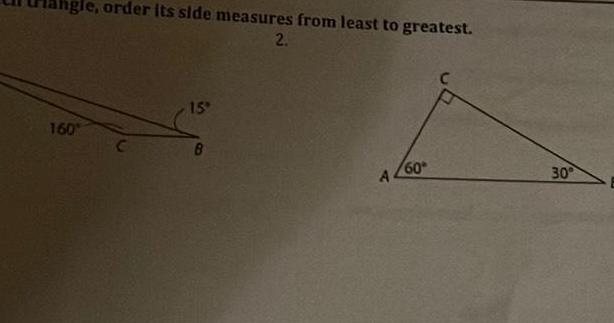
2D GeometryLesson 7 3 Checkpoint Once you have completed the above problems and checked your solutions complete below Complete the Lesson Reflection above by circling your current understanding of the I 1 Write the side lengths in order from shortest to greatest A B 45 18 2 Write the angles in order from least to greatest S T 25 15 65 U 70 C
Geometry
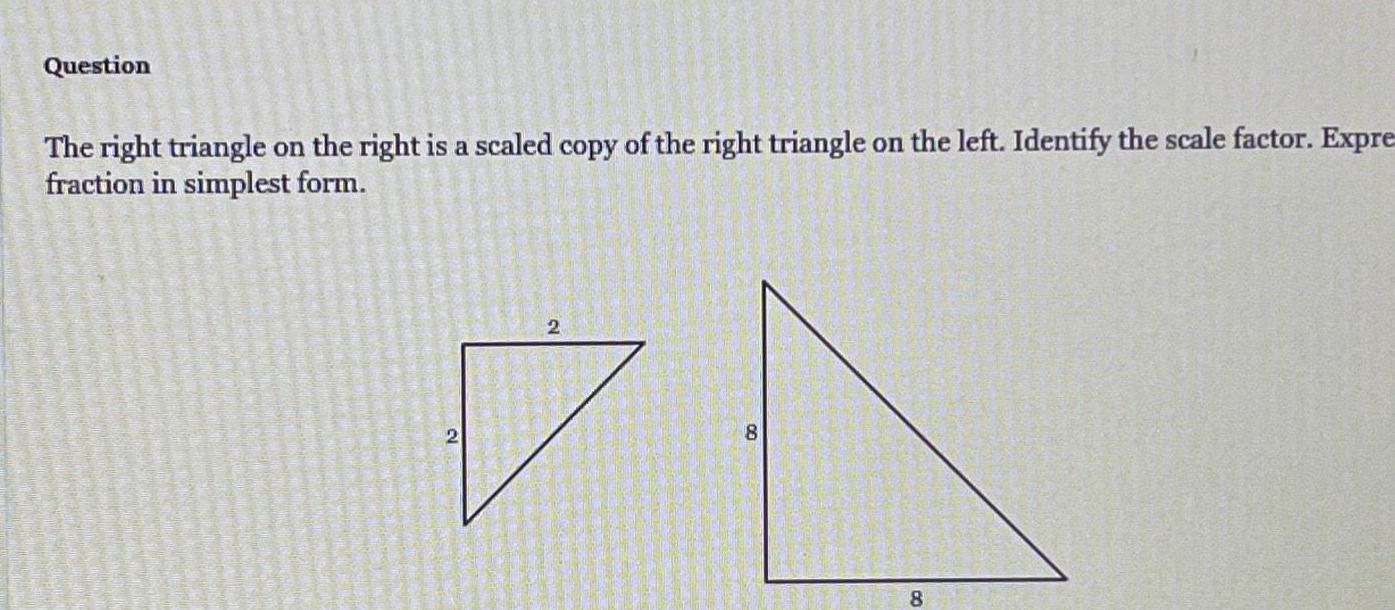
2D GeometryQuestion The right triangle on the right is a scaled copy of the right triangle on the left Identify the scale factor Expre fraction in simplest form 2 2 8 8
Geometry
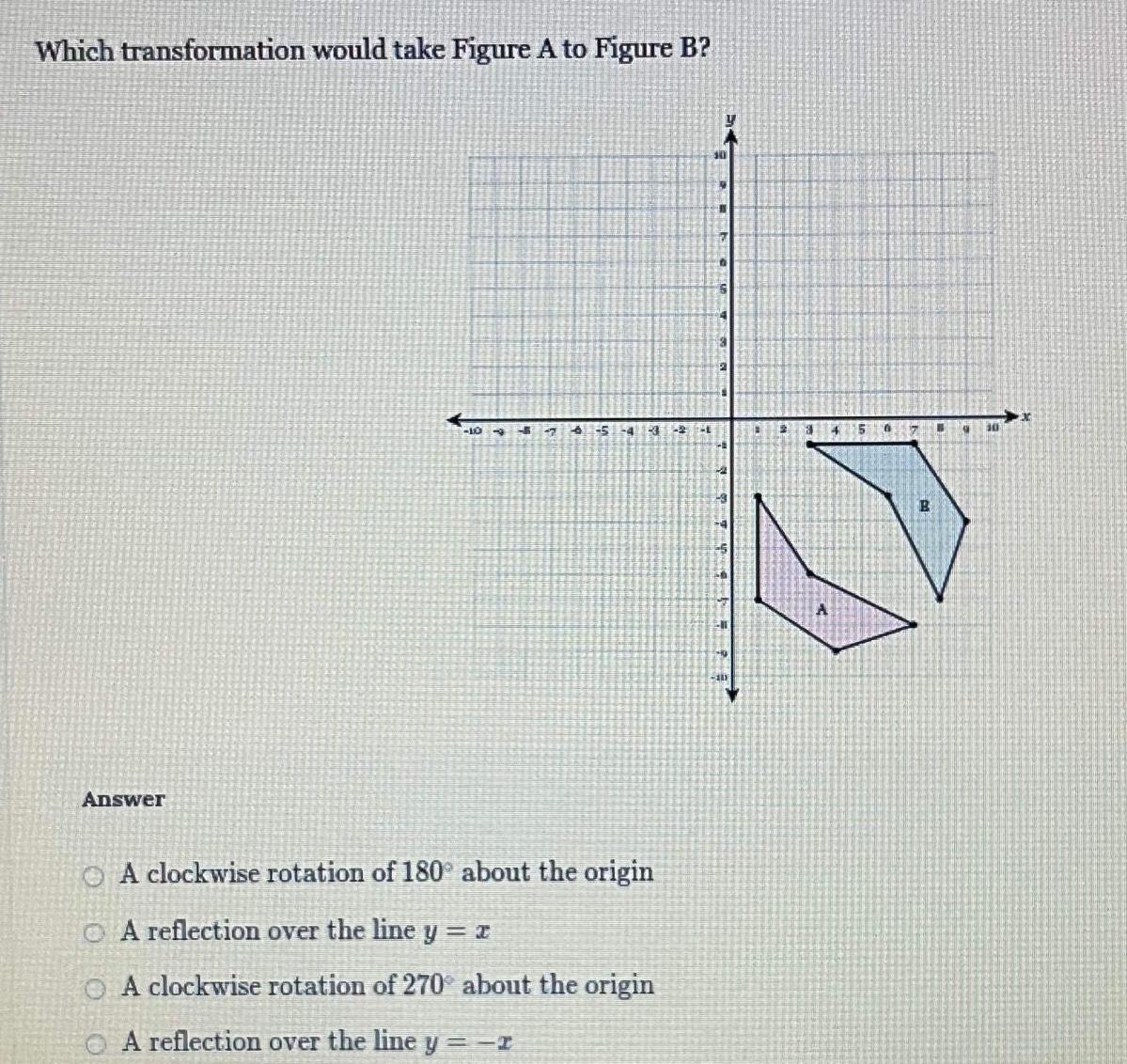
2D GeometryWhich transformation would take Figure A to Figure B Answer 10 47 5 4 341 A clockwise rotation of 180 about the origin A reflection over the line y x O A clockwise rotation of 270 about the origin A reflection over the line y r 241 301 14 H 7 Teh El 10 111 2 4 5 6 B H 30

Geometry
2D GeometryCool Down All Together Now Here is the image of triangle ABC and its dilation using center D and scale factor 2 DC CB A C A B C B H D 1 Why is segment B C on the same line as its corresponding side segment BC 2 Explain how you know that segment A C is parallel to its corresponding side segment AC 3 What relationship does angle ACB have with its corresponding angle A C B Explain or show your reasoning
Geometry
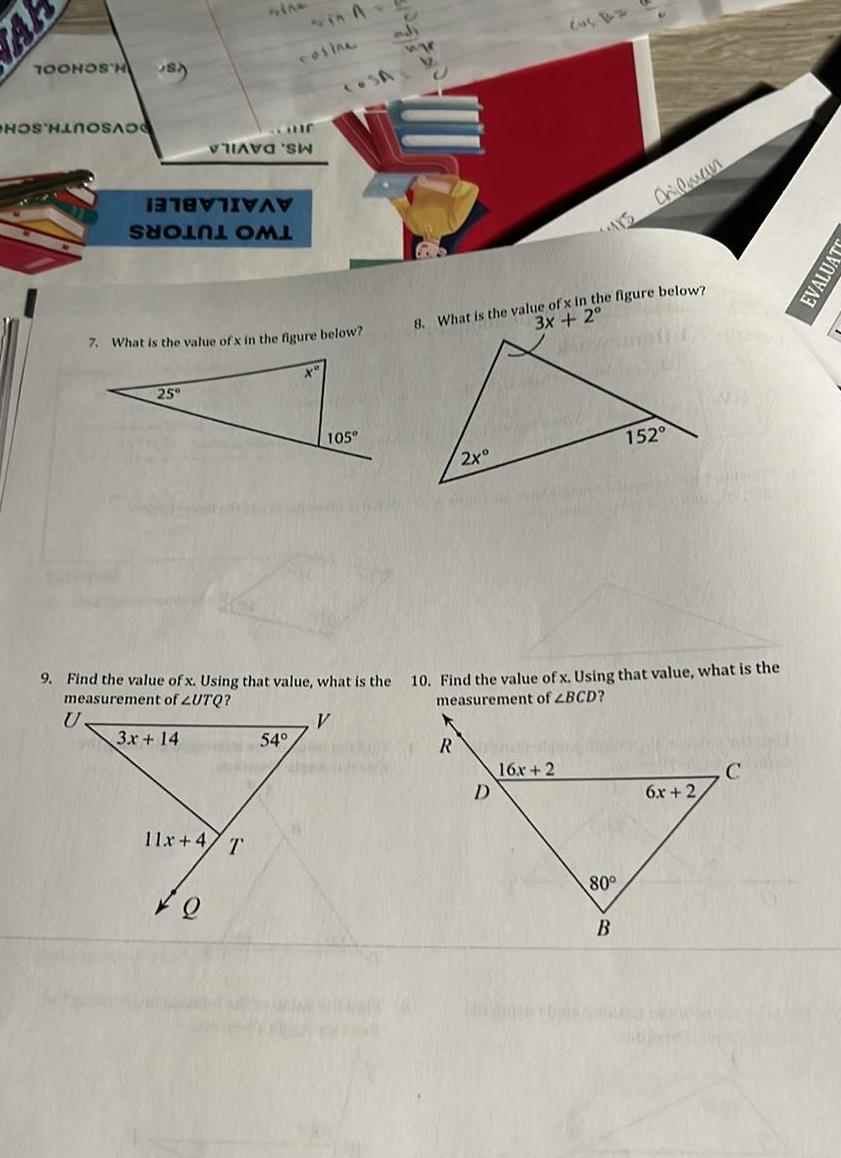
2D GeometryAR TOONOS H HO SA U VAN SHOE OML 25 sine 11x 47 T 7 What is the value of x in the figure below Q SA Suur W cosine 54 9 Find the value of x Using that value what is the measurement of LUTQ V 3x 14 to 105 adi wy V J YOU 8 What is the value of x in the figure below 3x 2 2x R 10 Find the value of x Using that value what is the measurement of 2BCD D Chilman 16x 2 80 B 152 6x 2 C EVALUATO

Geometry
2D Geometry6 Given the polar equation r 2 8 sin 0 The eccentricity is e The equation of the directrix is The shape of the curve is Select an answer

Geometry
2D GeometryPart 5 7 Let g x x 2x 3 a Find the vertex b Find the x intercepts zeros c Graph f x by plotting the points from parts a and b

Geometry
2D GeometryS of interior angles of a triangle sum to 180 50 Lesson 7 1 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Determine which of the following angle measures are correct Select two that apply A B 4x 11 5 10x 5x 5 R 60 11x 6 2 Determine which of the following angle measures are correct Select two that apply C A A OB C OD J easures Starting Getting there A OB C OD mLAQR 95 mzSQR 100 mZAQR 55 mzSRQ 45 Got it mZCAB 75 m2JAB 115 mzCBA 65 mzCBA 55

Geometry
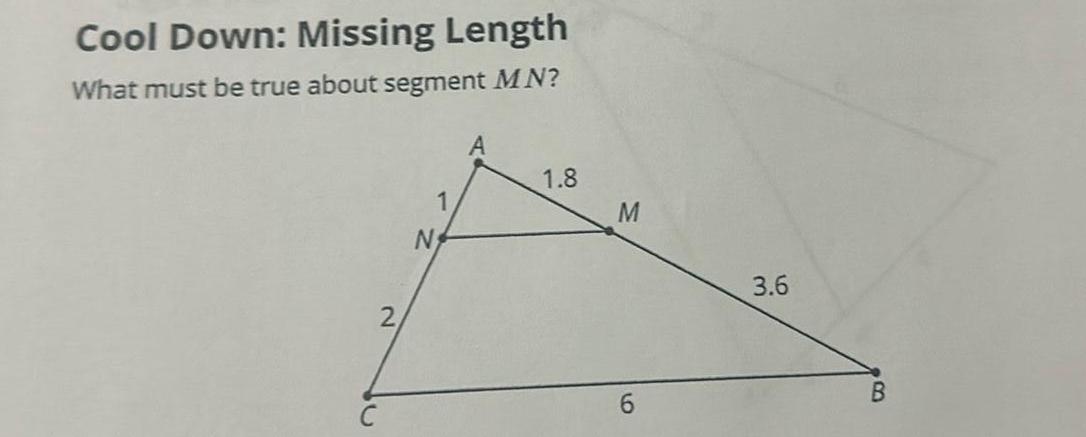
2D Geometry2 Your Turn 1 Remote interior angles For the figure shown find the unknown angle measure x For the figure shown find the unknown angle measure x Exterior angle OLUTASH EXPLAIN 3 Using Exterior Angles Read Explain 3 and complete Your Turn 1 2 adapted from Lesson 7 1 Show all your work 0 In the figure to the right we have the interior angles 21 22 and 23 of a triangle We also have the exterior angle 24 of the triangle 140 150 21 22 23 23 24 130 When we extend the side of a polygon the angle formed by the side of the polygon and the extended side is called an exterior angle Exterior angles form linear pairs with the interior angles The remote interior angles of a triangle are the angles that are not adjacent to the exterior angle m21 m2 m 4 Because they form a linear pair 23 and 24 are supplementary So 23 24 180 Also the sum of the measures of any triangle is 180 So 21 22 23 180 After substituting for 180 and simplifying we have 21 22 24 105 Thus the measure of the triangle s exterior angle 24 is equal to the sum remote interior angles 21 and 22 This conjecture can be formally stated as a theorem Exterior Angle Theorem
Geometry
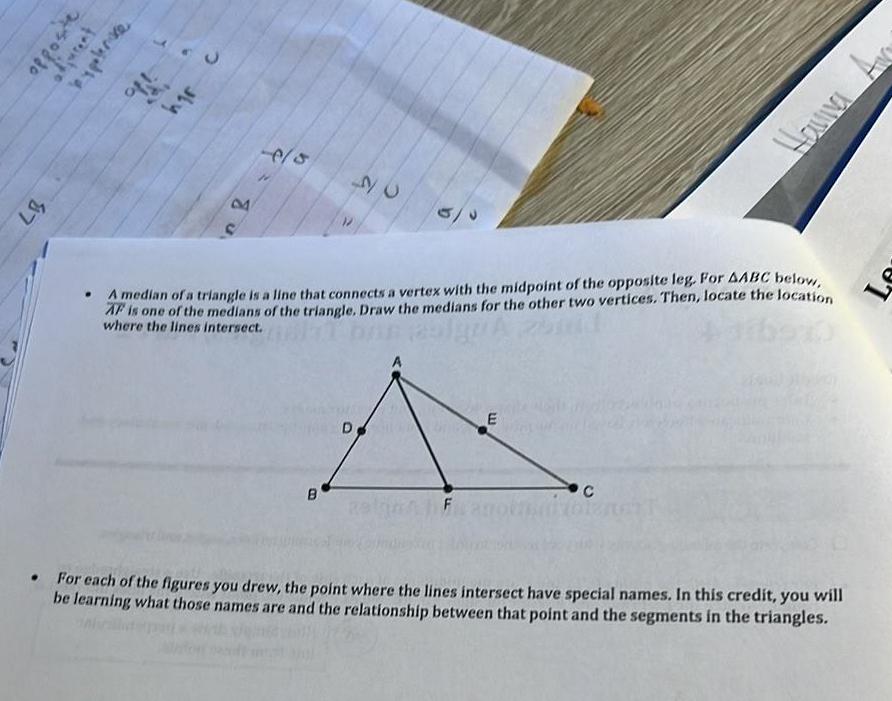
2D Geometry87 opposite bypolerice hgr 8 6 5 B 26 A median of a triangle is a line that connects a vertex with the midpoint of the opposite leg For AABC below AF is one of the medians of the triangle Draw the medians for the other two vertices Then locate the location where the lines intersect D F E Havia C For each of the figures you drew the point where the lines intersect have special names In this credit you will be learning what those names are and the relationship between that point and the segments in the triangles
Geometry
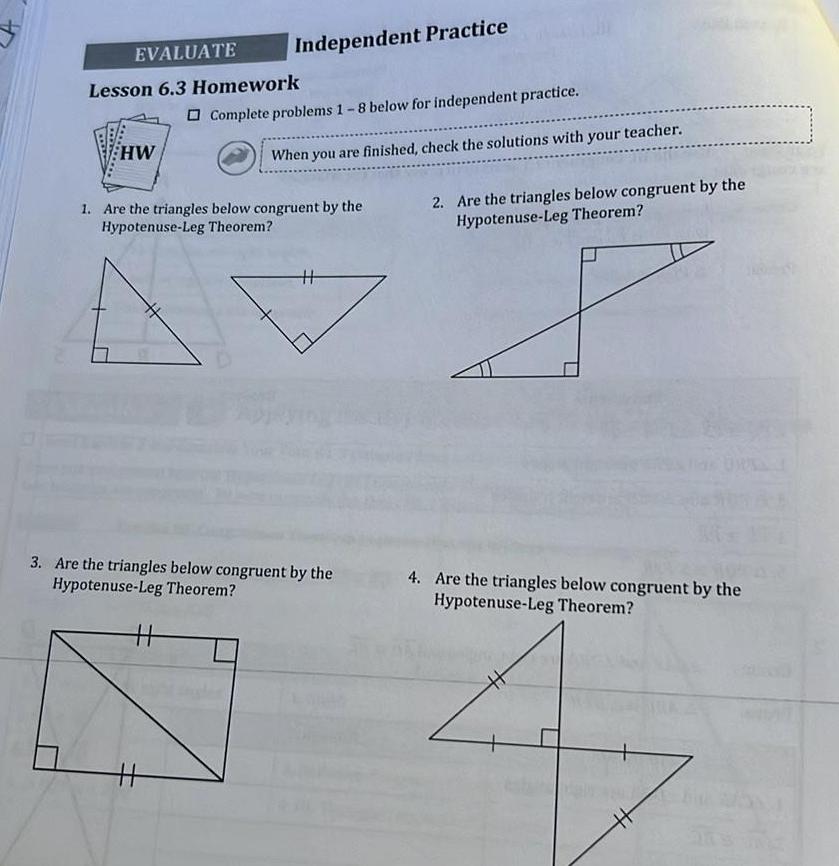
2D GeometryEVALUATE Lesson 6 3 Homework HW Independent Practice Complete problems 1 8 below for independent practice 11 When you are finished check the solutions with your teacher 1 Are the triangles below congruent by the Hypotenuse Leg Theorem 11 3 Are the triangles below congruent by the Hypotenuse Leg Theorem 2 Are the triangles below congruent by the Hypotenuse Leg Theorem 4 Are the triangles below congruent by the Hypotenuse Leg Theorem
Geometry
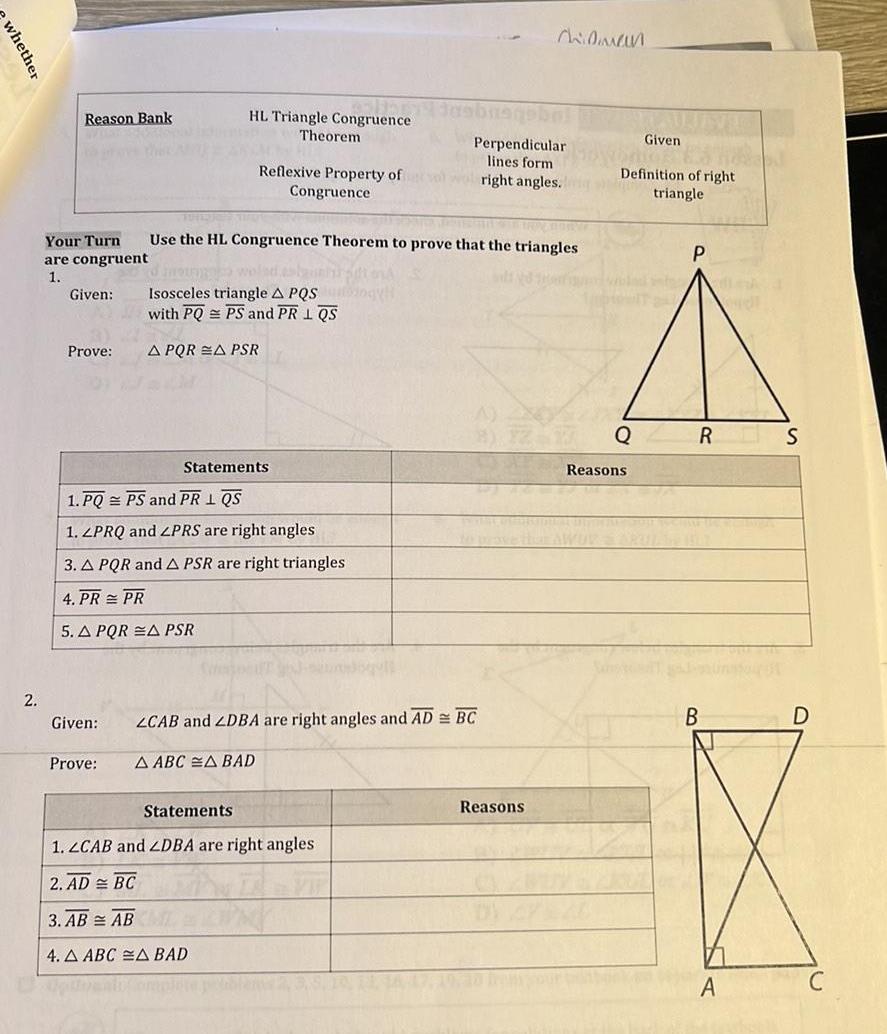
2D Geometrywhether 2 Reason Bank Your Turn are congruent 1 Given Prove Given Prove HL Triangle Congruence Theorem Reflexive Property of Congruence me wo Isosceles triangle A PQS Mogy with PQPS and PR 1 QS A PQR A PSR Statements 1 PQ PS and PR I QS 1 LPRQ and ZPRS are right angles 3 A PQR and A PSR are right triangles 4 PR PR 5 A PQR A PSR Use the HL Congruence Theorem to prove that the triangles Statements ZCAB and ZDBA are right angles and AD BC A ABC A BAD insbusqe Perpendicular lines form alwright angles 1 ZCAB and ZDBA are right angles 2 AD BC 3 AB AB 4 A ABC A BAD Chidman Reasons triangle Definition of right Q Given Reasons P A DE RS A D

Geometry
2D GeometryLearning Goal I can prove theorems about geometric figures using triangle congruence and similarity 19 07 Starting Lesson 6 3 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal G Getting there 1 Determine whether enough information is given to prove that the triangles are congruent by the HL Congruence Theorem Explain your answer AGKJ and AJHG K Got H
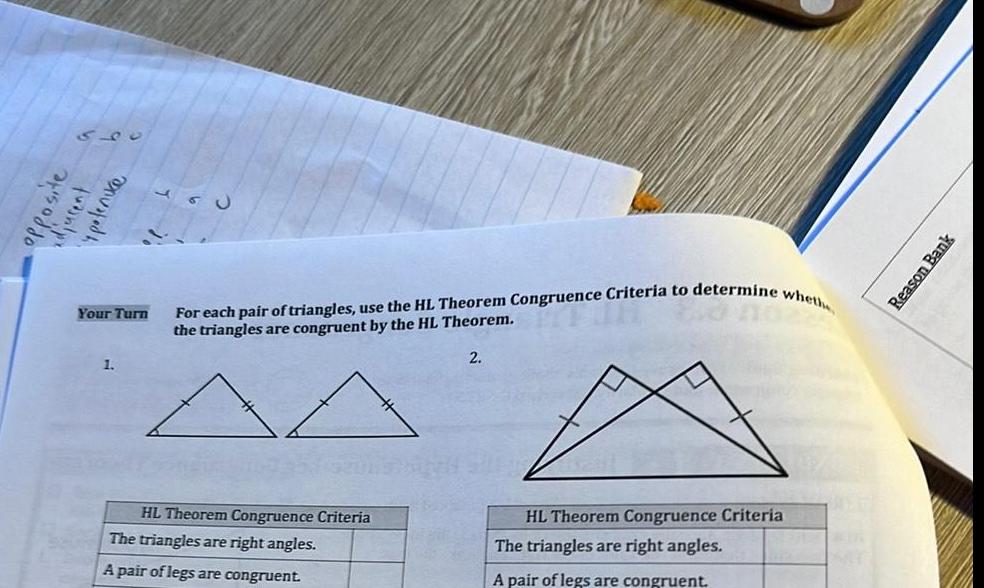
Geometry
2D Geometry550 du site y potenuce Your Turn 1 For each pair of triangles use the HL Theorem Congruence Criteria to determine whethe the triangles are congruent by the HL Theorem HL Theorem Congruence Criteria The triangles are right angles A pair of legs are congruent 2 HL Theorem Congruence Criteria The triangles are right angles A pair of legs are congruent Reason Bank

Geometry
2D Geometry5 What additional information would be enough to prove that AHIJ AKLM by HL I A IH LK B ZILL C LJ LM or I L D ZJ LM H J 7 What additional information would be enough to prove that AKLM AWVM by HL L domany M K March A LK LW B LK VW C ML MV or LK VW D ZKML LWMV K WAS APP pogrens 6 What additional information would be enough to prove that AXYZ AXYJ by HL Z bezmsidots 12 X A LZXY LJXY or LXYZ LXYJ B YZ YJ C XY XY D YZ YJ or ZX JX K 8 What additional information would be enough to prove that AWUVAKUL by HL W V A UV UL or WU KU B LWUV LKUL or V L C LWUV KUL or W 2K D LV ZL Optional Complete problems 2 3 5 10 13 16 17 19 20 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Geometry
2D GeometryLesson 6 2 Homework 1 Write whether the triangles below are congruent by ASA AAS or neither W Complete problems 1 6 below for independent practice 3 What additional information would be enough to 4 What additional information would be enough to prove that the two triangles are congruent by prove that AWVU NMLA by AAS AAS 0000 When you are finished check the solutions with your teacher U A B C D N M A ZWLN B VU ML C ZULL OD WU NL 2 Write whether the triangles below are congruent by ASA AAS or neither BC ZC LB LZ DB XZ ZD 2X X A O B C D 5 What additional information would be enough to 6 What additional information would be enough to prove that ADBC AXZC by AAS prove that ARVU AWUV by AAS R Z XZ GF 2X LG YZ EF XY GF determine whether W DA ZW LR OB C OD LRVU LWUV VW UR RV WU Optional Complete problems 2 5 7 12 from your textbook on separate lined paper finichod check the odd problems for solutions at the back of the textbook
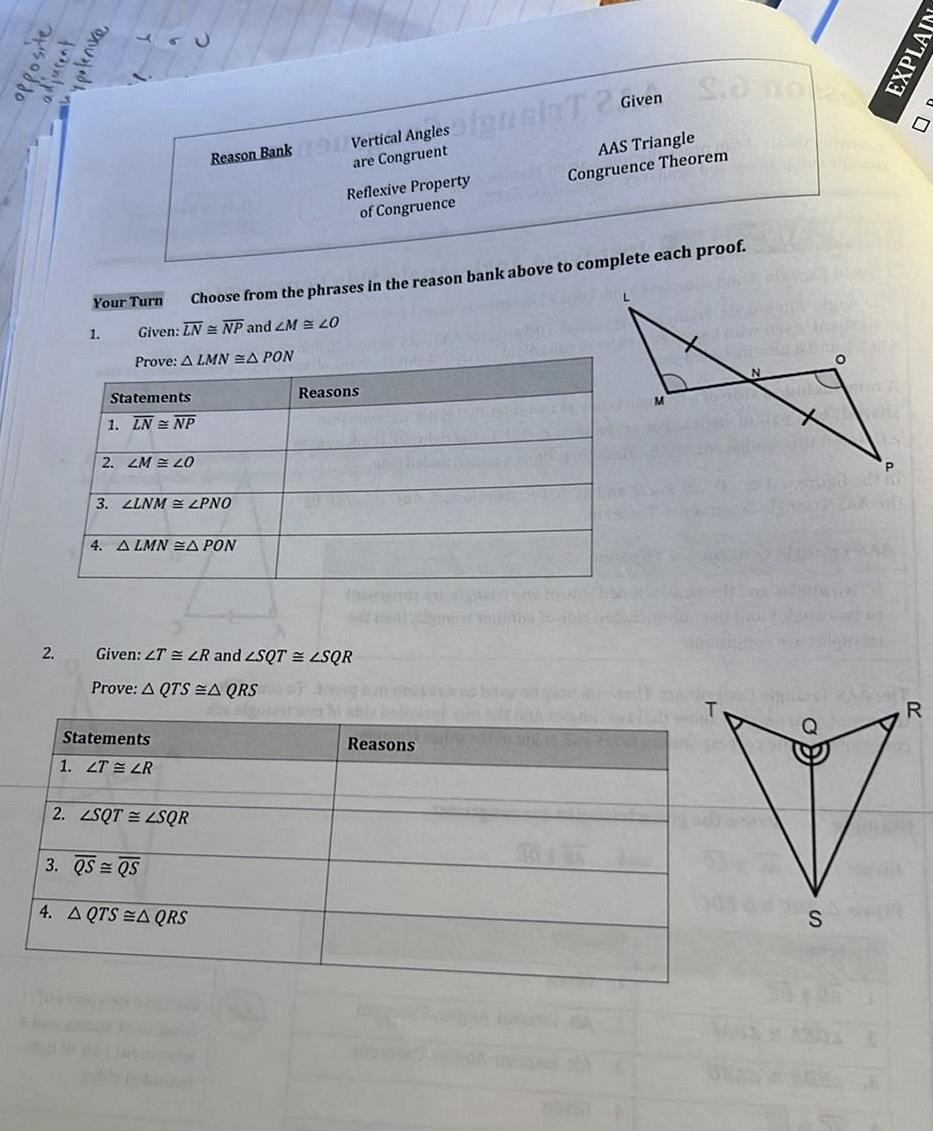
Geometry
2D Geometryopposite adjucent spolenice 2 Your Turn 1 Statements 1 LN NP 2 LM 20 3 LLNM LPNO Choose from the phrases in the reason bank above to complete each proof Given LN NP and 2M 20 Prove A LMN A PON 4 ALMNA PON Reason Bank Vertical Angles are Congruent Statements 1 LT LR 2 LSQT LSQR Given 2T LR and ZSQT ZSQR Prove A QTSA QRS 3 QS QS 4 AQTS AQRS Reflexive Property of Congruence Reasons signat T 2 Given Reasons So no AAS Triangle Congruence Theorem M SORP N S O R EXPLAIN

Geometry
2D Geometryurements Communicate effectively based on purpose task and audience using appropriate academic vocabulary and medium Angle vence ENGAGE Transformations and Angles Complete the following activity with your teacher in order to continue your learning on lines angles and triangles For triangle ABC the points D E and F are the midpoints of each side of the triangle Use a straightedge to roughly sketch the perpendicular bisector for sides AB BC and AC Name the point where the lines intersect 0 B D ob B E A anothe F For the following triangle ABC use a straightedge to sketch the angle bisectors for each of the angles Locate the location where the lines intersect Hint Simply draw a perpendicular line from these points C Hint Bisect LA LB and C

Geometry
2D GeometryWrite a two column proof 1 Given GJ GM GK bisects ZJGM Prove AGJK AGMK J M K Statement Rea





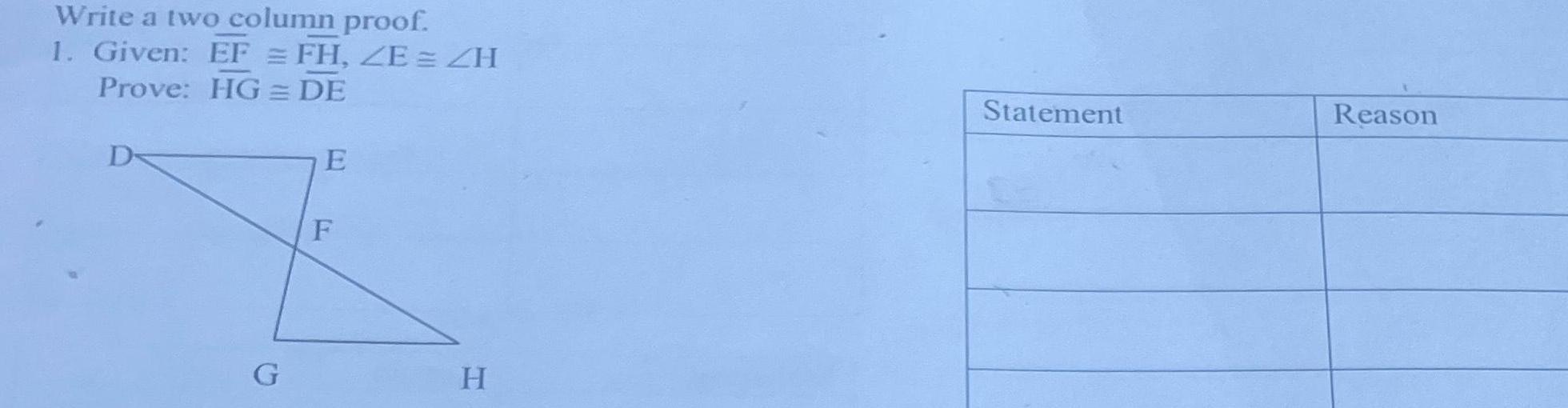
Geometry
2D GeometryWrite a two column proof 1 Given EF FH ZE H Prove HG DE D G E F H Statement Reason

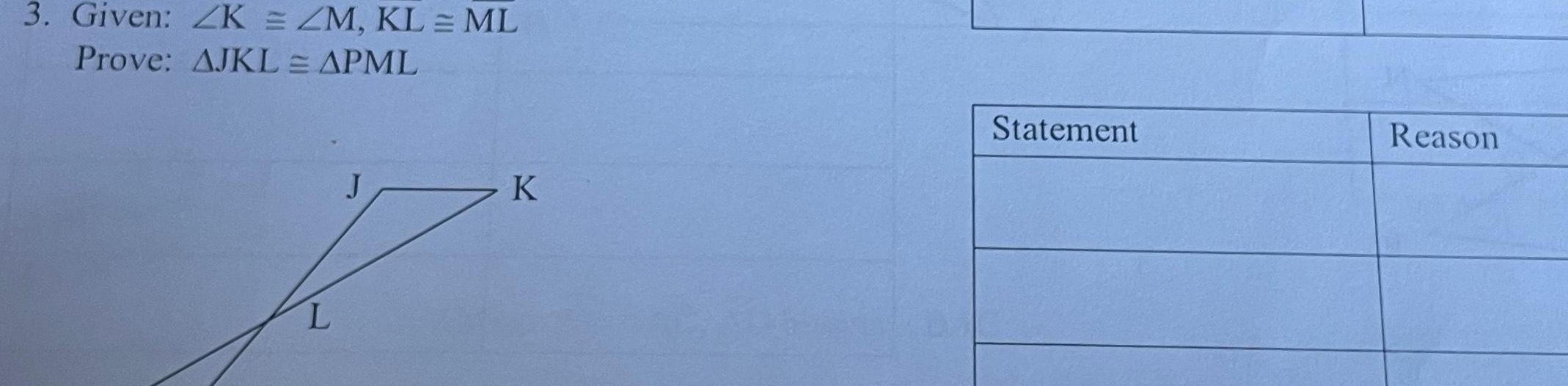

Geometry
2D Geometrythe object and the image congruent or not con Explain your answers The diagram shows triangle B on a coordinate grid Make four copies of the diagram On different copies of the diagram draw the image of B after each combination of transformations a b C d 5 1 followed by reflection in the x axis Translation Rotation of 180 centre 3 2 followed by reflection in the x axis Translation 3 5 clockwise centre 2 1 followed by rotation 90 Reflection in the line y 1 followed by rotation 90 anticlockwise centre 2 2 Think like a mathematician 6 5 4 3 2 B 6 5 4 3 2 1 2 3 4 5 6
Geometry
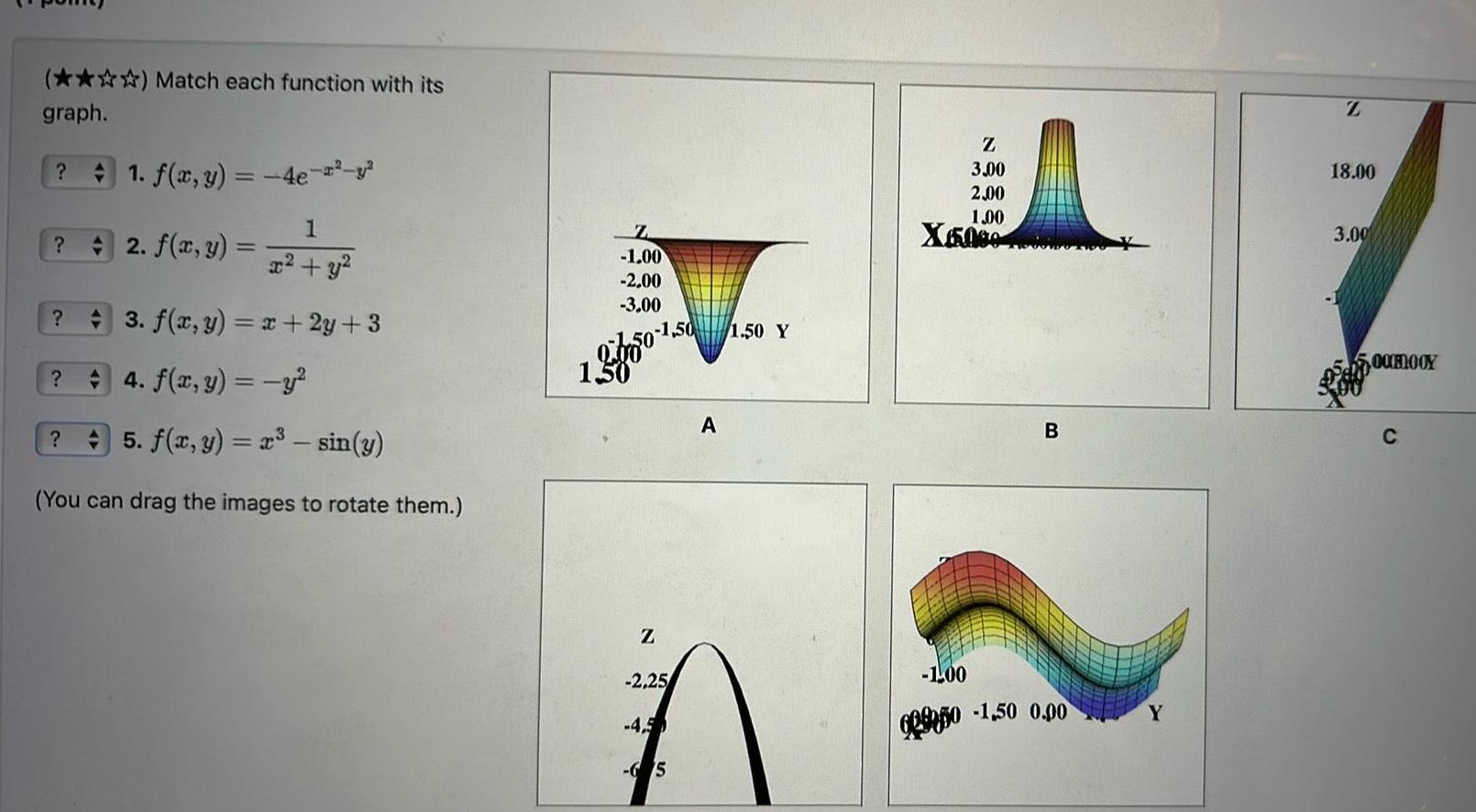
2D GeometryMatch each function with its graph 1 f x y 4e 1 x y 3 f x y x 2y 3 42 f x y 4 f x y y 5 f x y x sin y You can drag the images to rotate them Z 1 00 2 00 3 00 1 50 1 50 Z 2 25 4 5 65 A 1 50 Y Z 3 00 2 00 1 00 X5000 B 1 00 6950 1 50 0 00 Y Z 18 00 3 00 5 00ROOY C
Geometry
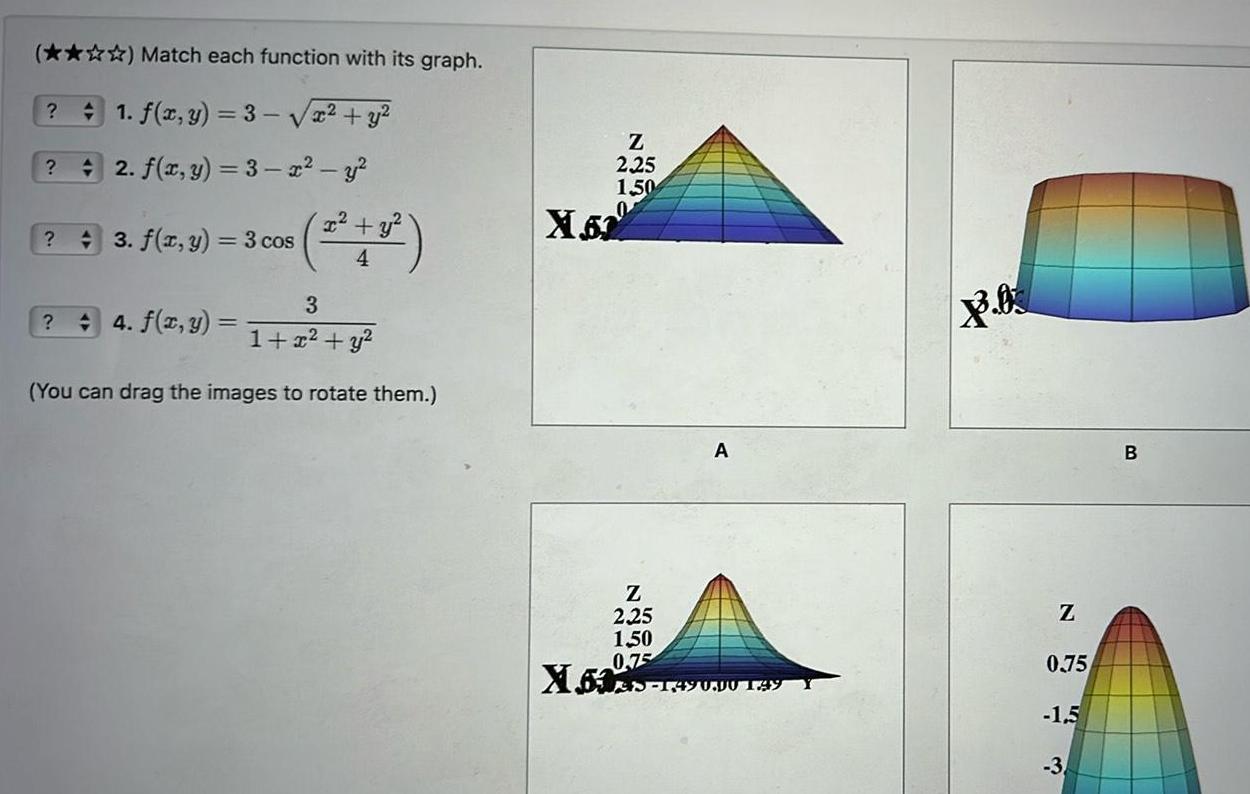
2D GeometryMatch each function with its graph 1 f x y 3 x y 2 f x y 3 x y 3 f x y 3 cos 4 3 2 4 f x y 1 2 y You can drag the images to rotate them Z 2 25 1 50 X 52 Z 2 25 1 50 0 75 X603 149 A 1 490 00 149 Z 0 75 1 5 3 B
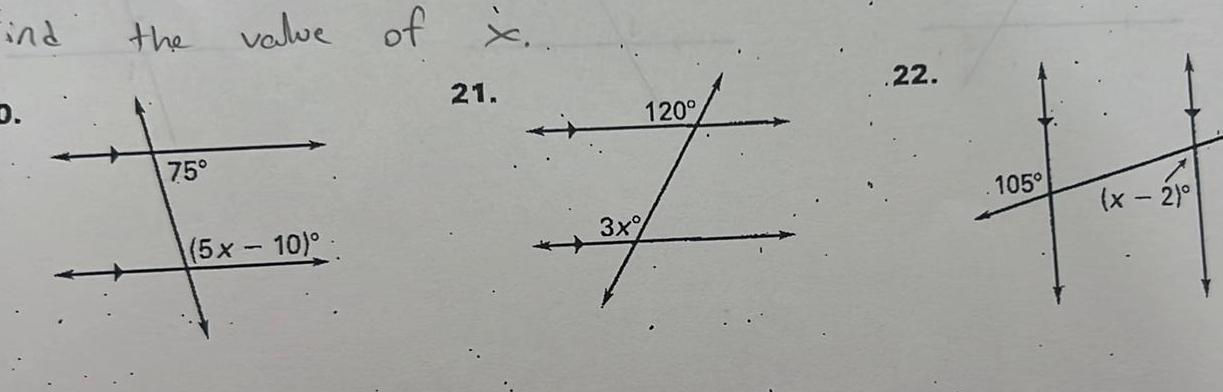
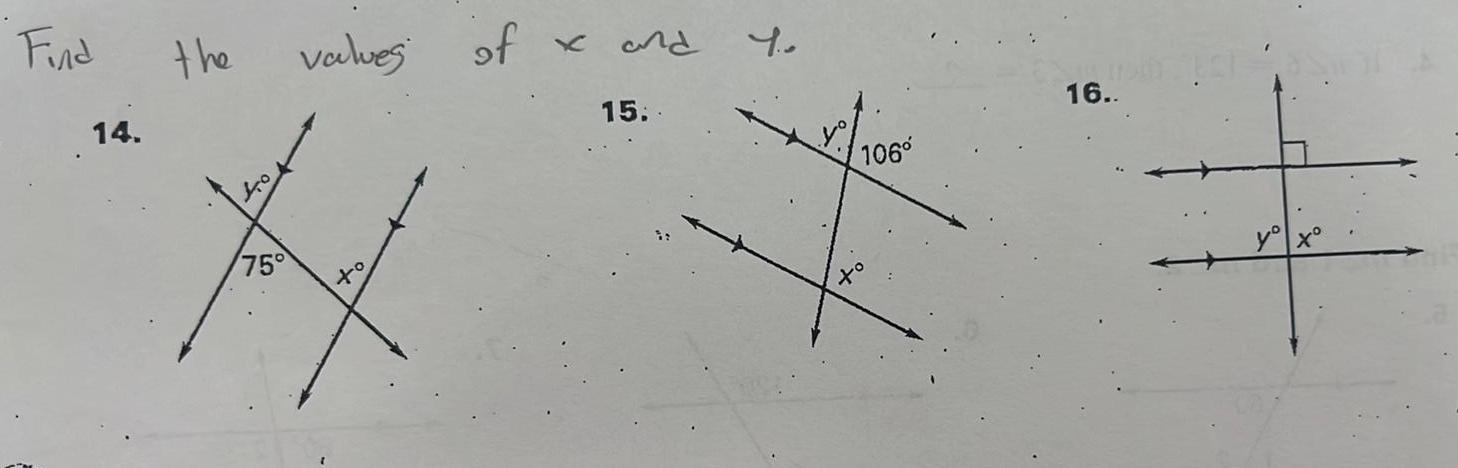
Geometry
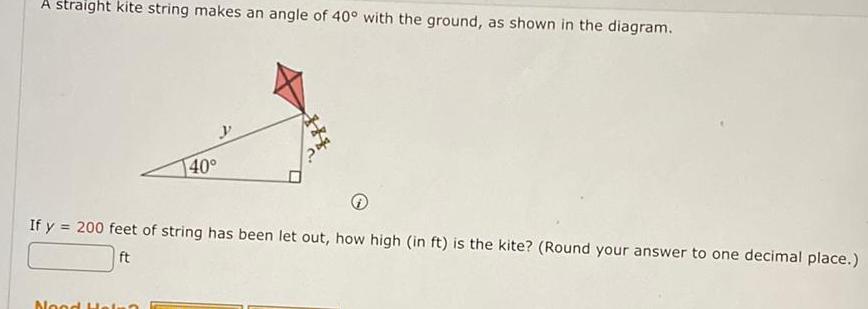
2D GeometryA straight kite string makes an angle of 40 with the ground as shown in the diagram 40 If y 200 feet of string has been let out how high in ft is the kite Round your answer to one decimal place ft Nood Hein
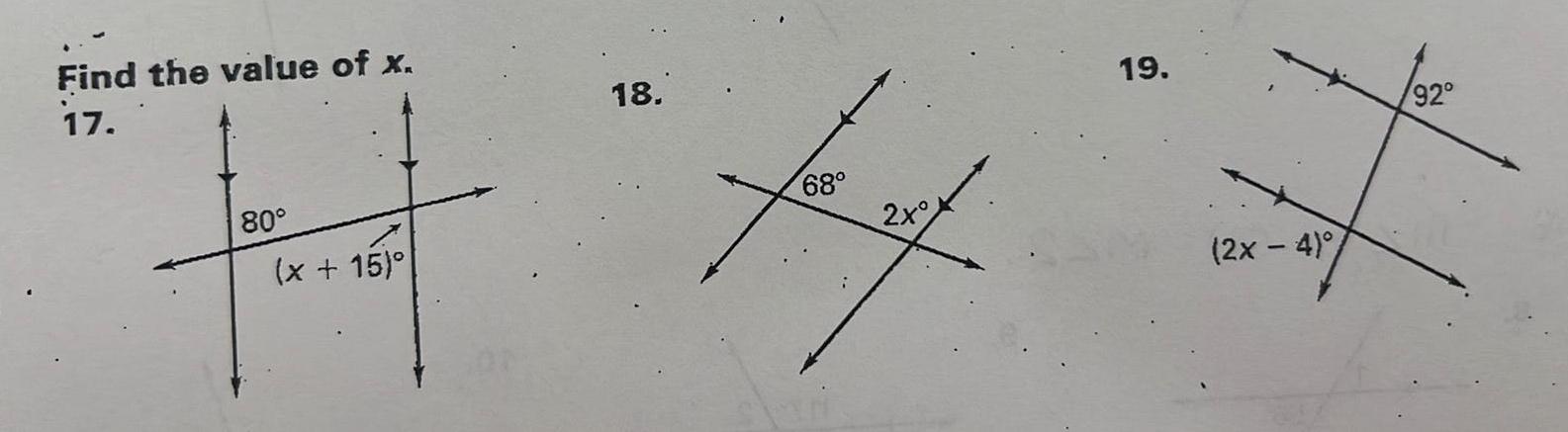
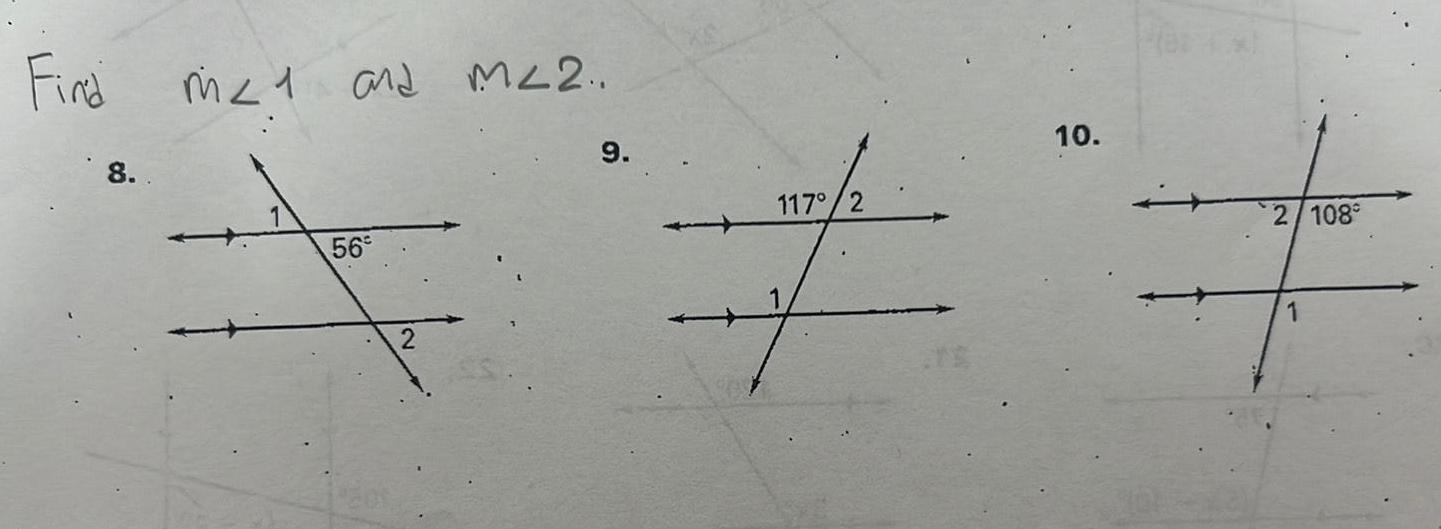

Geometry
2D Geometry7 Given quadrilateral TRAP with T 5 7 R 3 4 A 9 5 and P 1 10 Show TRAP is an isosceles trapezoid 3 4
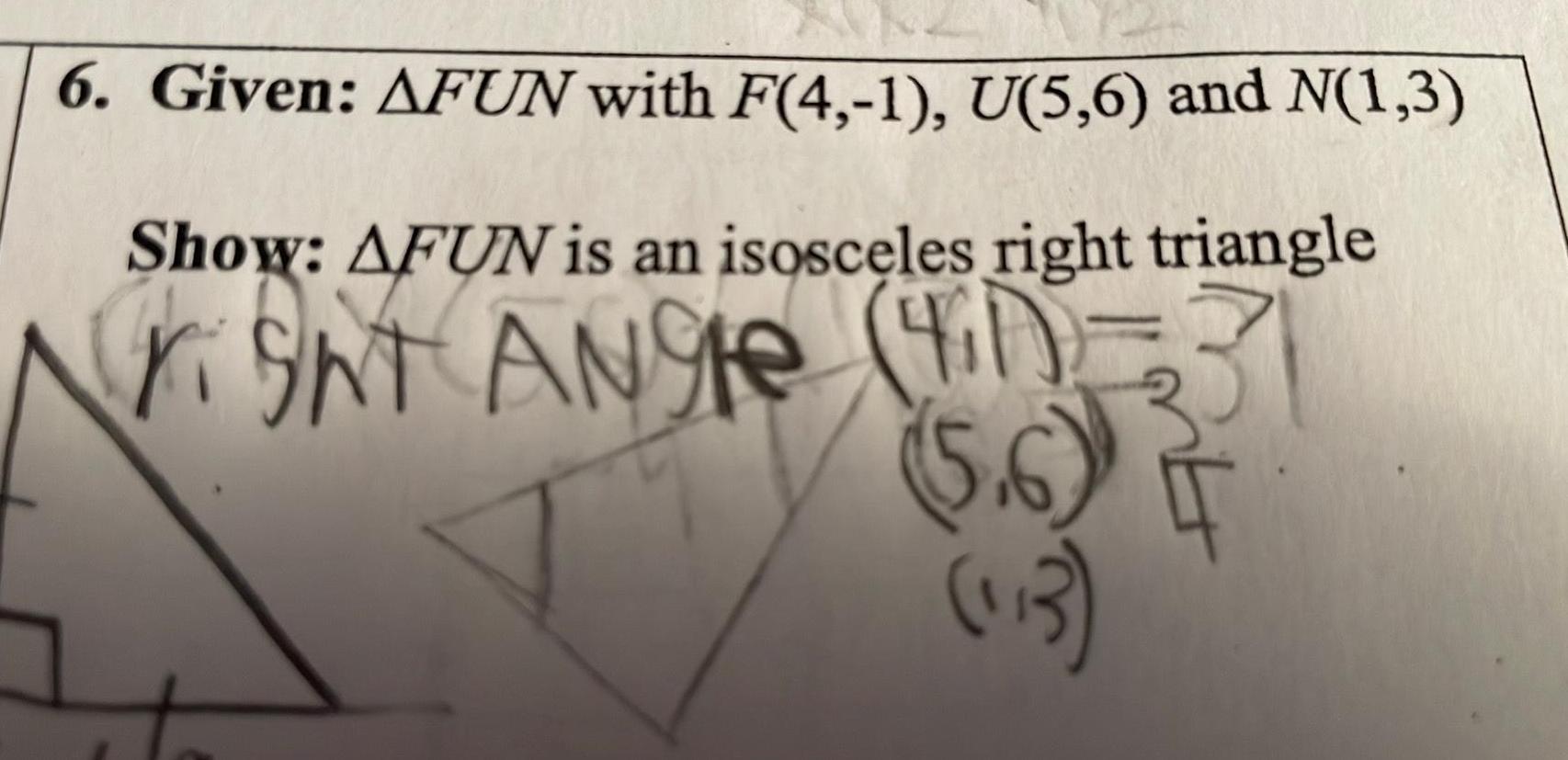
Geometry
2D Geometry6 Given AFUN with F 4 1 U 5 6 and N 1 3 Show AFUN is an isosceles right triangle righT ANgle 41 5 6 113
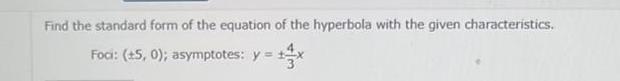
Geometry
2D GeometryFind the standard form of the equation of the hyperbola with the given characteristics Foci 5 0 asymptotes y x
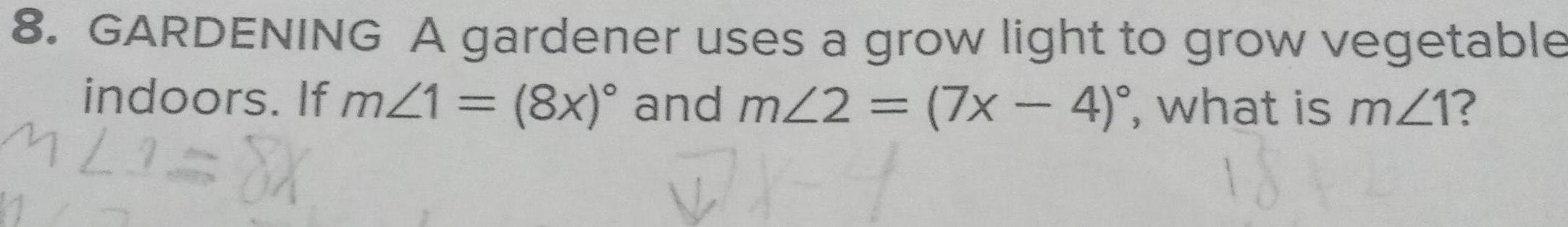
Geometry
2D Geometry8 GARDENING A gardener uses a grow light to grow vegetable indoors If m 1 8x and m 2 7x 4 what is m 1 M21 8X 7 1846 11