2D Geometry Questions and Answers
Geometry
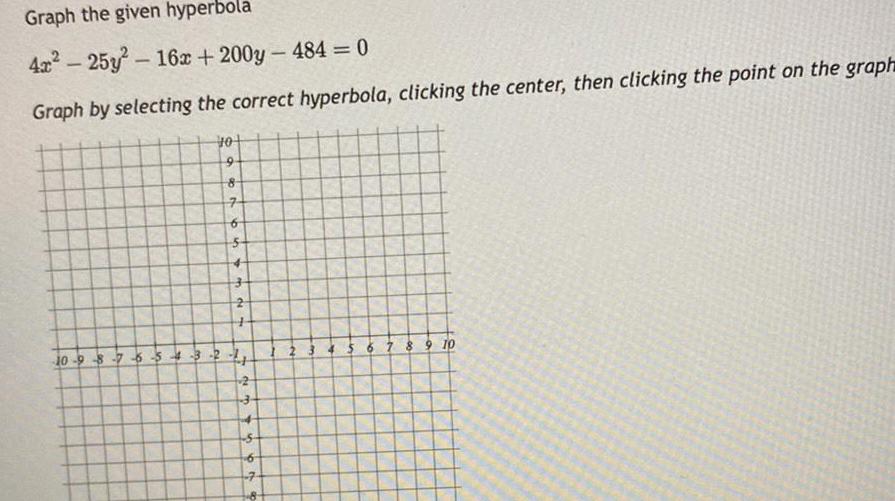
2D GeometryGraph the given hyperbola 4x 25y 16x 200y 484 0 Graph by selecting the correct hyperbola clicking the center then clicking the point on the graph 10 9 8 7 6 5 4 3 10 9 8 for 7 6 No 4 4 2 3 5676 5 8 9 10
Geometry
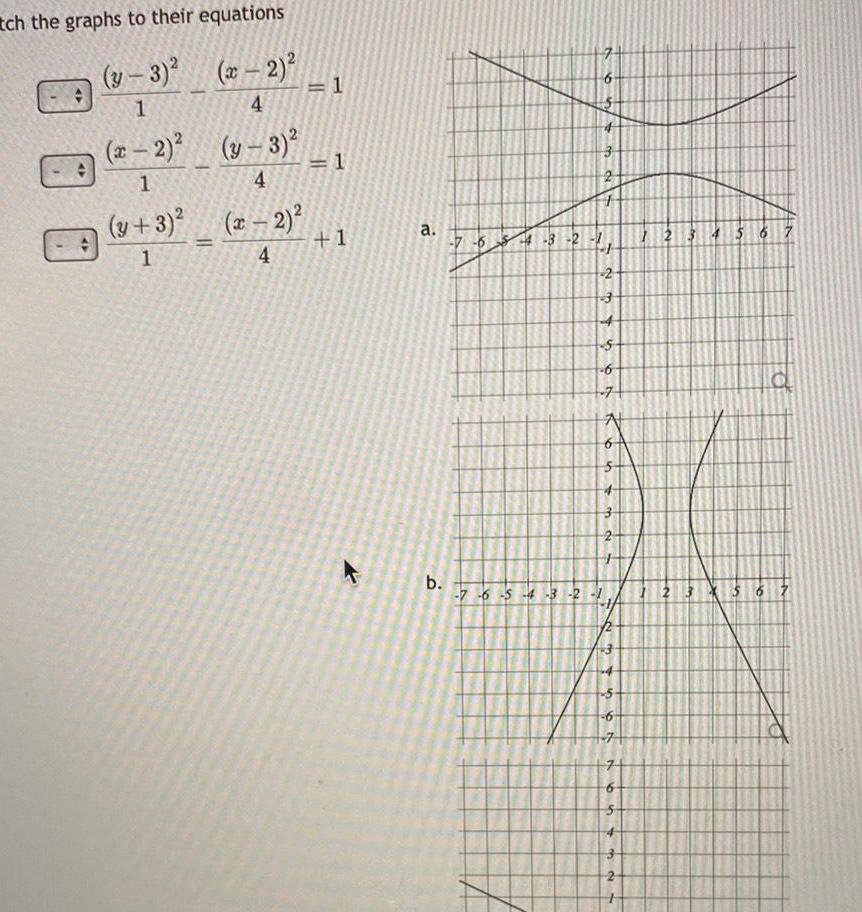
2D Geometrytch the graphs to their equations y 3 x 2 1 4 x 2 1 y 3 1 y 3 4 x 2 4 1 1 1 a b 7 7 654 3 2 1234 2 4 6 7 of 3 7 6 5 4 3 2 1 5 6 7 74 6 3 2 123 56 67
Geometry
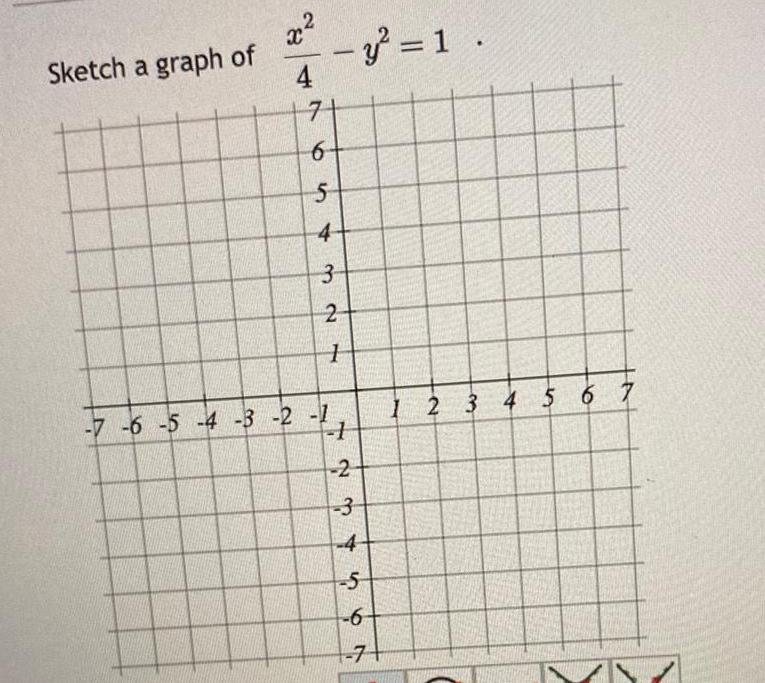
2D GeometrySketch a graph of x 4 y 1 71 65 6 4 32 3 7 7 6 5 4 3 2 1 1 2 3 4 5 6 1 71 1 2 3 4 5 6 7

Geometry
2D GeometryA swimming pool has the shape of a box with a base that measures 26 m by 19 m and a uniform depth of 2 9 m How much work is required to pump the water out of the pool when it 3 is full Use 1000 kg m for the density of water and 9 8 m s for the acceleration due to gravity Draw a y axis in the vertical direction parallel to gravity and choose one corner of the bottom of the pool as the origin For 0 sy 2 9 find the cross sectional area A y A y 494 Simplify your answer Set up the integral that gives the work required to pump the water out of the pool Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers OA JO dy OB CHEER dx
Geometry
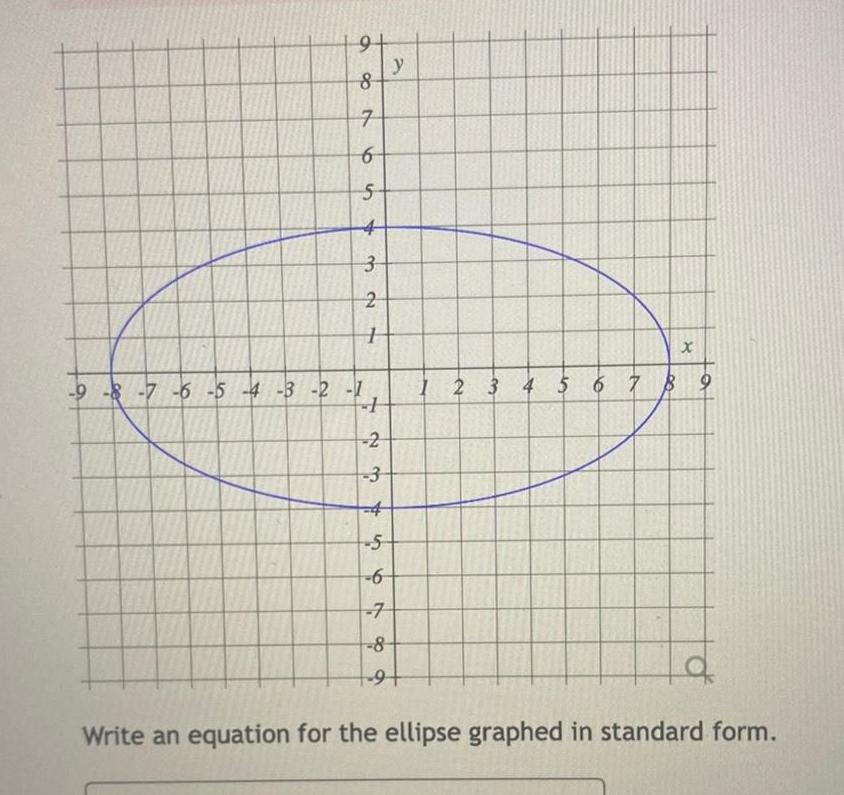
2D Geometry9 8 7 6 5 3 2 9 8 7 6 5 4 3 2 1 7 1 y 2 3 4 5 6 7 8 9 X 1 2 3 4 5 6 7 8 9 12 Write an equation for the ellipse graphed in standard form
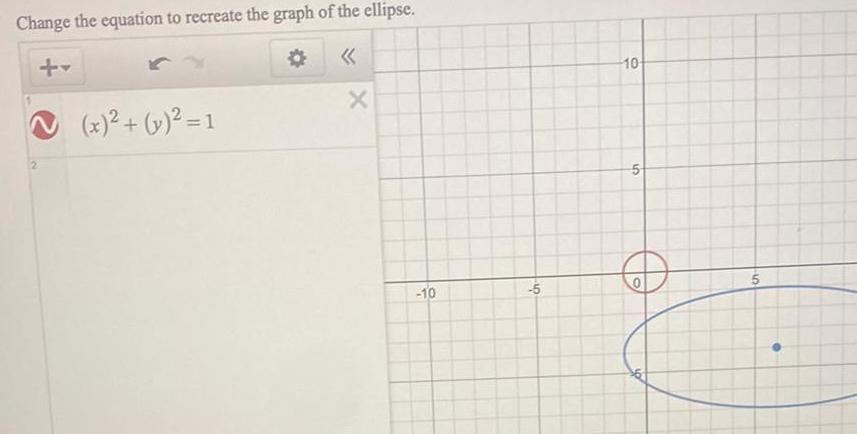
Geometry
2D GeometryChange the equation to recreate the graph of the ellipse 2 x y 1 X 10 5 10 5 O 10
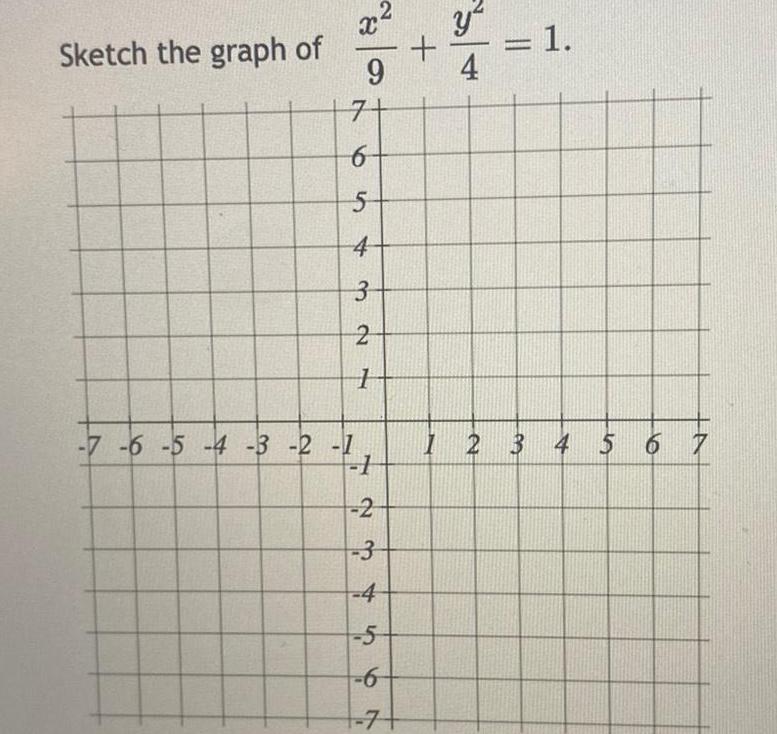
Geometry
2D GeometrySketch the graph of X 9 7 6 5 4 3 2 7 2 7 6 5 4 3 2 1 1 2 3 4 5 6 y 4 1 1 2 3 2 3 4 5 6 7
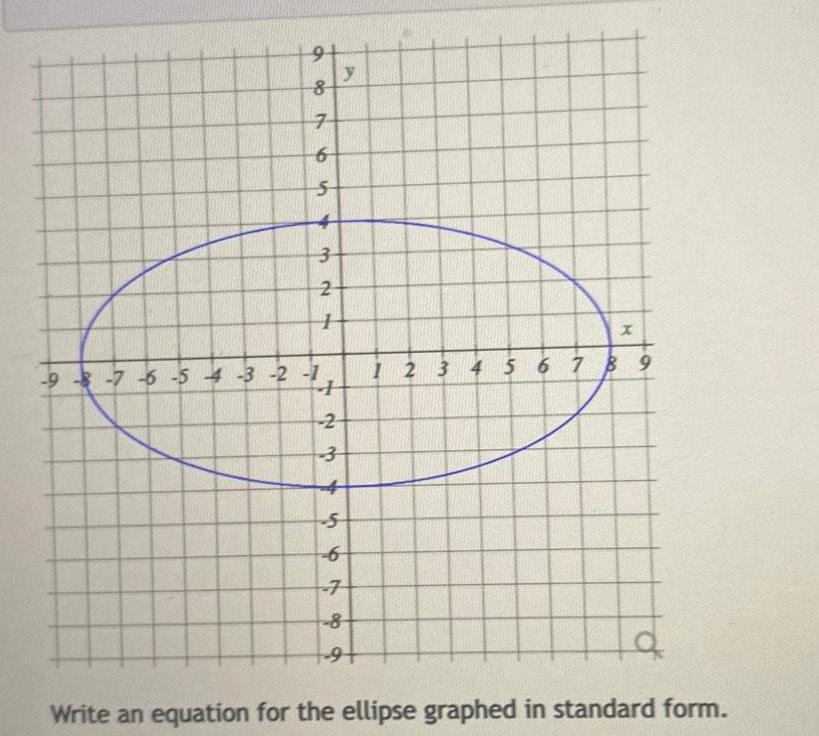
Geometry
2D Geometry91 y 8 6 ob 26 7 6 1 3 2 9 7 6 5 4 3 2 1 4 2 23 4 456 6 8 9 X 1 2 3 4 5 6 7 8 9 a Write an equation for the ellipse graphed in standard form
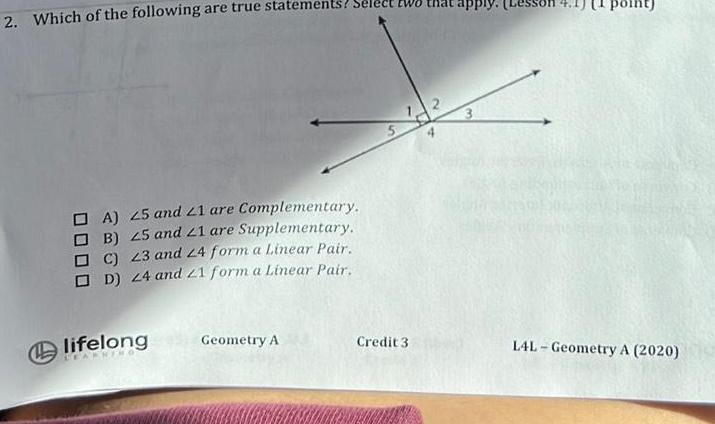
Geometry
2D Geometry2 Which of the following are true statements Sele A 25 and 21 are Complementary B 25 and 21 are Supplementary C 23 and 24 form a Linear Pair D 24 and 21 form a Linear Pair lifelong LEAKNE Geometry A Credit 3 L4L Geometry A 2020
Geometry
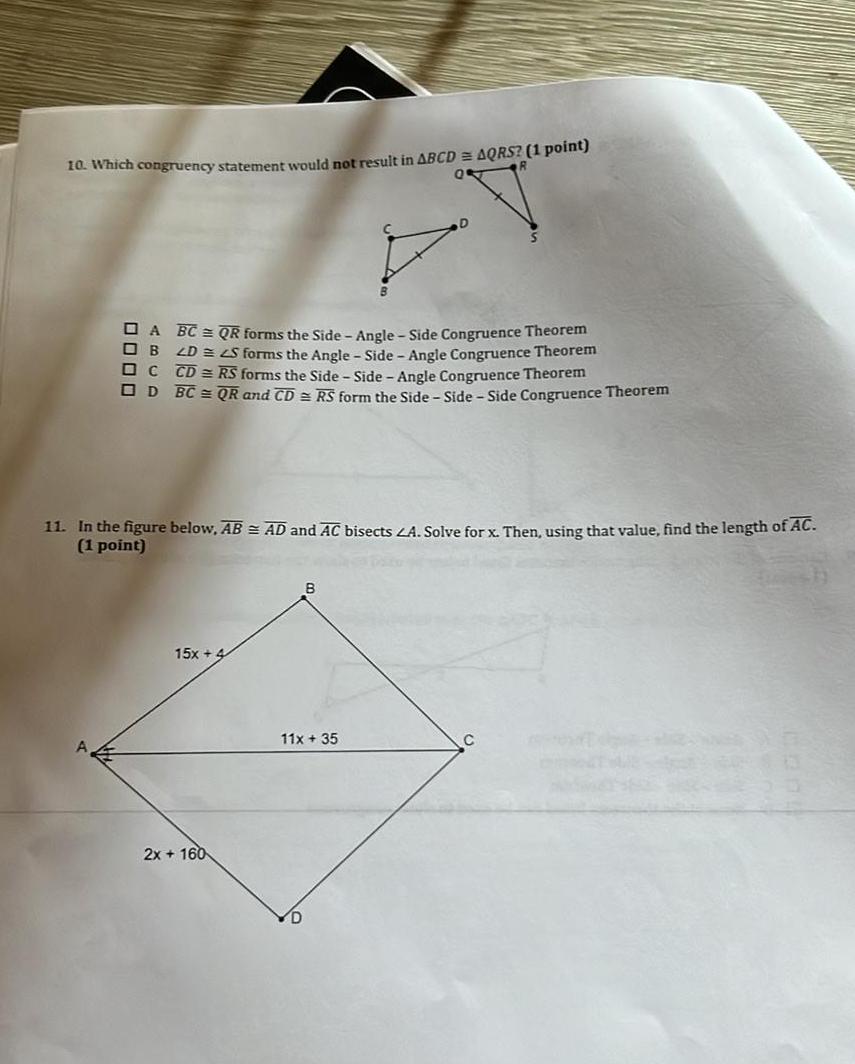
2D Geometry10 Which congruency statement would not result in ABCD AQRS 1 point A BC QR forms the Side Angle Side Congruence Theorem OB 2D S forms the Angle Side Angle Congruence Theorem C CD RS forms the Side Side Angle Congruence Theorem OD BC QR and CD RS form the Side Side Side Congruence Theorem 11 In the figure below AB AD and AC bisects A Solve for x Then using that value find the length of AC 1 point 15x 4 2x 160 B 11x 35 E 13

Geometry
2D GeometryYour Turn 1 Determine whether A DEFA GHJ Justify your reasoning EXPLAIN 2 Proving Triangles Are Congruent Using SAS Triangle Congruence Read Explain 1 and complete Your Turn 1 2 adapted from Lesson 5 3 Show all your work Given CD bisects AE Prove A ABC A EBD The SAS Triangle Congruence Theorem may be used as a reason in a proof To complete the proof you need to show that two sides and the included angle of one triangle are congruent to the corresponding sides and angle of the other triangle Example Use the figure to the right to complete the two column proof and AE bisects CD Statements 1 CD bisects AE 2 AB EB 3 AB EB 4 AE bisects CD 5 CB DB E H 2 5 cm 2 5 cm 77 2 9 cm 6 CB DB 4 LABC LEBD 5 AABC A EBD DO 1 7 cm 4 Given Reasons 1 Given 2 Definition of a Bisector 3 Definition of Congruence 5 Definition of a Bisector 6 Definition of Congruence 4 Vertical Angles are Congruent 5 SAS Triangle Congruence Theorem G 1 7 cm

Geometry
2D GeometryHW 1 What additional information would be enough to prove that the two triangles are congruent by SAS L Homework Complete problems 1 6 below for independent practice A HG ZX B TG 2X C LG LX D 2H ZY HHH H When you are finished check the solutions with your teacher A XHXY OBJH WY C ZW D 2N ZY 3 Determine if the triangles below are congruent If 4 Determine if the triangles below are congruent If so what properties are used in your logic so what properties are used in your logic M 5 State what additional information is required to prove AUML AKLM by SAS 2 What additional information would be enough to prove that the two triangles are congruent by SAS 6 State what additional information is required to prove AJHI AUSI by SAS Optional Complete problems 1 3 4 6 7 11 12 14 from your textbook on separate lined paper When you are finished check the odd problems for solutions at the back of the textbook

Geometry
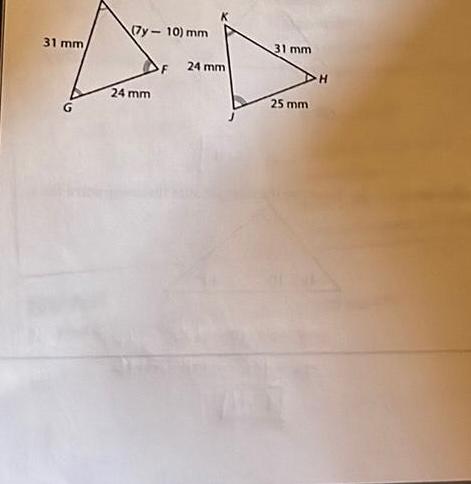
2D Geometry1 Find the values for x that results in A FGH A TUV 2 Find the values for y that results in A FGH A TUV 7y 4 T G 60 30 C 8x 12 cm 12 cm H


Geometry
2D GeometryHW 5 4 Homework 1 What additional information is needed to prove that the two triangles are congruent by SSS Complete problems 1 6 below for independent practice A HG VT BHFVT C LG LV D LF LT S G U tice When you are finished check the solutions with your teacher H 2 What additional information is needed to prove that the two triangles are congruent by SSS N 3 Determine if the triangles below are congruent 4 Determine if the triangles below are congruent If so what properties are used in your logic If so what properties are used in your logic 5 State what additional information is required to 6 State what additional information is required to prove AUMLAKLM by SSS prove AYGE AFGE by SSS M Y H F M ASN MN B LN LN CLM LS D LLNS ZLNM E Optional Complete problems 11 15 23 from your textbook on separate lined paner

Geometry
2D GeometryDetermine whether the triangles are congruent Explain your reasoning congrene papan you A 45 2 3 cm 61 C D 2 3 cm
Geometry
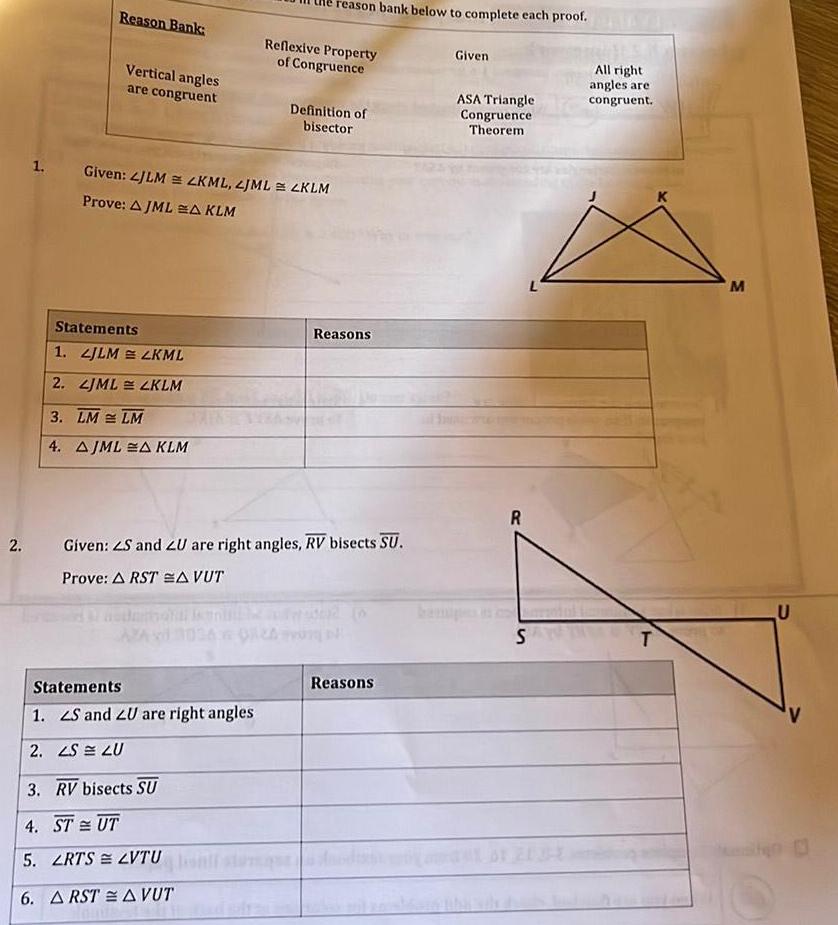
2D GeometryReason Bank Vertical angles are congruent Statements 1 JLM LKML 2 LJML LKLM 3 LM LM 4 AJMLA KLM 1 Given LJLM LKML LJML LKLM Prove AJMLA KLM AZAS reason bank below to complete each proof Reflexive Property of Congruence Statements 1 S and ZU are right angles 2 LS LU 3 RV bisects SU 4 STUT 5 LRTS LVTU 6 ARSTA VUT Definition of bisector 2 Given ZS and LU are right angles RV bisects SU Prove ARSTA VUT Reasons Reasons Given ASA Triangle Congruence Theorem R S All right angles are congruent T M U

Geometry
2D Geometrythose equidistant from the segment s endpoints ular bisector of a line segment are out lines and angles T T Lesson 4 4 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 If QR 12 and QR is a perpendicular bisector of TS determine which of the following claims are true 6x 4 RS 12 x 4 x 3 RS 5 RS 4 ST 10 QR 4 QT 16 2x 1 True Q90 True True True True True True True R R Q90 3x 8 False 2 If QS 4 and QR is a perpendicular bisector of TS determine which of the following claims are true False False False 4x 3 Starting False False False False Getting there S S Got it

Geometry
2D Geometryour Turn Tell whether lines m and n must be parallel from the given information If they are state your reasoning 1 45 27 1 8 2 7 3 6 4 5 m
Geometry
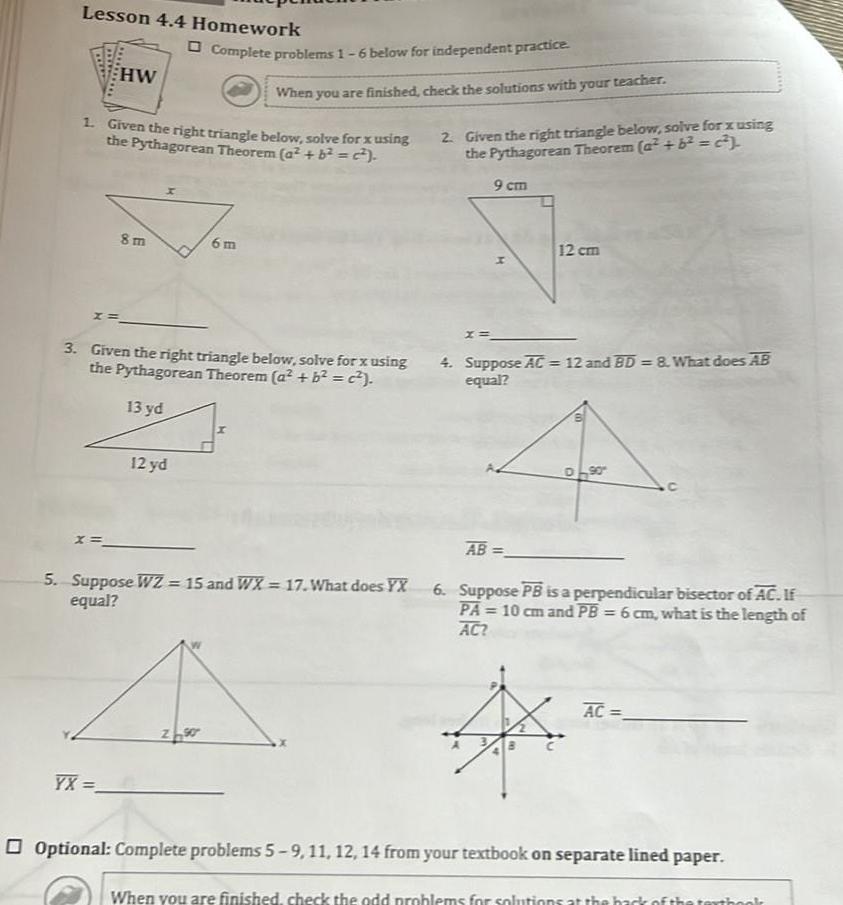
2D GeometryLesson 4 4 Homework x HW 1 Given the right triangle below solve for x using the Pythagorean Theorem a b c 8m YX Complete problems 1 6 below for independent practice 12 yd 3 Given the right triangle below solve for x using the Pythagorean Theorem a b 13 yd When you are finished check the solutions with your teacher 6m ZS 5 Suppose WZ 15 and WX 17 What does YX equal 2 Given the right triangle below solve for x using the Pythagorean Theorem a 6 2 9 cm 12 cm 4 Suppose AC 12 and BD 8 What does AB equal AB 90 6 Suppose PB is a perpendicular bisector of AC If PA 10 cm and PB 6 cm what is the length of AC AC Optional Complete problems 5 9 11 12 14 from your textbook on separate lined paper When you are finished check the odd problems for solutions at th

Geometry
2D GeometryLesson 4 3 Homework HW X x 1 Find the value of x that makes u v parallel X 26r 5 Complete problems 1 6 below for independent practice 2 Find the value of x that makes u v parallel 125 130 Independent Practice 6r 3 6r 4 45 3 Find the value of x that makes u v parallel 7x 1 When you are finished check the solutions with your teacher 17x 11 N 4 Find the value of x that makes us v parallel

Geometry
2D GeometryYour Turn 1 2 R 71 719 T Determine whether the given triangles are congruent Explain 38 D 700 S 38 U 71 71 W

Geometry
2D GeometryYour Turn If AD is 10 inches long BD is 6 inches long 1 Find the length of AB lifelong Geometry A Credit 3 A D B L4L Geometry A 2020 Page

Geometry
2D Geometry1 m24 m28 What type of angle pair is this Circle the theorem or postulate that proves all b Converse of the Same Side Interior Angles Postulate Converse of the Alternate Interior Angles Theorem Converse of the Corresponding Angles Theorem 4 3 2 8 5 6 ta
Geometry
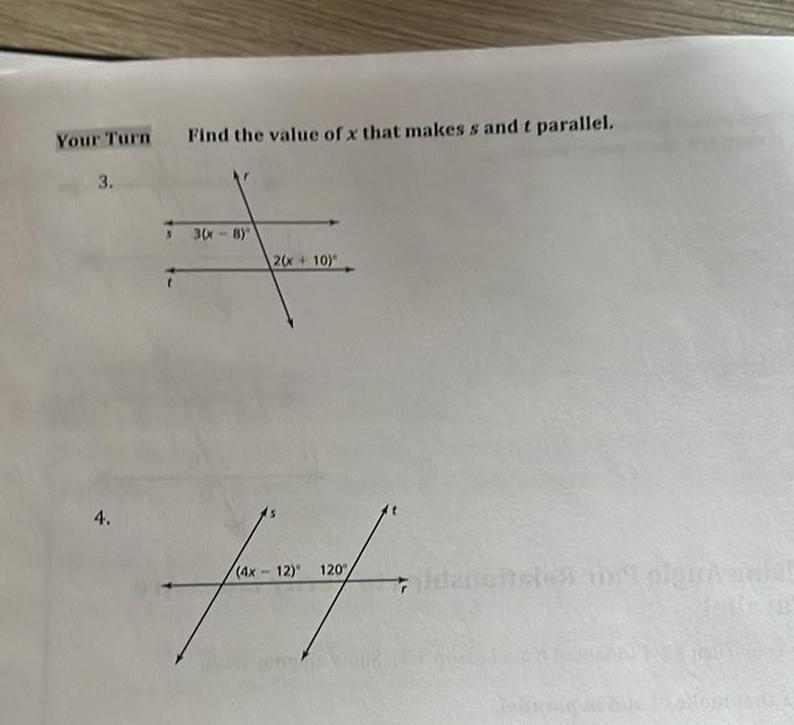
2D GeometryYour Turn 3 4 Find the value of x that makes s and t parallel 3 x 8 2 x 10 prof 4x12 120
Geometry
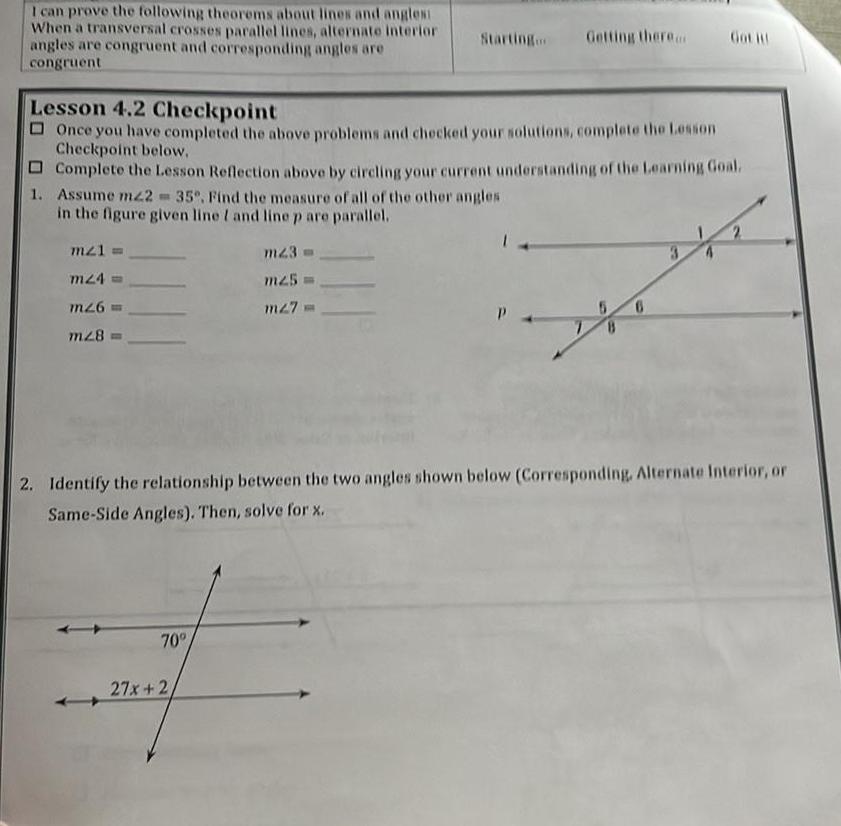
2D GeometryI can prove the following theorems about lines and angles When a transversal crosses parallel lines alternate interior angles are congruent and corresponding angles are congruent 1 Assume mz2 35 Find the measure of all of the other angles in the figure given line I and line p are parallel Lesson 4 2 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkpoint below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal m21 m24 m26 m28 70 Getting there mz3 m25 m27 27x 2 Got it 2 Identify the relationship between the two angles shown below Corresponding Alternate Interior or Same Side Angles Then solve for x

Geometry
2D Geometrythe value for y that results in A JKL A MNP 4y 12 mm 22 mm 15 mm 22 mm M P 15 mm 32 mm

Geometry
2D Geometry5 Find the value of x that makes u v parallel X 120 X 6 Find the value of x that makes u v parallel 14x 11 17x 1 v 95
Geometry
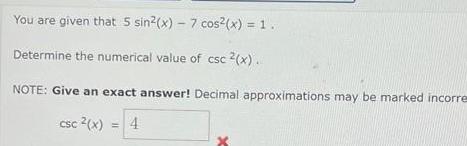
2D GeometryYou are given that 5 sin x 7 cos x 1 Determine the numerical value of csc 2 x NOTE Give an exact answer Decimal approximations may be marked incorre csc x 4
Geometry
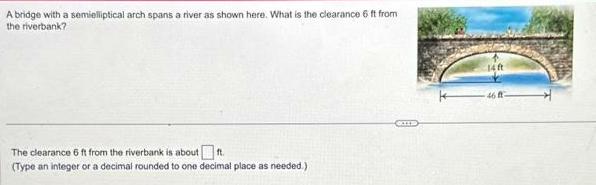
2D GeometryA bridge with a semielliptical arch spans a river as shown here What is the clearance 6 ft from the riverbank The clearance 6 ft from the riverbank is about ft Type an integer or a decimal rounded to one decimal place as needed GIES 14 ft
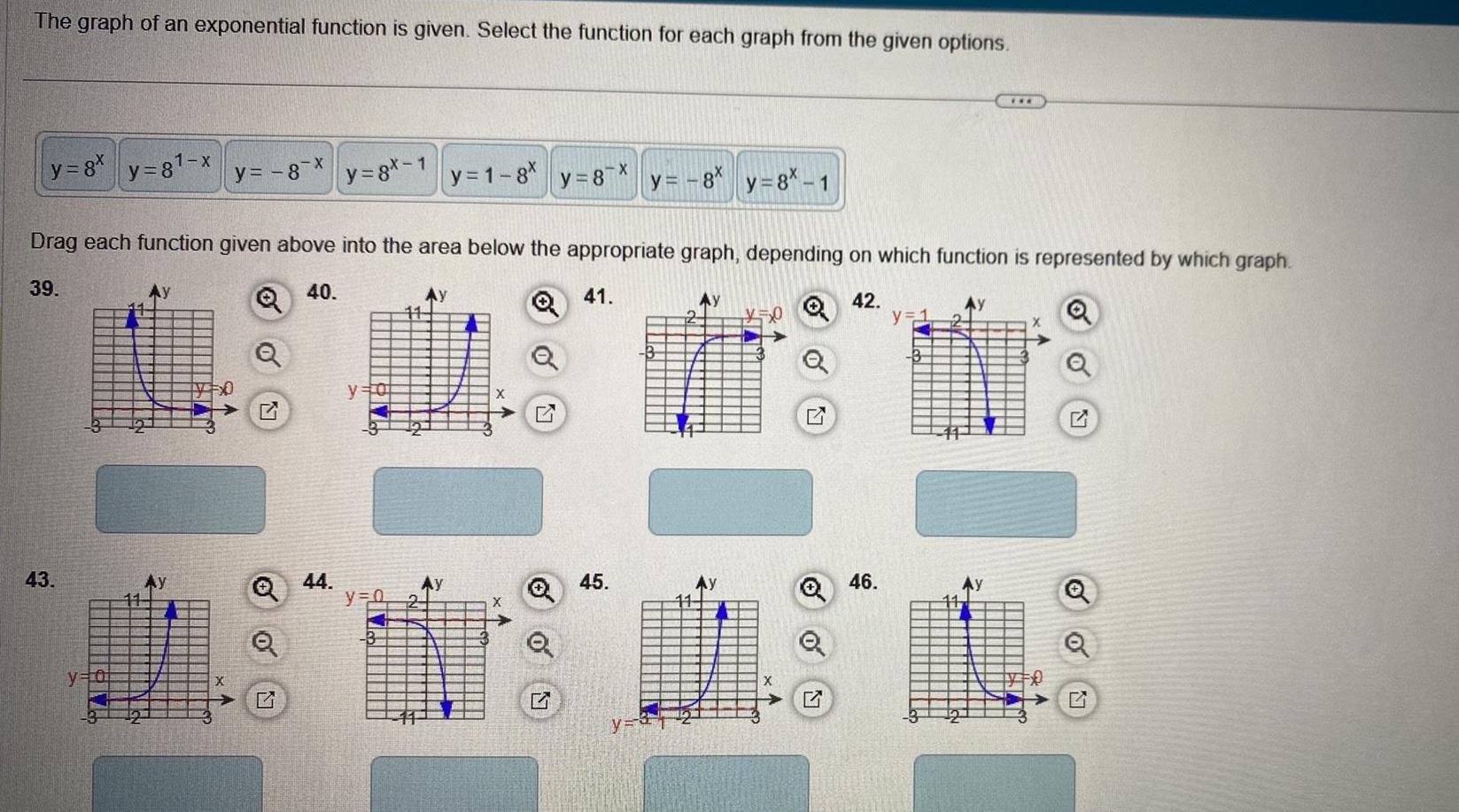
Geometry
2D GeometryThe graph of an exponential function is given Select the function for each graph from the given options y 8x y 8 x 43 y 8 x y 0 5x0 y 8x 1 44 Drag each function given above into the area below the appropriate graph depending on which function is represented by which graph 39 40 41 y 0 y 0 y 1 8x B y 8 x 45 y 8 y 8 1 y Ay y 0 G 42 46 y 1 F Ay FO Q
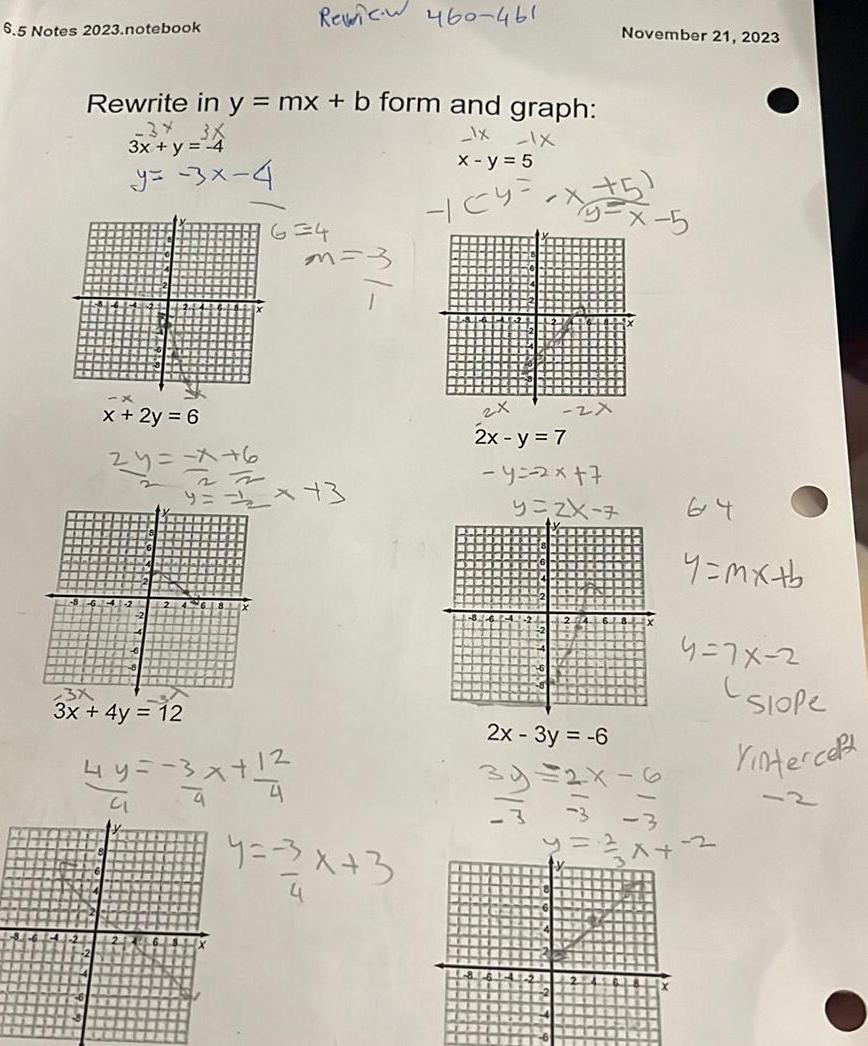
Geometry
2D Geometry6 5 Notes 2023 notebook Rewrite in y mx b form and graph IX IX 3 3X 3x y 4 x y 5 y 3x 4 x 2y 6 2y 6 Review 460 461 3x 3x 4y 12 6 4 27 9 2 43 4 m 3 y 3x 3 YCY November 21 2023 5 x 5 2x 2x y 7 y 2x 7 y 2X 7 2x 3y 6 39 2x 6 y mx b 4 7x 2 3 y x 2 Slope Vintercept
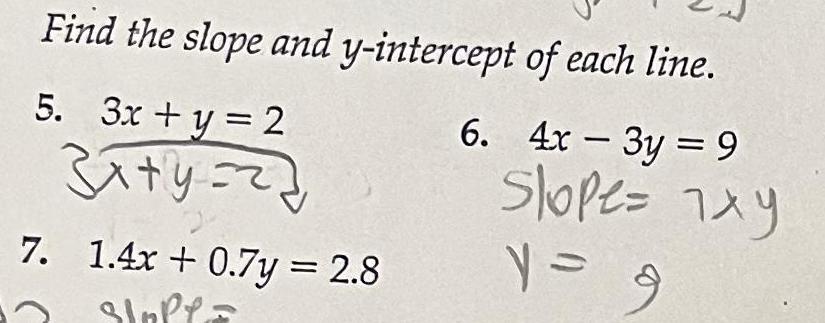
Geometry
2D GeometryFind the slope and y intercept 5 3x y 2 3x y 22 7 1 4x 0 7y 2 8 Sloffs of each line 6 4x 3y 9 Slope 7xy y 9
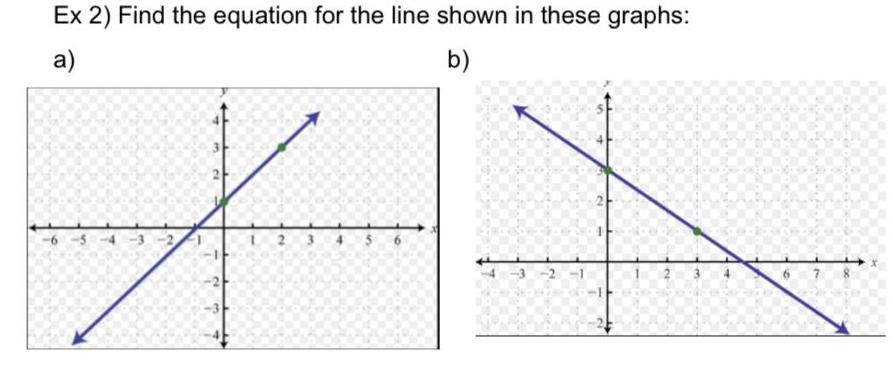
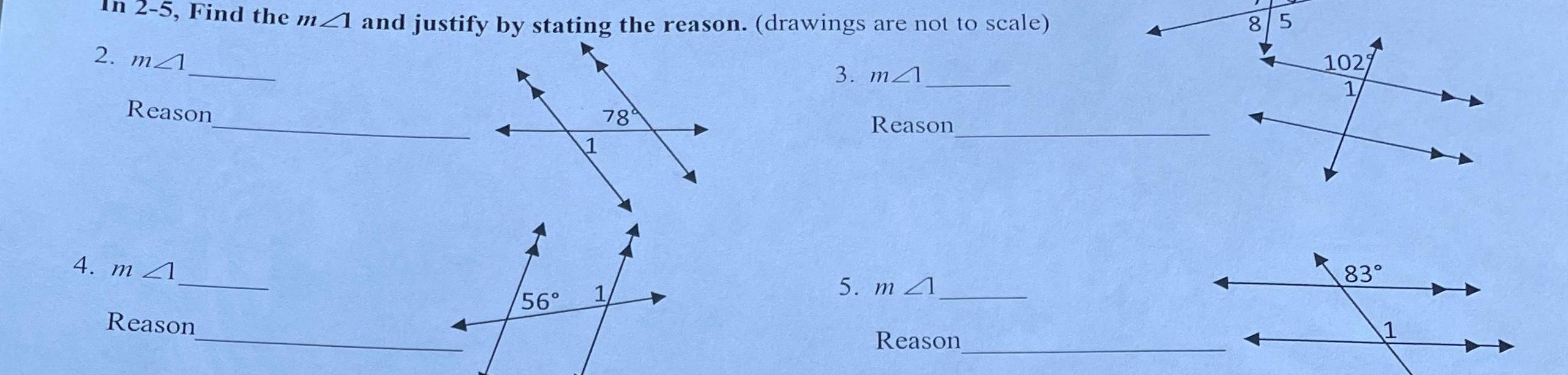
Geometry
2D Geometry2 5 Find the m4 and justify by stating the reason drawings are not to scale 2 m4 3 m4 Reason 4 m 4 Reason 56 78 1 Reason 5 m 4 Reason 8 5 1027 83 1
Geometry
2D GeometryEmployee net pay Lindsey Vater s weekly gross earnings for the week ended March 9 were 1 950 and her federal income tax withholding was 409 50 Assuming the social security tax rate is 6 and Medicare tax is 1 5 of all earnings what is Lindsey s net pay For interim computations carry amounts out to two decimal places Round your final answer to two decimal places
Geometry
2D GeometryThe payroll register of Heritage Co indicates 4 800 of social security withheld and 1 200 of Medicare tax withheld on total salaries of 80 000 for the period Federal withholding for the period totaled 17 540 Retirement savings withheld from employee paychecks were 3 200 for the period Journalize the entry to record the period s payroll If an amount box does not require an entry leave it blank Salaries Expense Social Security Tax Payable Medicare Tax Payable Employees Federal Income Tax Payable Retirement Savings Deductions Payable Salaries Payable Feedback Check My Work
Geometry
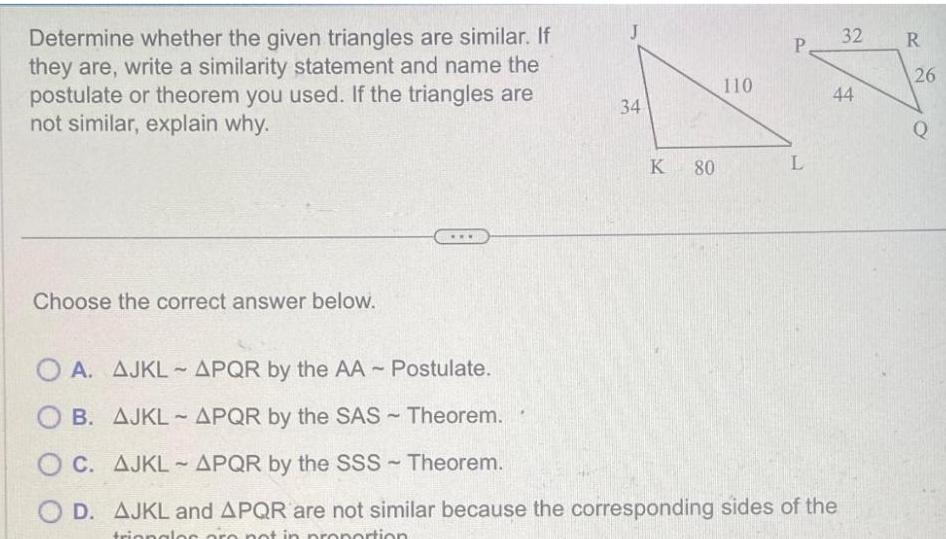
2D GeometryDetermine whether the given triangles are similar If they are write a similarity statement and name the postulate or theorem you used If the triangles are not similar explain why Choose the correct answer below 34 K 80 110 P L OA AJKL APQR by the AA Postulate OB AJKL APQR by the SAS Theorem OC AJKL APQR by the SSS Theorem OD AJKL and APQR are not similar because the corresponding sides of the triangles are not in proportion 32 R 44 26 Q

Geometry
2D GeometryThe lines represented by the equations 3y 2x 21 and y x 3 are Answer Attempt 1 out of 5 O neither parallel nor perpendicular O perpendicular O parallel the same line Submit Answer
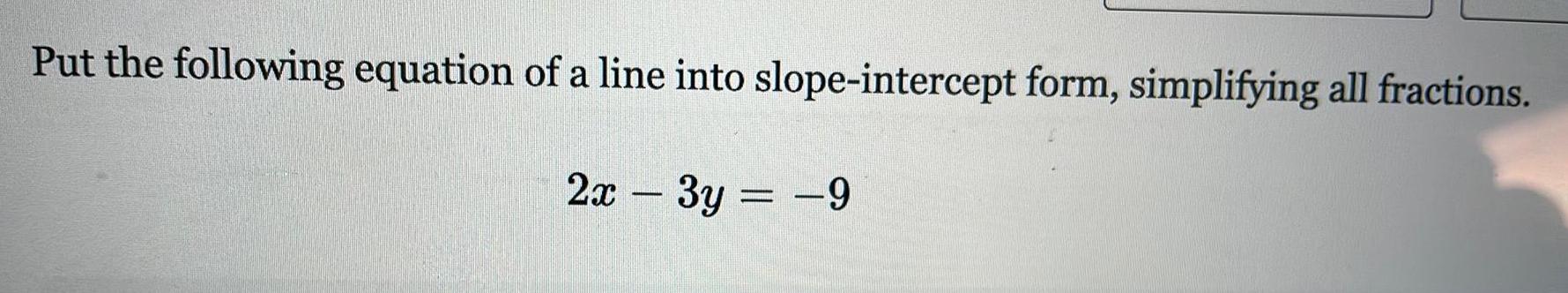
Geometry
2D GeometryPut the following equation of a line into slope intercept form simplifying all fractions 2x 3y 9

Geometry
2D GeometryUnit Circle What is the angle Name the Reference angle coterminal angle negative angles quadrants ordered pairs radians degrees sin cos 1
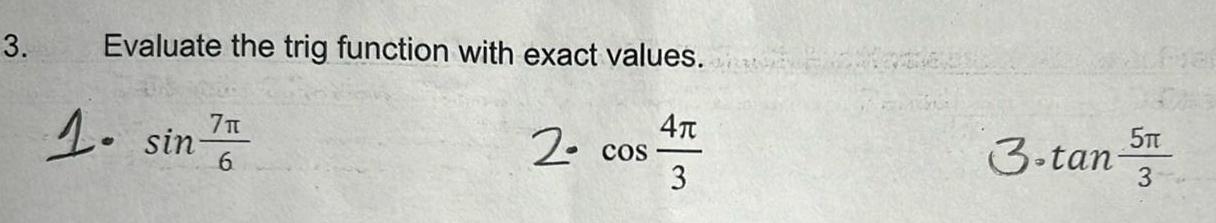

Geometry
2D GeometryProving That Alternate Interior Angles Are Congruent Read Explain 1 Explain2 and complete Your Turn 1 adapted from Lesson 4 2 Show all your work EXPLAIN 1 Alternate Interior Angles Theorem If two parallel lines are cut by a transversal then the pairs of alternate interior angles have the same measure Example 23 45 Given p q line p parallel to line q Prove m23 m25 Two Column Proof of the Alternate Interior Angles Theorem Statements Example Complete the proof by writing the missing reasons Choose from the following reasons You may use a reason more than once Refer to the reason bank below 1 pllq 2 23 and 26 are supplementary 3 m23 m26 180 4 25 and 26 are a linear pair 5 25 and 26 are supplementary 6 m25 m26 180 7 m23 m26 m25 m26 8 m43 m25 Reason Bank Substitution Property of Equality Reasons Same Side Interior Angles Postulate 1 2 3 4 5 6 7 8 Linear Pair Theorem P Definition of Supplementary Angles 9 1 4 3 5 6 At 8 7 Subtraction Property of Equality Given P 9

Geometry
2D GeometryGiven p q Prove m24 m28 Two Column Proof of the Vertical Angles Theorem Statements 1 pllq 2 24 and 26 are alternate interior angles 3 m24 m26 4 26 and 28 are vertical angles 5 m26 m28 Angles Theorem Refer to the reason bank below 6 m24 m28 Reason Bank Substitution Property of Equality Vertical Angles Theorem Reasons THE RE 1 Given 2 3 4 5 6 Definition of Vertical Angles Alternate Interior Angles Theorem 4 3 5 8 7 P 9 Definition of Alternate Interior Angles

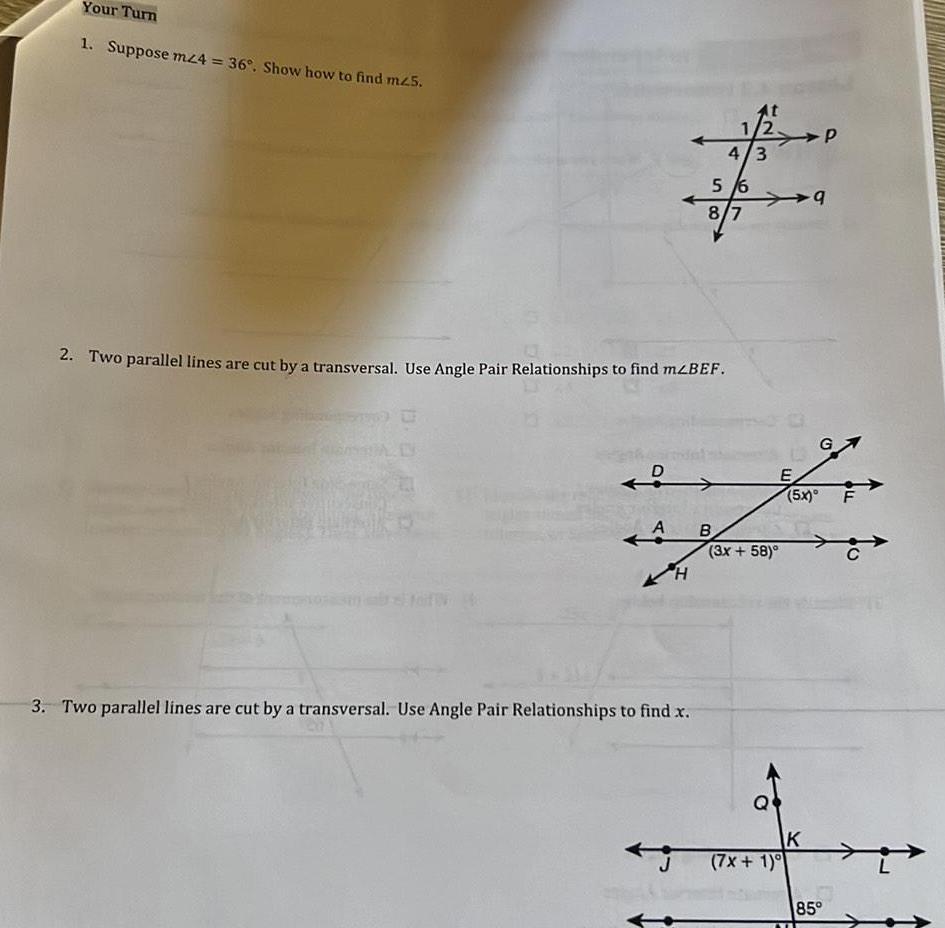
Geometry
2D GeometryYour Turn 1 Suppose mz4 36 Show how to find m25 2 Two parallel lines are cut by a transversal Use Angle Pair Relationships to find m BEF 0 D A H 3 Two parallel lines are cut by a transversal Use Angle Pair Relationships to find x 5 6 8 7 B 1 4 3 3x 58 7x 1 E 9 5x K G 5 85 FL
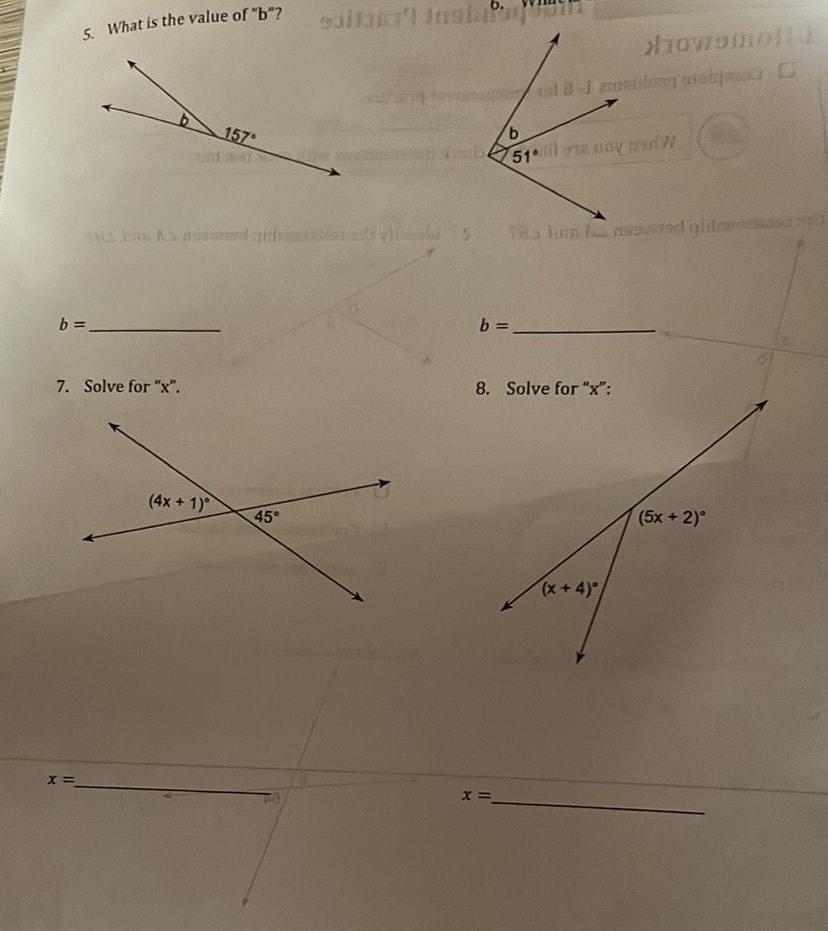
Geometry
2D Geometry5 What is the value of b b 7 Solve for x X 4x 1 157 45 salta inship b tal B 1 zounidony G b 51 il noy nad W X nowomoll E 518 lun wred gim 8 Solve for x x 4 O 5x 2

Geometry
2D GeometryCorresponding Angles Theorem If two parallel lines are cut by a transversal then the pairs of corresponding angles have the same measure Example 21 45 2 Name the four pairs of corresponding angles Then write an equation which shows that each of the angles has the same measure The first one is done for you Corresponding Angles 21 and 25 24 and 2 and 2 and Alternate Interior Angles Equation m21 m25 24 and 26 m and mz mz Alternate Interior Angles Theorem If two parallel lines are cut by a transversal then the pairs of alternate interior angles have the same measure Example 24 26 m2 1 m2 3 Name the two pairs of alternate interior angles Write an equation that shows that the angles have the same measure m2 Equation m24 mz6 5 m2 7 2 1 4 3 8 7

Geometry
2D Geometry4 1 Checkpoint Once you have completed the above problems and checked your solutions complete the Lesson Checkp below Complete the Lesson Reflection above by circling your current understanding of the Learning Goal 1 Which of the following groups of angles match the given property Select two that apply A E C LDEA and LCEA form a Linear Pair D LFEB and BED form a Linear Pair 60 F D B A LCEA is congruent to ZDEB through the Vertical Angles Theorem B LFEB is congruent to ZDEA through the Vertical Angles Theorem