3D Geometry Questions and Answers

Geometry
3D GeometryGive a cube ABCDA'B'C'D' with size of 14, point F is the midpoint of edge BB', point E lies on the edge BB' with the ratio BE : EB' = 5:2. Find the angle and the distance between lines AE and D'F

Geometry
3D GeometryA cylinder has a radius of 5 m and a height of 9 m. What is the volume of the cylinder? Round to the nearest tenth and use 3.14 or the calculator value for pi.
Geometry
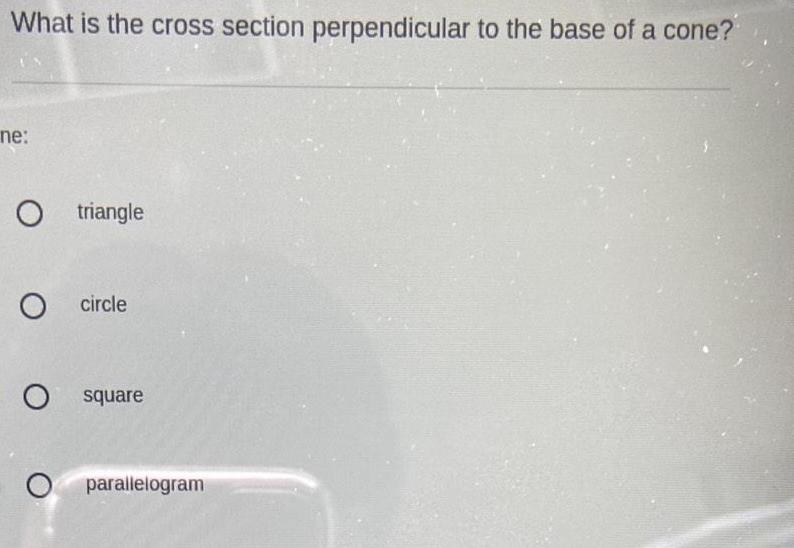
3D GeometryWhat is the cross section perpendicular to the base of a cone?
triangle
circle
square
parallelogram

Geometry
3D Geometrya. Given triangle ABC and circle CA centered at A with radius AC and circle CB centered at B with radius BC, how many intersection points do the two circles have and
where are the intersection point (s) located?
b. If two circles centered at A and B intersect in a single point C, then describe all of the possible relationships between AB, BC, and AC. Explain your answer.

Geometry
3D GeometryA ship leaves port and travels 85 miles into the sea at an angle of 2450. The ship then travels for 105 miles at an angle of 100. At that point the ship drops anchor. A helicopter, beginning from the same port, needs to join the ship as quickly as possible to rescue an injured passenger. At what angle should the helicopter fly in order to reach the ship? Round your answer to the nearest degree and do not include units.
Geometry
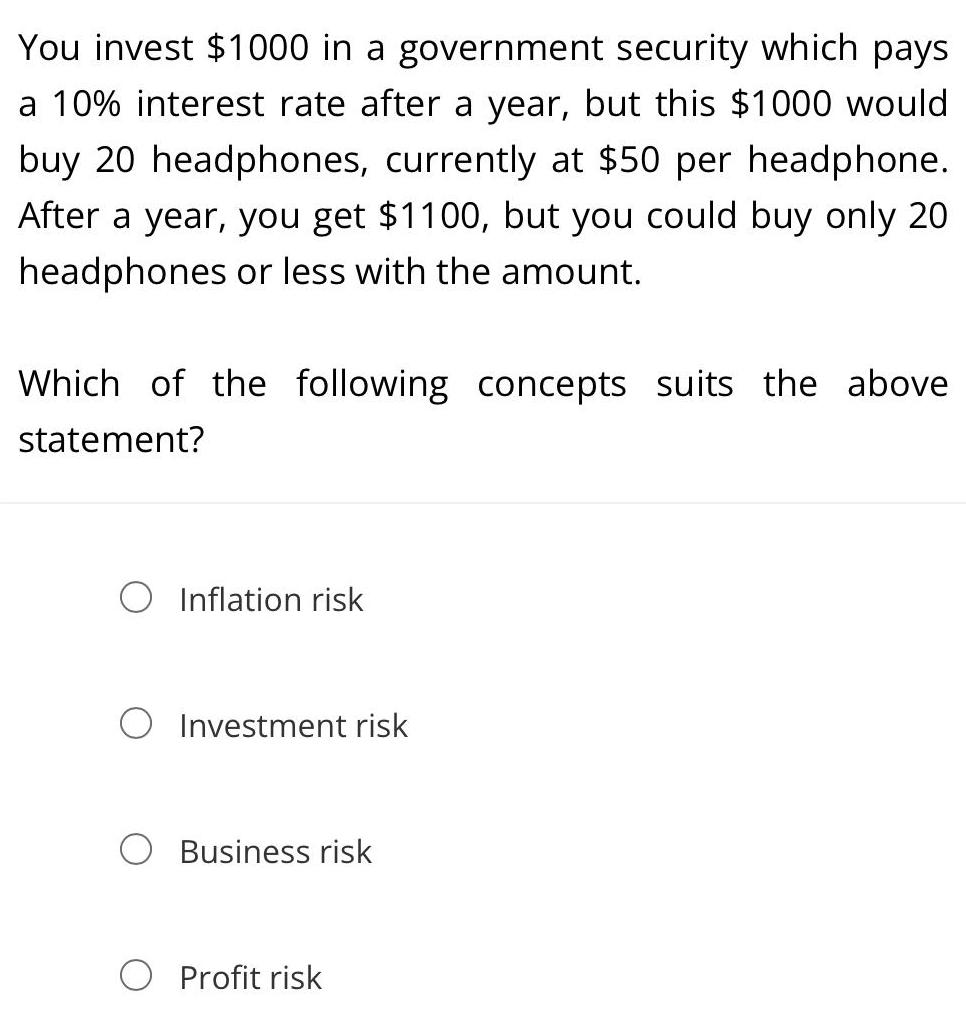
3D GeometryYou invest $1000 in a government security which pays
a 10% interest rate after a year, but this $1000 would
buy 20 headphones, currently at $50 per headphone.
After a year, you get $1100, but you could buy only 20
headphones or less with the amount.
Which of the following concepts suits the above
statement?
Inflation risk
Investment risk
Business risk
Profit risk

Geometry
3D GeometryWhat is the minimum number of faces that intersect to form a vertex of a polyhedron?
one
two
three
four
a number not listed here

Geometry
3D GeometryConsider a semi-spherical bowl machined out of wood (A drawing of a semi-spherical bowl can be found in UNIT- 4 Introduction, solved Example 3). The outer radius of the bowl is 12.0 cm and it is uniformly 2.0cm thick. What is the total surface area of the bowl (in units of m²)?
a. 10.4
b.0.104
c. 16.7
d.0.167

Geometry
3D GeometryThe equation of the ellipse that has a center at (3, 1), a focus at (1, 1), and a vertex at (-2, 1), is (x - c)²/A² + (y - D)²/B² =1 where
A =
B =
C=
D =

Geometry
3D GeometrySuppose the graph of y =4x²+bx+c intersects the x-axis at x = 4 and x = 8.
The vertex is at=________ (Enter your answer as an ordered pair)
The y-intercept is at=________


Geometry
3D Geometry2. (Edited/corrected
4/3/22.) Show that the intersection of H with the plane
x + 2y + 3z = 4 is a circle in H. What are its radius and the coordinates of its center?

Geometry
3D Geometryconsider on. Oxy, a circunference of equation (x-1)² · (4 + 2)² = 25. which of the following equations define a tangent line to this circunference? (A) X= A (B) x =S (c) y=-2 (D) y=3


Geometry
3D GeometryA right circular cylinder must have a volume of 100 m^3. Find the dimensions that should be used to make the cylinder using the least amount of material possible.

Geometry
3D GeometryLet G be a planar graph with 128 vertices and 378 edges, assuming that we colored 3 vertices located on the same face in green, and the rest in yellow, prove that it is possible to connect any pair of yellow vertices in a path that doesn't have any green vertices in it.
Geometry
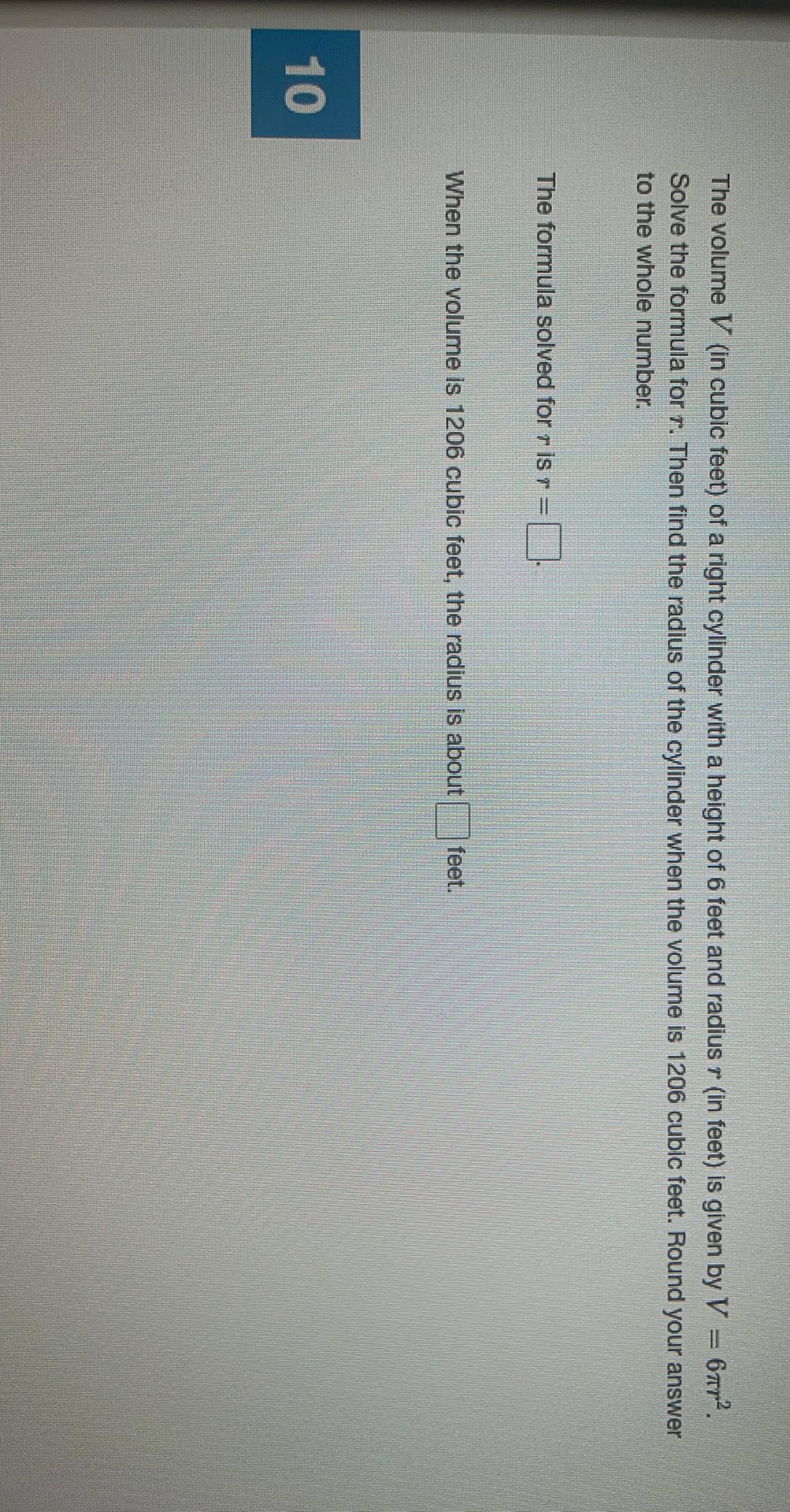
3D GeometryThe volume V (in cubic feet) of a right cylinder with a height of 6 feet and radius r (in feet) is given by V = 6πr². Solve the formula for r. Then find the radius of the cylinder when the volume is 1206 cubic feet. Round your answer to the whole number.
The formula solved for r is r = ___ .
When the volume is 1206 cubic feet, the radius is about ____ feet.

Geometry
3D GeometryA store has clearance items that have been marked down by 60%. They are having a sale, advertising an additional 25% off clearance items. What percent of the original price do you end up paying? _% Give your answer accurate to at least one decimal place.
Geometry
3D GeometryA cone has a volume of 108л and a base diameter of 12. What is the height of the cone? (1) 27 (2) 9 (3) 3 (4) 4

Geometry
3D GeometryAn isosceles right triangle whose legs measure 7 is continuously rotated about one of its legs to form a three-dimensional object. The three-dimensional object is a (1) cylinder with a diameter of 7 (2) cylinder with a diameter of 14 (3) cone with a diameter of 14 (4) cone with a diameter of 7

Geometry
3D GeometryA candle maker uses a mold to make candles like the one shown below.
The height of the candle is 14cm and the circumference of the candle at its widest measure is
31.416 cm. Use modeling to approximate how much wax, to the nearest cubic centimeter, is
needed to make this candle. Justify your answer.

Geometry
3D GeometryThe volume of a sphere is 5000π m². What is the surface area of the sphere to the nearest square meter?
1517 m²
195 m²
3033 m²
62,832 m²
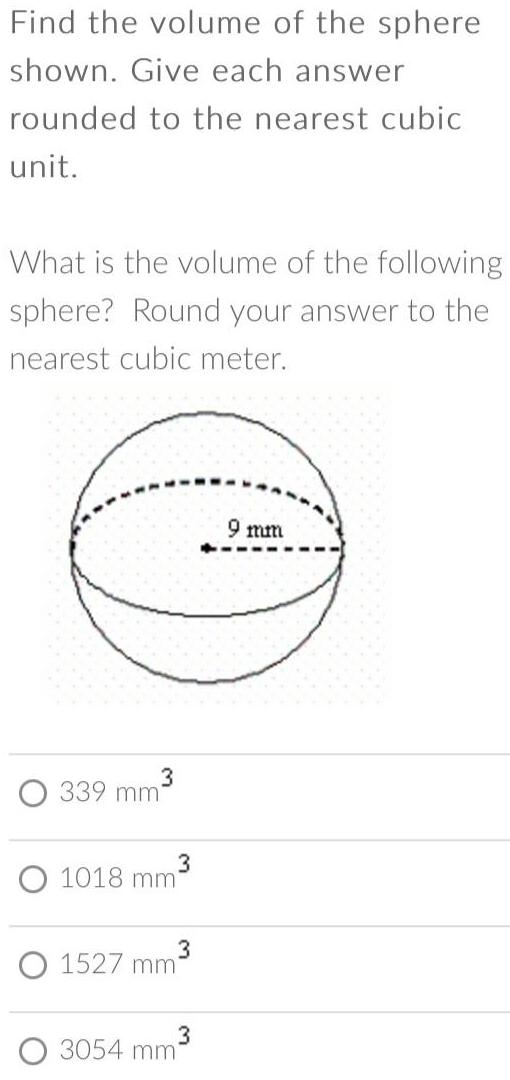
Geometry
3D GeometryFind the volume of the sphere
shown. Give each answer
rounded to the nearest cubic
unit.
What is the volume of the following
sphere? Round your answer to the
nearest cubic meter.
339 mm3
1018 mm3
1527 mm3
3054 mm3

Geometry
3D GeometryFind the surface area of the
sphere with the given
dimension. Leave your answer in
terms of π.
radius of 60 m
14,400 m²
7,200 m²
1,800 m²
3,600 m²

Geometry
3D GeometryA balloon has a circumference of 11 cm. Use the circumference to approximate the surface area of the balloon to the nearest square centimeter.
380 cm²
154 cm²
121 cm²
39 cm²
Geometry
3D GeometryConsider points A(1,4,7), B(2,-1,3), C(3,5,3), A'(2,3,5), B'(1, 1.-1) and C(1,-4,-2). Find a point P and a line h such that triangles ABC and A'B'C' are in perspective from a point P and from the line h, in which A corresponds to A', B corresponds to B' and C corresponds to C'.

Geometry
3D GeometryThree types of customers arrive at an airport: check baggage with 30% (that is for each arriving customer there is a 0.3 probability that this is a check baggage cus- tomer), purchase tickets (15%), and carry-on (55%). The interarrival-time distribution for all customers combined is EXPO(1.3); all times are in minutes and the first arrival is at time 0. The bag checkers go directly to the check-bag counter to check their bags-the time for which is distributed TRIA (2,4,5) -proceed to X-ray, and then go to the gate. The ticket buyers travel directly to the ticket counter to purchase their tickets-the time for which is distributed EXPO (7)-proceed to X-ray and then go the gate. The carry-ons travel directly to the X-ray, then go to the gate counter to get a boarding pass-the time for which is dis- tributed TRIA(1, 1.6, 3). All three counters are staffed all the time with one agent each. The X-ray time is EXPO(1): All travel times are EXPO(2), except for the carry ontime to the X-ray, which is EXPO(3). Create your model, your model need to record average system time from entrance to gate for all customers combined.

Geometry
3D GeometryThe volume of a right cone is 8917 units. If its circumference measures 187 units,
find its height.
Geometry
3D GeometryJoenni De jesus glass
Volume of a Cone Level 2
Jun 13, 9:49:43 PM
The volume of a right cone is 367 units. If its height is 12 units, find its
circumference in terms of .
Answer: _______units

Geometry
3D GeometryGiven the equation x² - 6x³-5x² +24x+4= 0, complete the following.
a. List all possible rational roots.
b. Use synthetic division to test several possible rational roots in order to identify one actual root.
c. Use the root from part (b) to solve the equation.
a. List all rational roots that are possible according to the Rational Zero Theorem.
(Use commas to separate answers as needed.)
b. Use synthetic division to test several possible rational roots in order to identify one actual root.
One rational root of the given equation is
(Simplify your answer.)
c. Use the root from part (b) to solve the equation.
The solution set is.
(Simplify your answer. Type an exact answer, using radicals as needed. USe integers or fractions

Geometry
3D GeometryThe United Nations stores statistics about all the live births in the United States. The latest data concerns the birthweights of infants born in 2015. The µ is 3056 grams and the σ is 514 grams. Calculate the total weight of twins, one born one standard deviation below the mean and the other born two standard deviations below the mean.
Provide your answer below:
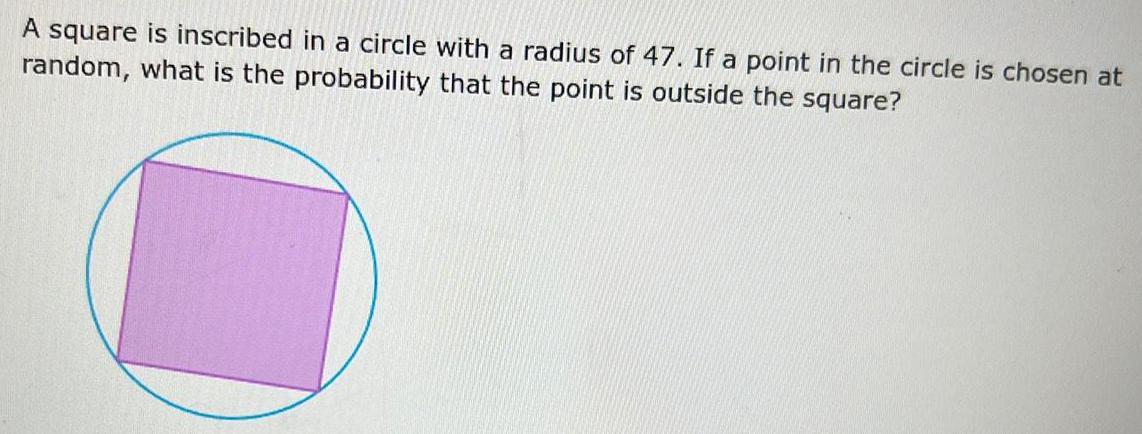
Geometry
3D GeometryA square is inscribed in a circle with a radius of 47. If a point in the circle is chosen at
random, what is the probability that the point is outside the square?

Geometry
3D GeometryGeometry
Hello, can someone help with this geometry
question?
The center of regular pentagon P is at the origin. One side of P is parallel to the x-axis.
Write the four rotation angles greater than 0° and less than 360° that map the pentagon onto itself.

Geometry
3D GeometryIn quadrilateral MNOP, ZMZN. Which of a parallelogram, trapezoid,
or rhombus could quadrilateral MNOP be?
parallelogram or rhombus
any of the three
parallelogram only
trapezoid only
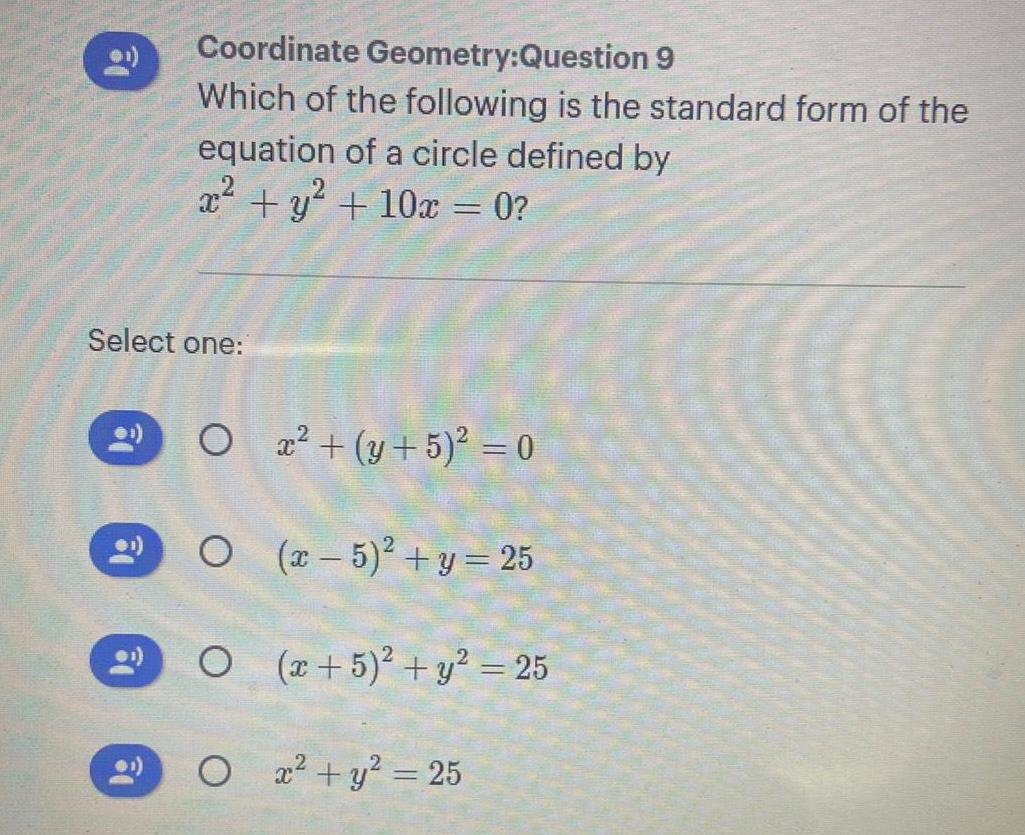
Geometry
3D GeometryCoordinate Geometry:Question 9 Which of the following is the standard form of the
equation of a circle defined by
x² + y² + 10x = 0?
Select one:
O x² + (y + 5)² = 0
O (x - 5)² + y = 25
O (x + 5)² + y² = 25
O x² + y² = 25
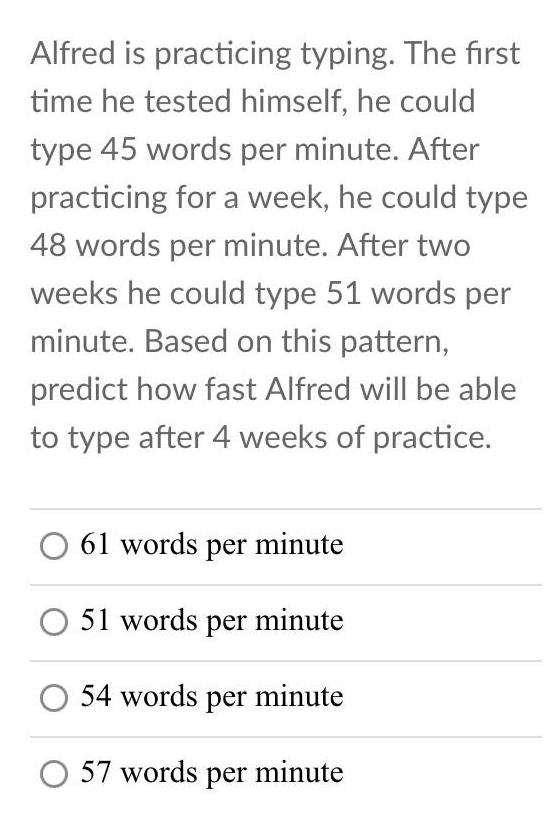
Geometry
3D GeometryAlfred is practicing typing. The first time he tested himself, he could type 45 words per minute. After Npracticing for a week, he could type 48 words per minute. After two
weeks he could type 51 words per minute. Based on this pattern,predict how fast Alfred will be able to type after 4 weeks of practice.
61 words per minute
51 words per minute
54 words per minute
57 words per minute

Geometry
3D GeometryIs the following definition of perpendicular reversible? If yes, write it as a true biconditional.Two lines that intersect at right angles are perpendicular.
Yes; if two lines are perpendicular,then they intersect at right angles.
Yes; if two lines intersect at right angles, then they are
perpendicular.
Yes; two lines intersect at right angles if (and only if) they are
perpendicular.
The statement is not reversible.

Geometry
3D GeometryWhat is the converse of thefollowing conditional? If a point is inthe fourth quadrant, then its coordinates are negative.
If a point is in the fourth quadrant then its coordinates are negative.
O If the coordinates of a point are not negative, then the point is not in
the fourth quadrant.
O If the coordinates of a point are negative, then the point is in the
fourth quadrant.
If a point is not in the fourth quadrant, then the coordinates of
the point are not negative.

Geometry
3D GeometryConstruct an experimental probability distribution. Use the 8-sided die link or random number generator in google classroom to simulate rolling two 8-sided dice 100 times. X represents the sum of the values found by rolling two 8-sided dice.
a. Construct a relative-frequency table.
b. Graph the experimental probability distribution.

Geometry
3D GeometryDraw your own triangle given the indicated measures and solve for the other parts using Sine Law. Write an explanation in each line of your solution.
1. <A = 73°, a = 18, b = 11
2. <A = 26°, < C = 35°,b=13
![Type the inverse of the matrix. Use decimals. If no inverse exists type "none".
[23]
25](https://media.kunduz.com/media/sug-question/raw/81089421-1659789932.1797178.jpeg?w=256)
Geometry
3D GeometryType the inverse of the matrix. Use decimals. If no inverse exists type "none".
[23]
25

Geometry
3D GeometryThe time-t price of a stock within the Black-Scholes framework is S(t). You are given:
(i) The stock pays continuous dividends at an annual rate of 0.02.
(ii) The stock's volatility is 0.3.
(iii) The continuously compounded risk-free interest rate is 0.06.
(iv) S(0)=50
A claim on the stock pays (S(2) - 50)³. Calculate the price of the claim at 0.

Geometry
3D GeometryProblem21.A circular cylinder is formed by rolling an 8 1/2x11" paper vertically and taping it with no overlap. A second cylinder is formed by rolling an 8-1/2 X11" paper horizontally and taping it with no overlap. What is the ratio of the volume of the 8 1/2 tall cylinder to 11" tall cylinder to the volume of th the 11" tall cylinder?
(A) 11/8 (B) 17/11 (C) 3/2 (D) 22/17 (E) 11/17
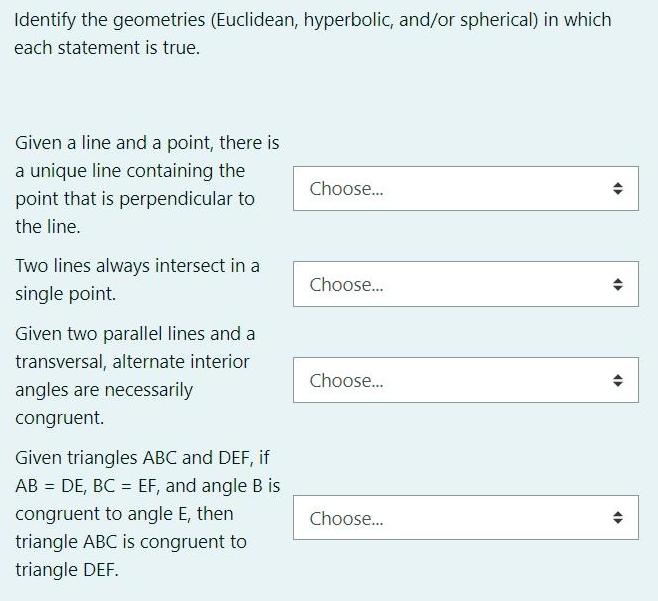
Geometry
3D GeometryIdentify the geometries (Euclidean, hyperbolic, and/or spherical) in which each statement is true.
Given a line and a point, there is a unique line containing the point that is perpendicular to the line.
Two lines always intersect in a single point.
Given two parallel lines and a transversal, alternate interior angles are necessarily congruent.
Given triangles ABC and DEF, if AB = DE, BC = EF, and angle B is congruent to angle E, then triangle ABC is congruent to triangle DEF.

Geometry
3D GeometryProblem 3. Let ABC be a triangle. Let C' be the midpoint of the
side AB. Let A' be a point on the side BC such that CA' = 2A'B.
Let B' be a point on the line AC such that CB' = 4CA. Let M be
the point of intersection of the line A'B' and the line CC'. Does the point M belong to segment CC? Find the ratio of CM: MC'.

Geometry
3D GeometryA curb is 4 inches high. The ramp from the sidewalk to the street follows the same guidelines as other ramps (no more than 4.8 degrees, so a 1: 12 ratio of vertical to horizontal). What is the horizontal distance for a ramp with a 4 inch vertical distance?
Image not drawn to scale.
Flared sides smoothly connect the ramp to the sidewalk. The guidelines say the flared sides must be no more than 5.7 degrees (1 : 10 ratio of vertical to horizontal). What is the horizontal distance for flared sides with a 4 inch vertical distance?
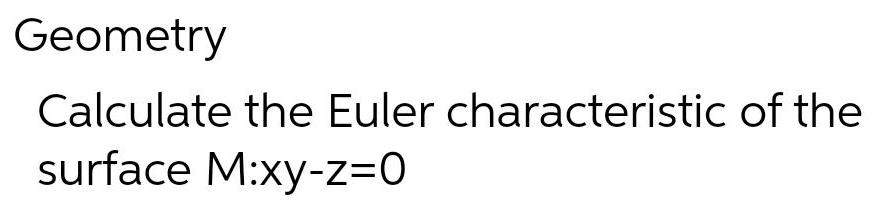
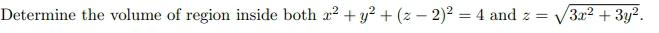
Geometry
3D GeometryDetermine the volume of region inside both x² + y² + (z-2)² = 4 and z =√3x² + 3y².

Geometry
3D GeometryThe voltage V. in an electric circuit is measured in millivolts (mV) and is given by the formula
V=0.2sin0.1m(t-0.5) +0.3, where t is the time in seconds from the start of an experiment. Use the graph of the function to estimate how many seconds in the 40 second interval starting at t= 0 during which the voltage is below 0.21mV.
Select one:
a. 14.06
b. 7.03
C 12.97
d. 27.16