3D Geometry Questions and Answers
Geometry
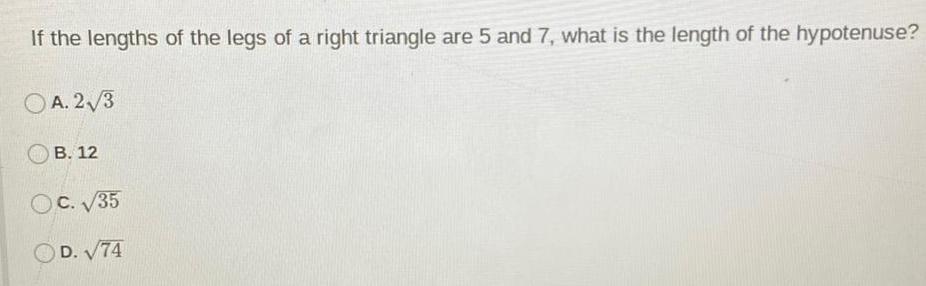
3D GeometryIf the lengths of the legs of a right triangle are 5 and 7, what is the length of the hypotenuse?
A. 2√3
B. 12
C. √35
D. √74

Geometry
3D GeometryAssume the Cartesian model for Euclidean geometry. Find the images of the points (0,0), (0, 2), and (2, 1) under the following isometries.
(a) The glide reflection GAB, where A = (-2,0) and B = (0, 1).

Geometry
3D GeometryFor a regular octagonal prism, suppose that the length of each base edge is 2.5 cm. and the apothem of each base is 3 cm. The altitude of the prism measures 4 cm. Find the total (surface) area and volume of the prism.

Geometry
3D GeometryImagine if you will that across the 26 stores assigned the $499.00 price point, an average of 127.4 phones were sold, whereas an average of 119.6 were sold for $519.00. Further, 117.8 were sold at the price point of $549 and 114.3 were sold for the price point of $599.00. Perform the appropriate multiple comparison test at alpha = .05, to see which means are significant from the others, if any.
According to your findings which means are pairwise different from each other and why?
Show all work
Geometry
3D GeometryWhat is Volume?
What are some ways knowing the volume of an object will help you in the real
world?

Geometry
3D GeometrySolve sin^2(t) = 8 cos(t) for all solutions 0 <t <2π
t=
Give your answers accurate to 2 decimal places, as a list separated by commas
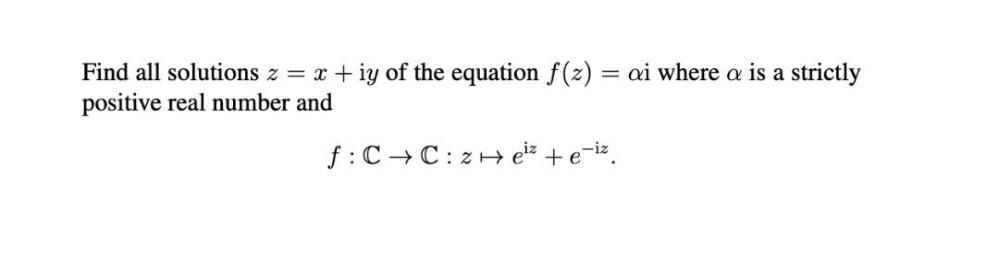
Geometry
3D GeometryFind all solutions z = x + iy of the equation f(x) = ai where a is a strictly positive real number and
f:C--> C:2 -->e^iz + e^-iz.

Geometry
3D GeometrySketch the following regions in cylindrical coordinates:
(a) 1 ≤r ≤ 3,0 ≤ θ ≤ π/2,0 ≤z≤1
(b) r² + z² = 9 (Hint: what is this in Cartesian coordinates?)
Geometry
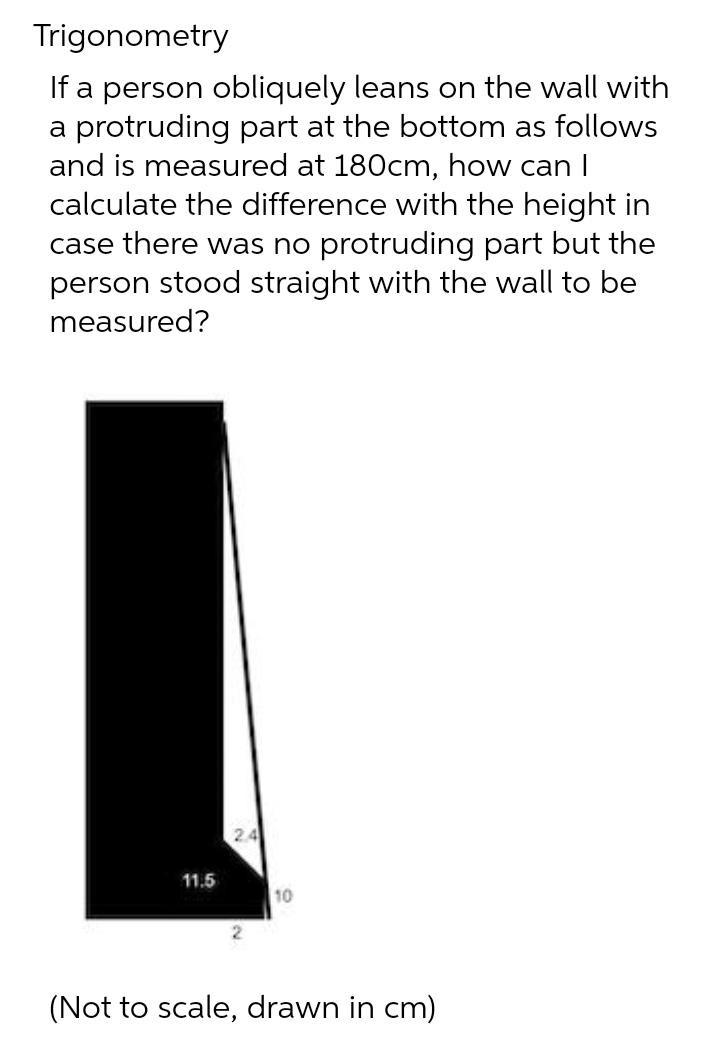
3D GeometryIf a person obliquely leans on the wall with a protruding part at the bottom as follows and is measured at 180cm, how can I calculate the difference with the height in case there was no protruding part but the person stood straight with the wall to be measured?

Geometry
3D GeometryAn action movie production team needs glass spheres to hold a green liquid that looks like an explosive. If all of the available 3,392.92 cubic
inches of the liquid is to be poured into 30 glass spheres, what should the diameter of each sphere be? Assume that each sphere is filled to the top.
A). 3 inches
B). 4 inches
C). 6 inches
D).8 inches
E). 9 inches
Geometry
3D GeometryA candle manufacturer sells cylindrical candles in sets of three. Each candle in the set is a different size. The smallest candle has a radius of 0.5 inches and a height of 3 inches. The other two candles are scaled versions of the smallest, with scale factors of 2 and 3. How much wax is needed to create one set of candles?
A. 27π cubic inches
B. 36π cubic inches
C. 53π cubic inches
D. 86π cubic inches
E. 98π cubic inches
Geometry
3D GeometryType the correct answer in the box. The volume of clay used to build a cylindrical pillar with a height of 9 centimeters is 324πt cubic centimeters. The area of the base of the pillar is ______ π Square centimeters.

Geometry
3D GeometryA satellite launch rocket has a cylindrical fuel tank. The fuel tank can hold V cubic meters of fuel. If the tank measures d meters across, what is the height of the tank in meters?
A)2V/πd²
B)4V/d²
C)V/πd²
D)4V/πd²
E)8V/πd²
Geometry
3D GeometryA cylindrical can has a radius of 7 inches and is 3 inches tall.
Find the volume of the can.
Volume =_________
Geometry
3D GeometryThe volume of a sphere with radius r is given by the formula V = 4/3πr³. Find the volume of a sphere with diameter 30 inches is __cubic inches.
Use 3.14 or the π key on your calculator. Round your answer to the nearest tenth if necessary.

Geometry
3D GeometryDetermine the type of the second-order
surface and find the coordinates of its center
(if it exists): 3x² + y² + 4z² - 2xy - 6xz+4yz + 4x - 2y - 6z= -=-1
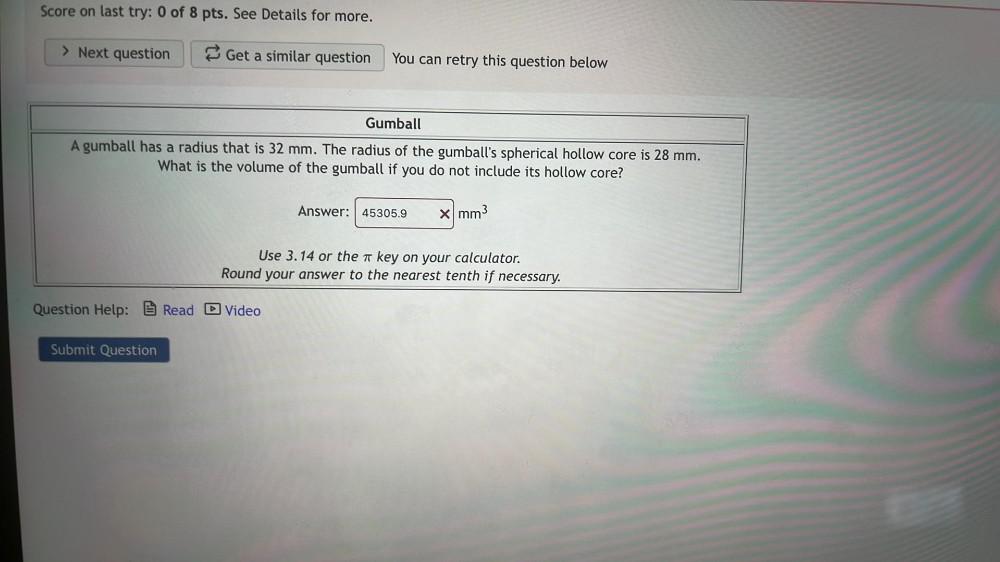
Geometry
3D GeometryA gumball has a radius that is 32 mm. The radius of the gumball's spherical hollow core is 28 mm. What is the volume of the gumball if you do not include its hollow core?
Answer: ______x mm³

Geometry
3D GeometryA regular right square pyramid has a lateral surface area of 161 m² and a total surface area of 235 m². Determine the length of the edges of its base, its slant height, its height and the length of its lateral edges. Express your answer to 3 sig figs.
1). Length of edges of the base =_____METRES
2). Slant height =____METRES
3). Height =____METRES
4). Length of the lateral edges =____METRES

Geometry
3D GeometryProblem 18. Let P = (0,1/2), Q=(1/2,0) and R = (-1/2,0).
1. Compute the perimeter of the hyperbolic triangle △PQR.
2. Compute the angles ∠PQR, ∠QRP and ∠QPR.

Geometry
3D GeometryCalculate the volume of a cylinder that is 5 cm tall with a radius of 4.3 cm. Round to the nearest tenth of a cubic cm Enter the number portion only.
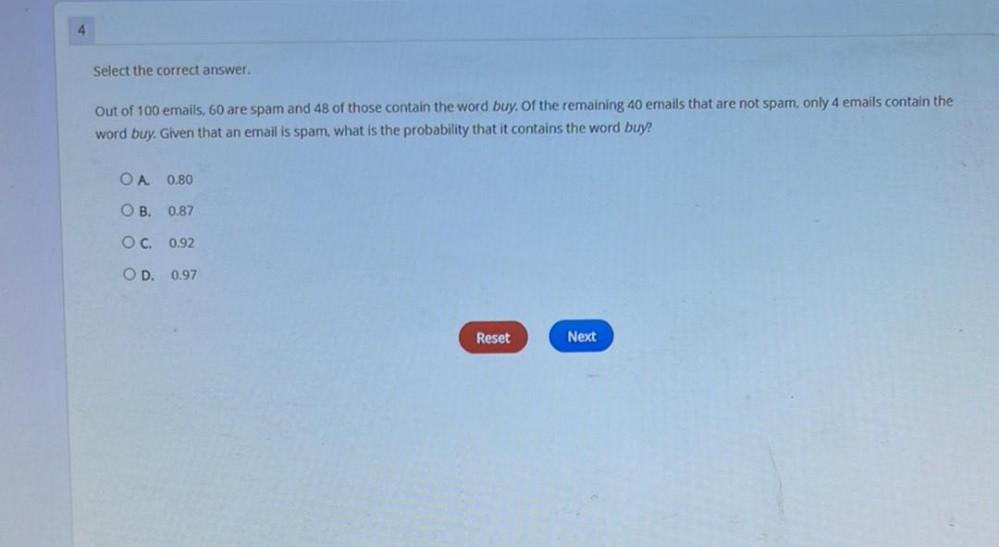
Geometry
3D GeometryOut of 100 emails, 60 are spam and 48 of those contain the word buy. Of the remaining 40 emails that are not spam, only 4 emails contain the word buy. Given that an email is spam, what is the probability that it contains the word buy?
A 0.80
B. 0.87
C. 0.92
D. 0.97
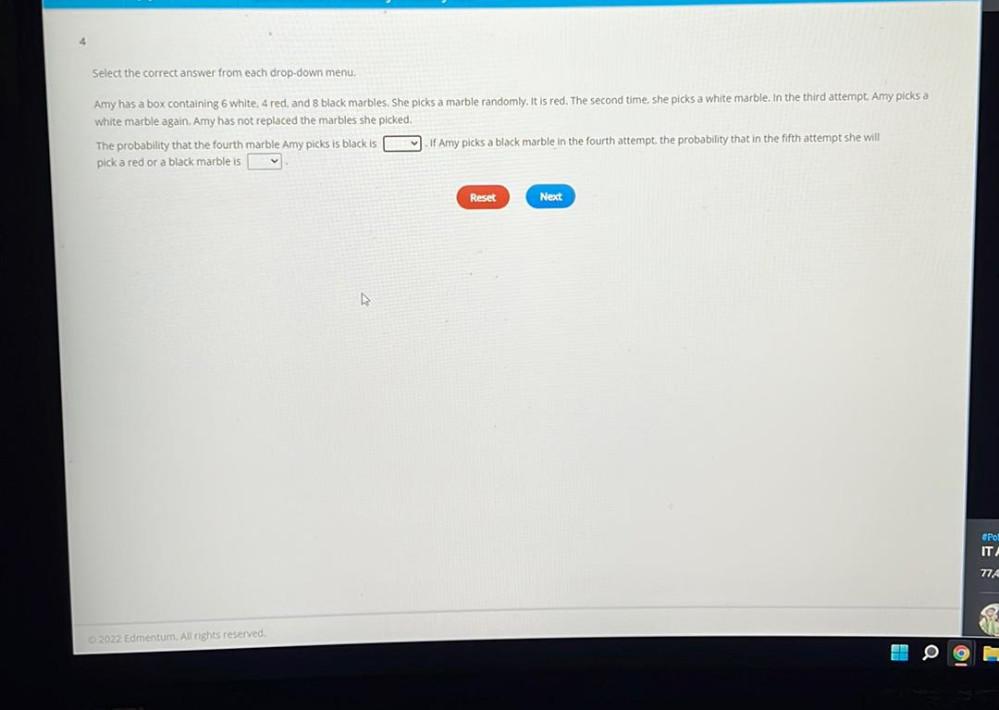
Geometry
3D GeometryAmy has a box containing 6 white. 4 red, and 8 black marbles. She picks a marble randomly. It is red. The second time, she picks a white marble. In the third attempt. Amy picks a white marble again. Amy has not replaced the marbles she picked.
The probability that the fourth marble Amy picks is black is______ If Amy picks a black marble in the fourth attempt, the probability that in the fifth attempt she will pick a red or a black marble is_____

Geometry
3D GeometryFind the shortest distance from the point P to the plane and find the point Q on the plane closest to P if P(2, 3, 0) and the plane has an equation 5x+y+z=1.
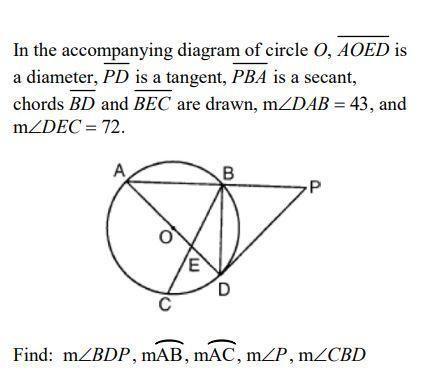
Geometry
3D GeometryIn the accompanying diagram of circle O, AOED is a diameter, PD is a tangent, PBA is a secant, chords BD and BEC are drawn, m∠DAB = 43, and m∠DEC = 72.
Find: m∠BDP, mAB, mAC, m∠P, m∠CBD

Geometry
3D GeometryThe given plane intersects the following paraboloid in an ellipse. Find the points on the ellipse that are nearest to and farthest from the origin.
x + y + 2z = 2; z = x² + y²
) (nearest point)
) (farthest point)

Geometry
3D GeometryWhich of the following statements is false?
A. A square is a regular quadrilateral.
B. The diagonals of a rectangle are perpendicular.
C. Opposite sides of a parallelogram are congruent.
D. A rectangle is an equiangular quadrilateral.
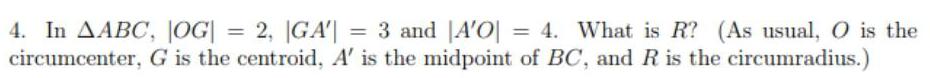
Geometry
3D GeometryIn AABC, |OG| = 2, |GA| = 3 and |A'O = 4. What is R? (As usual, O is the circumcenter, G is the centroid, A' is the midpoint of BC, and R is the circumradius.)

Geometry
3D GeometryUse spherical coordinates.
Evaluate ∫∫∫Ex y² dv, where E is the solid hemisphere x² + y² + z² ≤ 4, y ≥ 0.

Geometry
3D GeometryUse cylindrical or spherical coordinates, whichever seems more appropriate.
Find the volume of the smaller wedge cut from a sphere of radius a by two planes that intersect along a diameter at an angle of π/3

Geometry
3D GeometryUse cylindrical coordinates.
Evaluate ∫∫∫E (x - y) dV, where E is the solid that lies between the cylinders x² + y² = 1 and x^2 + y^2 = 16, above the xy-plane, and below the plane z = y + 4.

Geometry
3D GeometryOut of all points in the top half of the unit ball, what is the average distance from the origon?

Geometry
3D GeometryA stone pyramid in Egypt has a square base that measures 146 m on each side. The height is 94 m. What is the volume of the pyramid?
m³

Geometry
3D GeometryA cylindrical soup can has a radius of 1.3 in. and is 5 in. tall. Find the volume of the can.
Round your answer to the nearest tenth if necessary.

Geometry
3D GeometryA cone-shaped pile of sawdust has a base diameter of 36 feet, and is 14 feet tall. Find the volume of the pile.
Round your answer to the nearest tenth if necessary.

Geometry
3D GeometryCompute the volume of the cone shown if given are the slant height a =50 mi and height h=48 mi
Round your answer to two decimal places.
V=

Geometry
3D GeometryPlot the point whose spherical coordinates are given. Then find the rectangular coordinates of the point.
(a) (5, 3V/4,π/2)
(x, y, z) =
(b) (6, -π/3,π/4)
(x, y, z) =

Geometry
3D GeometryA video game is programmed using vectors to represent the motion of ob-
jects. The programmer is programming a human character's path to an object.
The object is 30 meters to the right, 20 meters in front of the human character.
Part One
Write a vector to represent the path to the object.
Part Two
How far is the object from the human character?
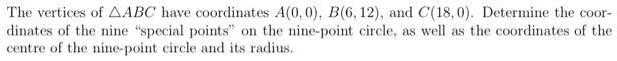
Geometry
3D GeometryThe vertices of ΔABC have coordinates A(0, 0), B(6, 12), and C(18,0). Determine the coordinates of the nine "special points" on the nine-point circle, as well as the coordinates of the centre of the nine-point circle and its radius.


Geometry
3D Geometry3. What is the biconditional of the following statement?
if a polygon is a hexagon, then it has six sides.
A. If a polygon is a pentagon, then it has six sides.
B. If a polygon is not a hexagon, then it doesn't have six sides.
C. If a polygon doesn't have six sides, then it is not a hexagon.
D. A polygon is a hexagon if and only if it has exactly six sides.
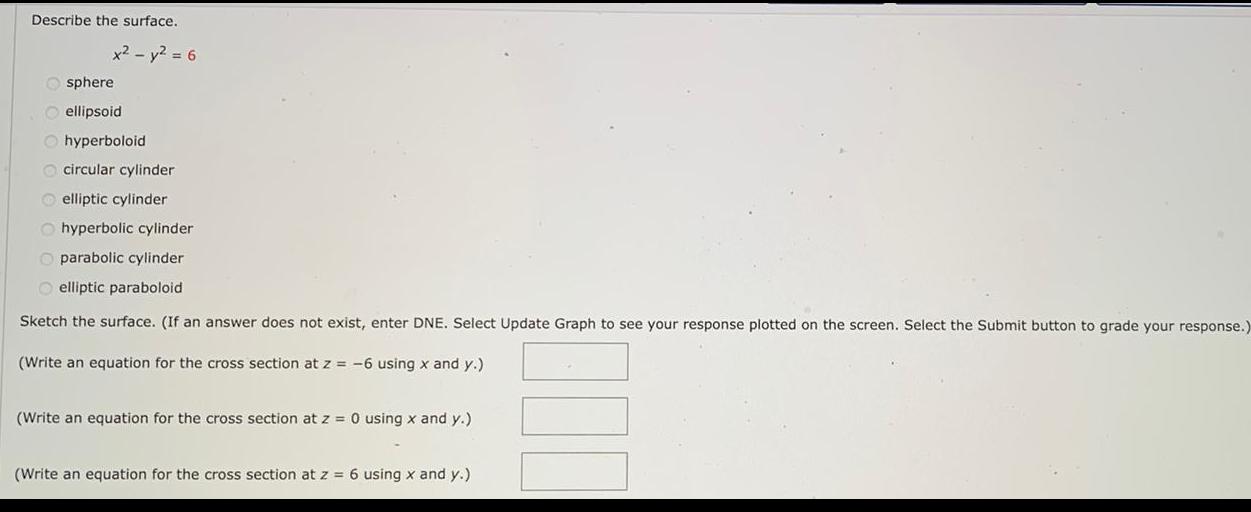
Geometry
3D GeometryDescribe the surface.
x² - y² = 6
sphere
ellipsoid
hyperboloid
circular cylinder
elliptic cylinder
hyperbolic cylinder
parabolic cylinder
elliptic paraboloid
Sketch the surface. (If an answer does not exist, enter DNE. Select Update Graph to see your response plotted on the screen. Select the Submit button to grade your response.)
(Write an equation for the cross section at z = -6 using x and y.)
(Write an equation for the cross section at z = 0 using x and y.)
(Write an equation for the cross section at z = 6 using x and y.)
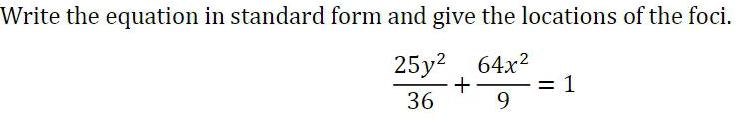
Geometry
3D GeometryWrite the equation in standard form and give the locations of the foci.
25y²/36 + 64x²/9 =1

Geometry
3D GeometryApply the KT conditions to solve the following NLP problem for optimality candidates:
min -x₁ +3
s. t. (3-x₁)³-X₂ + 2 ≥0
3x1 + x₂ ≥ 9
Verify the type of the achieved candidates by applying the second order condition.
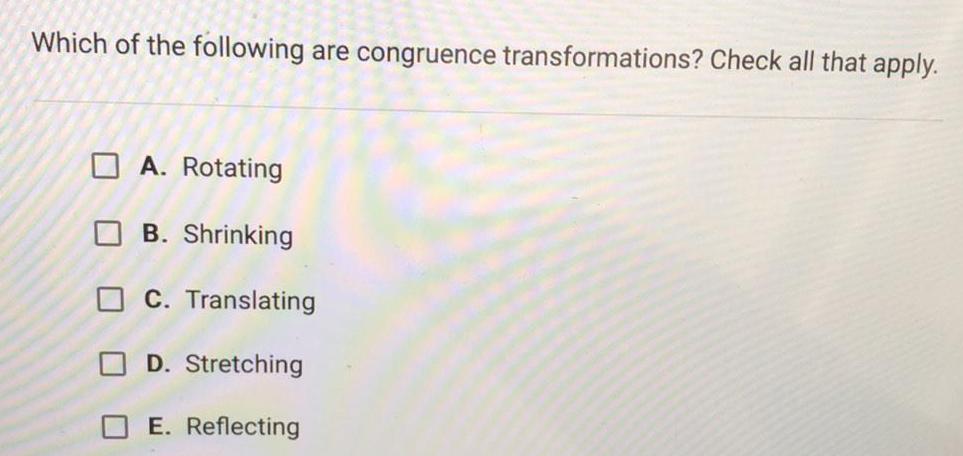
Geometry
3D GeometryWhich of the following are congruence transformations? Check all that apply.
A. Rotating
B. Shrinking
C. Translating
D. Stretching
E. Reflecting

Geometry
3D GeometryAssume that GHI ALMN. Which of the following congruence statements are correct? Check all that apply.
A. N= I
B. GH = LM
C. <L= I
D. M= H
E. IH = NM
F. IG = LM

Geometry
3D GeometryWrite the equation of the hyperbola that has a center at (-4, 6), a focus at (-10, 6), and a vertex at (-8,6).


Geometry
3D Geometry1. An inverted right closed conical tank has a base of 12m and 8m high and fully filled by water.
a. 302
b. 189
C. 47
Find the area of the wetted portion if the tank is opened
a. 302
b. 189
C. 47
Find the volume of the tank
a. 302
b. 189
c. 47
If the tank spilled half of the water contained, find the area left
a. 38
b.189
c.47
Find the volume left
a.38
b.189
c.47

Geometry
3D GeometryIn a beheaded cone placed a sphere so touch the pedestal, the top and the perpendicular space of beheaded cone. Area of the top of the beheaded cone is less than area of the pedestal. Find the ratio
of the beheaded with sphere volume.
a. (a+√a+1)/(2√a)
b. (a+√a+2)/(2√a)
c. (a+√a+3)/(2√a)
d. (a+√a+4)/(2√a)