Solution of triangles Questions and Answers

Geometry
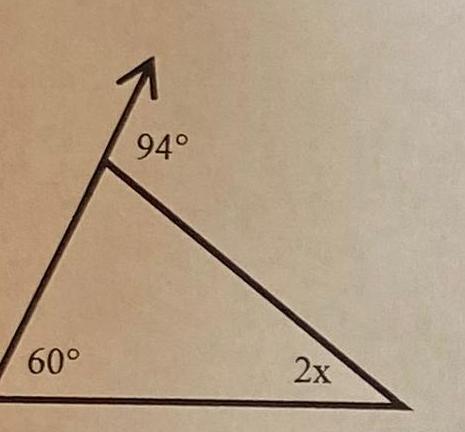
Solution of trianglesA cruise ship maintains a speed of 19 knots nautical miles per hour sailing from San Juan to Barbados a distance of 600 nautical miles To avoid a tropical storm the captain heads out of San Juan at a direction of 11 off a direct heading to Barbados The captain maintains the 19 knot speed for 11 hours after which time the path to Barbados becomes clear of storms a Through what angle should the captain turn to head directly to Barbados b Once the turn is made how long will it be before the ship reaches Barbados if the same 19 knot speed is maintained Barbados 600 11 San Juan
Geometry
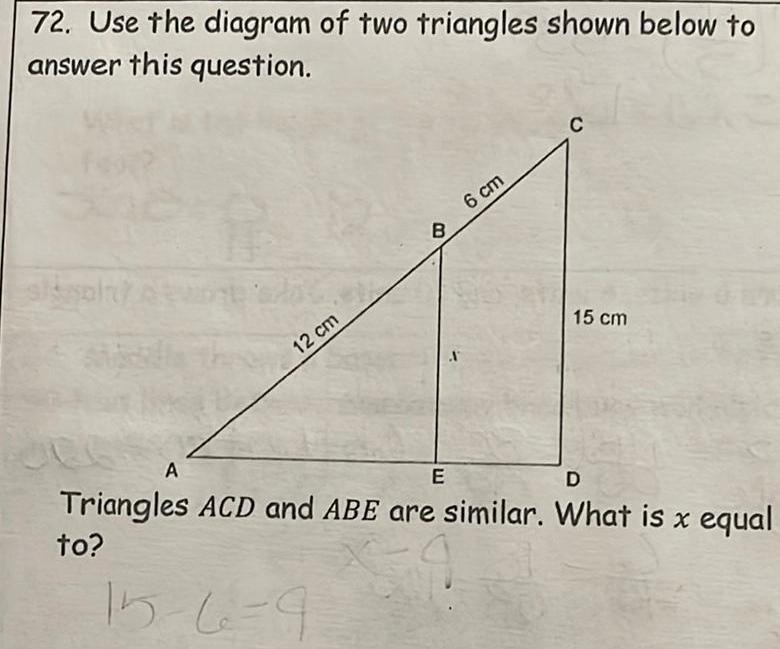
Solution of triangles72 Use the diagram of two triangles shown below to answer this question sisaln A 12 cm B 6 cm A C 15 cm E D Triangles ACD and ABE are similar What is x equal to 15 6 9 59
Geometry
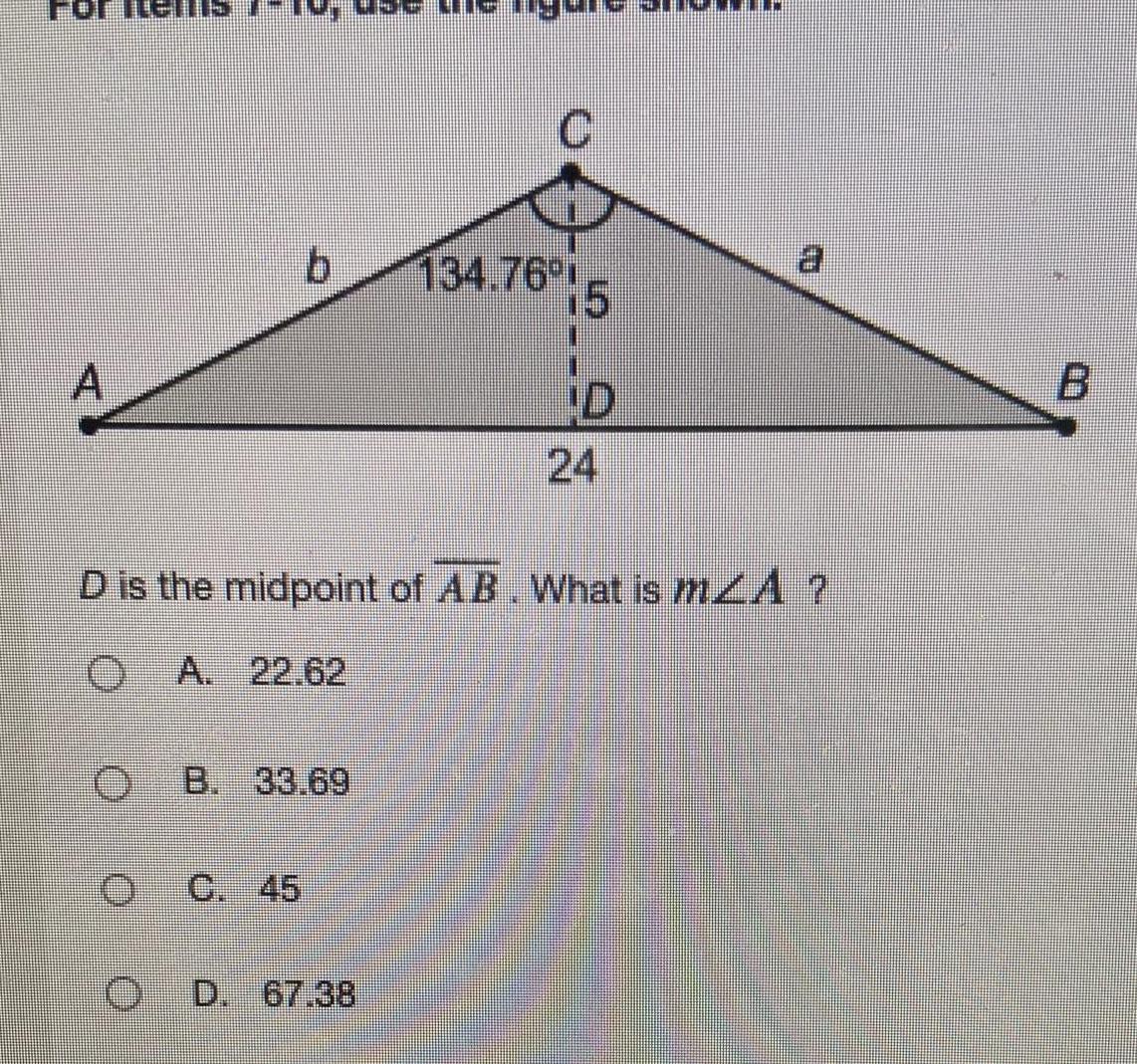
Solution of trianglesA O b B 33 69 C 45 C OD 67 38 134 76 D is the midpoint of AB What is mZA A 22 62 15 D 24 B
Geometry
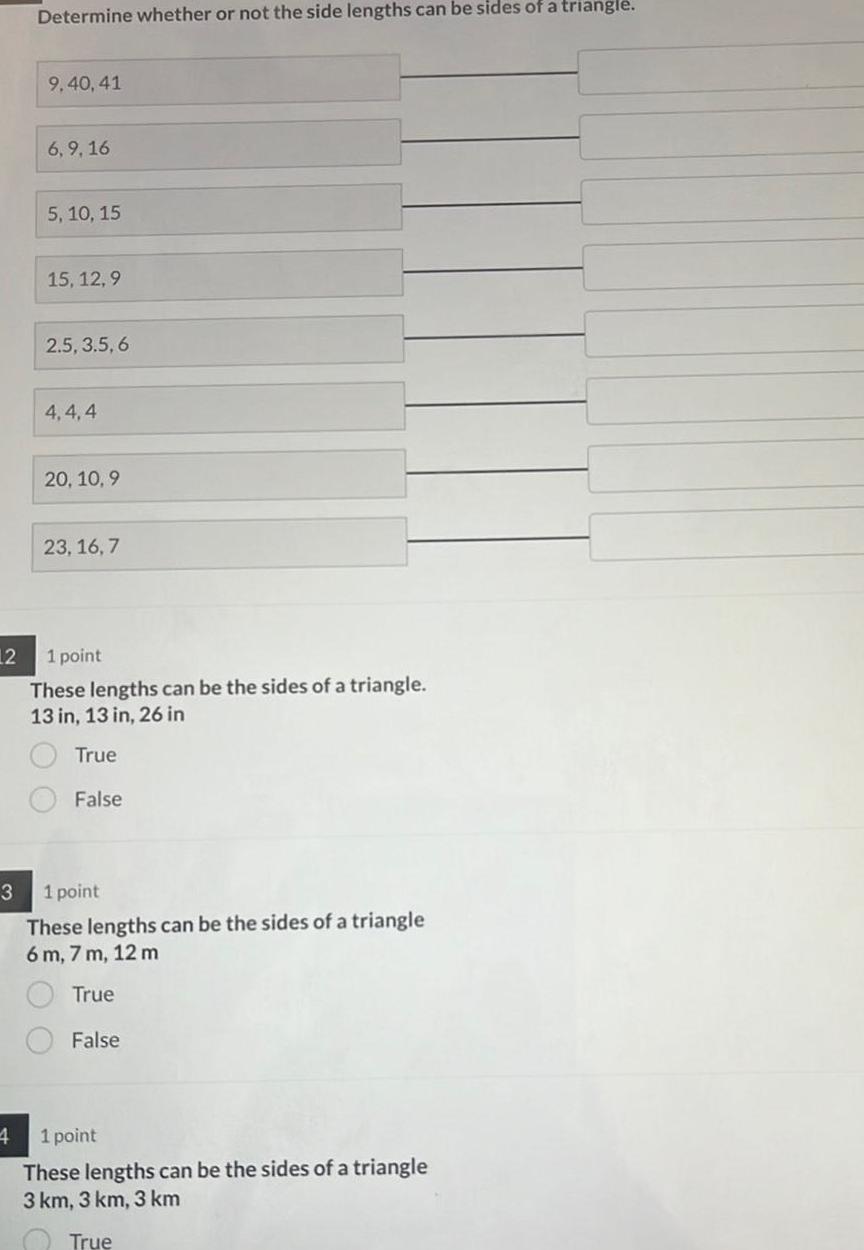
Solution of triangles12 3 4 Determine whether or not the side lengths can be sides of a triangle 9 40 41 6 9 16 5 10 15 15 12 9 2 5 3 5 6 4 4 4 20 10 9 23 16 7 1 point These lengths can be the sides of a triangle 13 in 13 in 26 in True False 1 point These lengths can be the sides of a triangle 6 m 7 m 12 m True False 1 point These lengths can be the sides of a triangle 3 km 3 km 3 km True
Geometry
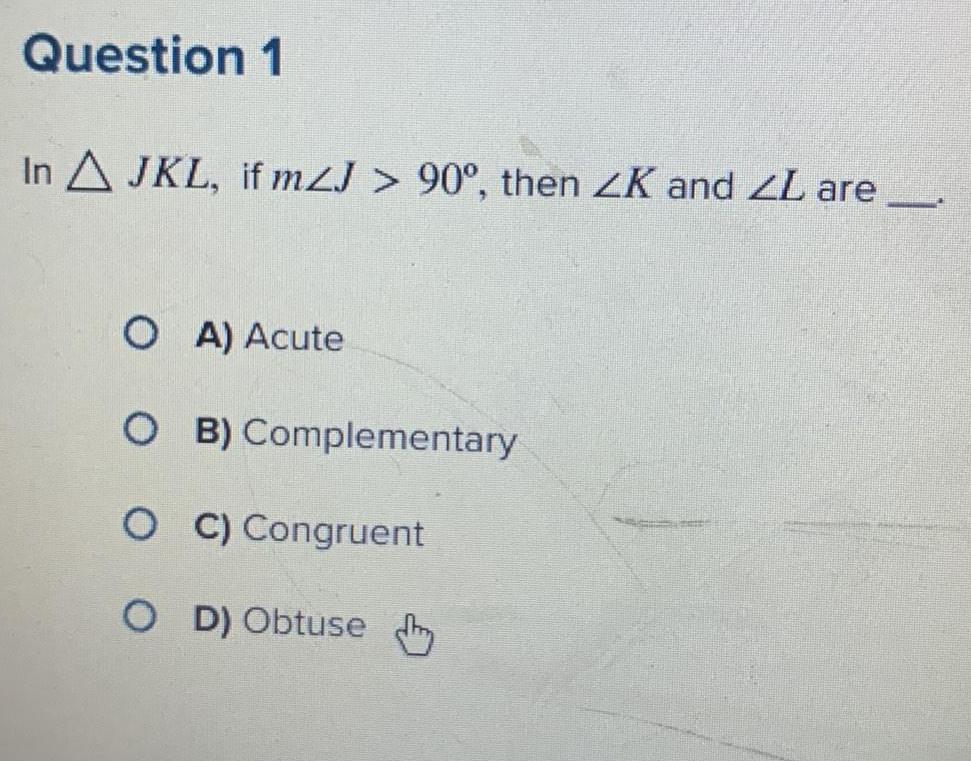
Solution of trianglesQuestion 1 In A JKL if mZJ 90 then ZK and ZL are OA Acute OB OC Congruent OD Obtuse Complementary
Geometry
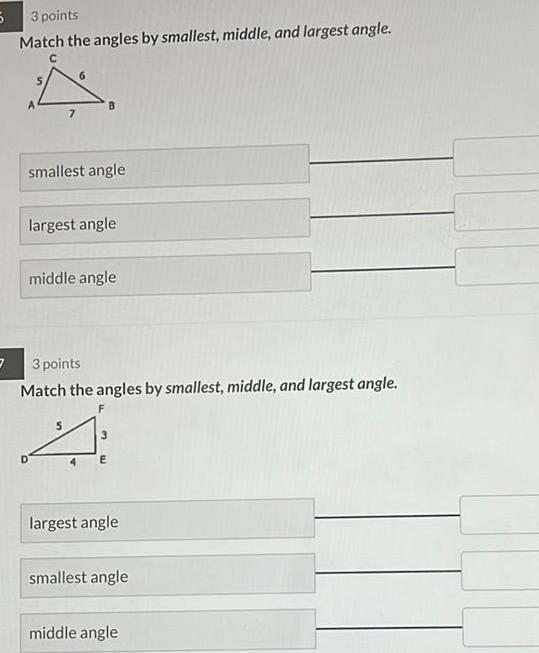
Solution of triangles5 3 3 points Match the angles by smallest middle and largest angle C smallest angle largest angle middle angle 3 points Match the angles by smallest middle and largest angle 4 largest angle smallest angle middle angle
Geometry
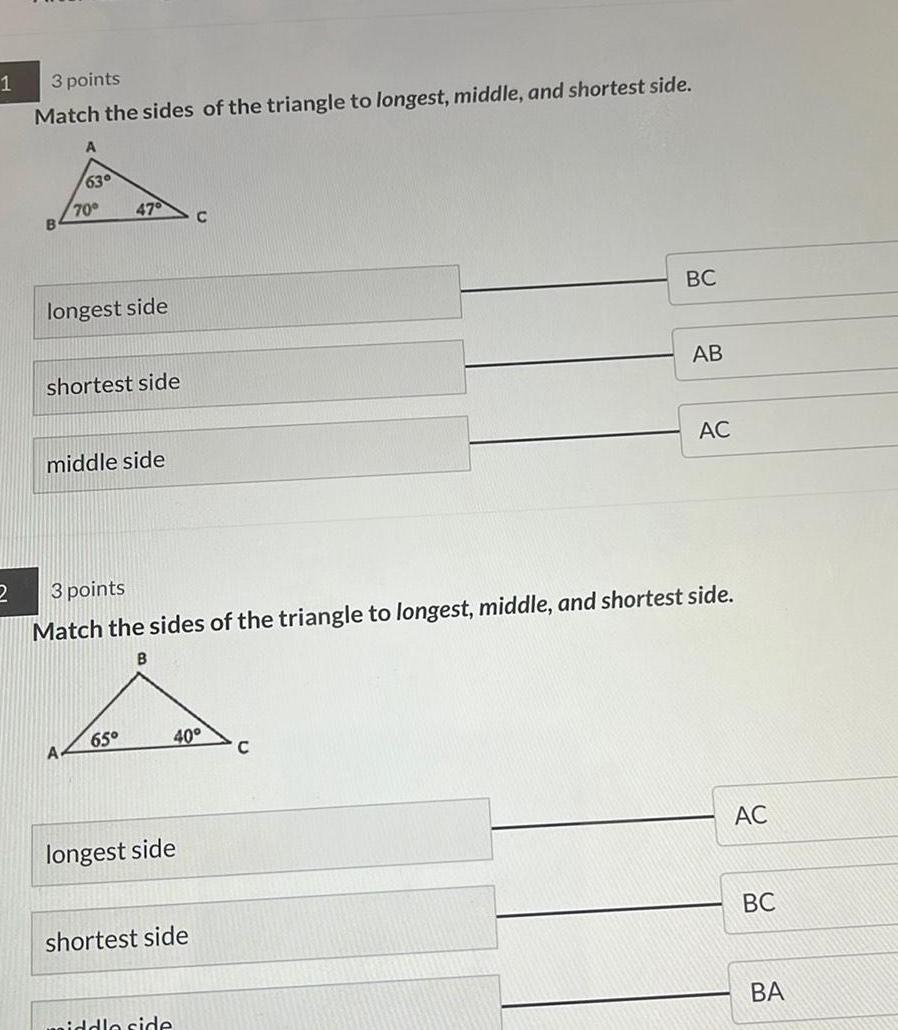
Solution of triangles1 2 3 points Match the sides of the triangle to longest middle and shortest side A 63 70 longest side A 47 shortest side middle side 65 3 points Match the sides of the triangle to longest middle and shortest side B longest side C 40 shortest side aiddle side BC C AB AC AC BC BA

Geometry
Solution of trianglesProblem 11 Let A B C be a triangle and let PO be an arbitrary point Let P1 be the 120 rotation of PO around A Let P2 be the 120 rotation of P1 around B Let P3 be the 120 rotation of P2 around C Let P4 be the 120 rotation of P3 around A etc Prove that if P2019 PO then ABC is equilateral
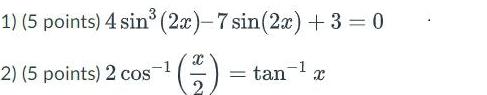
Geometry
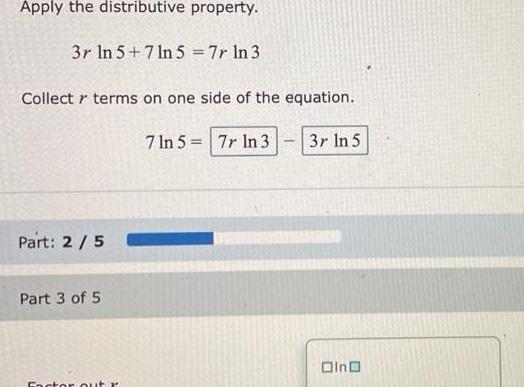
Solution of trianglesApply the distributive property 3r In 5 7ln 5 7r ln 3 Collect r terms on one side of the equation Part 2 5 Part 3 of 5 Factor out r 7 ln 5 7r In 3 3r ln 5 Oino
Geometry
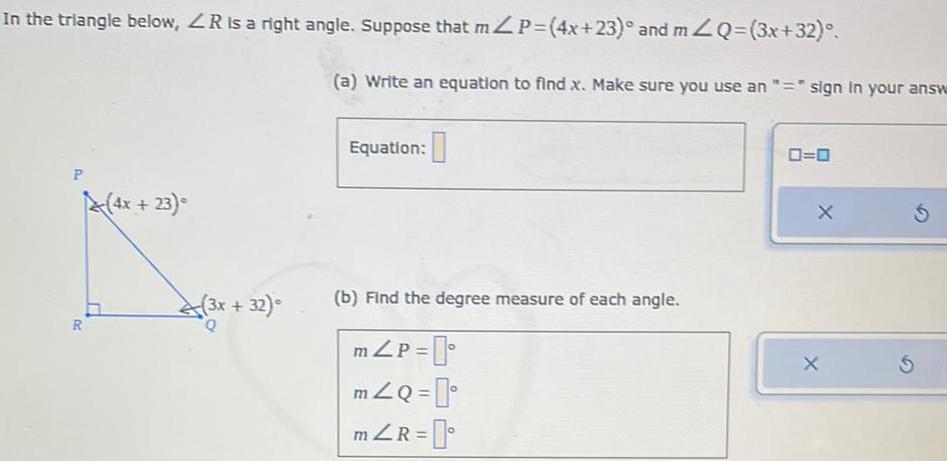
Solution of trianglesIn the triangle below ZR is a right angle Suppose that mZP 4x 23 and mZQ 3x 32 P R 4x 23 3x 32 Q a Write an equation to find x Make sure you use an sign in your answ Equation b Find the degree measure of each angle m P mZQ mZR 0 0 X X
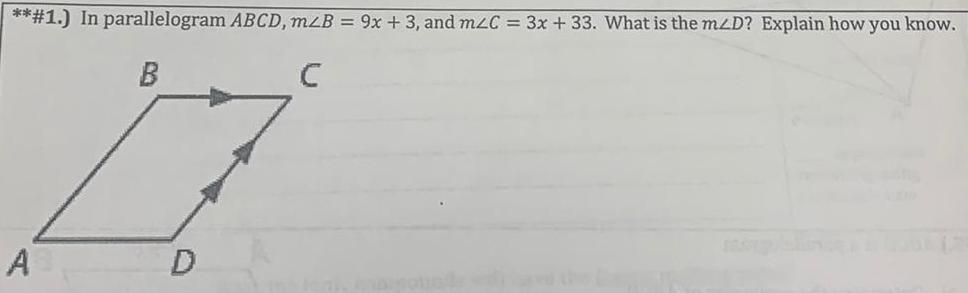
Geometry
Solution of triangles1 In parallelogram ABCD mzB 9x 3 and mzC 3x 33 What is the mzD Explain how you know B C 07 D A

Geometry
Solution of trianglesTriangle ABC has altitude h B A C X ih 27 D b y a C Move the options to the spaces to complete the proof of the Law of Cosines which becomes By the definition of cosine and multiplication y a cos C Then by subtraction and substitution x b acos C By the definition of sine and multiplication h a sin C By the Pythagorean Theorem by substitution By the distributive property the equation becomes which factors to Pythagorean Identity the final equation is h 1 2 a sin C cos C b 2ab cos C By the c asinC b a cos C 2 a sin C b 2ab cos C a cos C a b 2ab cos C
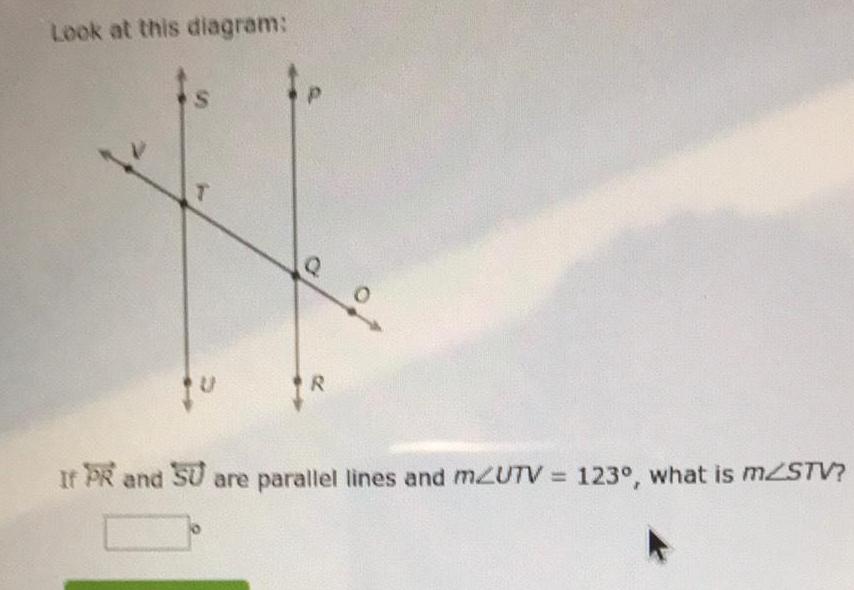
Geometry
Solution of trianglesLook at this diagram S T R If PR and SU are parallel lines and mZUTV 123 what is mZSTV
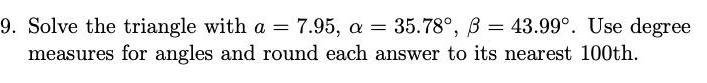
Geometry
Solution of triangles9 Solve the triangle with a 7 95 a 35 78 B 43 99 Use degree measures for angles and round each answer to its nearest 100th
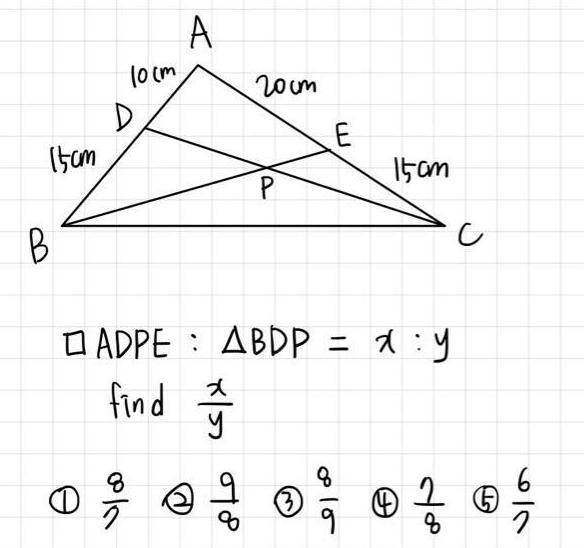
Geometry
Solution of triangles15cm B 10cm D A 200m P E 15cm ADPE ABDP x y find x 8 8 of a to s o f e 8 9 8

Geometry
Solution of trianglesnd all solutions to the following triangle Round your answers to one decimal place If either triangle is not possible enter NONE in each corresponding answer blank A 110 1 a 45 8 cm b 24 4 cm st triangle assume B 90 0 O cm cond triangle assume B 90
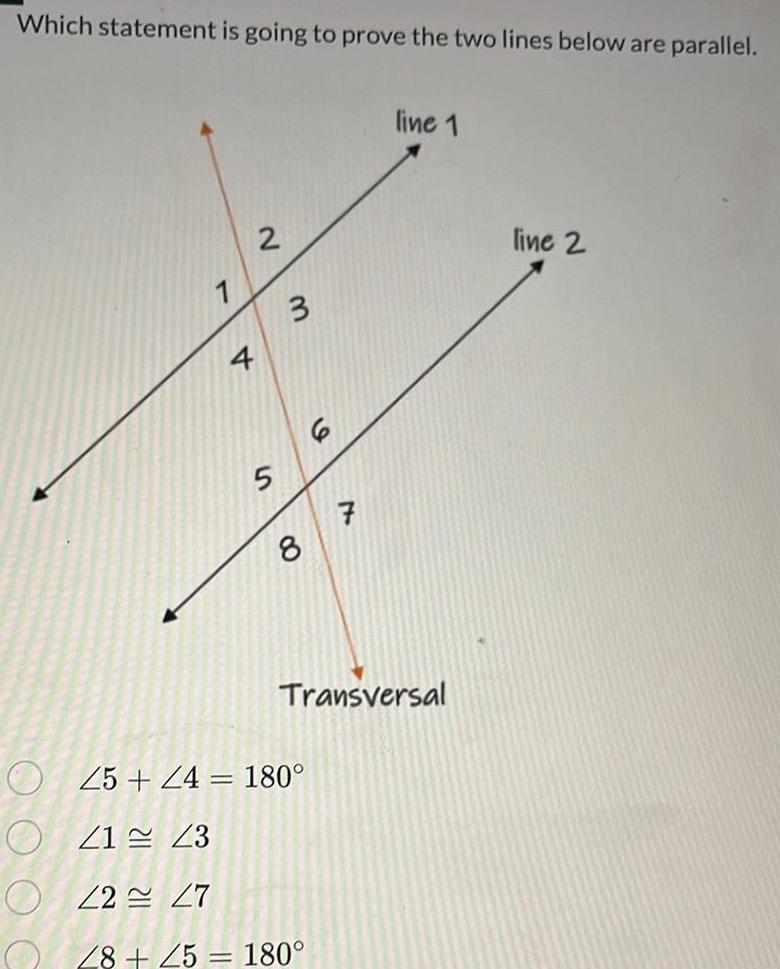
Geometry
Solution of trianglesWhich statement is going to prove the two lines below are parallel 4 2 5 3 7 25 24 180 41 43 22 27 28 25 180 line 1 Transversal line 2

Geometry
Solution of trianglesFor the following 2D system, a) find fixed points, b) linearize the system, c) classify eigenvalues of each fixed points and d) sketch phase-portrait.
x = y + x - x³
y = -y

Geometry
Solution of trianglesIn ΔWXY, w = 2.5 inches, y = 2.4 inches and ∠Y=122°. Find all possible values of ∠W, to the nearest 10th of a degree.
Geometry
Solution of trianglesTwo events, A and B, are independent.
P(A)=0.3
P(A and B)= 0.24
What is P(B)?

Geometry
Solution of trianglesWhich of the following triangles can be drawn?
an obtuse triangle with side lengths 5, 5, and 5 units
a triangle with two obtuse angles
a triangle with three acute angles
a triangle with one right angle, one obtuse angle, and one acute angle

Geometry
Solution of trianglesdiameter =
radius=
17. Find the diameter and radius of a circle with a circumference of 20.1 cm.
Geometry
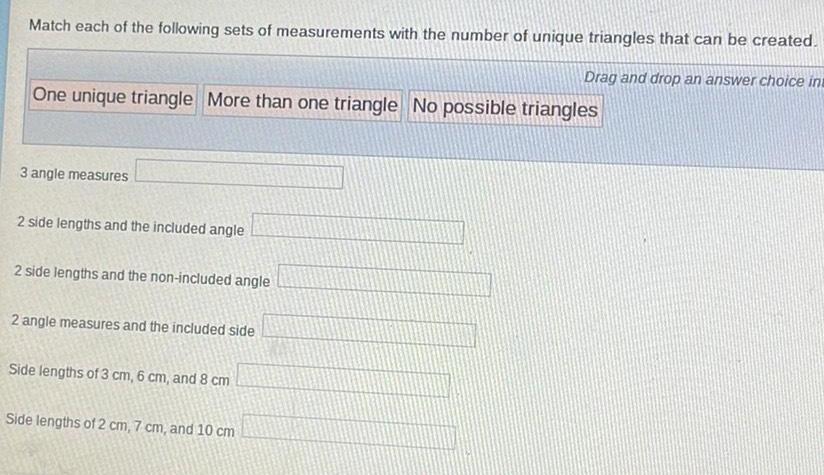
Solution of trianglesMatch each of the following sets of measurements with the number of unique triangles that can be created.
One unique triangle More than one triangle No possible triangles
3 angle measures
2 side lengths and the included angle
2 side lengths and the non-included angle
2 angle measures and the included side
Side lengths of 3 cm, 6 cm, and 8 cm
Side lengths of 2 cm, 7 cm, and 10 cm
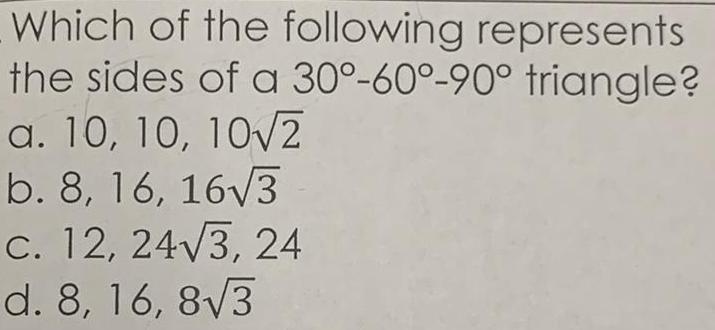
Geometry
Solution of trianglesWhich of the following represents the sides of a 30°-60°-90° triangle?
a. 10, 10, 10√2
b. 8, 16, 16√3
c. 12, 24√3, 24
d. 8, 16, 8√3

Geometry
Solution of trianglesTwo angles in a triangle measure (2.3x +25)° and (5.8x +11)°. What is the value
of x if the two angles are congruent to one another?
A. x = 34.2
B. x = 10.3
C. x = 6.6
D. x = 4
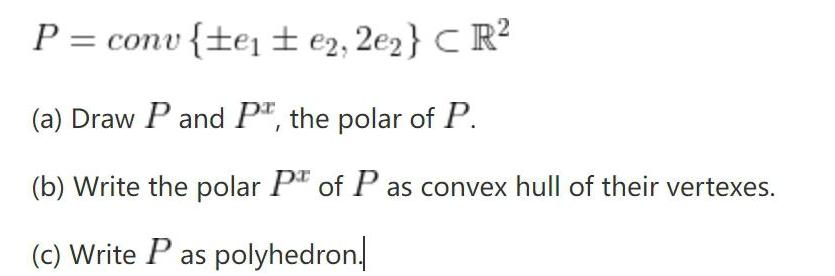
Geometry
Solution of trianglesP = conv{±e₁±e2, 2e₂}⊂CR²
(a) Draw P and PT, the polar of P.
(b) Write the polar P of P as convex hull of their vertexes.
(c) Write P as polyhedron.

Geometry
Solution of trianglesA right circular cylinder is circumscribed about a sphere whose radius is 3 inches. The number of cubic inches in the volume of the cylinder is
A) 108p
B) 18p
C) 54p
D) 36p
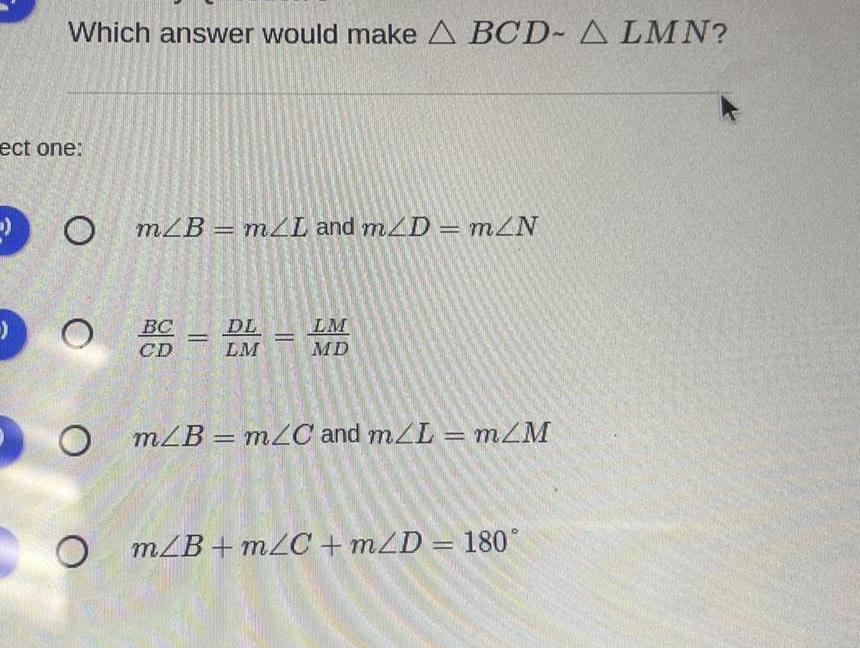
Geometry
Solution of trianglesWhich answer would make ΔBCD- ΔLMN?
m∠B = m∠L and m∠D = m∠N
BC/CD=DL/LM=LM/MD
m∠B=m∠C and m∠L = m∠M
m∠B+m∠C+m∠D = 180°

Geometry
Solution of trianglesABCD is a quadrilateral where AB = AD = 5 m, BC = CD = 7 m and the angle DAB = 80. Calculate the length of AC.

Geometry
Solution of trianglesFind the exact value of each expression.
(a) sin 40° cos 20° + cos 40° sin 20°
(b)sin 105°
(c)sin7π/12

Geometry
Solution of triangles(1 point) Let a be an angle, with 0 < a < 2π. Given cos(2a) and 3π/2 <2a < 27, find exact values of the six trigonometric functions.
Note: You are not allowed to use decimals in your answer.
sin(a) =
cos(a) =
tan(a) =
csc (a) =
sec (a) =
cot(a) =

Geometry
Solution of trianglesIn ∆PQR, p = 36 cm, q = 21 cm and r=17 cm. Find the measure of ∠Q to the nearest 10th of a degree.
Geometry
Solution of trianglesFind the final hourly wage if a $19.50 starting wage is increased by 2.5% each year for 7 years. The final hourly wage is $ Round your answer to the nearest cent.
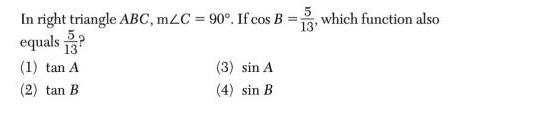
Geometry
Solution of trianglesIn right triangle ABC, mZC = 90°. If cos B = equals? 13 (1) tan A (2) tan B (3) sin A (4) sin B 5 13' which function also

Geometry
Solution of trianglesThe image of ΔDEF is ΔD'E'F'. Under which transformation will the triangles not be congruent? (1) a reflection through the origin (2) a reflection over the line y = x (3) a dilation with a scale factor of 1 (4) a dilation with a scale factor of centered at (2,3) centered at the origin

Geometry
Solution of trianglesTriangle A'B'C' is the image of ΔABC after a dilation followed by a translation. Which statement(s) would always be true with respect to this sequence of transformations? I. ΔABCΔA'B'C' II. ΔABCΔA'B'C' III. AB || A'B' IV. AA'= BB' (1) II, only (2) I and II (3) II and III (4) II, III, and IV
Geometry
Solution of trianglesSolve: 8r+ 4 = 6.
Write your answer as an integer, proper fraction, or mixed number in simplest form.
r=_________

Geometry
Solution of trianglesFind the similarity ratio and the rati of perimeters for two reguloctagons with areas of 18 in. 2 and50 in2
03:5; 9:25
03:5; 3:5
09:25; 9:25
09:25; 3:5
Geometry
Solution of trianglesSolve ΔABC subject to the given conditions.
A = 10.4°, C = 98.2°, b = 58

Geometry
Solution of trianglesSolve the following equation. Write your answer as an integer, proper fraction, or mixed number in simplest
form.
4q+ 11
10
=3
Geometry
Solution of trianglesIn a triangle ABC with circumcenter "O" and orthocenter "H", AC-24μ and OB=13μ.
Calculate BH.

Geometry
Solution of trianglesA triangle has sides of lengths 27,79, and 84. Is it a right triangle?
Explain.
O no; 27² + 79² = 84²
0yes; 27² +79² 84²
O no: 272+79284²
O yes; 27² +79² # 84²
Geometry
Solution of trianglesLet ABC be a triangle with AB<AC. Denote E the foot of the B-angle bisector, F the foot of the C-angle bisector, and P the intersection of EF and BC. If PB=13 and BC=6, find AB/AC.
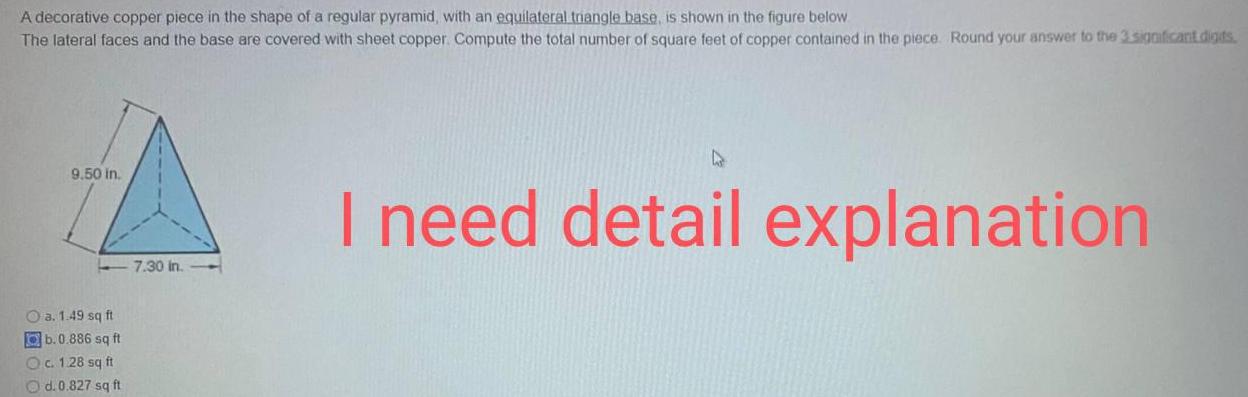
Geometry
Solution of trianglesA decorative copper piece in the shape of a regular pyramid, with an equilateral triangle base, is shown in the figure below.
The lateral faces and the base are covered with sheet copper. Compute the total number of square feet of copper contained in the piece. Round your answer to the 3 significant digits.
9.50 in.
a. 1.49 sq ft
b.0.886 sq ft
c. 1.28 sq ft
d. 0.827 sq ft
7.30 in.

Geometry
Solution of trianglesGiven AQRS = ATUV,QS = 3v + 2, and TV = 7v6, find the length of QS and TV.
08
02
O 20
09

Geometry
Solution of trianglesC. Directions: Complete the two-column proof. (10-15)Given: A LMN where IM <LN < MN Prove: MN+ IN > LM; MN + LM > LN; LM + IN > MN

Geometry
Solution of trianglesJay, Kay, and Ray found themselves far apart when they stopped forlunch while working in a field. Jaycould see Kay, then turn through 73°and see Ray. Kay could see Ray, then turn through 53° and see Jay. Raycould see Jay, then turn through 54°
and see Kay. Which two were farthest apart?
Kay and Ray
Ray and Jay
Jay and Kay
Kay and Ray were the same distance
apart as Ray and Jay.