Solution of triangles Questions and Answers
Geometry
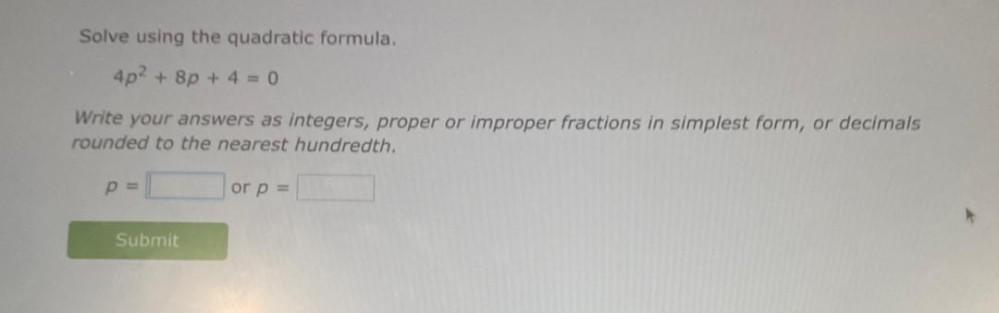
Solution of trianglesSolve using the quadratic formula.
4p² + 8p + 4 = 0 Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.
p= or p =
Geometry
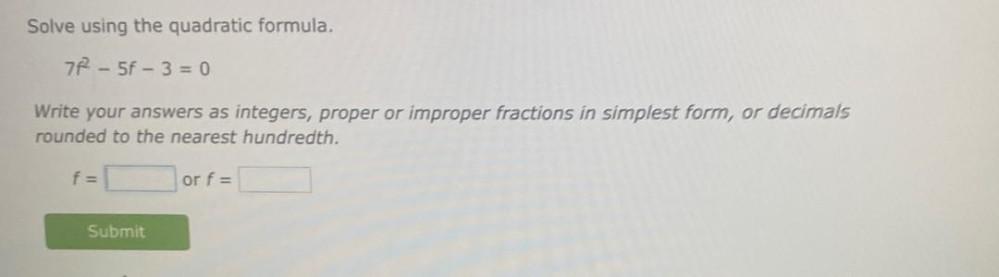
Solution of trianglesSolve using the quadratic formula.
7f² - 5f-3 = 0 Write your answers as integers, proper or improper fractions in simplest form, or decimals rounded to the nearest hundredth.
f = or f =
Geometry
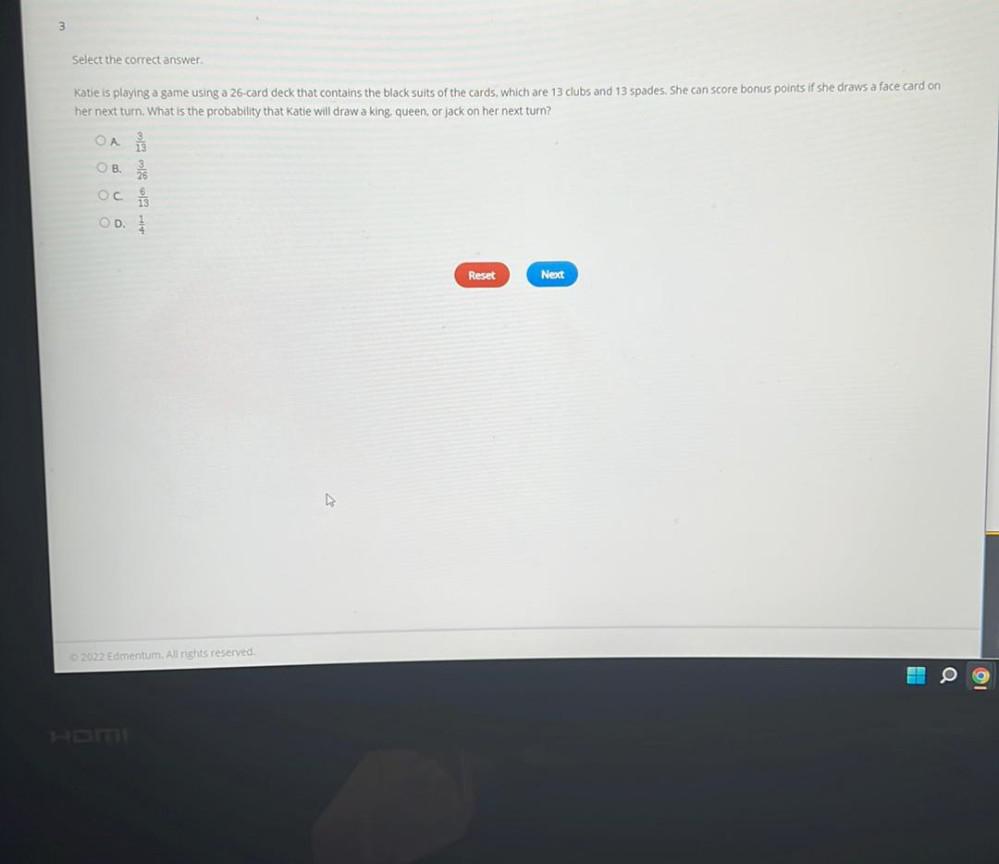
Solution of trianglesKatie is playing a game using a 26-card deck that contains the black suits of the cards, which are 13 clubs and 13 spades. She can score bonus points if she draws a face card on her next turn. What is the probability that Katie will draw a king, queen, or jack on her next turn?
A 3/13
B 3/26
C 6/13
D 1/4
Geometry
Solution of trianglesA survey of the men in a certain town showed that 35% of the men have blond hair and 14% of them have blond hair and blue eyes.
The probability that a randomly selected man has blue eyes, given that he has blond hair, is
Geometry
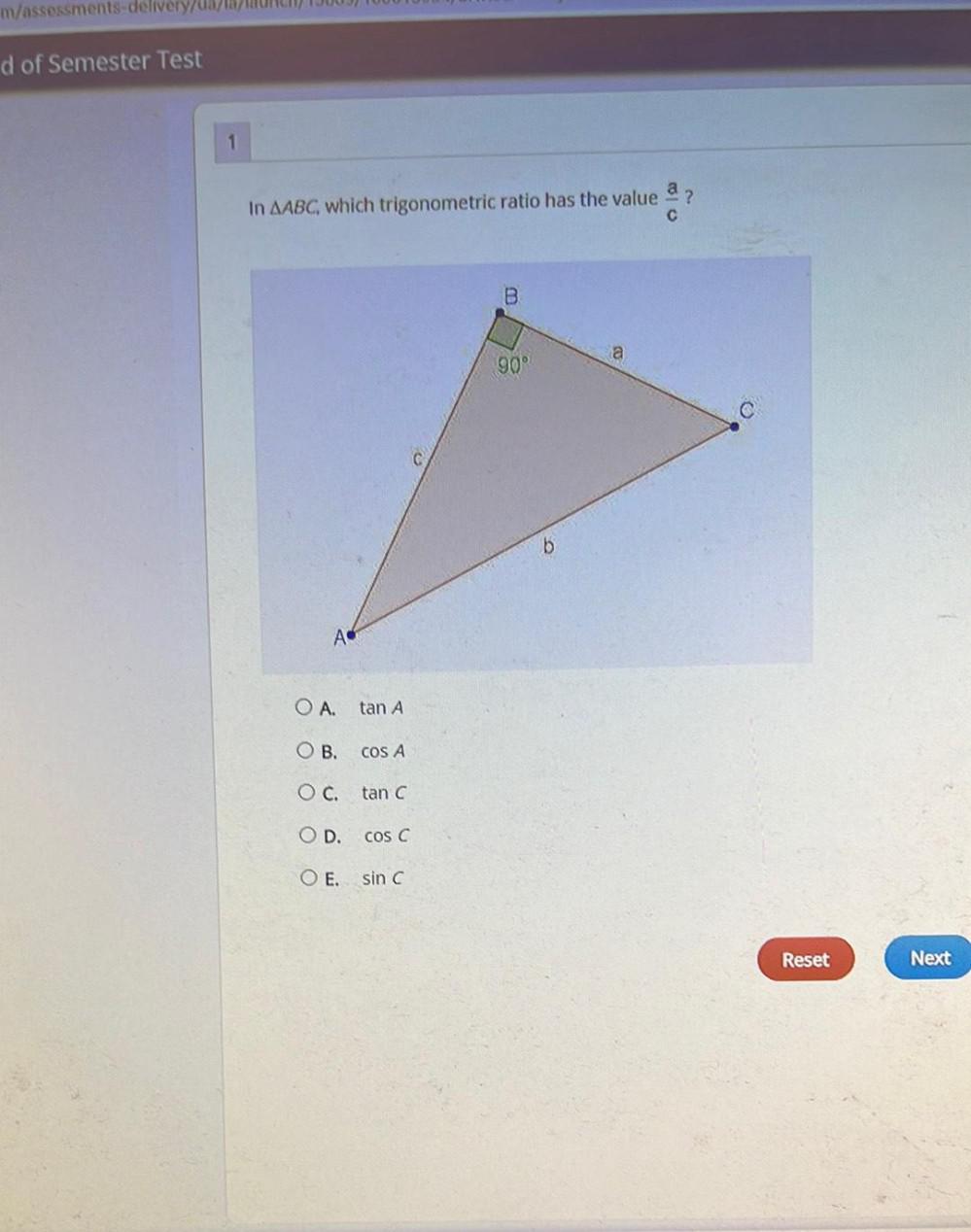
Solution of trianglesIn △ABC, which trigonometric ratio has the value a/c ?
A. tan A
B. Cos A
C. tan C
D. cos C
E. sin C
Geometry
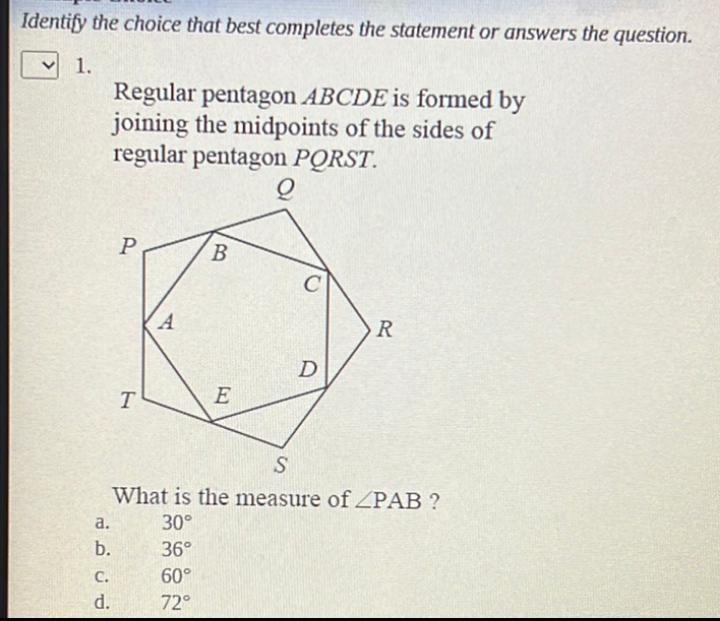
Solution of trianglesRegular pentagon ABCDE is formed by joining the midpoints of the sides of regular pentagon PORST.
What is the measure of PAB?
a. 30°
b. 36°
c. 60°
d. 72°

Geometry
Solution of trianglesUse the the triangles below to answer the following questions.
a). Are the triangles above similar? How do you know? Show your reasoning in a flowchart
b). Examine your work from part (a). Are the triangles also congruent ? Explain why or why not.

Geometry
Solution of trianglesIn triangle DEF, DE = 5 cm, angle D = 80°, and FE = 8 cm. Show that only one triangle can be drawn then solve the triangle to the nearest degree and nearest tenth of a centimetre.
Geometry
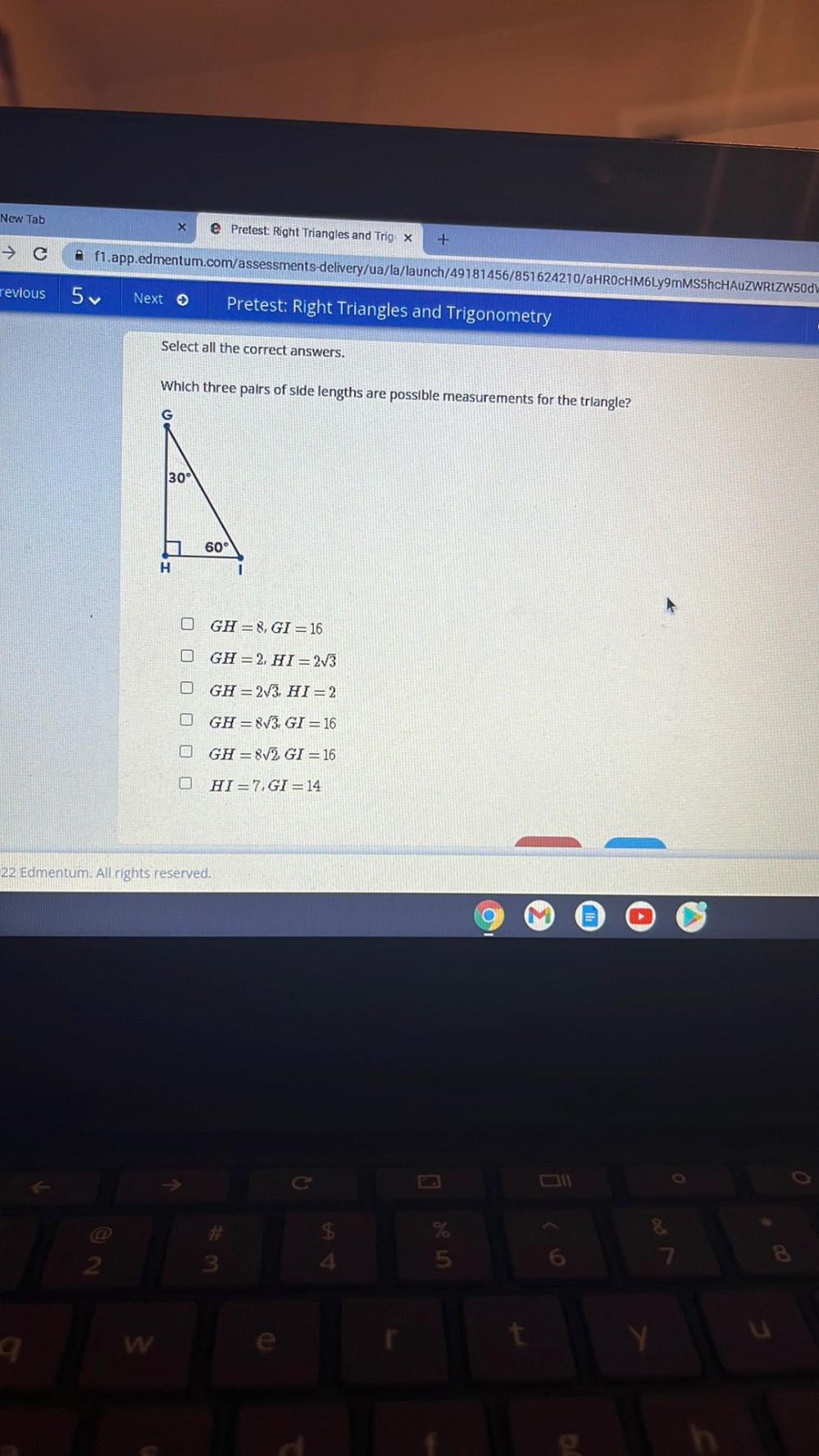
Solution of trianglesWhich three pairs of side lengths are possible measurements for the triangle?
GH=8, GI=16
GH=2, HI= 2√3
GH = 2√3, HI=2
GH=8√3, GI=16
GH = 8√2 GI = 16
HI 7, GI=14
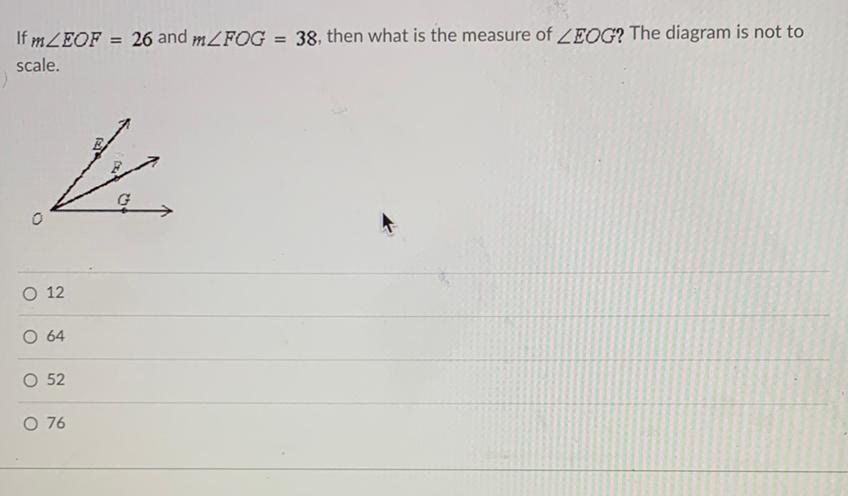
Geometry
Solution of trianglesIf m∠EOF=26 and m∠FOG = 38, then what is the measure of ∠EOG? The diagram is not to scale.
12
64
52
76

Geometry
Solution of trianglesSketch one cycle of the following graph and be sure to include an appropriate scale on each axis
: y = 3sin (0.5x-30)
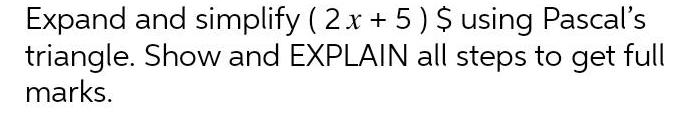
Geometry
Solution of trianglesExpand and simplify (2x + 5) $ using Pascal's triangle. Show and EXPLAIN all steps to get full marks.
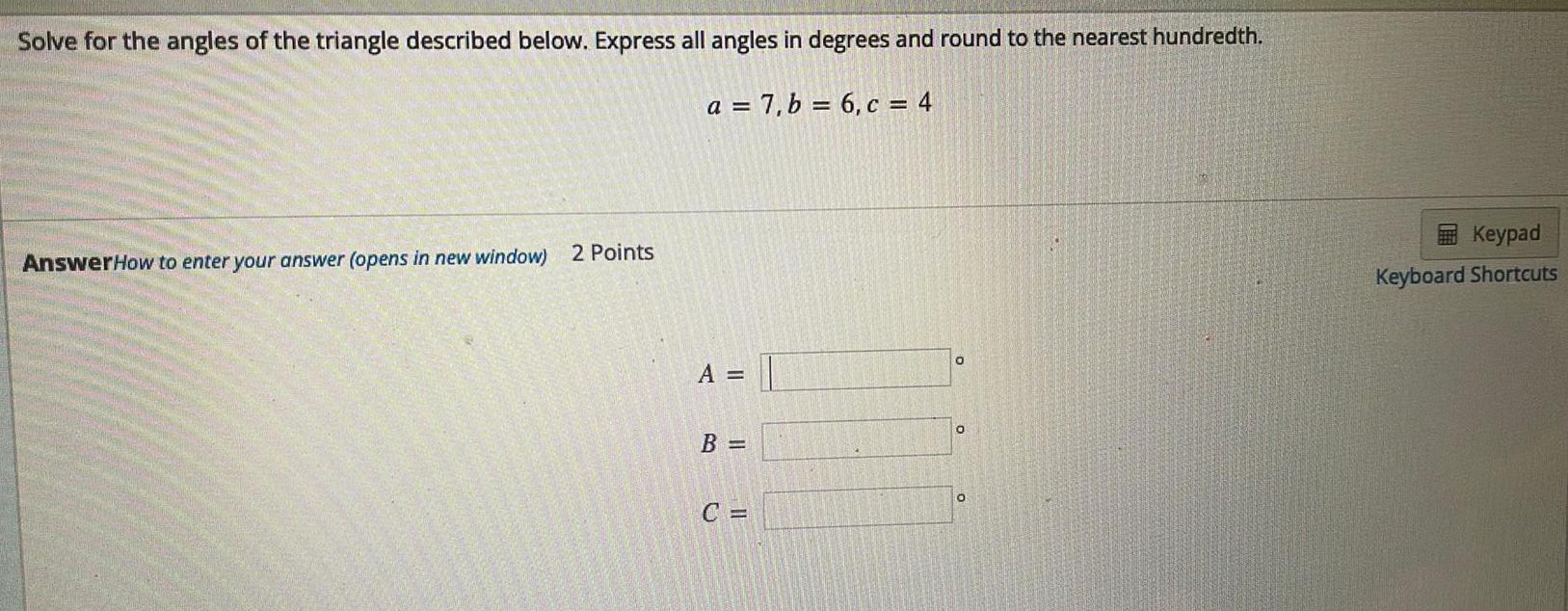
Geometry
Solution of trianglesSolve for the angles of the triangle described below. Express all angles in degrees and round to the nearest hundredth.
a = 7, b = 6, c = 4
Answer
A =
B =
C=
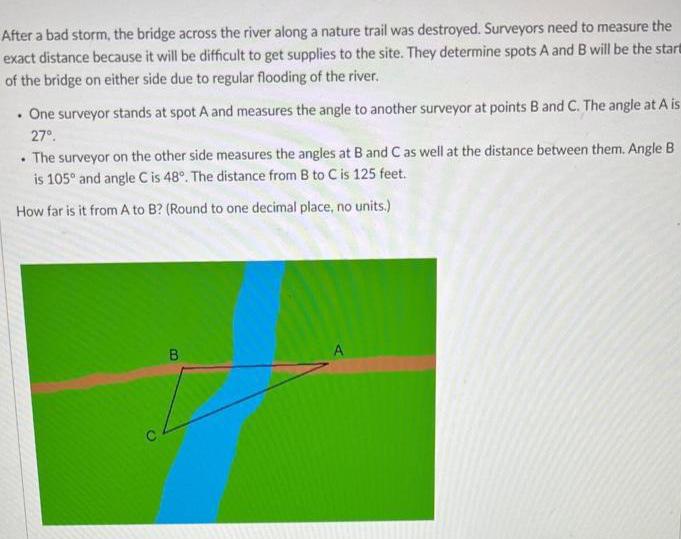
Geometry
Solution of trianglesAfter a bad storm, the bridge across the river along a nature trail was destroyed. Surveyors need to measure the exact distance because it will be difficult to get supplies to the site. They determine spots A and B will be the start of the bridge on either side due to regular flooding of the river.
. One surveyor stands at spot A and measures the angle to another surveyor at points B and C. The angle at A is 27º.
. The surveyor on the other side measures the angles at B and C as well at the distance between them. Angle B is 105° and angle C is 48°. The distance from B to C is 125 feet.
How far is it from A to B? (Round to one decimal place, no units.)

Geometry
Solution of trianglesSolve the right triangle (round values to one decimal place)
a=3.2 m, b= 19.0⁰° C = 90°
Geometry
Solution of trianglesThe incircle of AABC is tangent to BC at X. Suppose the incircle has radius 2, |BX|=3 and |CX| = 4. What is the length of the side AB?
Geometry
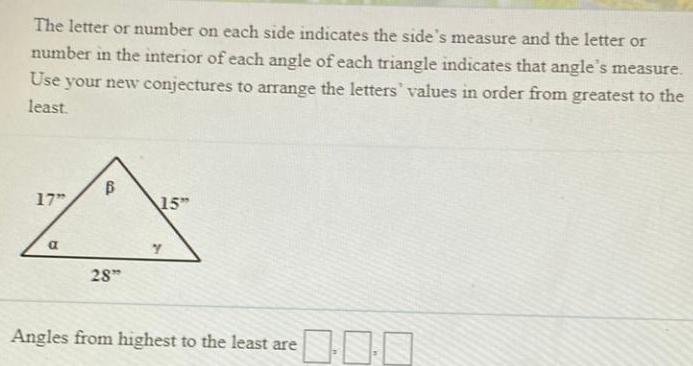
Solution of trianglesThe letter or number on each side indicates the side's measure and the letter or number in the interior of each angle of each triangle indicates that angle's measure. Use your new conjectures to arrange the letters' values in order from greatest to the least.
Angles from highest to the least are

Geometry
Solution of trianglesConsider this transistor in a common-emitter circuit (RE = 0). Design this common- emitter circuit to produce the IV (lc vs. VCE) characteristic and load line (LL) as shown in the graph. Your answers are the following: a drawing of the circuit; the values of Vcc, Rc, Van, and Ra; and the value for the current-axis LL intercept (this intercept is shown as "?" on the IV graph).
Geometry
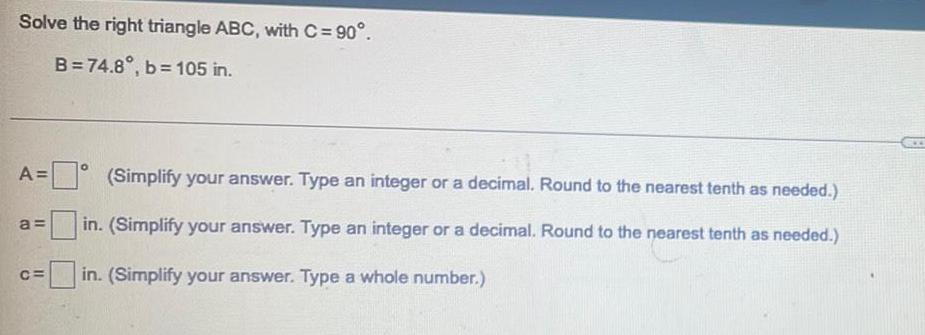
Solution of trianglesSolve the right triangle ABC, with C = 90°.
B=74.8°, b= 105 in.
A=___(Simplify your answer. Type an integer or a decimal. Round to the nearest tenth as needed.)
a=__(Simplify your answer. Type an integer or a decimal. Round to the nearest tenth as needed.)
C=___(Simplify your answer. Type an integer or a decimal. Round to the nearest tenth as needed.)

Geometry
Solution of trianglesA building 30.72 feet tall has a shadow that is 33.51 feet long. Find the angle of elevation of the sun to the nearest hundredth of a degree.
The angle of elevation is degrees.
(Round to the nearest hundredth as needed.)

Geometry
Solution of trianglesA(n)___triangle always has 2 congruent angles.
A. right
B. acute
C. isosceles
D. scalene

Geometry
Solution of trianglesLuis is flying a kite, holding his hands a distance of 9.75 feet above the ground play out. He measures the angle of elevation from his hand to the kite to be 35°. If the string from the kite to his hand is 140 feet long, how many feet is the kite above the ground? Round your answer to the nearest tenth of a foot if necessary.

Geometry
Solution of trianglesClassify the figure formed by A (-9,2), B (1,2), and C (-4,2-5√3).
equilateral triangle
isosceles (not right) triangle
a line
right scalene triangle
scalene (not right) triangle
right isosceles triangle

Geometry
Solution of trianglesIf the sides of a triangle are 12, 13, and 20 and the shortest side of a similar triangle measure 27, find the measure of the longest side of that triangle.
Geometry
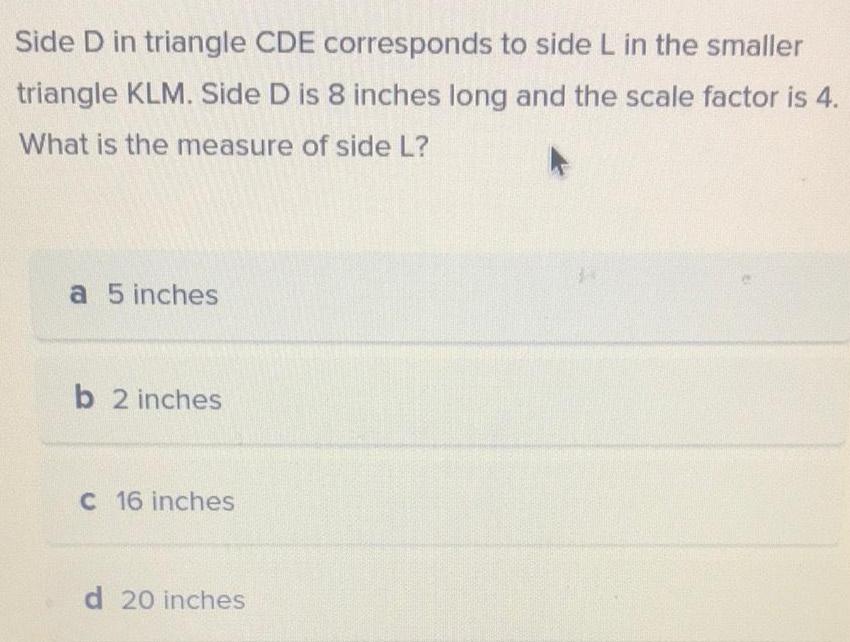
Solution of trianglesSide D in triangle CDE corresponds to side L in the smaller triangle KLM. Side D is 8 inches long and the scale factor is 4.
What is the measure of side L?
a 5 inches
b 2 inches
c 16 inches
d 20 inches

Geometry
Solution of trianglesGiven the equation y = 2cos3(x - 30°) + 1 has a maximum when x = 30°. Explain how to find other values of x when the same maximum value occurs.
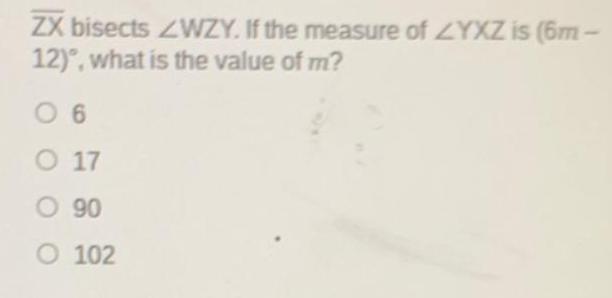
Geometry
Solution of trianglesZX bisects WZY. If the measure of YXZ is (6m-12), what is the value of m?
6
17
90
102

Geometry
Solution of trianglesHow many triangles exist that fit the following criteria?
C= 140, c = 6, a = 8

Geometry
Solution of trianglesUse the laws of sines and cosines to solve each triangle with the given parts. SHOW ALL WORK IN ORDER TO RECEIVE CREDIT. Round to the value that's given for angles and sides. If no triangle exists, state so. If two triangles exist, write a second set of answers underneath the first set of answers.
∠A = 36.6 ° a = 5.7 in, c= 8.4 in
m∠B=
m ∠ C=
b=

Geometry
Solution of triangles1. Choose the correct words to fill in the blanks.
The negation "No triangle is equilateral" is.That means that the original statement, "Some triangles are equilateral" is
true, false
true, true
false, false
false, true

Geometry
Solution of trianglesElsa rented a movie. She started the movie at 10:33 PM and it ended at 1:28 AM. How long was the movie?

Geometry
Solution of trianglesPaul's kitten jumped out of the house. It ran 21 feet, turned and ran 9 feet, and then turned 150° to face the house. How far away from the house is Paul's kitten? Round to the nearest hundredth.

Geometry
Solution of trianglesDetermine if the three numbers can be measures of the sides of a triangle. Write yes or no. Explain.
6, 7, 13
5, 10, 20
7, 12, 8
9, 10, 14
1, 2, 3
60, 70, 140

Geometry
Solution of trianglesFind the distance between A(-1, 5) and C(3, 5).
What is the distance between E(-3,-1) and F(4, -2)?
Is AMNP with vertices M(1, 4), N(-3, -2), and P(4, -3) an isosceles triangle? Explain.

Geometry
Solution of trianglesThe lengths of three sides of a triangle are given. Determine whether Each triangle is a right triangle.
9 mm, 40 mm, 41 mm
19 ft, 16 ft, 20 ft
Find the length of the diagonal of a rectangle whose length is 8 meters and whose width is 5 meters. (Example 3)

Geometry
Solution of trianglesWith the aid of a power reducing formula, 10sin²a = ?
Select the correct answer below:
5-10cos (2a)
5-5cos (2a)
5-5cos (4a)
5+5cos (2a)

Geometry
Solution of trianglesSolve the triangle.
a=7 c=6 B=97.9°
What is the length of side b? Select the correct choice below and, if necessary, fill in the answer box within your choice.
A. b= (Round to the nearest tenth.)
B. There is no solution.
What is the measure of angle C? Select the correct choice below and, if necessary, fill in the answer box within your choice.
A C=
B. There is no solution.
(Round to the nearest tenth.)
Geometry
Solution of trianglesThe points P = (15, −6,1,3), Q = (1, −3,0,8), R = (2,2, -14,5) form a right triangle in R^4. Which side is the hypotenuse?

Geometry
Solution of trianglesWhat is the measure of the largest angle of a triangle having sides of length 215, 309, and 278?
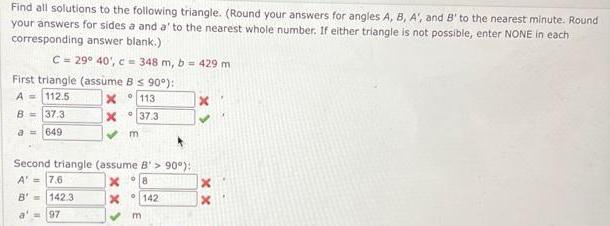
Geometry
Solution of trianglesFind all solutions to the following triangle. (Round your answers for angles A, B, A', and B' to the nearest minute. Round your answers for sides a and a' to the nearest whole number. If either triangle is not possible, enter NONE in each corresponding answer blank.)
C= 29° 40', c = 348 m, b = 429 m
First triangle (assume B ≤ 90°):
A =
B =
a =
Second triangle (assume B'> 90°):
A' =
B' =
a' =
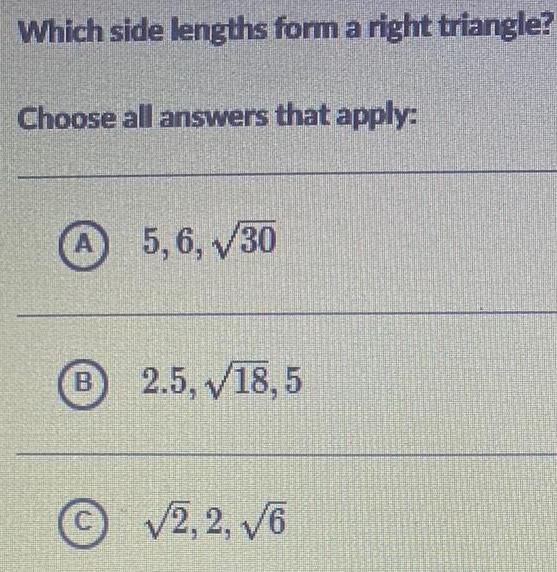
Geometry
Solution of trianglesWhich side lengths form a right triangle?
Choose all answers that apply:
A. 5,6,√30
B. 2.5, 18,5
C. √2,2, √6
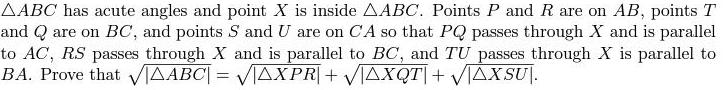
Geometry
Solution of trianglesAABC has acute angles and point X is inside AABC. Points P and R are on AB, points T and Q are on BC, and points S and U are on CA so that PQ passes through X and is parallel to AC, RS passes through X and is parallel to BC, and TU passes through X is parallel to BA. Prove that √|√△ABC|=√△XPR+√△XQT+√△XSUI.
Geometry
Solution of trianglesSolve the triangle with the given measures:
(a) B = 36.2°, C = 48.1°, and a = 10.6
(b) B= 22°, b = 2.5m, c = 4.9m
Geometry
Solution of trianglesSolve the triangle with the given measures:
(a) a = 3.4in, b = 2.6in, and C = 48°
(b) a = 6, b = 8, c = 10

Geometry
Solution of trianglesUse the Pythagorean Theorem to determine if the triangle is acute, obtuse, or right using the side lengths below.
9, 40, 41
right
obtuse
acute
Geometry
Solution of trianglesTwo sides and an angle are given below. Determine whether the given information results in one triangle, two triangles, or no triangle at all. Solve any resulting triangle(s)
b=4.c 5, B 10"
Select the correct choice below and, if necessary, fill in the answer boxes to complete your choice.
(Type an integer or decimal rounded to two decimal places as needed.)
OAA single triangle is produced, where CAN
and a
OB. Two triangles are produced, where the triangle with the smaller angle Chas C, A, and a and the triangle with the larger angle Chas C₂______and a₂
OC. No triangles are produced.

Geometry
Solution of trianglesA right triangle has legs of lengths 2cm and 5cm. Find the exact length of the hypotenuse, then use a calculator to approximate that length. Finally, approximate the measure of the non-right angles in the triangle. Draw and label the triangle for me and be sure to show me how you get your answers (as always).

Geometry
Solution of trianglesLet ABC be an equilateral triangle and let M be a point that does not lie on the circle described on the triangle. Show that the distances AM, BM and CM can form sides of a triangle.

Geometry
Solution of trianglesTo prove a theorem of geometry using rule-based systems, represent the following statements as production rules:
a. Corresponding sides of two congruent triangles are also congruent.
b. Corresponding angles of two congruent triangles are also congruent.
c. If corresponding sides of two triangles are congruent then the triangles are congruent.
d. If corresponding sides and the angle covered by them are equal then the triangles are congruent.
e. Base angles of an isosceles triangle are congruent.