Probability Questions and Answers
Statistics
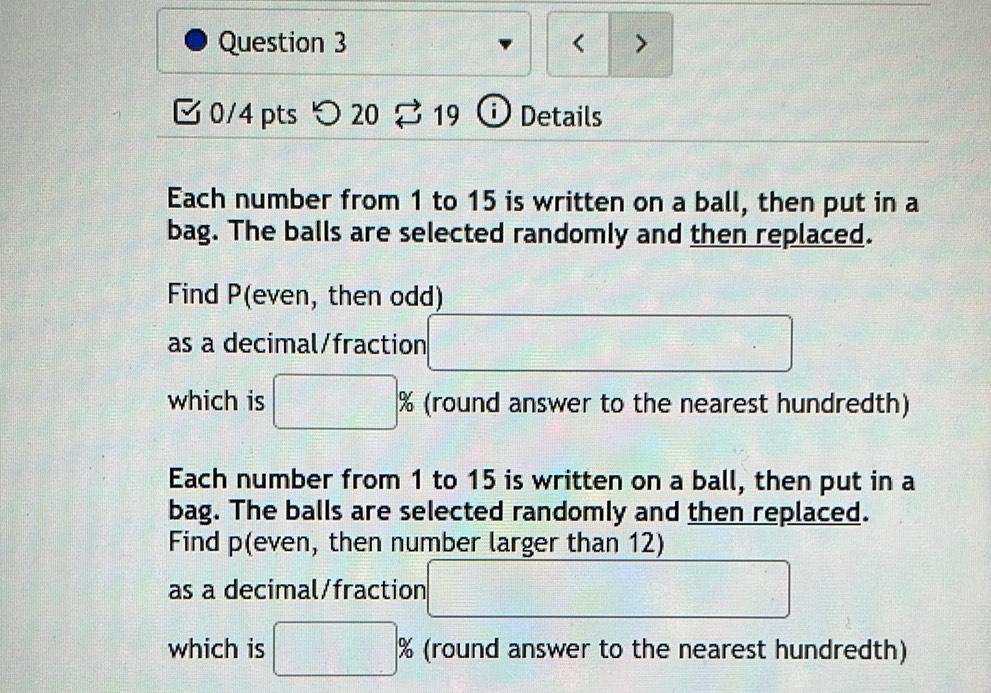
ProbabilityEach number from 1 to 15 is written on a ball, then put in a bag. The balls are selected randomly and then replaced.
Find P(even, then odd) as a decimal/fraction _________ which is _________ % (round answer to the nearest hundredth)
Each number from 1 to 15 is written on a ball, then put in a bag. The balls are selected randomly and then replaced.
Find p(even, then number larger than 12) __________ as a decimal/fraction which is _________ % (round answer to the nearest hundredth)
Statistics
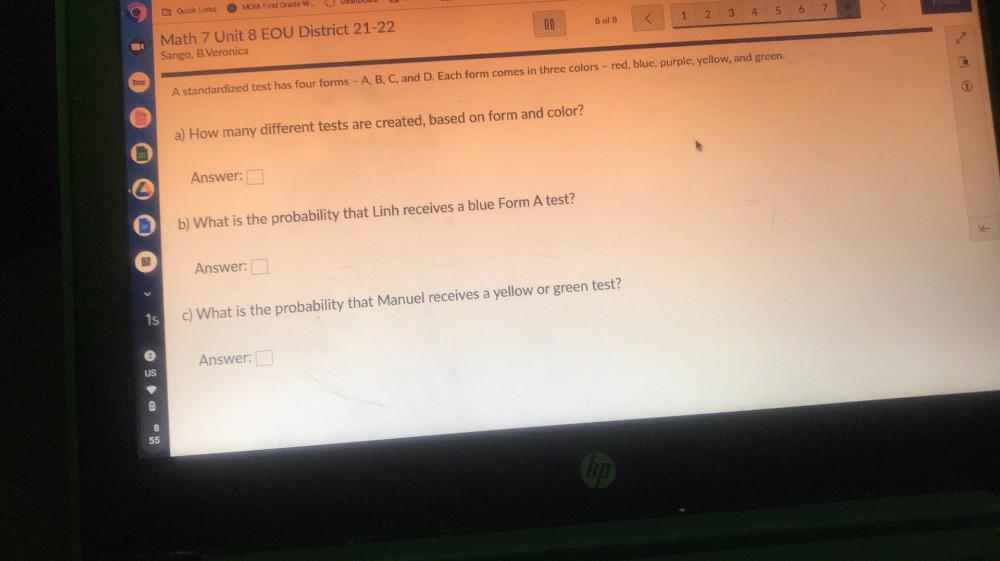
ProbabilityA standardized test has four forms - A, B, C, and D. Each form comes in three colors - red, blue, purple, yellow, and green.
a) How many different tests are created, based on form and color?
b) What is the probability that Linh receives a blue Form A test?
c) What is the probability that Manuel receives a yellow or green test?

Statistics
ProbabilityWhile studying to be a vet, Brad learns that different animals have different heart rates. This table shows the resting heart rate of a small dog:
Small dog
Time (minutes) Heartbeats
3 300
4 400
5 500
This equation describes the resting heart rate of a typical cat, where y represents the number of heartbeats and x represents the number of minutes:
y = 150x
Which animal has a slower heart rate?
a cat
a small dog
How much slower is its heart rate?
_________beats per minute slower
Statistics
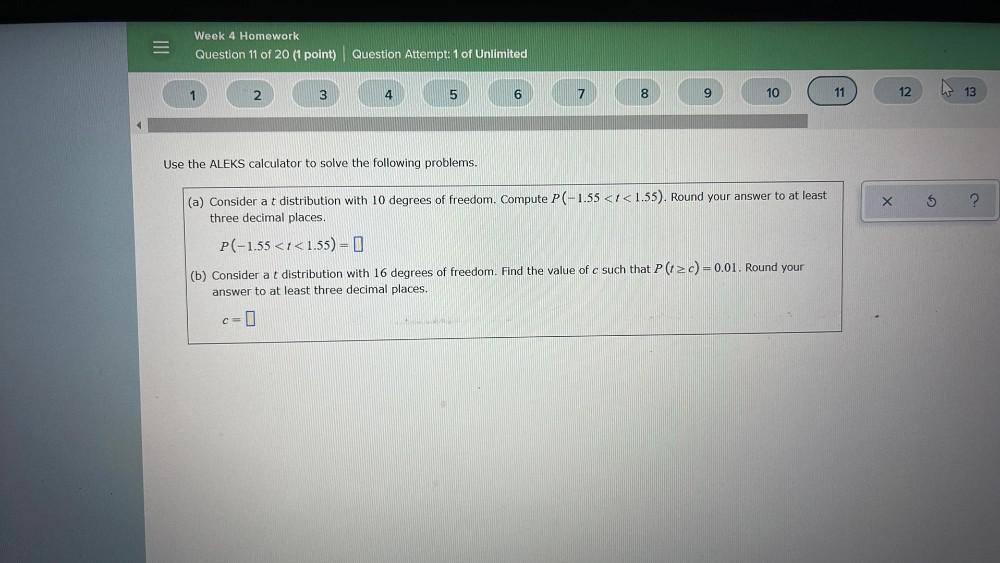
ProbabilityUse the ALEKS calculator to solve the following problems.
(a) Consider a t distribution with 10 degrees of freedom. Compute P(-1.55 <t<1.55). Round your answer to at least
three decimal places.
P(-1.55 <t< 1.55) =
(b) Consider a t distribution with 16 degrees of freedom. Find the value of c such that P(t> c)=.
Round your answer to at least three decimal places.
c=
![In a school, 30% of the students have brown eyes. Find
the experimental probability that in a group of 4 students,
at least one of them has brown eyes. The problem has been simulated by generating random numbers. The digits 0-9 were used. Let numbers "2", "4"and "8" represent the 30% of students with brown eyes. A sample of 20 random numbers is shown. Hint: First, count all of the random numbers that contain a 2, 4, or 8.
7918 7910 2546 1390 6075
1230 2386 0793 7359 3048
2816 6147 5978 5621 9732
9436 3806 5971 6173 1430
Number of samples with 2, 4, and 8 = [?]](https://media.kunduz.com/media/sug-question/raw/79087263-1659026464.804322.jpeg?w=256)
Statistics
ProbabilityIn a school, 30% of the students have brown eyes. Find
the experimental probability that in a group of 4 students,
at least one of them has brown eyes. The problem has been simulated by generating random numbers. The digits 0-9 were used. Let numbers "2", "4"and "8" represent the 30% of students with brown eyes. A sample of 20 random numbers is shown. Hint: First, count all of the random numbers that contain a 2, 4, or 8.
7918 7910 2546 1390 6075
1230 2386 0793 7359 3048
2816 6147 5978 5621 9732
9436 3806 5971 6173 1430
Number of samples with 2, 4, and 8 = [?]

Statistics
ProbabilityThe following data gives annual salaries (in thousands) of randomly chosen employees with college degrees. Some of these employees have only Bachelors' degrees and some have Masters'/PhDs. At α =0.05, can we claim that the mean salaries of employees with Bachelors' degrees are lower?
Bachelors': 89 78 67 89 100 65 45 37 68 68 78 80
Masters'/PhDs: 120 130 78 69 88 101 112 160 200 88
Test using: (a) a hypothesis test (b) a confidence interval

Statistics
ProbabilityEach person has a 75% probability of going to the Tahoe restaurant. You randomly select 8 people.
(a) What is the probability that 4 people will go to the restaurant?
(b) What is the probability that more than 6 people will go to the restaurant ?
(c) What is the probability that at most 7 people will go to the restaurant ?

Statistics
Probability100 adults and 100 teenagers were polled and asked if they liked the food choices found in the local food court at the mall. 21 of the adults liked the food court choices, and 96 of the teenagers liked the food court choices.
a) Make a two-way table for this data that shows the joint and marginal frequencies.
b) Make a two-way table that shows the joint and marginal relative frequencies.
c) Make a two-way table that shows the conditional relative frequencies based on the column totals.
d) What conclusions can you draw based on your results? Explain.

Statistics
ProbabilityThe monthly utility bills in a city are normally distributed, with a mean of $100 and a standard deviation of $12. Find the probability that a randomly selected utility bill is greater than $90.


Statistics
ProbabilityYou are measuring the length of squirrels from different sides of the Grand Canyon, to see if they are different species. Which of the following techniques should you use?
(a)Two sample t-test
(b)Fisher Exact Test
(c)adjusted Wald interval
(d)geometric mean
![If four out of four test subjects successfully complete a task, which of the following is the correct way to report your results?
With 95% confidence, [0.454, 1.056 ]percent of people will successfully complete this task.
With 95% confidence, over 45% of people will successfully complete this task.
With 95% confidence, [0.40, 0.76] of people will successfully complete this task.
With 95% confidence, only 45% of people will not successfully complete this task.](https://media.kunduz.com/media/sug-question/raw/79202250-1659025699.3831723.jpeg?w=256)
Statistics
ProbabilityIf four out of four test subjects successfully complete a task, which of the following is the correct way to report your results?
With 95% confidence, [0.454, 1.056 ]percent of people will successfully complete this task.
With 95% confidence, over 45% of people will successfully complete this task.
With 95% confidence, [0.40, 0.76] of people will successfully complete this task.
With 95% confidence, only 45% of people will not successfully complete this task.

Statistics
ProbabilityJeremy will roll a number cube numbered 1-6 twice. What is the probability of rolling an even number, then the number 3?

Statistics
ProbabilityThe cafeteria staff made sandwiches. Each sandwich had either rye or wheat bread, either ham or turkey, and either cheese or no cheese. The staff made an equal number of each type of sandwich. The sandwiches were placed on a tray. Without looking, Mary will choose a sandwich. What are the chances that Mary will get a sandwich with cheese?

Statistics
ProbabilityThe vanilly mandelic acid test is a urine test which was developed to detect the presence of neuroblastoma, a rare serious disease. This test gives a positive result in 70% of cases of neuroblastoma. 8 children with neuroblastoma are administered this test. We want to calculate the probability that the test will give an incorrect (negative) result for at least 2 children in this group. Which one of the following R commands gives this probability?
A) pbinom(2,8,0.7)
B) 1-pbinom (1,8,0.7)
C) pbinom(1,8,0.7)
D) pbinom (2,8,0.3)
E) 1-pbinom (1,8,0.3)
Statistics
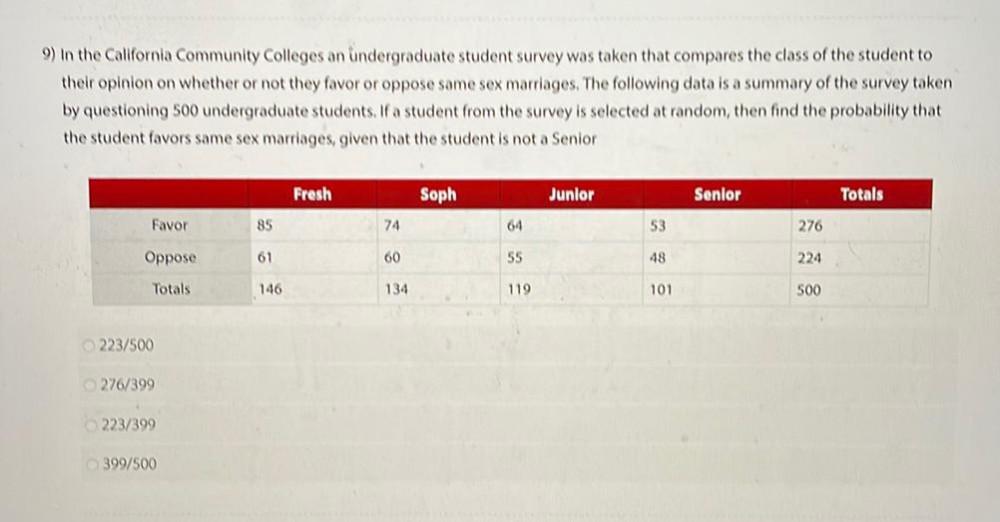
Probabilityin the California Community Colleges an undergraduate student survey was taken that compares the class of the student to their opinion on whether or not they favor or oppose same sex marriages. The following data is a summary of the survey taken by questioning 500 under -graduate students. If a student from the survey is selected at random, then find the probability that the student favors same-sex marriages, given that the student is not a Senior
Fresh Soph Junior Senior Totals
Favor 85 74 64 53. 276
Oppose 61 60 55 48. 224
Totals 146 134 119 101 500
a)223/500
b)276/399
c)223/399
d)399/500

Statistics
ProbabilityIn a busy coffee shop, which is a member of an international chain of coffee shops, 40% of customers order a pastry in addition to their drink. If 20 customers were selected at random during one business day, what is the probability that at least 11 of them did not order a pastry with their drink. Round your answer to 4 decimal places.
a)0.1275
b)0.3763
c)0.5956
d)0.7553
e)None of the above

Statistics
ProbabilityA spinner is divided into blue, yellow, and red parts. Gianna spun this spinner 400 times and listed her results in the table below. Select all of the estimated probabilities of the spinner landing on red.
COLOR FREQUENCY
Blue 198
Yellow 106
Red 96
A. 1/5
B. 6/25
C. 0.95
D. 0.24
E. 24%
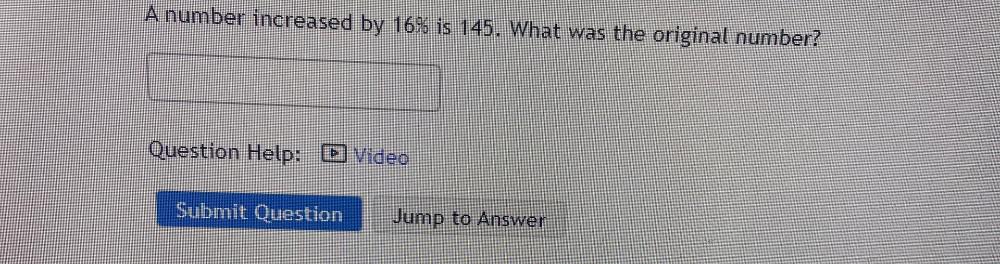

Statistics
ProbabilityCompute the amount of interest earned in the following simple interest problem. A deposit of $4,500 at 5% for 3 years:
$67.50
$6.75
$675.00
$6,750.00
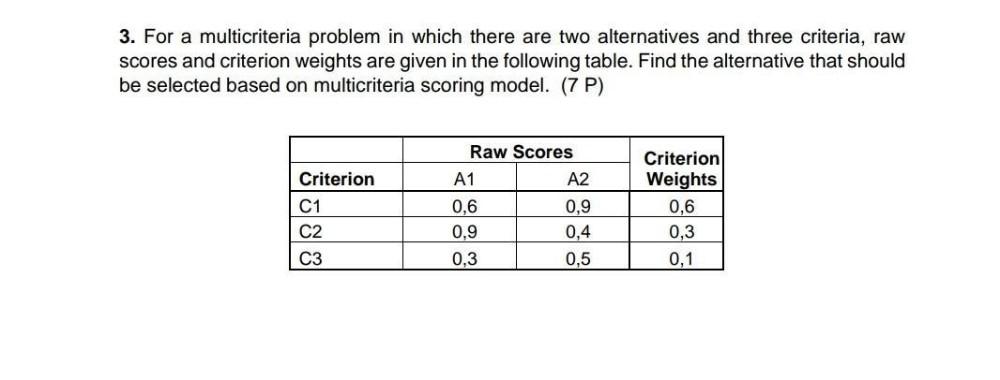
Statistics
ProbabilityFor a multicriteria problem in which there are two alternatives and three criteria, raw scores and criterion weights are given in the following table. Find the alternative that should be selected based on multicriteria scoring model.
Raw Scores
Criterion A1 A2 Weights Criterion
C1 0,6 0,9 0,6
C2 0,9 0,4 0,3
C3 0,3 0,3 0,1

Statistics
ProbabilityMiranda completed a random survey of 400 of the 3,256 students in her school. Now she wants to select part of this group of 400 to make estimates about the anticipated results. How should Miranda make her selection from the group of 400?
a)choose every Algebra class member
b)choose every athletics team member
c)choose every 13th survey
d)choose every B-average student

Statistics
ProbabilityWhich of the following is the most reasonable inference as to why age is a variable in many gender-wage studies?
Younger women are less likely to be discriminated against by employers than older women are, with other factors being equal.
Older women are likely to have entered the workforce at a time when women were traditionally paid significantly less than men.
Younger women have less knowledge about market conditions and thus are likely to accept lower wages than men for the same work.
Older women have more confidence and thus are more likely to aggressively negotiate for the same pay men in the profession receive.
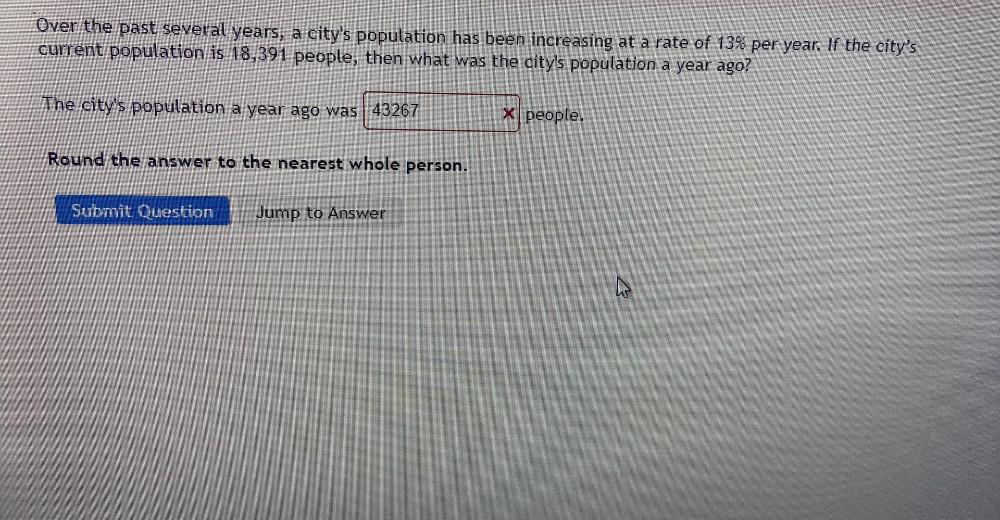
Statistics
ProbabilityOver the past several years, a city's population has been increasing at a rate of 13% per year. If the city's current population is 18,391 people, then what was the city's population a year ago?
The city's population a year ago was ____________ people.

Statistics
ProbabilityThe table below shows all of the outcomes to Jaime's experiment where he rolled a number cube and flipped a coin 370 times. According to Jaime's table, what is the probability (to the nearest whole number percentage) of rolling a number greater than or equal to 4 on the cube and having the coin land on tails?
Number Cube
1 2 3 4 5 6
Heads 34 28 29 32 27 31
Tails 30 32 30 31 33 33
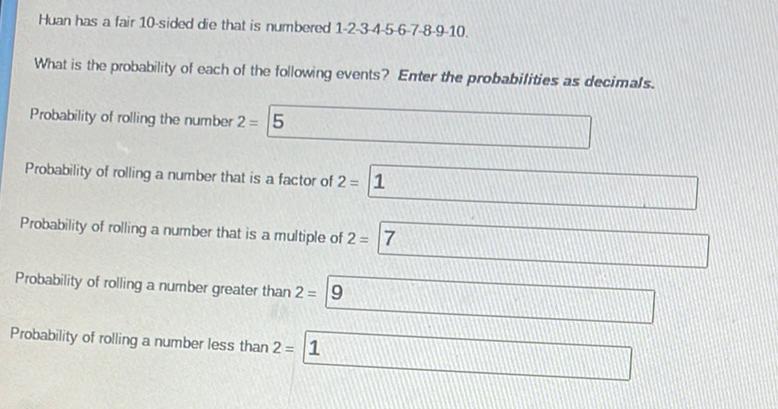
Statistics
ProbabilityHuan has a fair 10-sided die that is numbered 1-2-3-4-5-6-7-8-9-10.
What is the probability of each of the following events? Enter the probabilities as decimals.
a)Probability of rolling the number 2 = ___
b)Probability of rolling a number that is a factor of 2 = _____
c)Probability of rolling a number that is a multiple of 2 =____
d)Probability of rolling a number greater than 2 =______
e)Probability of rolling a number less than 2 =_____

Statistics
ProbabilityTim pays $2,000 annually for $150,000 worth of life insurance. At the end of 10 years, what will the cash value of his policy be?
Cash Value Of The Insurance Policy
Policy Anniversary Cash Value Per Unit
5th year $30.00
10th year $89.00
15th year $160.00
20th year $232.00
25th year $340.00
At the end of 10 years, what will the cash value of his policy be?
$20,000
$13,350
$150,000
$300,000
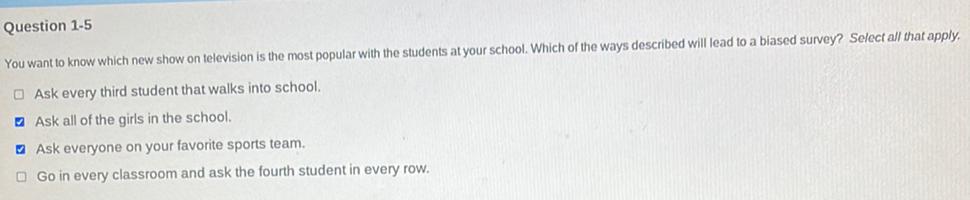
Statistics
ProbabilityYou want to know which new show on television is the most popular with the students at your school. Which of the ways described will lead to a biased survey? Select all that apply.
A. Ask every third student that walks into school.
B. Ask all of the girls in the school.
C. Ask everyone on your favorite sports team.
D. Go in every classroom and ask the fourth student in every row.
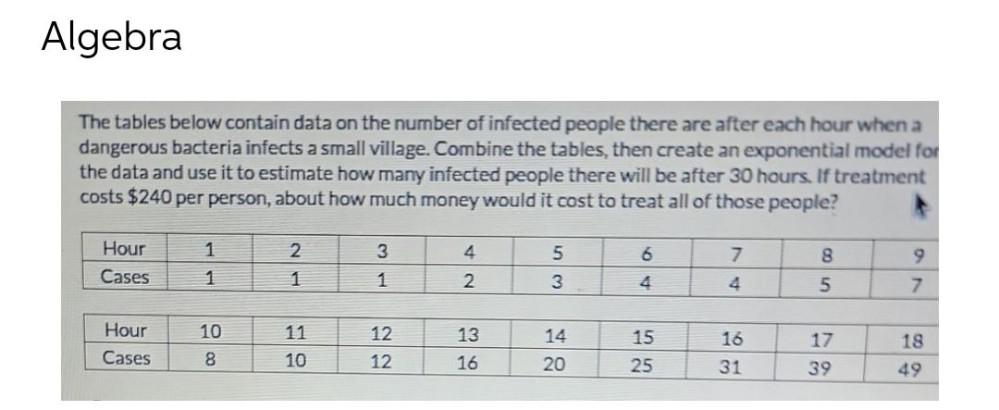
Statistics
ProbabilityThe tables below contain data on the number of infected people there are after each hour when a dangerous bacteria infects a small village. Combine the tables, then create an exponential model for the data and use it to estimate how many infected people there will be after 30 hours. If treatment costs $240 per person, about how much money would it cost to treat all of those people?
Hour 1 2 3 4 5 6 7 8 9
Case 1 1 1 2 3 4 4 5 7
Hour 10 11 12 13 14 15 16 17 18
Cases 8 10 12 16 20 25 31 39 49
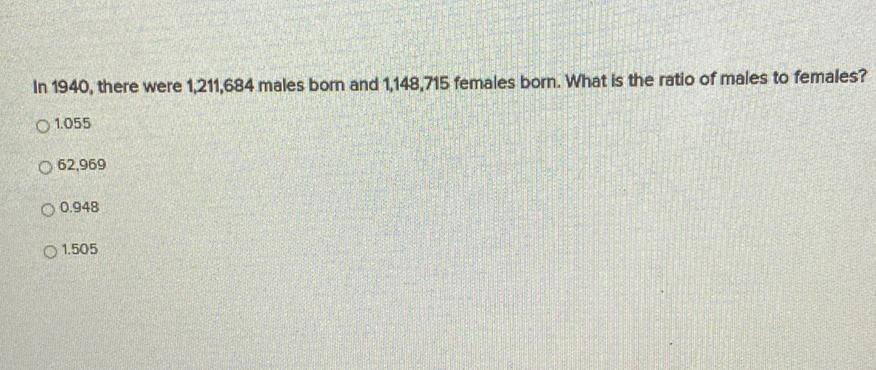
Statistics
ProbabilityIn 1940, there were 1,211,684 males born and 1,148,715 females born. What is the ratio of males to females?
1.055
62,969
0.948
1.505
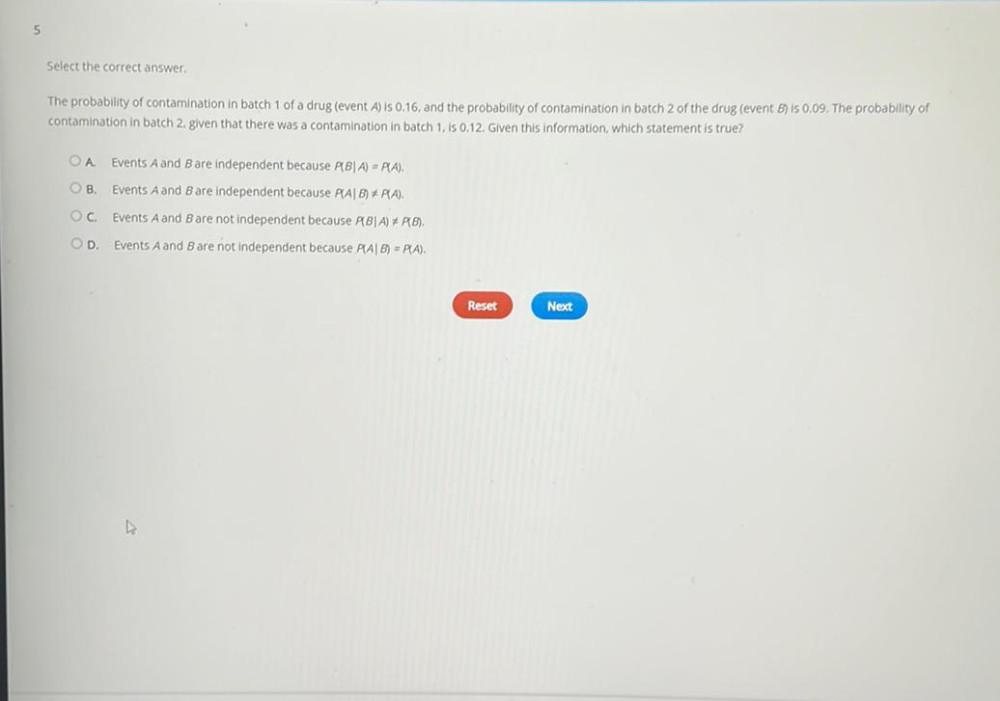
Statistics
ProbabilityThe probability of contamination in batch 1 of a drug (event A) is 0.16, and the probability of contamination in batch 2 of the drug (event B) is 0.09. The probability of contamination in batch 2. given that there was a contamination in batch 1, is 0.12. Given this information, which statement is true?
A. Events A and B are independent because P(BIA) = P(A).
B. Events A and B are independent because P(A| B) ≠P(A).
C. Events A and B are not independent because P(BIA)≠P(B).
D. Events A and B are not independent because P(A| B)=P(A).
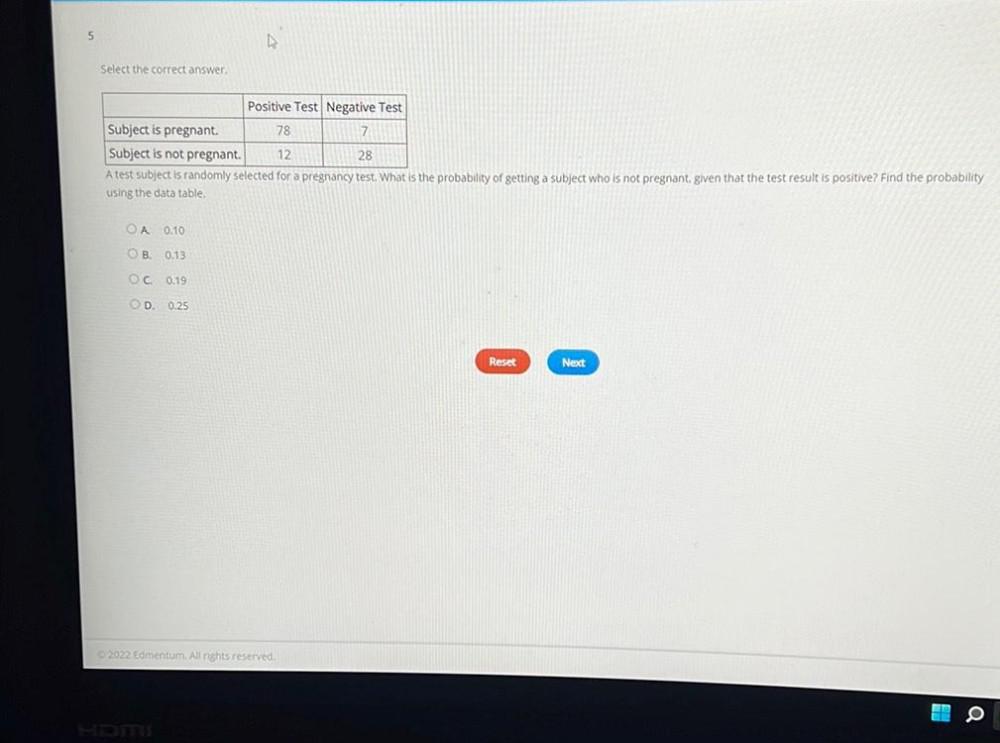
Statistics
ProbabilitySelect the correct answer.
Positive Test Negative Test
Subject is pregnant. 78 7
Subject is not pregnant. 12 28
A test subject is randomly selected for a pregnancy test. What is the probability of getting a subject who is not pregnant, given that the test result is positive? Find the probability using the data table.
A. 0.10
B. 0.13
C. 0.19
D. 0.25
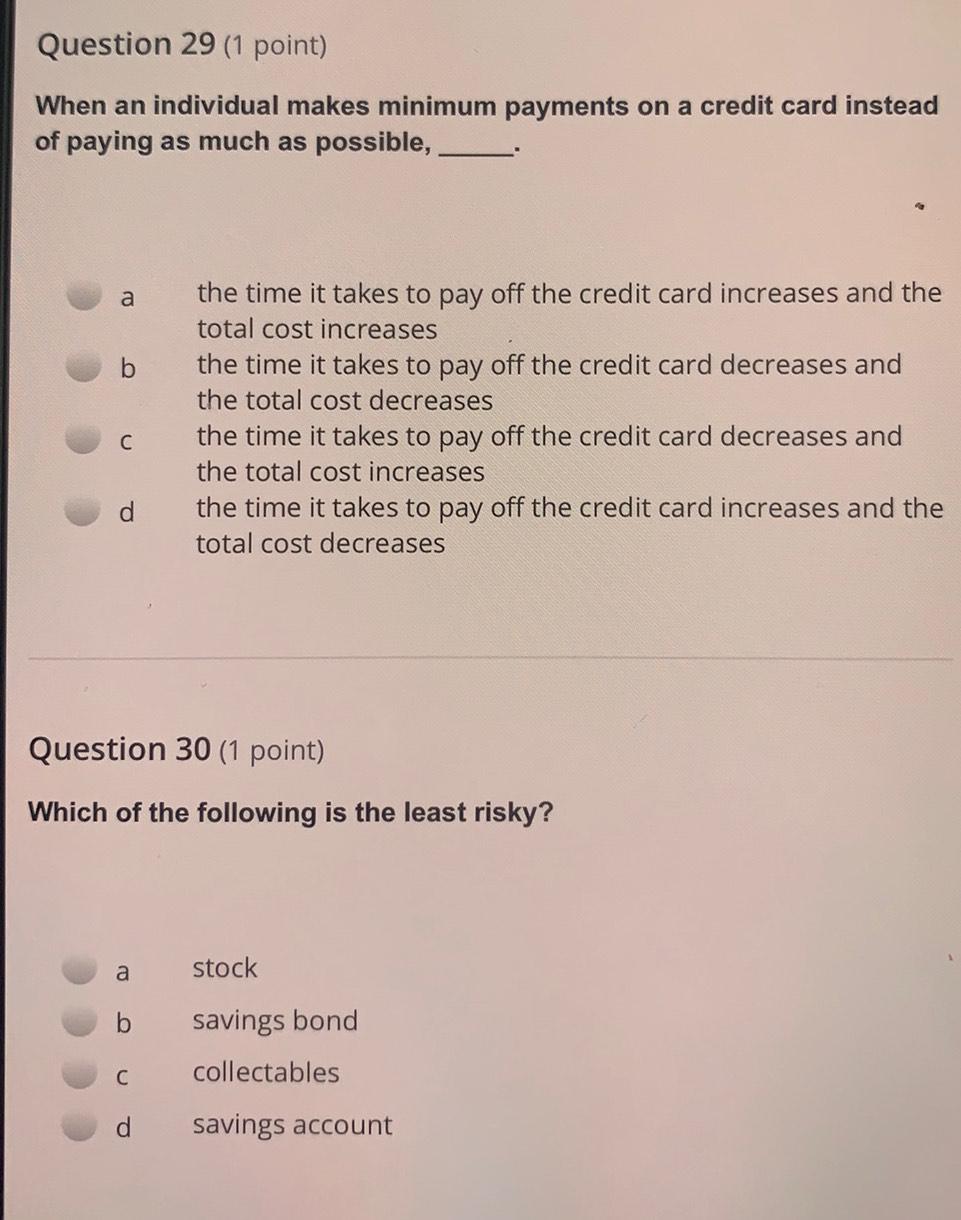
Statistics
ProbabilityWhen an individual makes minimum payments on a credit card instead of paying as much as possible,
A) the time it takes to pay off the credit card increases and the total cost increases
B) the time it takes to pay off the credit card decreases and the total cost decreases
C) the time it takes to pay off the credit card decreases and the total cost increases
D) the time it takes to pay off the credit card increases and the total cost decreases
30) Which of the following is the least risky?
A) stock
B) savings bond
C) collectables
D) savings account

Statistics
ProbabilityWhich situation is an example of confirmation bias?
A. A coach recruits a player he believes is excellent at stealing bases because he is on a high school track team. The player has made two of the last ten steal attempts. The coach has the player attempt to steal the base.
B. A coach recruits a player he believes is excellent at stealing bases because he is on a high school track team. The player has made eight of the last ten steal attempts. The coach has the player attempt to steal the base.
C. A coach recruits a player he believes is excellent at stealing bases because he is on a high school track team. The player has made nine of the last ten steal attempts. The coach has the player attempt to steal the base.
D. A coach recruits a player he believes is excellent at stealing bases because he is on a high school track team. Bases are loaded. The coach has the player attempt to steal the base.

Statistics
ProbabilityA chip is placed at point 0 on a number line. What is the approximate probability of seven movements to the right in a random walk, given ten total movements and a probability of 0.5 for taking a step in either direction?
A) 0
B) 0.12
C) 0.5
D) 1
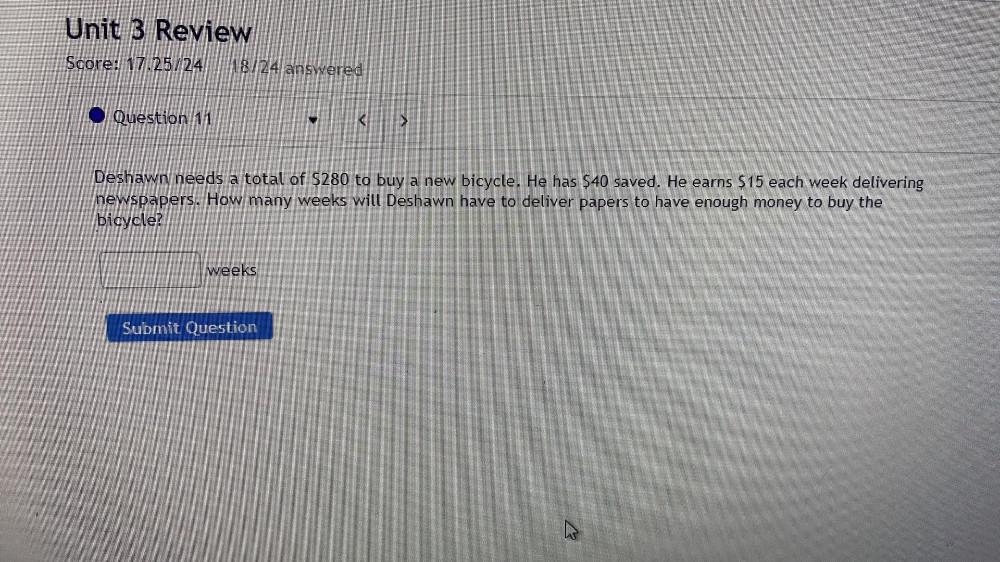
Statistics
ProbabilityDeshawn needs a total of $280 to buy a new bicycle. He has $40 saved. He earns $15 each week delivering newspapers. How many weeks will Deshawn have to deliver papers to have enough money to buy the bicycle?
___________________ weeks

Statistics
ProbabilityA gymnast is standing at point 0. She does a front tuck one movement forward each time the number one through four on a number cube is rolled and a back tuck one movement backward each time the number five or six is rolled. What is the probability of one forward movement, given three total movements?
A) 0
B) 0.22
C) 0.375
D) 0.5
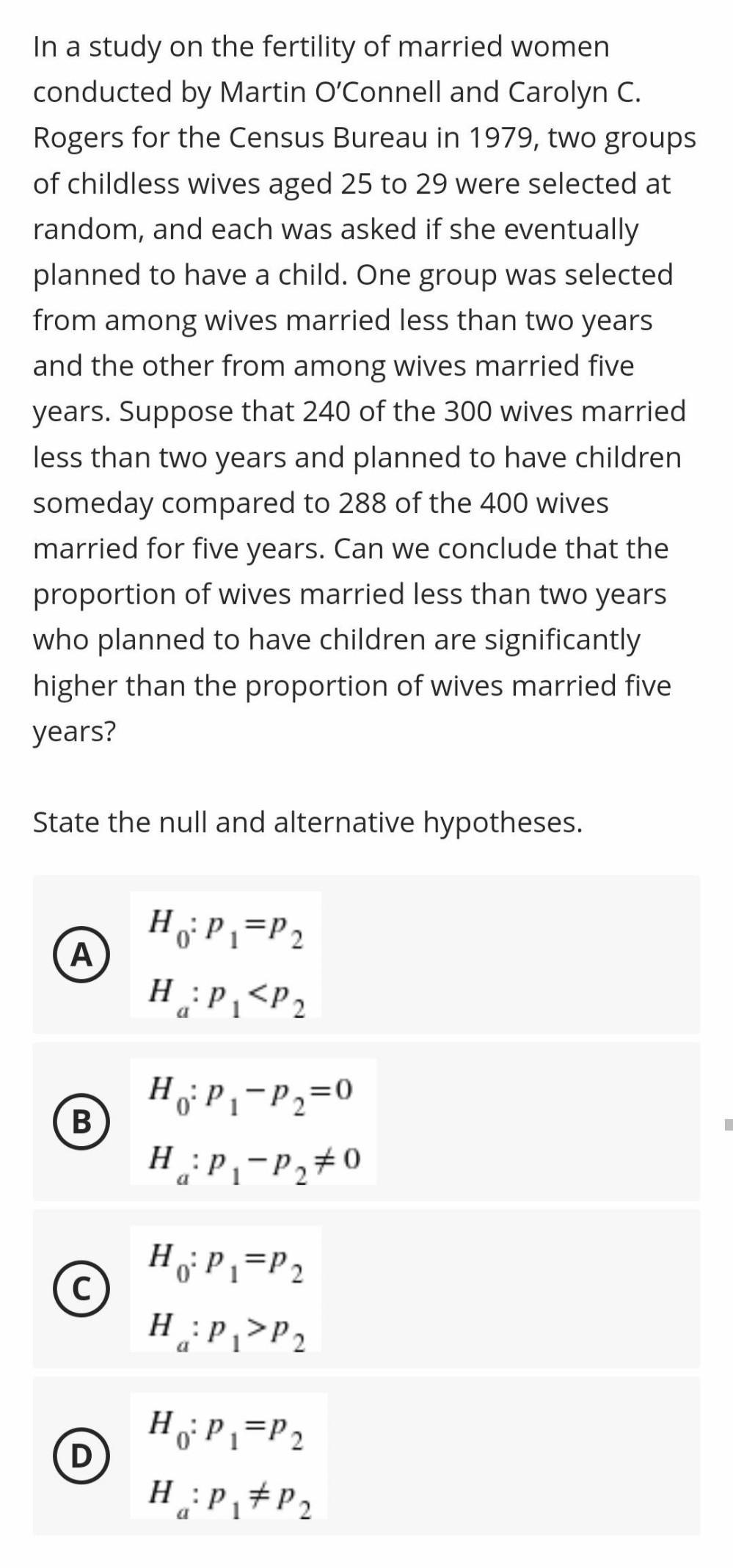
Statistics
ProbabilityIn a study on the fertility of married women conducted by Martin O'Connell and Carolyn C. Rogers for the Census Bureau in 1979, two groups of childless wives aged 25 to 29 were selected at random, and each was asked if she eventually planned to have a child. One group was selected from among wives married less than two years and the other from among wives married five years. Suppose that 240 of the 300 wives married less than two years and planned to have children someday compared to 288 of the 400 wives married for five years. Can we conclude that the proportion of wives married less than two years who planned to have children are significantly higher than the proportion of wives married five years?
State the null and alternative hypotheses.
A)H ₀ P₁ = P₂
Ha:P₁<P₂
b)H ₀:P₁-P₂=0
Ha:P₁-P₂≠0
C)H₀:P₁=P₂
H₁a: P₁ > P₂
d)H₀:P₁=P₂
Ha: P₁≠P₂

Statistics
ProbabilityThe Ericsson method is one of several methods claimed to increase the likelihood of a baby girl. In a clinical trial, results could be analyzed with a formal hypothesis test with the alternative hypothesis of p > 0.5, which corresponds to the claim that the method increases the likelihood of having a girl, so that the proportion of girls is greater than 0.5. If you have an interest in establishing the success of the method, which of the following P-values would you prefer: 0.999, 0.5, 0.95, 0.05, 0.01, 0.001? Why?
The P-value of___ is preferred because it corresponds to the sample evidence that most strongly supports the_____hypothesi that the method _____ effective.
Statistics
ProbabilityThere are eighteen students in a club. Four students are randomly chosen to sit on the float the club is entering in a parade. How many ways can you choose the four students?
3,060
73,440
3,080
72,240

Statistics
ProbabilityStart at point 0 on a number line. What is the probability of four movements to the right in a random walk, given eight total movements and the probability of a right movement is 0.5?
a) 0
b) 0.27
c) 0.5
d) 0.1

Statistics
ProbabilityEight acts applied for a talent contest. The acts are designated by unique letters: A, B, C, D, E, F, G, H. Five were randomly chosen to compete. What is the probability that the acts chosen will be scheduled to perform in this order:B G F E A?
1/6720
1/56
5/8
25/64
Statistics
ProbabilityA baseball player struck out eight of the player's last eleven times at bat. What is the probability that the player will strike out again the next time the player is at bat?
73%
0.73%
64%
0.64%

Statistics
ProbabilityA basketball player made two out of five 3-point shots in the last game. What probability can a coach assume the player will make a 3-point shot in the next game?
a) 0.4
b) 0.2
c) 0.6
d) 0.3

Statistics
ProbabilityWhich formula can be used to find the probability of one forward step in a random walk, beginning at location O, given two total steps and the probability of a forward step is 0.5?
a) P(1) = 2!/1!(1)! ×0.5¹(0.5)¹
b) P(1) = 2!/2! ×0.5¹(0.5)¹
c) P(1) = 2!/0! ×0.5¹(0.5)¹
d) P(1) = 5!/2!(3)! × 0.5²(0.5)³
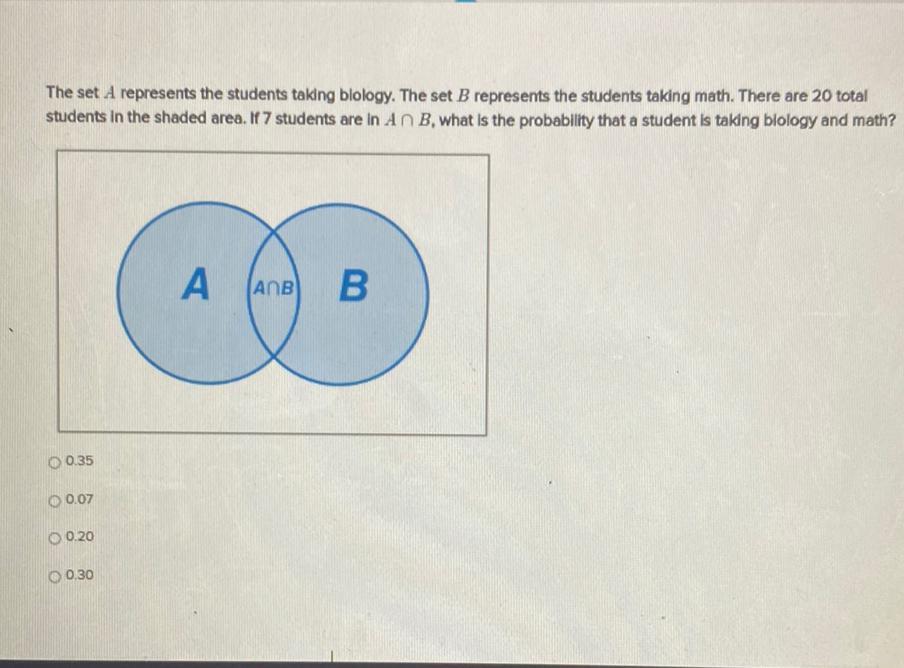
Statistics
ProbabilityThe set A represents the students taking biology. The set B represents the students taking math. There are 20 total students in the shaded area. If 7 students are in A∩B, what is the probability that a student is taking blology and math?
0.35
0.07
0.20
0.30
Statistics
ProbabilityThere are five sophomores, nine juniors, and seven seniors in a group. If you select one student at random, what is the probability of not picking a junior or a senior?
5/21
2/21
16/21
7/21
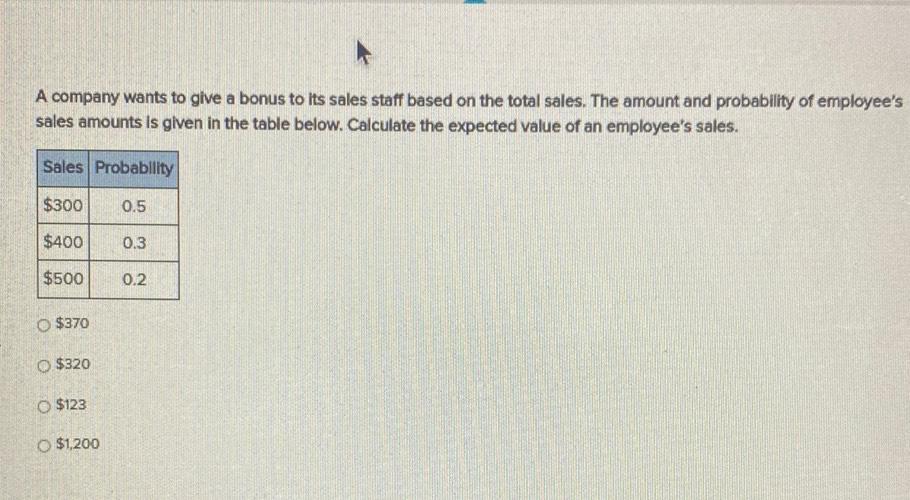
Statistics
ProbabilityA company wants to give a bonus to its sales staff based on the total sales. The amount and probability of employee's sales amounts is given in the table below. Calculate the expected value of an employee's sales.
Sales Probability
$300 0.5
$400 0.3
$500 0.2
$370
$320
$123
$1,200
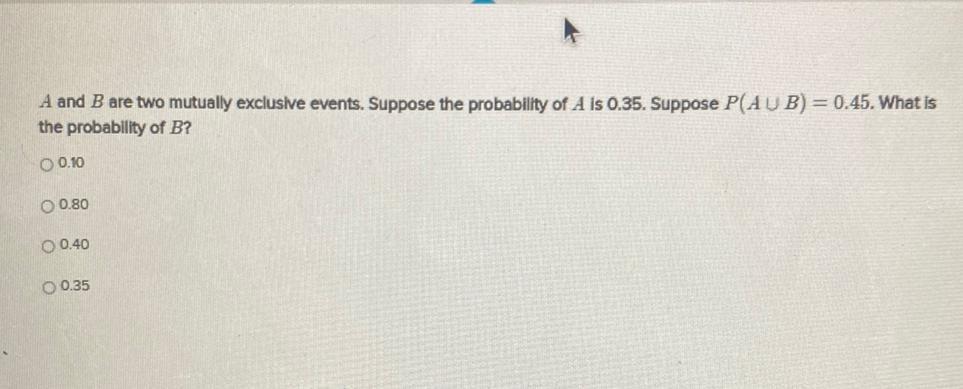
Statistics
ProbabilityA and B are two mutually exclusive events. Suppose the probability of A is 0.35. Suppose P(A⋃B) = 0.45. What is the probability of B?
a) 0.10
b) 0.80
c) 0.40
d) 0.35
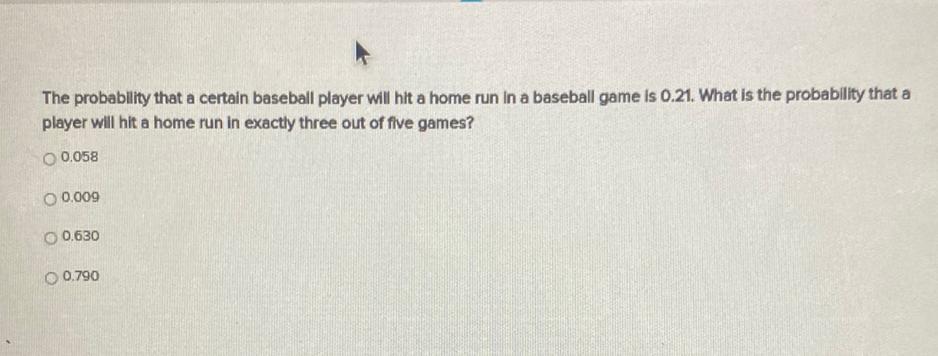
Statistics
ProbabilityThe probability that a certain baseball player will hit a home run in a baseball game is 0.21. What is the probability that a player will hit a home run in exactly three out of five games?
0.058
0.009
0.630
0.790