Probability Questions and Answers
Statistics
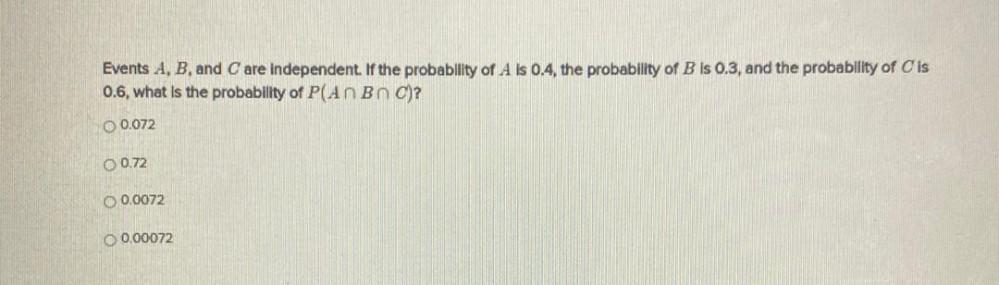
ProbabilityEvents A, B, and Care independent. If the probability of A is 0.4, the probability of B is 0.3, and the probability of C is 0.6, what is the probability of P(A∩B∩C)?
0.072
0.72
0.0072
0.00072
Statistics
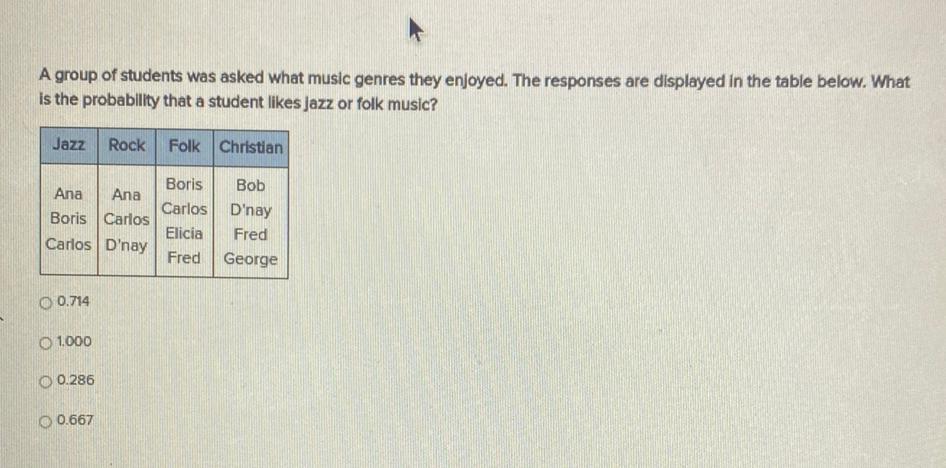
ProbabilityA group of students was asked what music genres they enjoyed. The responses are displayed in the table below. What is the probability that a student likes jazz or folk music?
Jazz | Rock | Folk | Christian
______________________________________________
Ana | Ana | Boris | Bob
Boris | Carlos | Carlos | D'nay
Carlos | D'nay | Elicia | Fred
| Fred | George
a) 0.714
b) 1.000
c) 0.286
d) 0.667

Statistics
ProbabilityYou buy a pair of Apple AirPods Pro on sale for $174.30 which is a discount of 30% off the original price. Write an equation that relates the sale price to the original price. Use p for original price. Now, solve the equation you wrote above to determine the original price.

Statistics
ProbabilityThe average life of an electric rice cooker is 5 years, with a standard deviation of 1 year. Assume the lives of these cookers follow a normal distribution. Find
(a) The probability that the mean life of a random sample of 9 machines falls between 5.7 and 8.1 years. (Answer in percent with 2 decimal places. No need to include the percent symbol)
(b) The value of to the left of which 85% of the means computed from random samples of size 9 would fall.(Answer in percent with 2 decimal places. No need to include the percent symbol)
Statistics
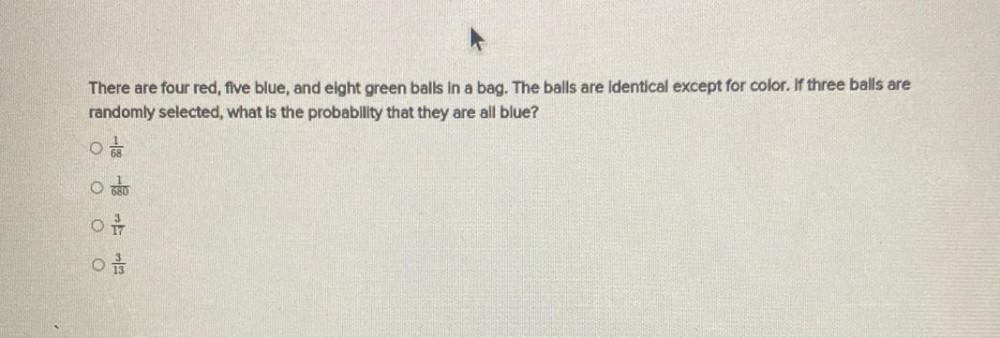
ProbabilityThere are four red, five blue, and eight green balls in a bag. The balls are identical except for color. If three balls are randomly selected, what is the probability that they are all blue?
1/68
1/680
3/17
3/13

Statistics
ProbabilityThe sample space S = {a, d, e, g}. Find the probability of the complement of (a, e, g}.
a) 0.25
b)0.50
b)0.75
c)0.33

Statistics
ProbabilityA random number generator selects numbers from ten to fifty. The results are in the table below.
Numbers 10s 20s 30s 40s 50s
Times 131 116 125 118 110
What is the experimental probability of selecting a number in the twenties?
a) 0.18
b) 0.19
c) 0.20
c) 0.21
Statistics
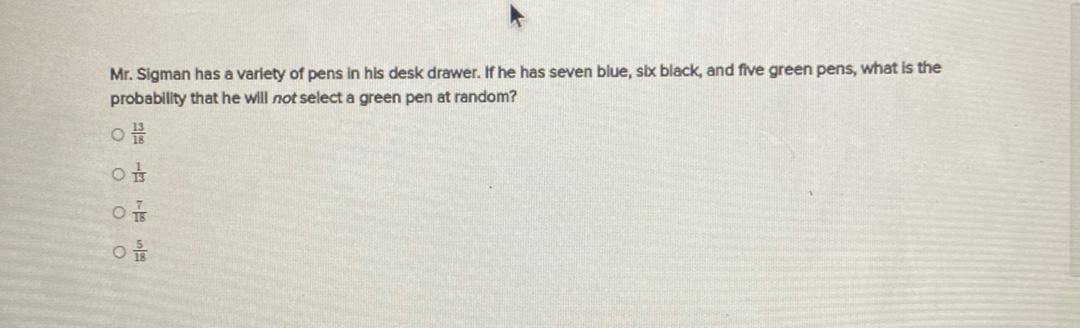
ProbabilityMr. Sigman has a variety of pens in his desk drawer. If he has seven blue, six black, and five green pens, what is the probability that he will not select a green pen at random?
a) 13/18
b) 1/13
c) 7/18
d) 5/18
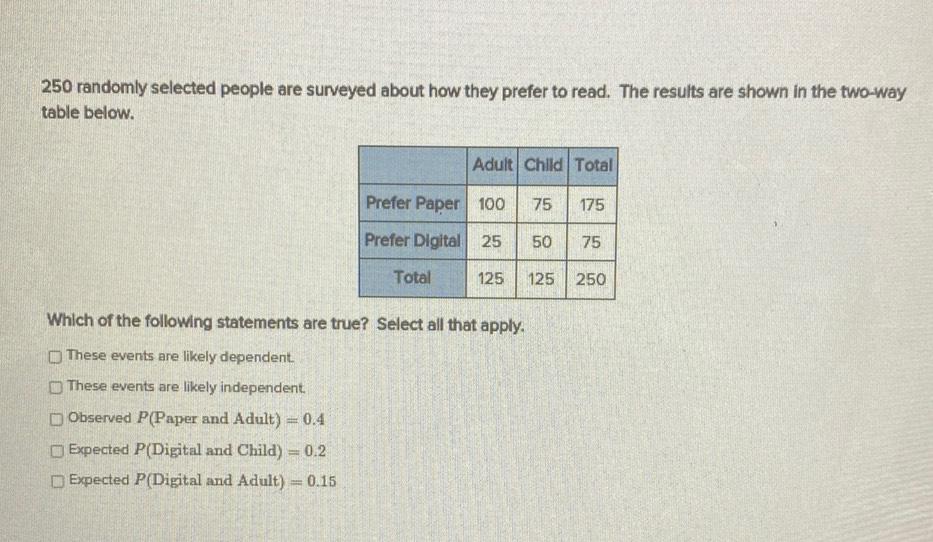
Statistics
Probability250 randomly selected people are surveyed about how they prefer to read. The results are shown in the two-way table below.
Adult Child Total
Prefer Paper 100 75 175
Prefer Digital 25 50 75
Total 125 125 250
Which of the following statements are true?Select all that apply.
These events are likely dependent.
These events are likely independent.
Observed P(Paper and Adult) = 0.4
Expected P(Digital and Child) = 0.2
Expected P(Digital and Adult) = 0.15

Statistics
ProbabilityThe probability of a student taking technology and woodshop is 0.078, and the probability that a student takes technology is 0.57. Which formula represents the probability that a given student takes woodshop given that they are taking technology?
P(B|A)= (0.078/0.57)
P(B|A) = (0.07/80.57)
P(B|A) ={(0.078)/(0.57)(0.057)}
P(B|A)= {(0.078)/0.078) (0.57)}

Statistics
ProbabilityThe table below gives the expected proportion of games where the player has the given number of hits in the game. If the baseball player plays in 100 games, what is the expected number of games with 2 hits?
Number of Hits in One Game Expected Proportion
0 0.62
1 0.31
2 0.05
3 0.015
4 0.005
5
50
0.5
20
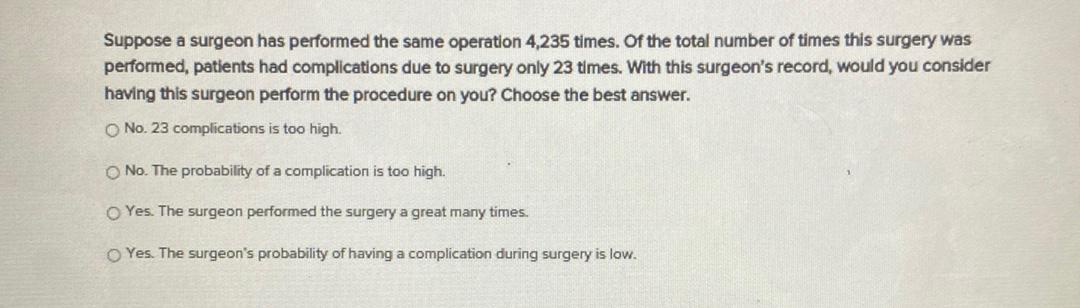
Statistics
ProbabilitySuppose a surgeon has performed the same operation 4,235 times. Of the total number of times this surgery was performed, patients had complications due to surgery only 23 times. With this surgeon's record, would you consider having this surgeon perform the procedure on you? Choose the best answer.
a) No. 23 complications is too high.
b) No. The probability of a complication is too high.
c) Yes. The surgeon performed the surgery a great many times.
d) Yes. The surgeon's probability of having a complication during surgery is low.

Statistics
ProbabilityFor a flash drive, there is a memory capacity of 2 GB, 4 GB, 8 GB, and 16 GB and there are five colors. What is the probability of selecting a 4 GB flash drive, assuming that the probabilities of selection are the same for all options?
1/20
1/5
1/3
1/2
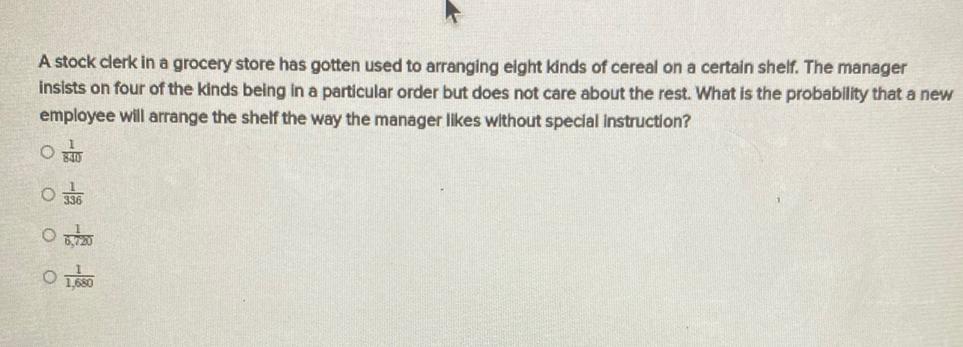
Statistics
ProbabilityA stock clerk in a grocery store has gotten used to arranging eight kinds of cereal on a certain shelf. The manager insists on four of the kinds being in a particular order but does not care about the rest. What is the probability that a new employee will arrange the shelf the way the manager likes without special instruction?
a) 1/840
b) 1/336
c) 1/6720
d) 1/1,680
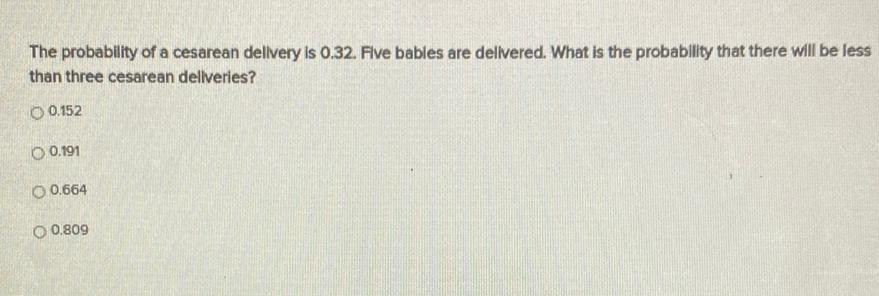
Statistics
ProbabilityThe probability of a cesarean delivery is 0.32. Five bables are delivered. What is the probability that there will be less than three cesarean deliveries?
0.152
0.191
0.664
0.809

Statistics
ProbabilityA and B are two independent events. Suppose the probability of A is 0.3, and the probability of B is 0.543. Which of the following is true? Select all that apply.
a) The probability that A and B occur is 0.1629.
b) The probability that A or B occurs is 0.6801.
c) The probability that A or B occurs is 0.1629.
d) The probability that A and B occur is 0.6801.

Statistics
ProbabilityFor the sample space S = {f, s, g, r, m}, where f denotes French, s Spanish, g German, r Russian, and m Mandarin, identify the probability of the complement of the event A = {f}.
a)P(A) = 1
b)P(A) = 4
c)P(A) =1/5
d)P(A) =4/5
Statistics
ProbabilityExplain why the following situation is a permutation: There are ten finalists in the science fair. How many ways could the top three be chosen (first, second, and third place)?

Statistics
ProbabilityDraw a probability tree diagram for the following scenario: Angelica's favorite meal is pizza, followed by ice cream for dessert. She orders pizza twice a week. If she orders pizza, the probability that she will have ice cream for dessert is 2/3. If she doesn't order pizza, then the probability that she eats ice cream for dessert is 1/4.

Statistics
ProbabilityThe probability of a hurricane on August 2 is 0.04. What is the probability of a hurricane on August 2 for three years in a row?
a) 0.000064
b) 0.000192
c) 0.120000
d) 0.001600
Statistics
ProbabilityIn some cases in hockey, the coach decides who will take a penalty shot. Player A makes 8/10 penalty shots, B makes 9/10, C makes 4/10, and D makes 1/10. Which player should the coach choose?
a)Player A
b) Player B
c) Player C
d) Player D

Statistics
ProbabilitySuppose the probability a resistor at a manufacturing company is defective (the probability of success) is 0.02. What is the probability a manager chooses a defective resistor on the third grab from the line?
0
0.00039
0.019
1

Statistics
ProbabilityThere is a housing lottery in a college for five houses among fifteen students, three students per house. What is the probability that a group of three friends will be assigned to the first house?
1/84
1/220
1/455
1/816

Statistics
ProbabilityWhich formula can be used to find the probability of four forward steps in a random walk, beginning at location 0, given ten total steps and the probability of a forward step is 0.5?
a) P(4)=10!/4!(6)! ×0.5⁴ (0.5)⁶
a) P(4) = 10!/(6)! ×0.5⁴ (0.5)⁶
c) P(4)= 10!/4! ×0.5⁴ (0.5)⁶
d) P(4)= 5!/2!(3)! x 0.5²(0.5)³
Statistics
ProbabilityA company is testing a product safety feature for a space heater. The likelihood that the safety feature fails is P(A) = 0.3. What is the probability that the safety feature does not fail in a series of three tests?
a) P(A')³ = 0.434
b) P(A')³= 0.343
c) P(A')³ = 0.7
d) P(A')³ = 0.3

Statistics
ProbabilityThe two-way table shows if campers can or can't swim.
Can Swim Can't Swim Total
Boys 28 22 50
Girls 32 18 50
Total 60 40 100
One girl will randomly be chosen. What is the experimental probability that she cannot swim?
9/50
9/29
2/5
9/20
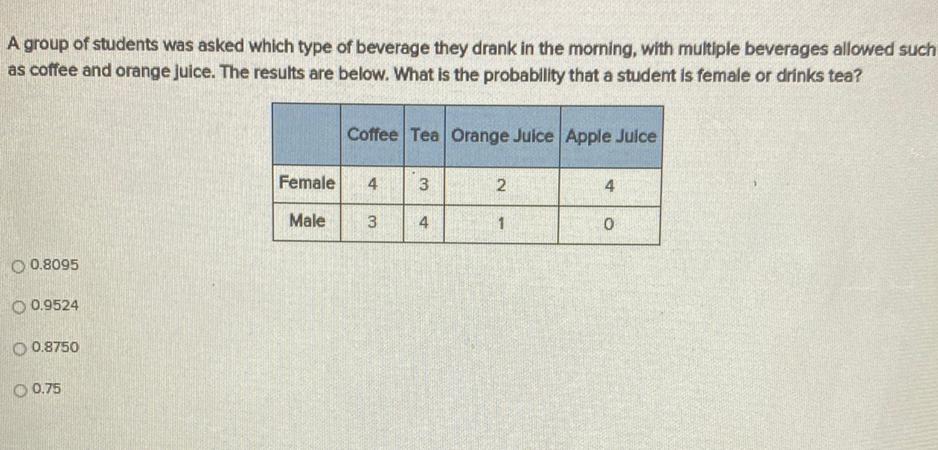
Statistics
ProbabilityA group of students was asked which type of beverage they drank in the morning, with multiple beverages allowed such as coffee and orange juice. The results are below. What is the probability that a student is female or drinks tea?
Coffee Tea Orange Juice Apple Juice
Female 4 3 2 4
Male 3 4 1 0
a) 0.8095
b) 0.9524
c) 0.8750
d) 0.75

Statistics
Probability45 students in a cooking course are asked which is their favorite fruit is out of an Orange, Apple, or Banana. The result of this survey is shown as Orange 10, Apple 16, Banana = 19
In R, estimate the probability that all three fruits have different numbers of students.

Statistics
ProbabilityLet A be the probability that a person in the United States has blood type A, 0.4. Let B be the probability that a person in the United States has blood type B, 0.11. Assume A and B are independent events. If two people from the United States are chosen at random, what is P(A⋂B)?
a) 0
b) 0.044
c) 0.51
d) 1
Statistics
ProbabilityUse the accompanying radiation levels(in W/kg)
for 50 different cell phones. Find the percentile corresponding to 1.47 W/kg.
The percentile corresponding to 1.47 W/kg is___.
(Round to the nearest whole number as needed.)

Statistics
ProbabilityYou play a game where you toss a ball into one of 5 targets while blindfolded. If you hit target 3, you win $15. It costs $4 to play. Construct a probability distribution for your winnings. Find your expected winnings.
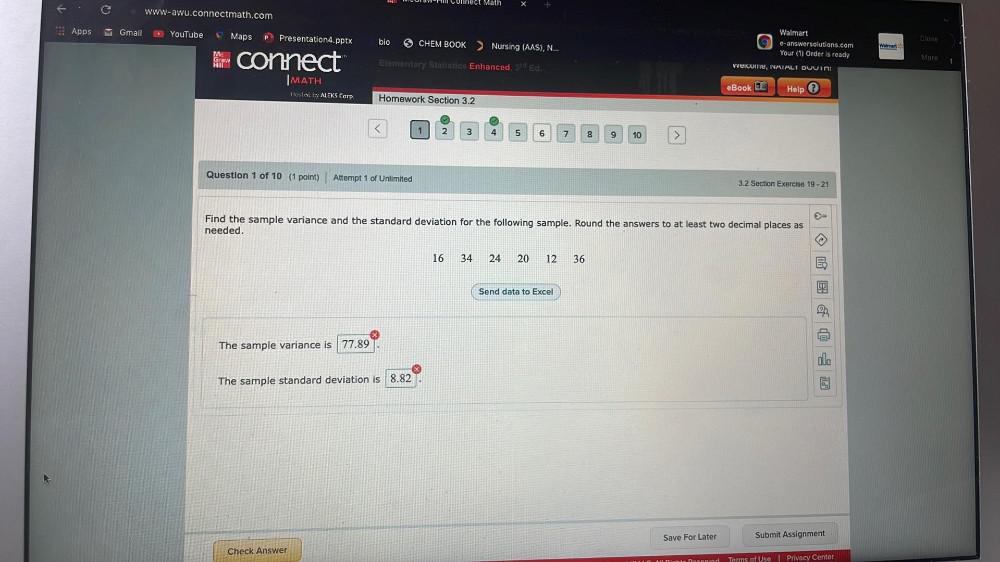
Statistics
ProbabilityFind the sample variance and the standard deviation for the following sample. Round the answers to at least two decimal places as needed.
16 34 24 20 12 36
The sample variance is _______.
The sample standard deviation is _______.

Statistics
ProbabilityRandomly selected college students answered a survey about their drinking habits during the last two weeks of the past semester. The table below represents the results of the survey.
15+ drinks during the last Less than 15 drinks during the last
two weeks of semester two weeks
Males 28 322
Females 10 562
If one college student is randomly selected, find the probability that the student
a) Drank a minimum of 15 drinks given that the student was a male.
b) Was a female or drank less than 15 drinks.

Statistics
ProbabilityLet X∼Exp(λ) and Y∼Exp(μ) be independent. Show that
(a) min(X,Y)∼Exp(λ+μ)
(b) P(X<Y)|min(X,Y)=λ/(λ+μ)

Statistics
ProbabilityCards: What is the probability of drawing a Queen or an 8 from a regular deck of cards?
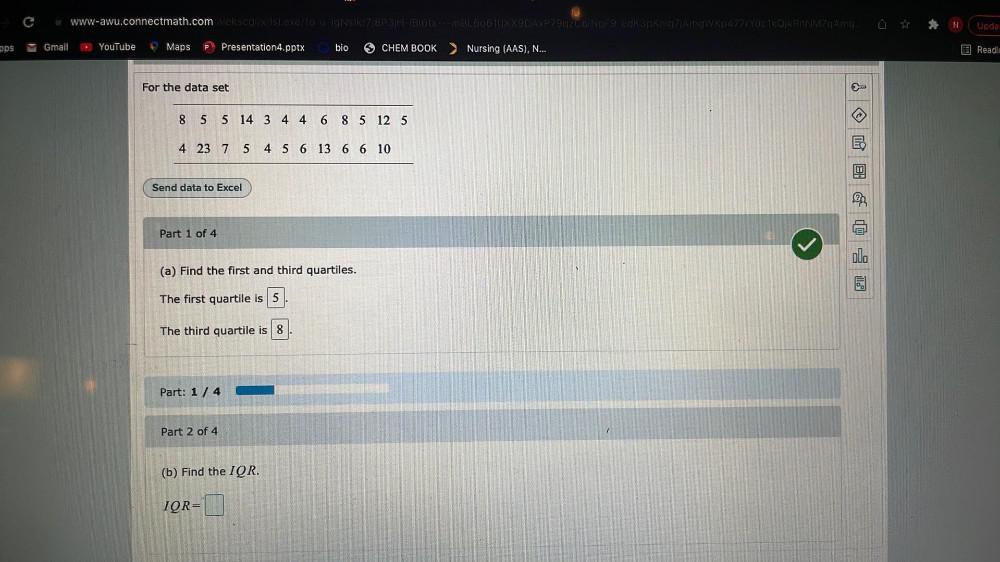
Statistics
ProbabilityFor the data set
8 5 5 14 3 4 4 6 8 5 12 5
4 23 7 5 4 5 6 13 6 6 10
Send data to Excel
Part 1 of 4
(a) Find the first and third quartiles.
The first quartile is ?
The third quartile is ?
(b) Find the IQR.
IQR=?
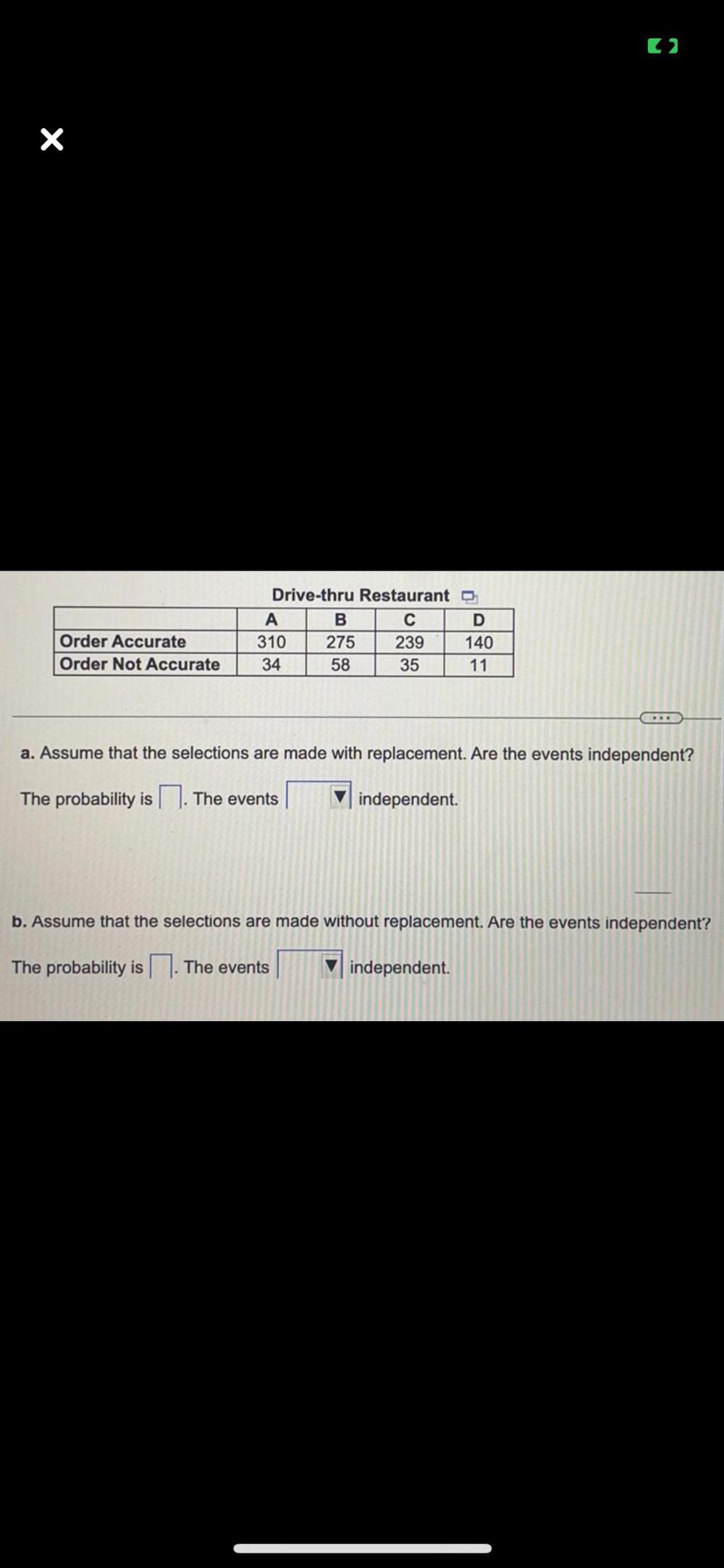
Statistics
ProbabilityDrive-thru Restaurant
A B C D
Order Accurate 310 275 239 140
Order Not Accurate 34 58 35 11
a. Assume that the selections are made with replacement. Are the events independent?
The probability is__________. The events ___________ independent.
b. Assume that the selections are made without replacement. Are the events independent?
The probability is___________ . The events _________ independent.
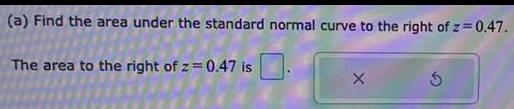
Statistics
Probability(a) Find the area under the standard normal curve to the right of z = 0.47.
The area to the right of z = 0.47 is

Statistics
ProbabilityUse the TI-84 Plus calculator to find the z-scores that bound the middle 82% of the area under the standard normal curve. Enter the answers in ascending orde and round to two decimal places.
The z-scores for the given area are __ and __

Statistics
ProbabilityContestants in a game show are each given four pairs of numbers (for example, 1 and 3, 5 and 4, and 6 and 1). A person in the audience is randomly picked and asked to roll two dice, one blue and one green. The blue die gives the first number. in the pair, and the green die gives the second number .theprobability that each player has of winning is? Show your work. numbers.

Statistics
ProbabilityA research scientist reports that mice will live a mean of 40 months
when their diets are sharply restricted and then enriched with vitamins
and proteins. Assuming that the lifetimes of such mice are normally
distributed with a standard deviation of 6.3 months, find the probability that a given mouse will live between 37 and 49 months.
A) 0.3920
B) 0.5845
C) 0.7205
D) 0.6080
E) 0.3888
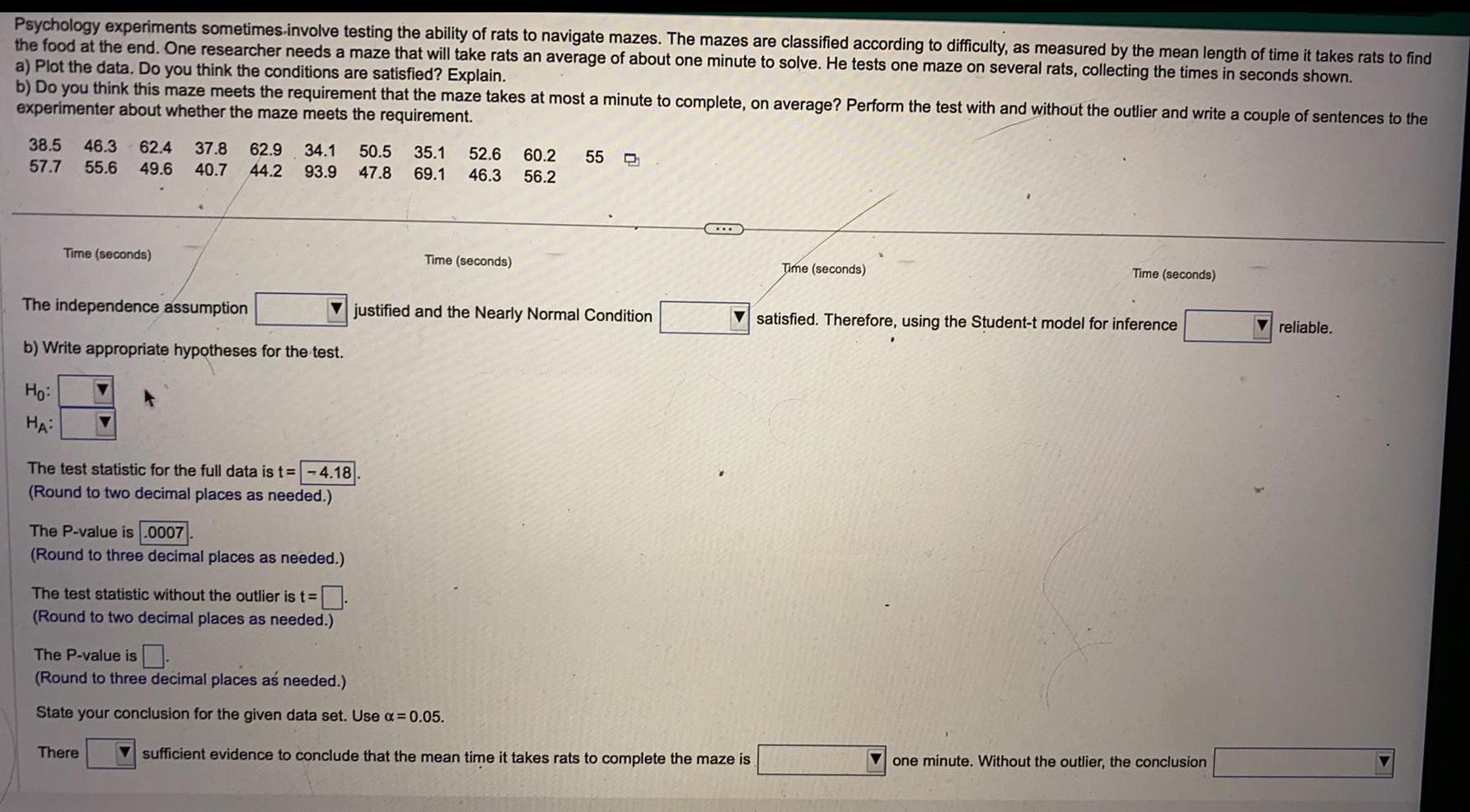
Statistics
ProbabilityPsychology experiments sometimes-involve testing the ability of rats to navigate mazes. The mazes are classified according to difficulty, as measured by the mean length of time it takes rats to find
the food at the end. One researcher needs a maze that will take rats an average of about one minute to solve. He tests one maze on several rats, collecting the times in seconds shown.
a) Plot the data. Do you think the conditions are satisfied? Explain.
b) Do you think this maze meets the requirement that the maze takes at most a minute to complete, on average? Perform the test with and without the outlier and write a couple of sentences to the
experimenter about whether the maze meets the requirement.

Statistics
ProbabilityA computer is generating passwords. The computer generates nine characters at random, and each is equally likely to be any of the 26 letters or 10 digits. Replications are allowed. What is the probability that the password will contain all letters? Round your answers to four decimal places.
The probability that the password will contain all letters is

Statistics
ProbabilityA fair 6-sided die is rolled four times. What is the probability that the sequence of rolls is 2, 4, 1, 3? Write your answer as a fraction or a decimal, rounded to four decimal places.
The probability that the sequence of rolls is 2, 4, 1, 3 is
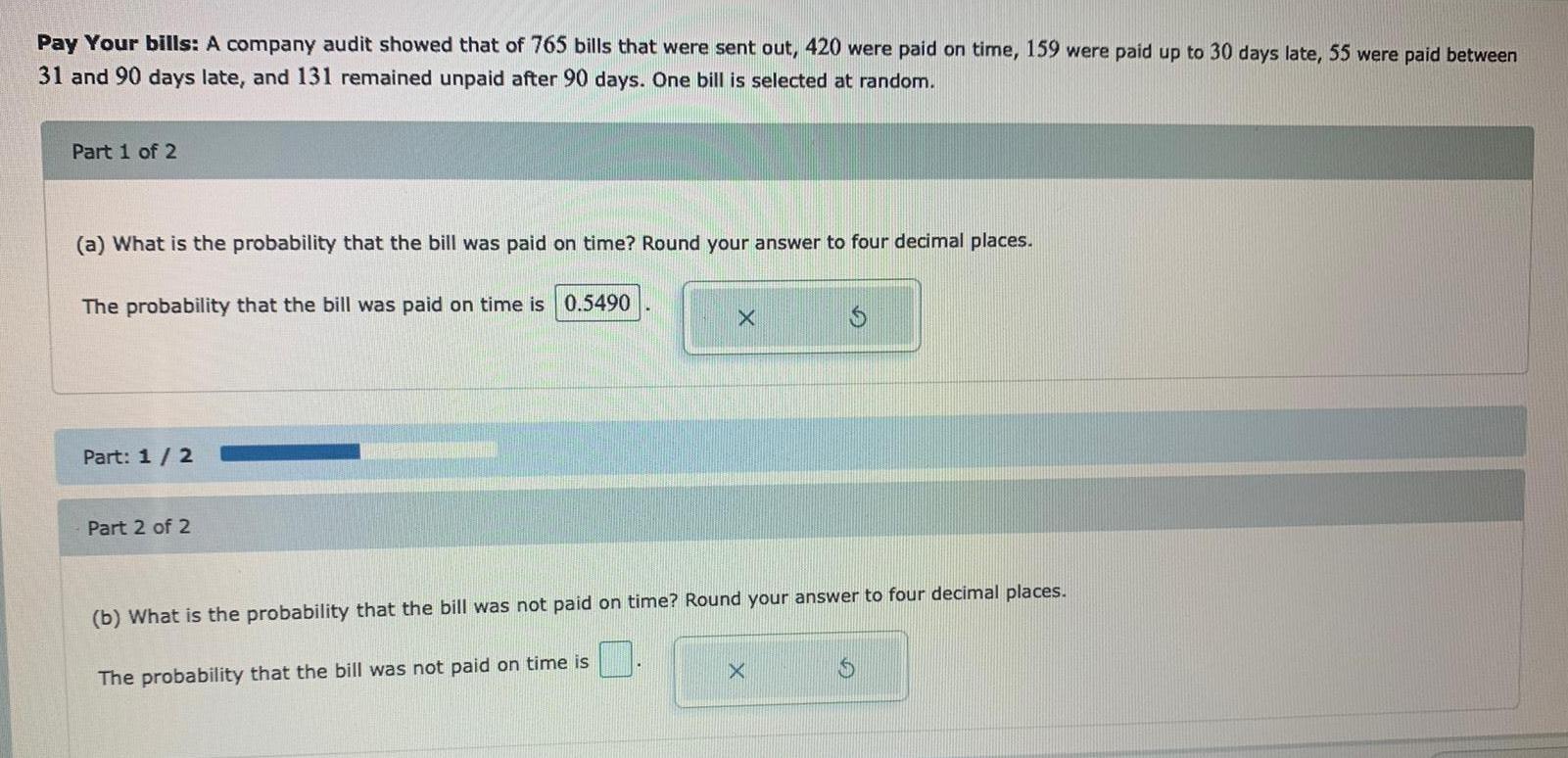
Statistics
ProbabilityPay Your bills: A company audit showed that of 765 bills that were sent out, 420 were paid on time, 159 were paid up to 30 days late, 55 were paid between 31 and 90 days late, and 131 remained unpaid after 90 days. One bill is selected at random.
(a) What is the probability that the bill was paid on time? Round your answer to four decimal places.
The probability that the bill was paid on time is
(b) What is the probability that the bill was not paid on time? Round your answer to four decimal places.
The probability that the bill was not paid on time is

Statistics
ProbabilityTrue-false exam: A section of an exam contains four true-false questions. A completed exam paper is selected at random, and the four answers are recorded. Round your answers to four decimal places if necessary.
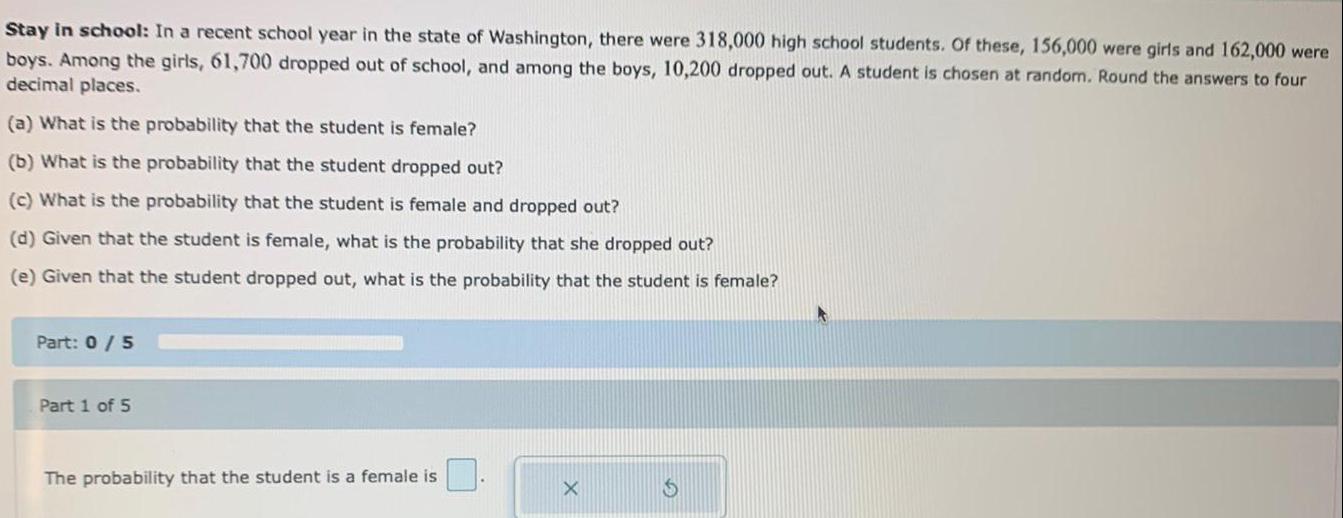
Statistics
ProbabilityStay in school: In a recent school year in the state of Washington, there were 318,000 high school students. Of these, 156,000 were girls and 162,000 were boys. Among the girls, 61,700 dropped out of school, and among the boys, 10,200 dropped out. A student is chosen at random. Round the answers to four decimal places.
(a) What is the probability that the student is female?
(b) What is the probability that the student dropped out?
(c) What is the probability that the student is female and dropped out?
(d) Given that the student is female, what is the probability that she dropped out?
(e) Given that the student dropped out, what is the probability that the student is female?
The probability that the student is a female is

Statistics
ProbabilityAssume that a fair die is rolled. The sample space is {1, 2, 3, 4, 5, 6}, and all the outcomes are equally likely. Find P (less than 2). Write your answer as a fraction or whole number.
P (less than 2) =

Statistics
ProbabilityThe average time it takes college freshmen to complete the Mason Basic Reasoning Test is 38.3 minutes. The standard deviation is 32 minutes. Assume the variable is normally distributed.
Find the probability that it will take a student between 30 and 45 minutes to complete the test.
a.0.021
b.0.9769
c.0.7255
d.0.2745

Statistics
ProbabilityA student answered 76 out of 100 homework questions correctly on the first try. What percent of homework questions were answered correctly on the first try?
The student answered% of homework corrections correctly on the first try