Differential equations Questions and Answers
Calculus
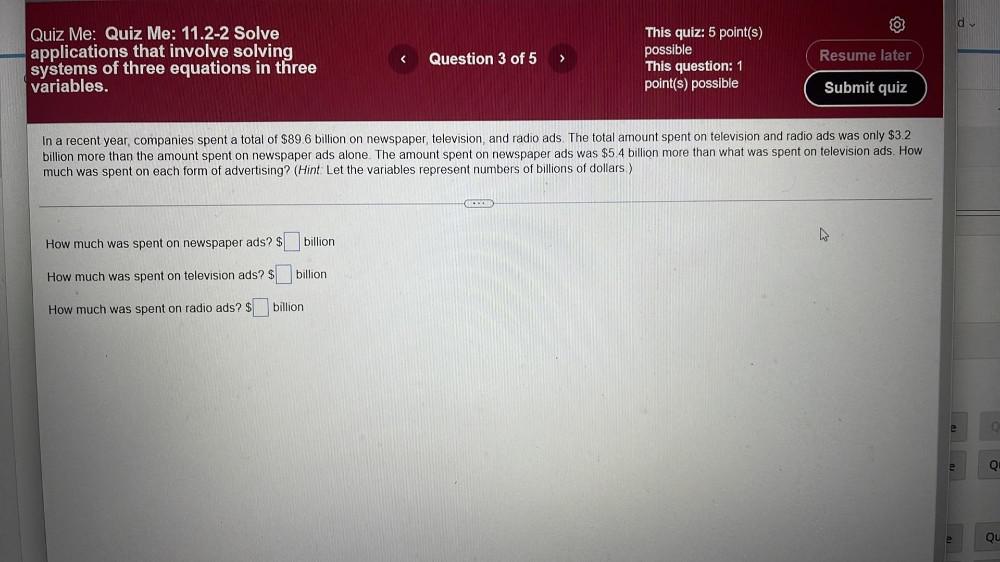
Differential equationsIn a recent year, companies spent a total of $89.6 billion. on newspaper, television, and radio ads. The total amount spent on television and radio ads was only $3.2 billion more than the amount spent on newspaper ads alone. The amount spent on newspaper ads was $5.4 billion more than what was spent on television ads. How much was spent on each form of advertising? (Hint: Let the variables represent numbers of billions of dollars.)
How much was spent on newspaper ads? $____ billion
How much was spent on television ads? $____ billion
How much was spent on radio ads? $____ billion

Calculus
Differential equationsGiven the function f(x)=3x³ (x²-2)(x+4), find the following:
a. The real zeros and the multiplicity of each (you may or may not need all blanks, just fill in what is needed).
ZERO:______ , _____ , ______ , ______
MULTIPLICITY:______ , _____ , ______ , ______

Calculus
Differential equationsLet's say we want to find the final grades for 3 girls, and we know what their averages are for tests, projects, homework, and quizzes.
Student Tests Projects Homework Quizzes
Alexandra 92 100 89 80
Megan 72 85 80 75
Brittney 88 78 85 92
We also know that tests are 65% of the grade, projects 10%, homework 5%, and quizzes 20%.
(A) Create three matrices. One for the categories (table above), one for their weights (sentence above) and one for their final grades. Label rows and columns on all three.
(B) What does 78 represent in your matrix above? Be specific.
(C) What was Brittney's final grade?
Calculus
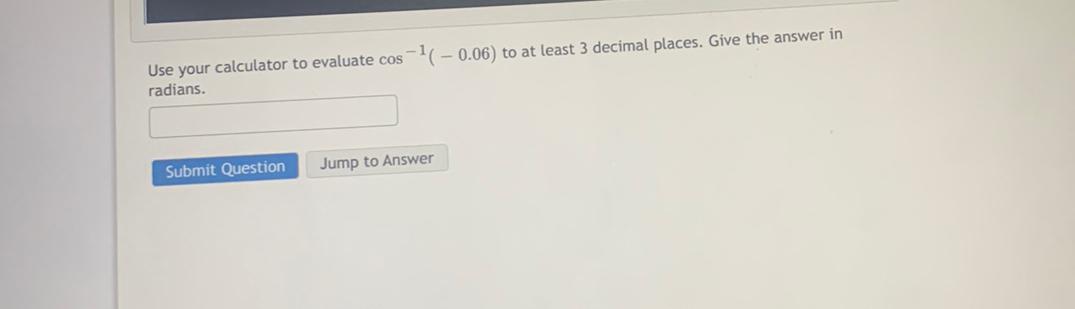
Differential equationsUse your calculator to evaluate cos‾¹(-0.06) to at least 3 decimal places. Give the answer in radians.
Calculus
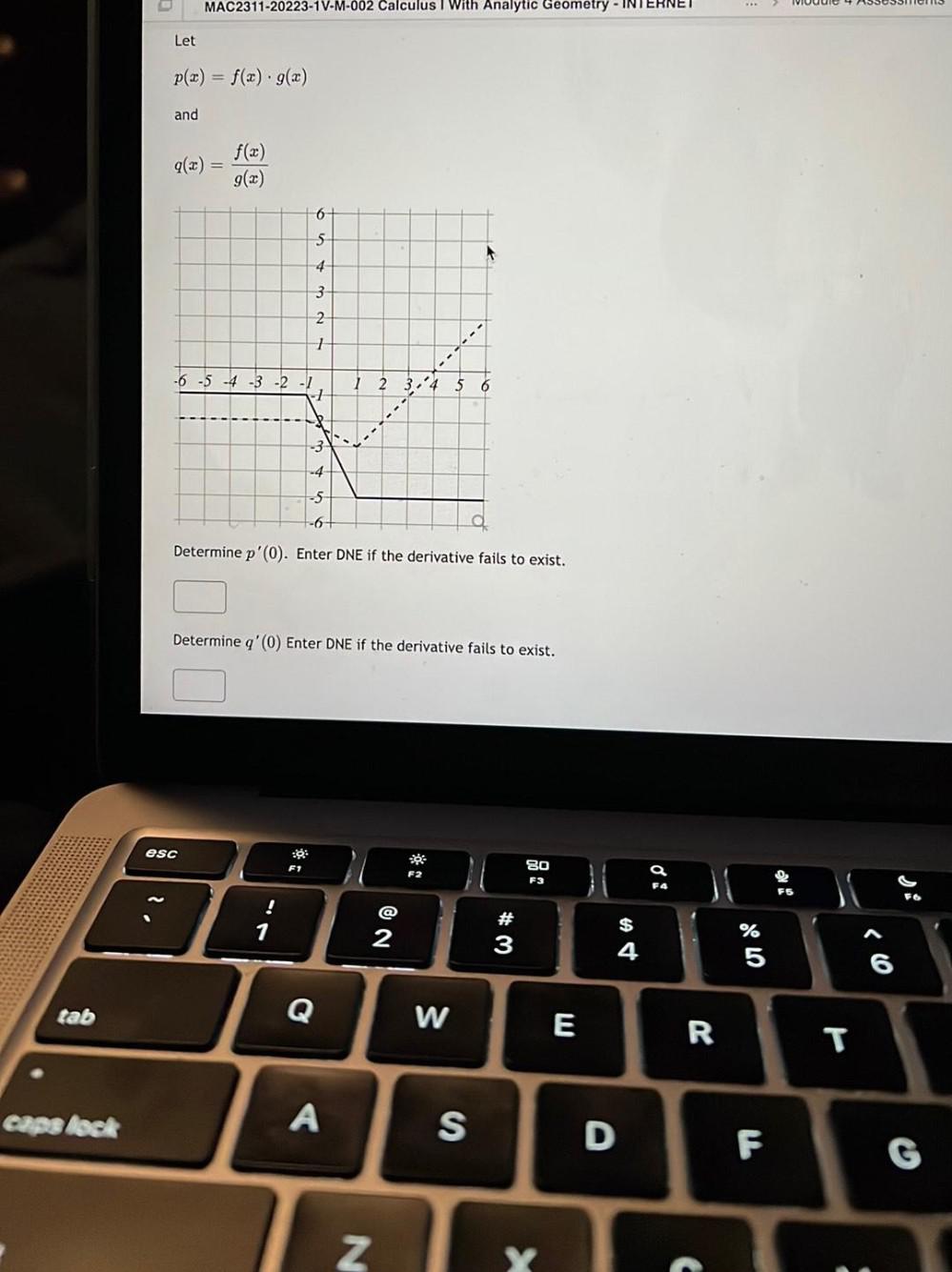
Differential equationsDetermine p'(0). Enter DNE if the derivative fails to exist.
Determine q'(0) Enter DNE if the derivative fails to exist.

Calculus
Differential equationsSolve the non homogeneous linear differential equations.
y"'-3y" + 3y' - y = x - 4e^x
Calculus
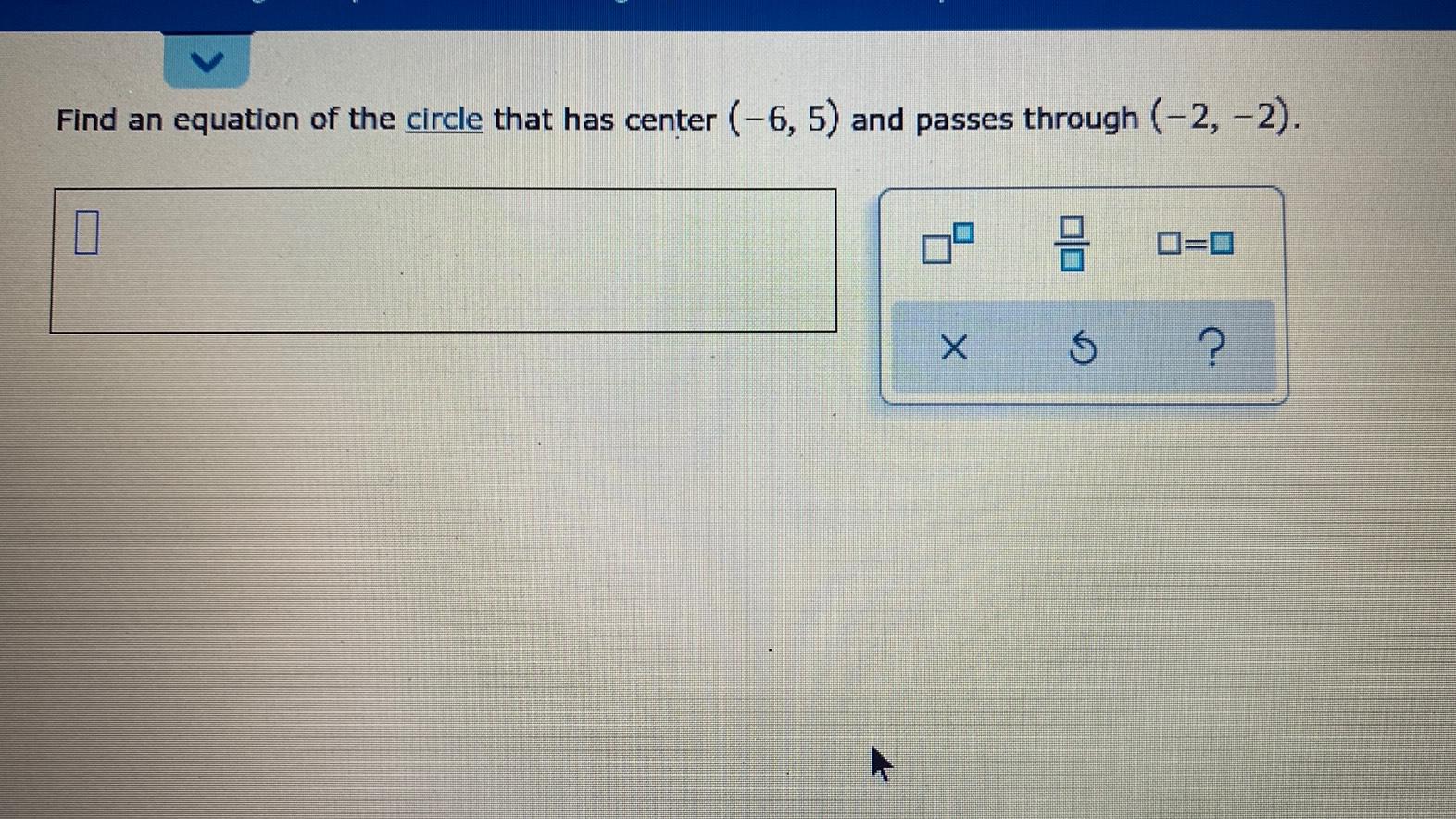
Differential equationsFind an equation of the circle that has center (-6, 5) and passes through (-2,-2).
Calculus
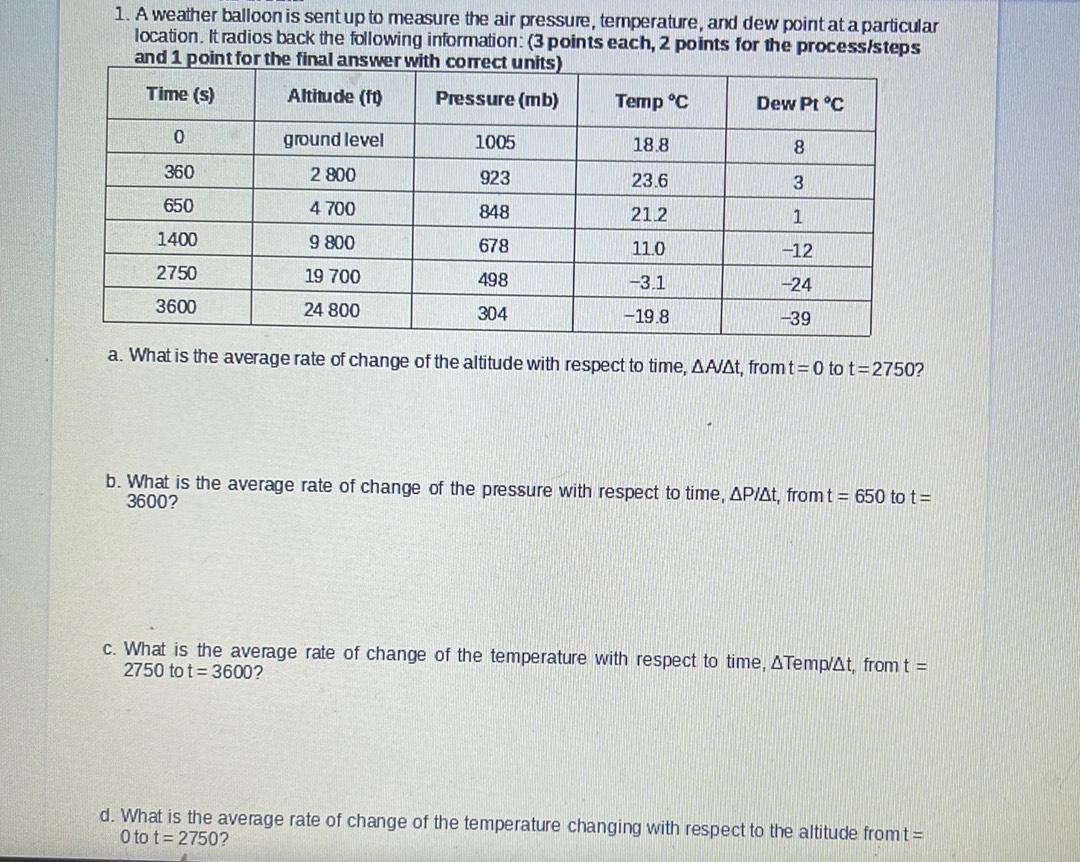
Differential equationsA weather balloon is sent up to measure the air pressure, temperature, and dew point at a particular location. It radios back the following information:
Time (s) Altitude (ft) Pressure (mb) Temp °C Dew Pt °C
0 ground level 1005 18.8 8
360 2 800 923 23.6 3
650 4 700 848 21.2 1
1400 9 800 678 11.0 -12
2750 19 700 498 -3.1 -24
3600 24 800 304 -19.8 -39
a. What is the average rate of change of the altitude with respect to time, △A/△t, from t=0 to t=2750?
b. What is the average rate of change of the pressure with respect to time, △P/△t, from t = 650 to t = 3600?
c. What is the average rate of change of the temperature with respect to time, △Temp/△t, from t = 2750 to t = 3600?
d. What is the average rate of change of the temperature changing with respect to the altitude from t = 0 to t = 2750?

Calculus
Differential equationsDetermine the value(s) of the constant k for which the following system of equations has
a). no solutions
b). one solution
c). infinitely many solutions
x + y = 6
2x + 2y = k
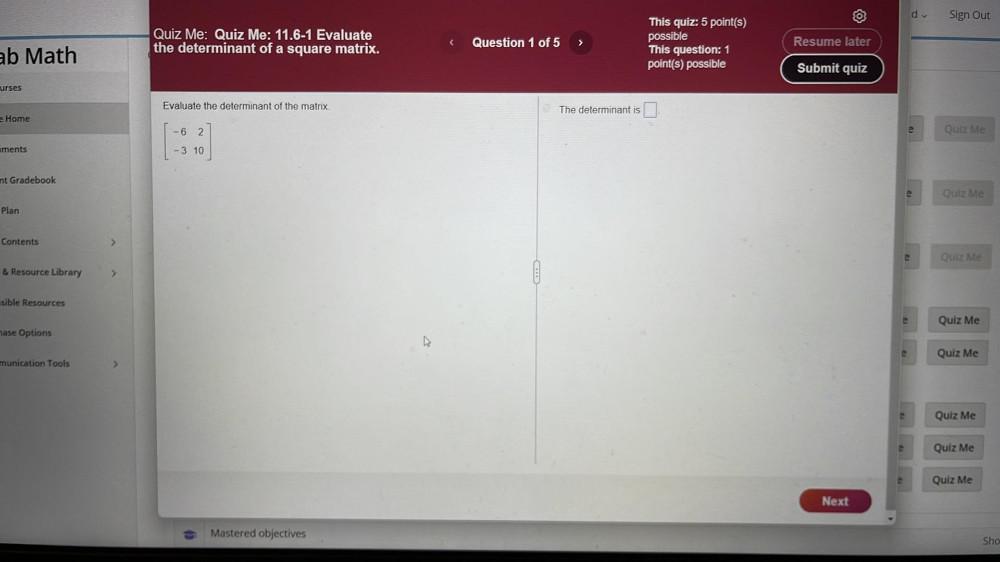

Calculus
Differential equationsWhat is the discriminant of 6x2 - 2x - 3=0
(a)76
(b)68
(c)29
(d)none of these

Calculus
Differential equationsSolve each of the following initial value problems:
(a) y'₁ = y₁+ 2y₂
y₂ = 2y₁ - y₂ ends A and B are fixed
y₁ (0) = 3, y₂(0) = 1 babe three springs are
(b) y₁ = y₁ - 2y₂ position. A force is exerted
y₂ = 2y₁ + y₂
y₁ (0) = 1, y₂(0) = -2
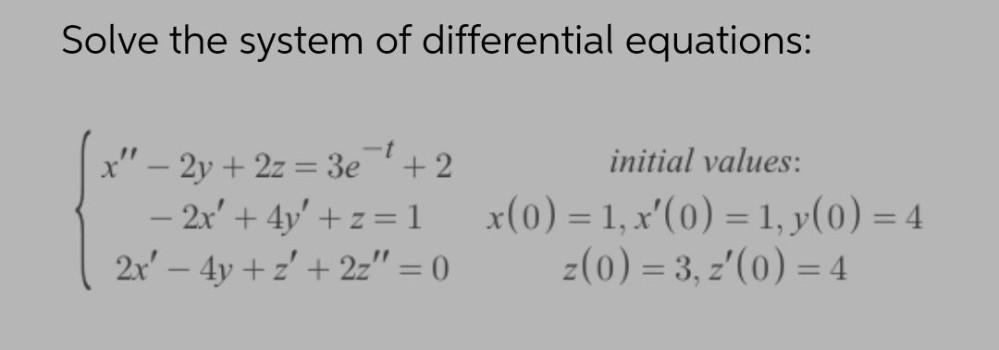
Calculus
Differential equationsSolve the system of differential equations:
x" - 2y + 2z = 3e^-t +2. initial values:
- 2x' + 4y' +z=1. x(0) = 1, x'(0)=1,y(0)=4
2x'-4y+z'+2z"=0 Z(0)=3,z'(0)= 4

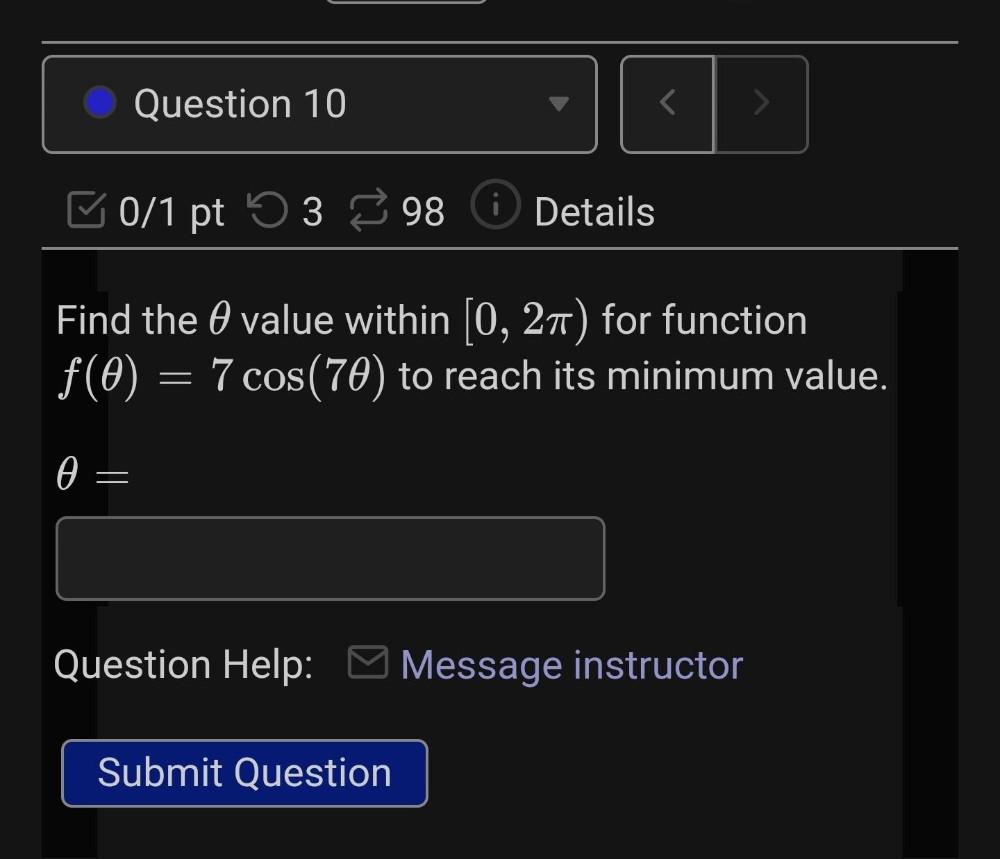
Calculus
Differential equationsFind the value within [0, 2π) for function f(θ) = 7 cos(7θ) to reach its minimum value.
θ=

Calculus
Differential equationsConsider the differential equation:
f'(x) = 3x + 1
1. Find the general solution for f(x).
2. Find the solution for the differential equation with the initial condition f(0) = 2.
3. Find the solution for the differential equation with the initial condition f(0) = -1. Graph both solutions.
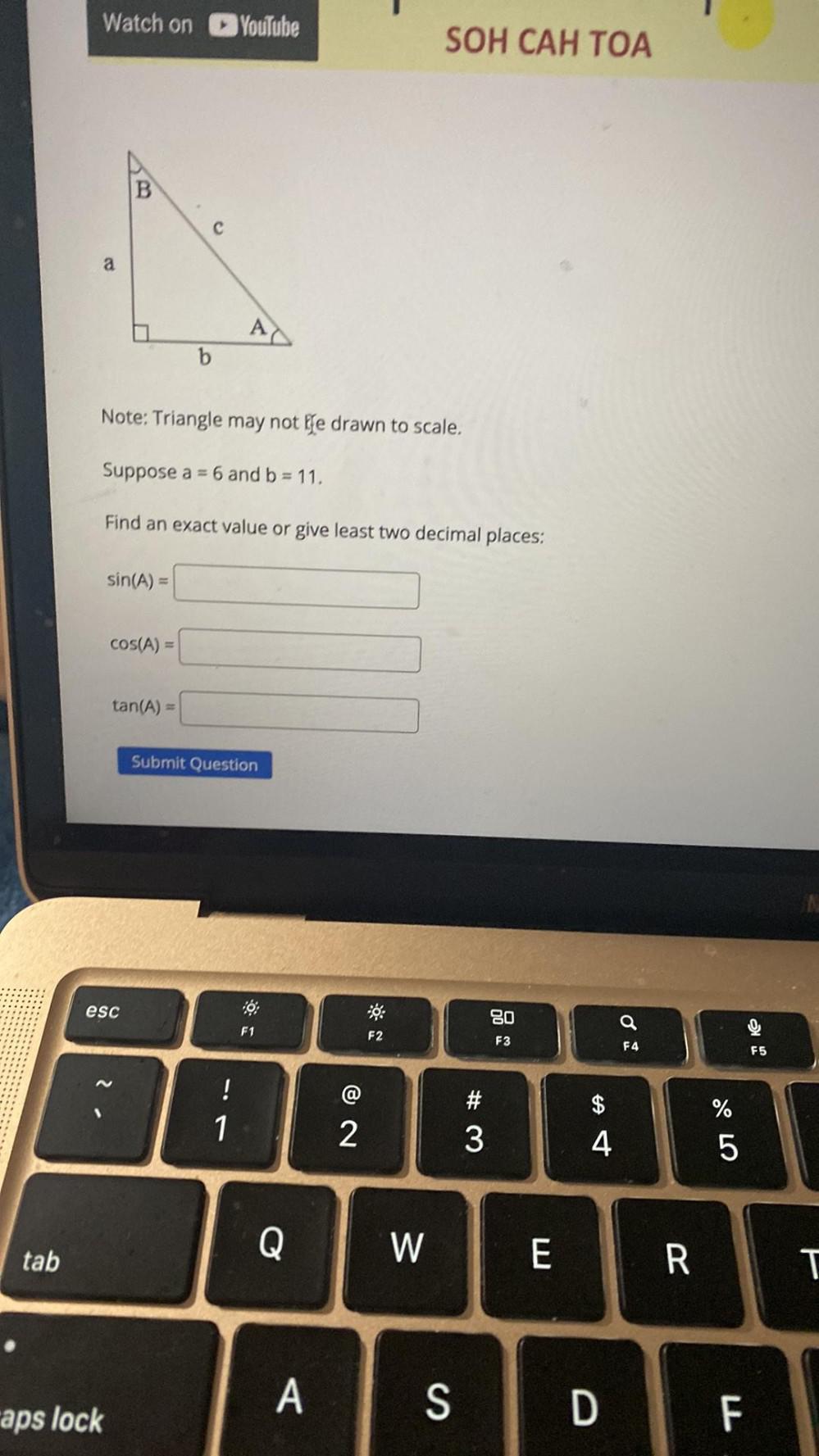
Calculus
Differential equationsSuppose a = 6 and b = 11.
Find an exact value or give least two decimal places:
sin(A) =
cos(A) =
tan(A) =

Calculus
Differential equationsTwo sides and an angle are given. Determine whether the given information results in one triangle, two triangles, or no triangle at all. Solve any triangle(s) that results.
B = 44°, b = 6, a = 31

Calculus
Differential equationsA man has 6 shirts and 5 ties. How many different shirt and tie arrangements can he wear? He can wear _______ different shirt and tie arrangements.
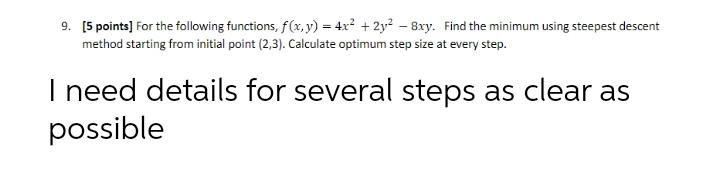
Algebra
Differential equationsFor the following functions, f(x,y) = 4x² + 2y2 – Bxy. Find the minimum using steepest descent method starting from initial point (2,3). Calculate optimum step size at every step.

Calculus
Differential equationsIf you make $2000 in Gross Income every month, but 35% is taken out in taxes, what will your monthly Net Income paycheck be?
a) $1200
b) $1675
c) $1300

Calculus
Differential equationsAt a computer store, a customer is considering 7 different computers, 8 different monitors, 9 different printers and 3 different scanners. Assuming that each of the components is compatible with one another and that one of each is to be selected, determine the number of different computer systems possible.
There are ___ different computer systems possible.

Calculus
Differential equationsUse the algorithm for Euler's method to determine approximations to the solution to the initial value problem
y' = 3x²(y + 2),0≤x≤ 1,y(0) = 1 h = 0.2
And compare these with the exact values given by y(x) = 3eˣ(³) - 2
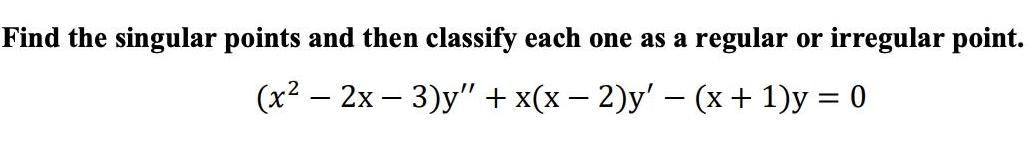
Calculus
Differential equationsFind the singular points and then classify each one as a regular or irregular point.
(x² - 2x - 3)y" + x(x − 2)y' - (x + 1)y=0

Calculus
Differential equationsAdmission into an amusement park for 4 children and 2 adults is $116.90. For 6
children and 3 adults, the admission is $175.35. Assuming a different price for
children and adults, what is the price of the child's ticket and the price of the adult
ticket?

Calculus
Differential equationsSketch the region of integration and change the order of integration
∫²₂ ∫√4-2²_0 f(x,y) dydx

Calculus
Differential equationsFind the dimensions of an open rectangular box of maximum volume and having an area of 48 ft² that can be constructed from a piece of cardboard. (Let / represent the length in feet, w the width in feet, and h the height in feet of the box.)
What is the volume of the box?

Calculus
Differential equationsFind equations of the tangent plane and the normal line to the given surface at the specified point.
x+y+z= 8exyz, (0, 0, 8)
(a) the tangent plane
(b) the normal line
(x(t), y(t), z(t)) =
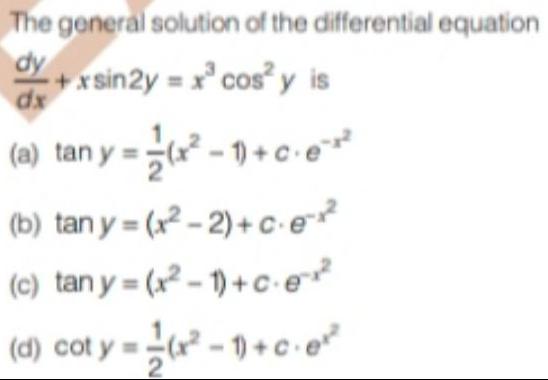
Calculus
Differential equationsThe general solution of the differential equation
dy dx + xsin2y = x³cos²y is
(a) tan y=(x²-1)+c.e²
(b) tan y=(x²-2)+c.e-x²
(c) tan y=(x²-1)+ c·e-x²
(d) cot y =(x²-1)+cex²


Calculus
Differential equationsTraffic signs re regulated by the Manual on Uniform Traffic Control Devices (MUTCD). The perimeter of a rectangular traffic sign is 104 inches. Also, its length is 8 inches longer than its width. Find the dimensions of this sign.
What is the length of the sign?
The length of the sign is

Calculus
Differential equations4. The top eyeglass retailers last year were XrayVision, YesSpecs and ZoomGlasses. Together, they accounted for 69% of total market sales. The combined share of Xray Vision and YesSpecs was twice the share of ZoomGlasses, and the share of Xray Vision is less than the combined share of ZoomGlasses and YesSpecs by 55.
What was the market share of each of the three companies?
Xray Vision:
YesSpecs:
ZoomGlasses:

Calculus
Differential equationsAssume that f(-1)= -2. Assume also that the graph of y=f(x) is symmetric with respect to the line x=2. Find another value for the function.

Calculus
Differential equationsThe general solution of the differential equation
xy' = y + √x² + y² for x > 0
is given by (with an arbitrary positive constant k)
(A) ky² = x + √x² + y²
(B) kx² = x + √x² + y²
(C) kx²=y+√x² + y²
(D) ky² = y + √x² + y²

Calculus
Differential equationsUse variation of parameters to find a general solution to the differential equation given that the functions y₁ and y₂ are linearly independent solutions to the corresponding homogeneous equation for t> 0.
ty" -(t+1)y' +y=3t³; y₁=e^ t, Y₂=t+1
A general solution is y(t) =c₁ e^ t+ c₂(t+1)-3t²
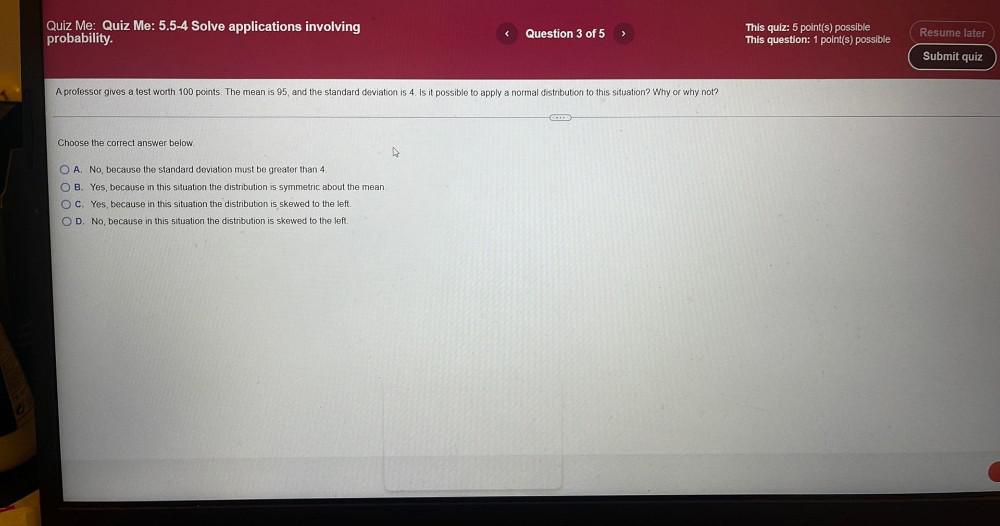
Calculus
Differential equationsA professor gives a test worth 100 points. The mean is 95, and the standard deviation is 4. Is it possible to apply a normal distribution to this situation? Why or why not?
Choose the correct answer below.
A. No, because the standard deviation must be greater than 4.
B. Yes, because in this situation the distribution is symmetric about the mean.
C. Yes, because in this situation the distribution is skewed to the left.
D. No, because in this situation the distribution is skewed to the left.
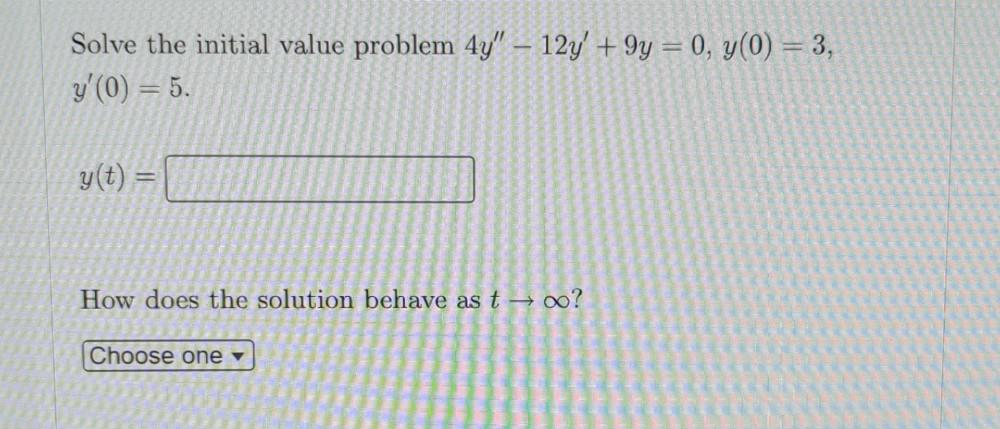
Calculus
Differential equationsSolve the initial value problem 4y" - 12y' +9y = 0, y(0) = 3,
y'(0) = 5.
y(t)=
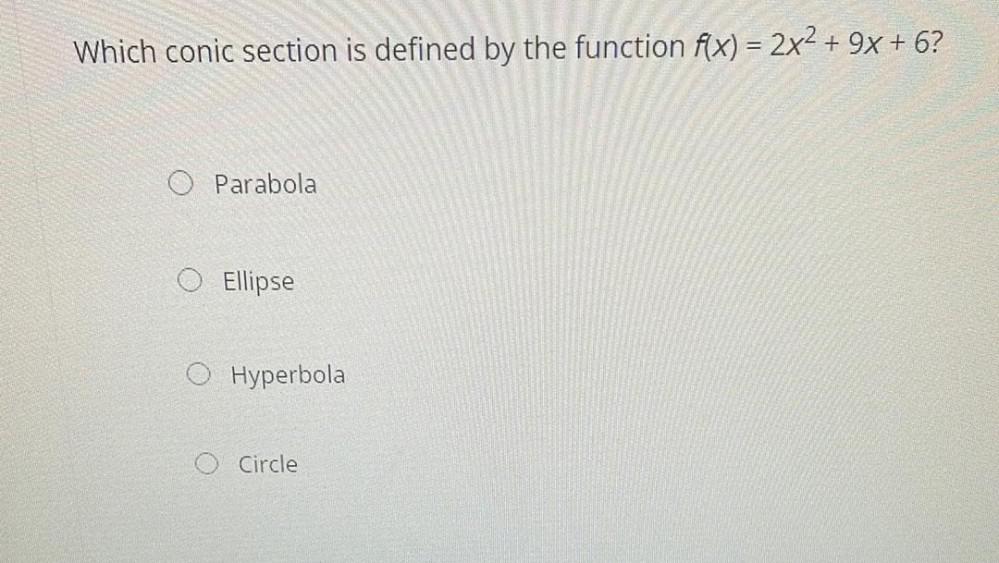
Calculus
Differential equationsWhich conic section is defined by the function f(x) = 2x² + 9x + 6?
Parabola
Ellipse
Hyperbola
Circle
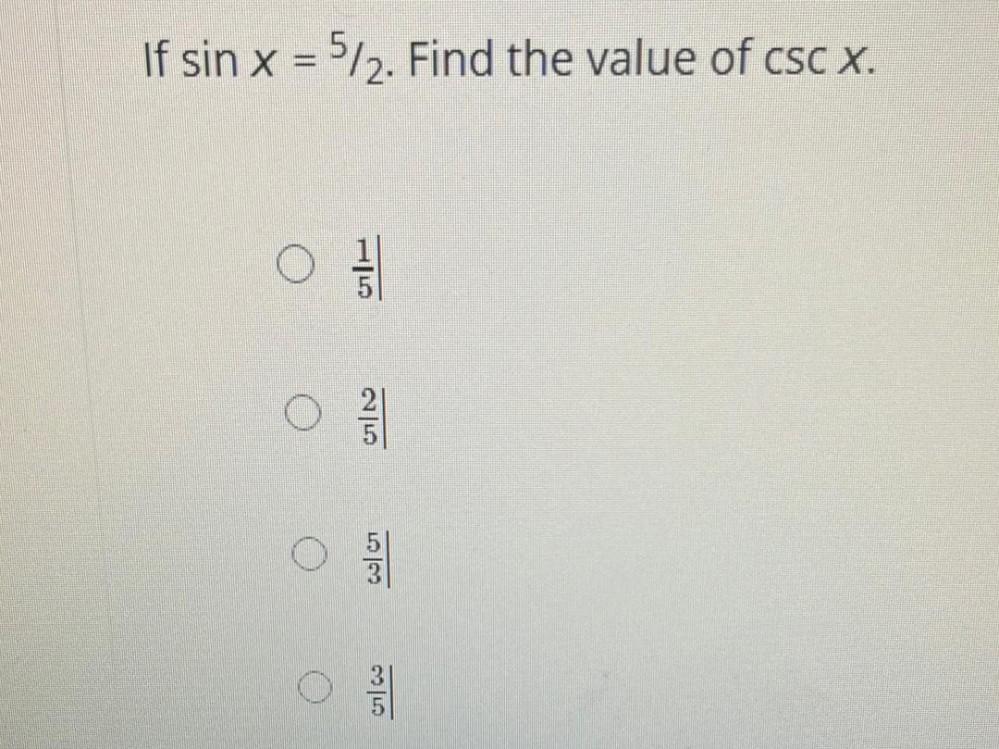
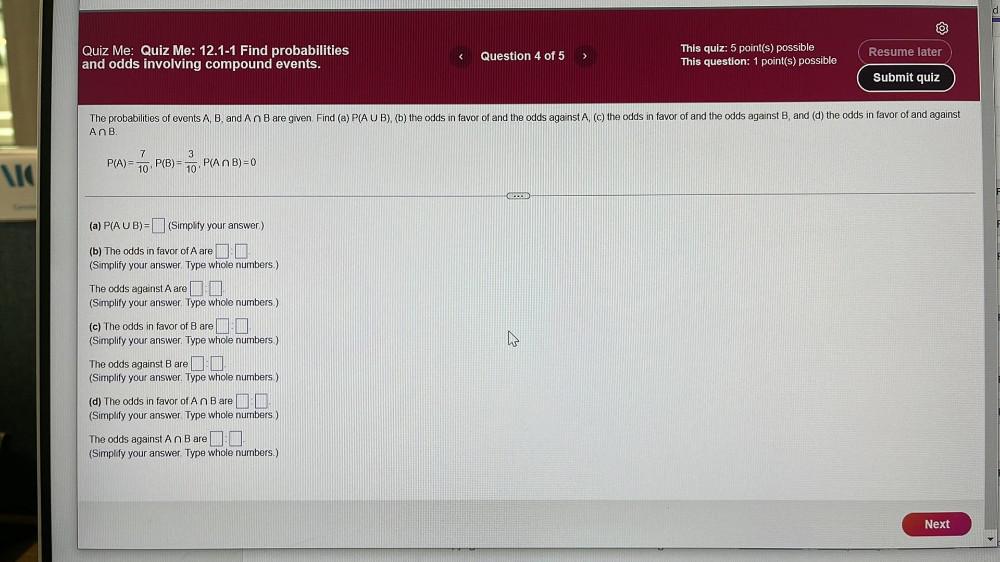
Calculus
Differential equationsThe probabilities of events A, B, and An B are given. Find (a) P(A U B), (b) the odds in favor of and the odds against A, (c) the odds in favor of and the odds against B, and (d) the odds in favor of and against A⋂B.
P(A) = 7/10, P(B) = 3/10, P(A⋂B)=0
(a) P(A U B) =
(Simplify your answer.)
(b) The odds in favor of A are
(Simplify your answer. Type whole numbers.)
The odds against A are
(Simplify your answer. Type whole numbers.)
(c) The odds in favor of B are
(Simplify your answer. Type whole numbers.)
The odds against B are
(Simplify your answer. Type whole numbers.)
(d) The odds in favor of An B are ☐☐
(Simplify your answer. Type whole numbers.)
The odds against An B are:
(Simplify your answer. Type whole numbers.)
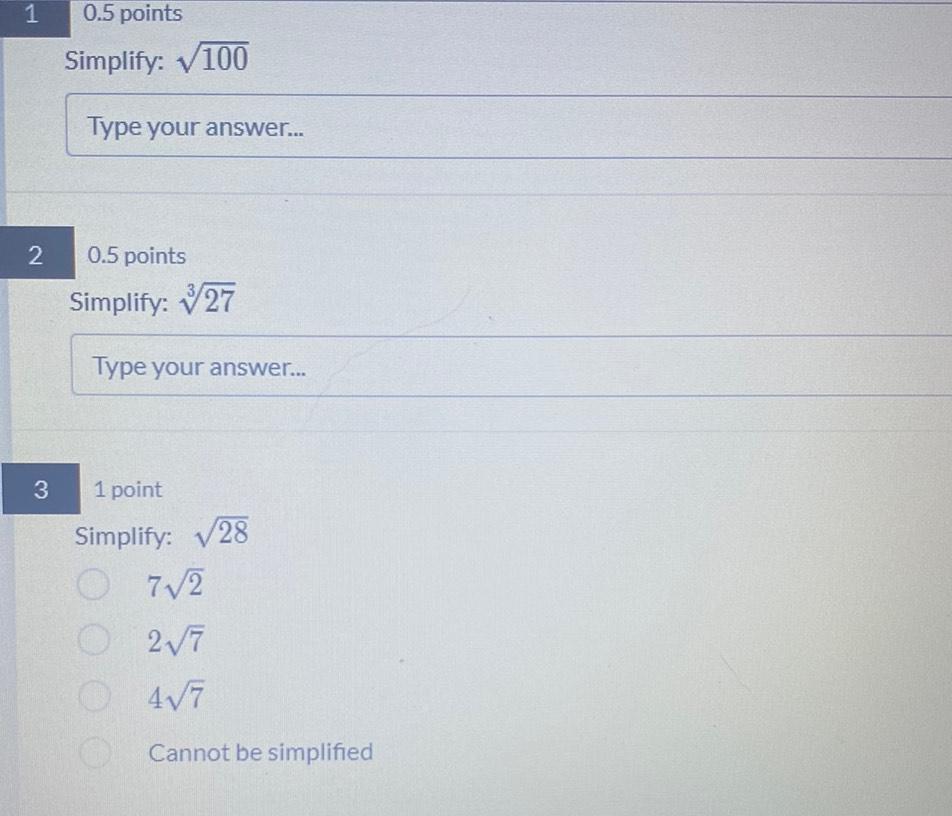
Calculus
Differential equationsSimplify: √100
Type your answer...
Simplify: ∛27
Type your answer...
Simplify: √28
7√2
2√7
4√7
Cannot be simplified

Calculus
Differential equationsDetermine whether the given equation is exact. If it is exact, solve.
(2xy²-3) dx +(4+2x²y)dy=0
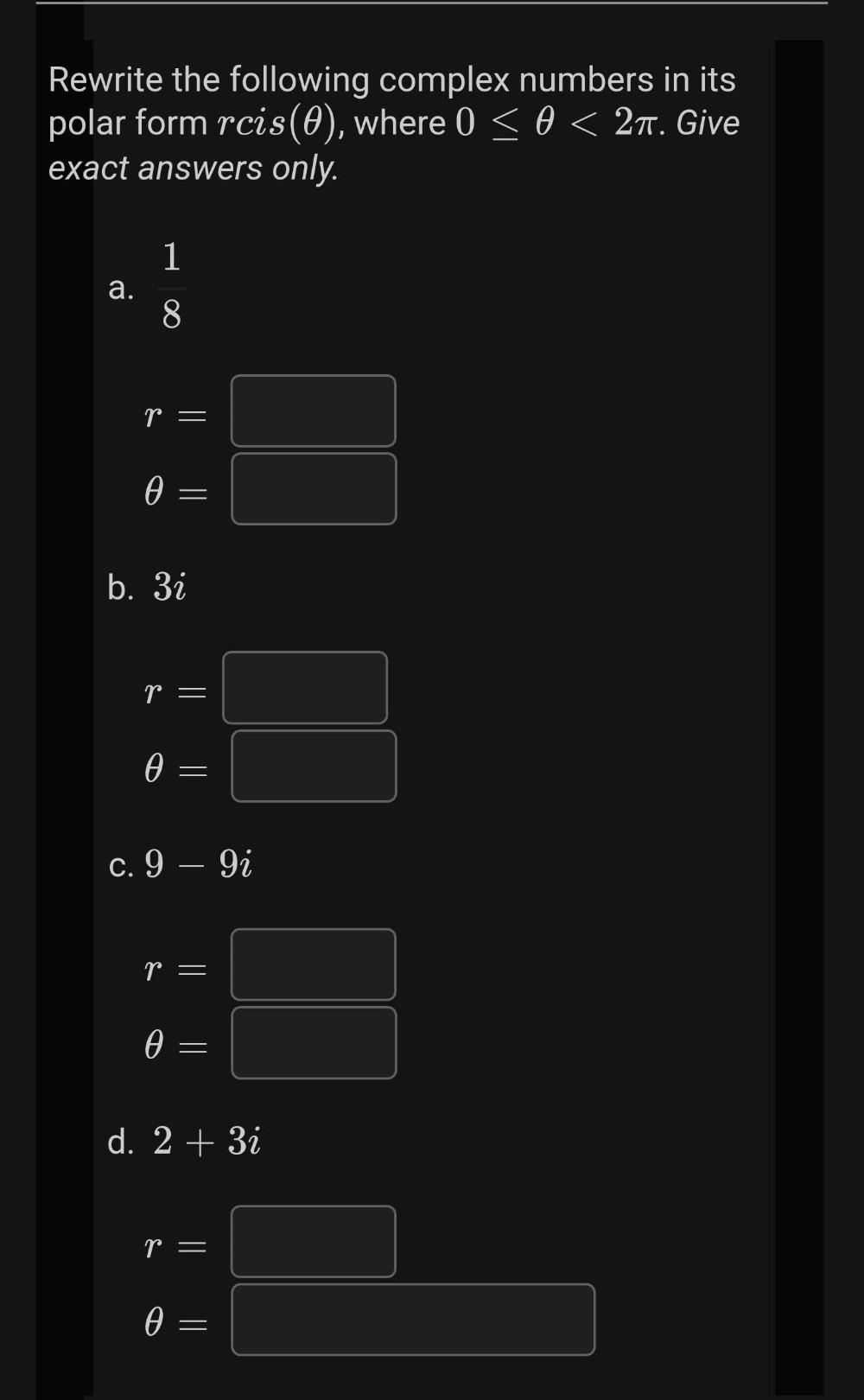
Calculus
Differential equationsRewrite the following complex numbers in its polar form rcis (θ), where 0 ≤ θ < 2π. Give exact answers only.
a. 1/8
r =
θ =
b. 3i
r =
θ =
c. 9 - 9i
r =
θ =
d. 2 + 3i
r =
θ =

Calculus
Differential equationsSolve the homogeneous system
x₁ +x3 +x4=0
x₂ +x3=0
x3+x4=0
by transforming the coefficient matrix (whose columns follow the order: x₁, x2, x3, x4) to r.r.e.f (otherwise, you may obtain a wrong answer).
Hint: Use the following free variables in order, if needed, t, s, w.
Answer: Don't leave spaces between symbols, letters, and numbers.

Calculus
Differential equationsUse trigonometric identities to establish the identity: tan(t) + cot(t) = 1/(sin(t) cos(t))
This question requires a file submission, so I am asking you to show at least 3 steps to get full credit.

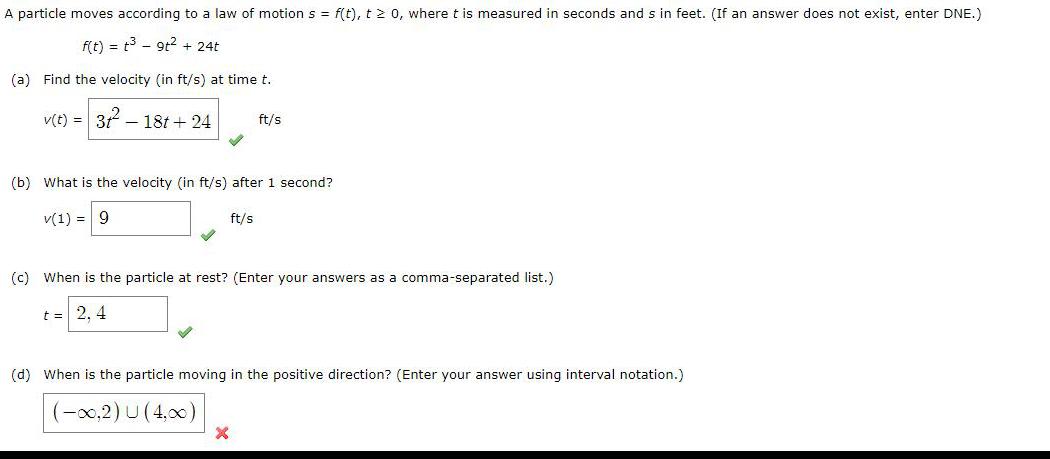
Calculus
Differential equationsA particle moves according to a law of motion s = f(t), t≥ 0, where t is measured in seconds and s in feet. (If an answer does not exist, enter DNE.)
f(t) = t³ 9t² + 24t
(a) Find the velocity (in ft/s) at time t.
v(t) = 3² 18t + 24
(b) What is the velocity (in ft/s) after 1 second?
v(1) = 9 ft/s
(c) When is the particle at rest? (Enter your answers as a comma-separated list.)
t = 2,4
(d) When is the particle moving in the positive direction? (Enter your answer using interval notation.)
(-∞0,2) U (4,00)

Calculus
Differential equationsFind the exact values of sin(x/2), cos(x/2) and tan(x/2) without solving for x.
If sec z=-7, and a is in quadrant 2.
sin(x/2)
cos(x/2)
tan(x/2)
![Find the general lower and upper sums (in terms of n) of the area of the region bounded by the x-axis and g(x) = 20x over [7, 8].
Lower Sum:
Upper Sum:
Determine the lower and upper sum when [7, 8] is divided into 10 subintervals.
Lower Sum:
Upper Sum:
Determine the lower and upper sum when [7, 8] is divided into 100 subintervals.
Lower Sum:
Upper Sum:
Determine the lower and upper sum when [7, 8] is divided into 1000 subintervals.
Lower Sum:
Upper Sum:
Use the above progression of lower and upper sums to determine the exact area of the region.
Net Area =](https://media.kunduz.com/media/sug-question/raw/84602296-1658660087.421247.jpeg?w=256)
Calculus
Differential equationsFind the general lower and upper sums (in terms of n) of the area of the region bounded by the x-axis and g(x) = 20x over [7, 8].
Lower Sum:
Upper Sum:
Determine the lower and upper sum when [7, 8] is divided into 10 subintervals.
Lower Sum:
Upper Sum:
Determine the lower and upper sum when [7, 8] is divided into 100 subintervals.
Lower Sum:
Upper Sum:
Determine the lower and upper sum when [7, 8] is divided into 1000 subintervals.
Lower Sum:
Upper Sum:
Use the above progression of lower and upper sums to determine the exact area of the region.
Net Area =
