Application of derivatives Questions and Answers

Calculus
Application of derivativesA fence must be built to enclose a rectangular area of 5000 ft2 Fencing material costs 1 per foot for the two sides facing north and south and 2 per foot for the other two sides Fin the cost of the least expensive fence The cost of the least expensive fence is

Calculus
Application of derivativesA fence must be built to enclose a rectangular area of 5000 ft Fencing material costs 3 per foot for the two sides facing north and south and 6 per foot for the other two sides Find the cost of the least expensive fence The cost of the least expensive fence is Simplify your answer

Calculus
Application of derivativesA baseball diamond has the shape of a square with sides 90 feet long see figure A player running from second base to third base at a speed of 27 feet per second is 24 feet from third base At what rate in ft sec is player s distance from home plate changing Round your answer to two decimal places 3rd ft sec Home

Calculus
Application of derivativesUse a calculator to make a table to approximate the following limit Confirm your result with l H pital s Rule lim 1 3h h 0 Complete the table below Round to four decimal places as needed h 10 1 10 2 1 h 10 10 4 1 3h h h 10 1 2 10 10 10 4 3 1 1 3h



Calculus
Application of derivativesSolve each equation for A Solve In 11x 1 5 for x 0 B Solve e 8 1 3 for x x 3
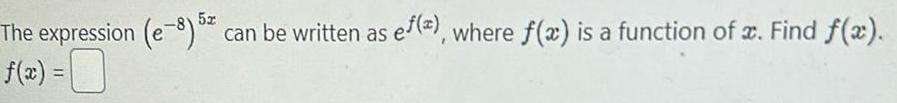
Calculus
Application of derivativesThe expression e 8 52 can be written as ef 2 where f a is a function of x Find f x f x 0

Calculus
Application of derivativesGiven functions Find 3x g x x 6 h x h x a hog x b State the domain in interval notation x

Calculus
Application of derivatives5 4 M 2 3 2 3 The minimum degree of the polynomial is 2 The minimum degree of the polynomial is 3 The minimum degree of the polynomial is 4 The minimum degree of the polynomial is 5 The minimum degree of the polynomial is 6 The leading coefficient is positive The leading coefficient is negative Based on the end behavior the polynomial is odd Based on the end behavior the polynomial is even


Calculus
Application of derivativesThe monthly profit for a company that makes picture frames depends on the price per frame The company determines that the profit is approximated by P x 50x 80 000x 2500 where x is the price per frame and P x is the monthly profit based on that price Find the price that generates the maximum profit

Calculus
Application of derivatives20 0 mL of water from a graduated cylinder is added to a beaker of water as shown below What is the new volume of water in the beaker 40 40 0 35 35 0 50 mL 40 mL 30 mL 20 mL 10 mL

Calculus
Application of derivativesA chunk of sulfur has a volume of 5 95 cm What is the mass of this sulfur Density of sulfur 2 07 g cm 0 348 g O 2 87 g O 3 88 g

Calculus
Application of derivativesPerform the following conversion 6 69 m s 1h 60 minutes 60 seconds 1 minute 1km 1 609 mi 1km 1000m O 0 334 mi h 15 0 mi h O249 mi h 13 4 mi h mi h

Calculus
Application of derivativesFind the following Simplify your answers completely f x 6x 9 g x 4 x a f g x 5x 5 b f g x 7x 13 c fg x d f g x 6x 33x 36 6x 9 4 x What is the domain of f g Enter your answer using interval notation x 4

Calculus
Application of derivativesDetermine the area enclosed by the functions g x 4x 3 and f x 6 x 2x 2 between x 4 and x 2

Calculus
Application of derivativesCompare the graph of the function with the graph of its parent function y X 1 Oy 8 is f x horizontally stretched 8 fold X X Oy y 8 is f x shifted to the left 8 units X Oy 8 X 8 Oy 8 X Oy 8 is f x is f x is f x shifted to the right 8 units 1 shifted down 8 units X vertically stretched 8 fold X

Calculus
Application of derivativesCompare the graph of the function with the graph of its parent function y x The graph of y x is a vertical shrink of f x x The graph of y x is a reflection about the origin of the graph of f x x x is a reflection about either axis of the graph of f x x as f x f x x is a reflection in the x axis The graph of y The graph of y O The graph of y x is identical to the graph of f x x

Calculus
Application of derivatives35 Velocity Use the results of Problem 33 to find the horizontal distance travelec by the bullet in 3 seconds Neglect the resistance of air on the bullet

Calculus
Application of derivativesf x 6 3 2 using transformations Show the Vertical Asymptote and the y intercept 10pts Sketch

Calculus
Application of derivatives1 Analyze the following the polynomial f x x x 1 x 4 a Determine the degree of f x 2 points x x x 1 x u x4 x 1 x 4 x4 x x 4 X4x4x4 4 x x x 4 X5 4x4 x3 4x b What is the end behavior of f x 2 points 5 odd coet 1 Pos rise Answer c What are the zeros of f x and their multiplicities 2 points x x 1 x u 0 X 0 Multip 2 X multip 1 X UHP 1 x 4 Multip d What does each multiplicity of each zero found in c mean for the graph of f x 2 points x 41 0 x 4 0 Answer e What is the y intercept of f x 2 points Answer Answer 5 falls left fise fi x 0 12 x i ml X 1 MI X 4 MI

Calculus
Application of derivativesGiven the function f x x 6 a Find the inverse function f x f x State domains and ranges below using interval notation b1 Domain of original function f x b2 Range of original function f x c1 Domain of inverse function f 2 c2 Range of inverse function f x

Calculus
Application of derivatives0 Type an exalt answer Simplify your answer Type any angle measures in de tan 32


Calculus
Application of derivativesSimplify your answers Type exact answers using radicals as needed Use intege fractions for any numbers in the expression Rationalize any denominators csc 2190 2 sec 2190 cot 2190 3 Simplify your answers Type exact answers using radicals as needed Use intege fractions for any numbers in the expression Rationalize any denominators

Calculus
Application of derivativestan 0 1 0 pe an integer or a decimal Use a comma to separate answers as needed

Calculus
Application of derivatives3x 4 an ingles 0 your answer Type an exact answer using radicals as needed Rationalize all dene

Calculus
Application of derivativesBearing A boat leaves the harbor entrance and travels 25 miles in the direction N 42 E The captain then turns the boat 90 and travels another 18 miles in the direction S 48 E At that time how far is the boat from the harbor entrance and what is the bearing of the boat from the harbor entrance See Figure 18 N 42 S 25 mi N 48 S FIGURE 18 18 mi

Calculus
Application of derivativesProblem 5 Determine which of the following series converge 77 1 5 2 n 4n n8 8n 6 n 1 n 3n n n A none of them B iii only C i and iii only D all of them E i only F i and G ii and iii only H ii only

Calculus
Application of derivativesLet f x be the number in thousands of computers sold when the price is x hundred dollars per computer Interpret the statements f 25 30 and f 25 6 Then estimate the number of computers sold if the price is set at 2525 pe computer What does f 25 30 imply OA When the price per computer is 2500 for every 100 price increase the sales increase by 30 000 computers OB When the price per computer is 3000 for every 100 price increase the sales increase by 25 000 computers OC 30 000 computers are sold when the price is set at 250 OD 30 000 computers are sold when the price is set at 2500

Calculus
Application of derivativesLet f t be the temperature of a cup of coffee t minutes after it has been poured Interpret f 5 180 and f 5 8 Estimate the temperature of the coffee after 5 minutes and 12 seconds that is after 5 2 minutes What does f 5 180 imply OA 5 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 180 degrees per minute OB 180 minutes after the coffee has been poured the temperature of the cup of coffee is 5 degrees OC 5 minutes after the coffee has been poured the temperature of the cup of coffee is 180 degrees OD 180 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 5 degrees per minute

Calculus
Application of derivativesAy 500 500 000 500 000 500 000 00 0 0 2 4 6 8 10 12 14 16 18 Years after 1980 e blue curve shows national health expenditures in billions of dollars The red curve shows its ivative C National health expenditures in billions of dollars from 1980 to 1997 are given by the function f t in the graph to the left a How much money was being spent at the beginning of 1982 billion
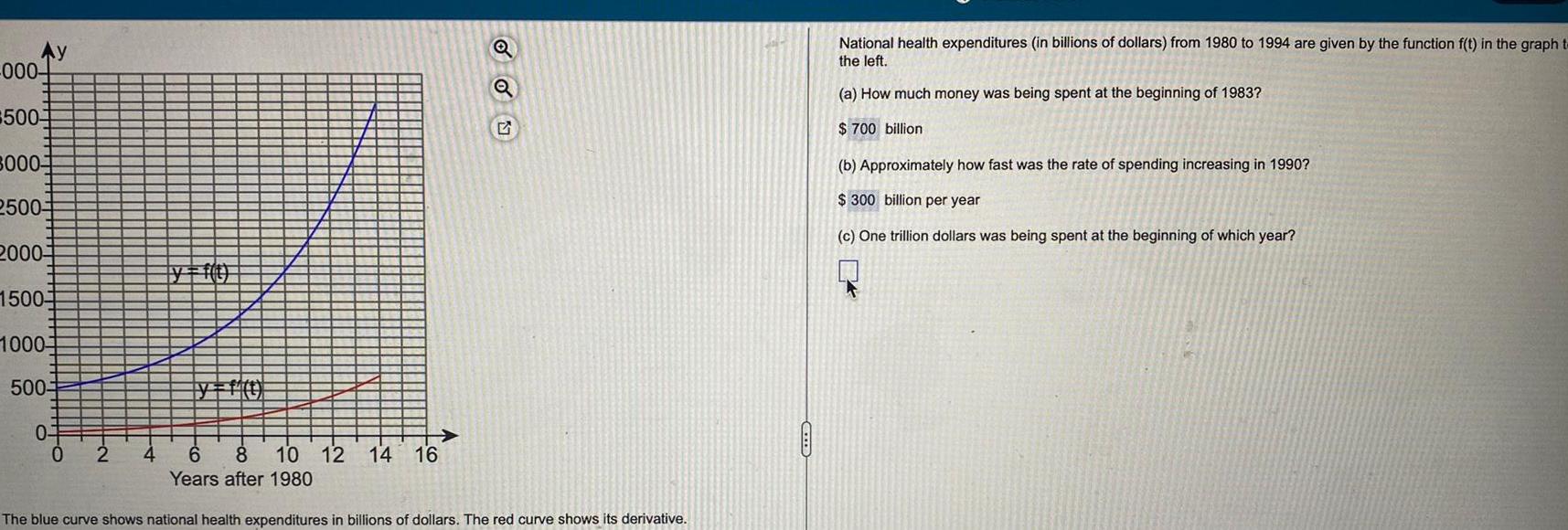
Calculus
Application of derivativesAy 000 500 3000 2500 2000 1500 1000 500 0 0 2 6 8 10 12 14 16 Years after 1980 The blue curve shows national health expenditures in billions of dollars The red curve shows its derivative Q 4 National health expenditures in billions of dollars from 1980 to 1994 are given by the function f t in the graph to the left a How much money was being spent at the beginning of 1983 700 billion b Approximately how fast was the rate of spending increasing in 1990 300 billion per year c One trillion dollars was being spent at the beginning of which year

Calculus
Application of derivativesLet f t be the temperature of a cup of coffee t minutes after it has been poured Interpret f 5 190 and f 5 8 Estimate the temperature of the coffee after 5 minutes and 36 seconds that is after 5 6 minutes What does f 5 190 imply EXOD OA 190 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 5 degrees per minute OB 190 minutes after the coffee has been poured the temperature of the cup of coffee is 5 degrees C 5 minutes after the coffee has been poured the temperature of the cup of coffee is rising at a rate of 190 degrees per minute OD 5 minutes after the coffee has been poured the temperature of the cup of coffee is 190 degrees

Calculus
Application of derivatives4 Evaluate a CSC b cos c tan 315 5TT 3 e sec 37 f fi cot 7 3 d 5TT 6 5 sin
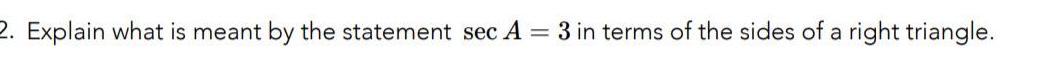
Calculus
Application of derivatives2 Explain what is meant by the statement sec A 3 in terms of the sides of a right triangle


Calculus
Application of derivativesComplete the table with exact trigonometric function values Do not use a calculator 0 225 sin 0 2 2 sin 0 2 COS COS tan 0 1 tan 0 cot 0 1 cot 0 sec sec CSC 2 CSC 0 1 225 2 Simplify your answer including any radicals Use integers or fractions for any numbers in the expression

Calculus
Application of derivativesFind exact values or expressions for the six trigonometric functions of angle A Do not use a calculator sin A cos A tan A Tuno csc A sec A cot A gore or simplified fractions A 45 53 28

Calculus
Application of derivativesLet f x be the number in thousands of computers sold when the price is x hundred dollars per computer Interpret the statements f 18 60 and f 18 4 Then estimate the number of computers sold if the price is set at 1850 per computer What does f 18 60 imply OA 60 000 computers are sold when the price is set at 180 B When the price per computer is 6000 for every 100 price increase the sales increase by 18 000 computers OC When the price per computer is 1800 for every 100 price increase the sales increase by 60 000 computers O D 60 000 computers are sold when the price is set at 1800
Calculus
Application of derivativesLet f x 1 x a Make two tables one showing values of f for x 0 01 0 001 0 0001 and 0 00001 and one showing values of f for x 0 01 0 001 0 0001 and 0 00001 1 b Estimate the value of lim 1 x X 0 1 c What mathematical constant does lim 1 x appear to equal x 0 Round to five decimal places as needed X 0 01 0 001 0 0001 f x Complete the following table of values of f for negative x values Round to five decimal places as needed X 0 01 0 001 0 0001 f x b An estimate for the value of the limit is Round to five decimal places as needed 0 00001 OA 2 OD e 1 OG 2 1 0 00001 1 c What mathematical constant does lim 1 x appear to equal X 0 OB e OE e 1 OH 1 II OC 2 1 OF OL x 1
Calculus
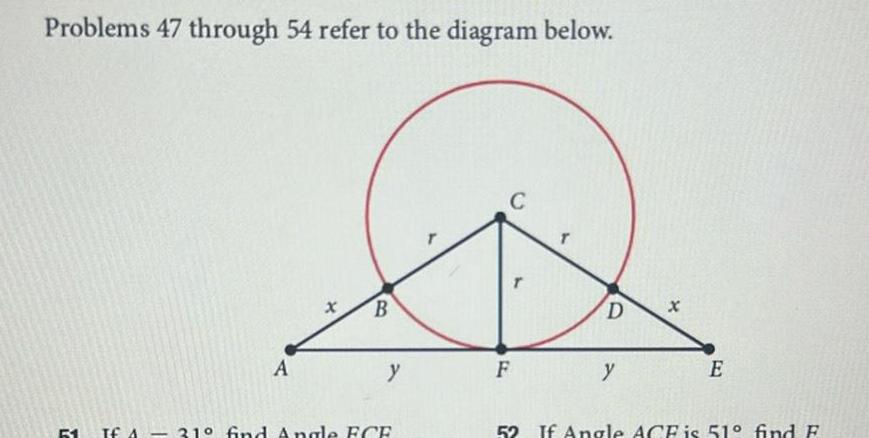
Application of derivativesProblems 47 through 54 refer to the diagram below Y A B y TE A 31 find Angle FCE C F T D y X E 52 If Angle ACE is 51 find F

Calculus
Application of derivativesUse the graph of g in the figure to evaluate the function or analyze the limit a g 1 b lim g x c lim g x X 1 X 1 e g 3 f lim g x h g 4 k lim g x X 4 d lim g x X 1 g lim g x x 3 j lim g x x 4 X 3 i lim g x X 4 a Select the correct answer below and if necessary fill in the answer box within your choice A g 1 Type an integer or a decimal OB The value g 1 does not exist because g is not defined at x 1 b Select the correct answer below and if necessary fill in the answer box within your choice OA lim g x X 1 OB The limit does not exist because g is not defined for all x sufficiently close to 1 with x 1 c Select the correct answer below and if necessary fill in the answer box within your choice Type an integer or a decimal F OA lim g x Type an integer or a decimal X 1 OB The limit does not exist because g is not defined for all x sufficiently close to 1 with x 1 AY 3 0 yag
Calculus
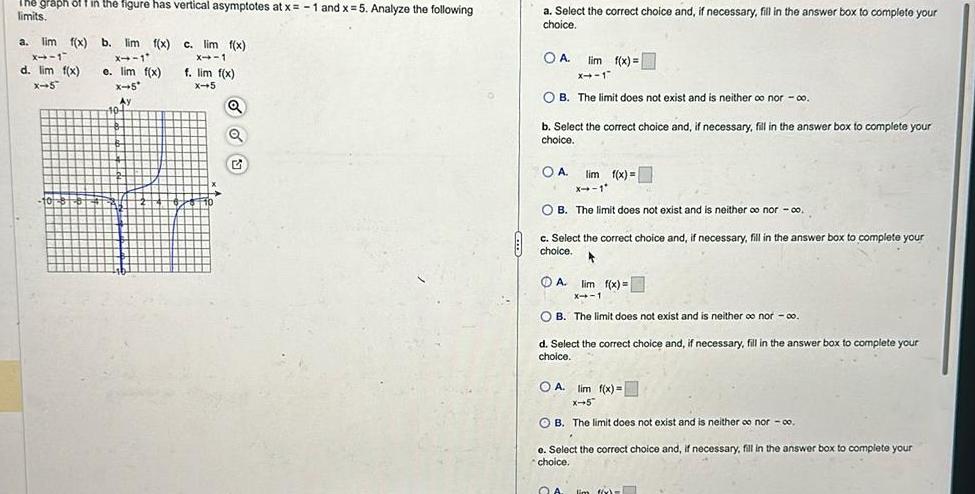
Application of derivativesThe graph off in the figure has vertical asymptotes at x 1 and x 5 Analyze the following limits a lim f x b lim f x x 1 X 1 e lim f x d lim f x x 5 X 5 Ay 10 c lim f x X 1 f lim f x X 5 Q Q a Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x x 1 OB The limit does not exist and is neither co nor co b Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x X 1 OB The limit does not exist and is neither oo nor co c Select the correct choice and if necessary fill in the answer box to complete your choice 4 A lim f x X 1 OB The limit does not exist and is neither oo nor co d Select the correct choice and if necessary fill in the answer box to complete your choice OA lim f x X 5 OB The limit does not exist and is neither co nor 00 e Select the correct choice and if necessary fill in the answer box to complete your choice QA lim f x

Calculus
Application of derivativesrmine a value of the g x x 3x 3x if x 1 ax 4 if x 1 ant a for wh X 1 g x exists and state the value of the limi possible Select the correct choice below and if necessary fill in the answer boxes to complete your choice OA The limit exists for a With that value for a lim g x X 1 OB There is no value of a for which lim g x exists X 1

Calculus
Application of derivativesDetermine the value of the constant a for which the function f x is continuous at 4 x 6x 8 X 4 a if x 4 if x 4 The function f x is continuous at 4 when a Type an integer or a fraction O
Calculus
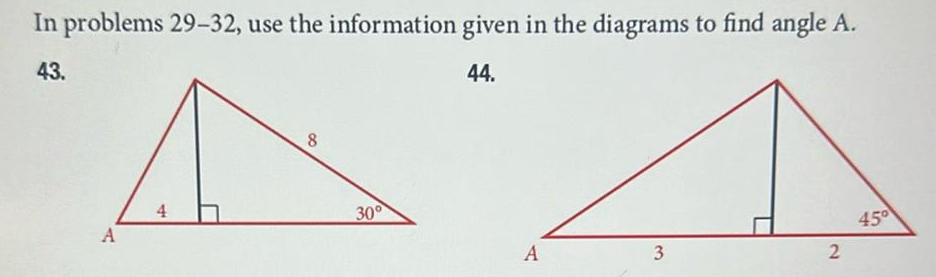
Application of derivativesIn problems 29 32 use the information given in the diagrams to find angle A 43 44 A 4 8 30 A 3 2 45
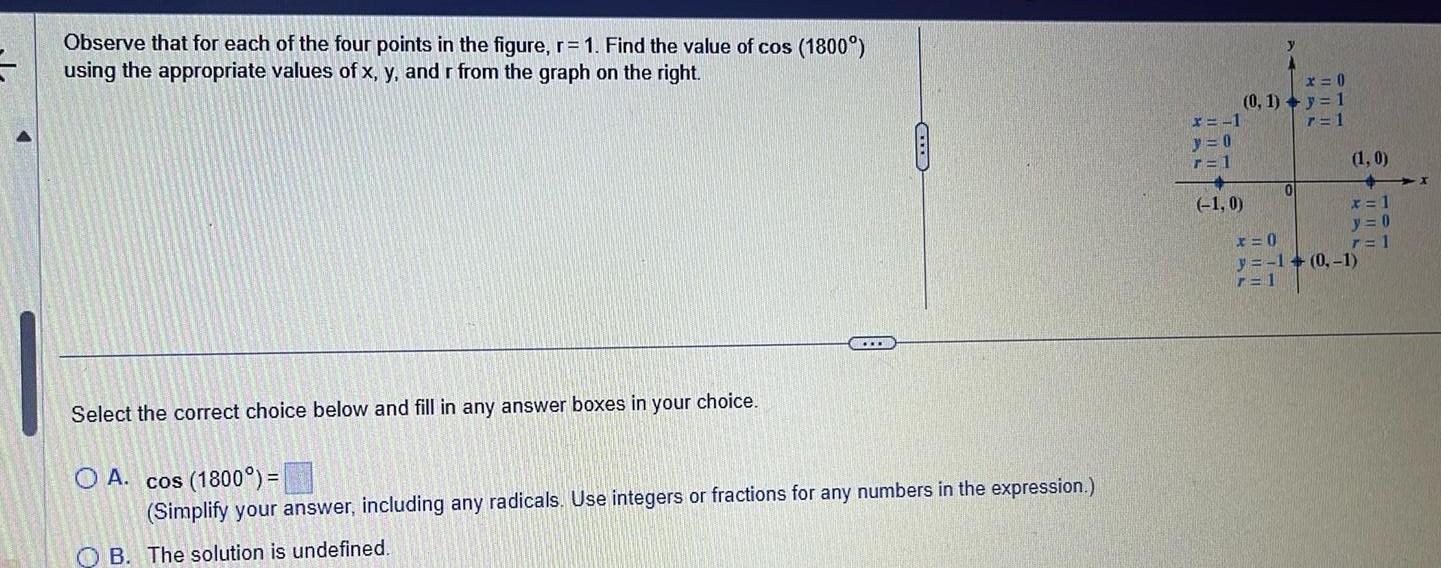
Calculus
Application of derivativesObserve that for each of the four points in the figure r 1 Find the value of cos 1800 using the appropriate values of x y and r from the graph on the right www Select the correct choice below and fill in any answer boxes in your choice O A cos 1800 Simplify your answer including any radicals Use integers or fractions for any numbers in the expression B The solution is undefined y x 0 0 1 y 1 7 1 x 1 y 0 r 1 1 0 0 1 0 x 1 y 0 r 1 x 0 y 1 0 1 r 1