Differential equations Questions and Answers

Calculus
Differential equationsA yeast culture is growing at the rate of W t 0 5e0 1t grams per hour If the starting culture weighs 5 grams what I will be the weight of the culture W t after t hours After 3 hours The weight of the culture after t hours will be W t



Calculus
Differential equationsall values of 0 if 0 is in the interval 0 360 and has the given function value sin 00 5791576 C alue s of 0 is are an integer or decimal rounded to five decimal places as needed Use a comma to s

Calculus
Differential equationsthe appropriate reciprocal identity to find the exact value of sec 0 for the given valu 6 9 9 95 0 an integer or a fraction

Calculus
Differential equationsLet f x be the number in thousands of computers sold when the price is x hundred dollars per computer Interpret the statements f 14 80 and f 14 2 Then estimate the number of computers sold if the price is set at 1425 per computer KIZB What does f 14 80 imply OA When the price per computer is 1400 for every 100 price increase the sales increase by 80 000 computers B 80 000 computers are sold when the price is set at 1400 OC When the price per computer is 8000 for every 100 price increase the sales increase by 14 000 computers D 80 000 computers are sold when the price is set at 140 What does f 14 2 imply OA When the price per computer is 1400 for every 1000 price increase the sales decrease by 2 000 computers c When the price per computer is 1400 for every 100 price increase the sales decrease by 2 000 computers If computers are sold for 1425 per computer 79 5 computers will be sold OB 14 000 computers are sold when the price is reduced by 200 OD 2 000 computers are sold when the price is set at 1400

Calculus
Differential equationsShow analytically that f is not differentiable at x 0 x 1 f x 2x x 0 x 0

Calculus
Differential equationsK Find the circular function values for the given number s State which functions are undefined for s Do not use calculator 3x 2 S A sin 3x 2 A cos OB The function is undefined Select the correct choice below and if necessary fill in the answer box to complete your choice Type an integer or a fraction 3r 2 Type an integer or a fraction 1 0 2

Calculus
Differential equationsA Ferris wheel is 40 meters in diameter and boarded from a platform that is 2 meters above the ground The six o clock position on the Ferris wheel is level with the loading platform The wheel completes 1 full revolution in 6 minutes How many minutes of the ride are spent higher than 35 meters above the ground

Calculus
Differential equationsEvaluate the function at each specified value of the independent variable and simplify If an answer is undefined enter UNDEFINED f x x 6 a f 8 14 b f 8 2 c f t UNDEFINED

Calculus
Differential equationsUse the graph of the function to find the domain and range of f Enter your answer using interval notatic domain range b 5 4 3 c 0 00 9 f 3 f 0 X d f 4 X 10 y 987654321 7 140 5 2 2 1 1 IIIII 1 123456789 2 Use the graph to find the indicated function values a f 4 3 5 9L 1 2 y f x 4 5 X


Calculus
Differential equationsLife is not about finding yourself Life is about creating yourself Lolly Daskal The rate at which water flows into a tank in gallons per hour is given by a positive continuous function R of time t The table below shows the rate at selected values oft for a 12 hour period 3 t hrs R gal hr 0 2 6 8 10 12 12 5 13 4 13 9 14 3 14 6 14 8 14 7 4 Use a midpoint Reimann sum with 3 subintervals to approximate the amount of water that flowed into the tank over the 12 hour period Use your calculator for 4 5 Show all work that leads to your answer 4 The total area enclosed between the curve y x 3x x 2 and the x axis on the interval 2 2 G 4 1 5 Find the average value of the function f x x 3x 8 on the interval 1 4 6 Given the graph of f x find f x dx

Calculus
Differential equationslim 8 X 6 X 6 a Calculate f x for each value of x in the following table 5 99 X 5 999 5 9999 0 0 6 001 6 0001 36 x 0 x 6 Type integers or decimals rounded to four decimal places as needed X a Calculate f x for each value of x in the following table b Make a conjecture about the vi 36 x 6 5 9 0 6 1 6 01

Calculus
Differential equationsgraph off and use it to make a conjecture about the values of f a lim f x lim f x and lim f x or s X a x a X 3 not exist x 1 a 1 conjecture about the value of f 1 Select the correct choice below and if necessary fill in the answer bo e your choice The value of f 1 Type an integer or a decimal The value of f 1 does not exist conjecture about the value of lim f x Select the correct choice below and if necessary fill in the answ X 1 Olete your choice The limit exists lim X 1 X 1 The limit does not exist Type an integer or a decimal

Calculus
Differential equationsvolume of a solid of revolution around the y axis with a function defined as a function of y Question efine R as the region bounded by the graphs f g y 2y 2y 2 y 1 y 0 and ne y axis Using the disk method what is the olume of the solid of revolution generated by otating R about the y axis Enter your answer terms of

Calculus
Differential equationsLet f x 9 X 3 X 3 lim x x 3 X a Calculate f x for each value of x in the following table 2 999 2 9999 5 99 5 999 5 9999 3 01 3 001 3 0001 f x 6 01 6 001 6 0001 x 3 Type integers or decimals rounded to four decimal places as needed f x lim 9 a Calculate f x for each value of x in the following table b Make a conjecture about the valu X x 9 x 3 2 9 5 9 3 1 6 1 2 99 b Make a conjecture about the value of lim X 9 X 3 X 3 Type an integer or a decimal

Calculus
Differential equationsDetermine the volume of a solid by integrating a cross section with a square or rectangle Question The solid S has a base described by the circle x y 9 Each cross section perpendicular to the x axis and the base is a square with one side in the base of the solid What is the volume of S Give the exact volume as your answer Do not include any units Provide your answer below
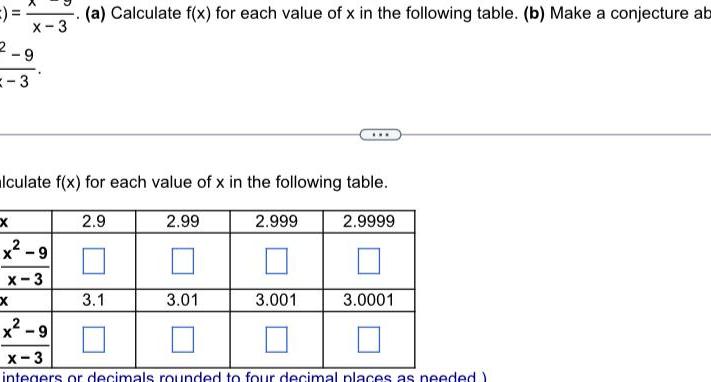
Calculus
Differential equations3 x X 3 9 Xx lculate f x for each value of x in the following table x 9 x 3 a Calculate f x for each value of x in the following table b Make a conjecture ab 2 9 3 1 2 99 3 01 2 999 3 001 2 9999 3 0001 x 9 x 3 integers or decimals rounded to four decimal places as needed

Calculus
Differential equationsThe equation r t cos 2t i sin 2t j t20 describes the motion of a particle moving along the unit circle Answer the following questions about the behavior of the particle a Does the particle have constant speed If so what is its constant speed b Is the particle s acceleration vector always orthogonal to its velocity vector c Does the particle move clockwise or counterclockwise around the circle d Does the particle begin at the point 1 0 a Select the correct choice below and fill in any answer boxes w your choice OA The particle s constant speed is OB The particle s speed is not constant

Calculus
Differential equationsThe equation r t 2t 5 1 312 3 j 3t k is the position of a particle in space at time t Find the particle s velocity and acceleration vectors Then write the particle s velocity at t 1 as a product of its speed and direction What is the velocity vector v t 0 0 0 j i
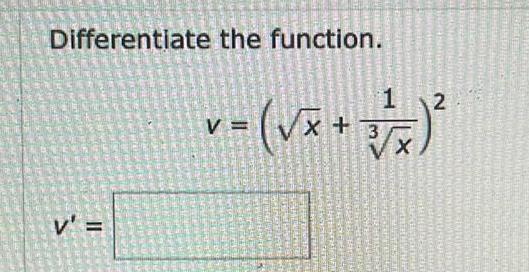
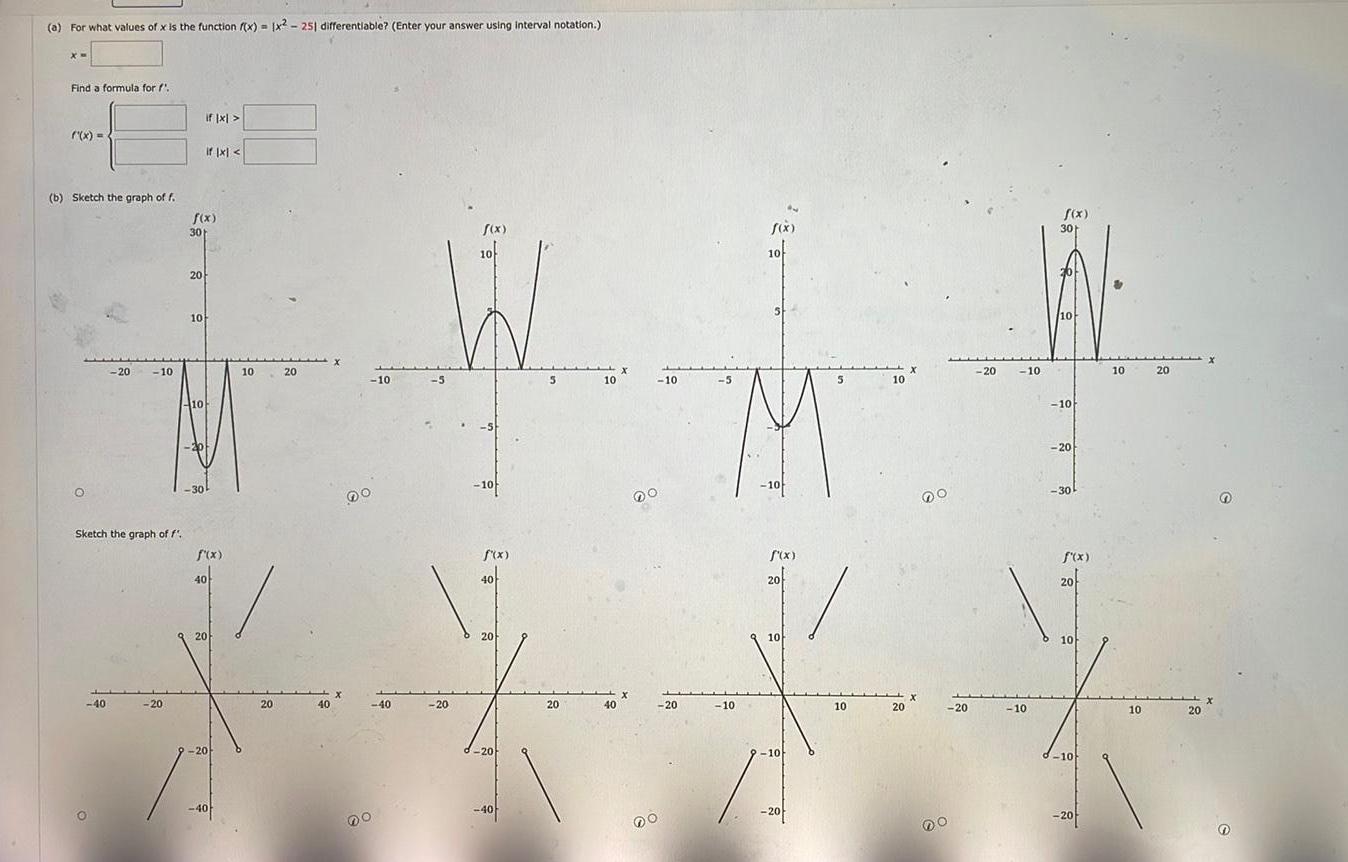
Calculus
Differential equationsa For what values of x is the function f x x2 251 differentiable Enter your answer using interval notation x Find a formula for f x b Sketch the graph of f if x if x f x f x f x 30 10 10 20 10 4 20 10 10 20 10 5 10 10 5 5 10 10 10 10 30k 40 O X 40 DO 40 40 20 X Do 20 20 Sketch the graph of f f x f x f x f x 40 20 40 20 20 20 10 10 X X X Y X 40 20 20 40 20 20 20 10 10 20 10 10 201 20 10 10 20 20 10 DO f x 30 10 10 20 30 10 20 20 20

Calculus
Differential equationsFind the first and second derivatives of the function f x 12x 2 4x4 x f x f x 11
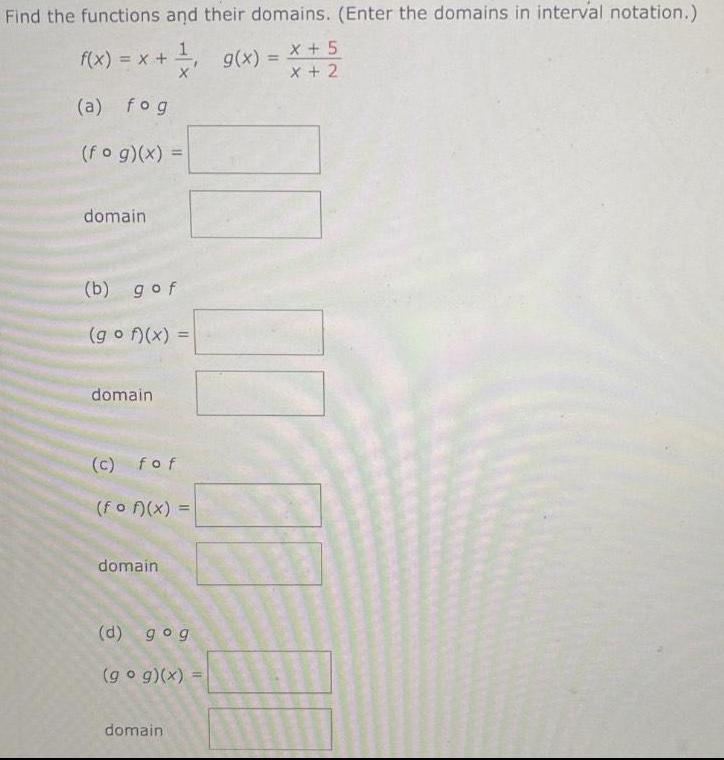
Calculus
Differential equationsFind the functions and their domains Enter the domains in interval notation g x g x x 5 X x 2 f x x a fog fog x domain b gof gof x domain c fof fof x domain d gog g g x domain

Calculus
Differential equationsThe function y f x is graphed below What is the average rate of change of the function f x on the interval 7 x 2 6 40 30 39

Calculus
Differential equationsse the identity cos s sin s 1 to find the value of x or y as appropriate Then assuming that s ne given point on the unit circle find the six circular function values for s 21 X 29 in s 29 OS S ans 21 29 x 0 Type an integer or a simplified fraction Type an integer or a simplified fraction 20 29 Type an integer or a simplified fraction Type an integer or a simplified fraction

Calculus
Differential equationsMultiply 21 sin 4 sin 0 3 23 2 cos 0 3 4 cos 0 5 25 1 sin 0 1 sin 0 27 1 tan 0 1 tan 8 29 sin cos 0 22 cos 2 cos 0 5 0 24 3 sin 0 2 5 sin 0 4 26 1 cos 0 1 cos 0 28 1 cot 0 1 cot 8 30 cos sin 8

Calculus
Differential equationsFind the required trigonometric ratio of using the given information 45 tan 0 sin 0 and 8 E QI and 6 and 0 E QI 2 3 46 tan 0 cos 0 3 4

Calculus
Differential equationsThe graphs of four derivatives are given below Match the graph of each function in a d with the graph of its derivative in I IV YA ya a c ya YA 0 VA A X YA V II b d III YA M v IV

Calculus
Differential equationsA 4 ft tall fence runs parallel to the wall of a house at a distance of 7 ft Find the length of the shortest ladder that extends from the ground to the house without touching the fence Assume the vertical wa of the house is 20 ft high and the horizontal ground extends 20 ft from the fence The length of the shortest ladder is ft Round the final answer to the nearest tenth as needed Round all intermediate values to the nearest thousandth as needed

Calculus
Differential equations2 Let f be the function given by f x x 3x x 2 A The tangent to the graph of fat the point P 2 8 intersects the graph off again at the point Q Find the coordinates of the point Q B Find the coordinates of point R the point where f x 0 6 Show that the segment QR divides the region between the graph of fand its 16 tangent at P into two regions whose areas are in the ration of 11 2 8 P2

Calculus
Differential equationsTutorial Exercise A ball is thrown into the air with a velocity of 46 ft s Its height in feet after t seconds is given by s t 46t 16t2 Find the velocity of the ball at time t 2 seconds Step 1 Let h s t 46t 16t2 give the height of the ball at time t Then the ball s velocity at time t a can be found by s t s a t a v a lim t a We are asked to find the velocity at t 2 therefore we use a v 2 lim s t s 2 t 2 t 2 lim t 2 lim t 2 46t 16t 46 16 2 46t 16t2 t 2 t 2 and have

Calculus
Differential equationsIf a rock is thrown upward on the planet Mars with a velocity of 11 m s Its height above the ground in meters after t seconds is given by H 11t 1 86t a Find the velocity in m s of the rock after 1 second 7 28 m s b Find the velocity in m s of the rock when t a 3 72 X m s c When in seconds will the rock hit the surface Round your answer to one decimal place t 5 91 S d With what velocity in m s will the rock hit the surface 4 08 X m s

Calculus
Differential equationsFind the shortest distance between 10 a and the curve y x 1 Select one a b C d 7 2 11 2 13 2 Lo VR TEA VR TEAM VRT VR

Calculus
Differential equationsSimplify the following trigonometric expression and verify that it equals sin D 8pts Show all steps cot D tan D sin D cos D Show all work only work typed into the space below will be graded Select the Insert drop down option in the menu below and use Equation to type your answer when you need to incorporate symbols equations or other math expressions

Calculus
Differential equationsOne possible way to simplify the trigonometric expression is shown Choose the correct substitution in each of the steps below from the answer bank provided Simplify secx cos x cotx sinx Step 1 secx cos x A sin x Step 2 secx cos x B Step 3 C cos a Step 4 D Answer Bank M Sin z cas m N Cos where A Select where B Select where C Select where D Select


Calculus
Differential equationsUse the general slicing method to find the volume of the following solid TI 2 2 and whose cross sections through the solid perpendicular to the x axis The solid whose base is the region bounded by the curve y 36 cos x and the x axis on are isosceles right triangles with a horizontal leg in the xy plane and a vertical leg above the x axis Set up the integral that gives the volume of the solid Use increasing limits of integration Select the correct choice below and fill in the answer boxes to complete your choice Type exact answers OA SO COL dx OB S dy y 36 cos x

Calculus
Differential equationsUse the given graph of the function f to answer the following questions Answer Formats D 2 Type your answers in interval notation Use INF and INF to denote o and co f x 3 2 2 x Enter NONE if it is not positive negative If there is more than one interval type your answer as a comma separated list For example a1 b1 a b If there is more than one interval type your answer as a comma separated list For example a b a b Part 1 The First Derivative Find the open interval s on which f x is positive negative Type your answers using interval notation 1 f z is positive 2 f z is negative Part 2 The Second Derivative Find the open interval s on which f a is positive negative Type your answers using interval notation 1 f z is positive 2 f z is negative

Calculus
Differential equationsThe graph on the right gives the annual per person retail availability of beef chicken and pork in Dounds from 2007 to 2012 What is the approximate annual per person retail availability of beef chicken and pork in 2012 The annual per person availability of beef in 2012 is approximately 62 pounds The annual per person availability of chicken in 2012 is approximately 60 pounds The annual per person availability of pork in 2012 is approximately 45 pounds G Points 0 67 of 1 Pounds 70 65 60 55 50 45 40 35 2007 2008 2009 2010 2011 Year

Calculus
Differential equationsDETAILS LARMPMT1 10 1 008 Use a protractor to sketch an angle with the given manure a 115

Calculus
Differential equationsK 5x 3x 7 0 to solve the equation If the solutions involve square roots give both the exact and approximate solutions B What are the exact solutions Select the correct choice below and if necessary fill in the answer box to complete your choice OA The solution s do es not involve s square roots The solution s is are x Simplify your answer Use a comma to separate answers as needed PALAKKA 3 149 10 The solution s involve s square roots The solution s is are x 3 149 10 Type an exact answer using radicals as needed Use a comma to separate answers as needed C There are no real solutions What are the approximate solutions Select the correct choice below and if necessary fill in the answer box to complete your choice A The exact solution s involve s square roots The approximate solution s is are x Round to three decimal places as needed Use a comma to separate answers as needed OB The solution s do es not involve s square roots so there is no approximate solution OC There are no real solutions

Calculus
Differential equations1 point Evaluate the Riemann sum for f x 6x 4x with n 6 taking the sample points to be right endpoints Illustrate with a diagram Riemann sum is 0 x 3

Calculus
Differential equationsFind the intersection of the line x y z 1 4 2 t 1 1 3 and the plane 2z4y 7z 26 0 An airplane is flying at an air speed of 420 km h on a heading of 210 A 45 km h wind is blowing at a bearing of 230 Determine the bearing and ground velocity of the airplane using geometric vectors

Calculus
Differential equationsProblems 9 through 14 refer to Figure 17 Remember The sum of the three angles in any triangle is always 180 C A D FIGURE 17 B 9 Find a if A 30 10 Find B if 45 11 Find a if A a 12 Find a if A 2a 13 Find A if B 30 and a 100 14 Find B if a B 80 and A 80



Calculus
Differential equationscal numbers of th following Answer Formats If the function does not have any enter NONE f x x 6x 19 x

Calculus
Differential equationsFind the positive numbers and y that minimize S x y provided xy 36 x Minimum Value The positive and y values where this minimum occurs 1 x 2 y 0