Limits & Continuity Questions and Answers

Calculus
Limits & ContinuityFor the functions f x 6 x and g x x 4x 60 find f g f g fg and Determine the domain for each function g What is the domain of fg Select the correct choice below and if necessary fill in the answer box to complete your choice OA The domain of fg is B The domain of fg is Use a comma to separate answers as needed OC The domain of fg is O O A Type your answer in interval notation x Simplify your answer f What is the domain of Select the correct choice below and if necessary fill in the answer box to complete your choice g B f The domain of is g Use a comma to separate answers as needed f
Calculus
Limits & Continuity1 Evaluate lim f x where x 0 f x sin 2x if x 1 n for some non zero integer n x 1 x otherwise Here x denotes the integer closest to x

Calculus
Limits & ContinuitySolve for the approximate solutions in the interval 0 27 List your answers separated by a comma round to two decimal places If it has no real solutions enter DNE 2 cos 0 2 cos 0 1 0

Calculus
Limits & ContinuityDirections Use your knowledge of geometric figures to set up an equation and solve for the missing variables X 400 ft v 36

Calculus
Limits & ContinuityMagnitude of a Vector The magnitude of a vector v is the length of that vector Example 2i 3j 2 3 4 9 13 Question Find 7i 4j For more information on this topic look in your textbook at section 6 6 You might also want to look at the Vectors presentation 17 33

Calculus
Limits & Continuityuppose a boat leaves port travels 10 miles turns 20 degrees and travels another 8 miles as shown in Figure How far fi port is the boat Round your answer to the nearest tenth and do not include units 8 mi 20 10 mi

Calculus
Limits & ContinuitySketch the curve O r 7 6 cos 0 5 y 5 12 10 8 6 4 2 2 Find the area that it encloses Read i Watch It 5 DSC X 12 12 10 8 6 4 2 5 5 2 4 6 8 10 o 2 X O 5 4 0 8 2 10 12

Calculus
Limits & Continuity9 5x is a The angle of the direction opposite the point 9 is 5x OF Step 3 We have found that the angle of the direction opposite the point 9 7 is a ST 4 Submit Skip you cannot come back r 8 Therefore a pair of polar coordinates that represent the same point as Therefore the point opposite 9 5 9 n s but with r 0 is should be our original point This is in fact an example of the general fact that r 6 represents the same point as

Calculus
Limits & Continuityunknown angle as shown in the figure The lengths of KL LM and MK are 105 millimeters 123 millimeters and 182 millimeters respectively What is the value of the unknown angle Round your answer to the nearest degree if necessary M 123 L 182 105 K

Calculus
Limits & ContinuityFind the angles of AABC given that 11 b 26 and c 20 Round your answers to the nearest tenth of a degree B 11 C 20 26 A

Calculus
Limits & ContinuityFind the angles of AABC given that a 11 b 20 and c 18 Round each angle to the nearest tenth of a degree and use that rounded value to find the remaining angles B 18 11 C 20

Calculus
Limits & ContinuityFind the angles of AABC given that a 12 b 21 and c 19 Round your answers to the nearest tenth of a degree Provide your answer below C A 21 7 19 12 B

Calculus
Limits & Continuitya What is a sequence OA sequence is an ordered list of numbers OA sequence is the sum of an ordered list of numbers A sequence is the product of an ordered list of numbers A sequence is the sum of an unordered list of numbers A sequence is an unordered list of numbers b What does it mean to say that lim nan 8 O The terms an approach infinity as 8 approaches n O The terms an approach 8 as n becomes large O The terms an approach infinity as 8 approaches n O The terms an approach infinity as n become large The terms a s an approach 8 as n becomes small c What does it mean to say that lim n O The terms an approach zero as n becomes large O The terms a become large as n becomes small O The terms a become small as n becomes small become small as n becomes large become large as n becomes large O The terms an O The terms an

Calculus
Limits & ContinuityA particle is moving with the given data Find the position of the particle s a t 2t 9 s 0 5 v 0 3 t
Calculus
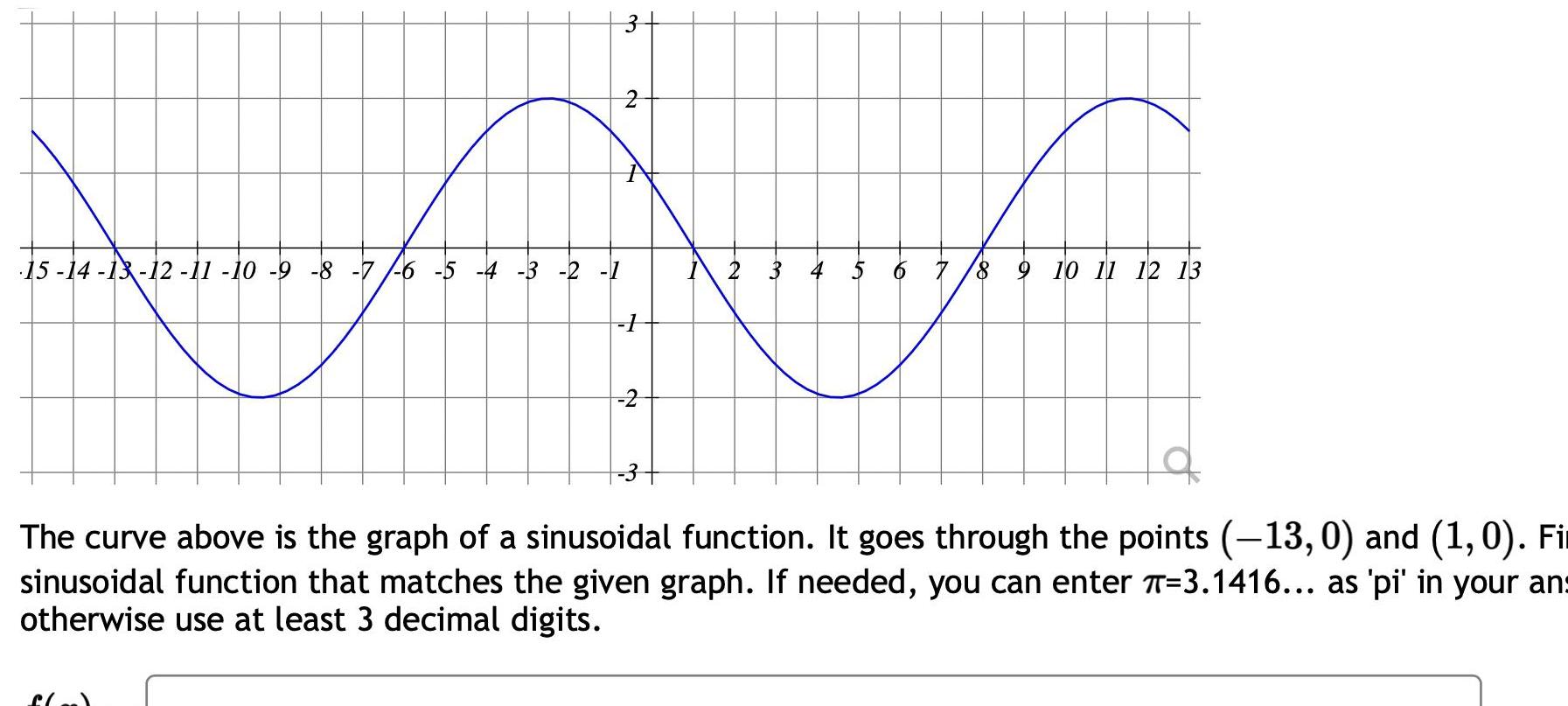
Limits & Continuity15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 3 f o N A N 1 2 3 4 5 6 7 8 9 10 11 12 13 The curve above is the graph of a sinusoidal function It goes through the points 13 0 and 1 0 Fi sinusoidal function that matches the given graph If needed you can enter T 3 1416 as pi in your an otherwise use at least 3 decimal digits

Calculus
Limits & ContinuityGiven that 0 x 2 which of the following gives all solutions to the equation cos 2x cos x sin 2x sin x Select the correct answer below O C 5x X x 5 and 7 x 4 and 5 4x 5x 10x 11x 16x 17x 99

Calculus
Limits & ContinuitySolve the equation 2tan a 2tan a given that a T Separate your answers with commas

Calculus
Limits & ContinuitySolve for 8sin 0 5 13 and 0 0 25 List your answers as exact answers in terms of separated by a comma if necessary Do not include 0 in your answer

Calculus
Limits & ContinuityDetermine all the values of 0 in the following equation if 0 0 2 12sin 0 5 4 Type your answers from least to greatest Provide your answer below

Calculus
Limits & ContinuityIf 2 2 2cos 0 2 where 0 0 2 what are the values of 0 Select the correct answer below 0 2 and 0 0 O 0 0 only 0 0 and 0 0 0 only 7x 0 0 7 only 7x

Calculus
Limits & ContinuityWe will now write a function that is the product of our two numbers where x represents the smaller number and x 56 represents the larger number as follows f x x x x

Calculus
Limits & ContinuityLet and w represent the length and the width of the rectangle measured in m Let A represent the area of the rectangle measured in m Writing an equation for A in terms of I and w gives us the following A m Let P represent the perimeter of the rectangle measured in m Writing an equation for P in terms of and w gives us the following P m

Calculus
Limits & ContinuityIf two numbers have a difference of 56 and we let x represent the smaller of these two numbers then the larger of these two numbers is given by the following

Calculus
Limits & ContinuityDeMoivre s Theorem For a complex number in polar form r cos i sin r cos no i sinne Question Calculate 3 cos 60 i sin 60 NOTE You will have to submit your scratchwork for these problems in the next question for full credit For more information on this topic look in your textbook at section 6 5 You might also want to look at the Complex Numbers presentation 81 cos 240 i sin 240 12 cos 240 i sin 240 81 cos 60 i sin 60

Calculus
Limits & ContinuityFind all missing measurements for the triangle with b 22 7 c 14 2 and A 22 Using the Law of Cosines a 22 7 Select 2 22 7 Select Select a Select O cos

Calculus
Limits & Continuity5x 2 sin cos 0 COS 2 Since it s something times something we can break our equation into smaller simpler equations 2 sin 2 0 OR cos sin 0 OR cos 2 First we ll solve sin sine of O That tells us that X 2 Select 2 sin 0 0 for 0 Select Select Select Select 5x 52 5x 2 Now we just multiply both sides of the equation by 2 to get x by itself and then pick out the solutions with 0 x T Choose the relevant solutions from the list below 0 Which angles make have a

Calculus
Limits & ContinuityNow we just multiply both sides of the equation by 2 to get x by itself and then pick out the solutions with 0 x T Choose the relevant solutions from the list below Select Select Select Select Select We still have to solve the other of our two smaller simpler equations COS 5x Which angles make have a cosine of 0 2 0 cos 0 0 for 0 Select That tells us that 5x and Select

Calculus
Limits & ContinuityExample Find all solutions to sin 3x sin 2x with 0 x 2 First we bring everything to one side of the equation sin 3x sin 2x 0 Next we use a sum to product formula from section 5 4 of our textbook to rewrite the left side of our equation as a product The relevant formula is sina sin 2 sin In the equation we re solving a Select a which means that B 2 a 2 Select x Select Select a x cos a 2 2 and 3 Our rewritten equation now looks like this 5x and

Calculus
Limits & ContinuityUsing the accompanying Colleges and Universities data to find 95 confidence intervals for the median SAT for each of the two groups liberal arts colleges and research universities Based on these confidence intervals does there appear to be a difference in the median SAT scores between the two groups Click here to view the Colleges and Universities data For the liberal art colleges the 95 confidence interval is 1240 8752 1275 7648 Use ascending order Round to four decimal places as needed For the research universities the 95 confidence interval is 1231 1310 Use ascending order Round to four decimal places as needed A 1 Liberal Arts Colleges Median SAT score 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 1166 1205 1207 1207 1222 1220 1222 1239 1250 1241 1244 1254 1258 1251 1261 1268 1294 1289 1300 1305 1297 1300 1311 1310 B Research Universities Median SAT score 1112 1139 1147 1171 1202 1225 1233 1215 1231 1277 1279 1275 1272 1278 1286 1310 1309 1328 1341 1342 1348 1360 1380 1399

Calculus
Limits & ContinuityUsing the accompanying Accounting Professionals data to answer the following questions a Find and interpret a 99 confidence interval for the mean years of service b Find and interpret a 99 confidence interval for the proportion of employees who have a graduate degree Click the icon to view the Accounting Professionals data a A 99 confidence interval for the mean years of service is 10 66 20 64 Use ascending order Round to two decimal places as needed Interpret the confidence interval Choose the correct answer below Save There is a 99 chance that the population mean years of service will be between the confidence interval A limits OB We are 99 confident that the sample mean years of service will be between the confidence interval limits Oc Of all the data values 99 of the population will fall between the confidence interval limits We are 99 confident that the population mean years of service will be between the confidence interval limits D b A 99 confidence interval for the proportion of employees who have a graduate degree is Use ascending order Round to two decimal places as needed 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 A Employee 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 B Years of Service Graduate Degree 19 Y 9 Y 9 N 14 Y 8 Y 26 Y 8 Y 20 N 10 N 10 N 6 N 8 N 16 Y 21 N 26 N 19 Y 28 N 17 N 8 Y 31 N C D

Calculus
Limits & ContinuityWhich of the answer choices given below is equivalent to the following trigonometric expression 3 cos x Select the correct answer below A A W 00 6 O cos 2x cos 4x cos 4x cos 4x O cos 2x cos 4x O cos 2x 8 cos 2x

Calculus
Limits & ContinuityFind a power series representation for f x 3x 5 1 2x 3 For which values of x is it valid

Calculus
Limits & Continuity2 Prove the Leibniz formula for n times differentiable functions f n fg n 1 f k g n k k k 0 where f k 0 k n is the kth derivative

Calculus
Limits & ContinuityWrite the sum as a product cos 18 7v cos 11 7v Note coefficients inside of the trigonometric functions should be entered as simplified decimal value do not enter fractions inside of the trig functions else they will be marked incorrect by the system F 11 example if your answer is enter 5 5 instead of 11 2

Calculus
Limits & ContinuitySimplify sin t cos t cos t sin t 2 sin 2t csc t to a single trig function

Calculus
Limits & ContinuityUse the spinner shown It is equally probable that the pointer will land on any one of the regions If the pointer lands on a borderline spin again If the pointer is spun twice find the probability that it will land on a color other than yellow for each spin 2 4 Type an integer or a simplified fraction Find the probability that the spinner will land on a color other than yellow for each spin green red yellow blue blue yellow red green

Calculus
Limits & ContinuityGraph the following function y sin 1 Drag the black dot to shift your graph in the desired direction Use the blue draggable dot to change the period Drag the orange dot to change the amplitude and or reflect with respect to the x axis The horizontal distance between the vertica dotted green lines corresponds to one period Note reference the sinusoidal function A sin Bx C D Provide your answer below 211 41 3 2 2 2 1 0 0 2 0 TT

Calculus
Limits & ContinuityA Use an indirect proof to prove the following GIVEN A ABC is not isosceles ADB CDB 6 PROVE AD DC D B C


Calculus
Limits & Continuity10 Given the series e 2 If the series converges indicate the value n 1 that it converges to If it diverges write diverges



Calculus
Limits & ContinuityGraph the following function y 3 sec x 7 2 Drag the movable red point to shift the function the black point to set the vertical asymptotes and the blue point whose value is printed on the graph at the correct set of coordinates You may click on a point to verify its coordinates Note Make sure to move the points in the direction of the phase shift represented in the function Provide your answer below 2TT 37 2 TT TR2 8 7 6 5 4 0 1 2 3 4 TR2 3TT 2 2TT

Calculus
Limits & ContinuityA company manufactures and sells x cellphones per week The weekly price demand and cost equations are given below p 400 0 1x and C x 20 000 140x A What price should the company charge for the phones and how many phones should be produced to maximize the weekly revenue What is the maximum weekly revenue The company should produce 2000 phones each week at a price of 200 Round to the nearest cent as needed The maximum weekly revenue is 400000 Round to the nearest cent as needed B What price should the company charge for the phones and how many phones should be produced to maximize the weekly profit What is the maximum weekly profit The company should produce phones each week at a price of Round to the nearest cent as needed

Calculus
Limits & Continuity3x 6 Sketch the following function f x BY HAND Determine the following 2 x x 6 characteristics and communicate your process Make sure to communicate these calculations without having to look at the graph The idea is that you can graph rational functions without technology and have the algebra to prove it x intercept s y intercept vertical asymptote s horizontal asymptote behaviours at the asymptotes It s okay to check Desmos for the sketch of the function but make sure it matches the information you have

Calculus
Limits & ContinuityConsidering only the values of a for which cos a csc a sec a is defined which of the following expressions is cos a csc a sec a Select the correct answer below Ocot a tan a tan a

Calculus
Limits & ContinuityOn the graph of f x cot x and the interval 2 0 for what value of x does f x 1 Choose the points in the figure Provide your answer below 2TT 3 2 0 3TT 8 TT 3 TT 2 2 1 2 0 0 1 2 3

Calculus
Limits & ContinuityWhat is the amplitude and period of the function f x 2 sin 7x Provide your answer below


Calculus
Limits & Continuityy tan 4x Drag either of the movable red points to set the asymptotes for one period of the given function Also place the blue point at the correct set of coordinates You may click on a point to verify its coordinates Provide your answer below TT 3TT 4 T2 TT 4 7 6 5 4 3 2 1 0 1 2 3 TT 4 TT 2 3TT 4 TT