Limits & Continuity Questions and Answers

Calculus
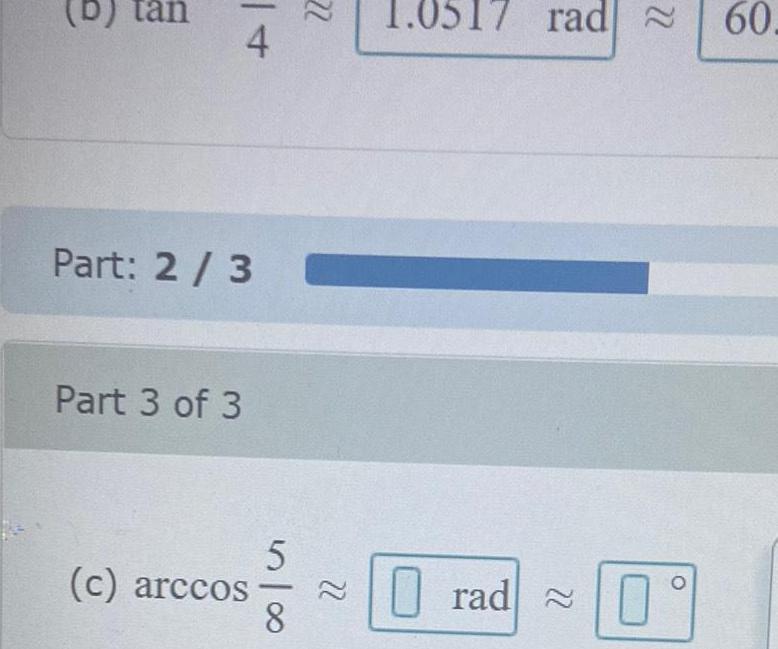
Limits & ContinuityUse a calculator to approximate the expression in radians rounded to 4 decimal places sec 1 5 3 22
Calculus
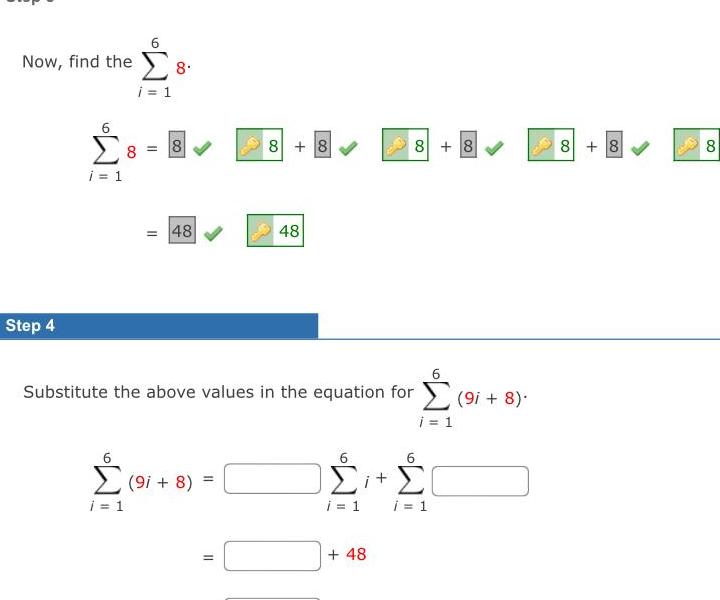
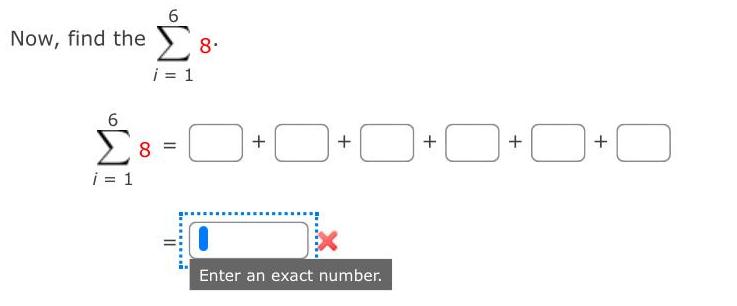
Limits & ContinuityNow find the 8 i 1 Step 4 i 1 8 8 48 9i 8 i 1 8 8 48 Substitute the above values in the equation for 9i 8 i 1 i 1 S 48 8 8 6 it E i 1 8 8 8
Calculus
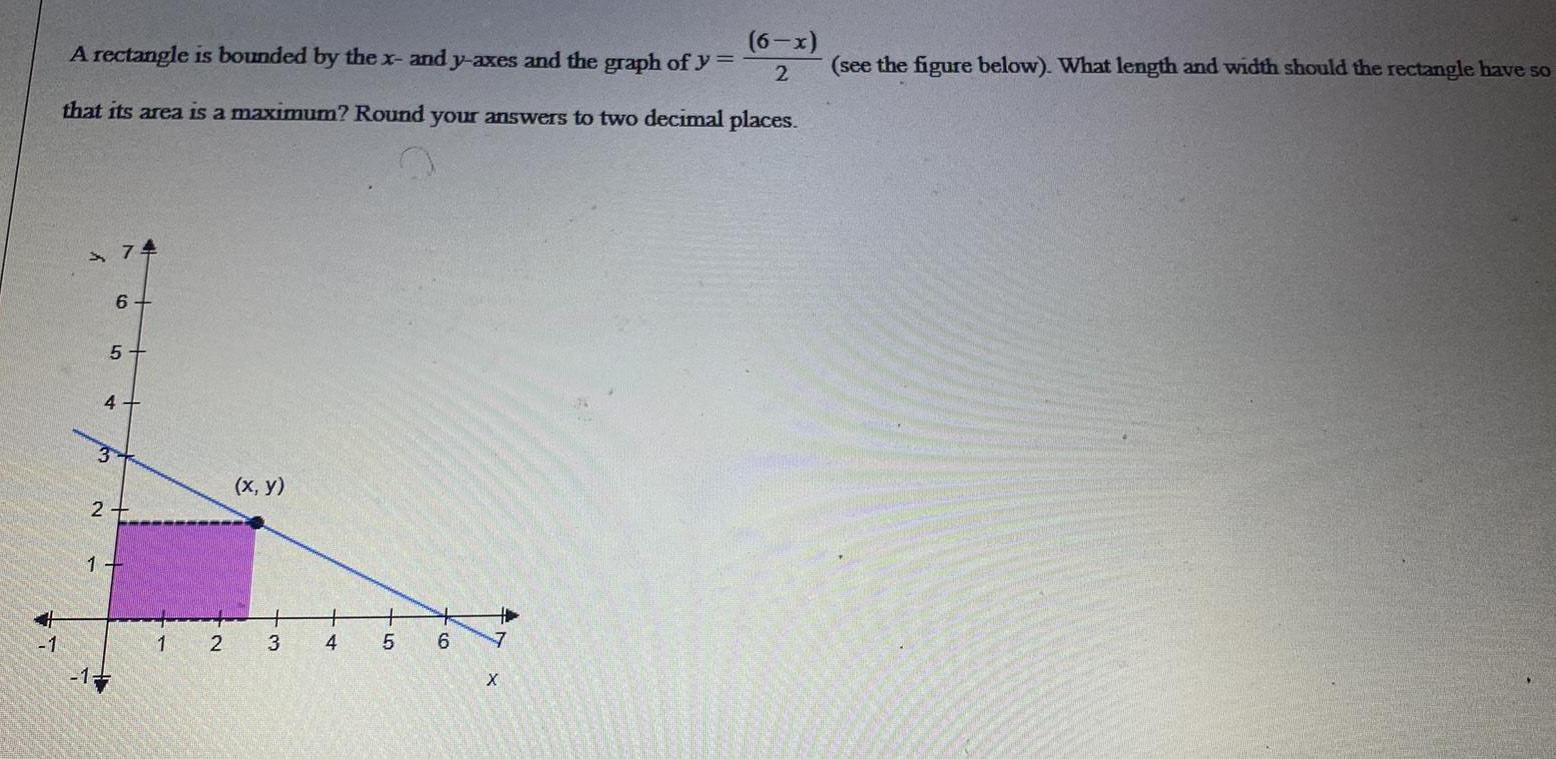
Limits & ContinuityA rectangle is bounded by the x and y axes and the graph of y 6 x 2 that its area is a maximum Round your answers to two decimal places 2 1 3 74 6 5 4 1 2 x y 3 4 5 6 4 7 X see the figure below What length and width should the rectangle have so
Calculus
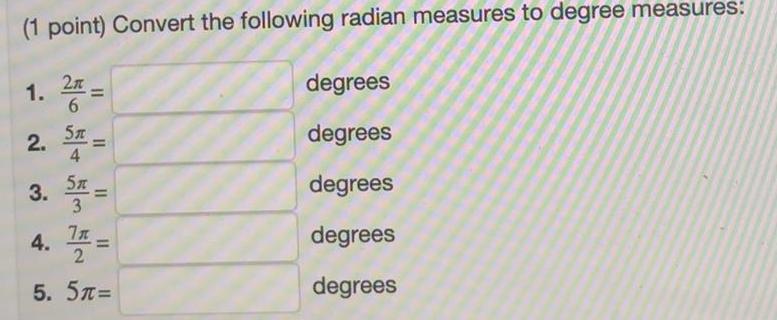
Limits & Continuity1 point Convert the following radian measures to degree measures 1 2 2 ST 3 S 3 II 4 11 2 5 5m degrees degrees degrees degrees degrees
Calculus
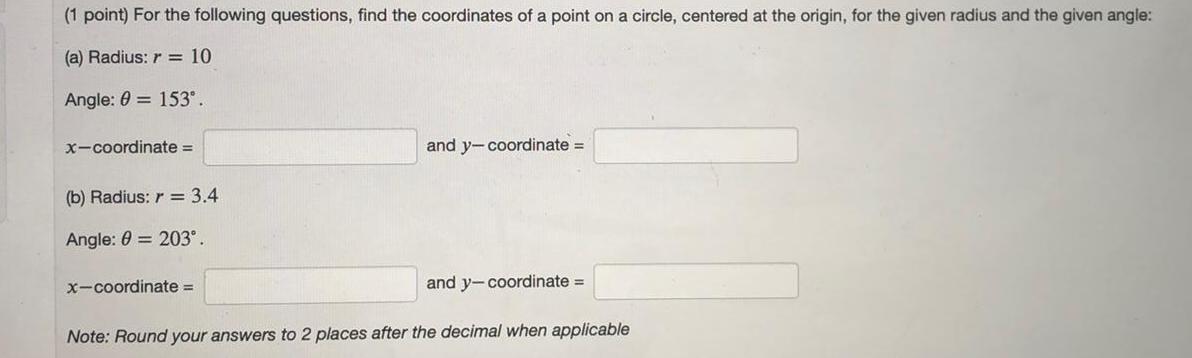
Limits & Continuity1 point For the following questions find the coordinates of a point on a circle centered at the origin for the given radius and the given angle a Radius r 10 Angle 0 153 x coordinate b Radius r 3 4 Angle 0 203 x coordinate and y coordinate and y coordinate Note Round your answers to 2 places after the decimal when applicable

Calculus
Limits & ContinuityUse the summation formulas to rewrite the expression without the summation notation Use the result to find the sums for n 10 100 1000 and 10 000 Step 1 IM i 1 Using the summation formula the expression Step 2 summation notation Therefore 6i 2 n i 1 6i 2 n 3 S 3 0005 Therefore S n 3 S Now to find the sums for 5 S n 3 n i 1 1 5 n W i 1 6i 2 6i 2 n 6i n i 1 can be 6 n n 1 2 2n can be written as the expression without the 2n 10 100 1000 and 10 000 substitute the value of in
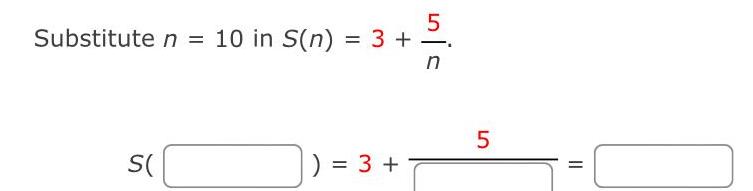

Calculus
Limits & ContinuityTutorial Exercise Find the sum Use the summation capabilities of a graphing utility to verify your result Step 1 WE i 1 9i 8 Use the following property of summation to find the sum a b a bi i 1 i 1 i 1 Write the sum using the above property 6 6 9i 8 i 1 i 1 i 6 i 1 i 1 9i 8

Calculus
Limits & Continuitypoints for the skipped part and you will not be able to come back to the skipped part Tutorial Exercise Find the sum Use the summation capabilities of a graphing utility to verify your result Step 1 Use the following property of summation to find the sum 9i 8 i 1 Step 2 6 9i 8 i 1 Write the sum using the above property Hence n a b a i 1 Step 3 6 6 9i 8 9 i 1 i 1 6 Since 9 is a constant use the following property of summation to find the sum 9i i 1 n i 1 ka k Using the above property 6 9i i 1 9i 9 6 9i i 1 n k a i 1 n n 20 bi i 1 i 1 9 9 6 9i 189 6 9i 8 i 1 9 6 i 1 i 9 1 2 3 9 21 189 8 3 4 5 6
Calculus
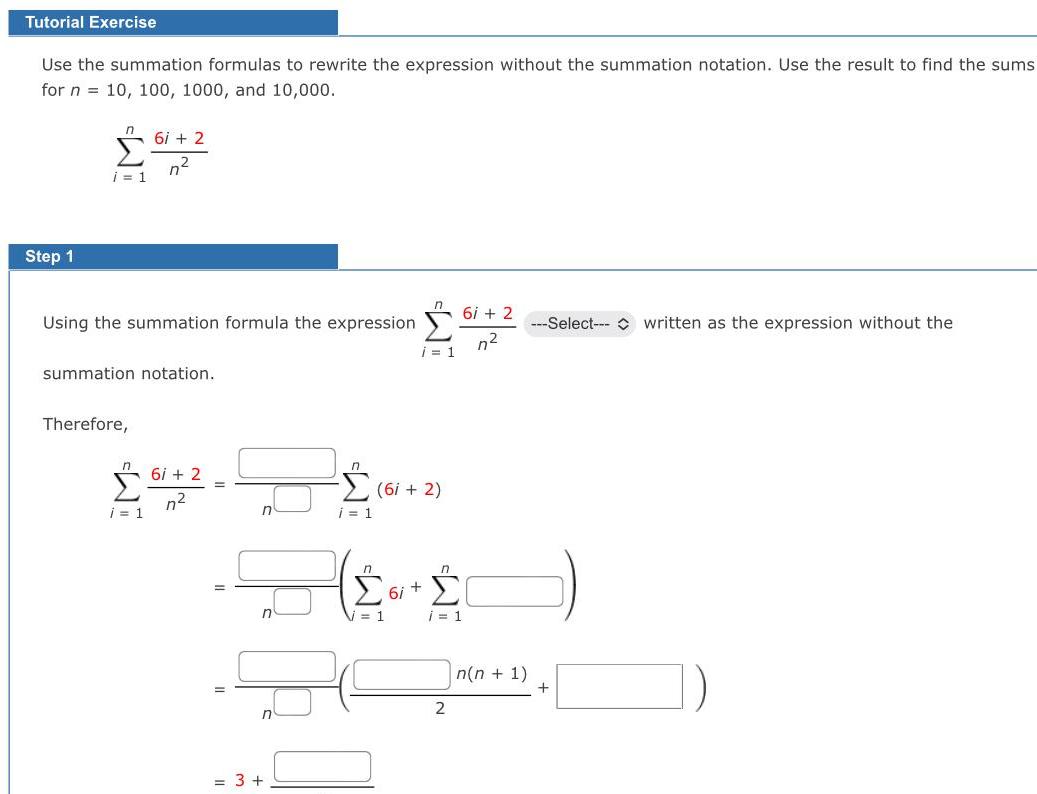
Limits & ContinuityTutorial Exercise Use the summation formulas to rewrite the expression without the summation notation Use the result to find the sums for n 10 100 1000 and 10 000 Step 1 i 1 6i 2 n Using the summation formula the expression summation notation Therefore 61 i 1 6i 2 n 3 i 1 n 61 i 1 6i 2 1 6i n i 1 2 6i 2 n n n 1 Select written as the expression without the

Calculus
Limits & ContinuityFind the sum by adding each term together Use the summation capabilities of a graphing utility to verify your result 7 k 0 C

Calculus
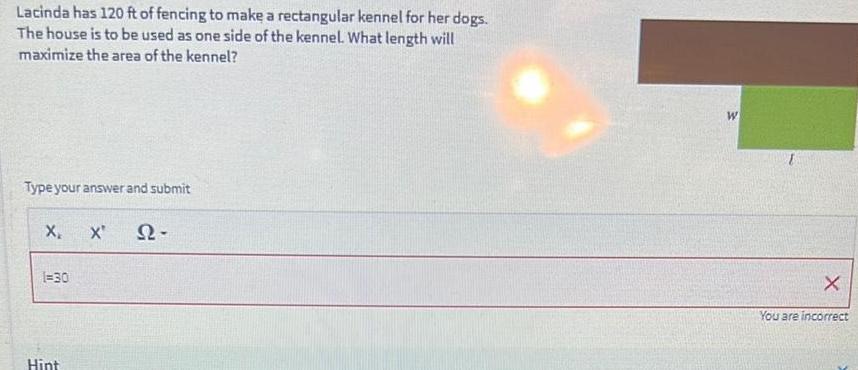
Limits & ContinuityLacinda has 120 ft of fencing to make a rectangular kennel for her dogs The house is to be used as one side of the kennel What length will maximize the area of the kennel Type your answer and submit X X Q2 1 30 Hint W X You are incorrect

Calculus
Limits & ContinuityThe wind chill index is modeled by the function W 13 12 0 6215T 11 37v0 16 0 39657v0 16 where T is the temperature C and v is the wind speed in km h When T 16 C and v 25 km h by how much in C would you expect the apparent temperature W to drop if the actual temperature decreases by 1 C Round your answers to two decimal places C drop What if the wind speed increases by 1 km h while the actual temperature stays constant at T 16 C C drop

Calculus
Limits & ContinuityDetermine the following limits Enter DNE if a limit fails to exist except in case of an infinite limit If an infinite limit exists enter or as appropriate 4x 5x lim 4x 2x 30x 4x 5x lim 4x 2x 30x Determine the equation of the horizontal asymptote that corresponds to the limit as n O Equation of horizontal asymptote O No horizontal asymptote corresponds to the limit as n o Determine the equation of the horizontal asymptote that corresponds to the limit as n O Equation of horizontal asymptote O No horizontal asymptote corresponds to the limit as n
Calculus
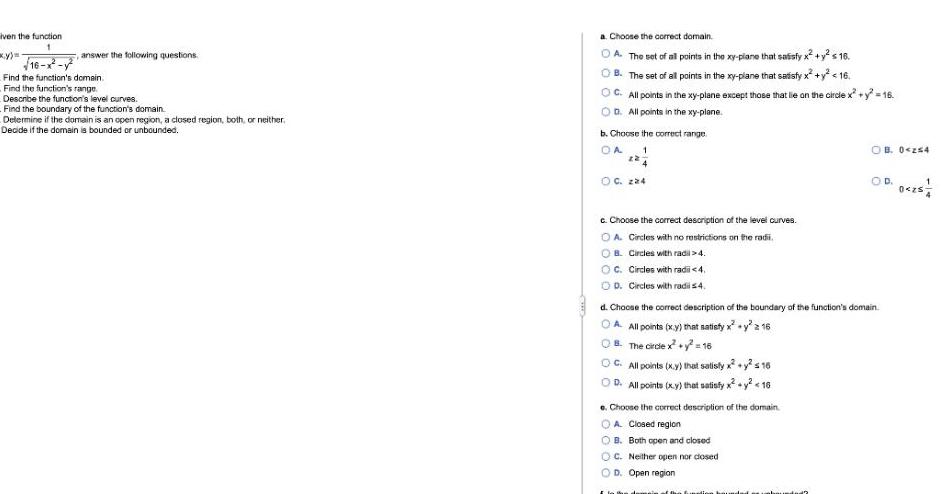
Limits & Continuityiven the function 1 16 answer the following questions Find the function s domain Find the function s range Describe the function s level curves Find the boundary of the function s domain Determine if the domain is an open region a closed region both or neither Decide if the domain is bounded or unbounded a Choose the correct domain A The set of all points in the xy piane that satisfy x y s 16 B The set of all points in the xy plane that satisfy x y 16 OC All points in the xy plane except those that lie on the circle x y 16 OD All points in the xy plane b Choose the correct range OA 1 OC 224 c Choose the correct description of the level curves OA Circles with no restrictions on the radi OB Circles with radi 4 OC Circles with radii 4 D Circles with radi s 4 C All points x y that satisfy x y 16 D All points x y that satisfy x y 16 d Choose the correct description of the boundary of the function s domain OA All points x y that satisfy x y 2 16 B The circle x y 16 e Choose the correct description of the domain OA Closed region OB Both open and closed OC Neither open nor closed OD Open region OB 0 254 I la Ban O D 0 25
Calculus
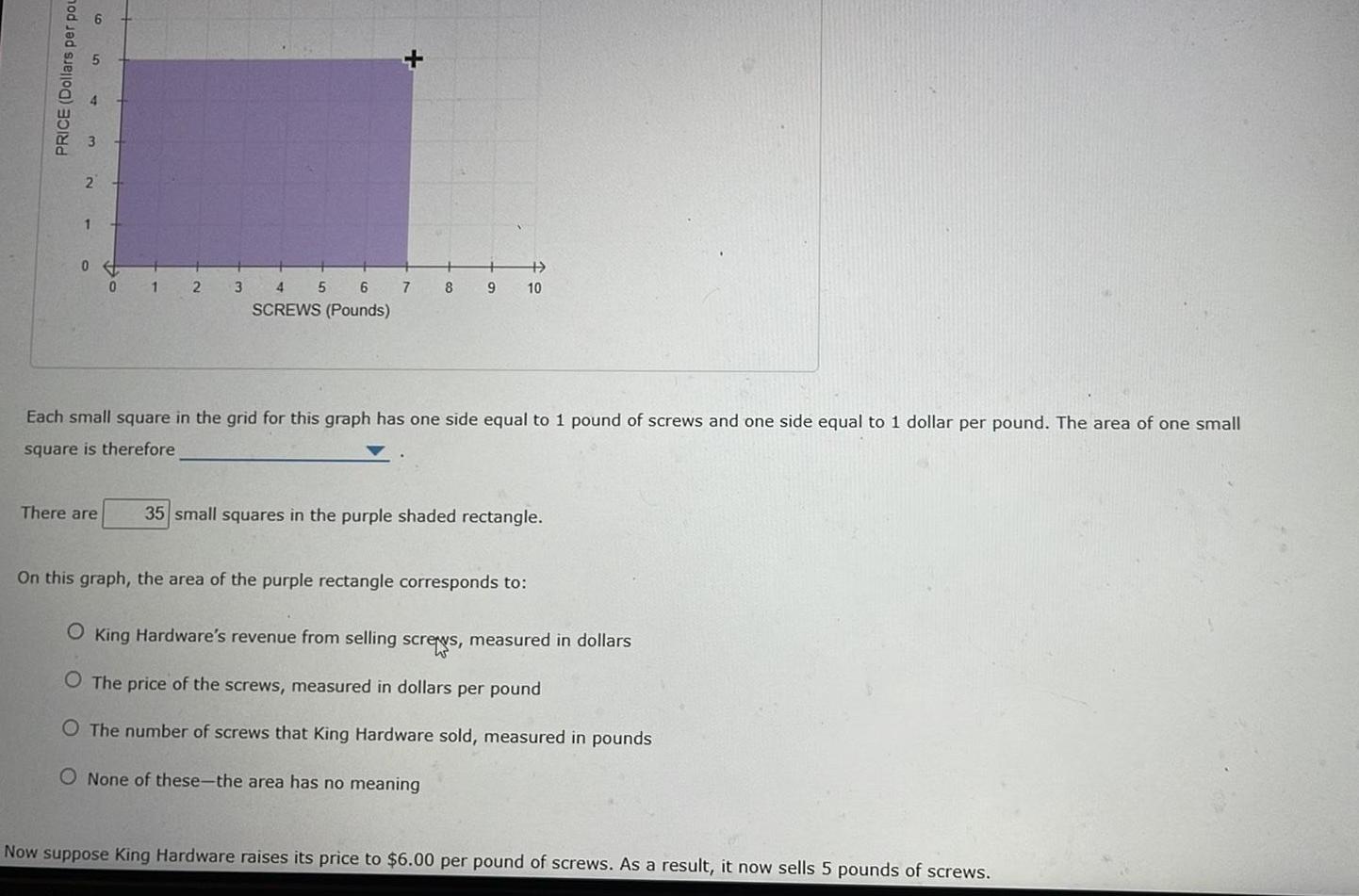
Limits & ContinuityPRICE Dollars per pou 1 0 1 2 3 There are 4 5 6 SCREWS Pounds 7 8 9 10 Each small square in the grid for this graph has one side equal to 1 pound of screws and one side equal to 1 dollar per pound The area of one small square is therefore 35 small squares in the purple shaded rectangle On this graph the area of the purple rectangle corresponds to O King Hardware s revenue from selling screws measured in dollars O The price of the screws measured in dollars per pound O The number of screws that King Hardware sold measured in pounds O None of these the area has no meaning Now suppose King Hardware raises its price to 6 00 per pound of screws As a result it now sells 5 pounds of screws

Calculus
Limits & ContinuityWhat is the percent abundance of the black eyed peas in this sample Sample Number Abundance Mass of Beans 1 3 Black Eyed Peas Cannellini Beans 187 113 2 9 Percent Abundance Weighted Average g 1 9 Enter

Calculus
Limits & ContinuityGiven sine 8 17 and cose 15 17 which of the following can be proven using a Pythagorean identity
Calculus
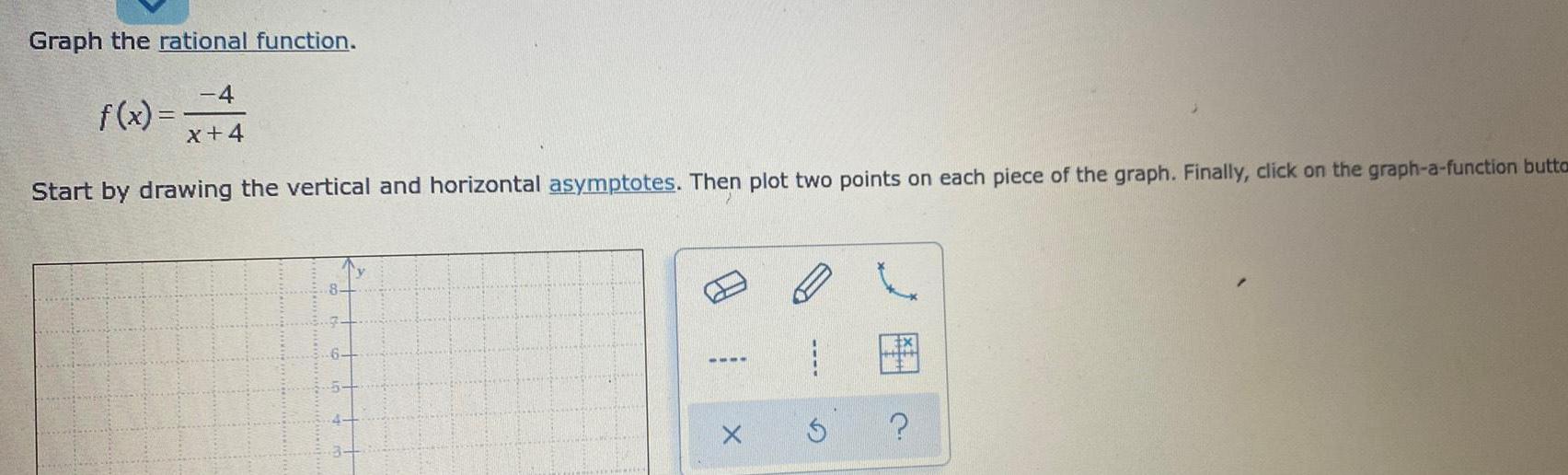
Limits & ContinuityGraph the rational function 4 x 4 Start by drawing the vertical and horizontal asymptotes Then plot two points on each piece of the graph Finally click on the graph a function butta f x X 5
Calculus
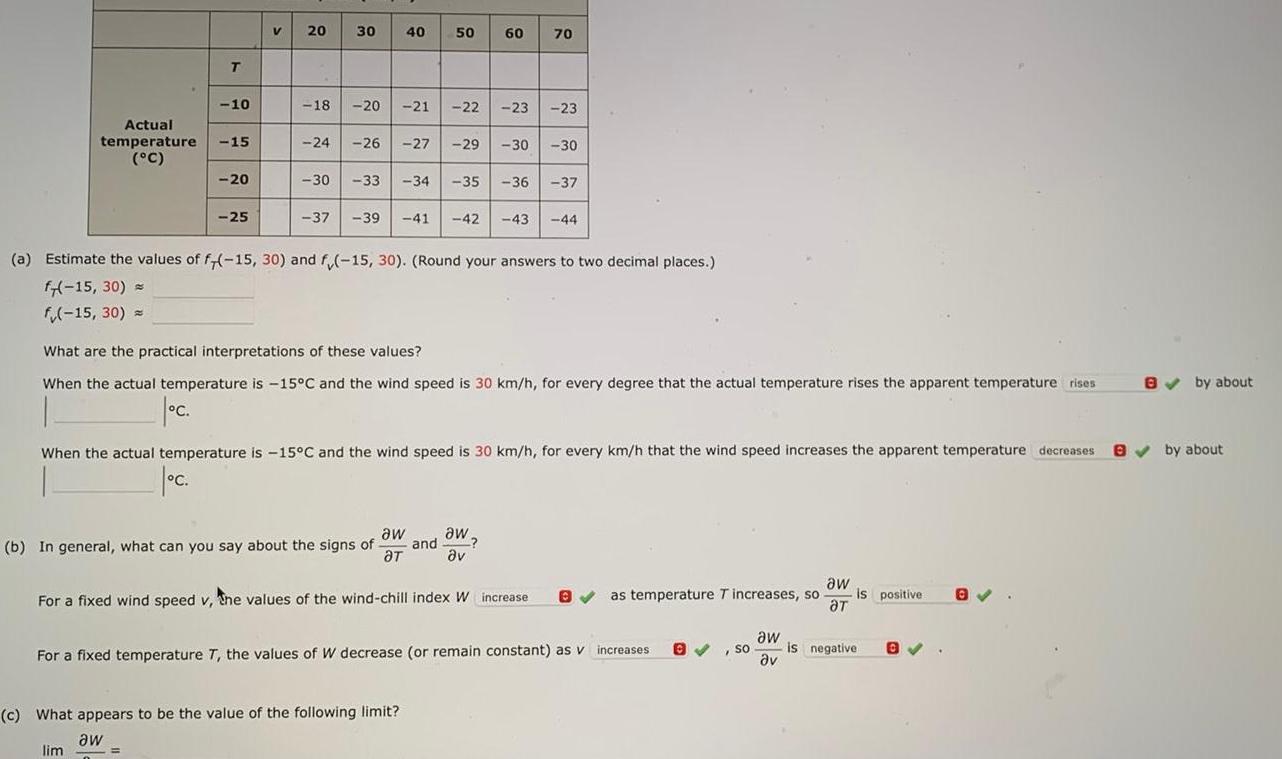
Limits & ContinuityT Actual temperature 15 C 10 C 20 lim 25 V 20 18 30 40 50 60 20 21 24 26 27 aw b In general what can you say about the signs of and T 30 33 34 35 37 39 41 42 22 23 23 c What appears to be the value of the following limit aw 29 30 30 a Estimate the values of f 15 30 and f 15 30 Round your answers to two decimal places f 15 30 f 15 30 36 What are the practical interpretations of these values When the actual temperature is 15 C and the wind speed is 30 km h for every degree that the actual temperature rises the apparent temperature rises 1 When the actual temperature is 15 C and the wind speed is 30 km h for every km h that the wind speed increases the apparent temperature decreases B by about C 70 43 aw v For a fixed wind speed v the values of the wind chill index W increase 37 44 For a fixed temperature T the values of W decrease or remain constant as v increases aw as temperature T increases so is positive T B SO aw is negative v BV B by about

Calculus
Limits & ContinuityFind the first partial derivatives of the function z x sin xy z x z av 11
Calculus
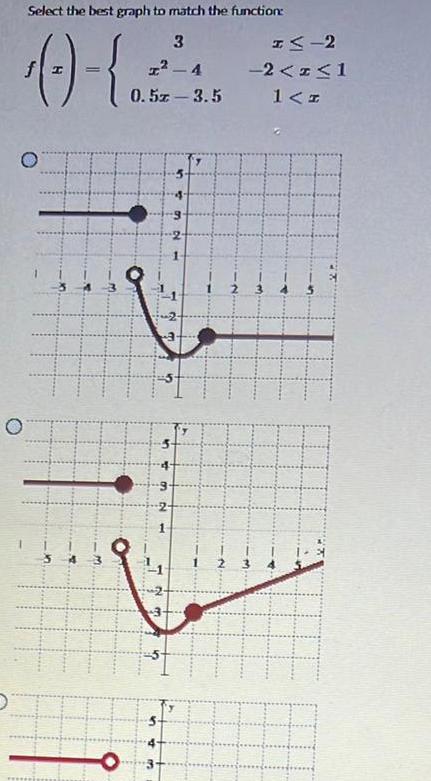
Limits & ContinuityO Select the best graph to match the function 3 0 I 4 0 5 3 5 n V 326 I 2 2 x 1 1 I
Calculus
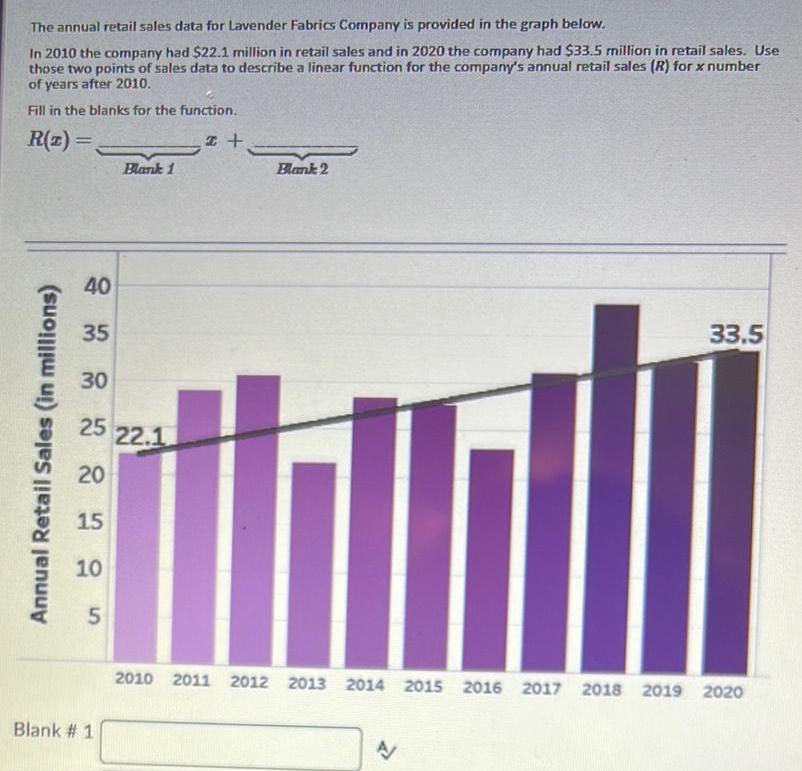
Limits & ContinuityThe annual retail sales data for Lavender Fabrics Company is provided in the graph below In 2010 the company had 22 1 million in retail sales and in 2020 the company had 33 5 million in retail sales Use those two points of sales data to describe a linear function for the company s annual retail sales R for x number of years after 2010 Fill in the blanks for the function R z I Annual Retail Sales in millions 40 35 30 25 22 1 20 15 10 5 Blank 1 Blank 1 Blank 2 33 5 2010 2011 2012 2013 2014 2015 2016 2017 2018 2019 2020 N
Calculus
Limits & ContinuityFind the intercepts of the graph of y 51 9 Do not enter any spaces in the answers The y intercept is the point Enter the x intercepts separated by a comma The x intercepts are the points A
Calculus
Limits & ContinuitySolve the following integral The answer can be determined by rules of antidifferentiation but some algebra may be required beforehand u6 2u 7 u u6 2u 7 du du CORRI
Calculus
Limits & ContinuityWrite the domain of the function in interval notation h x x 8 If necessary use inf for and capital U for union as in inf 0 U 2 inf means 0 U 2 Do not enter any spaces in the answer The domain of his 2



Calculus
Limits & ContinuityUse the graph of the function to determine the points on the graph that results from reflecting the graph horizontally across the Y axis Enter the coordinates of the points on the transformed graph a 4 1 Type your answer here b 3 3 Type your answer here c 2 2 Type your answer here d 1 1 Type your answer here e 2 1 Type your answer here f 4 2 Type your answer here Type your answer here Type your answer here Type your answer here Type your answer here Type your answer here Type your answer here
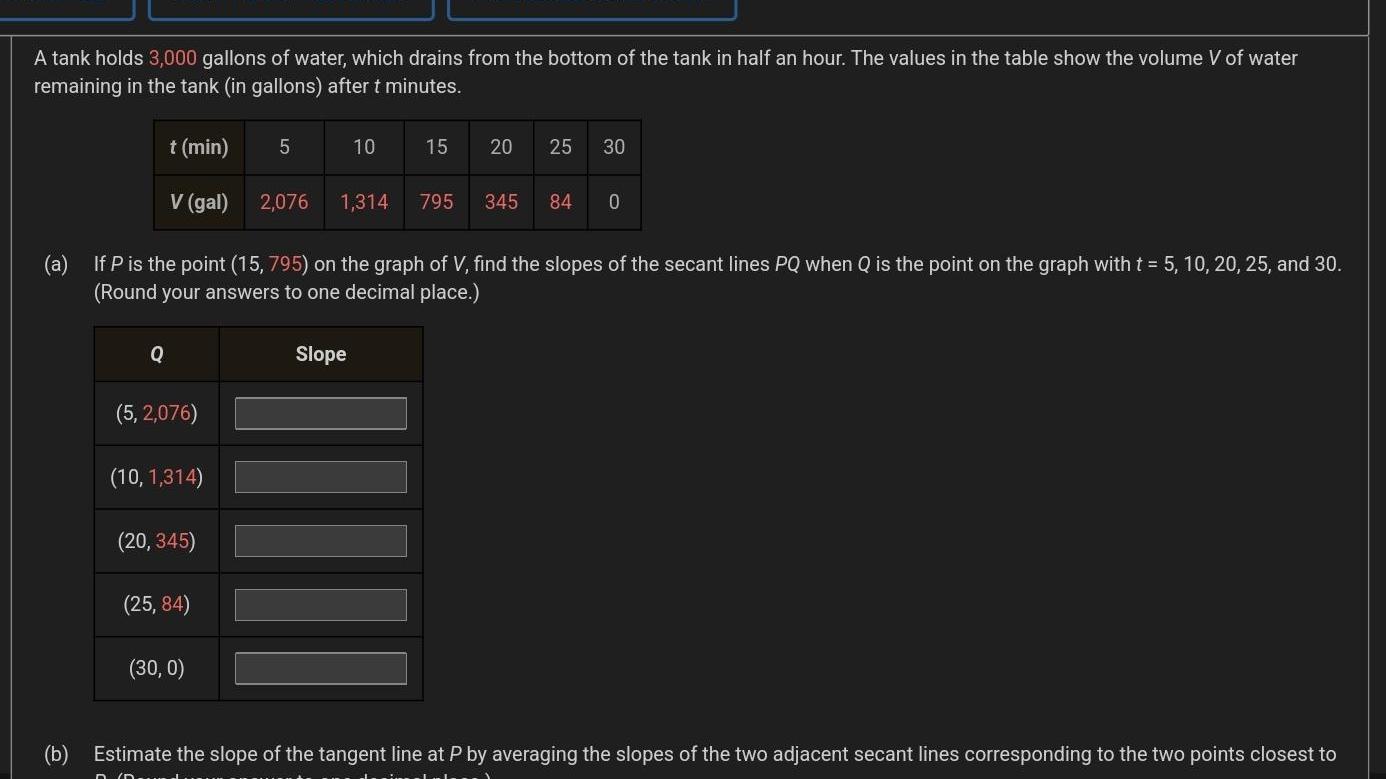
Calculus
Limits & ContinuityA tank holds 3 000 gallons of water which drains from the bottom of the tank in half an hour The values in the table show the volume V of water remaining in the tank in gallons after t minutes b t min V gal Q 5 2 076 10 1 314 20 345 a If P is the point 15 795 on the graph of V find the slopes of the secant lines PQ when Q is the point on the graph with t 5 10 20 25 and 30 Round your answers to one decimal place 25 84 5 30 0 2 076 10 15 Slope 20 25 30 1 314 795 345 84 0 Estimate the slope of the tangent line at P by averaging the slopes of the two adjacent secant lines corresponding to the two points closest to
Calculus
Limits & ContinuityLet f x x 2 Evaluate the function at the given values Then select the appropriate graph that represents this function a f 4 b f 3 c f 2 d f 1 Type your answer here Type your answer here Type your answer here to Type your answer here e f 0 Type your answer here The amph that
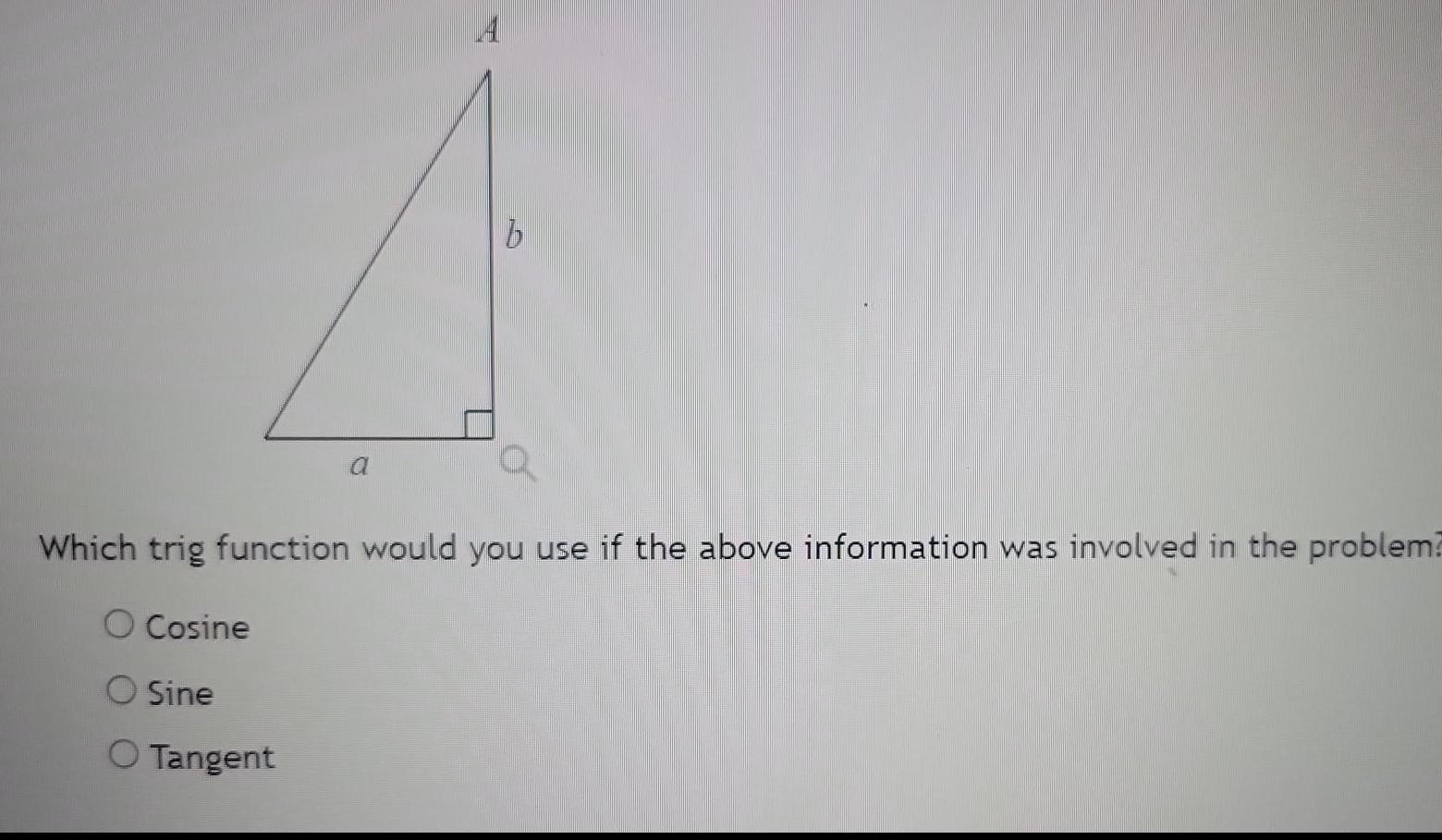
Calculus
Limits & ContinuityCosine A Which trig function would you use if the above information was involved in the problem O Sine O Tangent b
Calculus
Limits & Continuityfo U 2 6 5 Edan Lin TH C 675 GES E G Wil L TH him 7 LE In in 13 2011 15 2 4 2 E 2 3 17 J E 3 7 FH 2 2 7 2 15 Fill HIM 5 141 5 10 EA 123 7 2 173 2 5 1 2 3 2 2 3 4 5 234 FO 2 3 5 OT Z
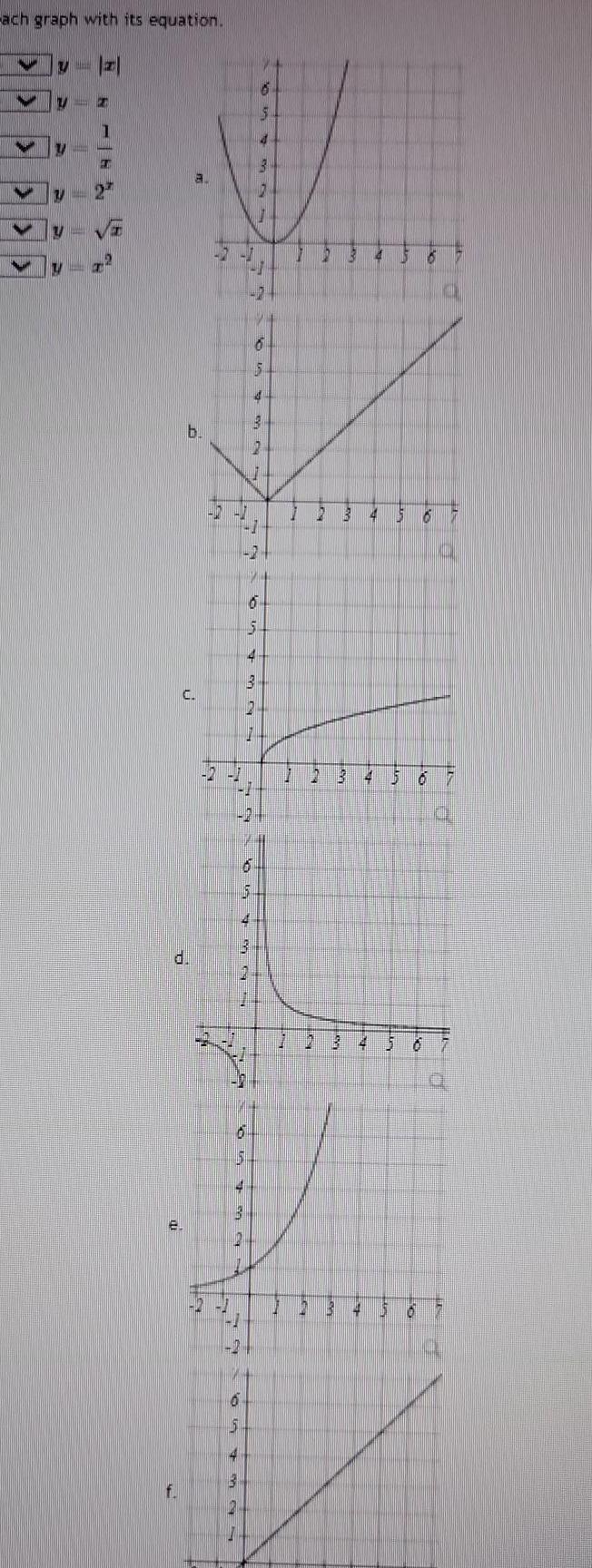
Calculus
Limits & Continuityach graph with its equation A V VL A Z n U 1 I f T 19 a b C d 20 5 4 3 2 0 5 4 19 5 4 3 2 17 6 5 4 3 2 1 19 4 3 2 6 6 I 6 5 4 3 P 16 3 4 14 4 G 5 6 9 19 0 7 1
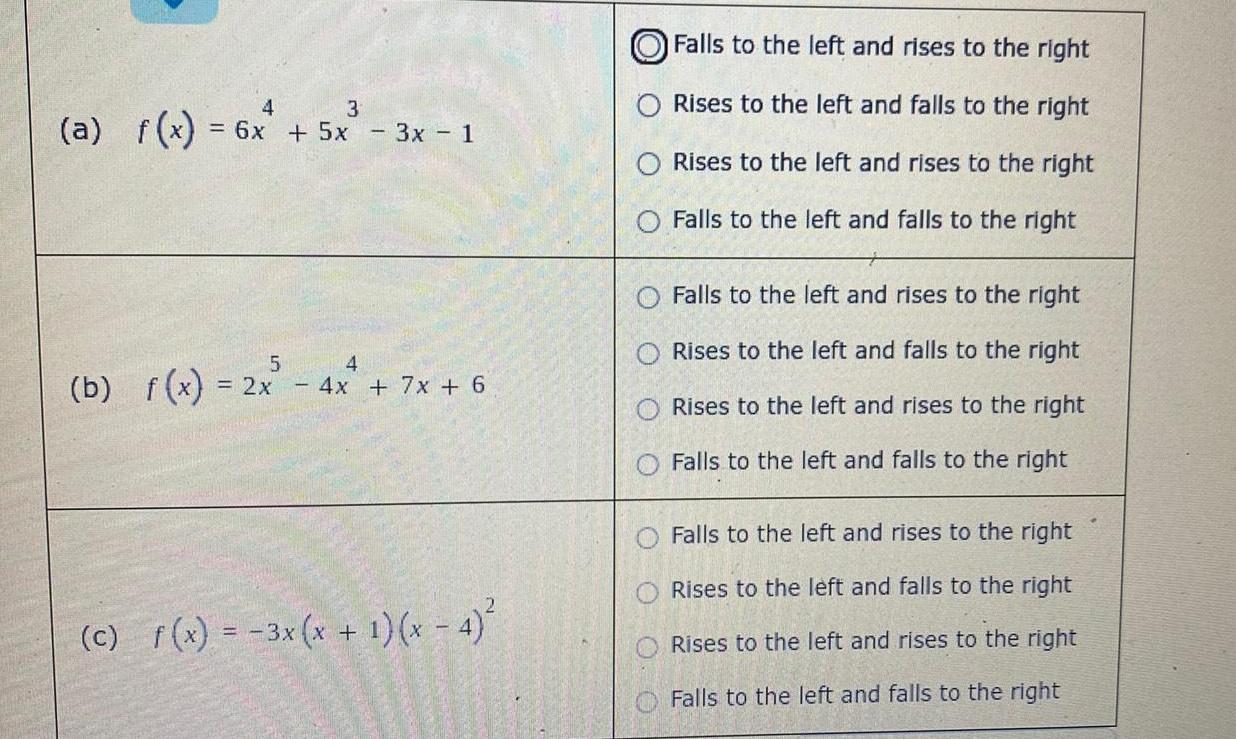
Calculus
Limits & Continuity4 3 a f x 6x 5x 3x 1 5 4 b f x 2x 4x 7x 6 c f x 3x x 1 x 4 OO OO Falls to the left and rises to the right Rises to the left and falls to the right Rises to the left and rises to the right Falls to the left and falls to the right Falls to the left and rises to the right Rises to the left and falls to the right Rises to the left and rises to the right Falls to the left and falls to the right Falls to the left and rises to the right Rises to the left and falls to the right Rises to the left and rises to the right Falls to the left and falls to the right
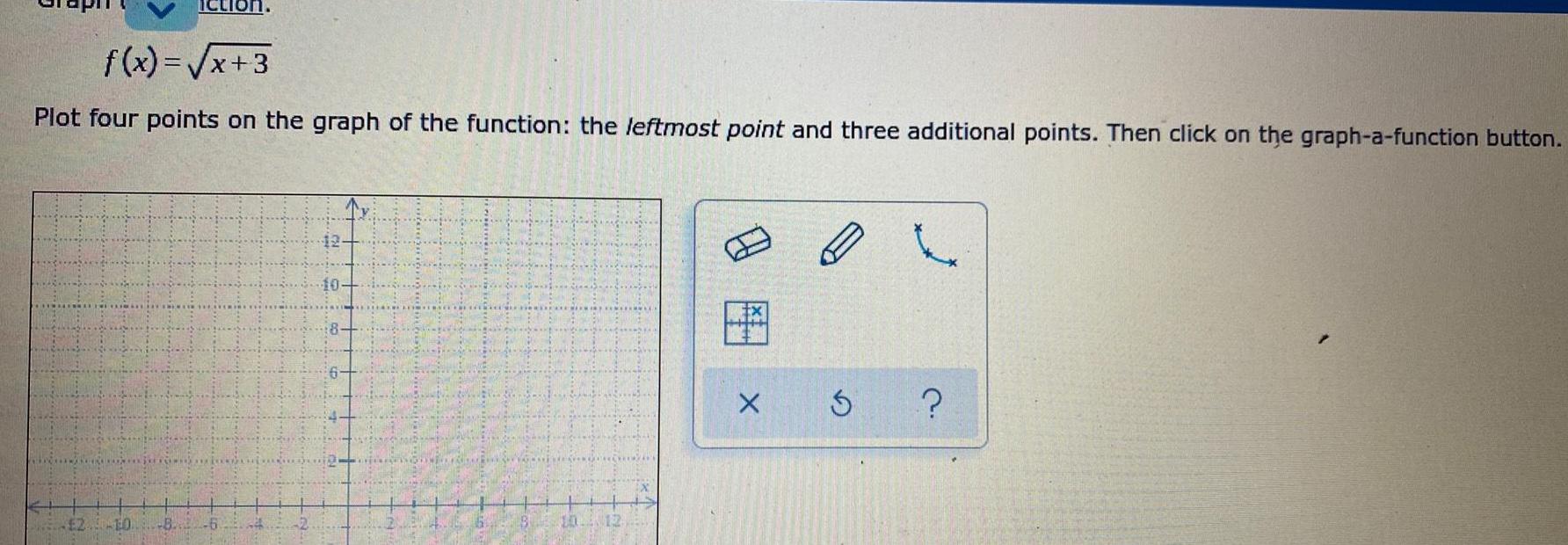
Calculus
Limits & Continuityf x x 3 Plot four points on the graph of the function the leftmost point and three additional points Then click on the graph a function button 2 10 8 6 10 X 5

Calculus
Limits & ContinuityConsider h y 3y 2 7 Determine the intervals on which h is decreasing Oh is decreasing on Oh is decreasing nowhere Determine the intervals on which h is increasing Oh is increasing on Oh is increasing nowhere Determine the value and location of any local minimum of f Enter the solution in y h y form If multiple solutions exist use a comma separated list to enter the solutions Oh has a local minimum at Oh has no local minimum Determine the value and location of any local maximum of f Enter the solution in y h y form If multiple solutions exist use a comma separated list to enter the solutions Oh has a local maximum at h has no local maximum
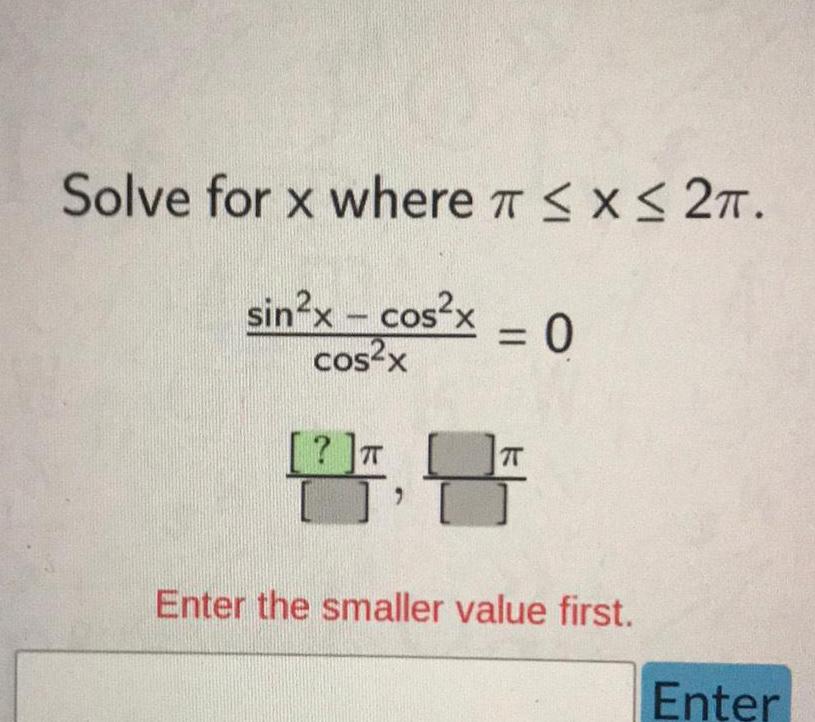
Calculus
Limits & ContinuitySolve for x where T x 2 sin x cos x cos x 0 2 Enter the smaller value first Enter

Calculus
Limits & ContinuityWrite the domain of the function in interval notation O a 0 00 Ob 0 5 U 5 Od 0 3 U 3 00 Q 2 5 U 5 3 U 3 00
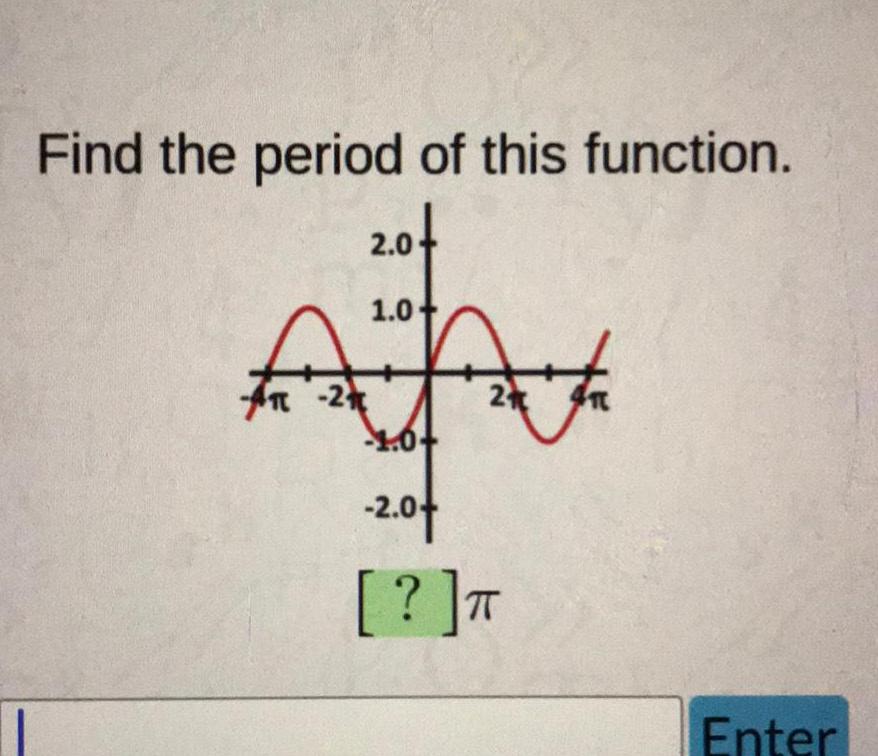

Calculus
Limits & ContinuityTo test this series for convergence d n 1 n n4 6 You could use the Limit Comparison Test comparing it to the series S n Completing the test it shows the series O Converges O Diverges 1 np where p
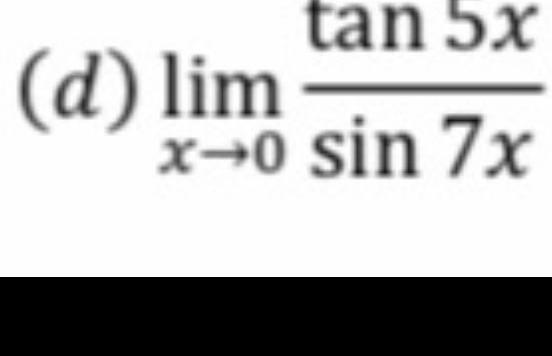

Calculus
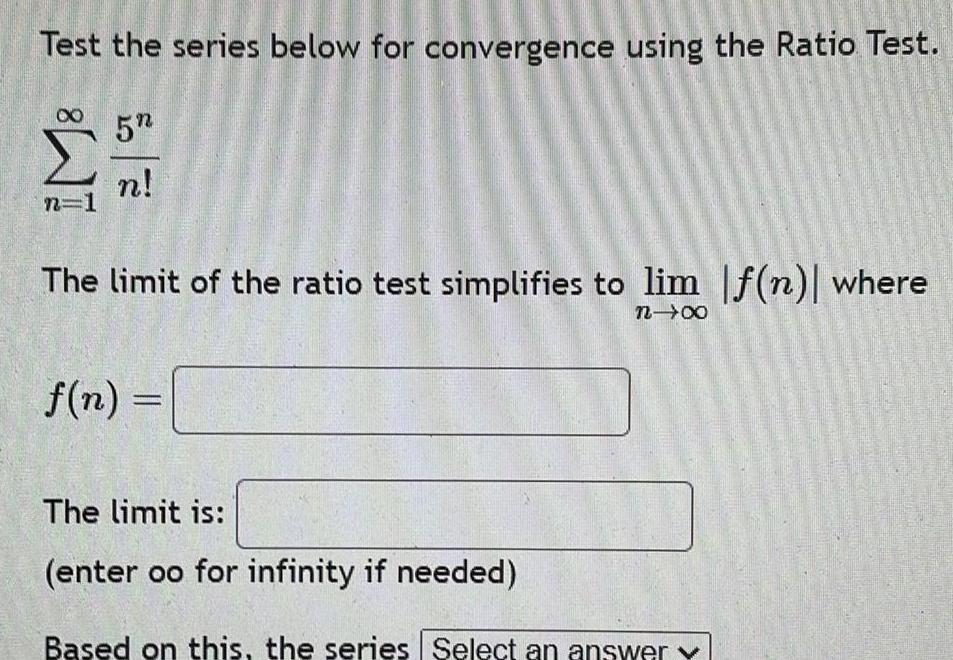
Limits & ContinuityTest the series below for convergence using the Ratio Test n 1 5 n The limit of the ratio test simplifies to lim f n where n f n C The limit is enter oo for infinity if needed Based on this the series Select an answer y

Calculus
Limits & Continuityet A R be a function that is continuous on AC R For n N define the function f by se x f x for x E A Prove that this f is continuous on A