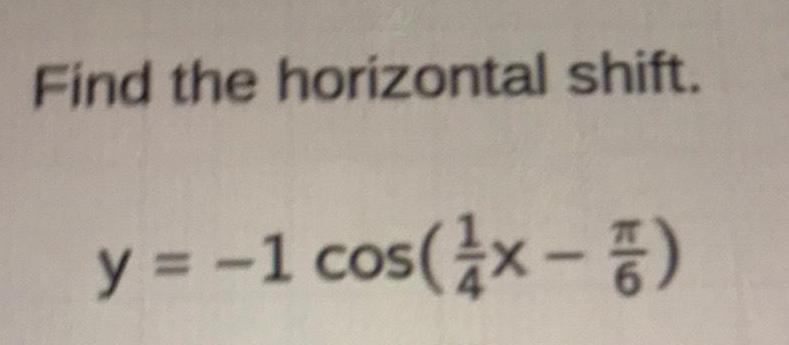Limits & Continuity Questions and Answers
Calculus
Limits & ContinuityWhat are the quotient and remainder when 5x4 - 3x² is divided by x³ -
x²
y x²³ - x² +1?
The quotient is and the remainder is.
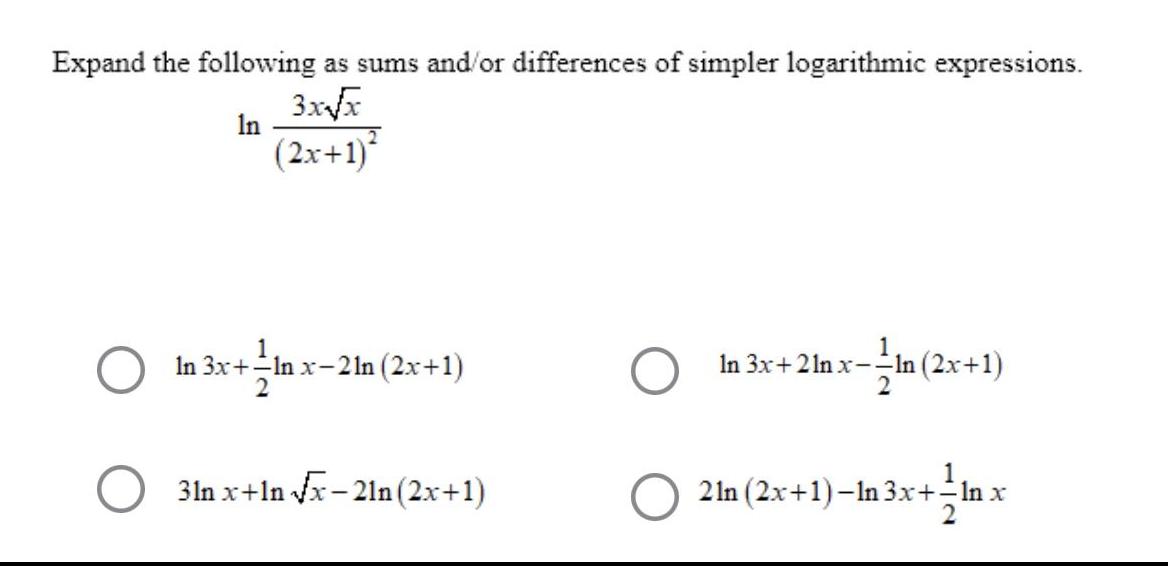
Calculus
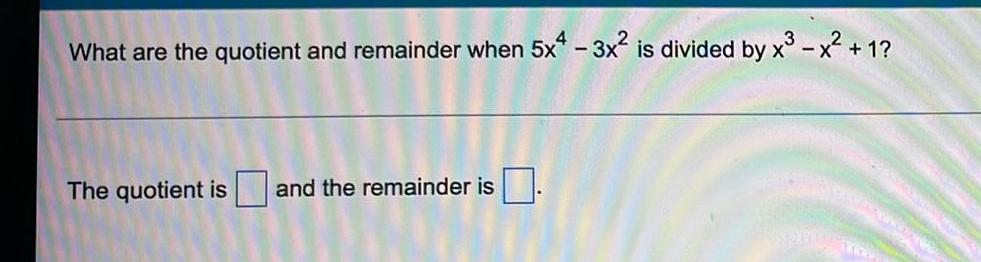
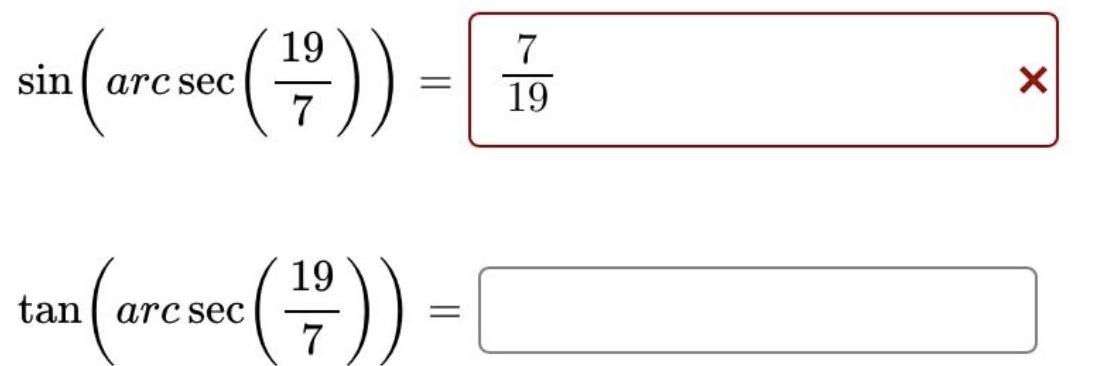
Limits & ContinuityExpand the following as sums and/or differences of simpler logarithmic expressions.
In
3x√√x
(2x+1)²
1
In 3x+-In x-21n (2x+1)
31n x+In √x-21n (2x+1)
1
In 3x+2lnx--In (2x+1)
x-In (2x+1)
1
21n (2x+1)-In 3x+ - ln
3x+ ln x
x

Calculus
Limits & ContinuitySelect the statement(s) that are true about sampling distributions.
1. The shape of all sampling distributions are approximately normal.
2. The mean of the sampling distribution of a is equal to the mean of the distribution from which the sample was taken.
3. The standard deviation of the sampling distribution of a is equal to the standard deviation of the distribution from
which the sample was taken divided by the sample size.
4. The shape of all sampling distributions are symmetrical.
01&3
2 only
3 only
0184
None of the above

Calculus
Limits & ContinuityA cell site is a site where electronic communications equipment is placed in a cellular network for the use of
mobile phones. The numbers of cell sites from 1985 through 2008 can be modeled by y =
237,101
1+1950e-0.355t
where t represents the year, with t=5 corresponding to 1985. Use the model to find the numbers of cell
sites in the year 2007
O209,071
O 207,071
O 211,071
O 210,071
O 208,071
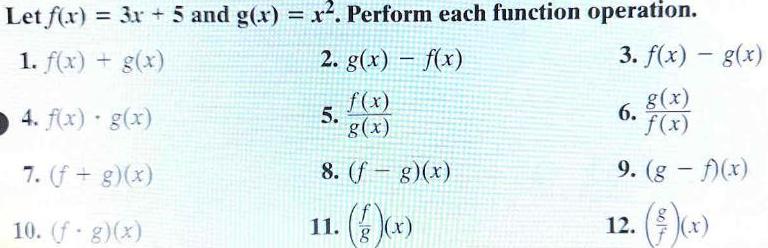
Calculus
Limits & ContinuityLet f(x) = 3x + 5 and g(x) = x². Perform each function operation.
2. g(x) = f(x)
1. f(x) + g(x)
-
3. f(x) - g(x)
4. f(x) · g(x)
7. (f + g)(x)
10. (f- g)(x)
.
f(x)
g(x)
8. (f- g)(x)
11. (g)(x)
5.
6.
f(x)
9. (g - f)(x)
12. ()(x)

Calculus
Limits & ContinuityA cheesecake has equally sized slices. Each slice is a different flavor. The diameter of the cheesecake is 10 inches, and the area of the
25T
slice of blueberry cheesecake is
12 square inches.
How many slices does the cheesecake have?
slices

Calculus
Limits & ContinuityA mass weighing 4 pounds is attached to a spring whose spring constant is 25 lb/ft. What is the period of simple harmonic motion?
S

Calculus
Limits & ContinuityA population of bees are dying at the rate proportional to the size of the initial hive, H(t), where t is measured in days. If the hive has 500 bees June 1st, and only 450 bees 15 days later, how many bees will there be 30 days later? Round your answer to the nearest bee, and assume the growth is proportional to initial population.
O 300
O 400
O 405
425
Calculus
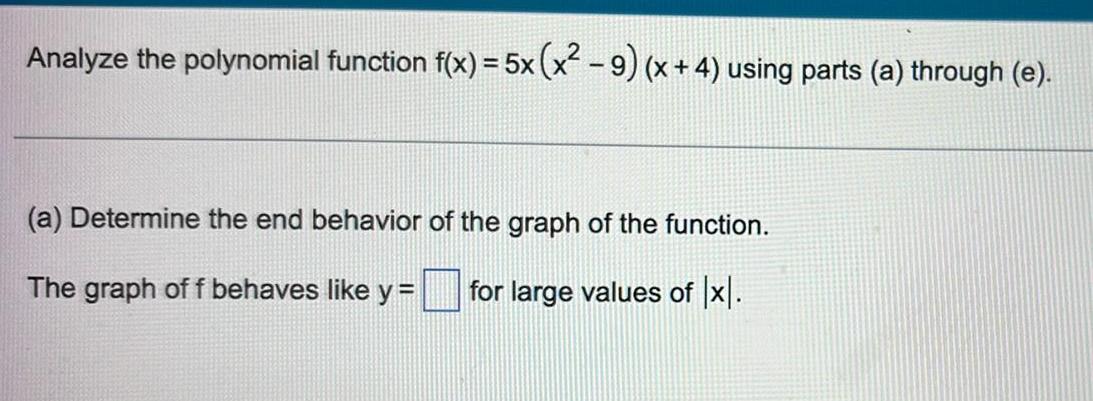
Limits & ContinuityAnalyze the polynomial function f(x) = 5x (x² − 9) (x + 4) using parts (a) through (e).
(a) Determine the end behavior of the graph of the function.
The graph of f behaves like y =___for large values of |x|.

Calculus
Limits & ContinuityFind a polynomial f (x) of degree 4 that has the following zeros.
5, 0, 7, -2
Leave your answer in factored form.
Calculus
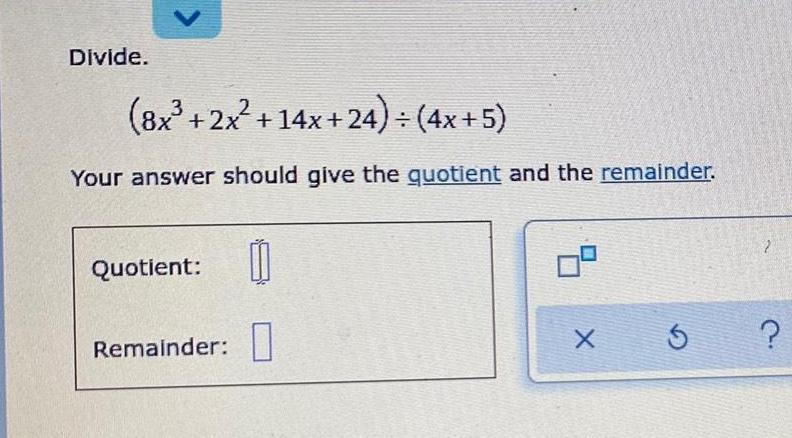
Limits & ContinuityDivide.
(8x²³ + 2x² +14x+24) ÷ (4x+5)
Your answer should give the quotient and the remainder.
Quotient:
Remainder:
0
9
X
5
?
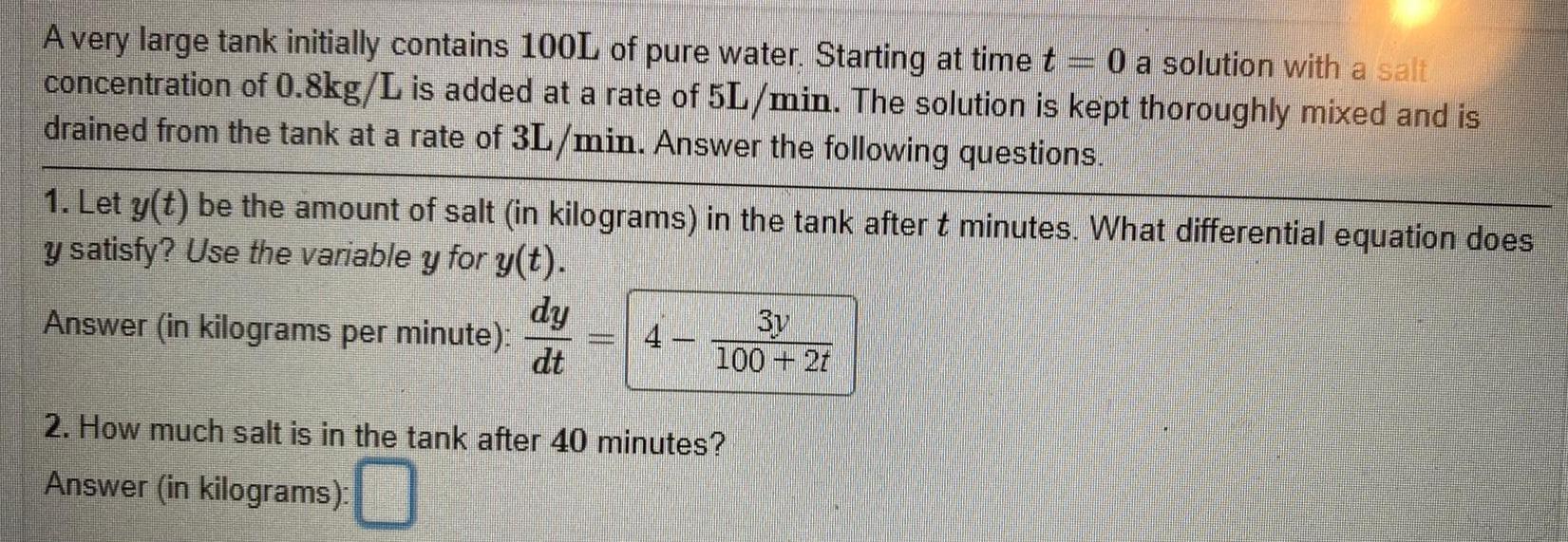
Calculus
Limits & Continuitywww
0 a solution with a salt
A very large tank initially contains 100L of pure water. Starting at time t
concentration of 0.8kg/L is added at a rate of 5L/min. The solution is kept thoroughly mixed and is
drained from the tank at a rate of 3L/min. Answer the following questions.
1. Let y(t) be the amount of salt (in kilograms) in the tank after t minutes. What differential equation does
y satisfy? Use the variable y for y(t).
Answer (in kilograms per minute):
dy
dt
m
3y
100 + 2t
2. How much salt is in the tank after 40 minutes?
Answer (in kilograms):
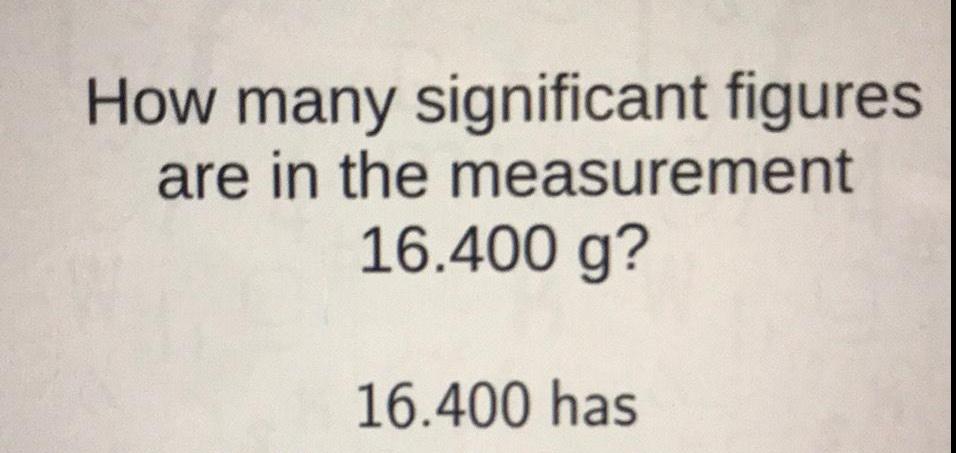

Calculus
Limits & ContinuityCalculate the volume of the
cube and report the answer
to the correct number of
significant figures.
2.20 cm x 2.215 cm x 2.2 cm

Calculus
Limits & ContinuityGraph the parabola.
2
y=x² +6x+4
Plot five points on the parabola: the vertex, two points to the left of the vertex, and two points to the right of the vertex. Then click on the grap
button.

Calculus
Limits & ContinuityA lighthouse is located 160 feet from the nearest point P on a straight shoreline. The revolving beacon in the lighthouse makes one revolution every 10 seconds. Find the rate at which a ray from the light moves along the shore at a point 115 feet from P.

Calculus
Limits & ContinuitySketch a graph of f(x)
Solution:
-
3
X - 2x² - 3x
2
x² + 3x + 2
Before answering this question, we need to factor
f(x). Factor f(x) completely and submit your
answer below.
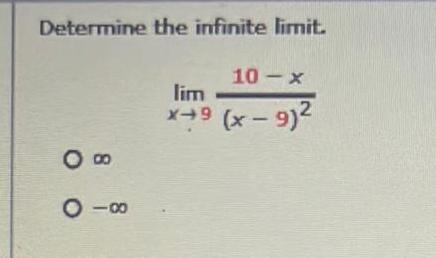

Calculus
Limits & ContinuityFor the function f, how would you remove the discontinuity? In other words, how would you define /(2) In order for fto be continuous at 27
(2)=1
f(x) =
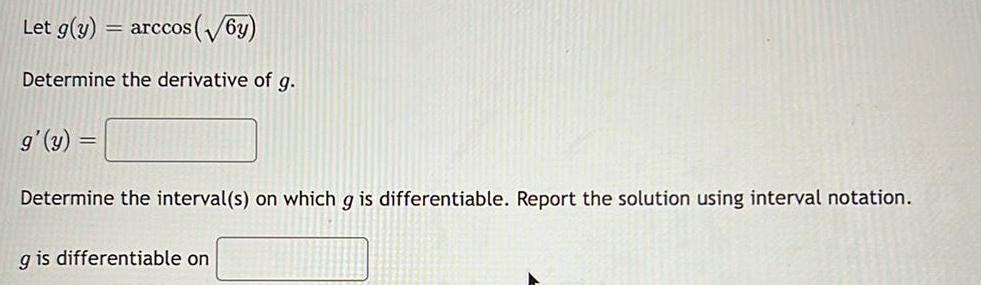
Calculus
Limits & ContinuityLet g(y) = arccos (√6y)
Determine the derivative of g.
g'(y)
Determine the interval(s) on which g is differentiable. Report the solution using interval notation.
=
g is differentiable on

![Find x where 0≤x≤ 2.
4√2 tan x-√√2 = 3√2 tan >
x
π
[?]'
+
T](https://media.kunduz.com/media/sug-question/raw/84128392-1660406992.6488218.jpeg?w=256)

Calculus
Limits & ContinuityUse Newton's method to approximate the indicated root of the equation correct to six decimal places. The positive root of 6 sin x = x² X =____
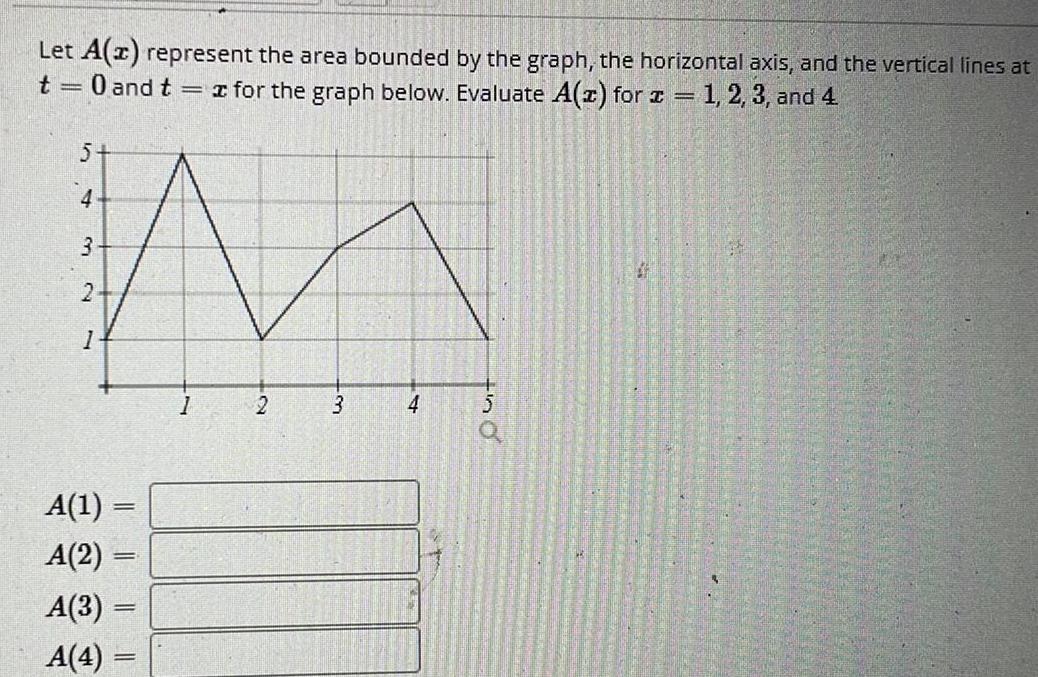
Calculus
Limits & ContinuityLet A(z) represent the area bounded by the graph, the horizontal axis, and the vertical lines at
t= 0 and t = for the graph below. Evaluate A(z) for x = 1, 2, 3, and 4
5
M
2
4
3
A(1) =
=
A(2)
-
A(3)
A(4) =
=
3
4

Calculus
Limits & ContinuityFind lim h(x), if it exists.
X→∞
f(x) = 4x² + 2x + 6
(a)
h(x) =
lim h(x) =
X→∞
(b) h(x) =
lim h(x) =
X-8
(c) h(x) =
=
lim h(x) =
X-8
f(x)
X
f(x)
x²
f(x)
+3
![Find x if π ≤ x ≤ 2π
2csc²x cos5x = √2cot²x cos²x
X=
[?] | JTC
2
4](https://media.kunduz.com/media/sug-question/raw/84128473-1660406728.2150514.jpeg?w=256)
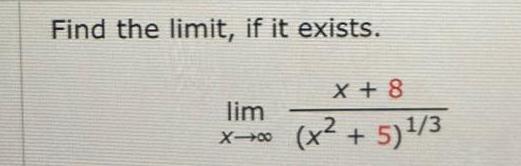
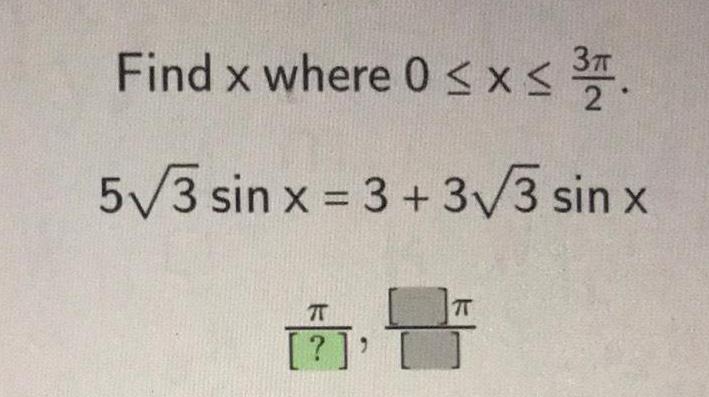
Calculus
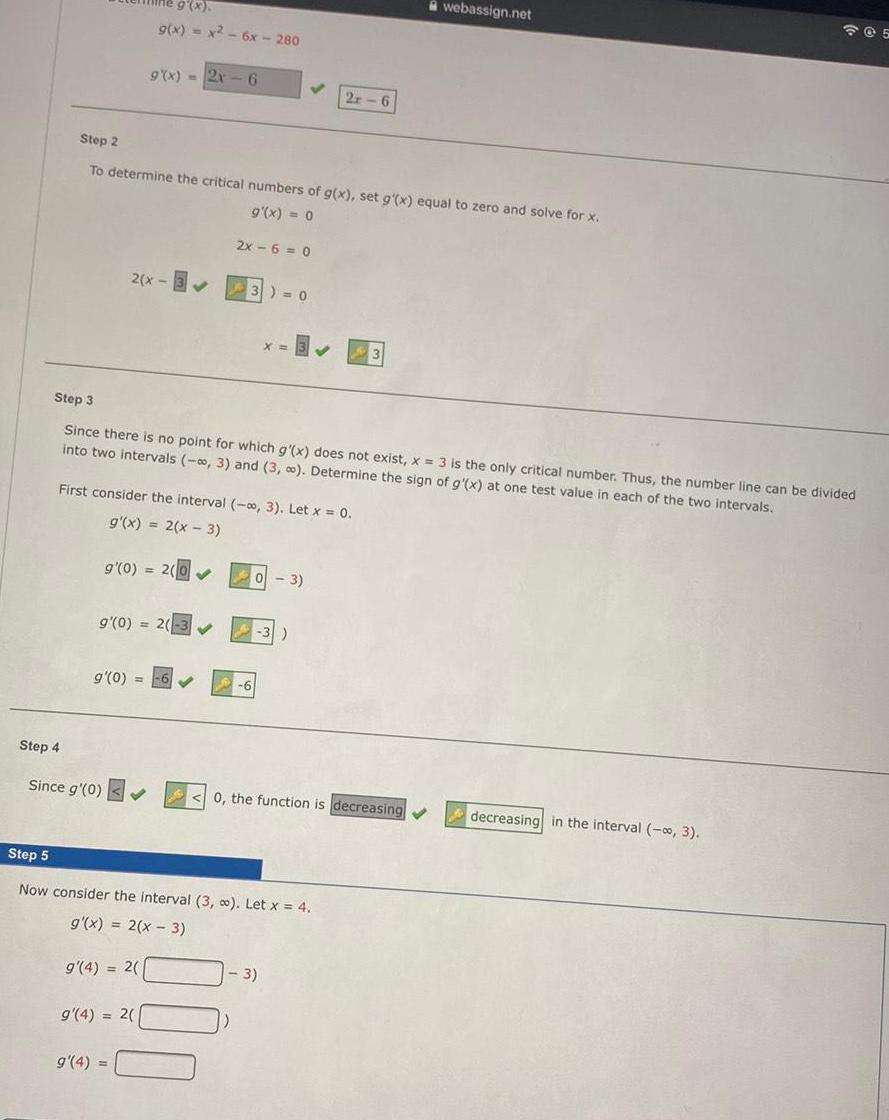
Limits & ContinuityStep 4
Step 2
To determine the critical numbers of g(x), set g'(x) equal to zero and solve for x.
g'(x) = 0
g(x).
g(x) = x² - 6x - 280
2(x-33) = 0
g'(0) =
9(x)=2x-6
g'(0) = 2(-3✔
Since g'(0) ✓
First consider the interval (-∞, 3). Let x = 0.
g'(x) = 2(x-3)
9'(0) = 2(0✔
Step 3
Since there is no point for which g'(x) does not exist, x = 3 is the only critical number. Thus, the number line can be divided
into two intervals (-∞, 3) and (3, ∞). Determine the sign of g'(x) at one test value in each of the two intervals.
g'(4) = 2(
g'(4) = 2(
g'(4) =
2x-6=0
✓
X=
Step 5
Now consider the interval (3, ∞). Let x = 4.
g'(x) = 2(x - 3)
2r-6
- 3)
-3)
- 3)
0, the function is decreasing ✔
webassign.net
205
decreasing in the interval (-∞, 3).
Calculus
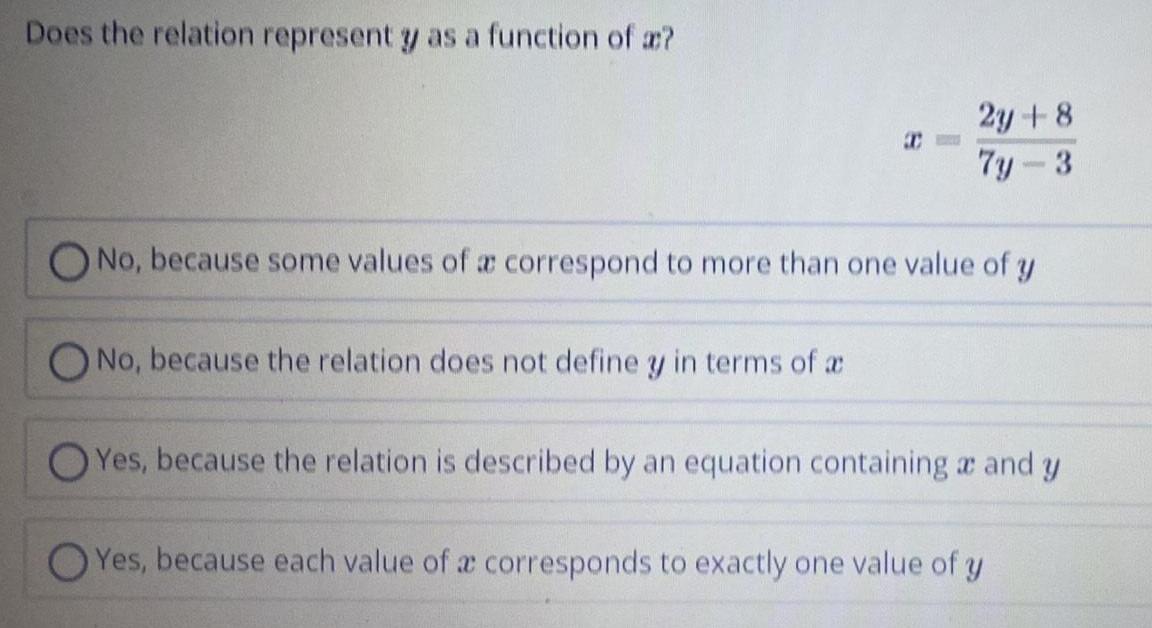
Limits & ContinuityDoes the relation represent y as a function of a?
2y +8
7y-3
No, because some values of a correspond to more than one value of y
No, because the relation does not define y in terms of a
Yes, because the relation is described by an equation containing and y
Yes, because each value of a corresponds to exactly one value of y

Calculus
Limits & ContinuityFind each limit if it exists.
5x3/2
(a)
(b)
(c)
lim.
x-* 8x²
lim
X→
+5
5x3/2
8x3/2 + 5
5x3/2
lim
x 8√x+5
→∞
11
11
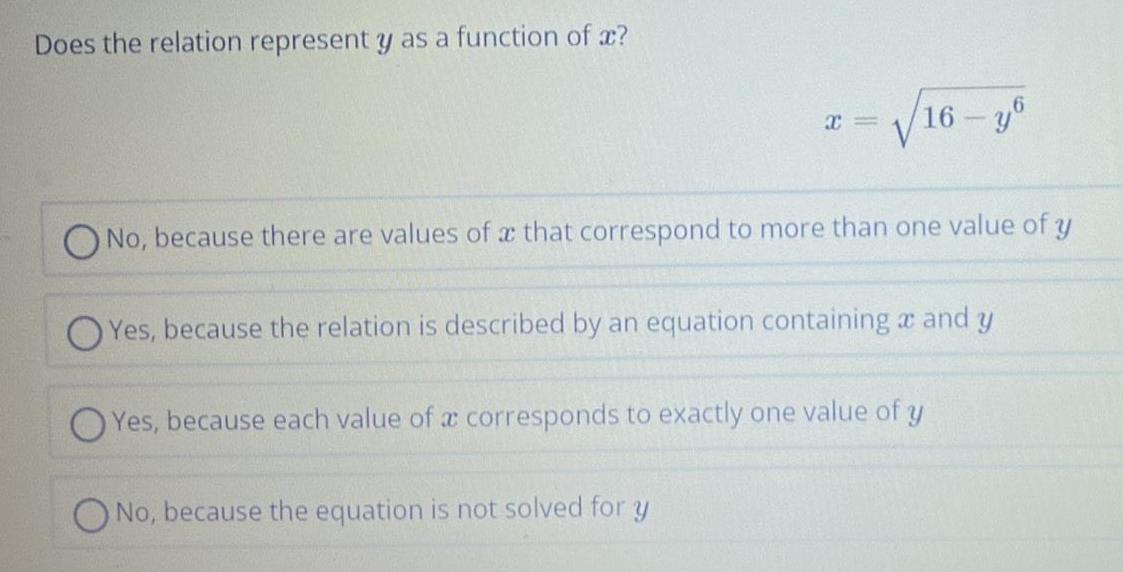
Calculus
Limits & ContinuityDoes the relation represent y as a function of x?
x=
√√16-y6
No, because there are values of a that correspond to more than one value of y
Yes, because the relation is described by an equation containing and y
No, because the equation is not solved for y
Yes, because each value of a corresponds to exactly one value of y
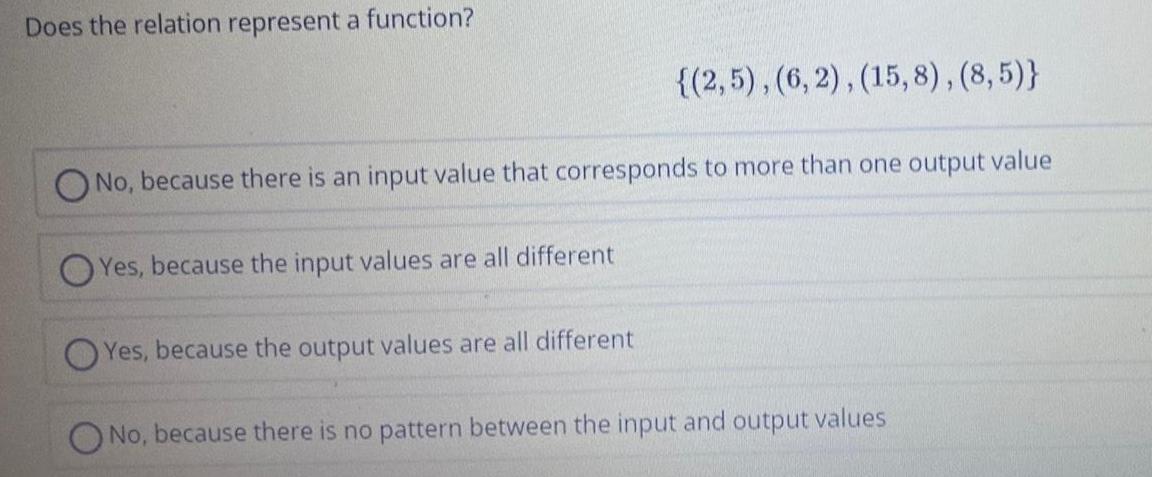
Calculus
Limits & ContinuityDoes the relation represent a function?
No, because there is an input value that corresponds to more than one output value
Yes, because the input values are all different
{(2,5), (6,2), (15,8), (8,5)}
Yes, because the output values are all different
No, because there is no pattern between the input and output values

Calculus
Limits & ContinuityDoes the relation represent a function?
No, because r appears as both an input value and an output value
Yes, because the ordered pairs are distinct
{(p, q), (r,s), (p,r)}
No, because the input value p corresponds to two different output values
Yes, because the output values are all different
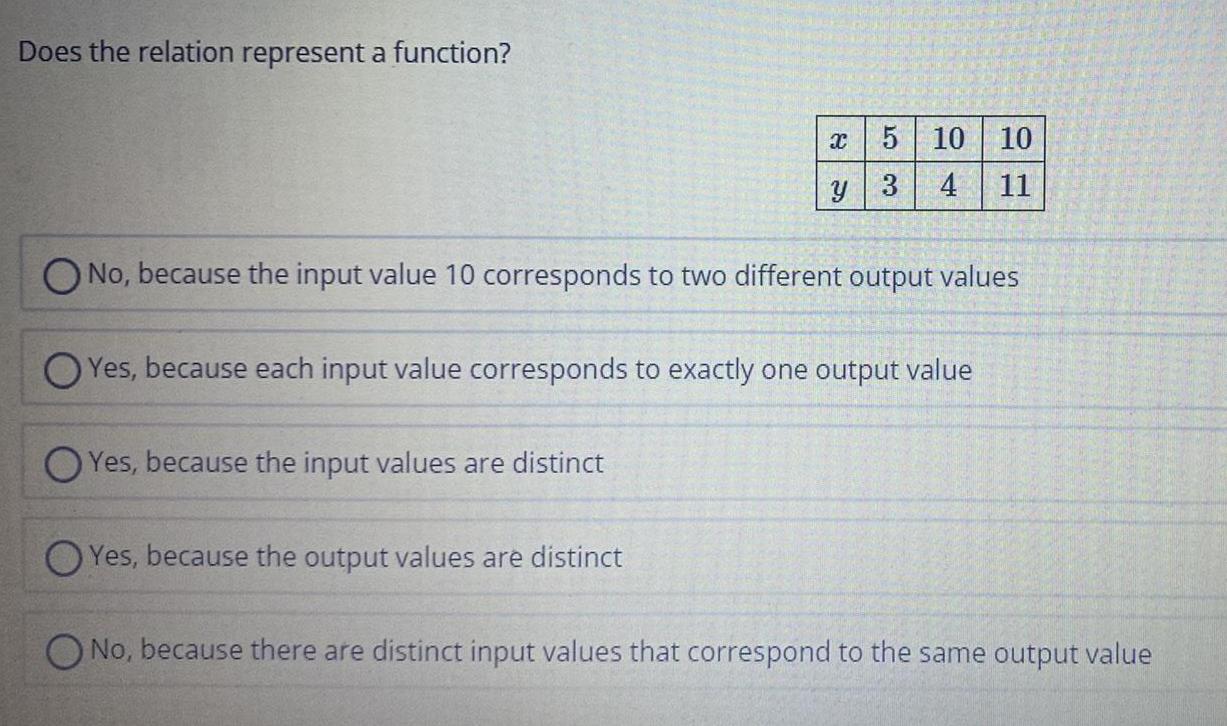
Calculus
Limits & ContinuityDoes the relation represent a function?
X
y
OYes, because the input values are distinct
OYes, because the output values are distinct
5
3
10 10
4 11
O No, because the input value 10 corresponds to two different output values
Yes, because each input value corresponds to exactly one output value
No, because there are distinct input values that correspond to the same output value

Calculus
Limits & Continuitytypes of numbers that make up the set of real numbers:
● Natural numbers: 1, 2, 3, 4, ...
• Integers:
,-3, -2,-1,0,1,2,3,...
●
Rational numbers: ratios of integers.
Examples:
2
***
5
--
23
0.23 =
100
Irrational numbers: real numbers that cannot be written as ratios of two
integers Examples: √2, T
35:
35
-
#6 Consider the set of numbers given in the set
{0,-8, 25, 27, √5, 0.492, -, V2, 0.3=
List the numbers that are
a) Natural numbers:
b) Integers:
c) Rational numbers:
d) Irrational numbers:
e) Real numbers:

Calculus
Limits & Continuity#7 Write an algebraic equation to represent the given information. Let x be the first number and y be
the second number.
a) the sum of the two numbers is 10
b) the first number is 2 more than the second number
c) the first number is twice the second number
d) The first number is 2 less than twice the second number
e) The square of the first number is 2 times the second number.
f) The total of the first number and ½ of the second number is 17.
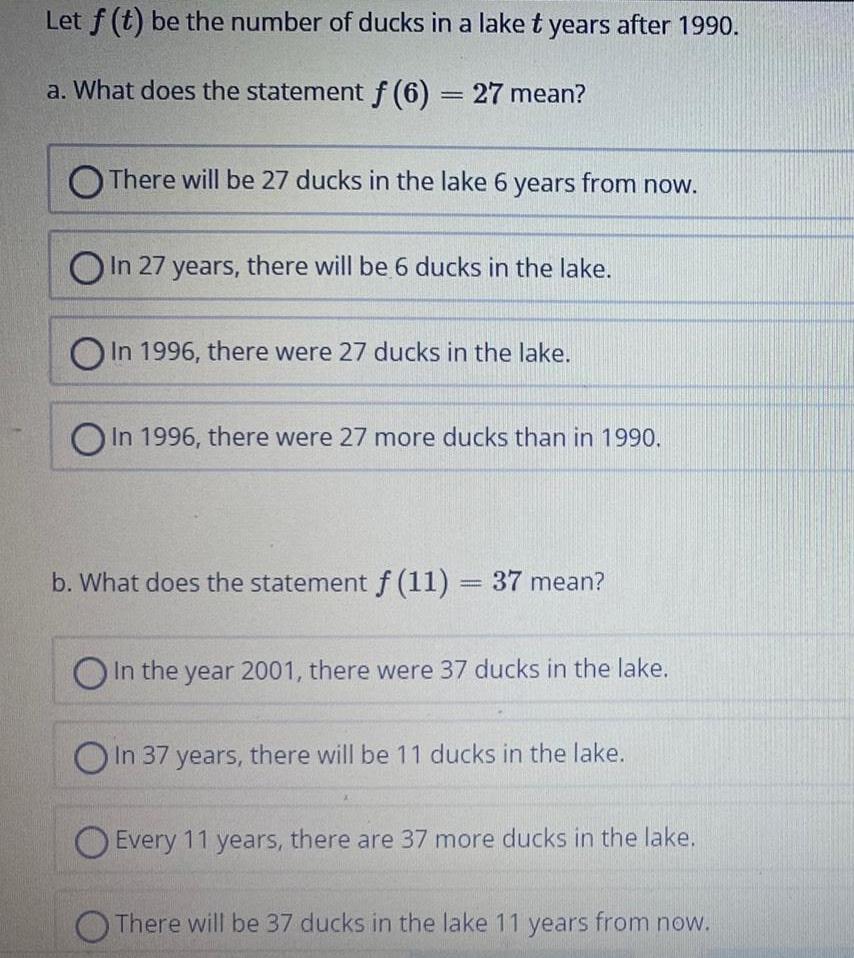
Calculus
Limits & ContinuityLet f (t) be the number of ducks in a lake t years after 1990.
a. What does the statement f (6) = 27 mean?
There will be 27 ducks in the lake 6 years from now.
In 27 years, there will be 6 ducks in the lake.
In 1996, there were 27 ducks in the lake.
In 1996, there were 27 more ducks than in 1990.
b. What does the statement f (11) = 37 mean?
O In the year 2001, there were 37 ducks in the lake.
O In 37 years, there will be 11 ducks in the lake.
Every 11 years, there are 37 more ducks in the lake.
There will be 37 ducks in the lake 11 years from now.
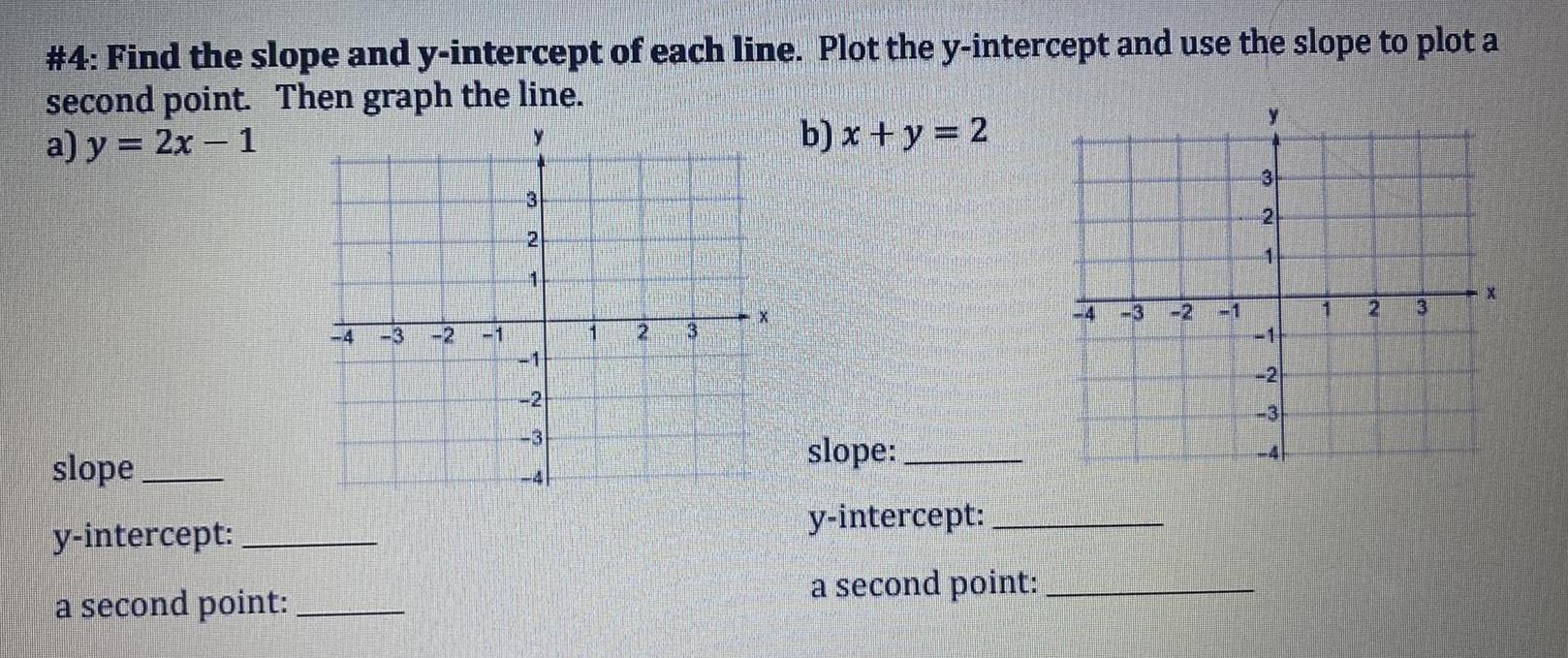
Calculus
Limits & Continuity#4: Find the slope and y-intercept of each line. Plot the y-intercept and use the slope to plot a
second point. Then graph the line.
a) y = 2x - 1
Y
b) x+y=2
slope
y-intercept:
a second point:
-4 -3 -2 -1
3
2
7
-2
-3
-4
2
3
X
slope:
y-intercept:
a second point:
-4 -3 -2
3
2
1
-
-2
-3
1
2
3
X
![An object oscillates as it moves along
the x-axis. Its displacement varies with
time according to the equation
x = 3 cos (8mt + 1)
where t is in seconds
What is the frequency of this motion?
[?] hertz](https://media.kunduz.com/media/sug-question/raw/84108965-1660406104.6580064.jpeg?w=256)
Calculus
Limits & ContinuityAn object oscillates as it moves along
the x-axis. Its displacement varies with
time according to the equation
x = 3 cos (8mt + 1)
where t is in seconds
What is the frequency of this motion?
[?] hertz
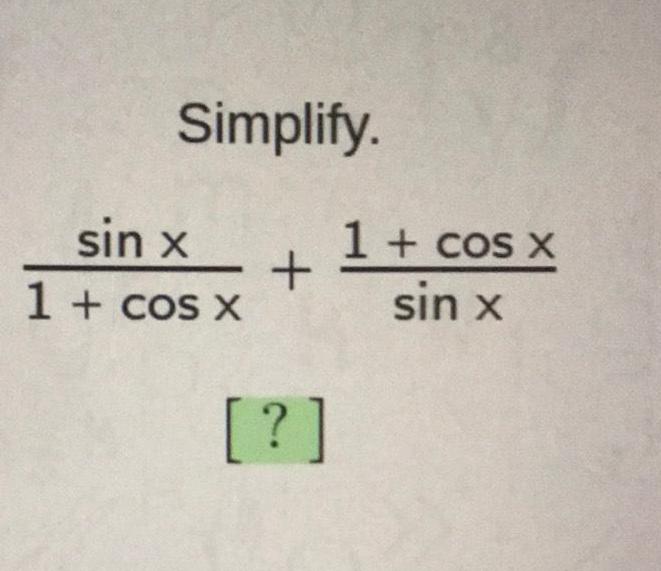

Calculus
Limits & ContinuitySolve the equation using U-substitution and enter the solution set below. Separate the solutions by a comma. Arrange the
solutions in order from smallest to largest. Do not insert any blank spaces in your answer. For fractional answers, use the /symbol,
e.g. 3/2.
(2x + 5)² - 7(2x + 5) - 30 = 0
![How many significant figures are in the number 24.32?
24.32 has [?] significant figures.](https://media.kunduz.com/media/sug-question/raw/84121140-1660405012.0489564.jpeg?w=256)
Calculus
Limits & ContinuityHow many significant figures are in the number 24.32?
24.32 has [?] significant figures.

Calculus
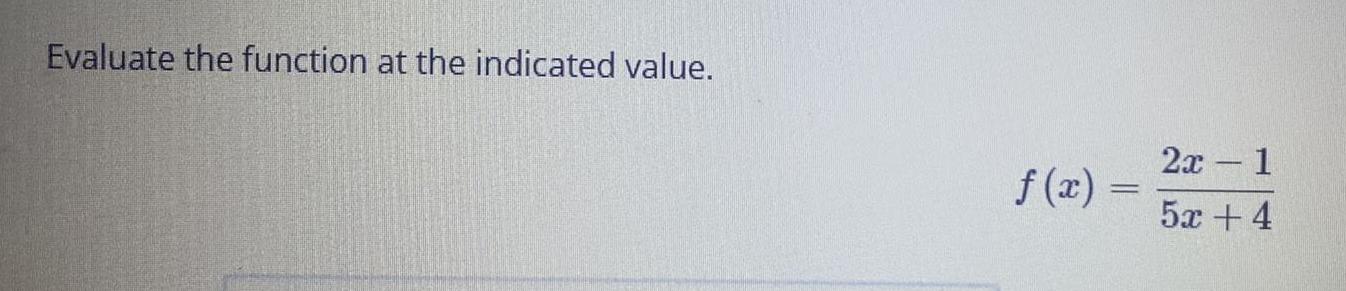
Limits & ContinuitySolve the equation. Enter your answer in solution set notation listing the solutions in order from smallest to largest separated by a comma. Do not include any blank spaces in your answer. (Example: (-1,5,8))
x³5x² - 4x + 20 = 0

Calculus
Limits & ContinuityThe equation describes a 3x2-y+z2
(A) elliptic paraboloid
(B) ellipse
(C) one-sheeted hyperboloid
(D) hyperbolic paraboloid
(E) two-sheeted hyperboloid
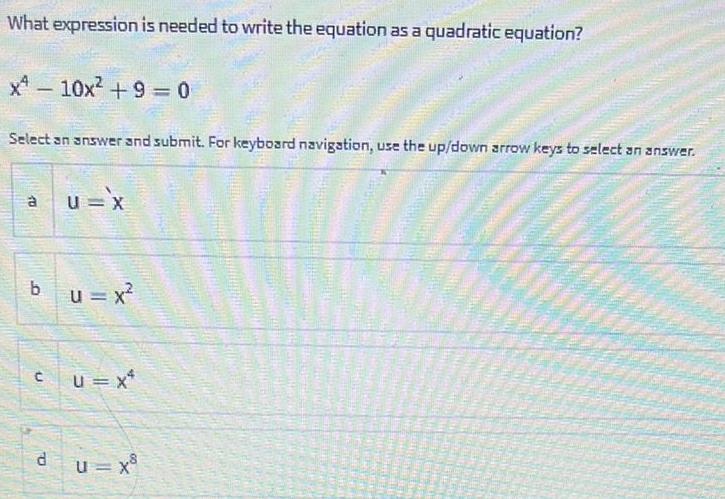
Calculus
Limits & ContinuityWhat expression is needed to write the equation as a quadratic equation?
x10x² +9=0
Select an answer and submit. For keyboard navigation, use the up/down arrow keys to select an answer.
a u='x
b u = x²
c u = x²
d u = x³

Calculus
Limits & ContinuityWhich vocabulary word has the following origin?from Latin acadēmia
A. persistent
B. resilient
C. eloquent
D. academy