Differential equations Questions and Answers
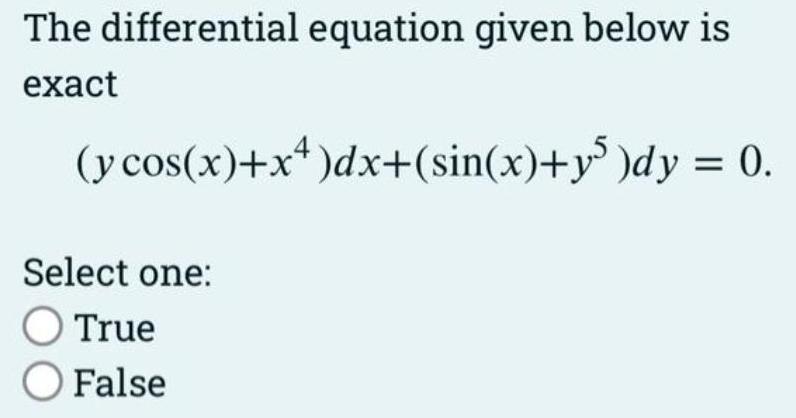
Calculus
Differential equationsThe differential equation given below is exact
(y cos(x)+x^4)dx+(sin(x)+y^5 )dy = 0.
Select one:
True
False

Calculus
Differential equationsThe bird flu is considered dangerous when the number of people getting sick is growing at a rate proportional to the number of people infected. Public health workers track bird flu infection rates and notice that the number of cases is doubling every day. Let F(t) be the number of people infected by the flu, where t is measured in days. Use differential equations to find the general solution to for F(t), where F(0) = 50 is the initial population.
A. F(t) = 50/e^0.6931t
B. F(t) = e^0.6931t/50
C. F(t) = 50e^-0.6931t
D. F(t) = 50e^0.6931t
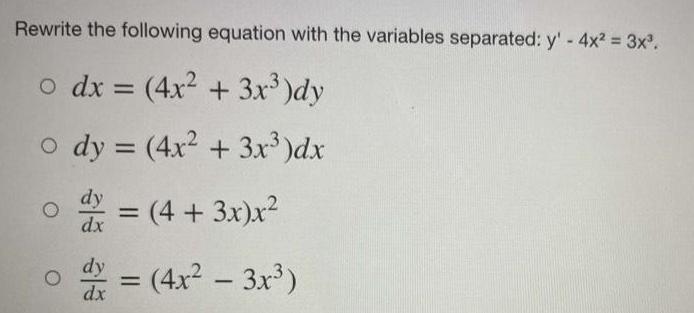
Calculus
Differential equationsRewrite the following equation with the variables separated: y' - 4x² = 3x³.
A. dx = (4x² + 3x³ )dy
B. dy = (4x² + 3x³)dx
C. dy/dx = (4 + 3x)x²
D. dy/dx = (4x²-3x³)
Calculus
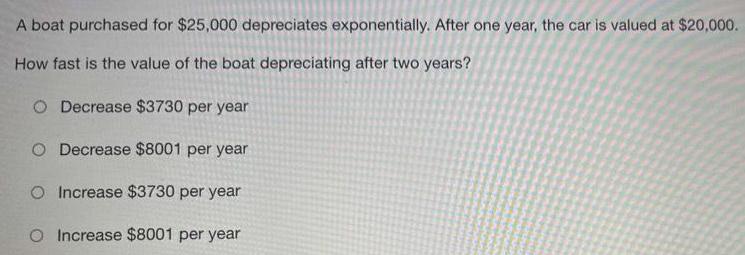
Differential equationsA boat purchased for $25,000 depreciates exponentially. After one year, the car is valued at $20,000. How fast is the value of the boat depreciating after two years?
A. Decrease $3730 per year
B. Decrease $8001 per year
C. Increase $3730 per year
D. Increase $8001 per year

Calculus
Differential equationsThe mess in a restaurant can be measured by M(t). Assume that M(0) = 0, the restaurant starts out each month completely clean. Over time the rate of change in the mess is proportional to (100-M). After 50 hours the restaurant had a mess index of 20. A completely messy restaurant has a value of 100. How many hours does it take for the restaurant to have a mess index of 90?
A. 493.89
B. 516.27
C. 523.75
D. 548.31
Calculus
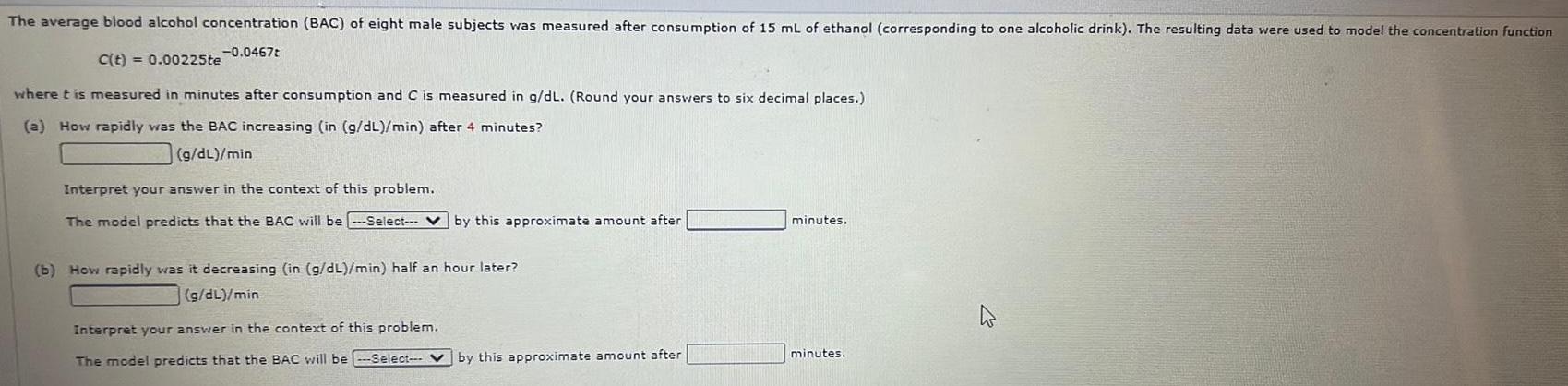
Differential equationsThe average blood alcohol concentration (BAC) of eight male subjects was measured after consumption of 15 mL of ethanol (corresponding to one alcoholic drink). The resulting data were used to model the concentration function
c(t) = 0.00225te^-0.0467t
where t is measured in minutes after consumption and C is measured in g/dL. (Round your answers to six decimal places.)
(a) How rapidly was the BAC increasing (in (g/dL)/min) after 4 minutes?
(g/dL)/min
Interpret your answer in the context of this problem.
The model predicts that the BAC will be by this approximate amount after minutes.
(b) How rapidly was it decreasing (in (g/dL)/min) half an hour later?
(g/dL)/min
Interpret your answer in the context of this problem.
The model predicts that the BAC will be by this approximate amount after minutes.
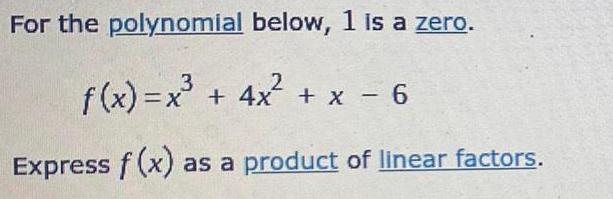
Calculus
Differential equationsFor the polynomial below, 1 is a zero.
3
f(x) = x³ + 4x² + x - 6
Express f(x) as a product of linear factors.

Calculus
Differential equationsSolve the initial value problem below using the method of Laplace transforms.
y" + 11y' + 30y = 56 e, y(0) = -6, y'(0) = 43

Calculus
Differential equationsA machine is rolling a metal cylinder under pressure. The radius of the cylinder
is decreasing at a constant rate of 0.02 inches per second and the volume is 240
cubic inches. At what rate is the length h changing when the radius r is 2.5
inches?