Vector Calculus Questions and Answers
Calculus
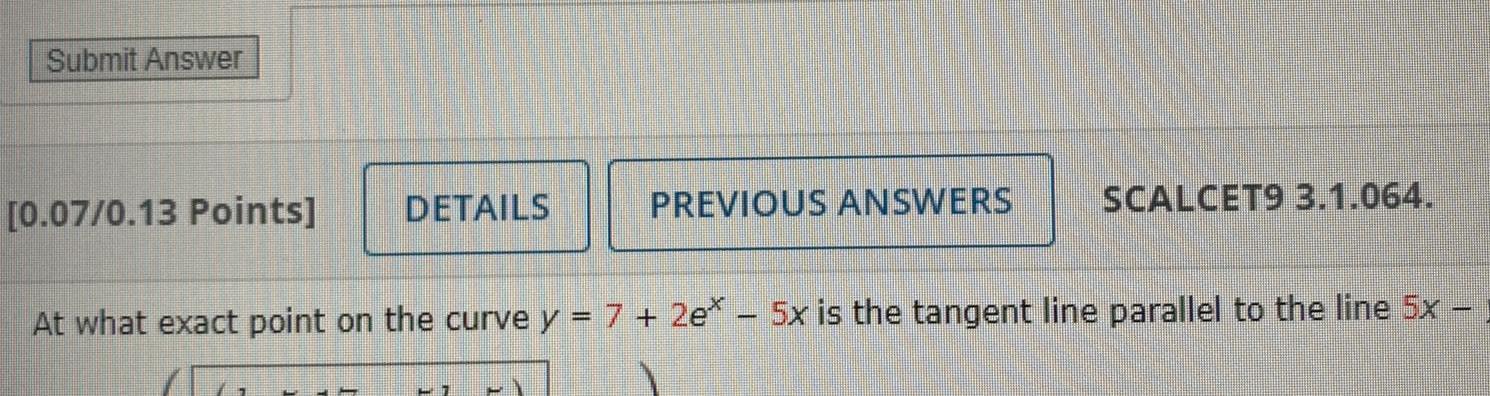
Vector CalculusSubmit Answer 0 07 0 13 Points DETAILS PREVIOUS ANSWERS 7 SCALCET9 3 1 064 At what exact point on the curve y 7 2e 5x is the tangent line parallel to the line 5x
Calculus
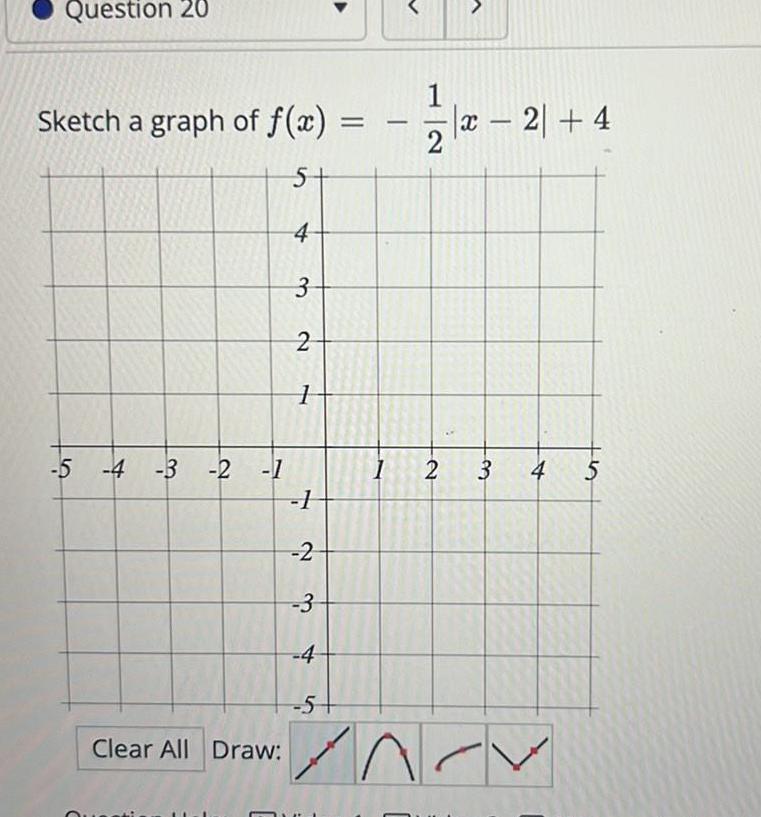
Vector CalculusQuestion 20 Sketch a graph of f x 5 4 3 5 4 3 2 1 Clear All Draw 2 1 1 2 3 4 5 1 12 14 x 2 4 2 2 3 4 5 ANCY

Calculus
Vector CalculusFind an equation of the tangent line to the curve y x x that is parallel to the line y 3 9x y x 12x 12 X Enhanced Feedback Please try again Find the derivative of the function set it equal to the slope of the given line then solve for x This will give you the x coordinate of the point at which the tangent line is parallel to the find the tangent line Remember that the slopes of two parallel lines are equal and the slope of the line y f a f a x a is f a
Calculus
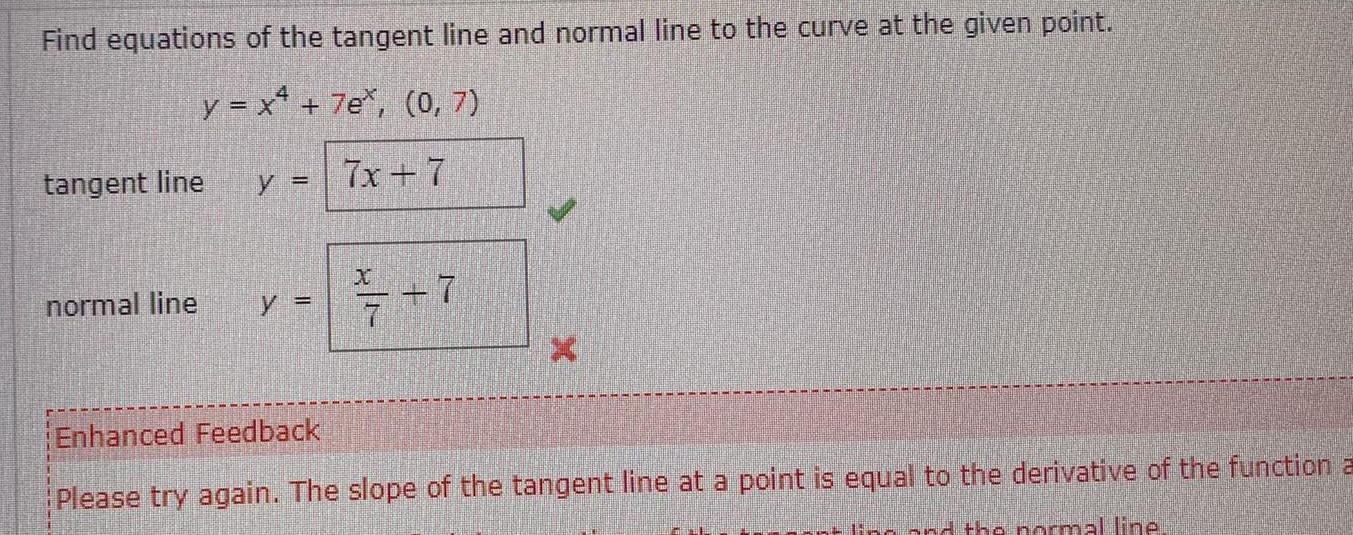
Vector CalculusFind equations of the tangent line and normal line to the curve at the given point y x 7e 0 7 7x 7 tangent line y normal line y 7 7 Enhanced Feedback Please try again The slope of the tangent line at a point is equal to the derivative of the function a ling and the normal line
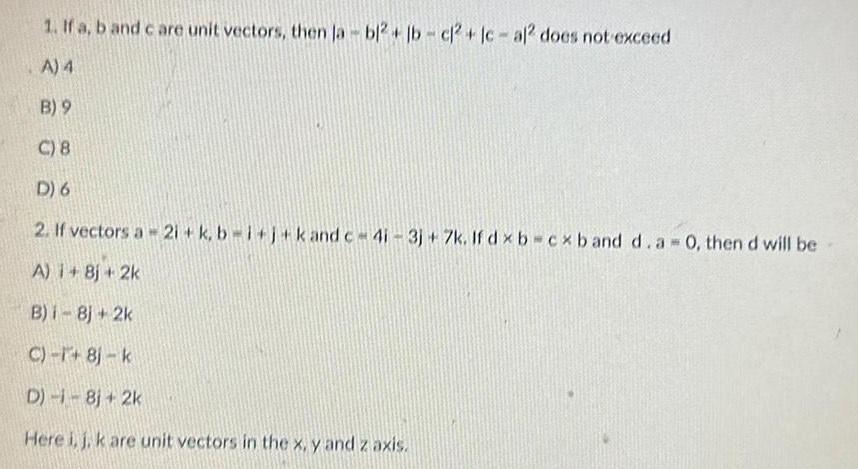
Calculus
Vector Calculus1 If a b and care unit vectors then la bl2 lb cl2 lc al does not exceed A 4 B 9 C 8 D 6 2 If vectors a 2i k b i j k and c 4i 3j 7k If dx b cx band d a 0 then d will be A 1 Bj 2k B i 8j 2k C 1 8j k D 1 8j 2k Here i j k are unit vectors in the x y and z axis
Calculus
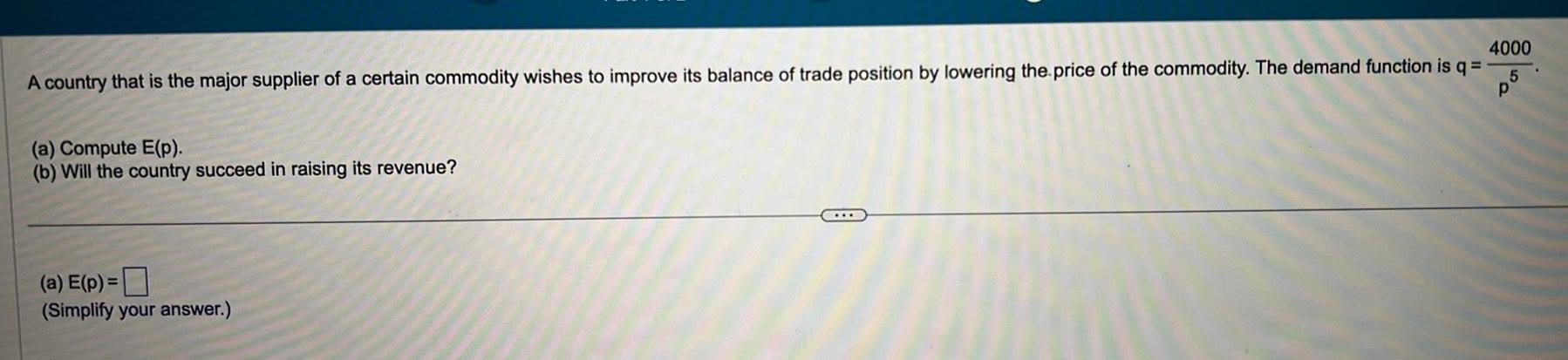
Vector CalculusA country that is the major supplier of a certain commodity wishes to improve its balance of trade position by lowering the price of the commodity The demand function is q p a Compute E p b Will the country succeed in raising its revenue a E p Simplify your answer 4000 5
Calculus
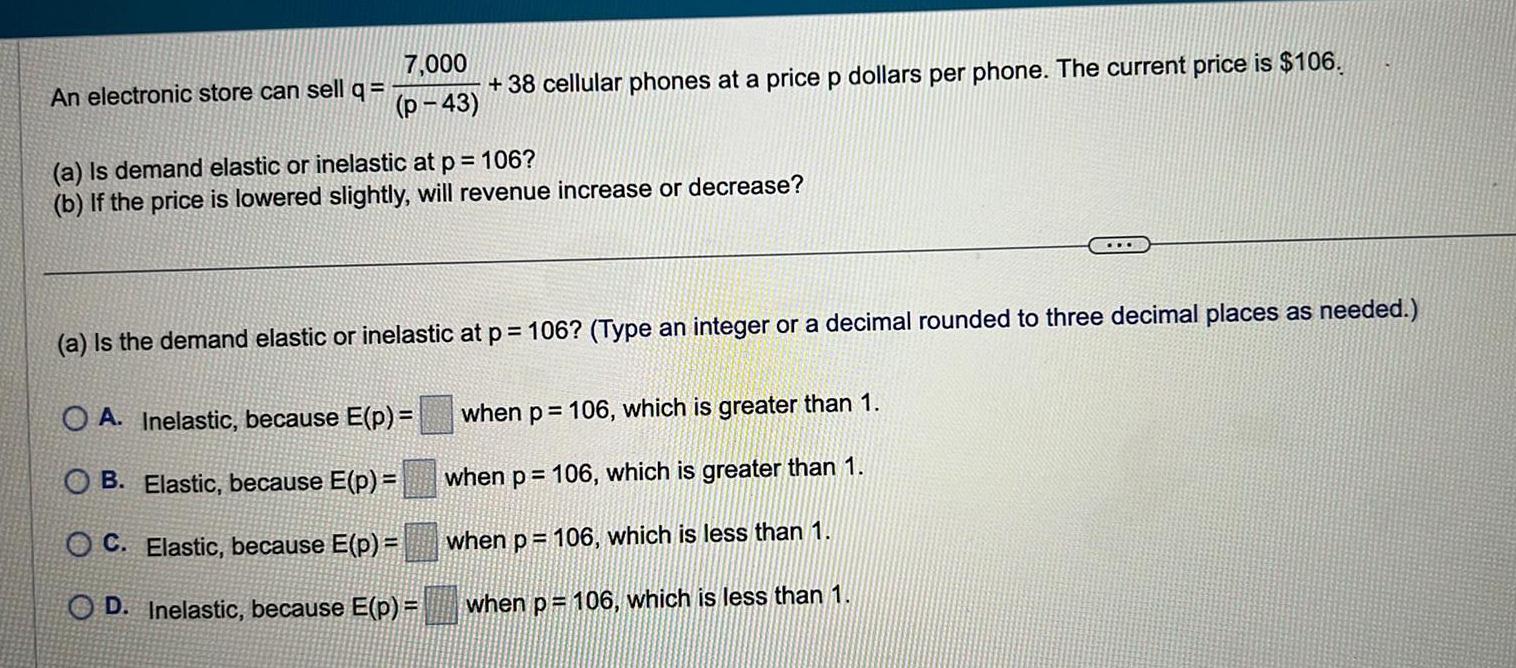
Vector CalculusAn electronic store can sell q 7 000 p 43 38 cellular phones at a price p dollars per phone The current price is 106 a Is demand elastic or inelastic at p 106 b If the price is lowered slightly will revenue increase or decrease a Is the demand elastic or inelastic at p 106 Type an integer or a decimal rounded to three decimal places as needed OA Inelastic because E p OB Elastic because E p OC Elastic because E p OD Inelastic because E p when p 106 which is greater than 1 when p 106 which is greater than 1 when p 106 which is less than 1 when p 106 which is less than 1
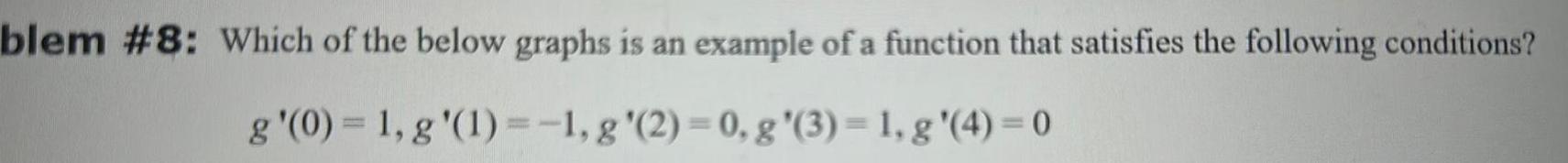
Calculus
Vector Calculusblem 8 Which of the below graphs is an example of a function that satisfies the following conditions g 0 1 g 1 1 g 2 0 g 3 1 g 4 0

Calculus
Vector CalculusA famous painting was sold in 1945 for 21 930 In 1993 the painting was sold for 29 5 million What rate of interest compounded continuously did this investment earn As an investment the painting earned an interest rate of Round to one decimal place as needed Points 0 of 1 SILB
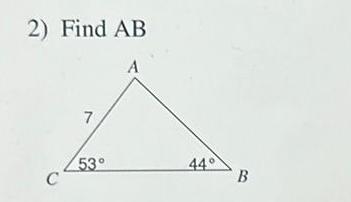

Calculus
Vector CalculusA hummingbird flies 382 m south then turns right and flies 146 m west What is the direction of the

Calculus
Vector CalculusLet A be a vector with magnitude A and components A and Ay In terms of components we can write A Az Ay Consider the following specific case A 52 0 km 84 0 km What is A Provide your answer below

Calculus
Vector CalculusPoints A company invests 20 000 in a CD that earns 9 compounded continuously How long will it take for the account to be worth 30 000 The account will be worth approximately 30 000 in about years Do not round until the final answer Then round to the nearest tenth as needed

Calculus
Vector CalculusWhen time is measured in days the decay constant for a particular radioactive isotope is 0 14 Determine the time required for a confined sample of the isotope to fall to 80 of its original value The time required for a confined sample of the isotope to fall to 80 of its original value is about Do not round until the final answer Then round to the nearest hundredth as needed days

Calculus
Vector Calculusplane is 120 mi north and 194 mi east of an airport Find x the angle the pilot should turn in order to fly directly to the airport Round your answer to the earest tenth of a degree 120 U Airport 194 X
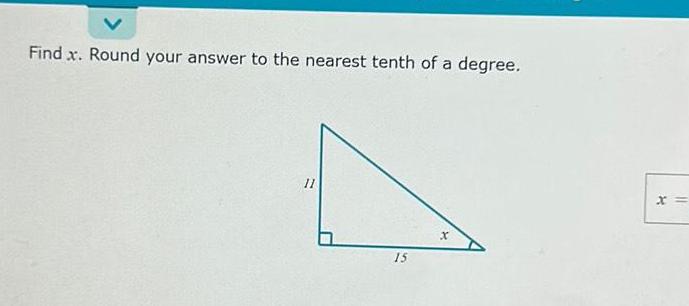
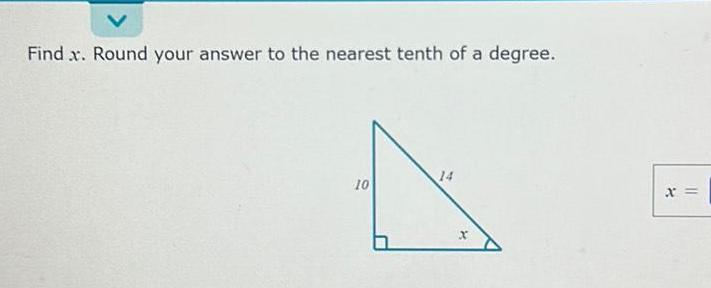
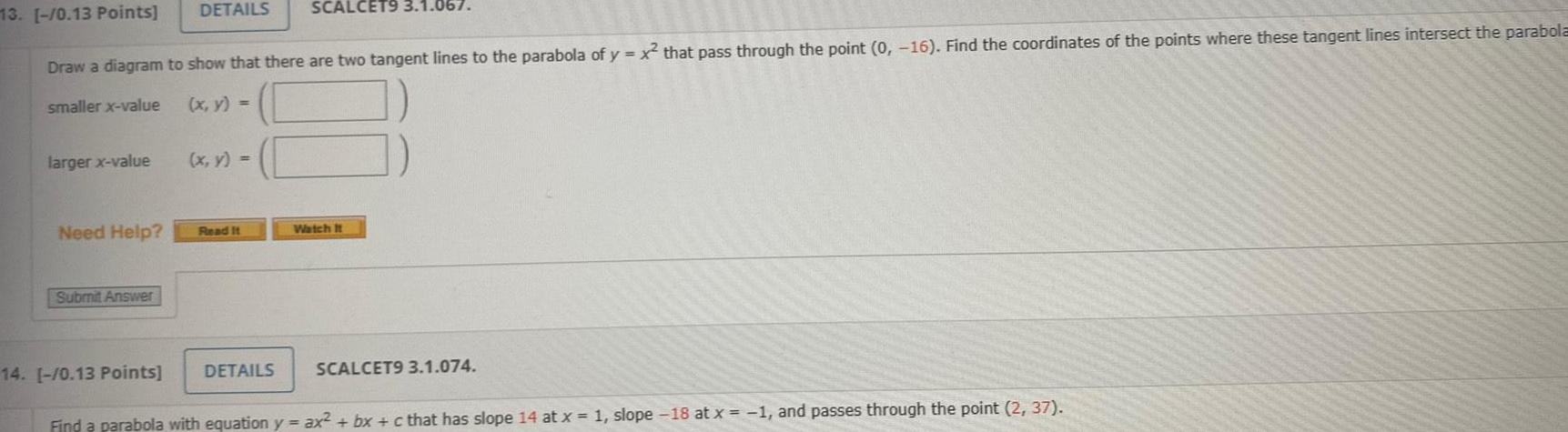
Calculus
Vector Calculuslarger x value 13 0 13 Points Draw a diagram to show that there are two tangent lines to the parabola of y x that pass through the point 0 16 Find the coordinates of the points where these tangent lines intersect the parabola smaller x value x y Need Help Submit Answer DETAILS 14 0 13 Points x y Read It SCALCET9 3 1 067 DETAILS Watch It SCALCET9 3 1 074 Find a parabola with equation y ax bx c that has slope 14 at x 1 slope 18 at x 1 and passes through the point 2 37

Calculus
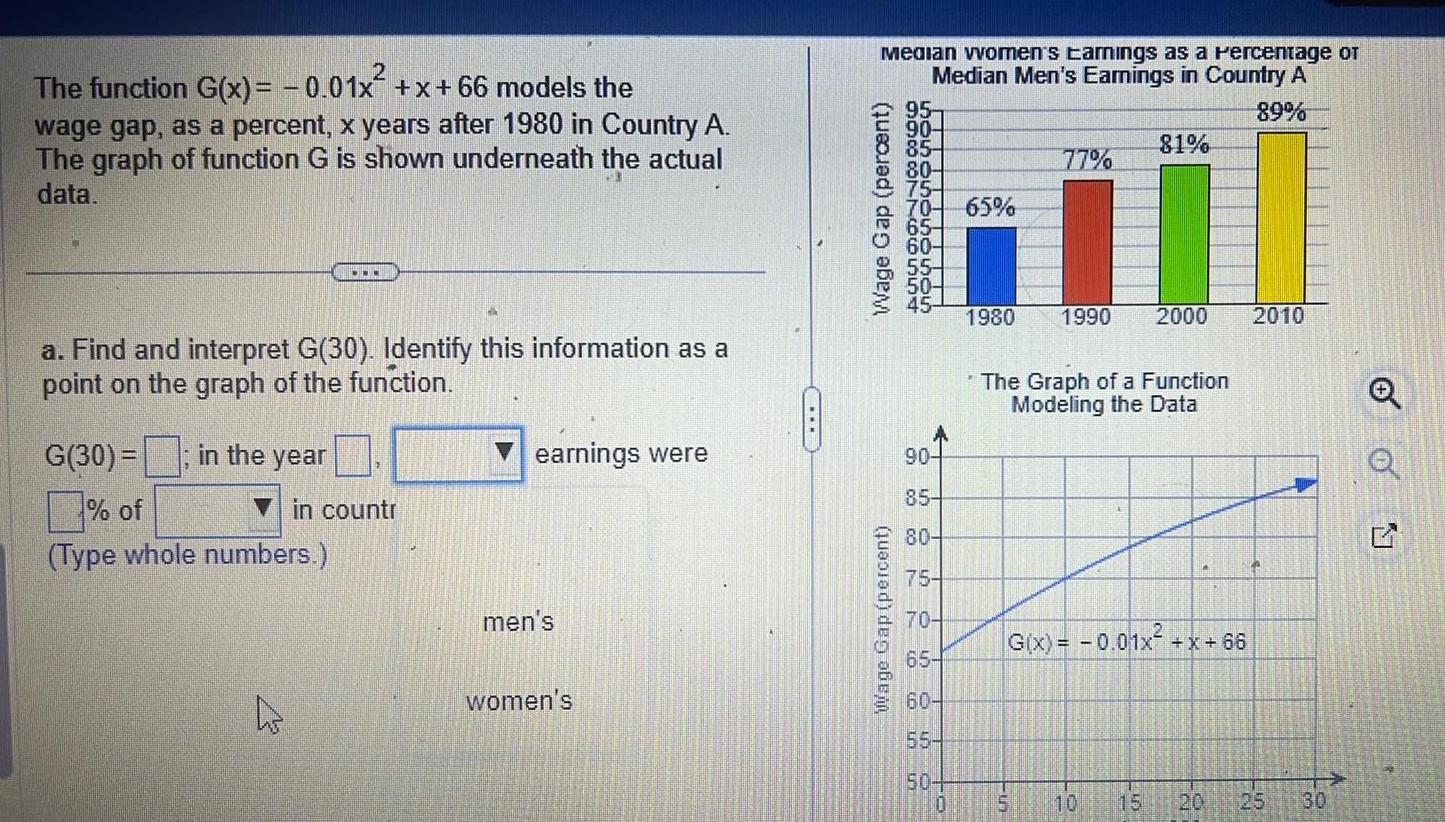
Vector Calculus2 The function G x 0 01x x 66 models the wage gap as a percent x years after 1980 in Country A The graph of function G is shown underneath the actual data a Find and interpret G 30 Identify this information as a point on the graph of the function G 30 of Type whole numbers in the year K in countr earnings were men s women s Median women s Earnings as a Percentage of Median Men s Earnings in Country A 89 Wage Gap percent quasjad des ab 95 90 85 otho LOLOS 80 75 70 65 65 60 55 50 90 85 80 75 70 65 60 55 504 77 1980 1990 The Graph of a Function Modeling the Data 10 5 0 81 G x 0 01x x 66 2000 15 18 20 2010 FN 2
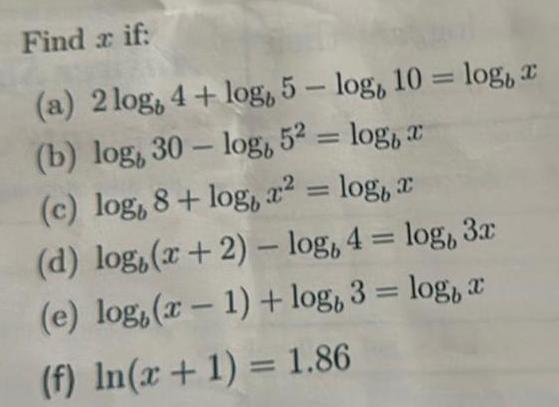
Calculus
Vector CalculusFind a if a 2log 4 log 5 log 10 log a b log 30 log 52 log c c log 8 log x log x d log x 2 log 4 log 3x e log x 1 log 3 log a f In x 1 1 86

Calculus
Vector CalculusWhat is the maximum value of z 3x 4y for the region given by the system I 0 y20 x y 11 3x 2y 30 Choose the correct answer for the question O a 44 O b 30 O c 56 d 48 e None of the options

Calculus
Vector CalculusGiven the function f x 7x 3 evaluate and simplify the expressions below See special instructions on how to enter your answers f a f a h f a h f a h Instructions Simplify answers as much as possible Expressions such as 4 x 2 and x 5 should be expanded Also collect like terms so 3r r should be writton
Calculus
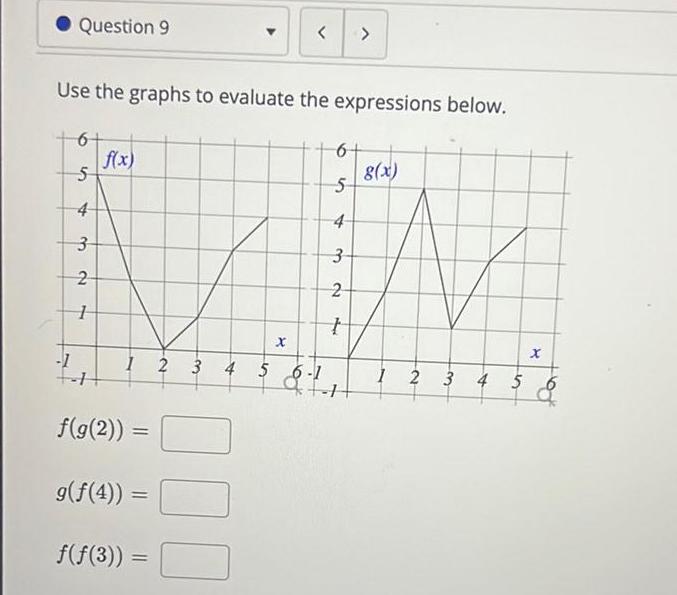
Vector CalculusQuestion 91 1 Use the graphs to evaluate the expressions below 6 5 4 3 2 1 f x f g 2 g f 4 f f 3 1 2 3 4 5 6 1 9 1 X 300 6 5 4 3 2 t g x 1 2 3 4 5 X

Calculus
Vector Calculusroblem 5 The value V in dollars of a truck owned by a company depreciates in value over time Its value t years after it is put in service is given by V t 36000 2400t a Find V 2 and interpret its meaning Be sure to include appropriate units b Find the inverse function t V c In words explain what the inverse function calculates d Use your answer to part c to evaluate t 10000 and interpret its meaning of t 10000 include units e Graph the functions V t and t V on separate axes and label all axes

Calculus
Vector CalculusThe temperature of a mug of hot chocolate in degrees Fahrenheit is given by H t 70 100 0 819 where t is the time in minutes after it is prepared a What is an appropriate domain for this situation Explain your reasoning b What is an appropriate range for this situation Explain your reasoning
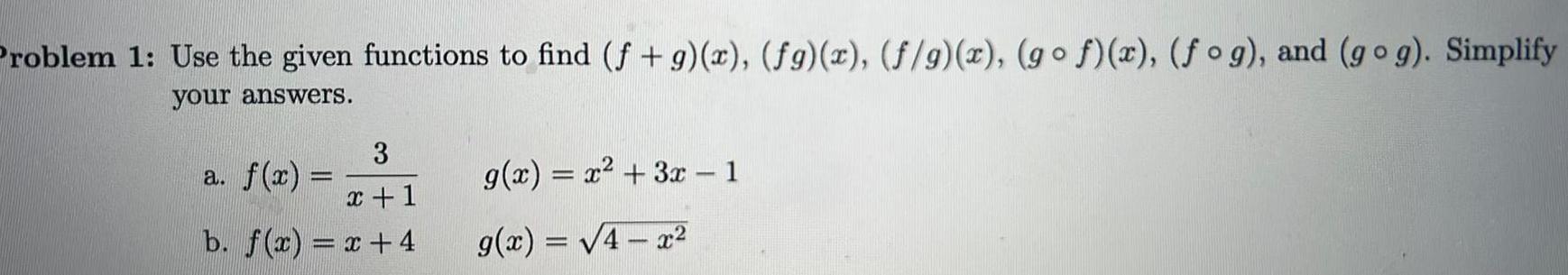
Calculus
Vector CalculusProblem 1 Use the given functions to find f g x fg x f g x gof x fog and gog Simplify your answers 3 x 1 b f x x 4 a f x g x x 3x 1 g x 4x

Calculus
Vector CalculusIndividual pathways PRACTER 1 4 0 11 14 MOLDATE 2 5 6 6 12 15 To answer questions online and to receive inmediate corrective feedback and fully worked solutions for all questions go to your learnON title at www jecplan com m Fluency Show that the following numbers are rational by writing each of them in fraction form 15 Show that the following numbers are rational by writing each of them in fraction form vinh 0 0002 10 Show that the following numbers are rational by writing each of them in fraction form 0 1 36 3 612 d 0 08 Write the first 8 digits of each of the following recurring decimals b 031 051 d 6011 Jacaranda Maths Queit 9 MARTER 3 7 10 13 16 17 0 5 we Write the first X digits of each of the following recurring decimals 7 024 89124 c 5 1234 4 5 1234 Write the following fractions as recurring decimals using doc notation Use a calculator Understanding From the following list of numbers 15 B 11 Write the following fractions as recurring decimals using dot notation Use a calculator 23 46 N 990 write down the natural numbers write down the rational numbers a 6 7 15 d a Write these numbers in order from smallest to largest 2 1 2 12 2 121 2121 212 K7 2 918 99 5 183 3 002 173 99 46 900 b write down the integers d write down the recurring decimals

Calculus
Vector CalculusProblem 3 Suppose that a linear system of equations in unknowns x y and has the following augmented matrix 1 2 3 2 3 3 2 4 2 Problem 3 3 Use Gauss Jordan elimination to solve the system for x y and z Enter the values of x y and z here separated by commas

Calculus
Vector CalculusProblem 5 Determine whether the following linear system has one solution no solutions or infinitely many solutions x14x2 6x3 6x4 3 4x16x27x3 5x4 4 8x1 2x2 3x3 9x4 16 A No solution B One solution C Infinitely many solutions

Calculus
Vector CalculusProblem 4 Use Gauss Jordan Elimination to solve the following system of equations 2x 2y 8z 2 x 5y 5z 2 6x 14y 26z 0 A x 3 51 B x 14 1 C x 3 5 D x 7 5 E x x 14 St F X y 4 y 3 1 z t 2 t y t z t 2 1 19 G x 3 5t H no solution I x y 2 1 x 1 51 4 y 3 1 2 t 8 y 2 z t t

Calculus
Vector Calculusblem 11 Find matrices A x and b that express the below system of linear equations as a single matrix equation Ax b 7x17x2 x3 6x4 2 2x1 4x2 8x3 5x4 2 3x1 2x2 4x3 7x4 1 C A A A 2 60 0 0 0 4 B A 2 E A 7 7 1 4 8 5 x 3 2 4 7 7 7 1 2 4 8 3 2 4 7 2 3 7 1 4 8 2 4 X X2 X X2 X3 b b 6 X1 8 0 b x3 D A 2 7 7 1 7 F A 2 3 3 2 4 7 7 1 6 60 4 8 5 X x3 3 2 4 7 8 7 4 2 5 4 1 8 0 X X3 X4

Calculus
Vector Calculusoblem 1 Use Gauss Jordan elimination to find the reduced row echelon form of the following matrix 132 2 1 A 0 0 1 E 0 0 6 1 2 3 1 5 0 23 0 1 0 0 1 0 0 1 0 1 00 WNIO WE 23 25 15 2 23 3 100 1 B 0 0 1 F 0 0 0 0 1 O 0 1 0 1 0 H2N 32 11 13 28 15 41 1 0 0 233 C 0 0 1 1 0 99 O 0 G 0 1 0 0 1 0 a NIO W NW NIO WIN 0 1 13 2 41 D H 002 5 1 0 0 0 1 10 0 1 00 0 10 0 15 1
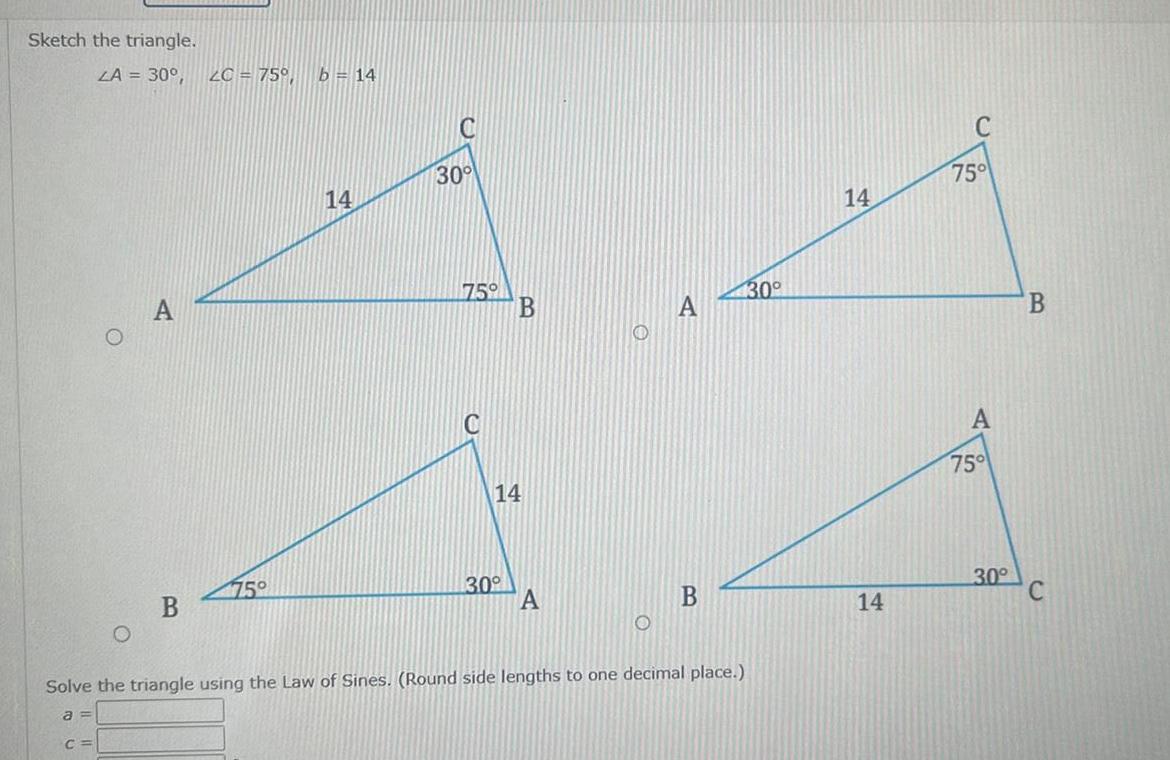
Calculus
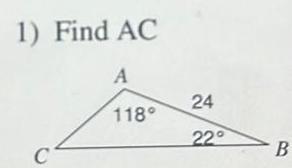
Vector CalculusSketch the triangle LA 30 2C 75 b 14 B 75 14 30 75 C B 14 30 A B Solve the triangle using the Law of Sines Round side lengths to one decimal place a C 30 14 14 C 75 A 75 30 B C
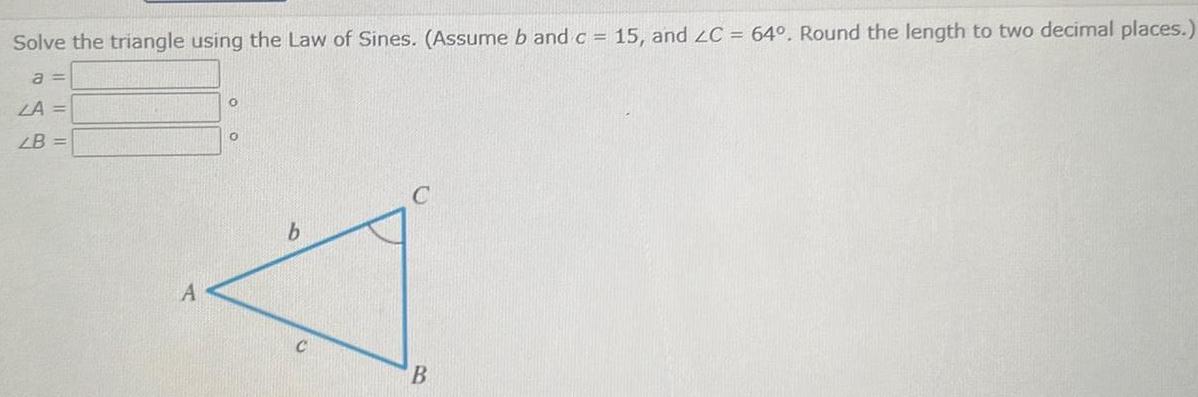
Calculus
Vector CalculusSolve the triangle using the Law of Sines Assume b and c 15 and 2C 64 Round the length to two decimal places a LA LB A O b C B

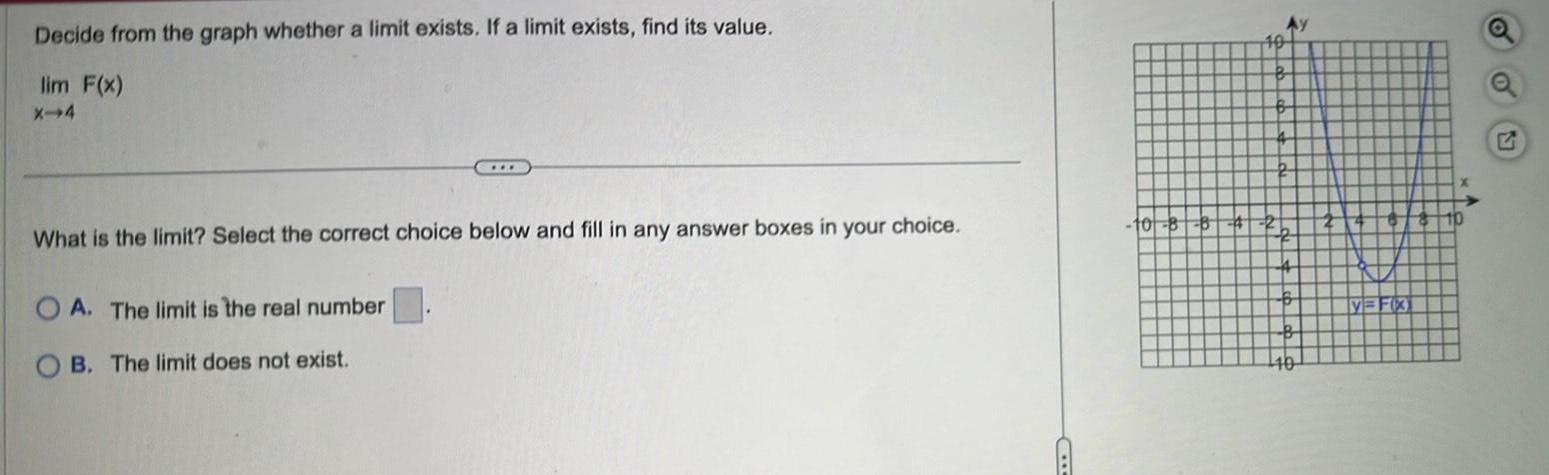
Calculus
Vector CalculusDecide from the graph whether a limit exists If a limit exists find its value lim F x X 4 What is the limit Select the correct choice below and fill in any answer boxes in your choice OA The limit is the real number B The limit does not exist 10 8 B 10 2b 4 B B V FX 10 A Q
Calculus
Vector CalculusWhat is the relationship between m and the slopes of the lines of a piecewise function Fon a b Given that F b F a m b a
Calculus
Vector CalculusSubmit Answer 5 5 X 5 5 DETAILS SCALCET9 2 XP 5 005 0 2 Submissions Used X 5 2 1 04 Points For the function f how would you remove the discontinuity In other words how would you define f 4 in order for f to be continuous at 4 2x 8
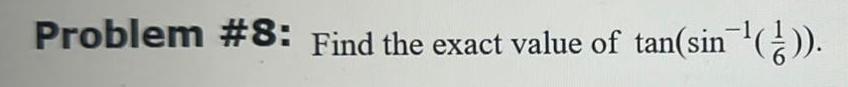
Calculus
Vector Calculus1 2 points Let v 5 2 and w 2 1 Compute and plot on a single set of axes each of the following vectors a v w b v w c proj w d proj 2w V
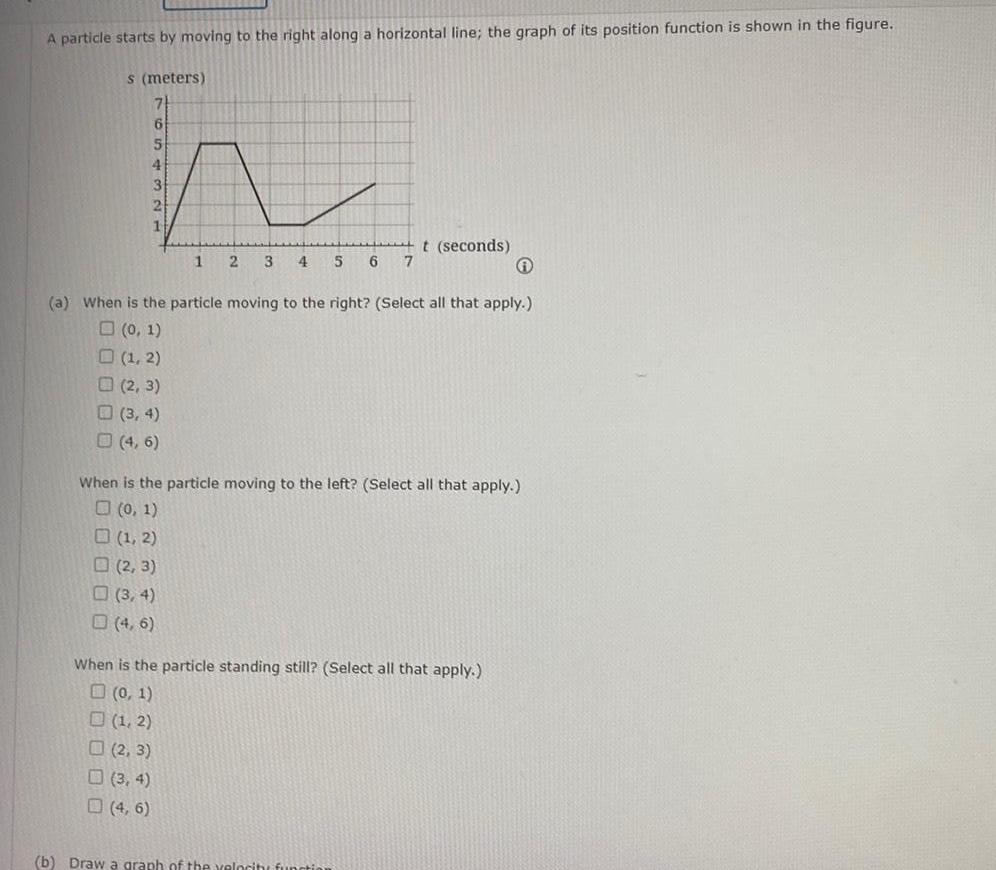
Calculus
Vector CalculusA particle starts by moving to the right along a horizontal line the graph of its position function is shown in the figure s meters 6 5 4 3 2 1 2 3 3 4 4 6 1 a When is the particle moving to the right Select all that apply 0 1 1 2 1 2 2 3 3 4 4 6 4 6 2 3 4 5 6 7 When is the particle moving to the left Select all that apply 0 1 t seconds When is the particle standing still Select all that apply 0 1 1 2 2 3 b Draw a graph of the velocity functi

Calculus
Vector CalculusGas mileage actually varies slightly with the driving speed of a car as well as with highway vs city driving Suppose your car averages 27 miles per gallon on the highway if your average speed is 52 miles per hour and it averages 26 miles per gallon on the highway if your average speed is 68 miles per hour Answer parts a and b below C a What is the driving time for a 2900 mile trip if you drive at an average speed of 52 miles per hour What is the driving time at 68 miles per hour The driving time at 52 miles per hour is hours Type an integer or decimal rounded to two decimal places as needed

Calculus
Vector CalculusComplete parts a through c below a A storage pod has a rectangular floor that measures 20 feet by 9 feet and a flat ceiling that is 8 feet above the floor Find the area of the floor and the volume of the pod b A lap pool has a length of 28 yards a width of 20 yards and a depth of 5 yards Find the pool s surface area the water surface and the total volume of water that the pool c A raised flower bed is 30 feet long 4 feet wide and 1 6 feet deep Find the area of the bed and the volume of soil it holds a The area of the floor of the pod is Typo on intogor or o donimel C

Calculus
Vector Calculusa f x Subsequently we used that fact to compare the value of the integral with the value of an antiderivative obtained by using integration rules Now suppose on one hand f x is integrable but cannot be differentiated using the integration rules available On the other hand the integral can be evaluated numerically for any value of x Many functions belong in this category For the moment however we focus on one particular function f x This function was the only power function not handled by the integration power rule consequently we could not obtain an expression for the antiderivative As we see in Section 7 1 an antiderivative can be found using our general expression in the first paragraph and it is the natural logarithmic function Procedure Go to desmos com 1 Plot the function f x over the interval 1 10 Go to the wrench at the top right of your screen and change the x axis to be 0 11 with 1 0 step and y scale to be 0 2 with 0 5 step Uncheck the box for minor gridlines 2 Without using calculus just by looking at the graph try to find a rough estimate of the area between the graph of f x and the x axis from x 1 to x 2 Hint what is the area of each rectangle Repeat this for x going from 1 to 5 Although tedious and inaccurate the process you just followed could be repeated to get an estimate of the area from x 1 to x a for any a 1 For any value of a we input the output is a number i e a function F a the area between f x and the x axis from x 1 to x a 3 In Desmos define F a to be the integral from 1 to a of 1 x dx To get an integral in desmos type int and the integral sign will appear a Evaluate F 2 b Evaluate F 5 c Do your estimates match your answers from question 2 4 Turn off the plot of f x Turn on the plot for F a if not already done Now graph In x on the interval from 0 1 to 10 In x 0 1 x 10 Zoom in or out as needed to see both graphs What do you notice 5 Evaluate In 0 5 and In 1 0 Interpret each of these answers in terms of the integral and area between the curve and the x axis Note we do not define In a for a 0 or for negative values of a 6 Evaluate the following In 2 In 5 In 5 In 2 5ln 2 In 2 5 In 5 2 In 2 5 7 State the logarithmic properties responsible for making the expressions equal 8 Interpret your answers from one side of the table either side in terms of the integral and area between the curve and the x axis The goal here is to see why in terms of the integral or area under the curve the right side equals the left side of the table We are looking for your thoughts here not a specific right answer 1 9 Type the integral dxinto Desmos Anything surprising How do you explain this 2 answer other than the fact we know F a is only defined for a 0 a Determine the exact value of this integral by hand 10 From Calculus A we learned that if a continuous function f on a closed interval a b takes values f a and f b at each end of the interval then it also takes any value between f a and f b at some point within the interval Since In 2 1 and In 5 1 by IVT there exists a value between x 2 and x 5 where In x 1 We obtain an approximation to

Calculus
Vector Calculus75 82 Evaluating inverse trigonometric functions Without using a calculator evaluate the following expressions 75 tan V3 77 sec 2 79 tan tan 7 4 1 81 csc sec 2 76 cot 1 3 78 csc 1 80 tan tan 3 4 82 tan tan 1
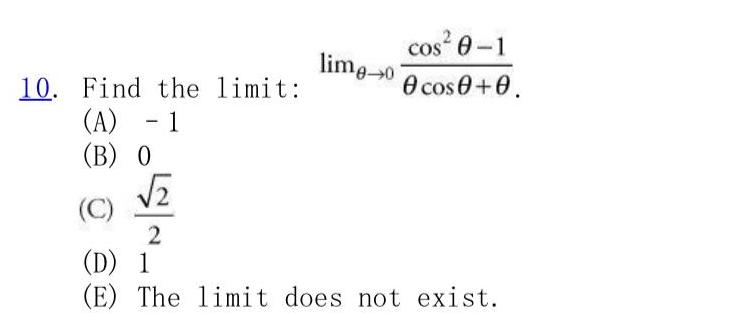
Calculus
Vector Calculus10 Find the limit A 1 B O lime o 2 cos 0 1 0 cos 0 0 C D 1 E The limit does not exist
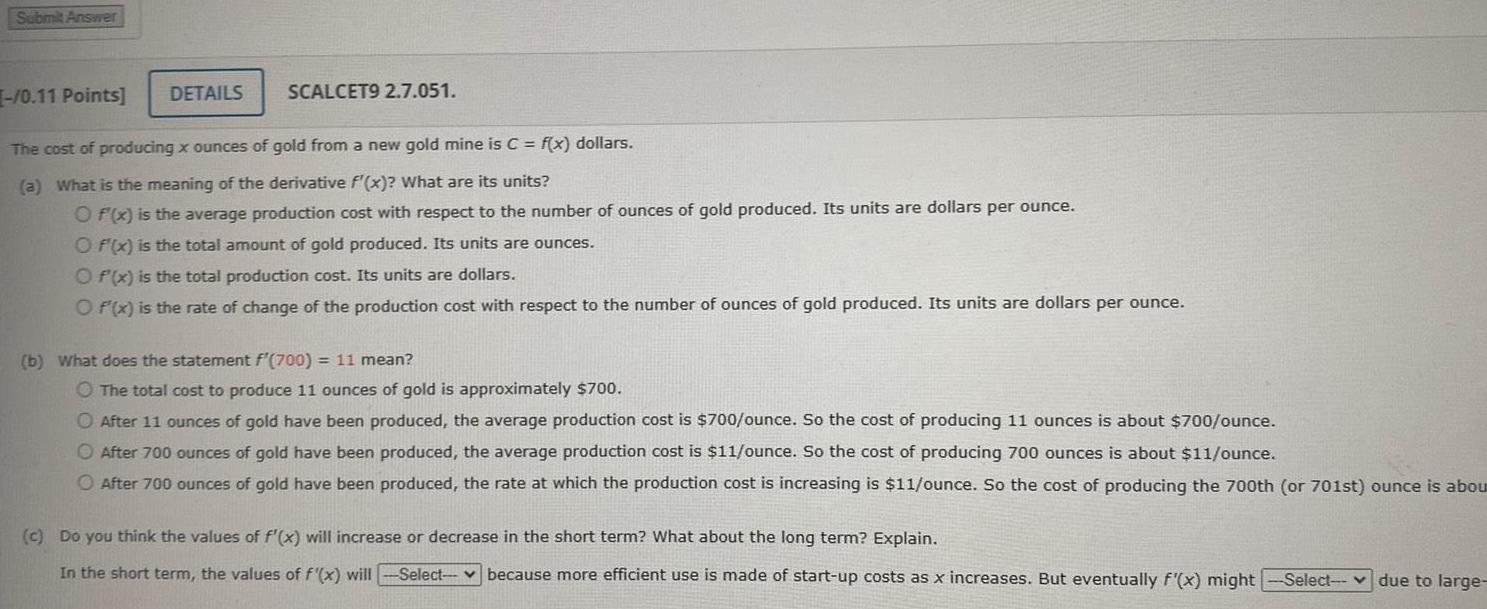
Calculus
Vector CalculusSubmit Answer 0 11 Points DETAILS SCALCET9 2 7 051 The cost of producing x ounces of gold from a new gold mine is C f x dollars a What is the meaning of the derivative f x What are its units O f x is the average production cost with respect to the number of ounces of gold produced Its units are dollars per ounce O f x is the total amount of gold produced Its units are ounces Of x is the total production cost Its units are dollars O f x is the rate of change of the production cost with respect to the number of ounces of gold produced Its units are dollars per ounce b What does the statement f 700 11 mean O The total cost to produce 11 ounces of gold is approximately 700 O After 11 ounces of gold have been produced the average production cost is 700 ounce So the cost of producing 11 ounces is about 700 ounce O After 700 ounces of gold have been produced the average production cost is 11 ounce So the cost of producing 700 ounces is about 11 ounce O After 700 ounces of gold have been produced the rate at which the production cost is increasing is 11 ounce So the cost of producing the 700th or 701st ounce is abou c Do you think the values of f x will increase or decrease in the short term What about the long term Explain In the short term the values of f x will Select because more efficient use is made of start up costs as x increases But eventually f x might Select due to large