Complex numbers Questions and Answers

1 2 3 1 2 3 2 3 12 3 0 20 Step 3 Here the maximum difference is 11 which corresponds to second column Third allocate in 2 3 cell X 3 min 25 15 15 3 4 17 9 2 3 14 16 15 15 10 7 7 7 16 18 15 10 7 7 4 11 20 Step 4 Here the maximum difference is 7 which corresponds to fourth column Fourth allocate in 1 4 cell X 4 min 0 10 0 4 20 20 11 0 9 9 20 18 10 7 18 0 2 15 11 25 2 H 0 11 10 20 25 11 0 2 20 10 11 0 18 Step 5 Here the maximum difference is 2 which corresponds to fourth column Fifth allocate in 3 4 cell X34 min 0 10 0 4 25 18 0 18 10 2 Step 6 Sixth allocate in 2 4 cell X24 min 10 10 10

Suppose there are n jobs J1 J2 two machines say M and M in order M M M first and M next Let t be the processing time for ith job in jth machine The list of jobs along with their processing times can be summarized as in the following table Jobs Processing time in M Processing time in M J t11 t21 above Jn which are to be processed in Jz t12 t22 Let x2j be the time for which the machine M remains idle after completing the j 1 th job and before starting jth job A job is assigned to machine My first and after it has been completely processed in machine M it is assigned to the machine M If the machine M is not free at any moment for processing a particular job then that job has to wait in a waiting line for its turn on the machine M In other words passing is not allowed Hence machine M will always be busy and will process the n jobs one by one After processing all the n jobs the machine M remains idle until all the n jobs are completed in the machine M However M may remain idle after the completion of some of the m jobs and before starting the next job The sequencing problem is to minimize the total idle time of the second machine M 32 Jn tin tzn Hence the total idle time for machine M is E 1X2j Thus the sequencing problem is to minimize E 12 The total elapsed time T is given by T Processing time idle time i e T j 121 1 2 Here some of the x2 may be zeros We observe that E 1 t2j is constant Hence minimizing T is equivalent to minimizing 1x2j Algorithm to find the optimum sequence for n jobs in 2 machines Step 1 List the jobs along with their processing times in a table as given Step 2 Find the minimum t j tzj for all j 1 2 n Step 3 If the smallest processing time is for the first machine M then place the corresponding job in the first available position in the sequence If it is for the second machine M then place the corresponding job in the last available position in the sequence Step 4 If there is a tie in the minimum of all the processing times then there arises three cases Case i Minimum among all processing times is same for the two machines i e minimum t j tzj t r tzs then place the rth job in the first available position in the sequence and the sth job in the last available position in the sequence Case it If the tie is for the minimum among the processing times tij on machine My only then place the jobs arbitrarily one after the other in the last available positions in the sequence Case iii If the tie is for the minimum among the processing times t2j on machine M only then place the jobs arbitrarily one after the other in the last available positions in the sequence

P t AP t 2P 1 t n 0 Po t AP t n 0 P z 0 02 P 0 lim At 0 1 0 1 Po t At Po t At P z t ed 2 1 Now Pn t can be defined as P t d z n dz t 0 Log P z t z 1 t E To determine E we put t 0 to get Log P z 0 E at e at n Multiplying both sides of A by z and taking summation for n 1 2 00 we get 0 Pr t 2 n 1 Pn t 2 1 Pn 1 t 2 P z t P t z P z t P z t 00 P z t P t z n 0 In general P t Classification of queueing models I Probabilistic queueing models 00 P t n 0 46 z 1 Model I Erlang Model This model is symbolically represented by MIMI o FCFS this denotes poisson arrival exponential inter arrival poisson departure exponential service time single server infinite capacity and first come first served service discipline Model II General Erlang Model Although this model is also represented by MIMI 00 FCFS but this is a general queueing model in which the rate of arrival and service depend on the length n of the line Model III this model represented by MIMI NIFCFS In this model capacity of the system is limited finite say n Obviously the number of arrivals will not exceed the number N in any case Model IV This model is represented by MIMIS 0o FCFS in which the number of stations is s in parallel Model V This model is represented by MEI 0o FCFS that is poisson arrivals Erlangian service time for k phases and a single server 46

service rate per busy service is u Therefore over all service rate when there are n units in the system may be obtained in the following two situations i And If n s all the customers may be served simulataneously There will be no queue s n number of servers may remain idle and then Hn nu n 0 1 2 s ii If n s all the servers are busy maximum number of customers waiting in queue will be n s then nu MODEL IV B MMS NIFCFS In model IV A if the maximum number in the system is limited to N then as in model III sp P 0 2n P su Where Po may be written as sp n s 1 p sp sp n s Virtually the same relationships hold between P and Po as in model IV A with infinite capacity Therefore Po 51 s 1 for 0 n N forn N sp Pon for o n s S pr Po s 0 for n N n 1 nu for 0 n s for s n N for s n N SP sp s s s 1 sp n n n s 1 p s 1 1 1 p N s 1 p 1 This queueing modrl with limited waiting room is valuable because of its relevance to many real situations and the fact that changes may be made to its properties by adjusting the number of servers or the capacity of the waiting room However while poission arrivals are common in practice negative exponential service times are less so and it is the second assumption in the system MIMs that limits its usefulness Example

Give a property of real numbers associative commutative addition or multiplication that justifies each step in the following equation 3x 1 2x 7 x 22 1 3x 2x 1 7 x 22 2 x 3 2 6 x 22 Sr 6 x 22 3 5x 6 6 x 22 6 Sr x 28 4 5r r r 28 r Solve the following equations for x show all steps 1 3 x 2 x 4 6 x 2 2 5 7 6 3 15 4 3 4 5 25 4 Part II Properties of Real Numbers Use the indicated properties of real numbers to complete the blanks of the following statements 73 1 50 43 Commutative property of Addition Associative property of Addition Additive Identity 2 1 6 7 8 5 7 11 14 16 4 fation 2x 1 5 X 3 Bu fat pitatiand w Multiplicative Inverse Commutative property of Multiplication Associative property of Multiplication Distributive property

158 or f is decreasing in MATHEMATICS Interval T T 5T 4 4 5 4 2 a increasing in 0 0 7 Sign of f x T 5T 4 4 Rationalised 2023 24 c 2x 9x 12x 1 e x 1 x 3 7 Show that y log 1 x 0 0 0 EXERCISE 6 2 1 Show that the function given by f x 3x 17 is increasing on 2 Show that the function given by f x e x is increasing on R 3 Show that the function given by f x Nature of function f is increasing 6 7 9m f is decreasing f is increasing sin x is c neither increasing nor decreasing in 0 4 Find the intervals in which the function f given by f x 2x 3x is a increasing b decreasing 5 Find the intervals in which the function f given by f x 2x 3x 36x 7 a increasing b decreasing 6 Find the intervals in which the following functions are strictly increasing decreasing a x 2x 5 b decreasing b 10 6x 2x d 6 9x x 2x x 1 is an increasing function of 2 x throughout its domain 8 Find the values of x for which y x x 2 is an increasing function 4 sin 0 9 Prove that y A is an increasing function of in

f x 3cos 3x Therefore f x 0 gives cos 3x 0 which or 3 0 17 2 into two disjoint intervals 0 implies 3x 0 Now f x 0 all xe T T fis increasing on or as x 2 Solution We have So x Therefore fis increasing in 0 0 is increasing or decreasing namely The points x BI6 Note that TC TU 4 TU 2 TC and x Ra R6 5T 3x TU Also the given function is continuous at x 0 and x 6 T The point x 6 B N 3 2 and decreasing on Rationalised 2023 24 and decreasing in T as 0 x 0 3x 6 Example 13 Find the intervals in which the function f given by f x sin x cos x 0 x 2 Now f x 0 gives sin x cos x which gives that 0 7 7 5 and ST 27 4 4 4 gives TU TU 6 2 f x sin x cos x f x cos x sin x TC x 0 if x 0 ST 3x 0 2 3 0 T 4 2 2 divides the interval 0 APPLICATION OF DERIVATIVES T T 6 2 as x 0 B 6 Fig 6 5 0 3x and f x 0 for 2 4 0 7 E2 ROBN TC T 5T 4 Fig 6 6 Therefore by Theorem 1 157 as 0 x 2 27 into three disjoint intervals e rejushed 2

1 Write out the first 4 terms of the series show that diverges n 2 1 to show how the series starts Then find the sum of the series or 4

3 y2 5 4 5x 2ys 10 4 0 5 4 3 2 4 2 4 2

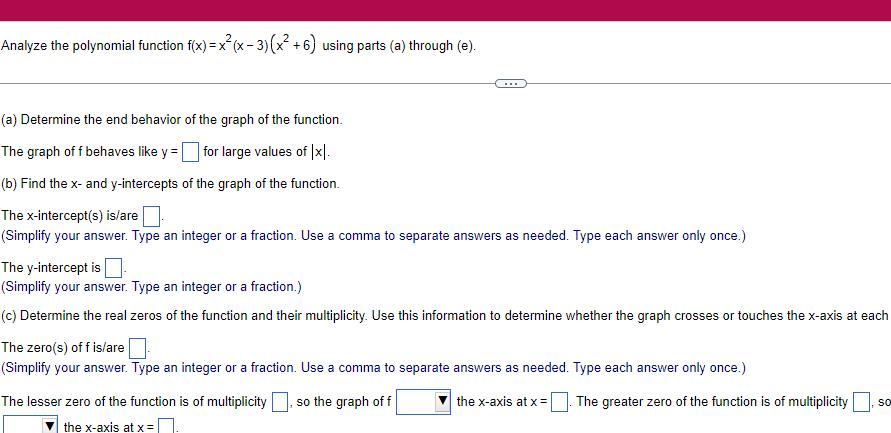
Analyze the polynomial function f x x x 3 x 6 using parts a through e a Determine the end behavior of the graph of the function The graph of f behaves like y for large values of Ix b Find the x and y intercepts of the graph of the function The x intercept s is are Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once The y intercept is Simplify your answer Type an integer or a fraction c Determine the real zeros of the function and their multiplicity Use this information to determine whether the graph crosses or touches the x axis at each The zero s of f is are Simplify your answer Type an integer or a fraction Use a comma to separate answers as needed Type each answer only once so the graph of f the x axis at x The lesser zero of the function is of multiplicity the x axis at x The greater zero of the function is of multiplicity SO

One pair of parallel sides are et different lengths vi Kite and V Shaped Kite Remember A square is also a rectangle as it has opposite sides squal A parallelogram has 2 thombus are special type en parallelogram A 2 pairs of adjacent equal sides Triangle Properties of Kite A Diagonals of a kite are perpendicular to each other One of the diagonals divides the kite into two modes A kite may or ay not be a parallelogram The sum of internal angles of a quadrilaterali 360 A square ra rectangle can be divided into two right angled triangles of equal sine by joining any two opposite vertices diagonally Opposite angles of a parallelogram are equal 3 Polygons A closed plane figure having more than 2 sides is a polygon in regular polygons all sides and all angles are equal Diagonals of a regular polygon are pal All polygons are classified according to the number of their sides Quadrilateral 4 ofequial and parallel sides so all rectangles guares and Dwap 30 In your day to day life you can see different types of polygon all around you In nature bectives are the best examples of hesagons A design of pentagon can be seen in football and hout Stop sight and wall clocks have wight sides so they are regalar tagms An opmed umbrella and star s a symbol of decagon STOP If a polygon has all tissides equal it called a regular polygos A regular polygim has all angles angles in it Let s Practice 1 Select any there objects having a flat tops Measure all sides of the sip using a divider and a ruler 2 What is the angle mame for half a relution What is the angle name for one fourth revolution 4 Draw five other situations of one fourth half and the fourth revolution on a clock The hour hand of a clock moves from 12 to 5 is the revolution of the hour hand more than one right angle What does the angle made by the hour hand of the clock look like when it moves from 577 is the angle mereed more than 1 night angle 7 Draw the following and check the angle with your RA tester 00 going from 12 to 2 from 6107 v trum 21052 from 4 to 8 List five situations where the angles made are 1 acute i obtuse angles are made 0 right angles v refles angles may be seen

Sketch the 2D vector field given by v yi xj 3 Find the first and second derivative of the vector function r 3 cos 2t 3 sin 4t 5t

Show that the equation sin sin is not an identity Which of the following values for can be used to show that the equation sin B sin B is NOT an identity A T 2 OC I B 2x OD O

Consider the following function g t 4t 0 Use the Leading Coefficient Test to determine the end behavior of g The graph of g Select an answer to the left and Select an answer to the right 4

Consider the polynomial function T 16 f x 6x 11c What is the degree of this polynomial Identify the constant term 12T Identify the leading coefficient Identify the leading term 14

Use transformations of the graph of y x to graph the function h x 2 x 3 4 D The graph of y x should be horizontally shifted to the right by 3 units reflected about the x axis and shifted vertically up by 2 units Now use the transformations of the graph of y x to graph h x 2 x 3 Choose the correct answer belo O C O D O A Q O B 3 24 1 32 4x1 37 3 02 1 Q Q

For the polynomial function below a List each real zero and its multiplicity b Determine whether the graph cross or touches the x axis at each x intercept c Determine the maximum number of turning points on the graph d Determine the end behavior that is find the power function that the graph of f resembles for large values of x f x 10 x 3 2 x 7 a Find any real zeros off Select the correct choice below and if necessary fill in the answer box to complete your choice A The real zero s of f is are Type an exact answer using radicals as needed Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed

3 20 3 18 10 Step 6 Sixth allocate in 3 4 cell X34 min 5 5 5 4 18 5 5 3 The initialz basic feasible solution is given by X11 5 X12 10 X22 5 X23 15 X24 5 X34 5 1 2 3 4 5 10 1 5 2 3 b 1 2 3 1 6 8 9 4 6 10 12 14 16 18 Minimum transportation cost 5 10 10 0 5 7 15 9 5 20 5 18 Rs 410 Exercise 1 Using North West Corner rule find out the initial basic feasible solution to the following TP 2 Least Cost Method 5 0 0 2 3 4 a 4 1 5 14 15 2 7 16 3 6 2 5 10 15 4 35 20 7 9 20 5 20 11 5 The procedure is as follows Step 1 Determine the smallest cost in the cost matrix of the transportation table Let it be Cij Allocate x min a b in the i j cell Step 2 If x j a cross off ith row of the transportation table and decrease b by aj If xij b cross off jth column of the transportation table and decrease a by bj If Xij a bj cross off either the first row or the first column but not both Step 4 Reneat stens 1 and 2 for the resulting table Reduce transportation table

Now we find the optimum sequence of the 6 jobs in two machines H and Kas usual in the following tables J4 J4 J4 J4 3 3 J3 Job seq J J J6 J 16 J3 J J6 J2 Js Jz Hence the optimal sequencing is J 13 1 16 12 15 Table to find minimum elapsed time Js Total M Time in Time out J5 Js out 0 2 2 8 7 10 12 10 21 21 21 33 33 33 42 42 17 8 2 7 M Time in Time 37 45 M3 Idle Idle time time M M3 Time in Time out 8 8 20 2 12 20 29 20 29 42 22 42 55 1 39 55 69 11 69 77 3 Minimum total elapsed time 77 Hrs Idle time for M 77 42 35 Idle time for M 17 77 45 17 32 49 8 0 0 0 0 0

t Light is Ligh articles 1 particte photon has energy Quantum TQuantum I photon a form of as energy Radiation energy Asafasa Electric field magnetic field light partides also light is particle wave behave as when light proticle move they mo duce Electric magnetic field he which as perpendicular Do light are considere an electromagnetic wave Speed 3 0 x108 m see Energy of Single photon 1 Energy ho s cycter wave per do Second planck s constant 6 626 110 7

At the age of 24 to save for retirement you decide to deposit 10 at the end of each month in an IRA that pays 5 5 compounded monthly a b Use the following formula to determine how much you will have in the IRA when you retire at age 65 P 1 r 1 A A P nt A Find the interest or a You will have approximately in the IRA when you retire Do not round until the final answer Then round to the nearest dollar as needec

What is an annuity Choose the correct answer below A An annuity is a checking account that pays interest B An annuity is a sequence of equal deposits made at equal time periods OC An annuity is a type of bank account that pays fixed interest rates if the principal is kept in the account for a specified amoun OD An annuity is a sequence of equal payments made at equal time periods

Solve for x 1 L x d X Simplify your answer

Change the percent to a decimal equivalent 2 10 10 The decimal equivalent is

The equation of the graph is f x Simplify your answer 10 10

Find the 3 degree polynomial with real coefficients depicted in the image below Note that 4i is a root of the polynomial Put your answer in the expanded form ax bx cx d 5 2 0 20 20 0 16 5

In this question we introduce a new definition Definition An n x n matrix is called happy if H On and H HT a Show that I is happy b Find a 2 x 2 happy matrix H I2 c Find all possible values for the determinant of a happy matrix H d Show that if H is an invertible happy matrix then H is hanni

Consider a generic quadratic function f x ax bx c with characteristics described below Determine the domain and range of f The vertex of the graph of f is 12 29 The graph of f a parabola opens downward The domain of f is The range of f is

Find the 3rd degree polynomial with real coefficients depicted in the image below Note that 2i is a root of the polynomial Put your answer in the expanded form ax bx cx d 5 0 0 2 1 0 5

Perform the operation below Enter your answer as a complex number in standard form 2 5i 3 7i

Find all complex roots real and or imaginary for the following polynomial Enter multiple answers separated by a comma f x x 4x 14x 20 roots

Ise division to rewrite the rational expression and use translations to sketch the graph by hand Then generate an mccurate depiction of the function with a graphing calculator f x X 5 X 6 Which of the following transformations are used to obtain the graph of f x from the graph of y Select all that apply A Shift the graph 1 unit upward B Shift the graph 6 units to the left c Reflect the graph about the y axis D Shift the graph 6 units to the right E Stretch the graph vertically by a factor of 6 OF Reflect the graph about the x axis G Shift the graph 1 unit downward H Shrink the graph horizontally by a factor of 6 Stretch the graph horizontally by a factor of 6 Shrink the an

Explain how the graph of the function f x can be obtained from the graph of y Then graph t and give the domain and range 1 To obtain the graph of f stretch the graph of y OA 9 Graph the function f x Choose the correct graph below Q G B x The domain of f x is Type your answer in interval notation vertically by a factor of 9 G OC Q OD o G

Explain how the graph of the function f x 2 can be obtained from the graph of y Then graph f and give domain and range To obtain the graph of 1 shift the graph of y The domain of f x is up Graph the function f x 2 Choose the correct graph below C 2 unit s G OD a a

Which of the graphs below have domain o 6 U 6 00 Q Q Q A 461 B L Use the letters below the graphs to answer the following question Graph s has have domain 6 U 6 00 Use a comma to separate answers as needed 10 C 1245 Q 2 16 X D

Write f x 3 5 x as the composition of two functions

A person standing close to the edge on top of a 56 foot building throws a ball vertically upward The quadratic function s t 16t 104t 56 models the ball s height above the ground in feet t seconds after it was thrown After how many seconds does the ball reach its maximum height seconds What is the maximum height of the ball feet W How many seconds does it take until the ball hits the ground seconds

Find the quadratic function that models the data in the table below 3 4 5 6 7 40 65 96 133 21 X y 2 1 0 5 16 0 1 1 2 8 8 176 9 10 280 225 The equation of the quadratic function that models the given data is y x x 0

Set f x 54x6 45x5 102x69x 35x 16x 4 Plot the function on the interval 2 2 and use Newton s Method to find all five roots in the interval Determine for which roots Newton converges linearly and for which the convergence is quadratic

A quadratic function has its vertex at the point 9 9 The function passes through the point 5 1 When written in standard form the function is f x a zh k where

Find all real solutions of the following Check your results 1 X 4 4 2 x 4x 2 Select the correct choice below and if necessary fill in the answer box es to complete your choice OA The solution s is are and the extraneous solution s is are Type exact answers using radicals as needed Use a comma to separate answers as needed OB The solution s is are and there are no extraneous solutions Type an exact answer using radicals as needed Use a comma to separate answers as needed OC There are no real solutions but an extraneous solution of Type an exact answer using radicals as needed Use a comma to separate answers as needed D There are no real solutions

POSSIBLE POINTS 2 A ball is thrown up in the air The function that represents the path of the ball is f t 16t2 80t 4 where f is the height in feet and t is the time in seconds What is the maximum height that the ball reaches feet

Write an equation for a parabola with x intercepts 4 0 and 3 0 which passes through the point 1 20 Write the equation

Solve the following inequality x 9x 8 0 Select the correct choice below and if necessary fill in the answer box OA The solution set is Type your answer in interval notation Use integers or fractions for any numbers in the expression OB There is no real solution

Write an equation in factored form for a parabola with x intercepts 2 0 and 4 0 and goes through the point 1 4 f x a x b x c a b C Type your answer as a fraction

Identify the interval s on which the function f x x 2x 3 is positive CHOOSE ALL THAT APPLY x 2 x 2 x 1 x 3 x 3 x 3 x 1 x 2 x 1 x 2 0x 1 x 3

ation of the cos 20 3 2 What are the solutions to cos 20 3 in the interval 0 0 2n Select the correct choice below and if necessary fill in the answer box to complete your choice 2 OA The solution set is 0 Simplify your answer Type an exact answer using as needed Type your answer in radians Use integers or fractions for any numbers in the expression Use a comma to separate as needed OB There is no solution

ll 2x 3 5 Determine the y intercept of a line with a slope of 2 that is a tangent to the curve y y 1 2x 4x 5

Suppose a sample of a certain substance decayed to 77 8 of its original amount after 300 days Round your answers to tv decimal places a What is the half life in days of this substance days b How long would it take the sample to decay to one third of its original amount days

x 1 234 2 345 3 456 y 12 342 11 45 16 56 which of the following is the equivalent of y of type x A 10x 30 B 9x 27 D 7x 21 C 8x 2 E 5x 20