Complex numbers Questions and Answers

Algebra
Complex numbersUse a half angle or reduction formula to fill in the blanks in the identity below cos 8x cos x
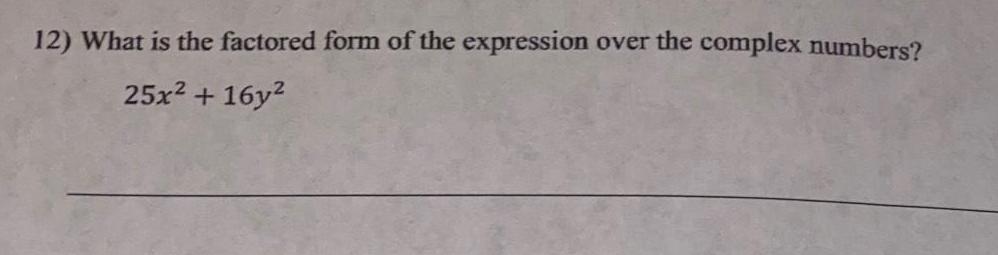
Algebra
Complex numbers12 What is the factored form of the expression 25x 16y over the complex numbers
Algebra
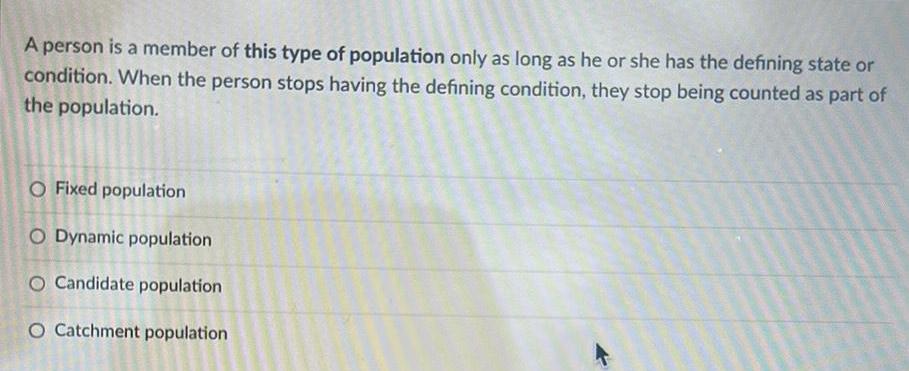
Complex numbersA person is a member of this type of population only as long as he or she has the defining state or condition When the person stops having the defining condition they stop being counted as part of the population O Fixed population O Dynamic population O Candidate population O Catchment population

Algebra
Complex numbersMacmillan Learning Solve the following equation for x log 3x log 4 x 1 Give an exact answer Use symbolic notation and fractions where needed Enter NO SOLUTION a solution

Algebra
Complex numbersApply It Group Problem Solving Tasks G In a class there is a 2 3 ratio of boys to girls If there are 30 students in the class how many boys are there

Algebra
Complex numbersWrite the expression below as a trigonometric function of a single angle Then evaluate cos 10 cos 18 sin 10 sin 18
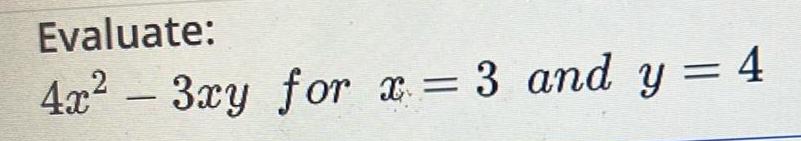

Algebra
Complex numbersFind the measure in radians of a central angle of a sector of area 12 square inches in a circle of radius 3 2 inches The central angle measures approximately radians Round to the nearest tenth

Algebra
Complex numbersThe weight of an object above the surface of the Earth varies inversely with the square of the distance from the center of the Earth Given the radius of the Earth is 3960 miles how much would a man weigh at the top of Mt Everest 5 5 miles above the surface of the Earth if he weighs 180 lbs on the surface of the Earth Round to the nearest 0 1 lb
Algebra
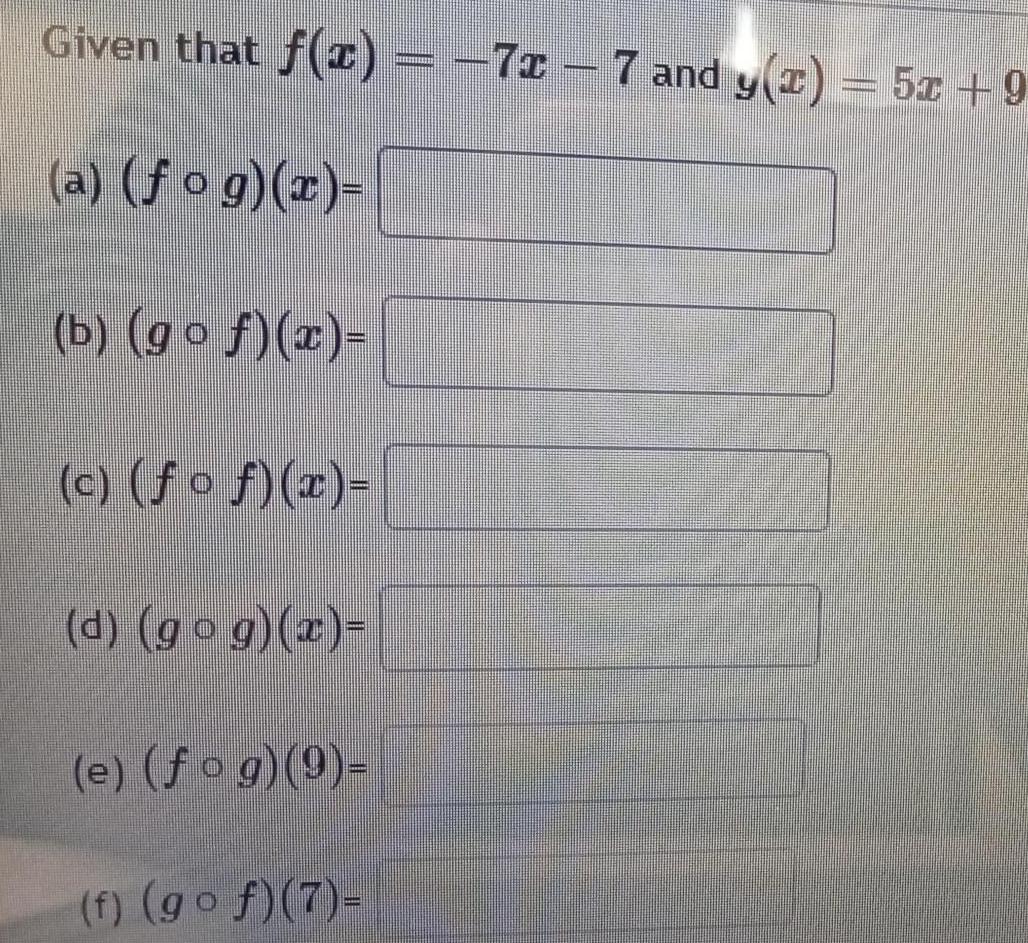
Complex numbersGiven that f x 71 7 and y x 5x 9 www a fog x b gof x c o x d go g x e fog 9 f gof 7

Algebra
Complex numbersFind the equation of the einele with center 1 2 and paring through the pofit 912 in stondend forem

Algebra
Complex numbersFind the equation of live passing through the point 210 a perpendicular to the line to the answer

Algebra
Complex numbers230 MATHEMATICS Proof Let fand g be two functions such that d or or Rationalised 2023 24 f dx 10x dx fx 0x dx 0 Hence f x dx g x dx C where C is any real number Why f x dx fg x dx C So the families of curves f x dx C C ER and g x dx C C R are identical Hence in this sense f x dx and 120x dx dx Note The equivalence of and g x dx C C R is customarily expressed by writing f x dx g x dx without mentioning the parameter II f x g x dx ff x dx f g x dx Proof By Property 1 we have d Also On the otherhand we find that ecode f x dx f800 de dx g x dx f x g x f x g x Thus in view of Property II it follows by 1 and 2 that f f x g x dx f x dx f g x dx IV For any real number k fk f x dx k f x dx shed Rationalised 2023 24 Proof By the Property 1 f x dx k f x kaff x dx k f x dx k ffox dx INTEGRALS M www 1 2 231

Algebra
Complex numbers1 Example 4 Express tan Solution We write ii Take x cos 0 then proceeding as above we get sin tan COS X 1 sin x Example 5 Write cot Therefore cot 3 tan tan tan tan 1 X 1 x 1 1 COS X Solution Let x sec 0 then x 1 1 N sin 2sine cose sin Sin20 20 2 sin x X X X sin COS sin COMME 17 2 2 2 X x COS sin 2 3 X COS sin 2 X COS sin 2 Prove the following 1 3sin x sin 3x 4x xe X 0 T X tan 4 2 X X X sin 2 sin cos 2 2 2 sin 2 3cos x cos 4x 3x XE X 2 X 2 tan T X 4 2 Rationalised 2023 24 le of you 1 sec 0 Write the following functions in the simplest form 1 x 1 x 1 in the simplest form EXERCISE 2 2 in the simplest form 1 tan INVERSE TRIGONOMETRIC FUNCTIONS 29 1 tan cot cot 0 0 sec x which is the simplest form 0 1 tan 0 X 1 x 2 cos x NORT COS X 1 cos x ublished 0 x T

Algebra
Complex numberstrigonometric functions In fact they will be valid only for some values of x for which inverse trigonometric functions are defined We will not go into the details of these values of x in the domain as this discussion goes beyond the scope of this textbook Let us recall that sin x then x sin y and if x sin y then y sin x This is equivalent to For suitable values of domain similar results follow for remaining trigonometric functions 28 sin sin x x x 1 1 and sin sin x x x E 2 MATHEMATICS We now consider some examples Example 3 Show that 1 sin 2x 1 x 2 sin X 1 ii sin 2x 1 x 2 cos x Solution tan Rationalised 2023 24 i Let x sin 0 Then sinx 0 We have 1 Example 4 Express tan Solution We write 25x5 1 2 x 2 sin 2x 1 x sin 2 sin 0 1 sin 0 COS X 1 sinx ii Take x cos 0 then proceeding as above we get sin tan x 1 not sin 2sine cos0 sin sin2 2 sin x 2 COS 2 2 X 2 X 2 sin COS X 2 2 X X cos sin COS sin 2 x 2 sin the simplest form t to be reputasted x 2 cos x
Algebra
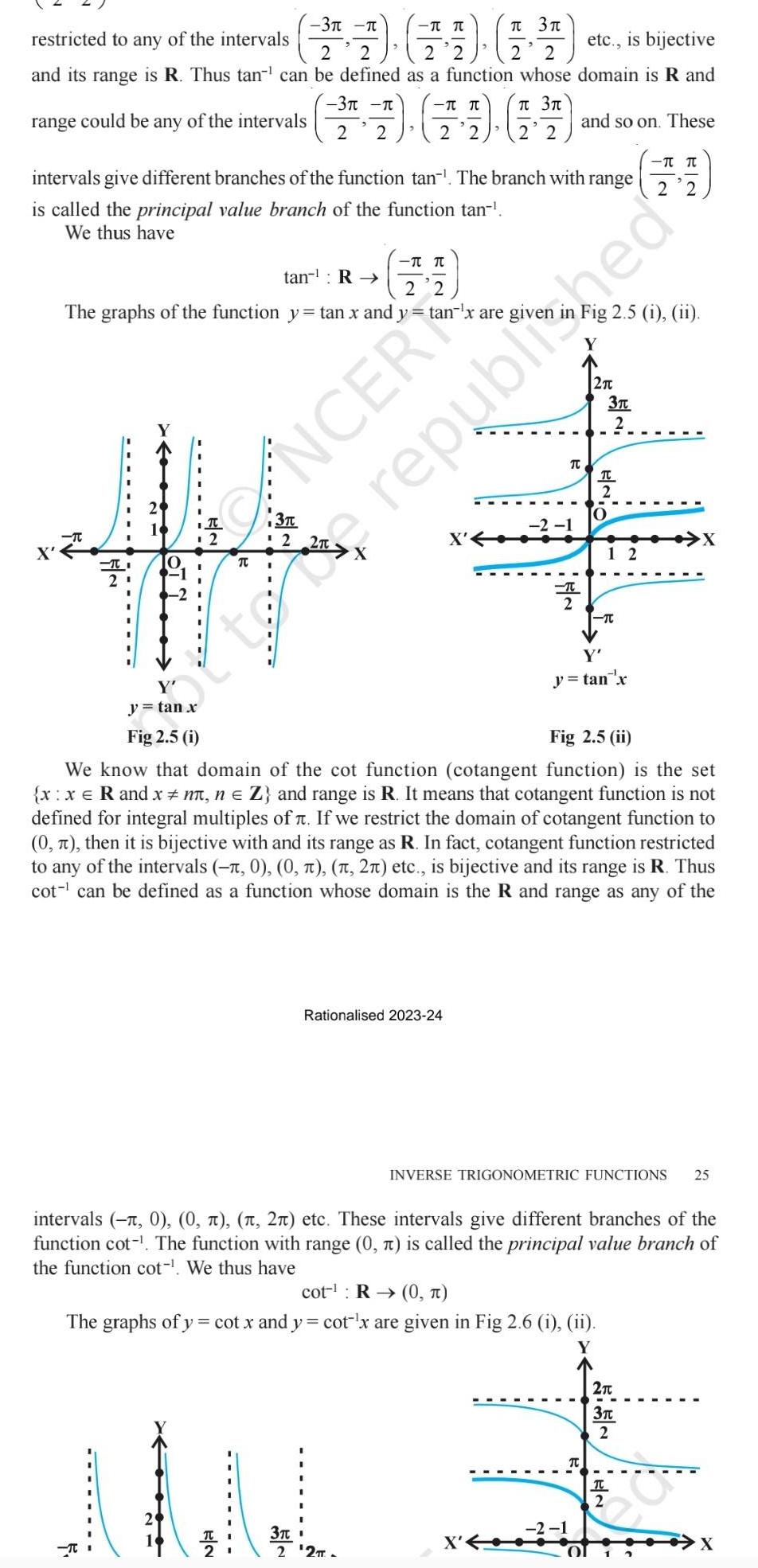
Complex numbersrestricted to any of the intervals 1 1 14 etc is bijective 2 2 2 2 2 and its range is R Thus tan can be defined as a function whose domain is R and 3 3 range could be any of the intervals 2 2 2 2 T intervals give different branches of the function tan The branch with range is called the principal value branch of the function tan We thus have tan R The graphs of the function y tan x and ytan x are giver 2 y tan x Fig 2 5 i T T 3 CANCER T TT 2 2 3 2 TI 21 T Rationalised 2023 24 3 t 2 2TT 2 1 T 2 and so on These 74 2 2 Fig 2 5 i ii Y 2 2 1 Fig 2 5 ii We know that domain of the cot function cotangent function is the set x x R and x n n Z and range is R It means that cotangent function is not defined for integral multiples of If we restrict the domain of cotangent function to 0 then it is bijective with and its range as R In fact cotangent function restricted to any of the intervals 0 0 2 etc is bijective and its range is R Thus cot can be defined as a function whose domain is the R and range as any of the cot R 0 The graphs of y cot x and y cot x are given in Fig 2 6 i ii 3T 2 TC 2 O Y y tan x T intervals 1 0 0 2 etc These intervals give different branches of the function cot The function with range 0 is called the principal value branch of the function cot We thus have 12 INVERSE TRIGONOMETRIC FUNCTIONS 25 republished T 2T 3 2 X
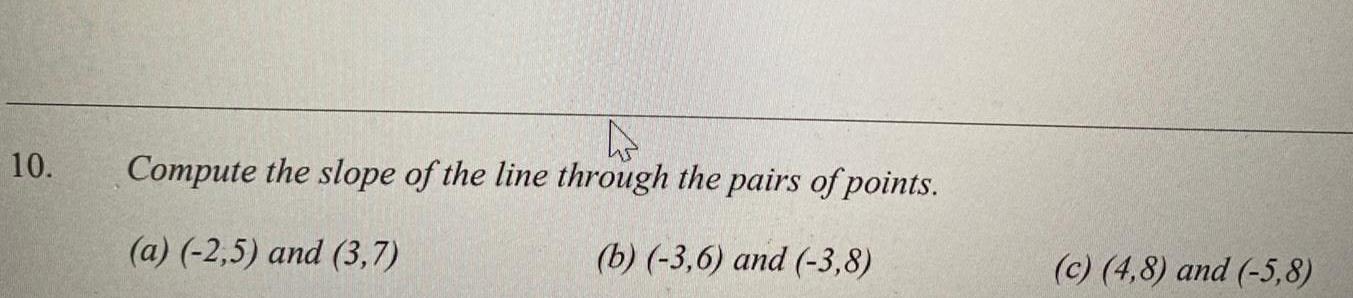
Algebra
Complex numbers10 4 Compute the slope of the line through the pairs of points a 2 5 and 3 7 b 3 6 and 3 8 c 4 8 and 5 8

Algebra
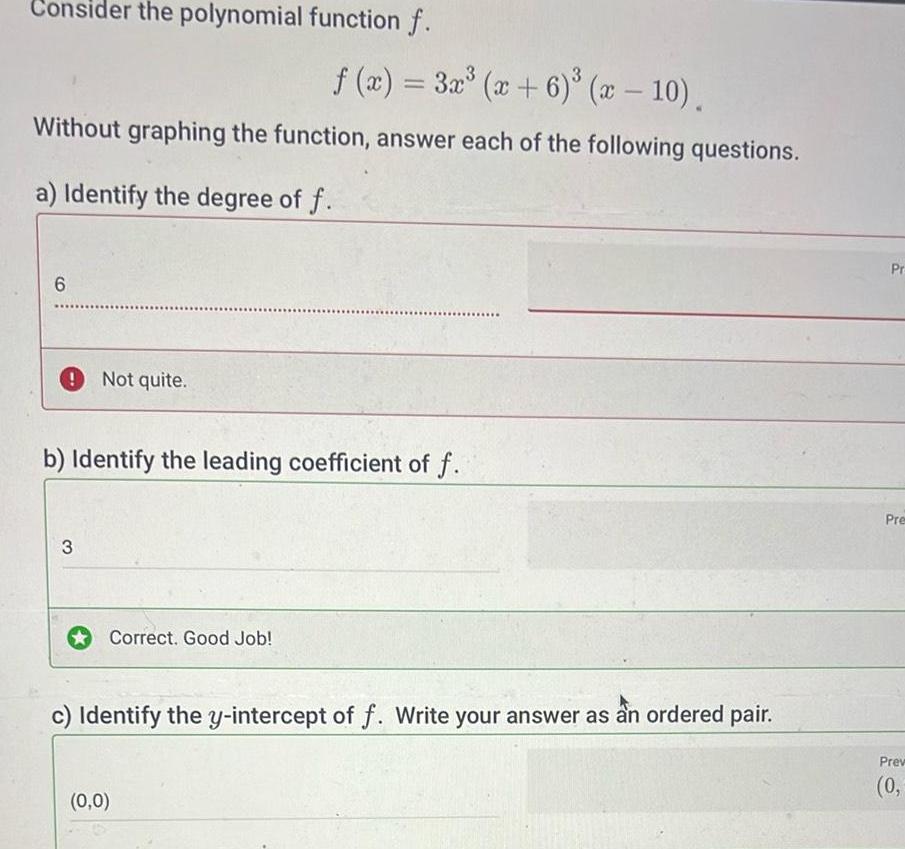
Complex numbersConsider the polynomial function f f x 3x x 6 x 10 Without graphing the function answer each of the following questions a Identify the degree of f 6 Not quite b Identify the leading coefficient of f 3 Correct Good Job c Identify the y intercept of f Write your answer as an ordered pair 0 0 Pr Pre Prev 0



Algebra
Complex numbersf x 3x x 6 x 10 Without graphing the function answer each of the following questions a Identify the degree of f b Identify the leading coefficient of f c Identify the y intercept of f Write your answer as an ordered pair d Describe the end behavior of f As x xo f x As x o f x O As x f x As x o f x As a o f x As o f x
Algebra
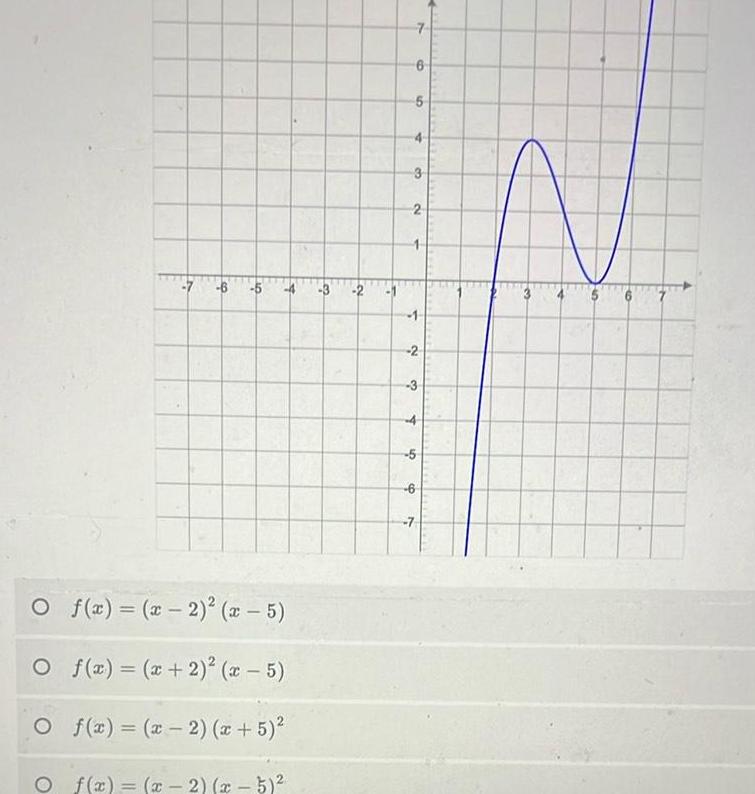
Complex numbersT O do 149 4 O f x x 2 x 5 O f x x 2 x 5 f x x 2 x 5 O f x x 2 x 5 t 2 5 7 6 5 4 3 2 1 2 3 4 5 7 6

Algebra
Complex numbers5 Suppose that x 13 is a point in Quadrant II lying on the unit circle Find x Write the exact value not a decimal approximation X 8
Algebra
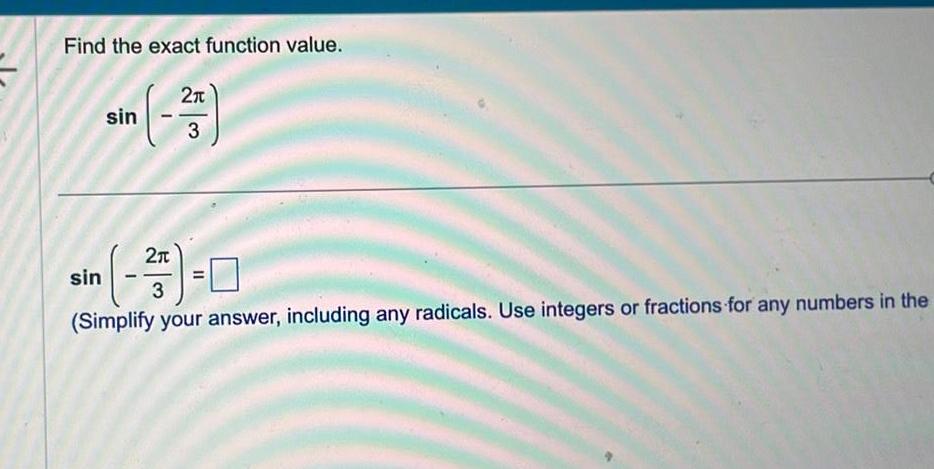
Complex numbersFind the exact function value 3 sin in 25 0 3 Simplify your answer including any radicals Use integers or fractions for any numbers in the
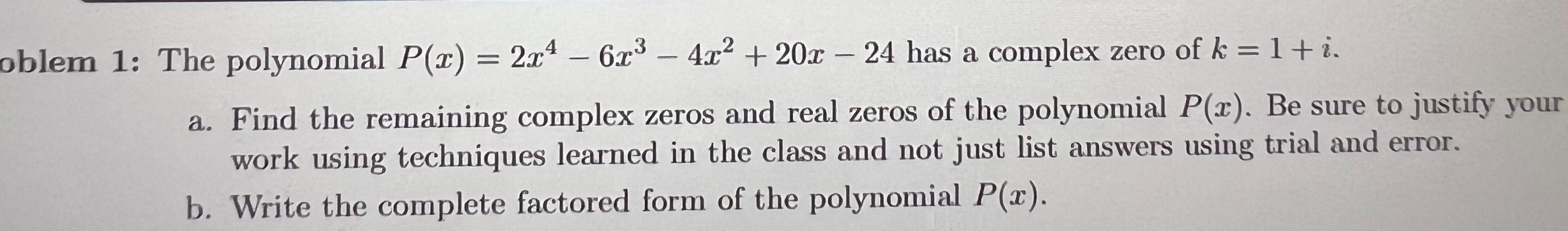
Algebra
Complex numbers4 oblem 1 The polynomial P x 2x 6x 4x 20 24 has a complex zero of k 1 i a Find the remaining complex zeros and real zeros of the polynomial P x Be sure to justify your work using techniques learned in the class and not just list answers using trial and error b Write the complete factored form of the polynomial P x
Algebra
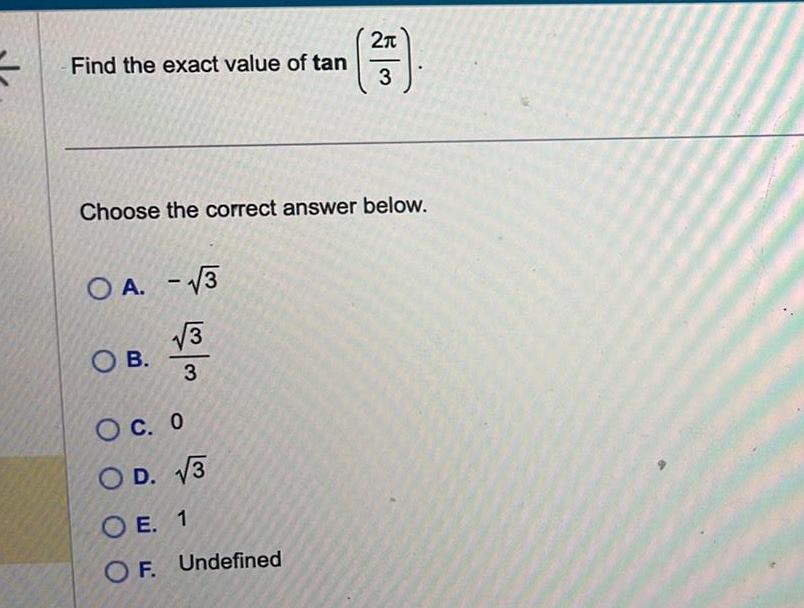
Complex numbersFind the exact value of tan Choose the correct answer below OA 3 3 3 OB 2 3 OC 0 OD 3 OE 1 OF Undefined


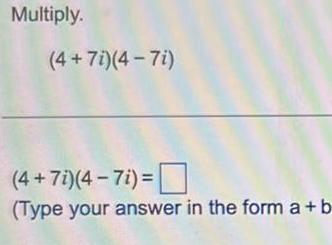
Algebra
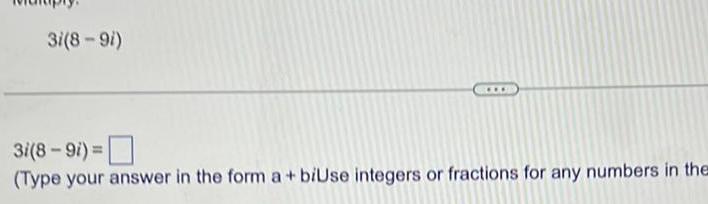
Complex numbers3i 8 9i 3i 8 9i Type your answer in the form a biUse integers or fractions for any numbers in the
Algebra
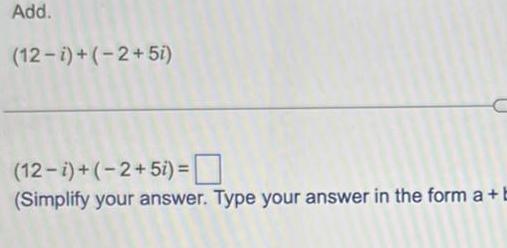
Complex numbersAdd 12 1 2 5i C 12 i 2 5i Simplify your answer Type your answer in the form a b

Algebra
Complex numbersFull Solutions to these problems must be uploaded to Canvas before the deadline Solutions must be organized legible and all papers must be stapled Points will be deducted for incomplete reasoning and disorganized work even if your answers are correct No late submissions will be accepted Problem 1 Solve each inequality symbolically and state the solution set using interval notation 3y 2y 1 a b TT 4x c 1 d 3 L1 8 1 8x 2 3 2t 5y 7x 2 7 2 52 3 un granha of f r and a r to solve each equation or inequality For each inequality use 1
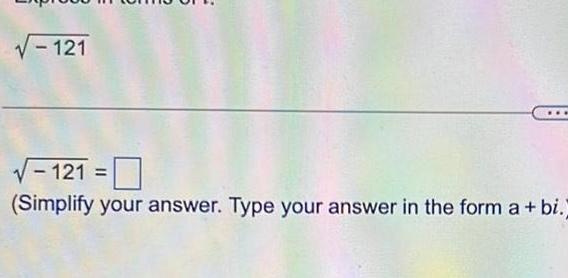
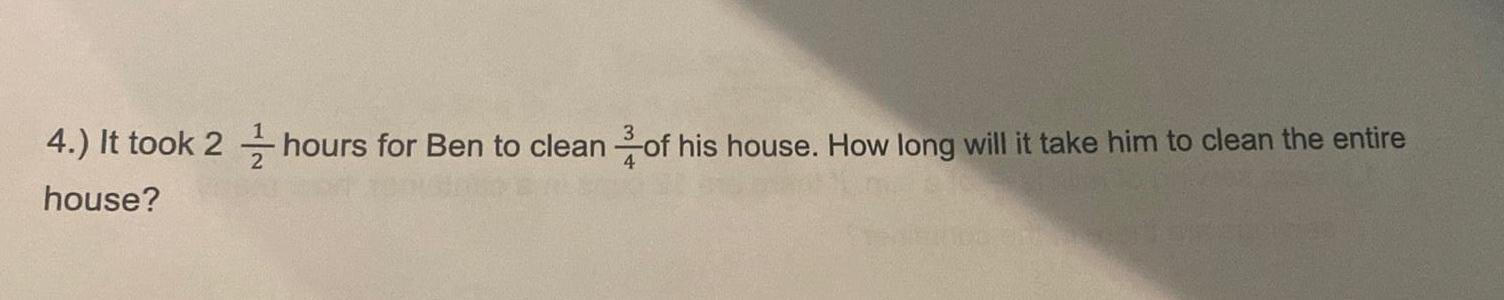
Algebra
Complex numbers4 It took 2 hours for Ben to clean of his house How long will it take him to clean the entire house

Algebra
Complex numbers5 The ratio of sugar to salt in a recipe is 20 3 If Jessica is following the recipe and using 4 cups of sugar how much salt will she need to use

Algebra
Complex numbers4 In of an hour Becca completes of a project How many total hours will it take her to complete the project a hours c 1 hours b 1 hour d hours

Algebra
Complex numbers3 At a grocery store peppers cost 1 25 a pound How much money would a customer be charged for four and a half pounds of peppers

Algebra
Complex numbers2 George is on the track team and can run 50 meters in 8 seconds If he runs at the same rate about how many seconds will it take him to reach the 375 meter mark

Algebra
Complex numbersYou must show work for ALL problems to get 1 Amy types 130 words in 2 minutes If she types for 45 minutes how many words will she type
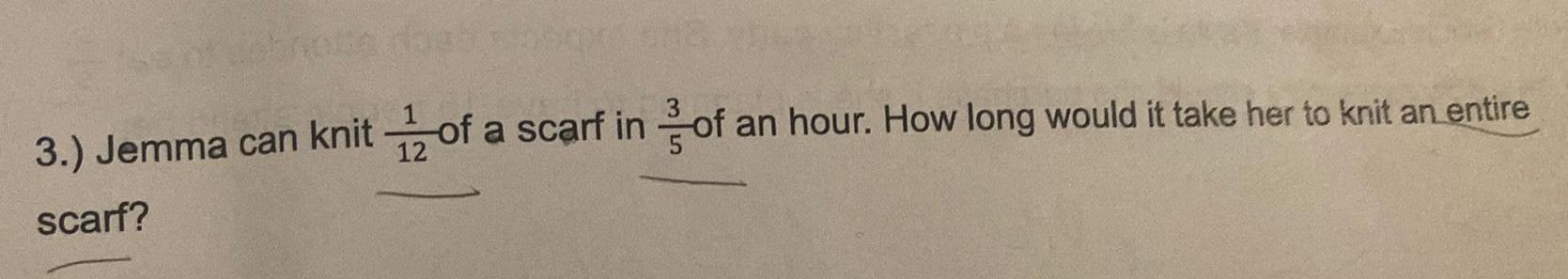
Algebra
Complex numbers3 Jemma can knitof a scarf in of an hour How long would it take her to knit an entire scarf
Algebra
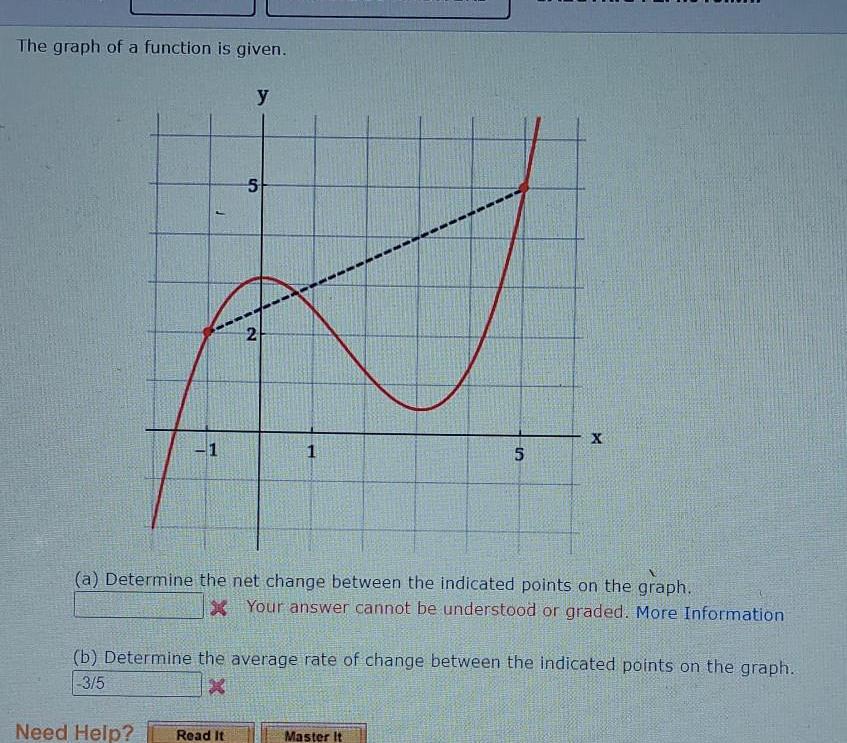
Complex numbersThe graph of a function is given J 1 y 5 2 Need Help Read It 1 5 a Determine the net change between the indicated points on the graph X Your answer cannot be understood or graded More Information b Determine the average rate of change between the indicated points on the graph 3 5 X Master It
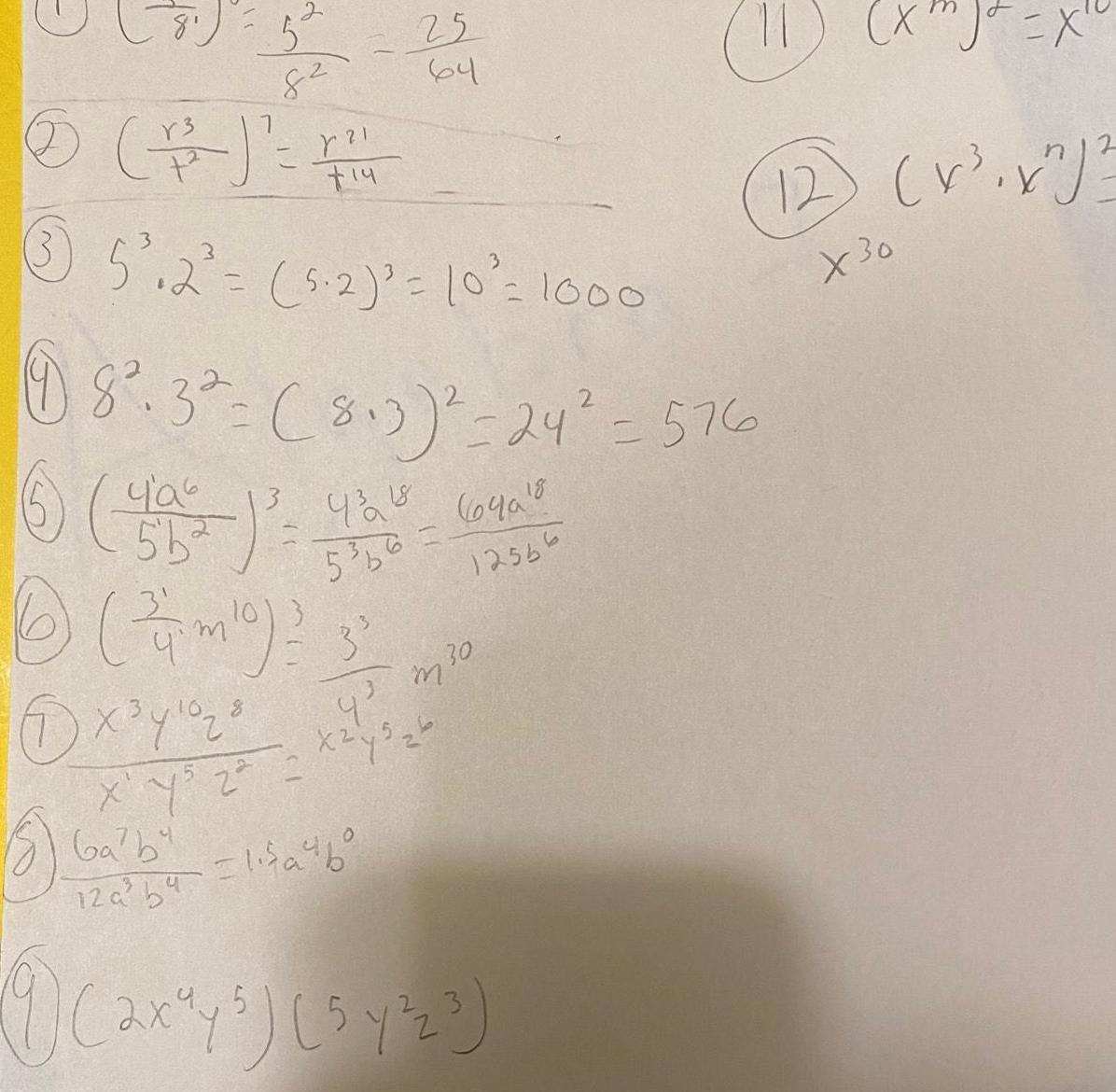
Algebra
Complex numbers23 24 5 25 64 93218 5356 3 5 2 5 2 10 1000 18 3 813 24 576 64018 12556 4a6 6 19 6 7m 0 3 1x y 0 4 m 0 30 zb 2 x y 2 x y J EX 12 x x X 30 6 bm b Hab by 12a b4 1 2x 4 54 23

Algebra
Complex numbersUffit Stope Write the slope intercept form of the equation of the line through the given point with th slope 5 1 12 1 through 2 3 slope A y x 2 B y 4x 2 y x 2 D y 4x 2 2 2 through 1 3 slope 2 A y x 5 C y 2x 5 B y 2x 5 D y 4x 5

Algebra
Complex numbers1 3 Point Slope Write the slope intercept form of the equation of the line through the given point with the given slope 1 through 2 3 slope 5232 A y x 2 B y 4x 2 5 C y x 2 D y 4x 2 3 through 3 3 slope undefined 1 A y x 1 3 B x 3 C y 3 D y x 1 3 2 2 through 1 3 slope 2 4 A y x 5 C y 2x 5 4 through 5 4 slope 7 A y x 2 3 2 7 3 B y x 2 2 7 3 C y x 2 2 B y 2x 5 D y 4x 5 3 7 D y x 2 2 3 2

Algebra
Complex numbers7 through 3 1 and 1 3 A y 1 x 3 B y 1 5 x 3 C y 1 5 x 3 D y 3 5 x 1 11 Slope A y 0 C 0 x 1 2 B y 5 3x D y 5 4x Write the point slope form of the equation of each line given the slope and y intercept 9 Slope 0 y intercept 5 7 5 A y 5 3x C y 5 0 y intercept 0 8 1 B y x 2 D v 2x 8 through 3 4 and 0 4 A y 3 x 4 8 8 B y 4 x 3 3 12 C y 3 x 4 8 D y 3 x 4 4 10 10 Slope y intercept 5 A y 36x 5 5 7 B y 5 C y x 5 tx D y 5 x 5 12 Slope2 y intercept 1 A y 1 2x C y 1 4x B y 1 5x D y 1 4x
Algebra
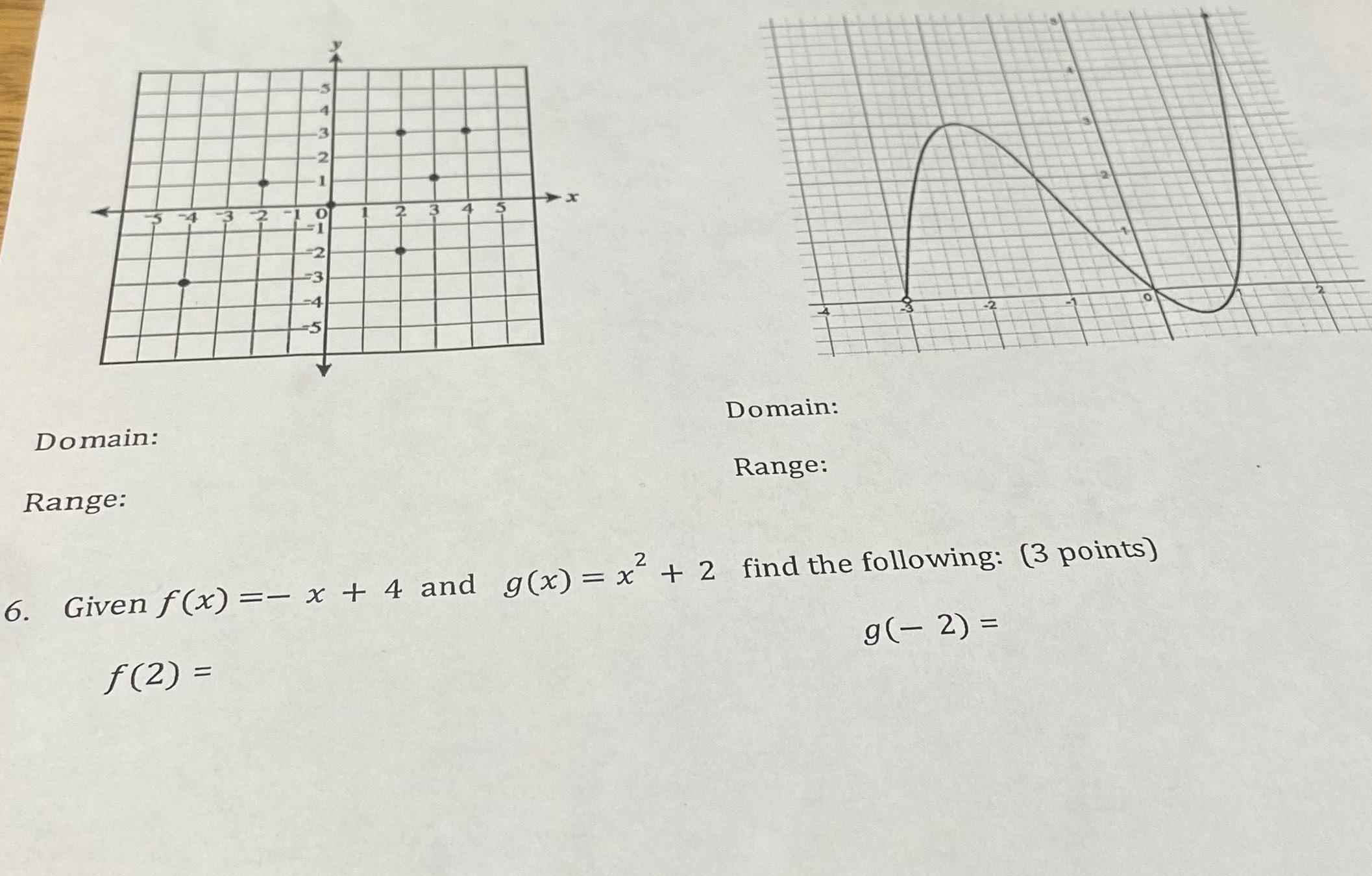
Complex numbersDomain Range 3 4 2 1 10 1 2 3 4 5 2 3 5 Domain Range 2 O 6 Given f x x 4 and g x x 2 find the following 3 points f 2 g 2

Algebra
Complex numbers4 Find the value of each unknown angle in this diagram There are five unknown angles 104 Z 56 Y X d of it all 41x12 b X y