Limits & Continuity Questions and Answers
Calculus
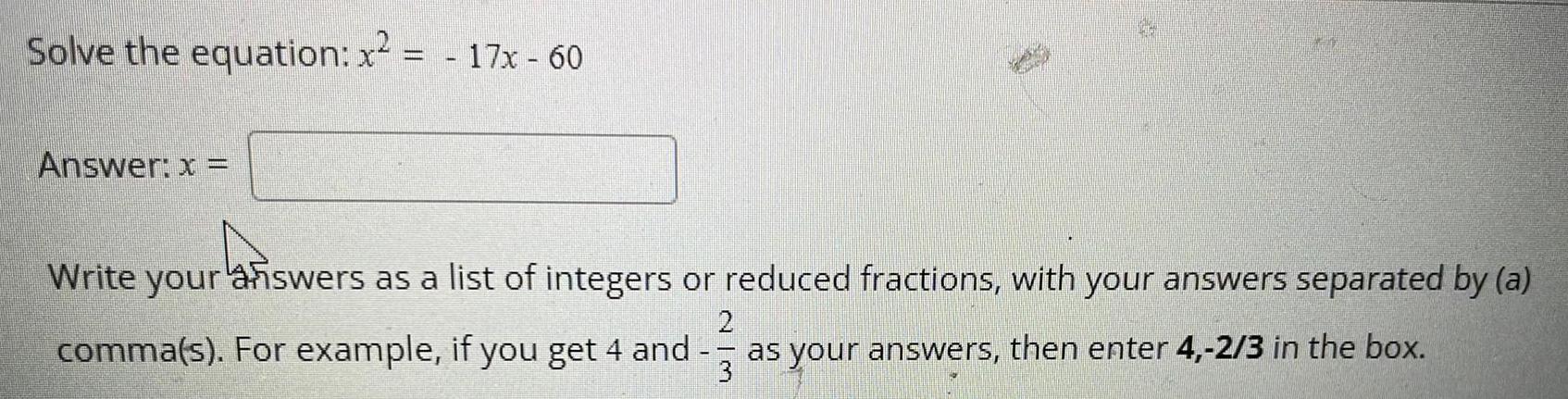
Limits & ContinuitySolve the equation: x² = - 17x - 60
Answer: x =
Write your answers as a list of integers or reduced fractions, with your answers separated by (a)
comma(s). For example, if you get 4 and
2
as your answers, then enter 4,-2/3 in the box.
3

Calculus
Limits & ContinuityConsider the quadratic function `f(x) = x^2-2x-8.
Determine the following:
The smallest x-intercept is `x = `
The largest x-intercept is `x =
The y-intercept is `y =
Calculus
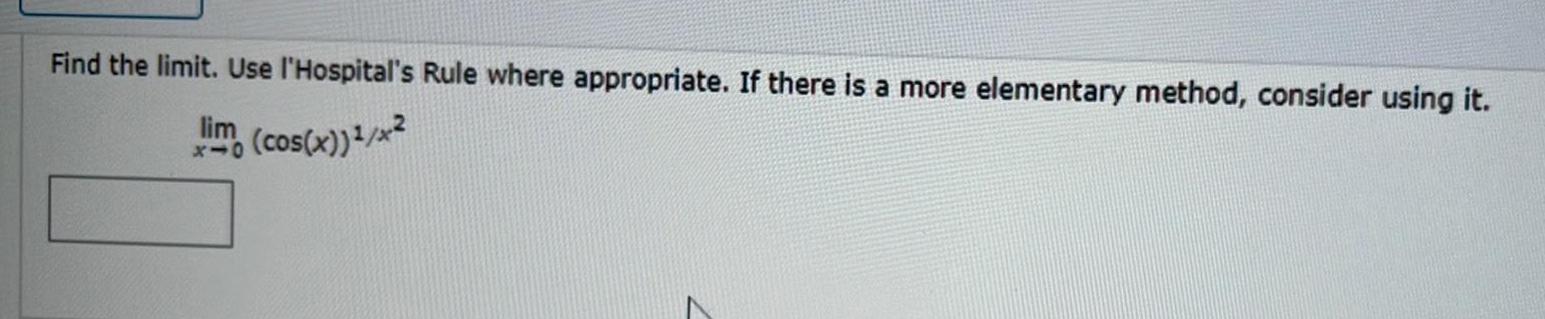
Limits & ContinuityFind the limit. Use l'Hospital's Rule where appropriate. If there is a more elementary method, consider using it.
lim (cos(x))¹/²
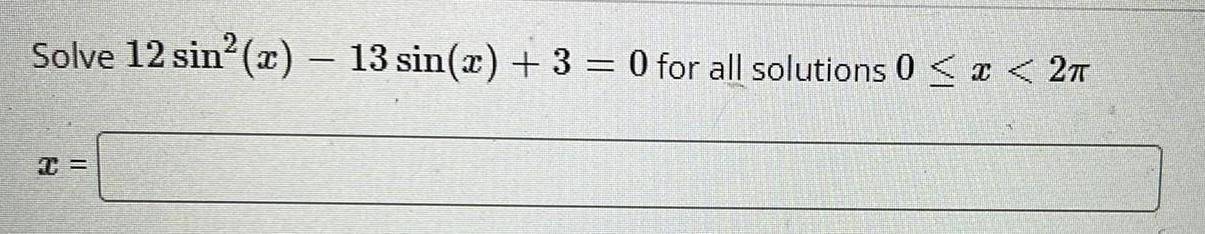


![A pedestrian walks 7.4 kilometers west
and then 9.2 kilometers south.
What is the angle of the
pedestrian's resultant vector?
Hint: Draw a vector diagram.
[?]°](https://media.kunduz.com/media/sug-question/raw/83393305-1660312550.8561485.jpeg?w=256)
Calculus
Limits & ContinuityA pedestrian walks 7.4 kilometers west
and then 9.2 kilometers south.
What is the angle of the
pedestrian's resultant vector?
Hint: Draw a vector diagram.
[?]°

Calculus
Limits & ContinuityConsider the number of fish, y, in a certain population.
dy
dt
The annual rate of change of a fish population is given by
What is the meaning of 0.1y in this differential equation?
= 0.1y-b.
O There is an increase in the fish population each year, equal to 10% of the current population.
There is an increase in the fish population each year, equal to 1% of the current population.
O There is a decrease in the fish population each year due to harvesting, equal to 10% of the current fish
population.
O There is an increase in the fish population each year, equal to 50 fish each year.
![If 3 sin ²x
+ 3 cos²x = 4, then find the number of solutions of the
equation in the interval [0, 2x]](https://media.kunduz.com/media/sug-question/raw/83401080-1660312433.9707685.jpeg?w=256)
Calculus
Limits & ContinuityIf 3 sin ²x
+ 3 cos²x = 4, then find the number of solutions of the
equation in the interval [0, 2x]
Calculus
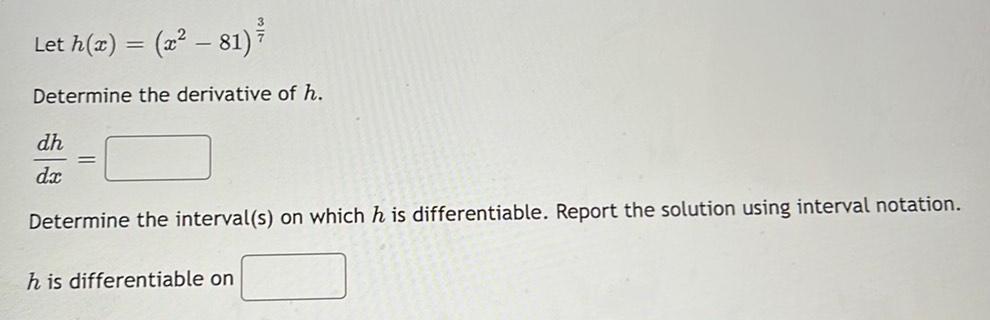
Limits & ContinuityLet h(x) = (x² − 81) ²
-
Determine the derivative of h.
dh
dx
Determine the interval(s) on which h is differentiable. Report the solution using interval notation.
h is differentiable on
![Find the absolute extrema of the function on the interval [2, 10].
g(x)
=
Absolute minimum:
X
In(x)
at x =
Absolute maximum:
at x =](https://media.kunduz.com/media/sug-question/raw/83439921-1660312314.7577598.jpeg?w=256)
Calculus
Limits & ContinuityFind the absolute extrema of the function on the interval [2, 10].
g(x)
=
Absolute minimum:
X
In(x)
at x =
Absolute maximum:
at x =
![Find all values of 8 (in rad) that satisfy the equation over the interval [0, 2π].
√3
2
sin(0)
smaller value
larger value
0 =
0
-
rad
rad](https://media.kunduz.com/media/sug-question/raw/83440122-1660312257.083293.jpeg?w=256)
Calculus
Limits & ContinuityFind all values of 8 (in rad) that satisfy the equation over the interval [0, 2π].
√3
2
sin(0)
smaller value
larger value
0 =
0
-
rad
rad
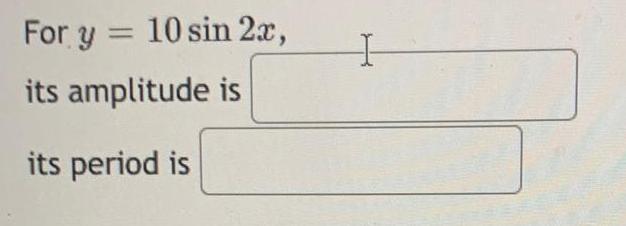

Calculus
Limits & ContinuityA boat sails 285 miles south and
then 132 miles west.
What is the magnitude of the
boat's resultant vector?
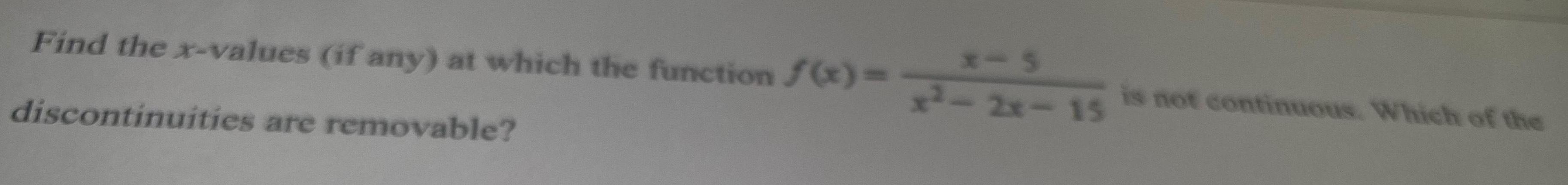
Calculus
Limits & ContinuityFind the x-values (if any) at which the function f(x)=
discontinuities
are removable?
x-S
x²-2x-15
is not continuous. Which of the

Calculus
Limits & Continuity(3x+12 if x < -2
if x>-2
if x = -2
Let f(x)=√x+38
2
Select all statements below that you agree with.
Note: You may be checking more than one box. No partial credit.
Of(-2) is defined.
Olim f(x) exists.
x--2
O lim f(x)=f(-2).
x--2
The function is continuous at x = -2.
The function is not continuous at x = -2.
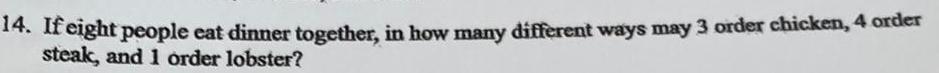
Calculus
Limits & Continuity14. If eight people eat dinner together, in how many different ways may 3 order chicken, 4 order
steak, and 1 order lobster?
![Suppose that limf(x) = 10 and lim g(x)=14. Find the following limit.
lim [f(x)g (x)]](https://media.kunduz.com/media/sug-question/raw/83305657-1660311928.411592.jpeg?w=256)
Calculus
Limits & ContinuitySuppose that limf(x) = 10 and lim g(x)=14. Find the following limit.
lim [f(x)g (x)]

Calculus
Limits & ContinuityProblem 12. Determine the amplitude and period of the function y = 3 cos
the function over its single period using five key points.
(x). Then, graph
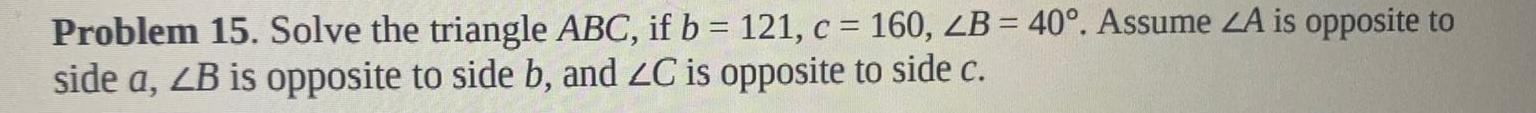
Calculus
Limits & ContinuityProblem 15. Solve the triangle ABC, if b = 121, c = 160, LB = 40°. Assume LA is opposite to
side a, LB is opposite to side b, and ZC is opposite to side c.
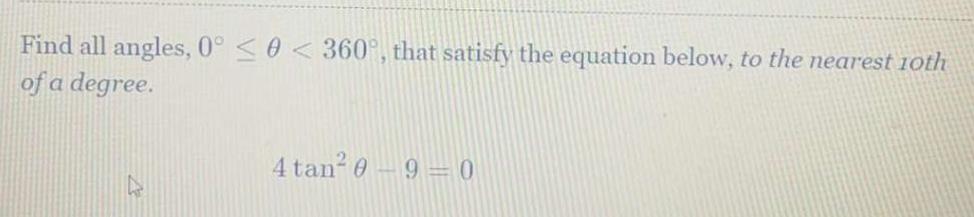
Calculus
Limits & ContinuityFind all angles, 0° ≤ 0 < 360°, that satisfy the equation below, to the nearest 10th
of a degree.
4 tan² 090
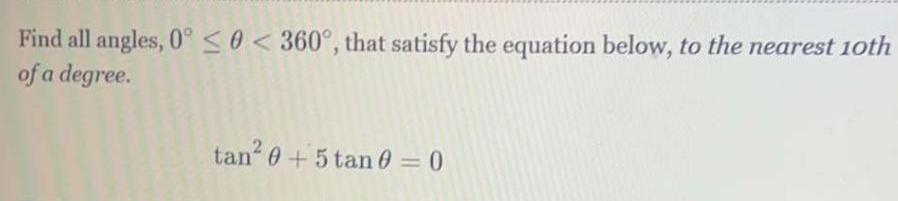
Calculus
Limits & ContinuityFind all angles, 0° ≤0 < 360°, that satisfy the equation below, to the nearest 10th
of a degree.
tan²0+5 tan 0 = 0
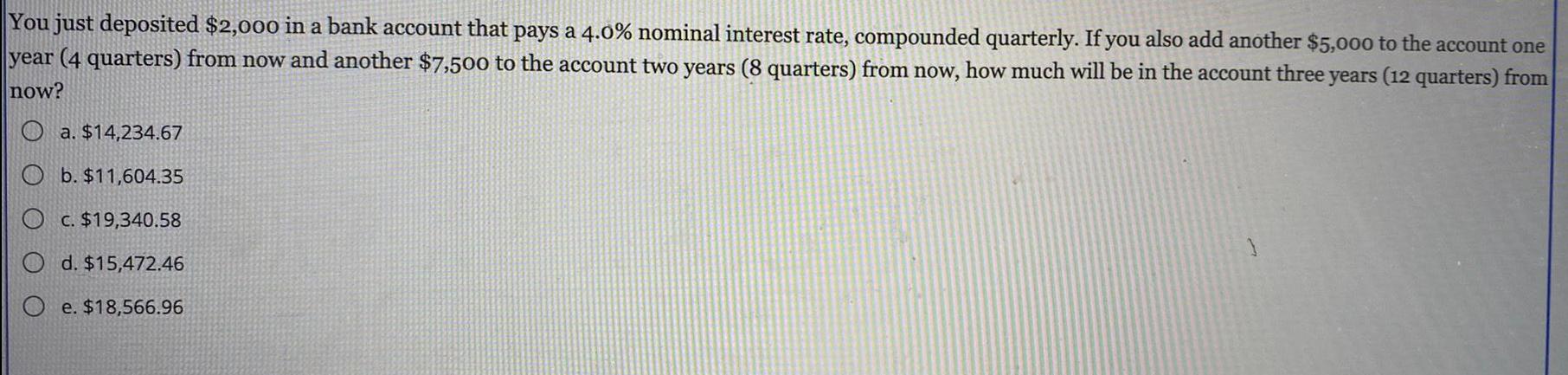
Calculus
Limits & ContinuityYou just deposited $2,000 in a bank account that pays a 4.0% nominal interest rate, compounded quarterly. If you also add another $5,000 to the account one
year (4 quarters) from now and another $7,500 to the account two years (8 quarters) from now, how much will be in the account three years (12 quarters) from
now?
Oa. $14,234.67
Ob. $11,604.35
O c. $19,340.58
d. $15,472.46
e. $18,566.96

Calculus
Limits & ContinuityGranville Co. recently purchased several shares of Kalvaria Electronics' preferred stock. The preferred stock has a before-tax yield of 8.60%. If the company's
tax rate is 15%, what is Granville Co.'s after-tax yield on the preferred stock? Assume a 70% dividend exclusion for tax on dividends. (Round your final answer
to two decimal places.)
a. 9.53%
b. 7.47%
c. 8.95%
d. 8.21%
e. 8.79%
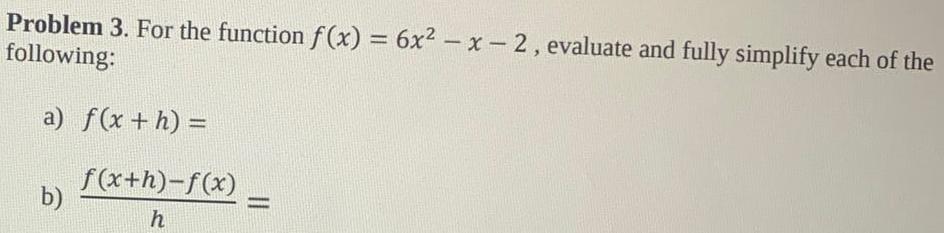
Calculus
Limits & ContinuityProblem 3. For the function f(x) = 6x²-x-2, evaluate and fully simplify each of the
following:
a) f(x + h) =
b)
f(x+h)-f(x)
h
=
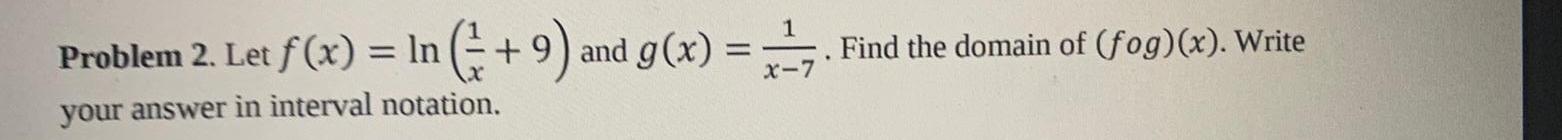
Calculus
Limits & ContinuityProblem 2. Let f(x) = ln (+9) and g(x) =
1
X-7
your answer in interval notation.
Find the domain of (fog)(x). Write
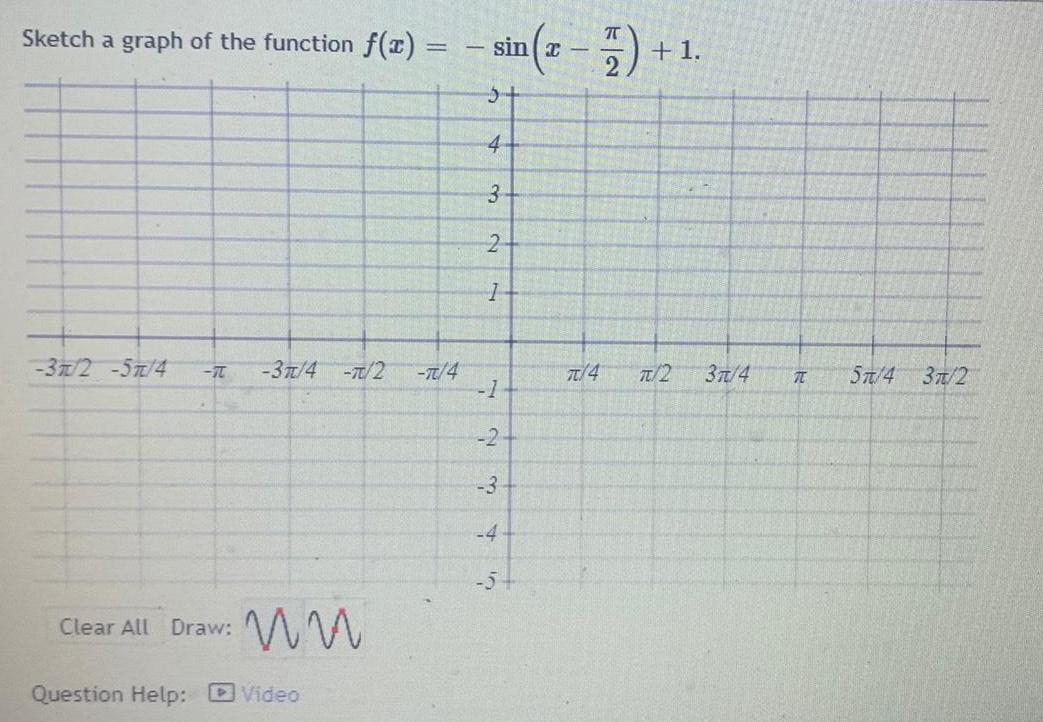
Calculus
Limits & ContinuitySketch a graph of the function f(x) =
-37/2 -57/4 -7 -3π/4 -π/2 -π/4
Clear All Draw: M
Question Help: Video
sin|t —
5+
4
3
2
1
-1
-2-
-3
-4
+1.
π/4 π/2
3π/4
T
5/4 3/2
![8. [-/3 Points]
DETAILS
(x, y)
WANEFMAC7 15.4.012.
Use Lagrange multipliers to solve the given optimization problem.
Find the minimum value of f(x, y) = x² + y2 subject to xy2 = 16.
fmin
Also find the corresponding points (x, y).
(x, y) =
(smaller y-value)
(larger y-value)](https://media.kunduz.com/media/sug-question/raw/83164450-1660311607.7031121.jpeg?w=256)
Calculus
Limits & Continuity8. [-/3 Points]
DETAILS
(x, y)
WANEFMAC7 15.4.012.
Use Lagrange multipliers to solve the given optimization problem.
Find the minimum value of f(x, y) = x² + y2 subject to xy2 = 16.
fmin
Also find the corresponding points (x, y).
(x, y) =
(smaller y-value)
(larger y-value)
![Find the area of this triangle if
B = 5 radians, a = 9, and c = 7.
A.
b
B
a
[?] square units
-c C](https://media.kunduz.com/media/sug-question/raw/83164540-1660311601.7262936.jpeg?w=256)
Calculus
Limits & ContinuityFind the area of this triangle if
B = 5 radians, a = 9, and c = 7.
A.
b
B
a
[?] square units
-c C

Calculus
Limits & ContinuityA colony of an animal begins with one pair of mature animals, which will produce a pair of offspring (one male, one female) each month. Assume that all animals mature in 1 month and produce a pair of offspring (one
male, one female) after 2 months. If no animals ever die, how many pairs of mature animals are there after 6 months? (Hint: A Fibonacci sequence models this colony.)
The number of pairs of mature animals after 6 months is
C
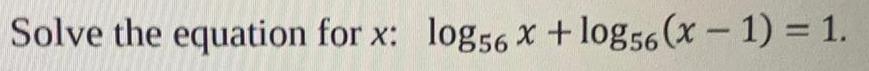

Calculus
Limits & ContinuityProblem 13. Find all solutions of the equation 2 cos x − 2 sin x cos x = 0 on the interval
-
[0, 27). Give the exact values only.
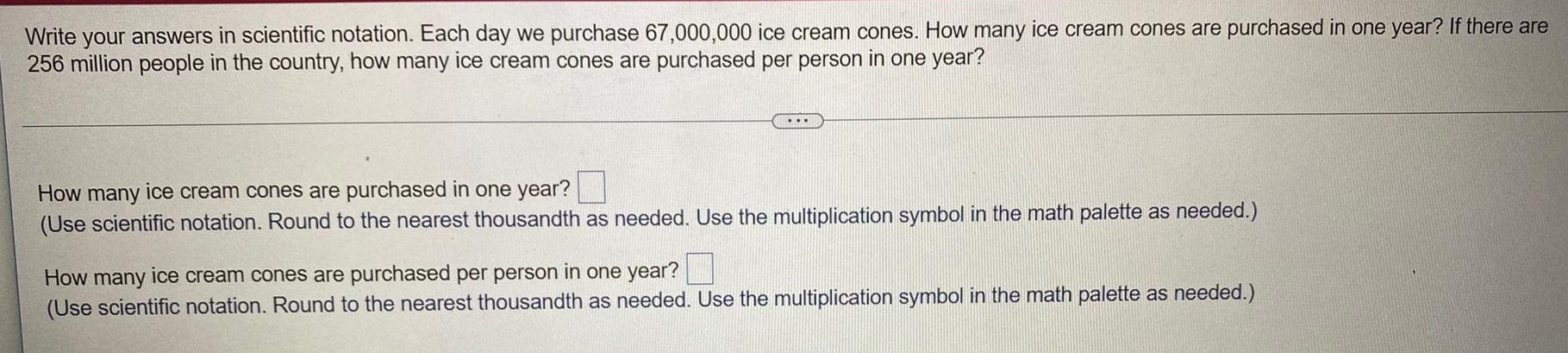
Calculus
Limits & ContinuityWrite your answers in scientific notation. Each day we purchase 67,000,000 ice cream cones. How many ice cream cones are purchased in one year? If there are
256 million people in the country, how many ice cream cones are purchased per person in one year?
How many ice cream cones are purchased in one year?
(Use scientific notation. Round to the nearest thousandth as needed. Use the multiplication symbol in the math palette as needed.)
How many ice cream cones are purchased per person in one year?
(Use scientific notation. Round to the nearest thousandth as needed. Use the multiplication symbol in the math palette as needed.)

Calculus
Limits & ContinuityHow many years will it take $5,000 to grow to $9,800 if it is invested at 2.50% compounded continuously?
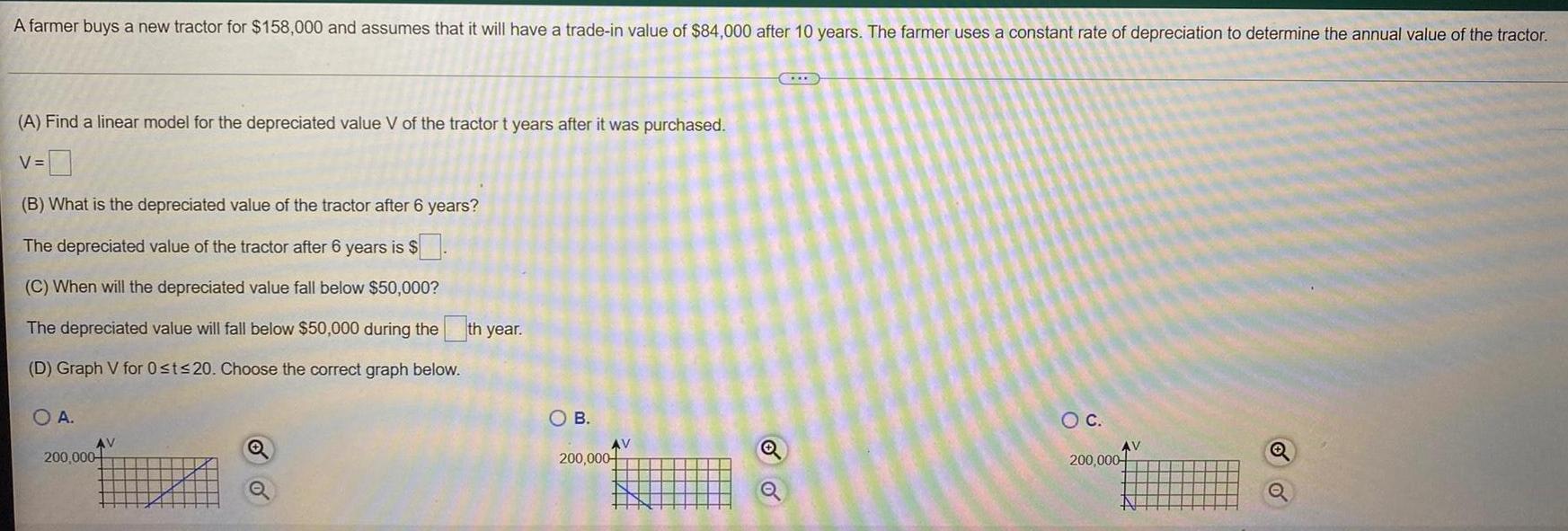
Calculus
Limits & ContinuityA farmer buys a new tractor for $158,000 and assumes that it will have a trade-in value of $84,000 after 10 years. The farmer uses a constant rate of depreciation to determine the annual value of the tractor.
(A) Find a linear model for the depreciated value V of the tractor t years after it was purchased.
V=
(B) What is the depreciated value of the tractor after 6 years?
The depreciated value of the tractor after 6 years is $
(C) When will the depreciated value fall below $50,000?
The depreciated value will fall below $50,000 during the
(D) Graph V for 0≤t≤20. Choose the correct graph below.
O A.
200,000
AV
Q
Q
th year.
O B.
AV
Hemm
200,000+
(...)
Q
O C.
200,000
Q

Calculus
Limits & ContinuityA popular movie debuted in 4530 theaters and earned an average of $12,801 per cinema the weekend of the debut. Find the amount that the movie earned in its first
weekend. Write the answer in scientific notation.
***
The amount that the movie earned in its first weekend is about $
(Use scientific notation. Use the multiplication symbol in the math palette as needed. Round to the nearest hundredth as needed.)

Calculus
Limits & ContinuityProblem 7.
a) Describe the transformation(s) that can be applied to the function g(x) = e* to obtain the
graph of f(x) = e¯* + 7.
b) State the domain and range of f(x).
c) Sketch the graph of f(x).

Calculus
Limits & ContinuityMantle Corporation is considering two equally risky investments:
A $5,000 investment in preferred stock that yields 6.75%.
A $5,000 investment in a corporate bond that yields 10.00%.
.
What is the breakeven corporate tax rate that makes the company indifferent between the two investments? Assume a 70.00% dividend exclusion for tax on
dividends. (Do not round your intermediate answer and round your final answer to two decimal places.)
O a. 50.13%
O b. 46.87%
OC. 37.08%
Od. 34.23%
Oe. 40.75%
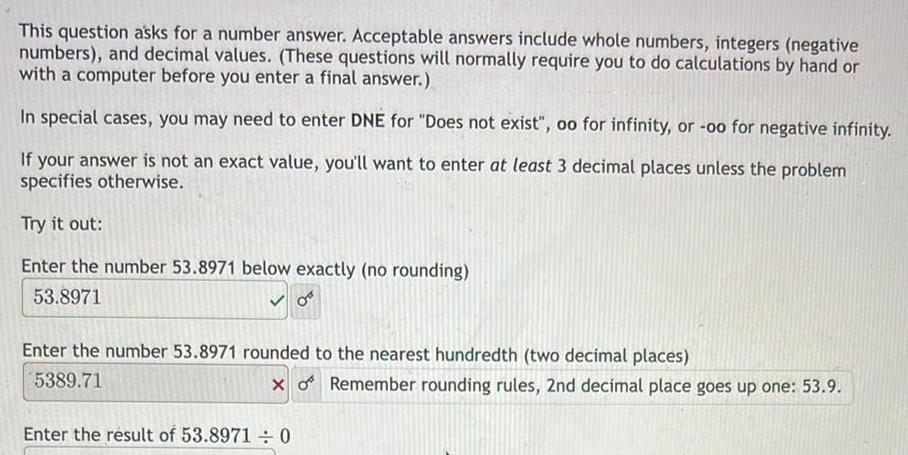
Calculus
Limits & ContinuityThis question asks for a number answer. Acceptable answers include whole numbers, integers (negative
numbers), and decimal values. (These questions will normally require you to do calculations by hand or
with a computer before you enter a final answer.)
In special cases, you may need to enter DNE for "Does not exist", oo for infinity, or -oo for negative infinity.
If your answer is not an exact value, you'll want to enter at least 3 decimal places unless the problem
specifies otherwise.
Try it out:
Enter the number 53.8971 below exactly (no rounding)
53.8971
✓0
Enter the number 53.8971 rounded to the nearest hundredth (two decimal places)
5389.71
XoRemember rounding rules, 2nd decimal place goes up one: 53.9.
Enter the result of 53.89710

Calculus
Limits & ContinuityUsing the Law of Sines to solve for all possible triangles if ZB = 50°, a = 109, b = 46.
If no answer exists, enter DNE for all answers.
ZA is
degrees
LC is
degrees
C=
Assume LA is opposite side a, B is opposite side b, and ZC is opposite side c.
Question Help: Video

Calculus
Limits & ContinuityGiven the triangle below, find the angle A and length of side x
Note: picture is NOT drawn to scale, but you can assume an angle that appears acute is acute and
angle that appears obtuse is obtuse.
19
36
O
X
A
12
C
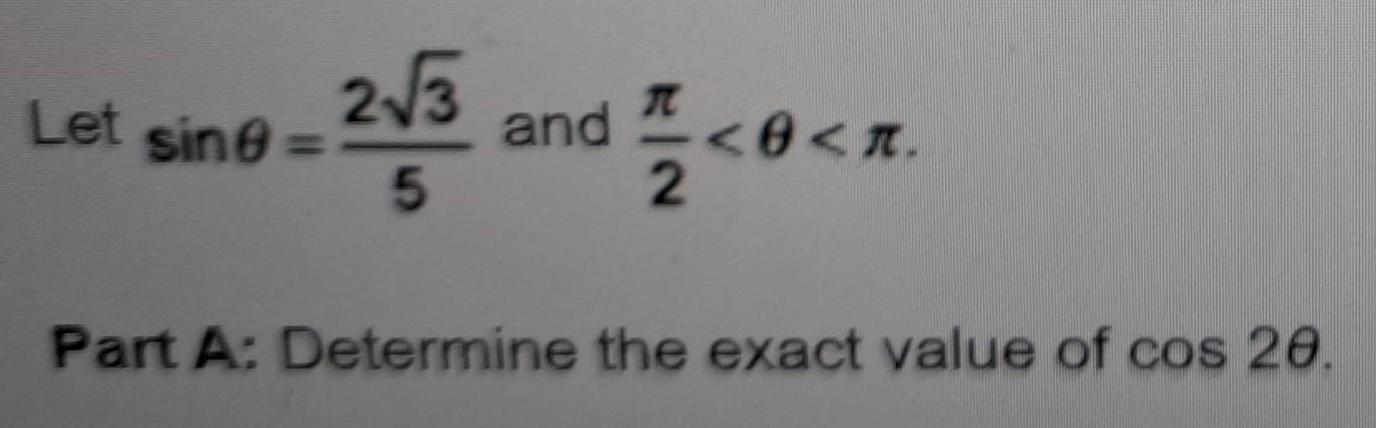

Calculus
Limits & ContinuityEvaluate the polynomial
2
P(b) = 4b² - 11b + 10;
function for the given values of the variable.
find P(4) and P(0).

Calculus
Limits & ContinuityIf the statement is always true, explain why. If not, give a counterexample.
If f is a function such that lim f(x) exists, then f(0) exists.
X-0
Choose the correct answer below.
O A. The statement is always true. Although it is possible for f(0) to exist without lim f(x) existing, it is not possible for lim f(x) to exist without f(0) also existing.
X-0
X→0
OB.
O D.
X
The statement is not always true. For example, if f(x) =
x²
X - 1
The statement is not always true. For example, if f(x) =
X
OC. The statement is always true. It is always the case that lim f(x) = f(c).
X-C
1
1
then lim f(x) = 0 but f(0) does not exist.
X→0
then lim f(x) = 0 but f(0) does not exist.
X-0

Calculus
Limits & ContinuityLet e
11
12
Part A: Determine tan 8 using the sum formula. Show all necessary work in the calculation. (5 points)
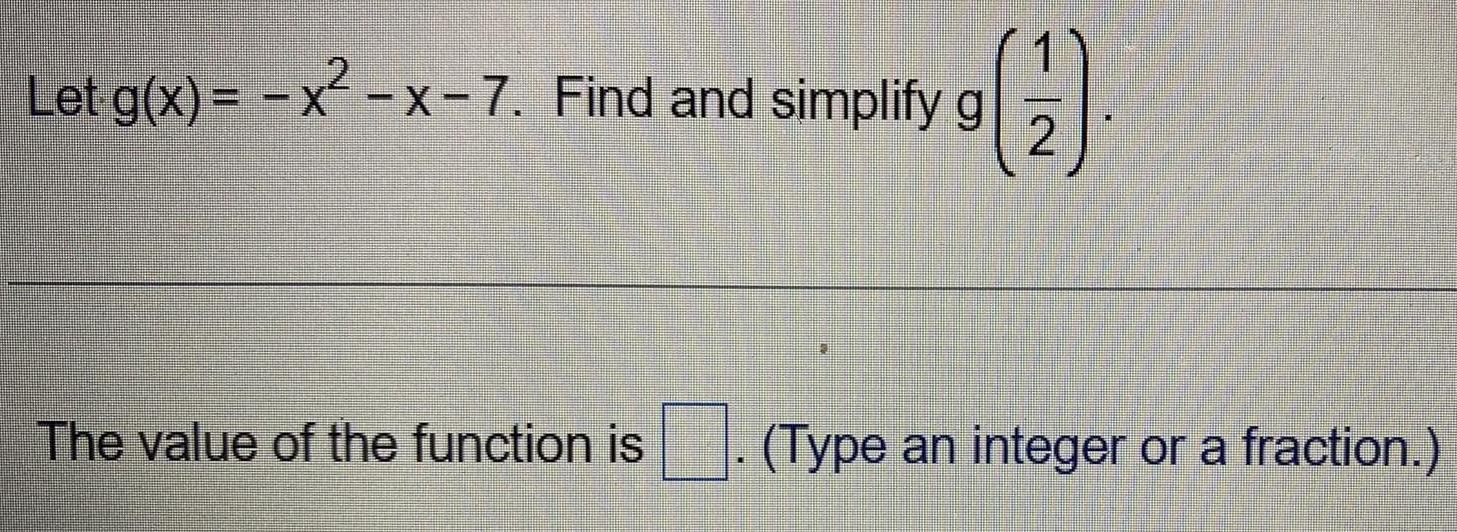
Calculus
Limits & ContinuityLet g(x) = − x² - x-7. Find and simplify g
y (17)
2
The value of the function is
(Type an integer or a fraction.)

Calculus
Limits & ContinuityUsing the Law of Sines to solve the triangle if ZA = 37°, 4C = 69°, b = 12:
LB is
degrees;
a=
;
C=
;
Round to two decimal places if needed.
Assume LA is opposite side a, LB is opposite side b, and C is opposite side c.
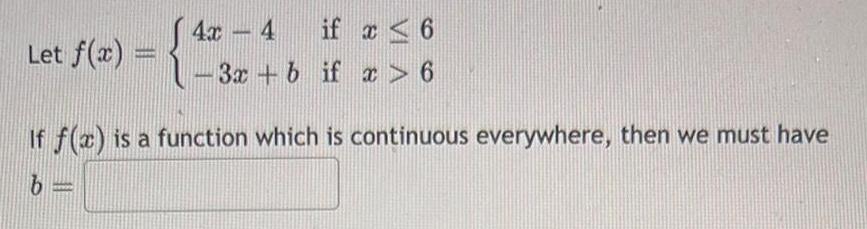
Calculus
Limits & ContinuityLet f(x) =
(4x - 4
if x < 6
3x + b if x > 6
BAL
If f(x) is a function which is continuous everywhere, then we must have
b=
wwwww