Limits & Continuity Questions and Answers
Calculus
Limits & ContinuityFind the minimum of 3X+Y(3X-1+3Y-1-1)
There is a hint given by teacher that is
multiplying by 3 and add 1.

Calculus
Limits & ContinuityFind the values of a and b such that the
following function
4a cos(x + 3)- b. 2x+5, if x < -3,
f(x) = -4,
if x = -3,
ax² + bx - 7,
is continuous at x = -3. Justify your
answer by the definition of the continuity.
if x > -3,

Calculus
Limits & Continuity4. Extra Credit. (10 Points.) Consider the problem of solving for functions u(x, y), defined on x² + y² ≤ 1,
such that
(i) Au = 0, and
(ii) u = 0 at all points in the boundary x² + y² = 1.
Show that the only solution to this problem is the zero function: u(x, y) = 0.
Hint: Consider the vector field F = uvu.
Can you make the same conclusion if we replace replace condition (ii) with "Vun = 0 at all points on
the boundary" (so the function becomes "flat" as you approach the boundary). If not, what is a conclusion
about u you can make?
Remark: The two "boundary conditions" in this problem are two very common ones you'll find in differen-
tial equations.
Calculus
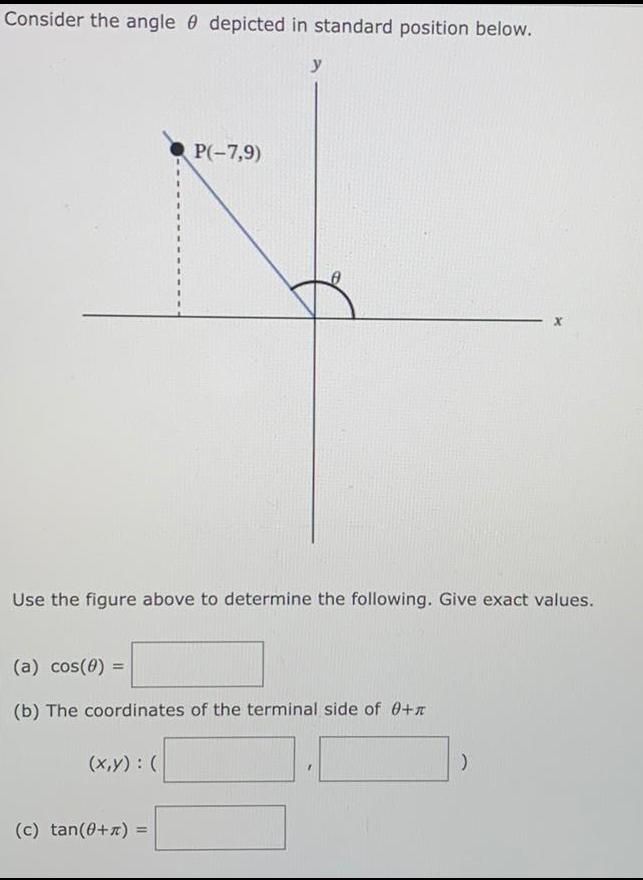
Limits & ContinuityConsider the angle depicted in standard position below.
P(-7,9)
Use the figure above to determine the following. Give exact values.
(x,y) : (
y
(a) cos(0) =
(b) The coordinates of the terminal side of 0+
(c) tan(0+) =
)
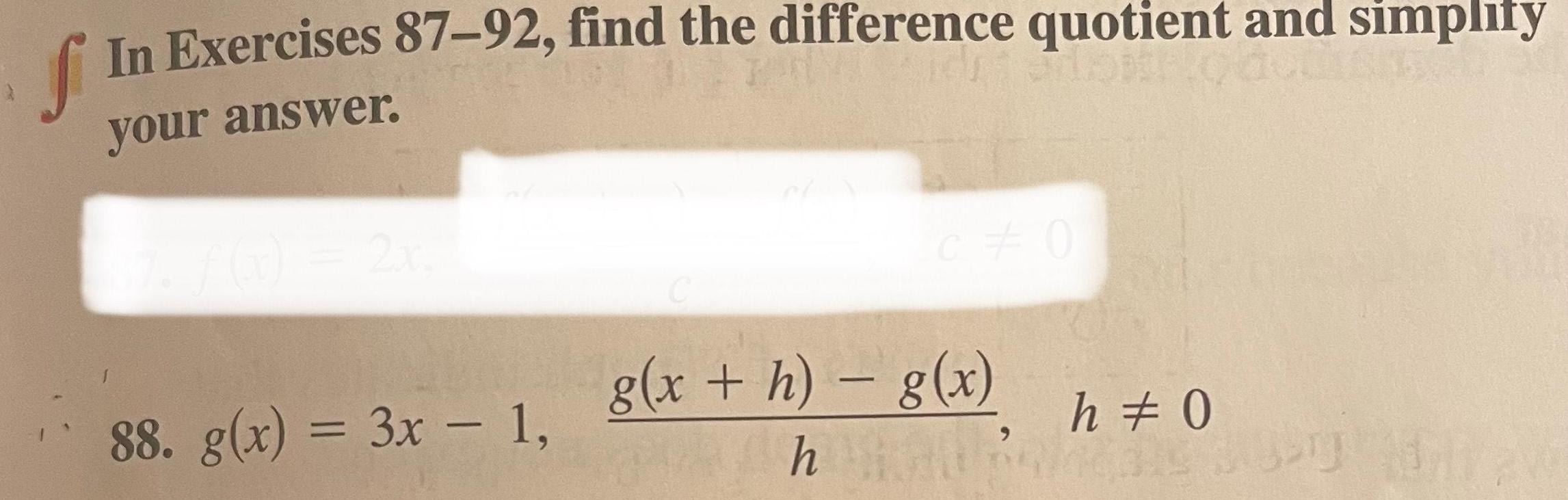
Calculus
Limits & ContinuityIn Exercises 87-92, find the difference quotient and simplity
S
Slon
your answer.
88. g(x) = 3x - 1,
C
c#0
-
g(x + h) = g(x)
him
h #0
2009072
Calculus
Limits & ContinuityDate:
Period
Calculus AB
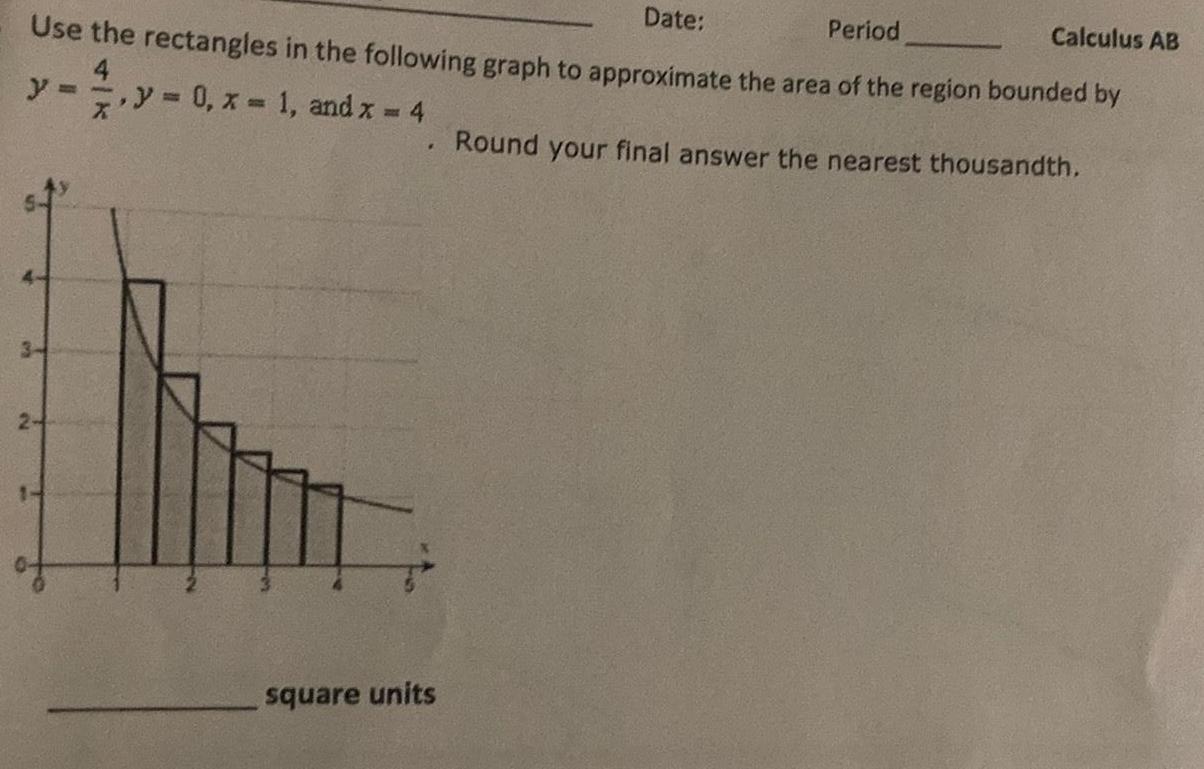
Use the rectangles in the following graph to approximate the area of the region bounded by
4
y=y=0, x= 1, and x = 4
Round your final answer the nearest thousandth,
square units

Calculus
Limits & ContinuityDetermine the tax free Roc, capital Gain,
Dividend, End basis, End
basis shareholder basis= 130,000 AAA= 450,000
E&P= 350,000 Distribution=300,000
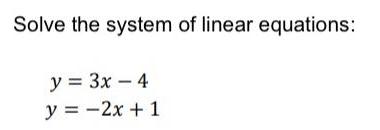
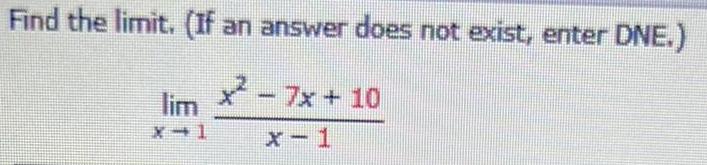
Calculus
Limits & ContinuityFind the limit. (If an answer does not exist, enter DNE.)
x² - 7x + 10
x-1
X-1

Calculus
Limits & Continuityy = xe-2x, 0≤x≤ In(3)
On this interval, the maximum value(s) occur at x =
In(3)
two of these are correct
0
1
2
Calculus
Limits & ContinuityWrite the augmented matrix of the given system of equations.
x - 4y = 9
6x + 7y = 4
The augmented matrix is

Calculus
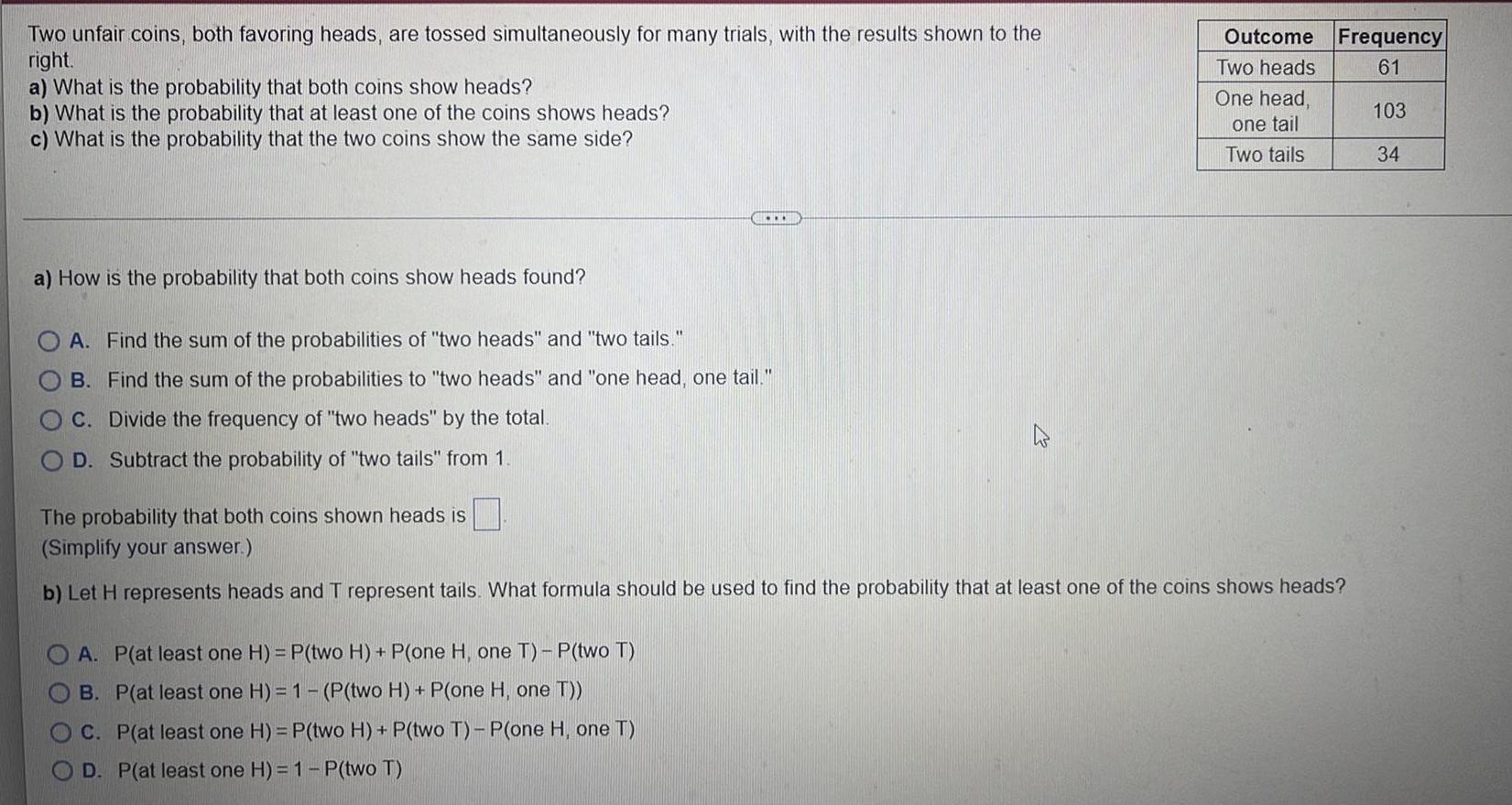
Limits & ContinuityTwo unfair coins, both favoring heads, are tossed simultaneously for many trials, with the results shown to the
right.
a) What is the probability that both coins show heads?
b) What is the probability that at least one of the coins shows heads?
c) What is the probability that the two coins show the same side?
...
a) How is the probability that both coins show heads found?
A. Find the sum of the probabilities of "two heads" and "two tails."
B. Find the sum of the probabilities to "two heads" and "one head, one tail."
C. Divide the frequency of "two heads" by the total.
D. Subtract the probability of "two tails" from 1.
A. P(at least one H) = P(two H) + P(one H, one T) - P(two T)
B. P(at least one H) = 1 (P(two H) + P(one H, one T))
C. P(at least one H) = P(two H) + P(two T) - P(one H, one T)
D. P(at least one H) = 1- P(two T)
Outcome Frequency
61
103
34
Two heads
One head,
one tail
Two tails
The probability that both coins shown heads is
(Simplify your answer.)
b) Let H represents heads and T represent tails. What formula should be used to find the probability that at least one of the coins shows heads?
![Find the value of the constant c so that the function below is a probability density function for a random variable over the specified interval.
1
f(x) = = x over [2,c]](https://media.kunduz.com/media/sug-question/raw/82810020-1660233047.9061556.jpeg?w=256)
Calculus
Limits & ContinuityFind the value of the constant c so that the function below is a probability density function for a random variable over the specified interval.
1
f(x) = = x over [2,c]
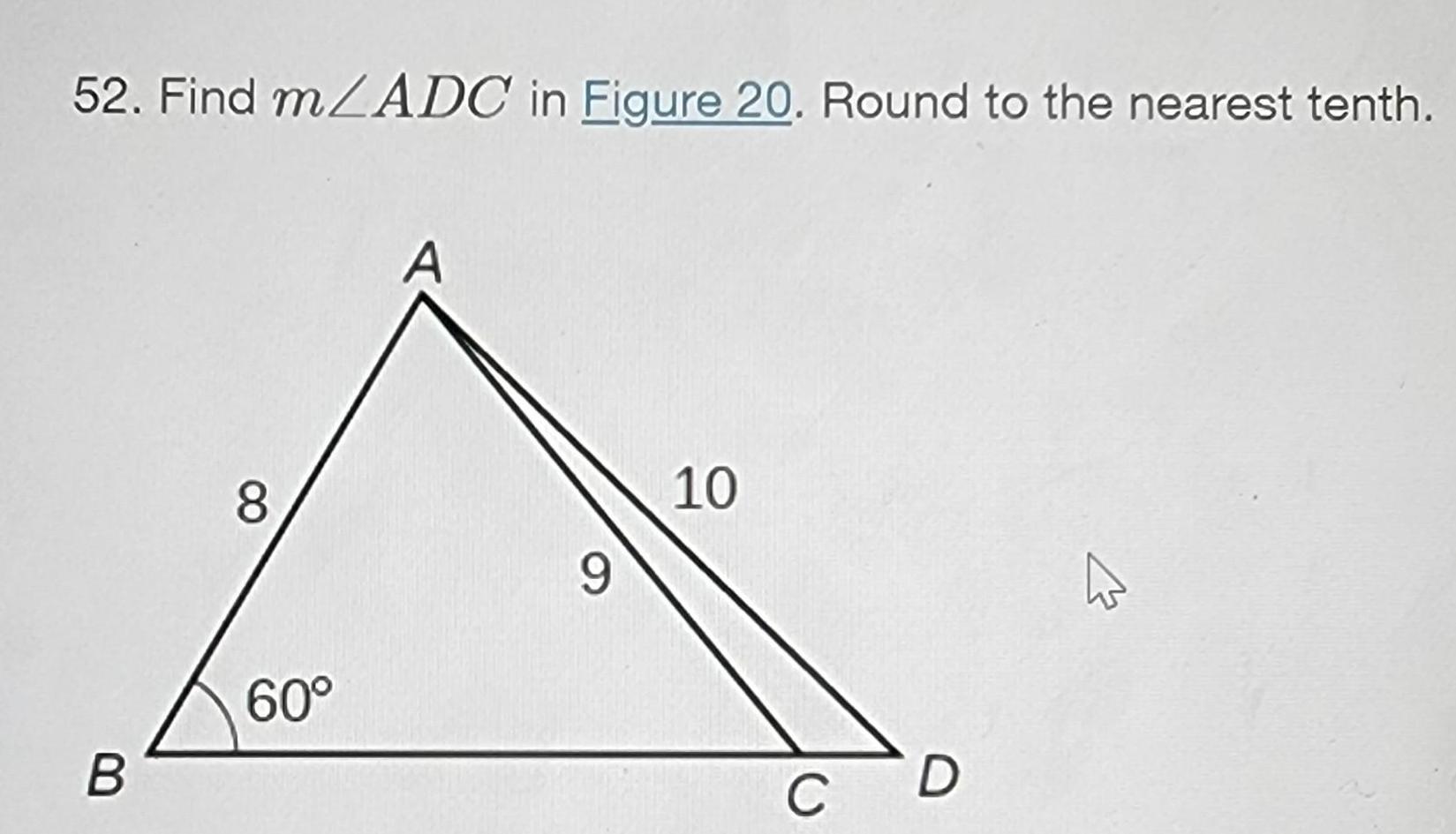
Calculus
Limits & Continuity52. Find m/ADC in Figure 20. Round to the nearest tenth.
B
8
60°
9
10
C
D
M
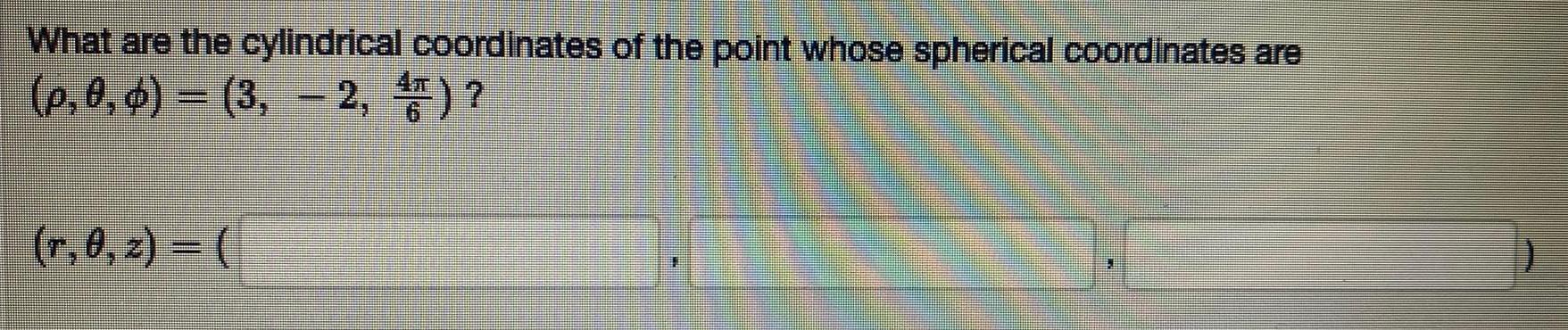
Calculus
Limits & ContinuityWhat are the cylindrical coordinates of the point whose spherical coordinates are
(p, 0, d) – (3, – 2,)?
(r,0,2)=(

Calculus
Limits & ContinuityA spinner marked off in 5 equal-size regions, numbered 1 through 5, is spun twice. Let event E be that the outcome of both spins is 4 and event F be that the sum
of the two outcomes is 7.
a) Write the sample space, S. Use ordered pairs such as (2,3), and so on.
b) Find P(E) and P (E').
c) Find P(F) and P (F').
d) Find P(EUF).
OC. S= {(1,1), (1,2), (1,3), (1,4), (1,5), (2,2), (2,3), (2,4), (2,5), (3,3), (3,4), (3,5), (4,4), (4,5), (5,5)}
D. S = {(1,2), (1,3), (1,4), (1,5), (2,1), (2,3), (2,4), (2,5), (3,1), (3,2), (3,4), (3,5), (4,1), (4,2), (4,3), (4,5), (5,1), (5,2), (5,3), (5,4)}
b) P(E)=
(Simplify your answer.)
P(E') =
(Simplify your answer.)
c) P(F) =
(Simplify your answer.)
P(F') =
(Simplify your answer.)
d) P(EUF) =
(Simplify your answer.)
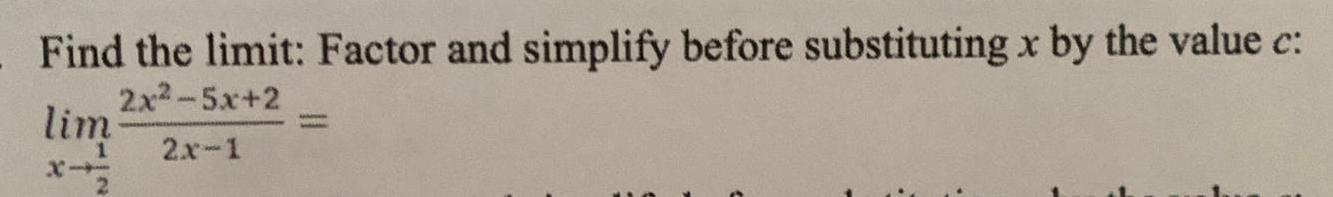
Calculus
Limits & ContinuityFind the limit: Factor and simplify before substituting x by the value c:
2x²-5x+2
lim
2x-1

Calculus
Limits & ContinuityEvaluate the limit, if it exists. (If an answer does not exist, enter DNE.)
lim x cos
X-0

Calculus
Limits & ContinuityUse transformations to graph the function f(x) = -2+4*-2. Determine its domain, range, and horizontal
asymptote.
Which transformations must be applied to obtain the graph of f(x) = -2+4*-2? Select all that apply.
A. Horizontal shift
B. Reflection about the x-axis
C. Horizontal compression or stretch
D. Vertical shift
E. Vertical compression or stretch
F. Reflection about the y-axis
Use the graphing tool to graph the function.
*
Click to
enlarge
graph
What is the domain of f(x) = -2+4*-22

Calculus
Limits & ContinuityA graphing calculator is recommended.
Use the Squeeze Theorem to show that lim x cos(9x) = 0.
x10
Illustrate by graphing the functions f(x) = -x², g(x) = x² cos(9x), and h(x) = x² on the same screen.
Let f(x) = -x², g(x) = x² cos(9x), and h(x) = x². Then ?s cos(9x) ≤ ? ✓
=
2≤ x² cos(9x) ≤ 2 ✓
Since lim x)= lim h(x) =
X-0
X10
by the Squeeze Theorem we have lim g(x) =
110
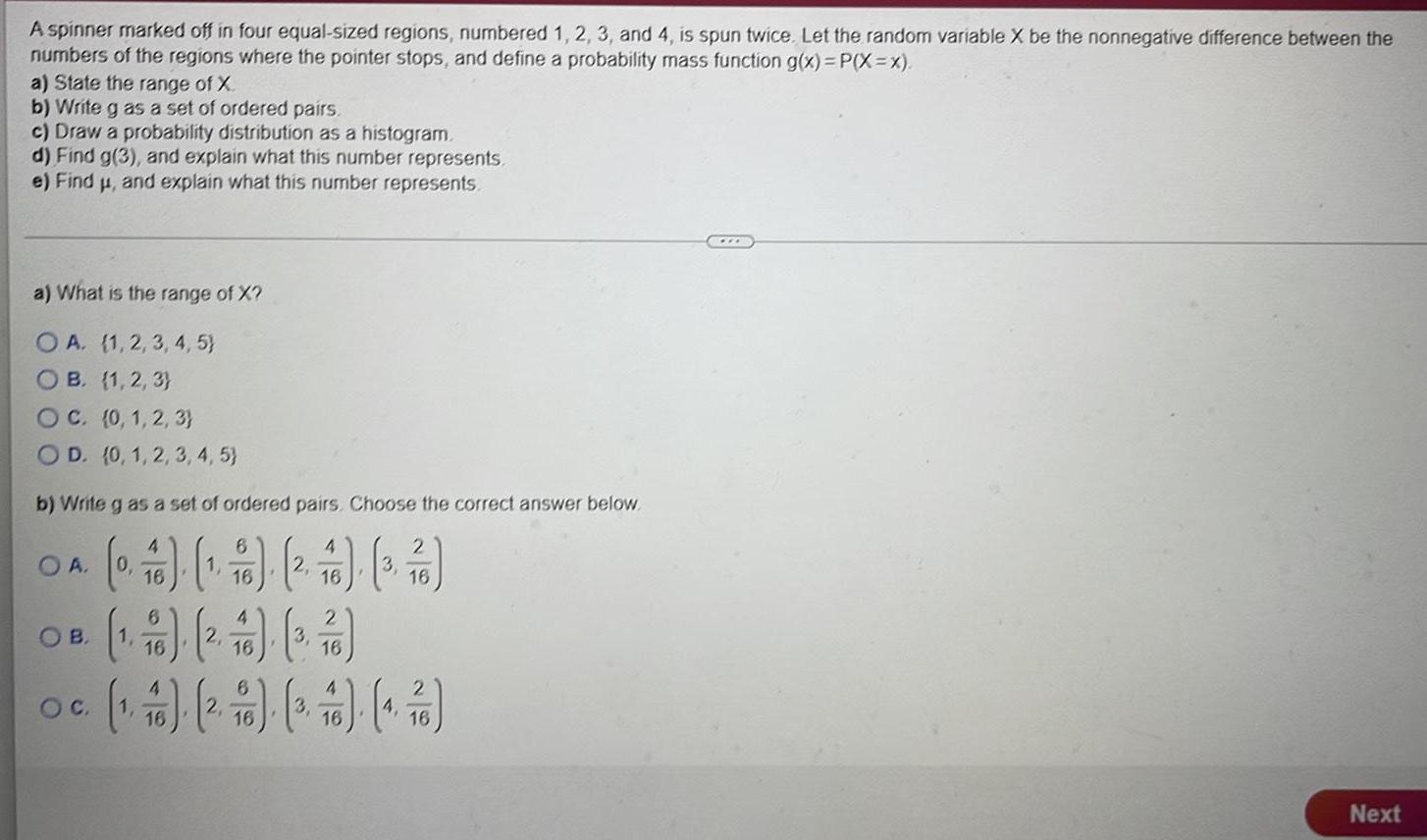
Calculus
Limits & ContinuityA spinner marked off in four equal-sized regions, numbered 1, 2, 3, and 4, is spun twice. Let the random variable X be the nonnegative difference between the
numbers of the regions where the pointer stops, and define a probability mass function g(x)=P(X=X).
a) State the range of X.
b) Write g as a set of ordered pairs.
c) Draw a probability distribution as a histogram.
d) Find g(3), and explain what this number represents.
e) Find µ, and explain what this number represents.
a) What is the range of X?
OA. (1, 2, 3, 4, 5)
OB. (1,2,3)
O C. (0, 1, 2, 3)
OD. (0, 1, 2, 3, 4, 5)
b) Write g as a set of ordered pairs. Choose the correct answer below.
4
6
2
(0) (¹)
1,
(2) (376)
16
16
16
OA.
OB.
O C.
4
2
(1.6) (2. 6) (3, ²76)
16
16
4
4
2
(¹6) (2)
96) (3, 76). (4, ²76)
16
16
16
16
Next

Calculus
Limits & Continuity1
->(x+6).
Consider the functions f(x) = 7x-6 and g(x)=
(a) Find f(g(x)).
(b) Find g(f(x)).
(c) Determine whether the functions f and g are inverses of each other.
(a) What is f(g(x))?
f(g(x)) =
(Simplify your answer.)
Give any values of x that need to be excluded from f(g(x)). Select the correct choice below and fill in any answer boxes within your choice.
A. x#
(Use a comma to separate answers as needed.)
B. No values should be excluded from the domain.
(b) What is g(f(x))?
g(f(x)) =
(Simplify your answer.)
Give any values of x that need to be excluded from g(f(x)). Select the correct choice below and fill in any answer boxes within your choice.
OA. x#
(Use a comma to separate answers as needed.)

Calculus
Limits & ContinuityEvaluate the limit using the appropriate Limit Law(s). (If an answer does not exist, enter DNE.)
4-5
lim
t-2 21²-3t+8
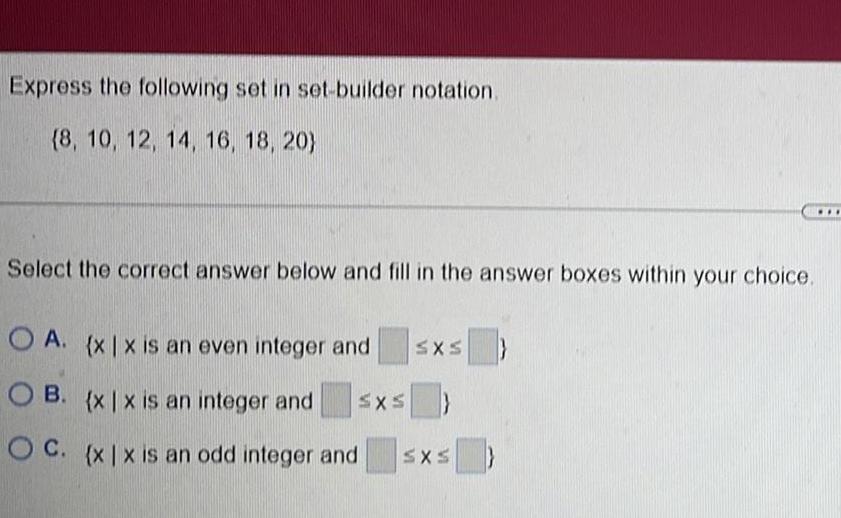
Calculus
Limits & ContinuityExpress the following set in set-builder notation.
(8, 10, 12, 14, 16, 18, 20)
Select the correct answer below and fill in the answer boxes within your choice.
OA. {x|x is an even integer and SXS
OB. {x|x is an integer and SXS
OC. (x | x is an odd integer and
SXS
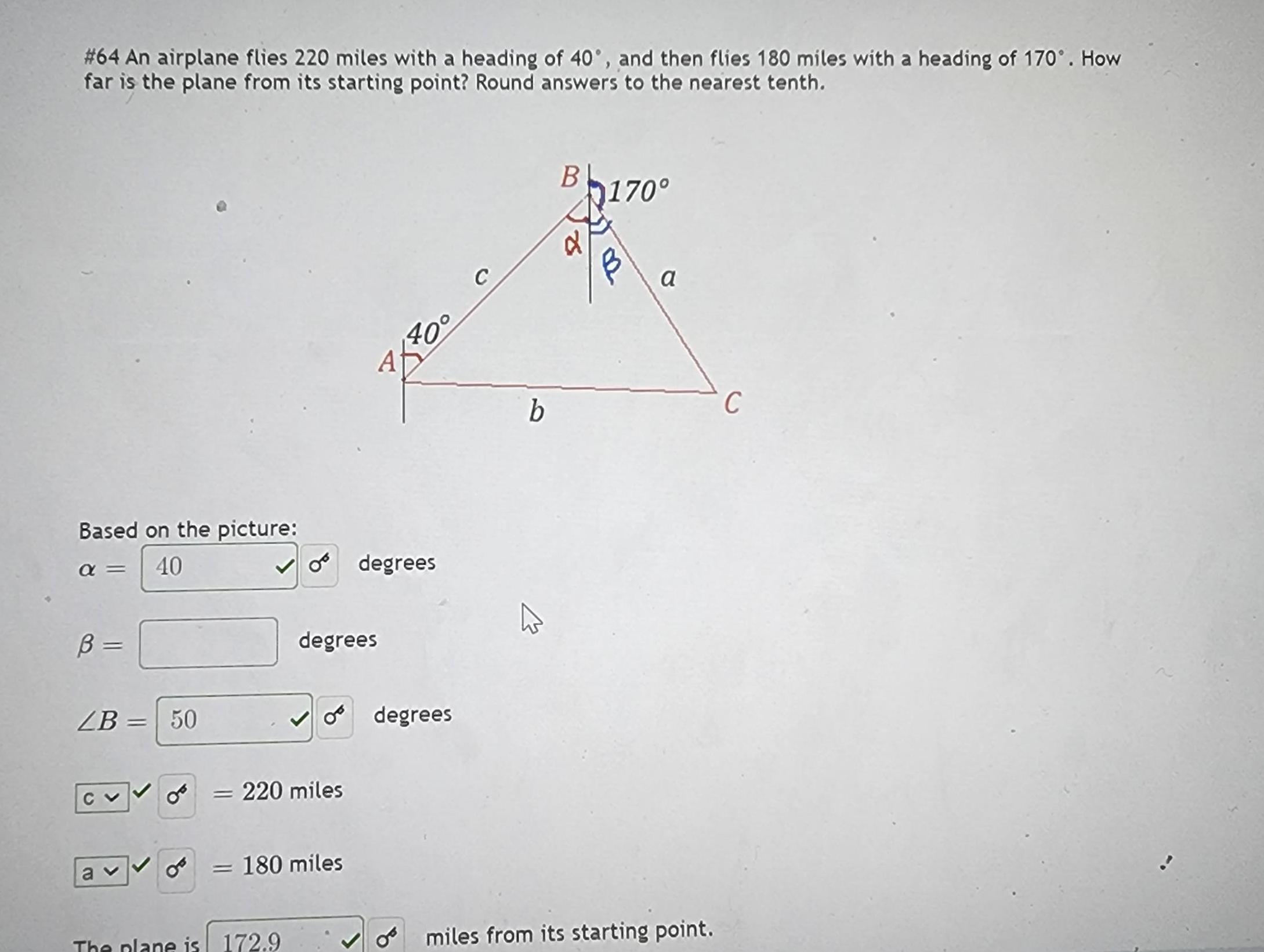
Calculus
Limits & Continuity#64 An airplane flies 220 miles with a heading of 40°, and then flies 180 miles with a heading of 170°. How
far is the plane from its starting point? Round answers to the nearest tenth.
Based on the picture:
α =
40
B =
LB =
50
CVV OF
av of
The plane is 172.9
A
of degrees
degrees
= 220 miles
= 180 miles
40°
o degrees
C
b
4
B
170°
a
miles from its starting point.
C
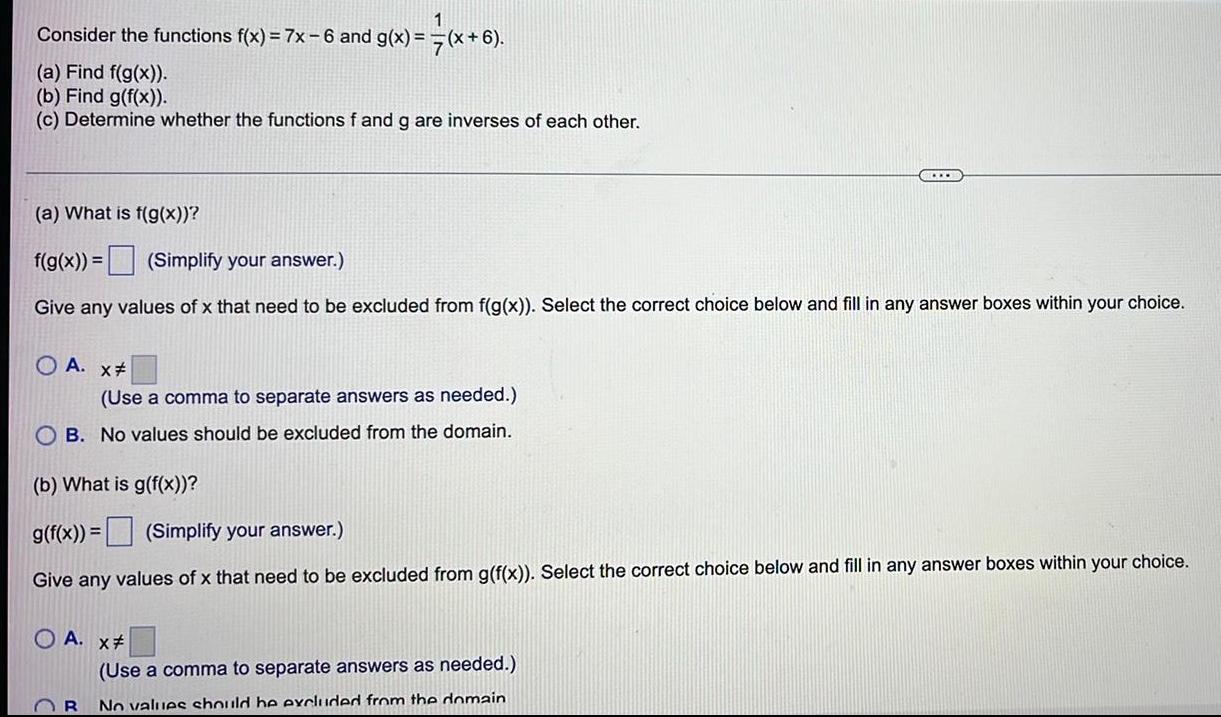
Calculus
Limits & Continuity1
Consider the functions f(x) = 7x − 6 and g(x) = (x + 6).
(a) Find f(g(x)).
(b) Find g(f(x)).
(c) Determine whether the functions f and g are inverses of each other.
(a) What is f(g(x))?
f(g(x)) =
(Simplify your answer.)
Give any values of x that need to be excluded from f(g(x)). Select the correct choice below and fill in any answer boxes within your choice.
OA. x#
(Use a comma to separate answers as needed.)
OB. No values should be excluded from the domain.
(b) What is g(f(x))?
g(f(x)) =
(Simplify your answer.)
Give any values of x that need to be excluded from g(f(x)). Select the correct choice below and fill in any answer boxes within your choice.
OA. x#
(Use a comma to separate answers as needed.)
OR No values should be excluded from the domain
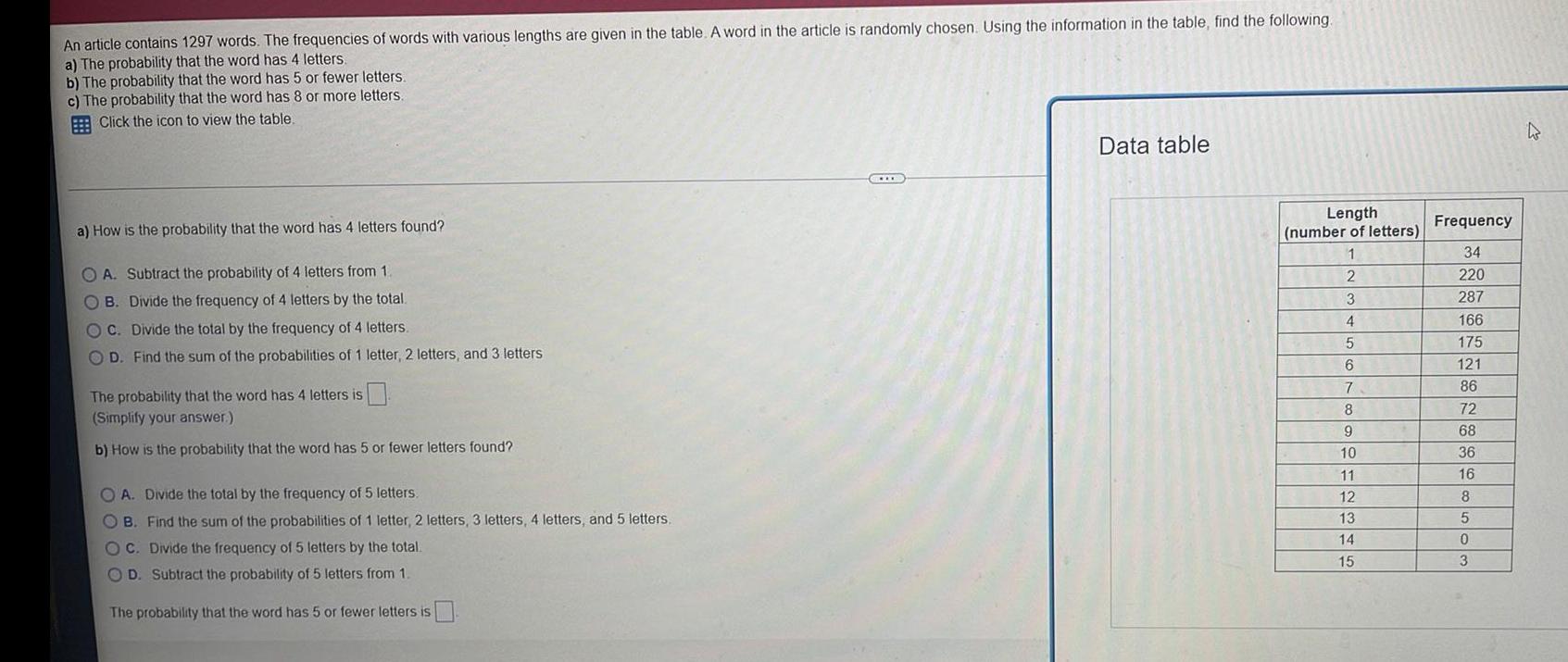
Calculus
Limits & ContinuityAn article contains 1297 words. The frequencies of words with various lengths are given in the table. A word in the article is randomly chosen. Using the information in the table, find the following.
a) The probability that the word has 4 letters.
b) The probability that the word has 5 or fewer letters.
c) The probability that the word has 8 or more letters.
Click the icon to view the table.
a) How is the probability that the word has 4 letters found?
OA. Subtract the probability of 4 letters from 1.
OB. Divide the frequency of 4 letters by the total.
OC. Divide the total by the frequency of 4 letters.
OD. Find the sum of the probabilities of 1 letter, 2 letters, and 3 letters
The probability that the word has 4 letters is
(Simplify your answer.)
b) How is the probability that the word has 5 or fewer letters found?
OA. Divide the total by the frequency of 5 letters.
OB. Find the sum of the probabilities of 1 letter, 2 letters, 3 letters, 4 letters, and 5 letters.
OC. Divide the frequency of 5 letters by the total.
OD. Subtract the probability of 5 letters from 1.
The probability that the word has 5 or fewer letters is
GEILE
Data table
Length
(number of letters)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Frequency
34
220
287
166
175
121
86
72
68
36
16
8
5
0
3
W

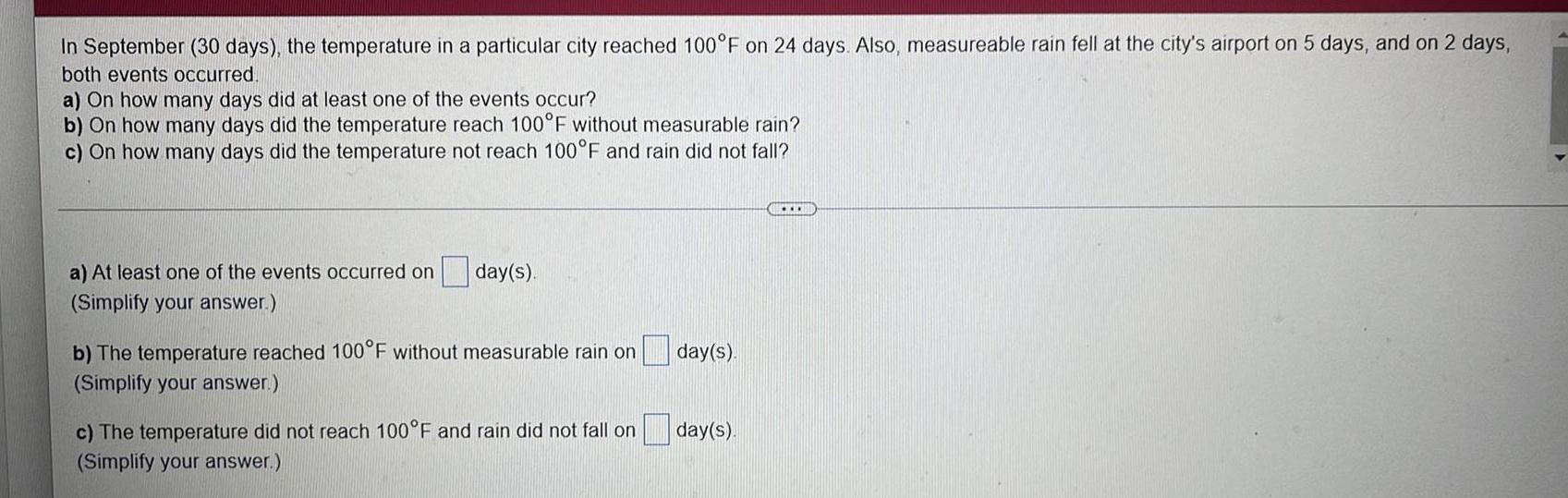
Calculus
Limits & ContinuityIn September (30 days), the temperature in a particular city reached 100°F on 24 days. Also, measureable rain fell at the city's airport on 5 days, and on 2 days,
both events occurred.
a) On how many days did at least one of the events occur?
b) On how many days did the temperature reach 100°F without measurable rain?
c) On how many days did the temperature not reach 100°F and rain did not fall?
a) At least one of the events occurred on
(Simplify your answer.)
day(s).
b) The temperature reached 100°F without measurable rain on
(Simplify your answer.)
c) The temperature did not reach 100°F and rain did not fall on
(Simplify your answer.)
day(s).
day(s).
...

Calculus
Limits & ContinuityA test has many multiple-choice items, each with four answer choices. A student receives 1 point for every correct answer, and each incorrect answer brings a penalty
1
(loss) of
of a point. If Chris guesses on every question, what score can he expect on the test?
3
Chris can expect to get a score of
(Simplify your answer.)
.…..

Calculus
Limits & ContinuityExpress the following set using set-builder notation.
{March, May}
Choose the correct answer below.
A. {x|x is a month in the first quarter of the year}
B. {x|x is a month of the year}
C. {x|x is a month that begins with M}
OD. The set has no elements.
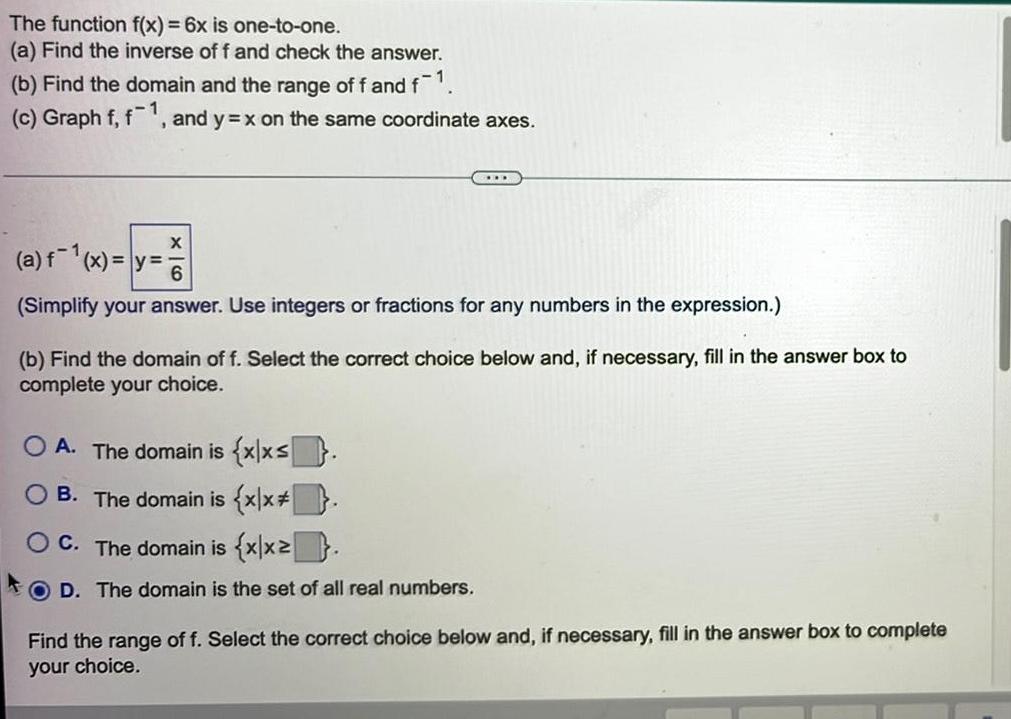
Calculus
Limits & ContinuityThe function f(x) = 6x is one-to-one.
(a) Find the inverse of f and check the answer.
(b) Find the domain and the range of f and f
(c) Graph f, f1, and y=x on the same coordinate axes.
X
..
(a) f(x)=y=
(Simplify your answer. Use integers or fractions for any numbers in the expression.)
(b) Find the domain of f. Select the correct choice below and, if necessary, fill in the answer box to
complete your choice.
OA. The domain is {x|xs.
B. The domain is {x|x*}.
OC. The domain is {x|x²}.
OD. The domain is the set of all real numbers.
Find the range of f. Select the correct choice below and, if necessary, fill in the answer box to complete
your choice.

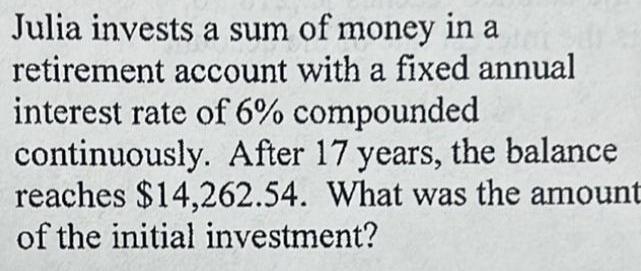
Calculus
Limits & ContinuityJulia invests a sum of money in a
retirement account with a fixed annual
interest rate of 6% compounded
continuously. After 17 years, the balance
reaches $14,262.54. What was the amount
of the initial investment?

Calculus
Limits & ContinuityFor the following exercises, determine whether the
graphs of the polar equation are symmetric with
respect to the x -axis, the y -axis, or the origin.
r² = 6 cos(20)
2
x-axis
y-axis
origin
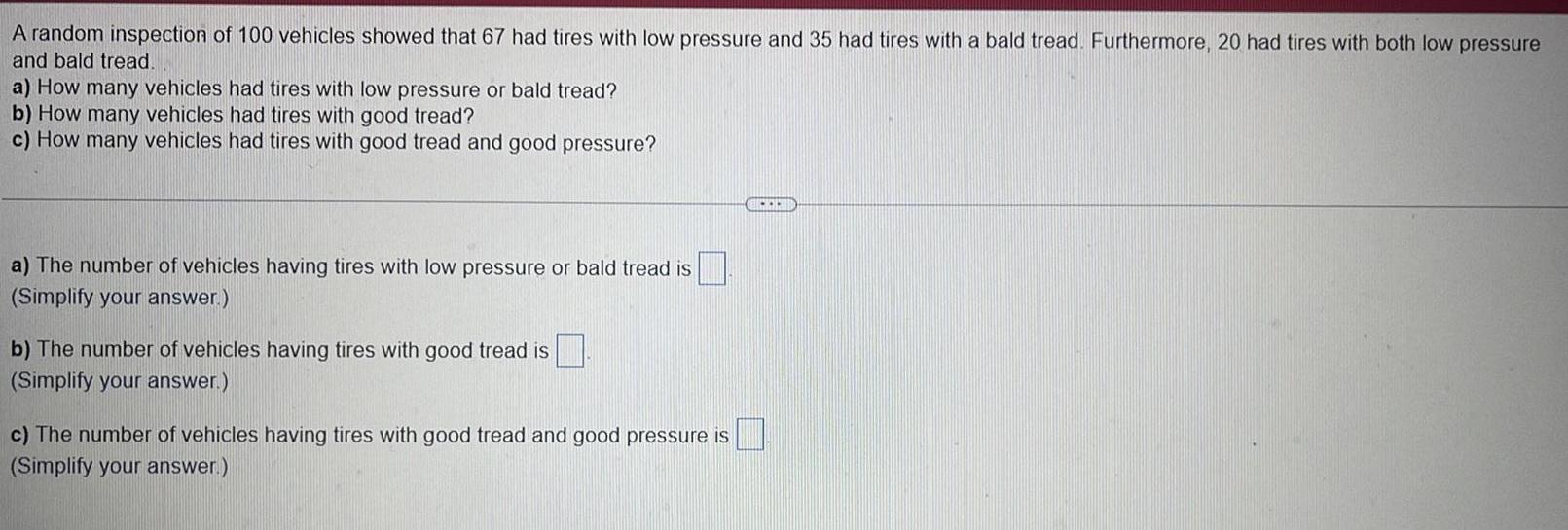
Calculus
Limits & ContinuityA random inspection of 100 vehicles showed that 67 had tires with low pressure and 35 had tires with a bald tread. Furthermore, 20 had tires with both low pressure
and bald tread.
a) How many vehicles had tires with low pressure or bald tread?
b) How many vehicles had tires with good tread?
c) How many vehicles had tires with good tread and good pressure?
a) The number of vehicles having tires with low pressure or bald tread is
(Simplify your answer.)
b) The number of vehicles having tires with good tread is
(Simplify your answer.)
c) The number of vehicles having tires with good tread and good pressure is
(Simplify your answer.)
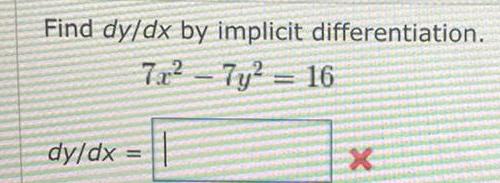
![Consider the function
A. The function f(x) has vertical asympototes at x=
B. f(x) is concave up on the region
C. The inflection point for this function is
the direction of concavity also changes at
on the interval [-20, 15].
Answer the following questions for f (enter points in ascending order, i.e. smallest x values first; enter intervals in ascending order also):
to
and
f(x) =
and
x3
x²-1
and x=
and
to
where the function is undefined.](https://media.kunduz.com/media/sug-question/raw/82678259-1660231293.12076.jpeg?w=256)
Calculus
Limits & ContinuityConsider the function
A. The function f(x) has vertical asympototes at x=
B. f(x) is concave up on the region
C. The inflection point for this function is
the direction of concavity also changes at
on the interval [-20, 15].
Answer the following questions for f (enter points in ascending order, i.e. smallest x values first; enter intervals in ascending order also):
to
and
f(x) =
and
x3
x²-1
and x=
and
to
where the function is undefined.
Calculus
Limits & ContinuityFor a week, a clothing company tracks the amounts spent by its customers, with the results shown to the right.
a) What is the probability that a randomly chosen customer spent $120 or more?
b) What is the probability that a randomly chosen customer did not spend less than $80?
c) What is the probability that a randomly chosen customer spent between $40 and $159.99?
a) What formula should be used to find the probability that a randomly chosen customer spent $120 or more?
A. P($120 or more) = P($120-$159.99)
B. P($120 or more) = 1 - P($120 - $159.99)
O C. P($120 or more) = P($120-$159.99) + P($160-$199.99) + P($200 or more)
O D. P($120 or more) = P($120-$159.99) + P($160 - $199.99) - P($200 or more)
The probability that a randomly chosen customer spent $120 or more is
(Simplify your answer.)
b) What formula should be used to find the probability that a randomly chosen customer did not spend less than $80?
A. P(not less than $80)=P($0-$39.99)+ P($40-$79.99) + P($80 - $119.99)
B. P(not less than $80)=P($80 - $119.99)
DIADO
6440 001
Amount spent Frequency
37
57
94
97
42
11
$0-$39.99
$40-$79.99
$80-$119.99
$120-$159.99
$160 $199.99
$200 or more

Calculus
Limits & ContinuityA spinner marked off in eight equal-sized regions, numbered 1, 2, 3, 4, 5, 6, 7, and 8, is spun once. Let the random variable X be the number of the region where the
pointer stops, and define a probability mass function f(x)=P(X=x).
a) State the range of X.
b) Write f as a set of ordered pairs.
c) Draw the probability distribution as a histogram.
d) Find f(8), and explain what this number represents.
e) Find μ, and explain what this number represents.
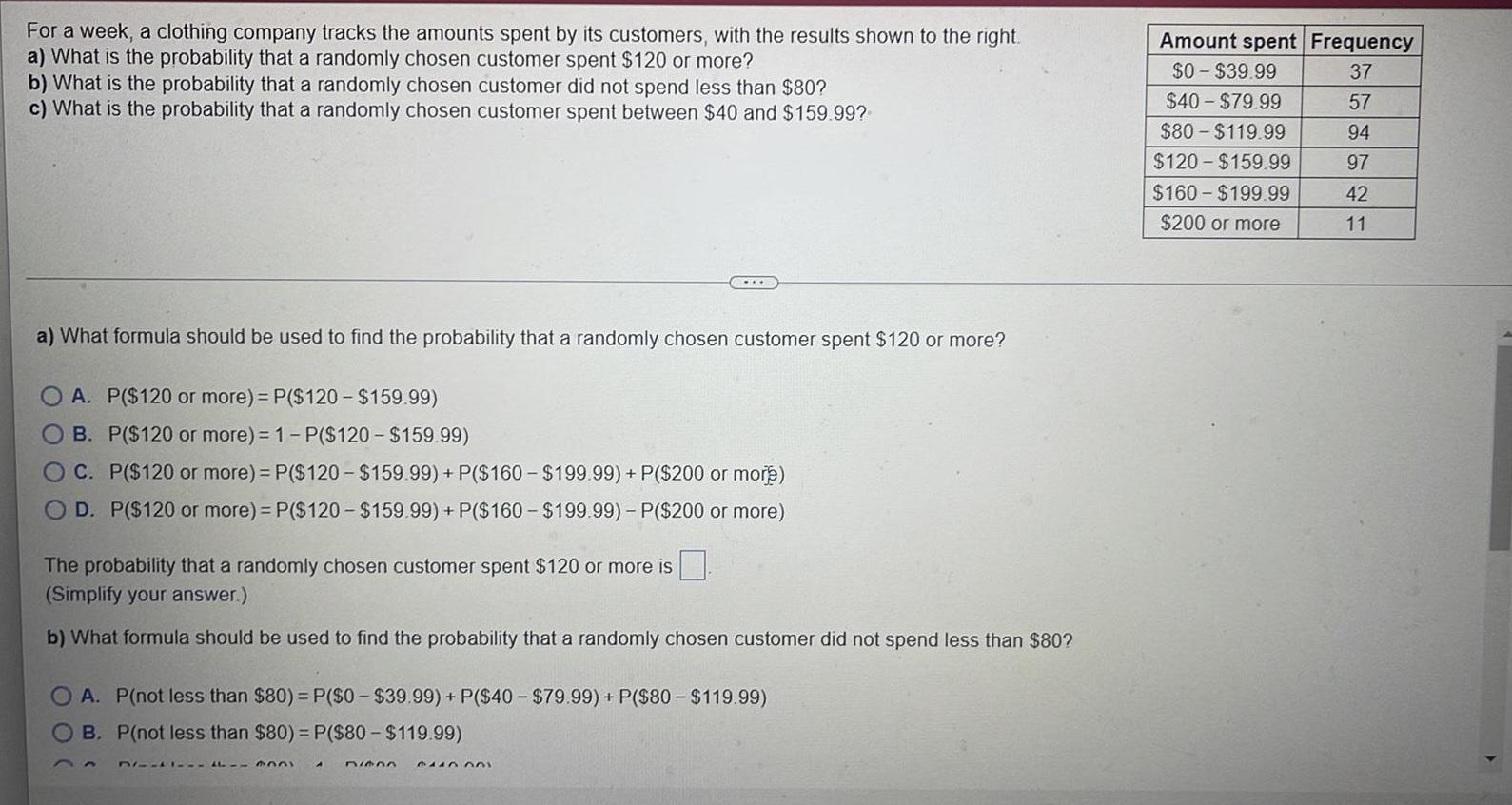
Calculus
Limits & ContinuityPart 1 of 4
A box with a square base and open top must have a volume of 415292 cm³. We wish to find the dimensions
of the box that minimize the amount of material used.
First, find a formula for the surface area of the box in terms of only a, the length of one side of the square
base.
A(x)=
=
I
Question Help: 55 Video & Written Example 2 Message instructor

Calculus
Limits & ContinuityA survey of 100 people showed that 26 own a car, 62 own a bicycle, and 12 own both a car and a bicycle. How many people own a car or a bicycle?
The number of people that own a car or a bicycle is
(Simplify your answer.)
...

Calculus
Limits & ContinuityUse roster form to write the elements of the following set, or state that the set has no elements.
The seasons
Choose the correct answer below.
OA. (Spring, Summer}
B. (Fall, Winter}
C. (Spring, Summer, Fall, Winter}
D. (Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}
OE. Ø


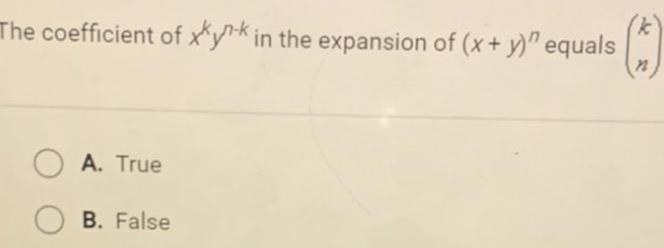
Calculus
Limits & ContinuityThe coefficient of xkyk in the expansion of (x + y)" equals
OA. True
B. False
k
n
Calculus
Limits & ContinuitySuppose the heights of the members of a population follow a normal
distribution. If the mean height of the population is 68 inches and the
standard deviation is 4 inches, 99.7% of the population will have a height
within which of the following ranges?
OA. 56 inches to 80 inches
OB. 60 inches to 76 inches
C. 64 inches to 72 inches
D. 52 inches to 84 inches
Calculus
Limits & ContinuityIf fis continuous on (-00, 00), what can you say about its graph? (Select all that apply.)
The graph of f has a hole.
The graph of f has a jump.
The graph of f has a vertical asymptote.
Onone of these
Calculus
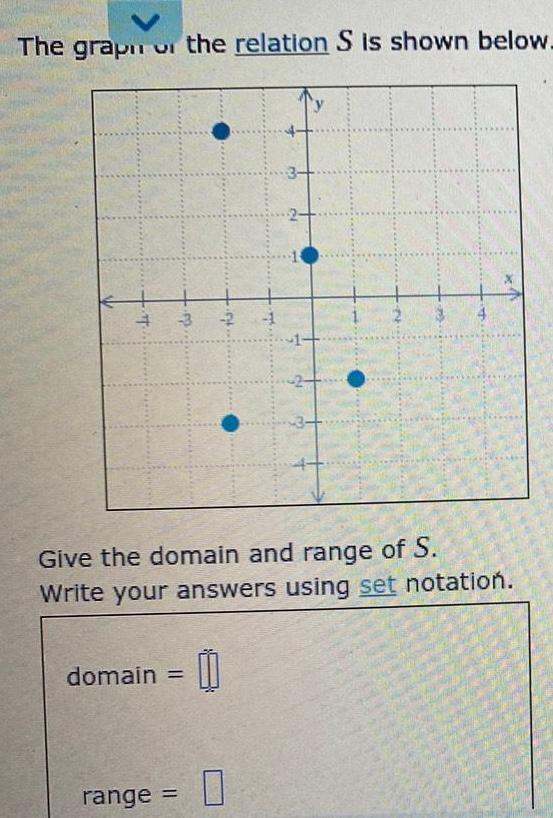
Limits & ContinuityThe grap the relation S is shown below.
-3
Give the domain and range of S.
Write your answers using set notation.
domain =
range =
00
2
0