Simple harmonic motion Questions and Answers
Physics
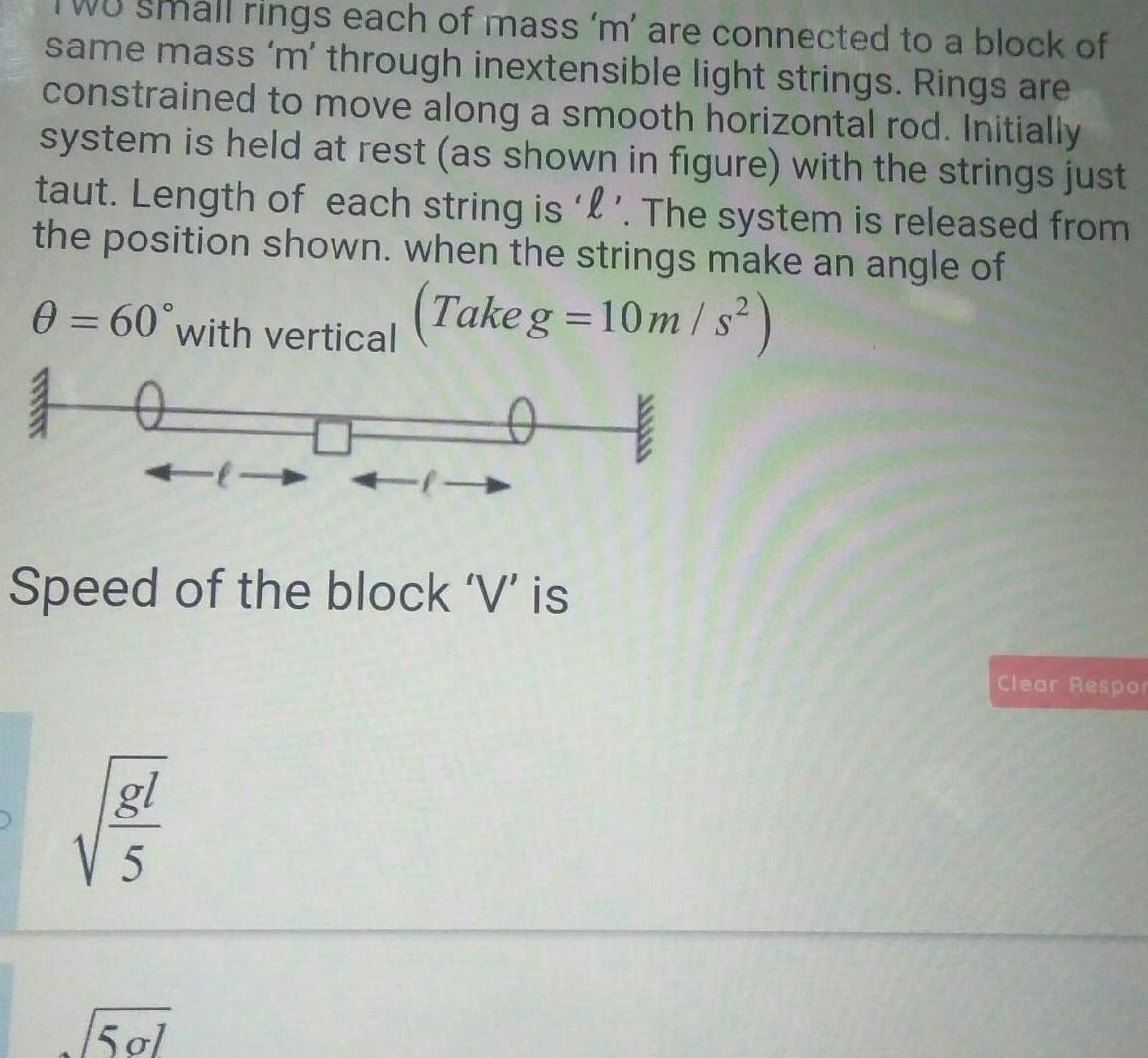
Simple harmonic motionrings each of mass m are connected to a block of same mass m through inextensible light strings Rings are constrained to move along a smooth horizontal rod Initially system is held at rest as shown in figure with the strings just taut Length of each string is l The system is released from the position shown when the strings make an angle of 0 60 with vertical Take g 10m s 10 t Speed of the block V is gl 505 15 gl Clear Respor

Physics
Simple harmonic motion26 Average velocity of a particle executing SHM in one complete vibration is any velocity NEET 2019 2 Aw 2 zero 3 Aw Aw 4 2
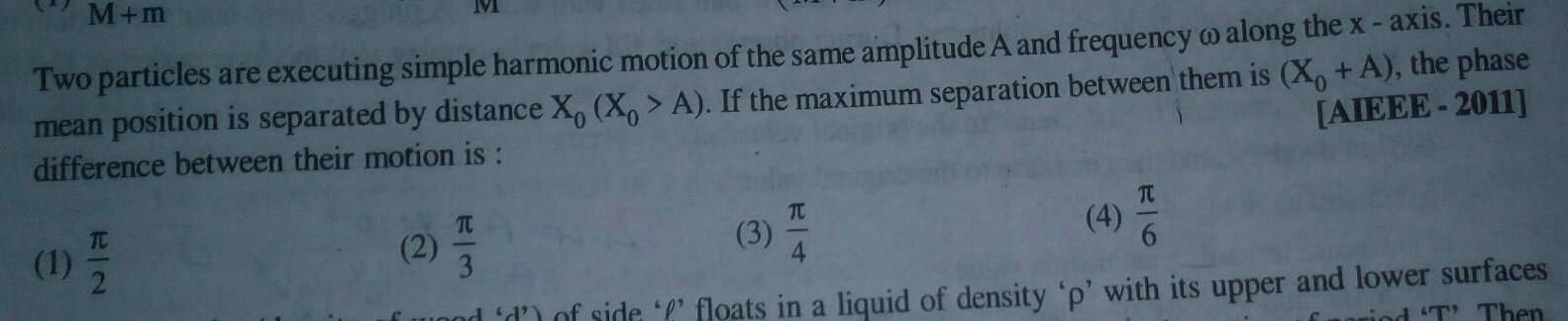
Physics
Simple harmonic motionM m Two particles are executing simple harmonic motion of the same amplitude A and frequency o along the x axis Their mean position is separated by distance X X A If the maximum separation between them is X A the phase difference between their motion is AIEEE 2011 1 7 2 M 2 T 3 3 TC 4 TU and d of side floats in a liquid of density p with its upper and lower surfaces rind T Then
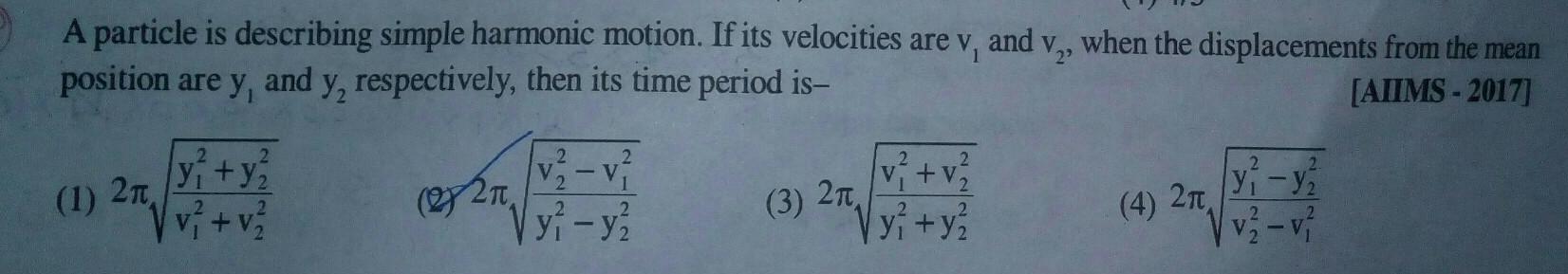
Physics
Simple harmonic motionA particle is describing simple harmonic motion If its velocities are v and v when the displacements from the mean position are y and y respectively then its time period is AIIMS 2017 1 2n 2 2 y y v v 22 2 2 v v y y 3 2 2 v v 2 y y 4 2 y y v2 v

Physics
Simple harmonic motionThe displacement of a particle from its mean position in m is given by y 0 2 sin 10nt 1 5p cos 10nt 1 5n The motion of particle is A B C Periodic but not SHM non periodic Simple harmonic motion wit S Correct Answer
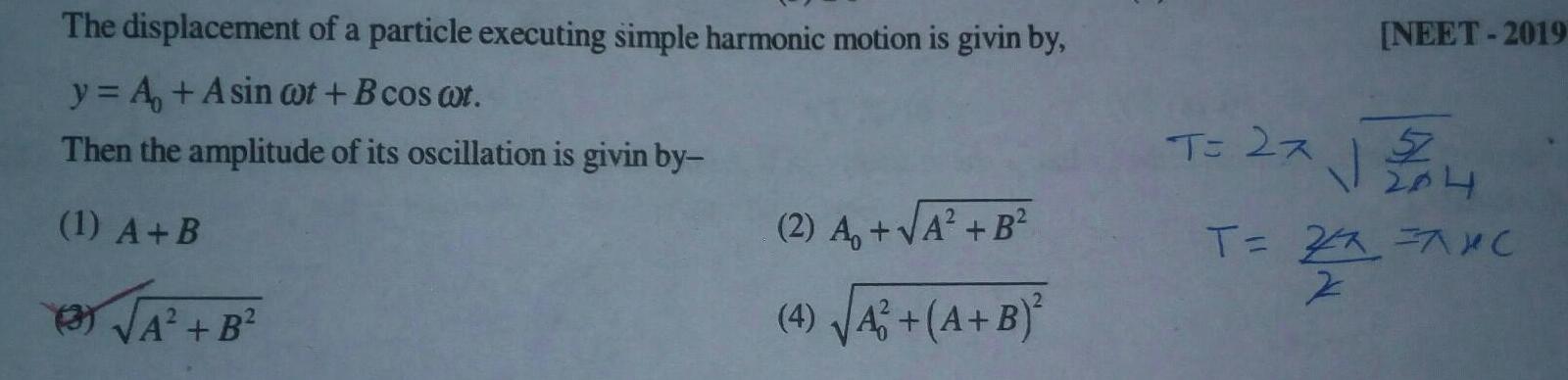
Physics
Simple harmonic motionThe displacement of a particle executing simple harmonic motion is givin by y A Asin wot B cos wt Then the amplitude of its oscillation is givin by 1 A B B 2 A A B 4 A A B NEET 2019 T 2x 27 2 04 T 27 7XC Z
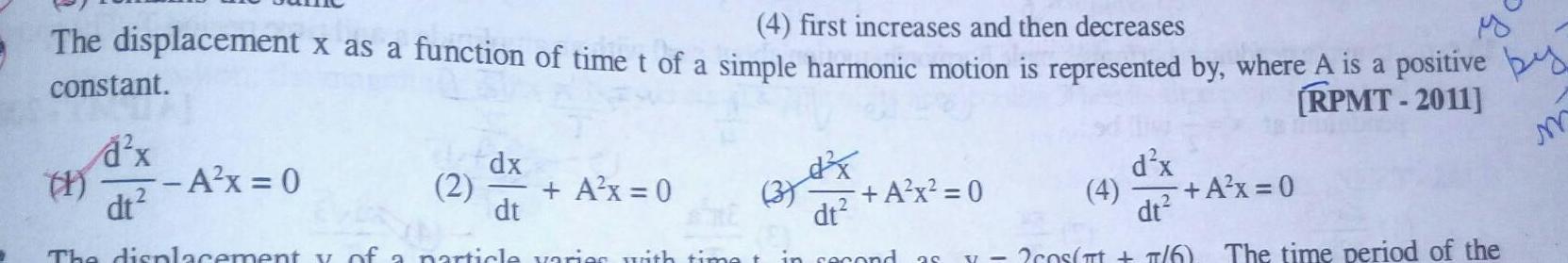
Physics
Simple harmonic motionThe displacement x as a function of time t of a simple harmonic motion is represented by where A is a positive by constant 4 first increases and then decreases yo RPMT 2011 m a x dt A x 0 dx 2 A x 0 dt A x 0 dt d x The displacement y of a particle varies with time t in second as X cos 7 6 The time period of the dt A x 0

Physics
Simple harmonic motionIn forced oscillation of a particle the amplitude is maximum for a frequency of the force while the energy is maximum for a frequency oo of the force then Cit is a suenance AIEEE 2004 Condition 0 0 2 w 3 0 when damping is small and o when damping is large 4 c

Physics
Simple harmonic motionA mass of 2 0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure The mass of the spring and the pan is negligible When pressed slightly and released the mass executes a simple harmonic motion The spring constant is 200N m What should be the minimum amplitude of the motion so that the mass gets AIPMT 2007 detached from the pan Take g 10 m s elllll m
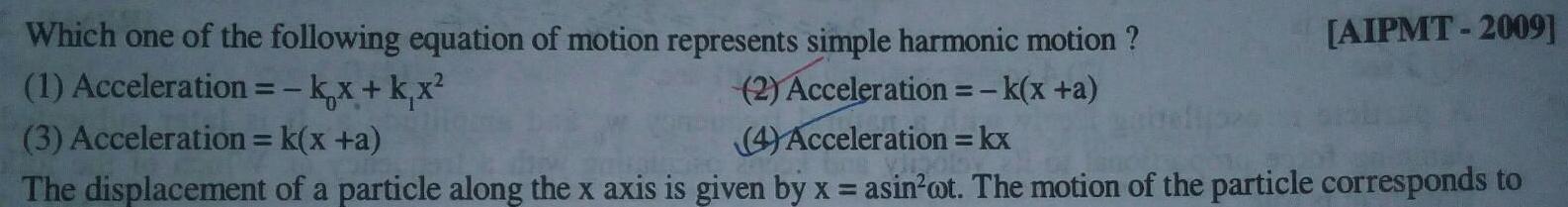
Physics
Simple harmonic motionAIPMT 2009 Which one of the following equation of motion represents simple harmonic motion 1 Acceleration kx k x 2 Acceleration k x a 4 Acceleration kx 3 Acceleration k x a The displacement of a particle along the x axis is given by x asin ot The motion of the particle corresponds to
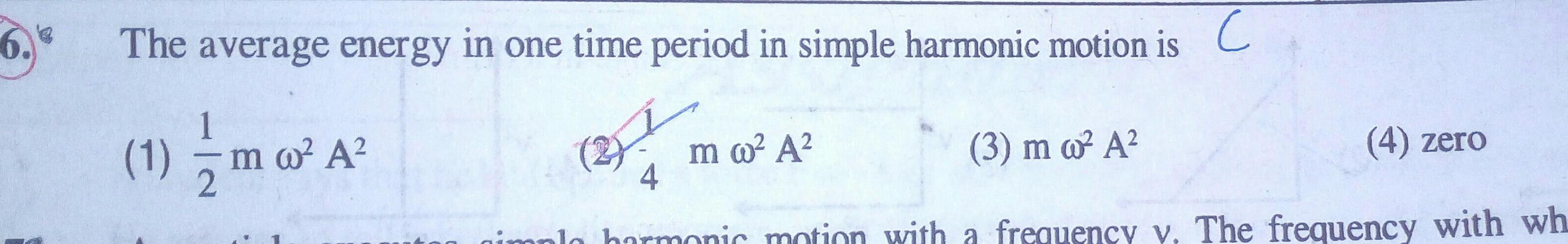
Physics
Simple harmonic motion6 e The average energy in one time period in simple harmonic motion is C 1 m A 2 m w A 3 m A 4 4 zero harmonic motion with a frequency y The frequency with wh

Physics
Simple harmonic motionA particle of mass m is executing oscillations about the origin on the x axis Its potential energy is U x k x whe k is a positive constant If the amplitude of oscillation is a then its time period T is AIIMS 2008 1 proportional to 1 2 independent of a 3 proportional to a 4 proportional to a 2

Physics
Simple harmonic motionTwo particle are oscillating along two close parallel straight lines side by side with the same frequency and ampli tudes They pass each other moving in opposite directions when their displacement is half of the amplitude The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles The phase AIPMT 2011 difference is 1 0 2 2 3 3 T 4 6

Physics
Simple harmonic motionA toy car of mass m is having two similar rubber ribbons attached to it as shown in the figure The force constant of each rubber ribbon is k and surface is frictionless The car is displaced from mean position by x cm and released At the mean position the ribbons are undeformed Vibration period is m 2k 1 2 2 2 m 2k k 3 2T k 4 2T m k k

Physics
Simple harmonic motion1 Straight line 2 Circle 3 Ellipse 4 Figure of eight Two mutually perpendicular simple harmonic vibrations have same amplitude frequency and phase When superimpose the resultant form of vibration will be 1 A circle 2 An ellipse 3 A straight line 4 A parabola
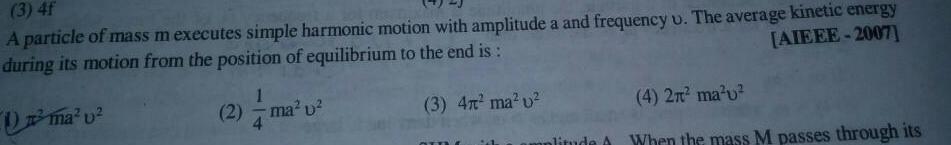
Physics
Simple harmonic motion3 4f A particle of mass m executes simple harmonic motion with amplitude a and frequency u The average kinetic energy during its motion from the position of equilibrium to the end is AIEEE 2007 ma v 3 4n ma u 1 2 ma v 4 2 ma u When the mass M passes through its

Physics
Simple harmonic motion1 3 5 2 25 9 3 A body executes simple harmonic motion The potential energy P E the kinetic energy K E and total ener T E are measured as function of displacement x Which of the following statements is true K E is maximum when x 0 2 T E is zero when x 0 2 K E is maximum when x is maximum 0 4 P E is maximum when x IRA 2 V AZ
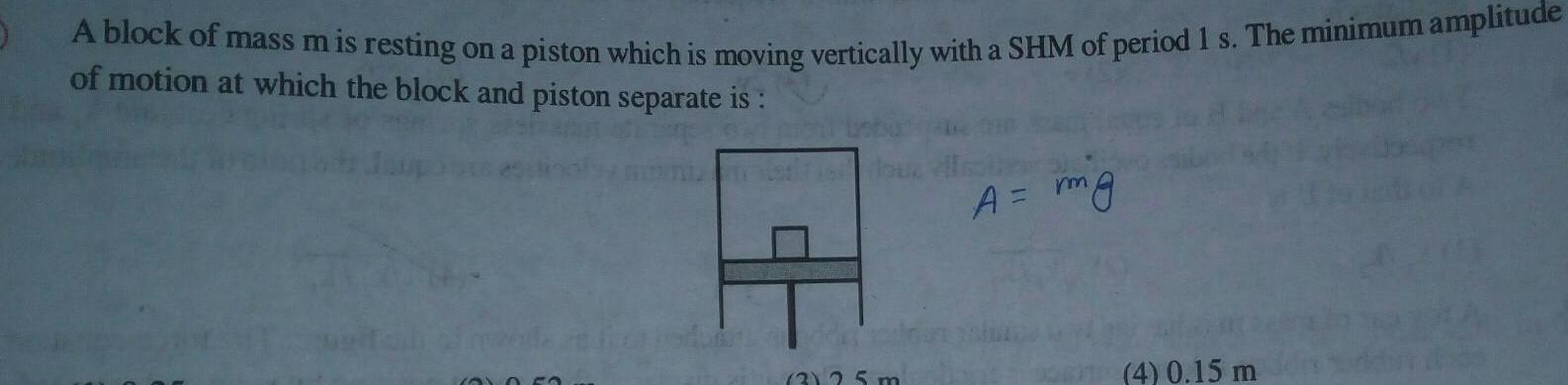
Physics
Simple harmonic motionA block of mass m is resting on a piston which is moving vertically with a SHM of period 1 s The minimum amplitude of motion at which the block and piston separate is O 0 50 2 25 m A mg 4 0 15 m
Physics
Simple harmonic motion33 When an oscillator completes 100 oscillation its ampliutde reduced to of initial value What will be its amplitude 3 when it completes 200 oscillation 400 27 1 1 2 2 3 3 4

Physics
Simple harmonic motionThe time period of a particle in simple harmonic motion is equal to the time between consecutive appearance of th particle at a particular point in its motion This point is 1 the mean position gnols 2 an extreme position 3 between the mean position and the positive extreme an position and the negative extreme

Physics
Simple harmonic motion70 A wall clock uses a vertical spring mass system to measure the time Each time the mass reaches an extreme position the clock advances by a second The clock gives correct time at the equator If the clock is taken to the poles it will 4 give correct time 1 run slow 2 run fast 3 stop working A pendulum clock keeping correct time is taken to high altitudes 1 it will keen correct time
Physics
Simple harmonic motion1 0 25 m 2 0 52 m 3 2 5 m A particle moves on the X axis according to the equation x x sin oot The motion is simple harnomic 1 with amplitude x 2 with amplitude 2x T 3 with time period 2 S of amplitude of 0 1m When the particle passes through th 4 with time period

Physics
Simple harmonic motion1 A 2 2A 1 2 al potom s The distance moved by a particle in simple harmonic motion in one time period is L A 2 2A 3 4A 4 zerc gimple harmonic motion is equal to the time between cc

Physics
Simple harmonic motionA student says that he had applied a force F k x on a particle and the particle moved in simple harmonic motion He refuses to tell whether k is a constant or not Assume that he has worked only with positive x and no other force acted on the particle 1 As x increases k increases 3 As x increases k remains constant 2 As x increases k decreases 4 The motion cannot be simple harmonic in proportional to

Physics
Simple harmonic motion32 Two bodies M and N of equal masses are suspended from two separate massless spring of force constants k and k respectively If the two bodies oscillate vertically such that their maximum velocities are equal the ratio of the amplitude M to to that of N is A W ALW AL 33 Ar k AL K AL 53 3 ki ditic
Physics
Simple harmonic motionDU KX 2 2 U KX 3 U K The kinetic energy and potential energy of a particle executing simple harmonic motion will be equal when displacement amplitude a is 1 2 a 2 2 a 2 3a when the displacement is half of the

Physics
Simple harmonic motionThe displacement of a particle in simple harmonic motion in one time period is 1 A AS 2 2A 1 2 al otome 3 4A 4 zer The distance moved by a particle in simple harmonic motion in one time period is
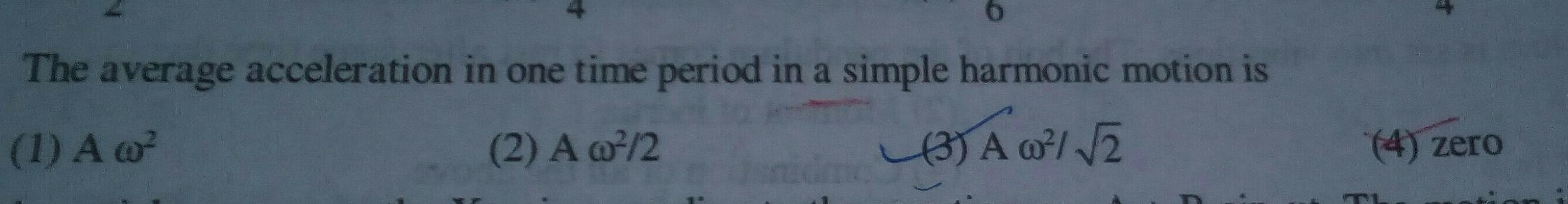
Physics
Simple harmonic motion6 The average acceleration in one time period in a simple harmonic motion is 1 A w 2 A w 2 3 A 00 2 4 zero

Physics
Simple harmonic motionThe distance between the point of suspension and the centre of gravity of a compound pendulum is and the rac of gyration about the horizontal axis through the centre of gravity is k then its time period will be 1 2 l k g l k lg l k g inimum period of oscillation will be 27 2 2 3 2T 4 2 2k eg
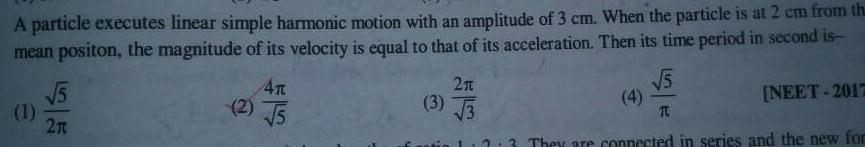
Physics
Simple harmonic motionA particle executes linear simple harmonic motion with an amplitude of 3 cm When the particle is at 2 cm from th mean positon the magnitude of its velocity is equal to that of its acceleration Then its time period in second is 5 1 2n 2 4T 5 2 t 3 3 5 T NEET 2017 2 3 They are connected in series and the new for

Physics
Simple harmonic motionThe force constant of a spring is k and that of another is 3k Now both spring are stretched through same distance if work done on springs are w and W2 respectively then O W1 W2 O W1 3W2 O W 3W W2 9W1
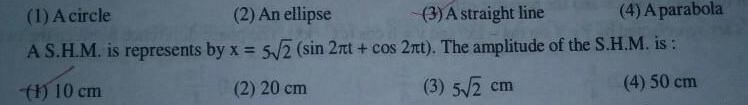
Physics
Simple harmonic motion1 A circle 2 An ellipse 3 A straight line 4 A parabola A S H M is represents by x 5 2 sin 2nt cos 2nt The amplitude of the S H M is 1 10 cm 2 20 cm 3 5 2 cm 4 50 cm

Physics
Simple harmonic motionThe composition of two simple harmonic motions of equal periods at right angle to each other and with a pha difference of results in the displacement of the particle along 1 Straight line 2 Circle 3 Ellipse 4 Figure of eight Tun mutually perpendicular simple harmonic vibrations have same amplitude frequency and phase When t
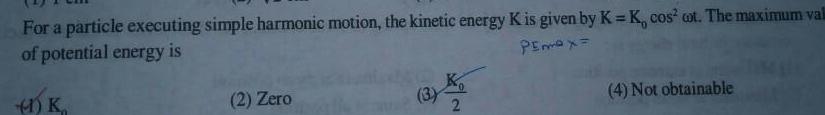
Physics
Simple harmonic motionFor a particle executing simple harmonic motion the kinetic energy K is given by K K cos cot The maximum val of potential energy is Pemax 1 K 2 Zero 4 Not obtainable
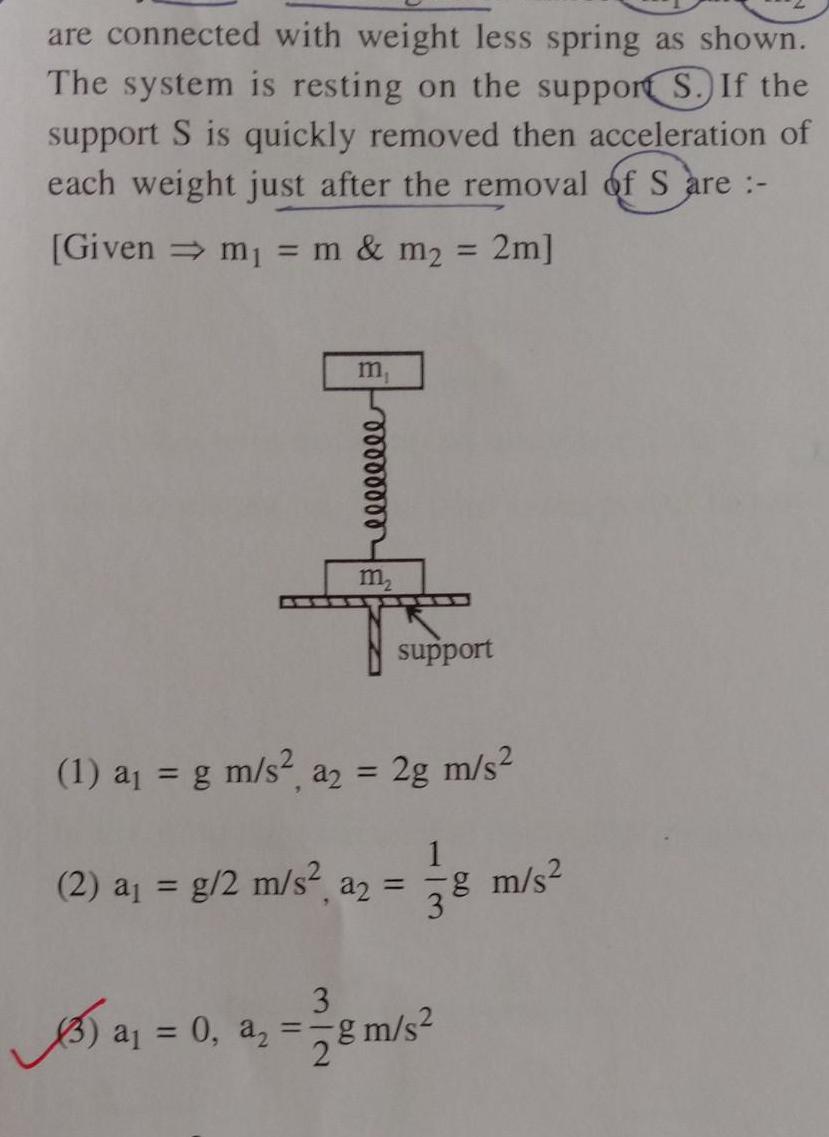
Physics
Simple harmonic motionare connected with weight less spring as shown The system is resting on the support S If the support S is quickly removed then acceleration of each weight just after the removal of S are Given m m m 2m 5 00000000 m support 1 a g m s a2 2g m s Xal 2 a g 2 m s a 1 78 3 3 a 0 a g m s 2 8 m s

Physics
Simple harmonic motionA simple harmonic oscillator has an amplitude a and time period T The time required by it to travel from x a tox a 2 is Rad and f Sara T A T 6 B T 4 C T 3 D T 2 x A 2 Your Answer A 32

Physics
Simple harmonic motionThe figure shows the displacement time graph of a particle executing S H M If the time period of oscillation is 2s the equation of motion of its SHM is farger vert af SHMERY in m 10 A 5 for de 2 1 s A x 10sin nt n 3 B x 10sin t C x 10sin nt 6 D x 10sin 2nt n 6 Your Answer C

Physics
Simple harmonic motionA particle perform SHM of amplitude A along a straight line When it is at a distance of A from its mean position Its kinetic energy gets increased by 2 amount ma 4 due to an impulsive force The new amplitude of the particle becomes O 2A O PA OA

Physics
Simple harmonic motionA particle perform simple harmonic motion with amplitud A and time period T Average speed of the particle over the time interval during which it travels a distance of A 2 starting from extreme position is 4 A 04A T 0 3A 3A 2T O A 3T 26

Physics
Simple harmonic motionA block of mass m is resting on a piston as shown in figure which is moving vertically in an SHM of period 1 s The minimum amplitude of motion at which the block and piston separate is g n 0 25 m 0 52 m O 2 5 m 0 15 m

Physics
Simple harmonic motionA simple pendulum 50 cm long is suspended from the root of a cart accelerating in the horizontal direction with constant acceleration 3g m s The period of small oscillations of the pendulum about its equilibrium position g m s L 50 cm 1 0 s O 2 S O a 3g m s
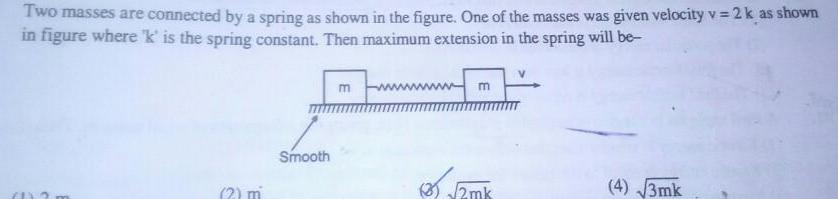
Physics
Simple harmonic motionTwo masses are connected by a spring as shown in the figure One of the masses was given velocity v 2 k as shown in figure where k is the spring constant Then maximum extension in the spring will be a 2 m Smooth m m 2mk 4 3mk
Physics
Simple harmonic motionStationary wave is represented by y A sin 100t cos 0 01x where y and A are in mm t in sec and x in m The velocity of the wave 1 1 m s 2 10 m s 3 10 m s In stationary wave 4 not derivable wave to form a s
Physics
Simple harmonic motionA travelling wave on a string is given by y Asin ax t The displacement and velocity of oscillation of a point a 0 56 cm 12 sec A 7 5 cm x 1 cm and t Is is 1 4 6 cm 46 5 cm s 1 3 1 76 cm 7 5 cm s 2 3 75 cm 77 94 cm st 4 7 5 cm 75 cm s mond frequency Hz is propagating in a string in the negative x

Physics
Simple harmonic motion1 f In case of a forced vibration the resonance wave becomes very sharp when the 1 applied periodic force is small 2 quality factor is small 3 damping force is small 4 restoring force is small both transvere S and longitudinal P sound waves in the ea
Physics
Simple harmonic motionThe period of a simple pendulum that is 1 00 m long on another planet is 133s What is the acceleration due to gravity on this planet if the mass of the pendulum bob is 1 5 kg 20 7 m s O24 5 m s O 22 3 m s 26 8 m s

Physics
Simple harmonic motionA block of mass m rests on a platform The platform is given up and down SHM with an amplitude d What can be the maximum frequency so that the block never leaves the platform Question Type Single Correct Type 1 g d 2 3 1 2 gid 1 2 9 d
Physics
Simple harmonic motionWhen a body of mass m is suspended from a spiral spring of natural length L the spring gets stretched through a distance h The potential energy of the stretched spring is mgh2 mgh 1 2 mgh pressib 4 mg L h w as ds Jw dr 55
Physics
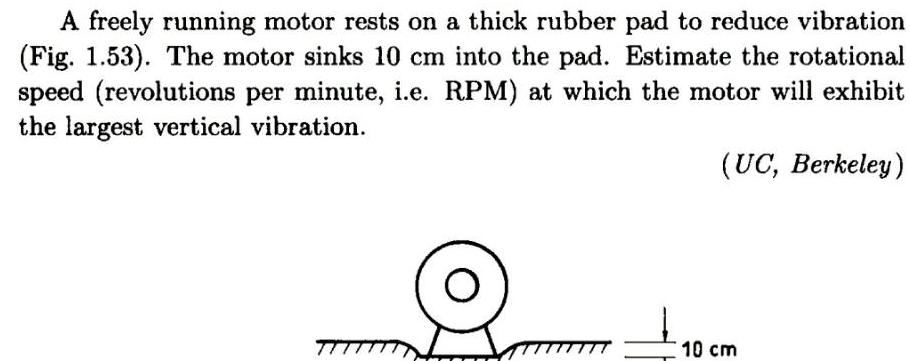
Simple harmonic motionA freely running motor rests on a thick rubber pad to reduce vibration Fig 1 53 The motor sinks 10 cm into the pad Estimate the rotational speed revolutions per minute i e RPM at which the motor will exhibit the largest vertical vibration UC Berkeley TT 10 cm

Physics
Simple harmonic motionNet force acting on the rod is 1 2qE leftwards 3 Zero 1 2T 3 2 9 m AO me 2qE A light insulating rod AB with two small identical metal balls connected to its ends is placed in a uniform electric field with its length parallel to the electric field Charges on the balls are q and q as shown mass of each ball is m and length of the rod is Assume that the space is gravity free 2ml qE 2 4 2 If the rod is rotated in anticlockwise direction by angle 90 from the position shown torque acting on the rod will be 1 qEl clockwise 2 2qEl anticlockwise 3 qEl anticlockwise 4 2qEl clockwise 38 If the rod is slightly disturbed from the position shown it oscillates with time period 4 FO q m 2 2T Em 2qE rightwards 2qE upwards B me qE E me 4gE