Simple harmonic motion Questions and Answers
Physics
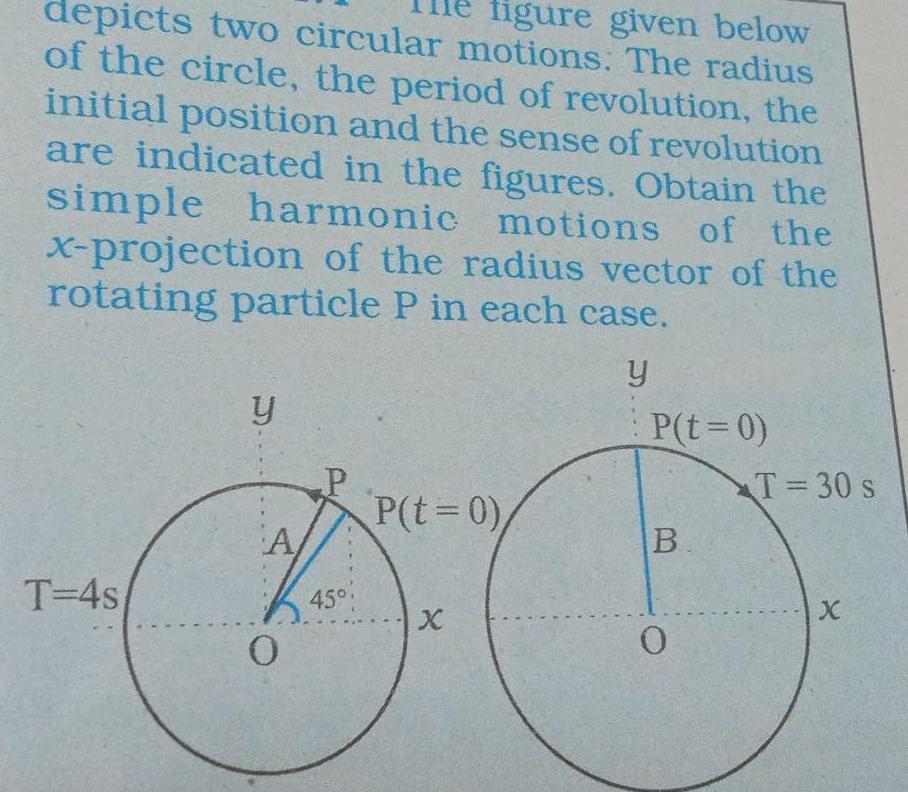
Simple harmonic motiondepicts two circular motions The radius ligure given below of the circle the period of revolution the initial position and the sense of revolution are indicated in the figures Obtain the simple harmonic motions of the x projection of the radius vector of the rotating particle P in each case y T 4s y A 0 45 P t 0 X P t 0 B 0 T 30 s X

Physics
Simple harmonic motionextreme position and lowest position are equal The angle 9 of thread deflection in the extreme position will be 1 tan 2 2 tan 2 3 tan 1 2 4 2 tan 1 2

Physics
Simple harmonic motionA simple pendulum of length 1 metre suspended from the ceiling of a lift executes oscillation with a period of 6 25 sec If the lift is moving up with an acceleration a find a take g m s e the acceleration of the lift unwards then
Physics
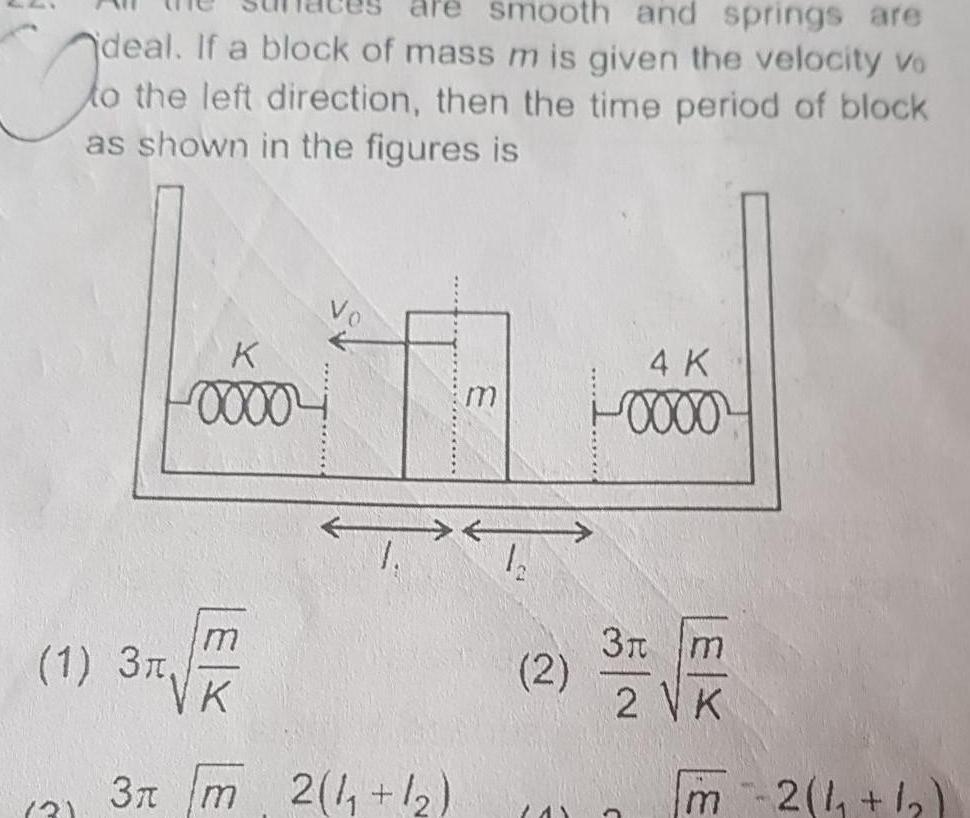
Simple harmonic motionsmoot and springs are deal If a block of mass m is given the velocity Vo the left direction then the time period of block as shown in the figures is To 31 1 3T K 0000 m K 3 m 2 1 1 m 1 2 2 4 K 0000 3r m 2 VK C m2 1 1
Physics
Simple harmonic motionFor a particle executing simple harmonic motion the KE is given by K K cos wt Then maximum value of potential energy for given particle 1 May be K 2 Must be K 3 May be less than K 4 Roth 1 3

Physics
Simple harmonic motionllustration 18 A simple pendulum of length l is made to oscillate with a solid sphere density D in a non viscous fluid of density p find the period of oscillation D pl
Physics
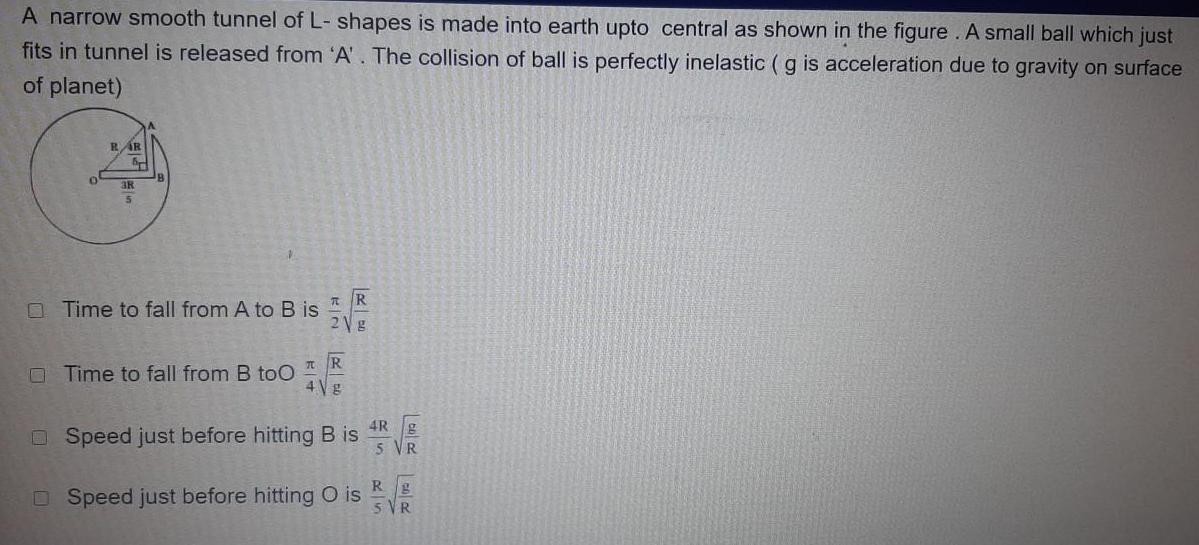
Simple harmonic motionA narrow smooth tunnel of L shapes is made into earth upto central as shown in the figure A small ball which just fits in tunnel is released from A The collision of ball is perfectly inelastic g is acceleration due to gravity on surface of planet 0 RAR 3k Time to fall from A to B is Time to fall from B too T R 2Vg 7 R 4Vg Speed just before hitting B is DSpeed just before hitting O is 4Rg 5 VR Rg 5 VR

Physics
Simple harmonic motionCategorise the following function of time cos ot as a S H M b Periodic but not S H M Also find the period Hint cos wf 3 cos wt cos3wt 4
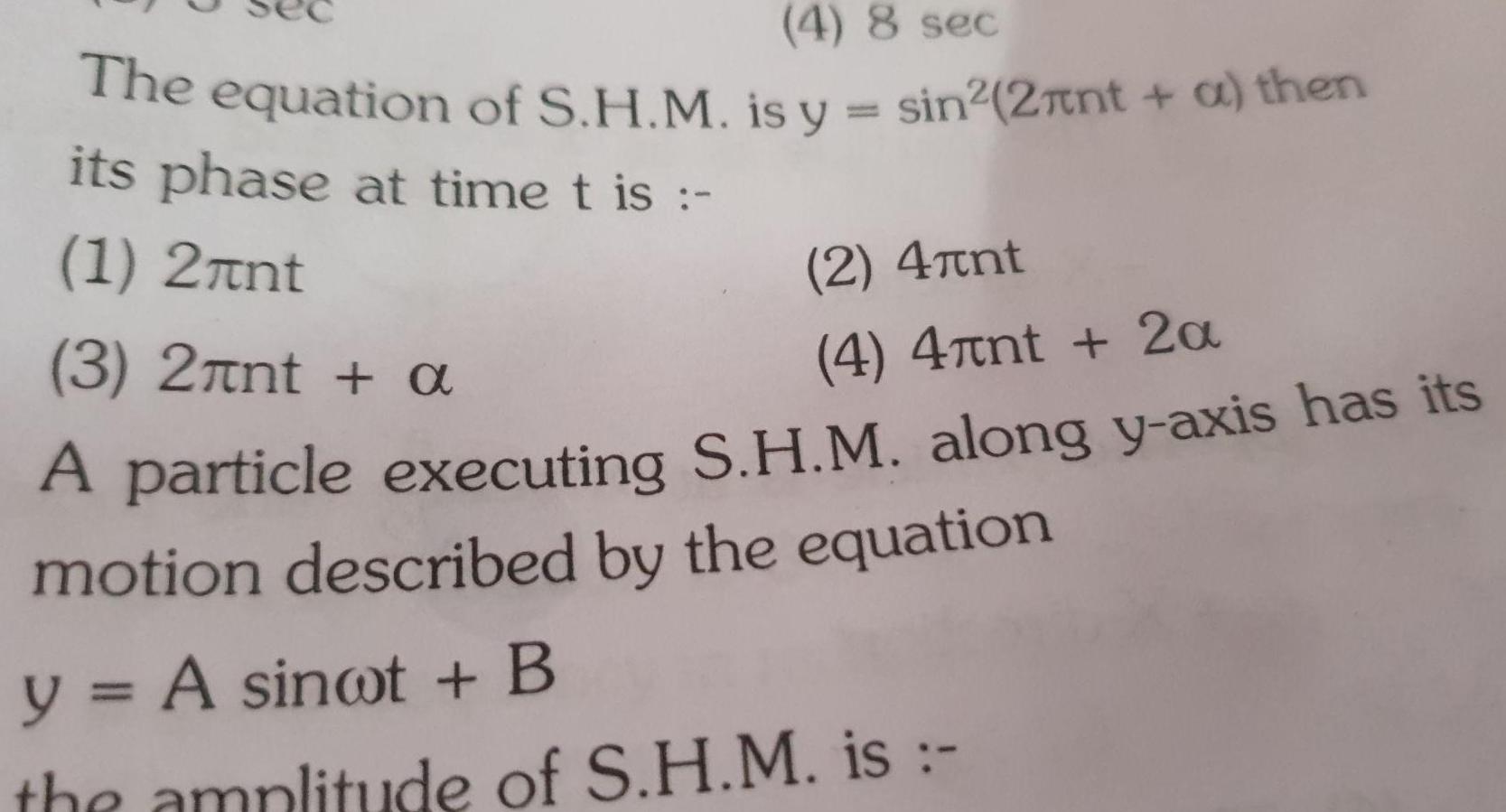
Physics
Simple harmonic motion4 8 sec The equation of S H M is y sin 2 nt a then its phase at time t is 1 2nt 2 4 nt 3 2 nt a 4 4 nt 2a A particle executing S H M along y axis has its motion described by the equation y A sinot B the amplitude of S H M is

Physics
Simple harmonic motionThe young s modulus of material of a thin ring shaped elastic body is Y The mass of ring is m area of cross section is A its initial radius is R Ring is a little elongated then left alone At what time will ring circumference be same as it was initially Neglect loss of energy 1 3 2 TMR 8YA mR YA 2 4 3 2 mR YA KmR V2YA
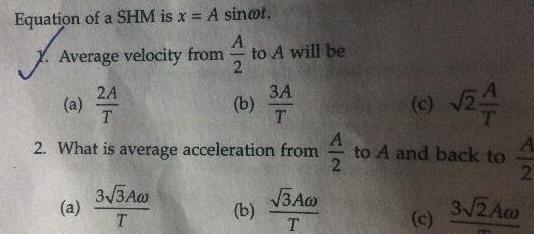
Physics
Simple harmonic motionEquation of a SHM is x A sintot A Average velocity from 2 a 2A T 2 What is average acceleration from a to A will be 3 3 Aw T b 34 3A T b 3AG T A 2 c 24 to A and back to c 2 3 2Aw

Physics
Simple harmonic motionX The equation of a wave is given by Y A sin V k where is the angular velocity and v is the linear velocity The dimensions of k is

Physics
Simple harmonic motionis placed on a horizontal platform which undergoes vertical simple harmonic motion of angular frequency The amplitude of oscillation is gradually increased The coin will leave contact with the platform for the first time a at the mean position of the platform b for an amplitude of c for an amplitude of 00 3 0 3 2006

Physics
Simple harmonic motionof the 23 The string the spring and the pulley shown in figure 12 E9 are light Find the time period of the mass m p k eeeeee m Figure 12 E9 T mg ma IR kk ft ky za R Solve the previous problem if the pulley has a moment of nertia I about its orig d th MV 29 Find the in figure near the v t B 2gh 9 2 t 0 55

Physics
Simple harmonic motionC 0 25 sec D 0 5 sec The maximum acceleration of a particle in SHM is made two times keeping the maximum speed to be constant It is possible when A amplitude of oscillation is doubled while frequency remains constant B amplitude is doubled while frequency is halved C frequency is doubled while amplitude is halved D frequency is doubled while amplitude remains constant

Physics
Simple harmonic motion4 Time period of a simple pendulum of length is T and time period of uniform rod of same length l pivoted about one end and oscillating in a vertical plane is T2 Amplitude of oscillations in both the cases is small then T 21 1 3 3 3 T is T 2 2 1 4 13

Physics
Simple harmonic motion1 A particle with total energy E is moving in a potential energy region U x Motion of the particle is restricted to the region when 1 U x E 2 U x E 3 U x 0 4 U X E

Physics
Simple harmonic motiontion 25 A small block of mass m is attached to three springs with respective stiffness constants k k and ks see fig Find the period of oscillations if the block is slightly pressed against the spring with stiffness constant k Will your answer be the same if the block be pressed against the spring with stiffness 000000 constant k 90

Physics
Simple harmonic motion6 Points A block with a mass of 4 00 kg connected to a spring is undergoing simple harmonic motion The block has a maximum velocity of 4 50 m s Some time later the block has compressed the spring by 10 0 cm coming to a complete stop What is the period of oscillations 0 3185 0 115

Physics
Simple harmonic motionEquation of a wave travelling along x axis on string is given as y 3 sin 3 14x 314t where x and y in cm and t in second Maximum velocity of particle is 9 4 m s 1 12 3 m s 1 6 2 m s 1 8 5 m s 1
Physics
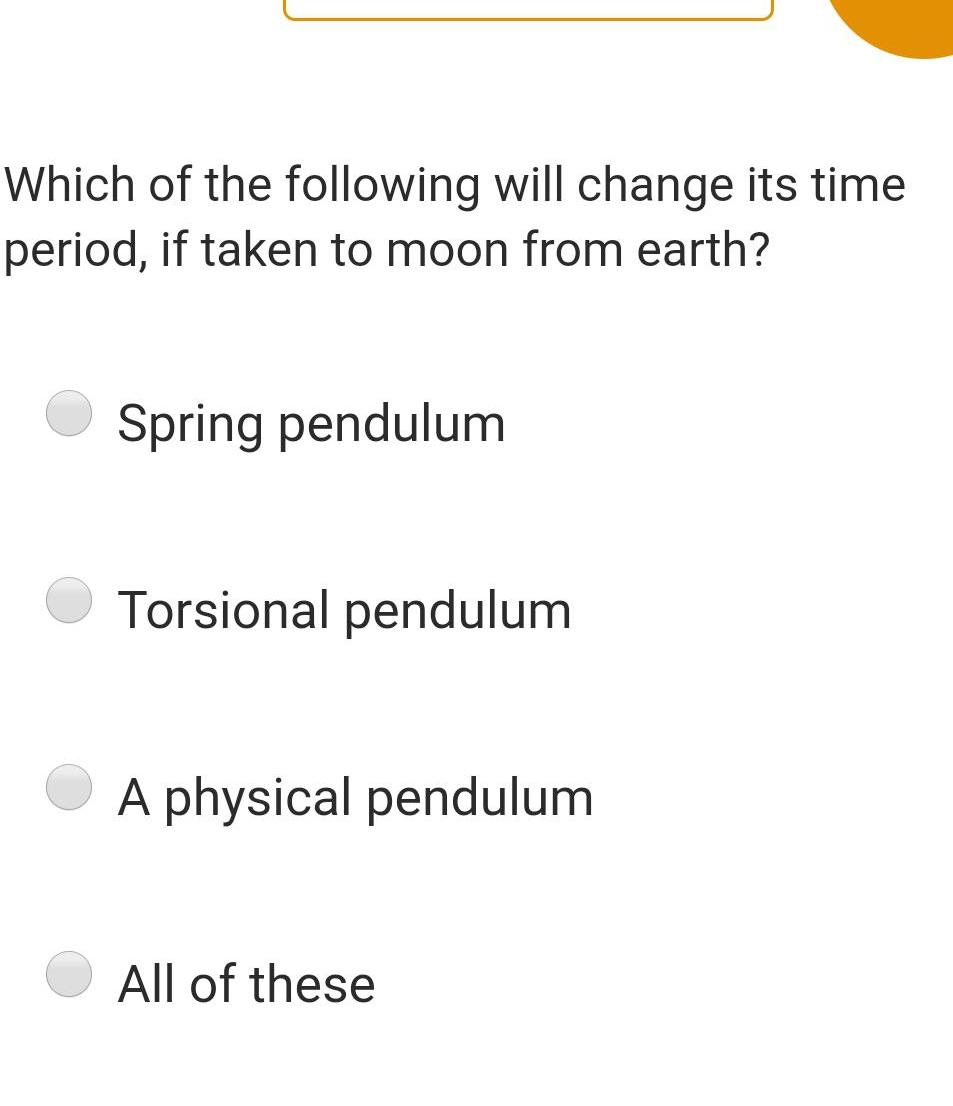
Simple harmonic motionWhich of the following will change its time period if taken to moon from earth Spring pendulum Torsional pendulum A physical pendulum All of these

Physics
Simple harmonic motionA simple pendulum has time period T The point of suspension is now moved upward according to the relation y Kt K 1 m s where y is the vertical displacement The time period now becomes T The ratio of T is g 10 m s T T2 2 1 6 5 2 56 3 1 4 5
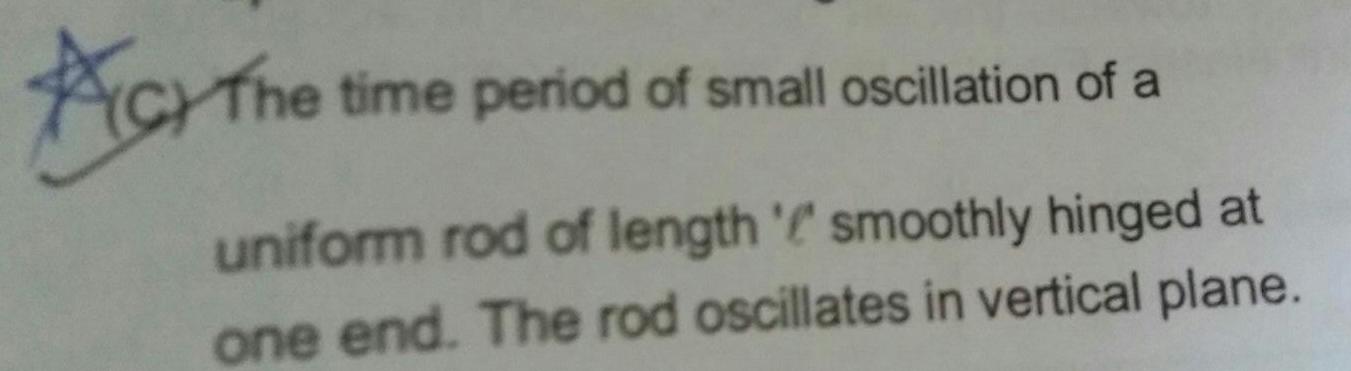
Physics
Simple harmonic motionThe time period of small oscillation of a uniform rod of length smoothly hinged at one end The rod oscillates in vertical plane

Physics
Simple harmonic motionD The frequency of oscillation of an electric dipole moment having dipole moment p and rotational inertia I oscillating in a uniform electric field E is given 1 1 2 I PE 3 2 PEII 2 1 2 PE I 4 2 IPE

Physics
Simple harmonic motionA particle execute S H M with frequency f Find frequency with which its kinetic energy oscilla A particle of mass 10g is placed in potential field given by V 50x 100 erg g What will be freque of oscillation of particle

Physics
Simple harmonic motionA particle performing S H M is found at its equilibrium at t 1 s and it is found to have a speed of 0 25 m s at t 2 s If the period of oscillation is 6s Calculate amplitude of oscillation 1 3 2n m 2 m 3 3 4r 6 T m 3 4 m 8f
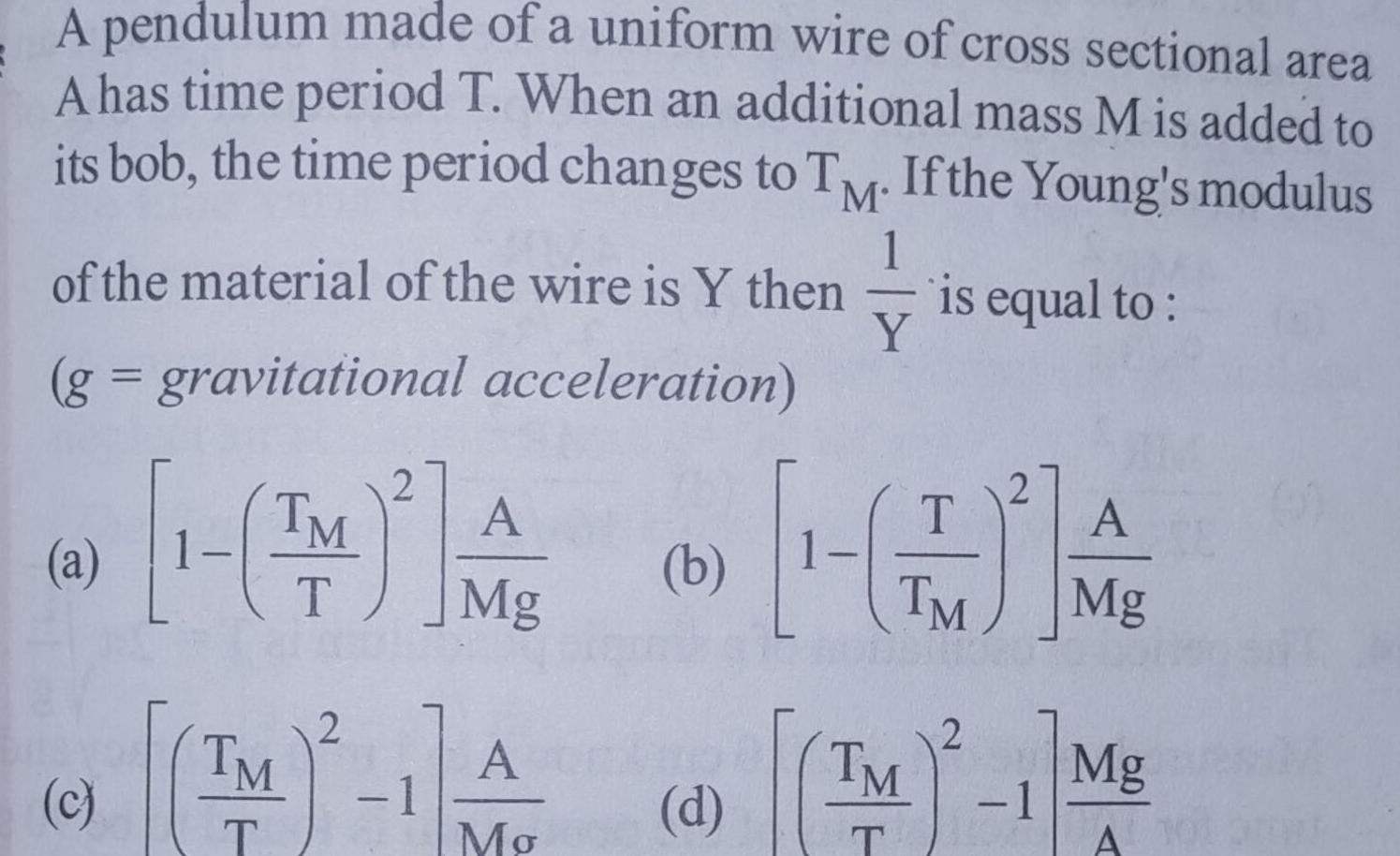
Physics
Simple harmonic motionA pendulum made of a uniform wire of cross sectional area A has time period T When an additional mass M is added to its bob the time period changes to TM If the Young s modulus 1 of the material of the wire is Y then is equal to Y g gravitational acceleration a c TM T TM 2 2 1 A Mg A Mo b T TM A Mg 2 d M 1 Mg TM T A 101 amat

Physics
Simple harmonic motion0 If a simple harmonic motion is represented by dt its time period is a 2 a b 2T a d x 2 c 2 ax 0 d 2
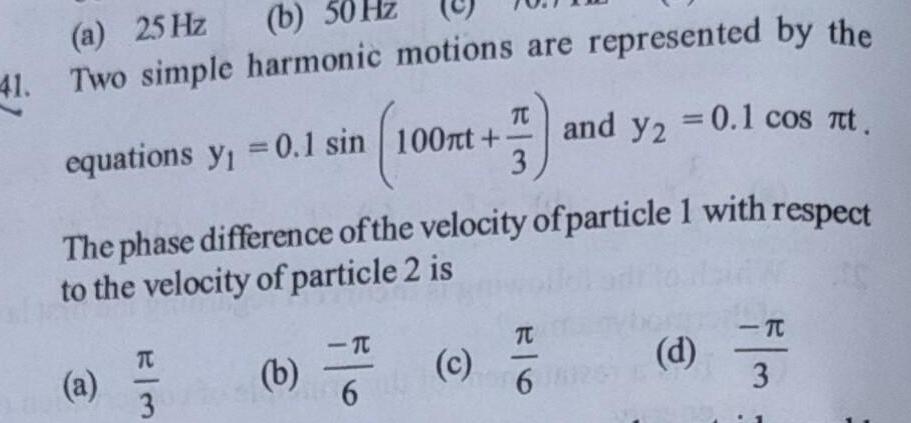
Physics
Simple harmonic motiona 25 Hz b 50 Hz 41 Two simple harmonic motions are represented by the equations y 0 1 sin 100nt a The phase difference of the velocity of particle 1 with respect to the velocity of particle 2 is W 3 b 539 F 0 c and y2 0 1 cos t TC 6 d TC 3

Physics
Simple harmonic motionThe bob of a simple pendulum is a spherical hollow ball filled with water A plugged hole near the bottom of the oscillating bob gets suddenly unplugged During observation till water is coming out the time period of oscillation would a first decrease and then increase to the original value b first increase and then decrease to the original value c increase towards a saturation value d remain unchanged
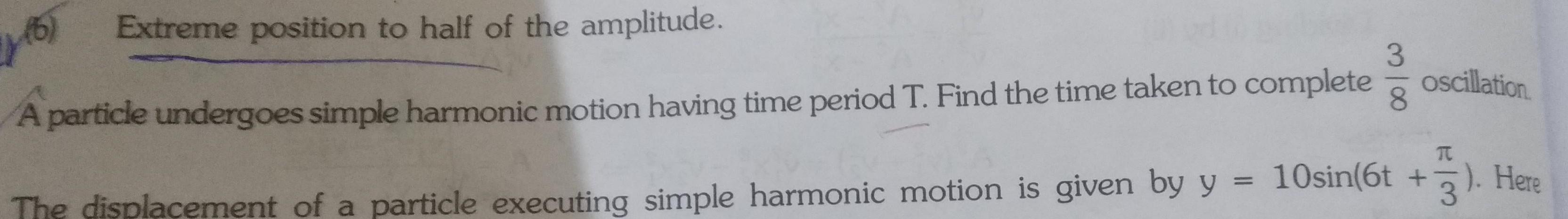
Physics
Simple harmonic motion116 Extreme position to half of the amplitude A particle undergoes simple harmonic motion having time period T Find the time taken to complete 3 8 oscillation T The displacement of a particle executing simple harmonic motion is given by y 10sin 6t 3 Here
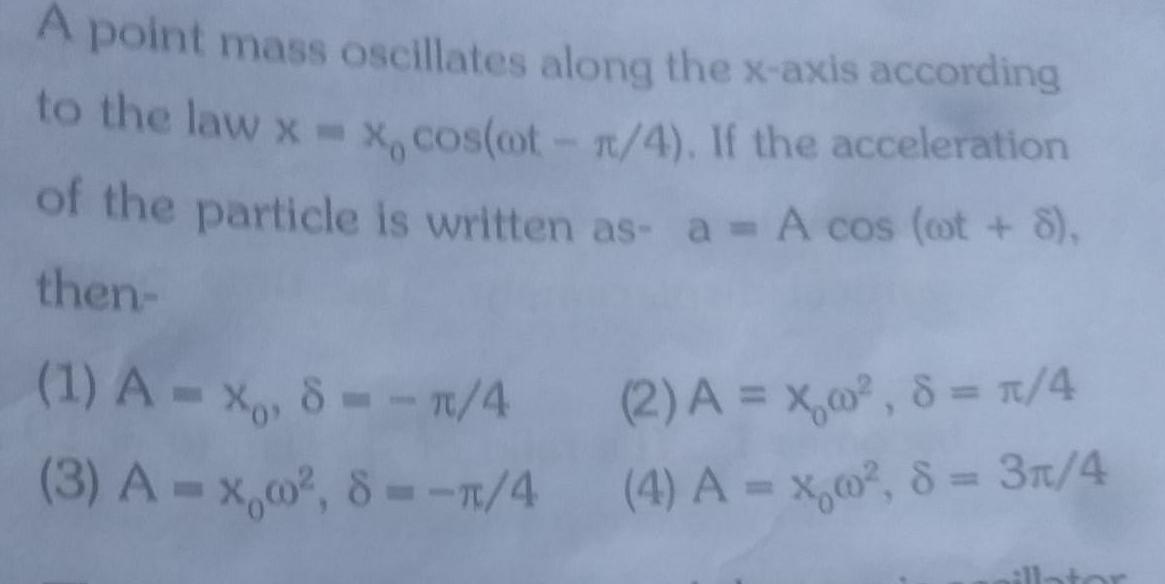
Physics
Simple harmonic motionA point mass oscillates along the x axis according to the law x x cos oot 4 If the acceleration of the particle is written as a A cos oot 8 then 1 Axo 8 4 3 A x w 8 1 4 4 2 A x 0 8 4 4 A x 0 8 3 4 illator
Physics
Simple harmonic motionThe maximum velocity of a particle executing simple harmonic motion with an amplitude 7 mm is 4 4 m s The period of oscillation is a 0 01s c 0 1 s b d 10 s 100 s

Physics
Simple harmonic motionblock attached to an end of a vertical spring whose other end is fixed to the ceiling of a stationary lift stretches the spring by length equilibrium It s time period when lift moves up with an acceleration g 2 is

Physics
Simple harmonic motionA man of mass 60 kg standing on a plateform executing S H M in the vertical plane Th displacement from the mean position varies a y 0 5 sin 2 ft The minimum value of f fe which the man will feel weightlessness at th highest point is y is in metres 1 3 g 4 T 2g2MA 2T 2 4 ng 4 2 2g

Physics
Simple harmonic motionWedge A is fixed while wedge B slides down on a smooth surface The vessel C having a simple pendulum of length I can slide down vertically on a smooth surface of wedge B Find the time period of the pendulum 90 111 C A O2n O O Zero Infinity

Physics
Simple harmonic motionTwo object P and Q of masses 2m and m are connected to two springs of spring constant 2k and k respectively Other ends of springs are connected to rigid walls as shown Initially springs are compressed by length 2A and A respectively and then released 0 0 J 2h vooooo 2m 2AAQ Smooth surface k oooooo Time period of P and Q remains same before and after the collision irrespective of the fact whether collision between masses is perfectly elastic or perfectly inelastic Time period of P and Q remains same before and after the collision only if collision between the objects is perfectly elastic Time period of P and Q remains same before and after the collision only if collision between the objects is perfectly inelastic If collision is perfectly inelastic amplitude of SHM of combined mass is A

Physics
Simple harmonic motionBlock A of mass m connected with spring of spring constant K is executing SHM for which x x a sinot Block B of same mass connected with spring of spring constant K is executing SHM for which x x a sino t Block B collides with block A elastically at time t 0 then displacement time equation for block A will be K wwwww A B O x a Ox a a m VK Ox a 00 E Xo a 00 K m m K TWO FOO sin co t sin co t sin co t sin co t D

Physics
Simple harmonic motionWhen displacement of a particle executing SHM is one fourth of its amplitude Chen what fraction of total energy is kinetic energy 15 16 0 1

Physics
Simple harmonic motionA block of mass 20 g connected to a harmonic motion with frequency of 04 Nm 05 Nm 1 O2 Nm 01 Nm 1 spring of spring constant K executes sim Hz Value of K is

Physics
Simple harmonic motionThe piston in a cylinder head of locomotive is having stroke length of 6 cm The piston is executing SHM with an angular frequency of 200 rad min 1 Its maximu speed is O 10 cms 1 15 cms 1 12 cms 1 16 cms 1
Physics
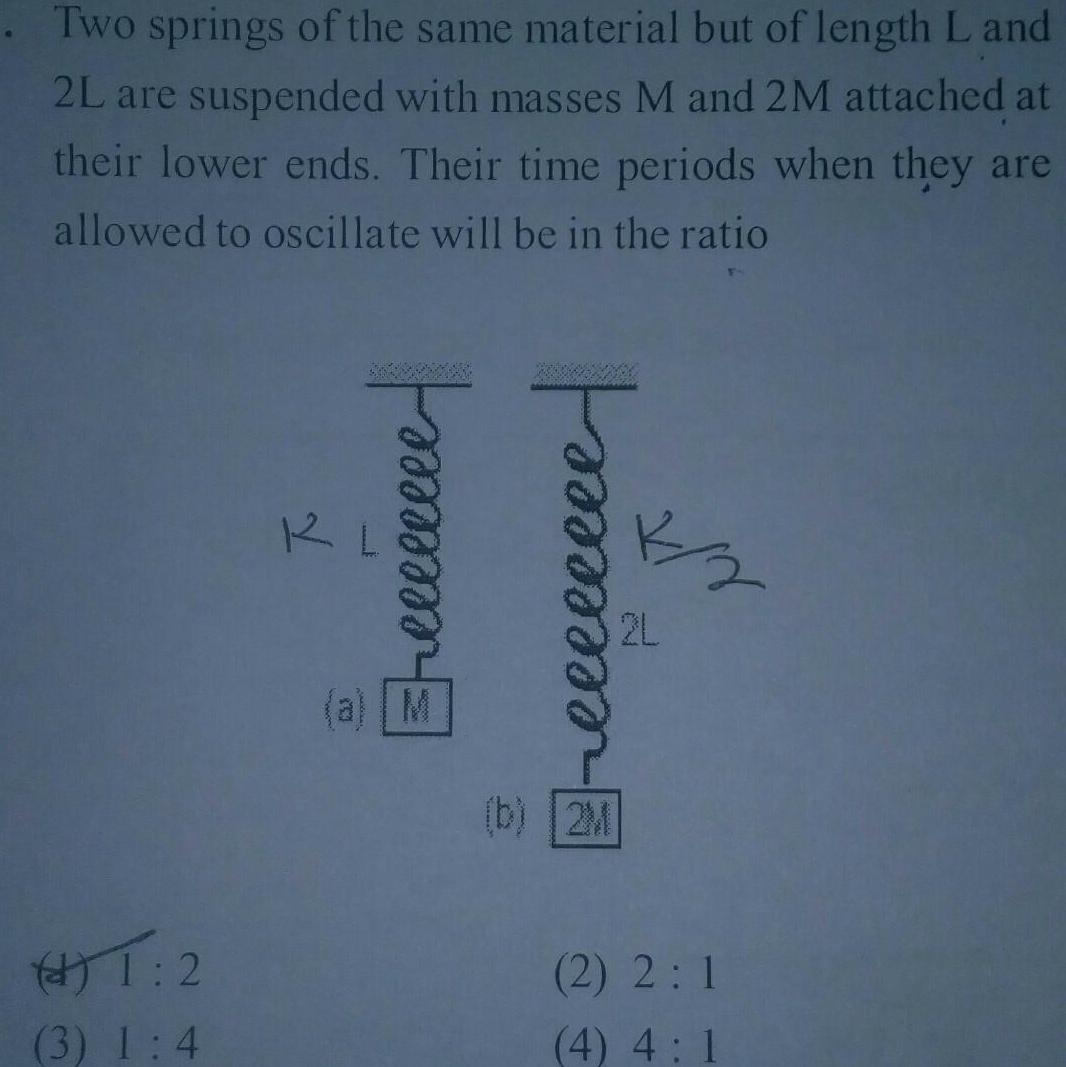
Simple harmonic motionTwo springs of the same material but of length L and 2L are suspended with masses M and 2M attached at their lower ends Their time periods when they are allowed to oscillate will be in the ratio 1 2 3 1 4 a Eeeeeeeee reeeeeeee b 2M 7 2 2L 2 2 1 4 4 1
Physics
Simple harmonic motion12 A particle performing SHM is found at its equilibrium at t 1 sec and it is found to have a speed of 0 25 m s at t 2 sec If the period of oscillation is 6 sec Calculate amplitude of oscillation T 3 1 m 2 3 2 m 41 6 3 m T 4 S mla 3 6 251 13 A t 2 1

Physics
Simple harmonic motionA particle performs SHM with a period T and ampli tude a The mean velocity of the particle over the time interval during which it travels a distance a 2 from the extreme position is 1 a T 2 2a T 4 a 2T 13a T

Physics
Simple harmonic motionA point particle of mass 0 1 kg is executing S H M of amplitude of 0 1 m When the particle passes through the mean position its kinetic energy is 8 10 J The equation of motion of this particle when the initial phase of oscillation is 45 can be given by 1 0 1 cos 4t 41 5 TU 2 0 1sin 4t 4 4 0 2 sin 3 0 4 sin t TC TU H 4 C 2t

Physics
Simple harmonic motionFigure shows a smooth horizontal table in x y plane between two identical fixed walls Two identical springs are connected to the small ball The length of the springs in the free state is The ball is shifted slightly from the equilibrium position in two different ways once along the axis OX and second along the y axis and it begins to perform vibrations The time period for these motions is T and T respectively A Motion along x axis is simple harmonic B Motion along y axis is simple harmonic C T 2n A A B B C C D D m 2k D T 2 2k Y mi 000000 000000 k k X
Physics
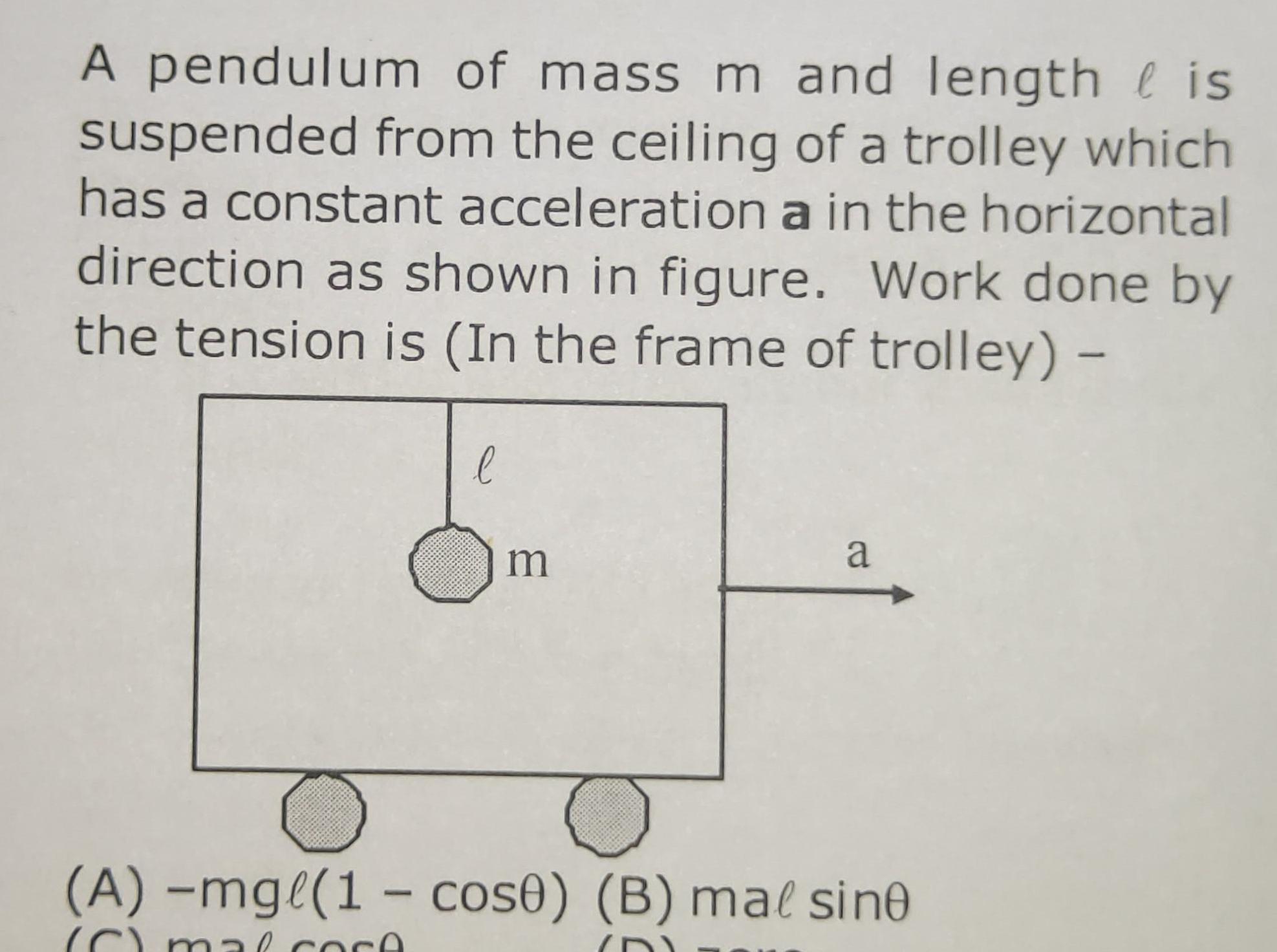
Simple harmonic motionA pendulum of mass m and length is suspended from the ceiling of a trolley which has a constant acceleration a in the horizontal direction as shown in figure Work done by the tension is In the frame of trolley l m a A mg 1 cos0 B mal sine C mal core

Physics
Simple harmonic motionA force of 10 N stretches a spring 0 2 m A 250 g mass attached to this spring is vibrated from a position 10 cm below the equilibrium position with an initial velocity of 0 2 m s upwards Find the equation of motion

Physics
Simple harmonic motionTwo springs both have spring constant k and relaxed length zero They are each stretched to a length and then attached to two identical masses 1 and 2 and a wall as shown in figure The masses ar simultaneously released Immediately afterwards the magnitudes of the accelerations of 2 k fecer l A mass 1 is C mass 2 is 1 m k sellele l kl m 2kl m m B mass 1 is zero D mass 2 is kl m

Physics
Simple harmonic motion1 A simple harmonic motion having an amplitude A and time period T is represented by the equation y 5 sin t 4 m Then the values of A in m and T in sec are A A 5 T 2 T B A 10 T 1 ID 10 T 2