Complex numbers Questions and Answers
Algebra
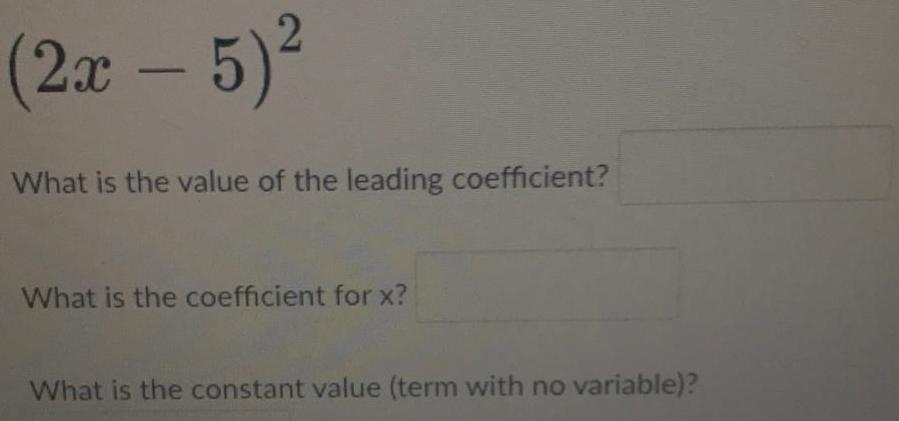
Complex numbers(2x - 5)²
What is the value of the leading coefficient?
What is the coefficient for x?
What is the constant value (term with no variable)?

Algebra
Complex numbersThe best way to graph a line from data points is to graph the points and then pick two of those points (that seem to fit the trend) to build a line from.
Select one:
True
False

Algebra
Complex numbersThe graph of y=f(x) is shown in blue. Draw the graph of y = 3f(x), shown in red, by determining how a stretch or compression will transform the location of the indicated blue points. Drag the movable red points to the desired coordinates.

Algebra
Complex numberscube roots of 125( cos(5π/6) + / sin(5π/6))
(a) Find the roots of the given complex number in trigonometric form. (Let 0 ≤ θ < 2π.)
smallest -value Zo
largest -value
Z1
Z2
(b) Write each of the roots in standard form. (Round all numerical values to four decimal places.)
Z0
Z1
Z2
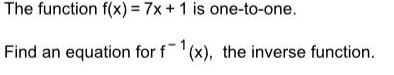
Algebra
Complex numbersThe function f(x) = 7x + 1 is one-to-one.
Find an equation for f-1(x), the inverse function.
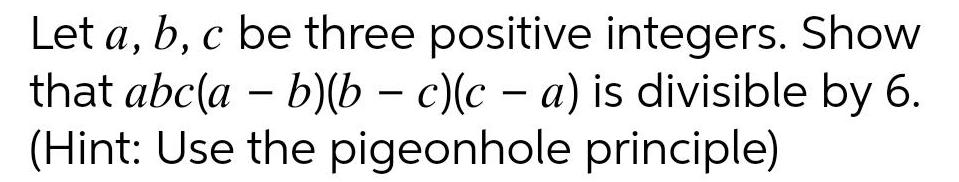
Algebra
Complex numbersLet a, b, c be three positive integers. Show that abc(a - b)(b − c)(c − a) is divisible by 6. (Hint: Use the pigeonhole principle)

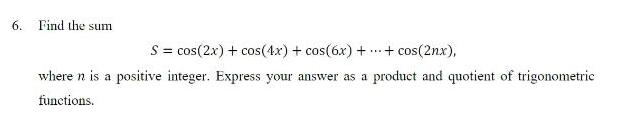
Algebra
Complex numbersFind the sum
S = cos(2x) + cos(4x) + cos(6x) + ... + cos(2nx),
where n is a positive integer. Express your answer as a product and quotient of trigonometric functions.

Algebra
Complex numbersA hospital records the number of floral deliveries its patients receive each day. For a two-week period, the records show
15, 27, 26, 24, 18, 21, 26, 19, 15, 28, 25, 26, 17, 23
Use a three-period moving average and report the MAE (Mean Absolute Error) for the period of forecasting. Use 2 numbers after thendecimal point.


Algebra
Complex numbers1 Write down the first 10 terms of the Fibonacci sequence.
2 Give a recursive definition for this sequence.
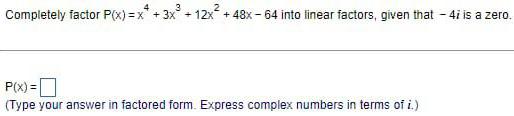
Algebra
Complex numbersCompletely factor P(x)=x^4 + 3x^3 + 12x^2 +48x-64 into linear factors, given that - 4i is a zero.
P(x) =
(Type your answer in factored form. Express complex numbers in terms of i.)

Algebra
Complex numbersFind an nith-degree polynomial function with real coefficients satisfying the given conditions. If you are using a graphing utility, use it to grach the function and verify the real zeros and the given function w
n=3;
2 and 2i are zeros
f(1)=5
f(x)=
(Type an expression using x as the variabile Simplify your answer)
Algebra
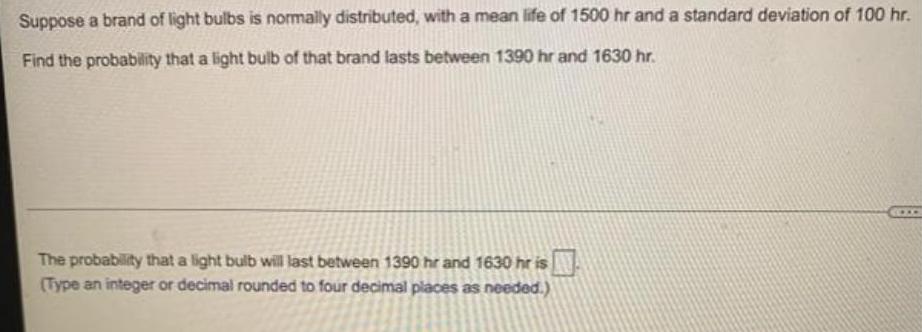
Complex numbersSuppose a brand of light bulbs is normally distributed, with a mean life of 1500 hr and a standard deviation of 100 hr.
Find the probability that a light bulb of that brand lasts between 1390 hr and 1630 hr.
The probability that a light bulb will last between 1390 hr and 1630 hr is

Algebra
Complex numbersConsider the following autonomous DE.
y' = 4(y - 1)^2(y - 3)
Choose all correct answers.
There are two critical points.
If y(1) = 4, then the solution is an increasing function.
One critical point is semi-stable.
y = 3 is a solution.
One critical point is a repeller.
If y(0) = 2, then lim y(x) = 3
One critical point is an attractor.

Algebra
Complex numbersA small craft in Lake Ontario sends out a distress signal. The coordinates of the boat in trouble are (8, 10). The Coast Guard's Moonlight II (rescue boat) is at the coordinates (18, 19), and the Coast Guard's Moonlight IV is at coordinates (-14,9). Which Coast Guard boat is closer to the distressed craft?
Moonlight II
Moonlight IV
Neither. They are equally far away.
Algebra
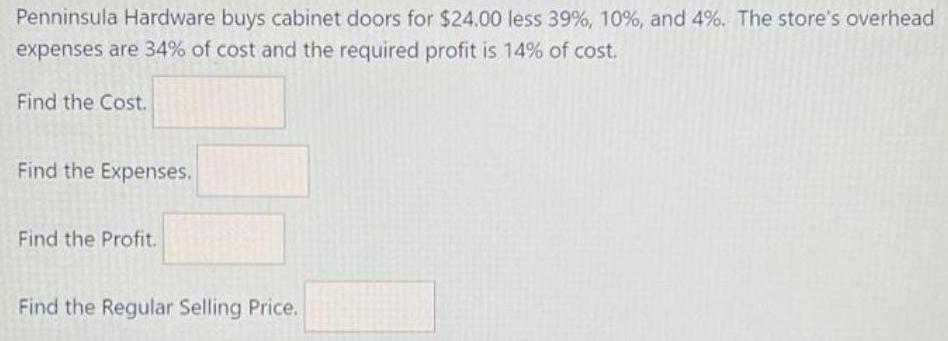
Complex numbersPenninsula Hardware buys cabinet doors for $24.00 less 39%, 10 %, and 4%. The store's overhead
expenses are 34% of cost and the required profit is 14% of cost.
Find the Cost.
Find the Expenses.
Find the Profit.
Find the Regular Selling Price.

Algebra
Complex numbersA ship leaves its port and sails on a bearing of N36°20'E, at speed 25.4 mph. Another ship leaves the same port at the same time and sails on a bearing of S53°40'E, at speed 18.7 mph.
How far apart are the ships after 4 hours? ...miles
(Round to the nearest integer as needed.)

Algebra
Complex numbersConvert to an exponential equation.
log 0.1 = -1
The equivalent equation is.
(Type in exponential form.)

Algebra
Complex numbersFind the product of the complex numbers. Leave the answer in polar form.
Z₁ = cos3π/4 +i sin 3π/4
Z₂ = cos 2π/3 +isin 2π/3

Algebra
Complex numbersFind a polynomial with real coefficients of the specified degree that has the given zeros.
Degree 3; zeros: -2, and -4-i

Algebra
Complex numbersThis question is about the fox and rabbit population in a forest. If the fox population increases the rabbit populatio starts to decrease since each fox eats 0.075 rabbits in day. On the other hand, the decreasing population of the rabbi results in decreased fox population. Therefore number of rabbits in the forest will affect the fox population: The fo population is increased by the 10% of rabbit population in each day. The daily birth rate for rabbits is given by 20% Assume that initially there are 10 rabbits and 5 foxes.
a. Using the information given find the rabbit population after one month.
b. Determine the steady state populatiouns
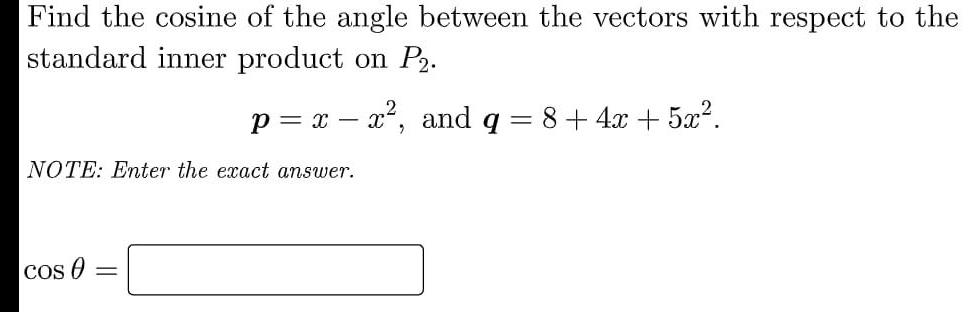
Algebra
Complex numbersFind the cosine of the angle between the vectors with respect to the standard inner product on P2.
p= x - x², and q = 8 + 4x + 5x².
NOTE: Enter the exact answer.

Algebra
Complex numbersfind three additional polar represntation of the point (0, 7pi/6) using -2pi< θ <2pi

Algebra
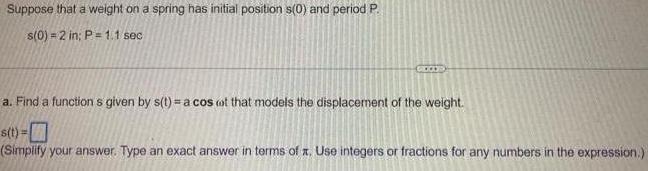
Complex numbersSuppose that a weight on a spring has initial position s(0) and period P.
s(0) = 2 in; P = 1.1 sec
a. Find a function s given by s(t)= a cost that models the displacement of the weight.
s(t)=0
(Simplify your answer. Type an exact answer in terms of x. Use integers or fractions for any numbers in the expression.)

Algebra
Complex numbersThe position (m)-time(sec) data for a moving body is given: 0 0.25 0.5 0.75 1.25 1.5 13 10.2 17.2 26.2 33.1 39.1 Approximate the velocity at time t = 1.25 sec by using central differences (b) Approximate the acceleration at time t = 1.25 sec by using central differences
Algebra
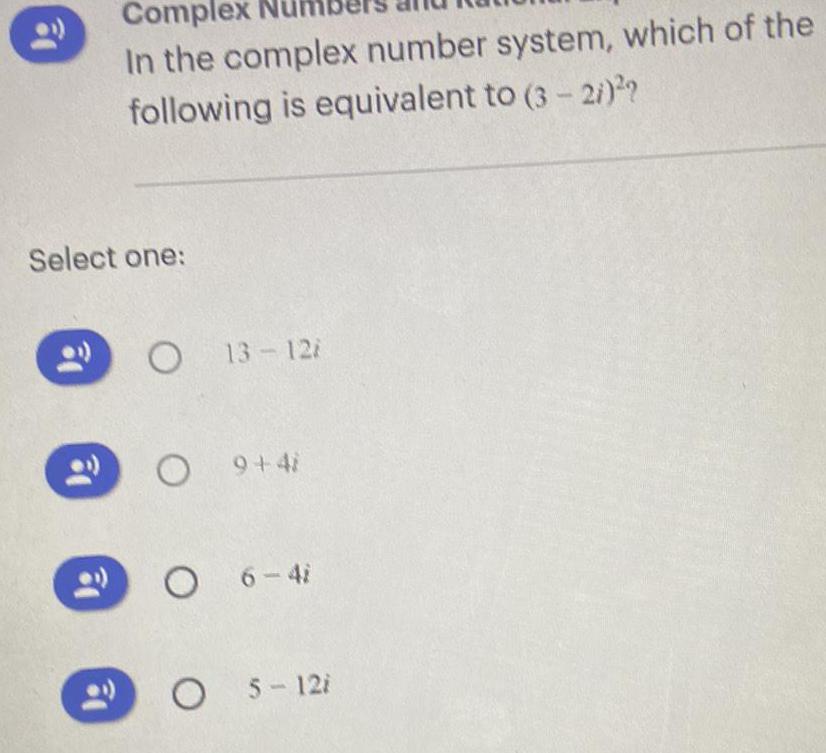
Complex numbersComplex In the complex number system, which of the following is equivalent to (3-2i)²?
Select one:
13-12i
9+4i
6-4i
5-12i
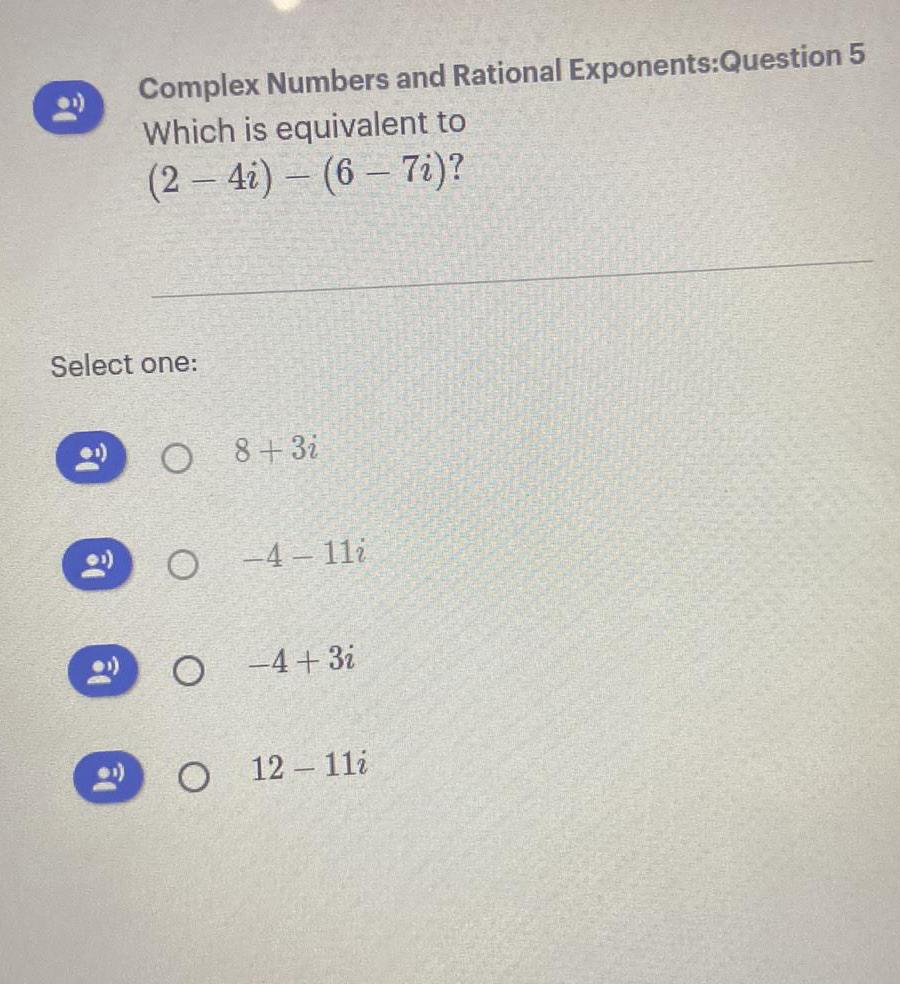
Algebra
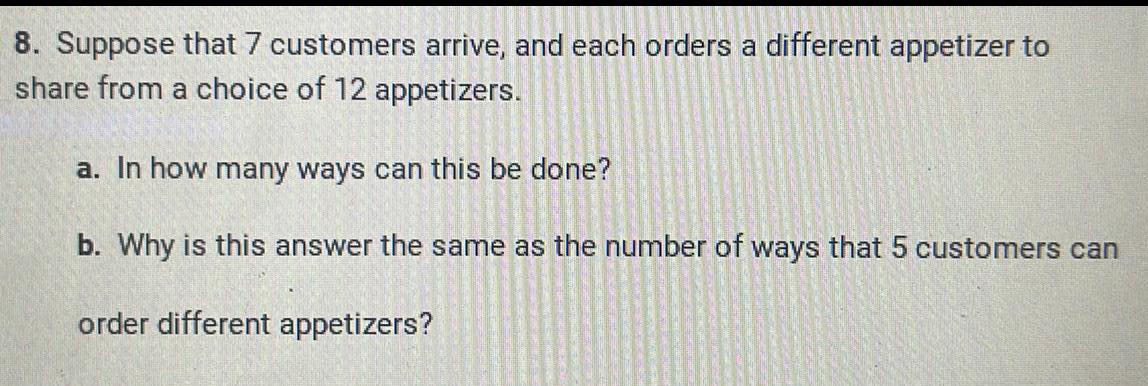
Complex numbersSuppose that 7 customers arrive, and each orders a different appetizer to share from a choice of 12 appetizers.
a. In how many ways can this be done?
b. Why is this answer the same as the number of ways that 5 customers can order different appetizers?

Algebra
Complex numbersSuppose you roll two standard number cubes.
What is the theoretical probability of getting a sum of 7?
What is the sample space?
How many outcomes are there?

Algebra
Complex numbersLet A be a (mx n) matrix. Is it possible to describe the range of A as the null spaces of another matrix? If so, how would you do it? Provide solid arguments and a concrete example.

Algebra
Complex numbersA food processing facility froze 45,000 kg of blueberries in a blast freezer to -20 °C before being packaged. How much heat was removed from the blueberries if the starting temperature was 18°C?
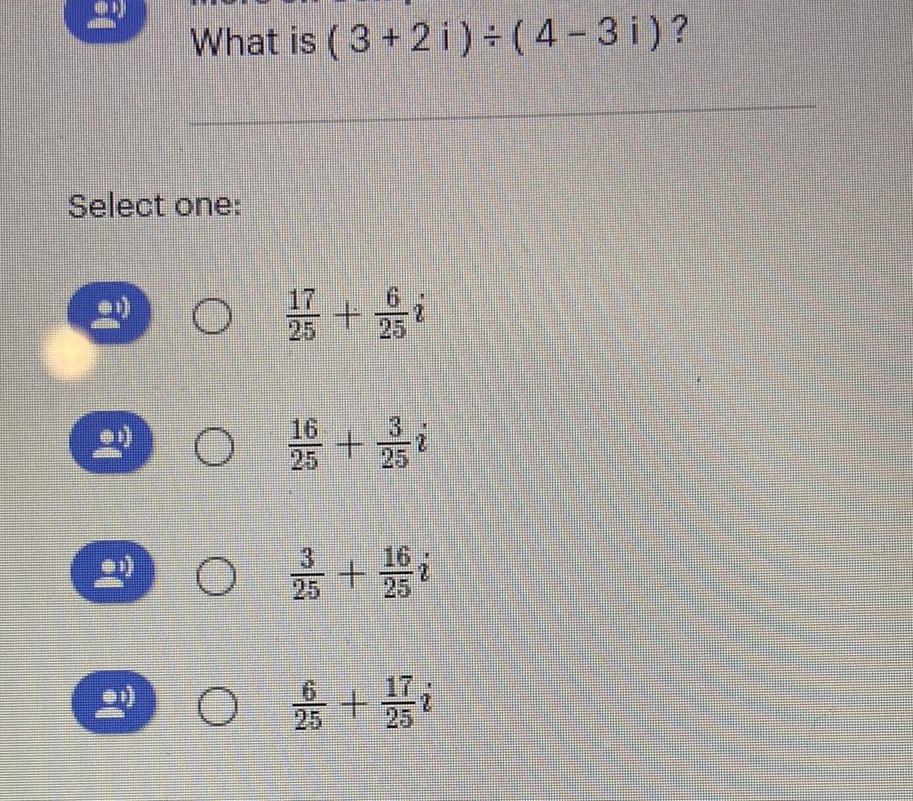
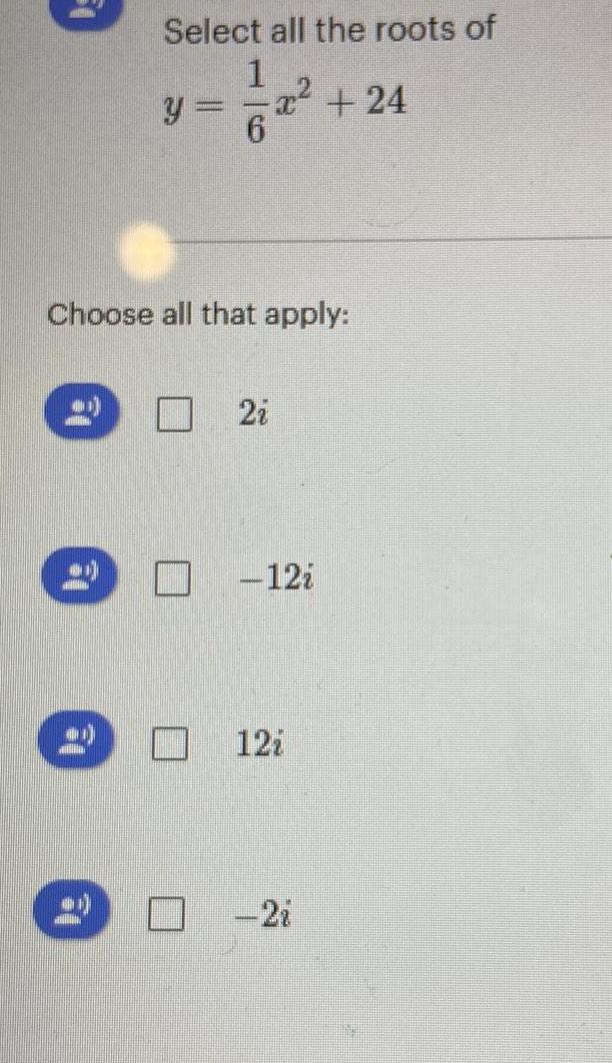
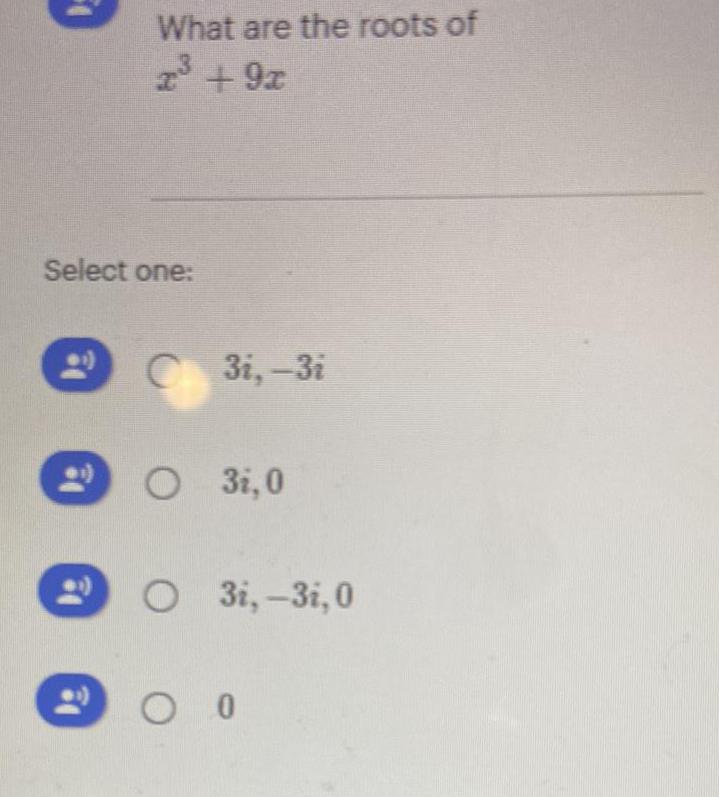
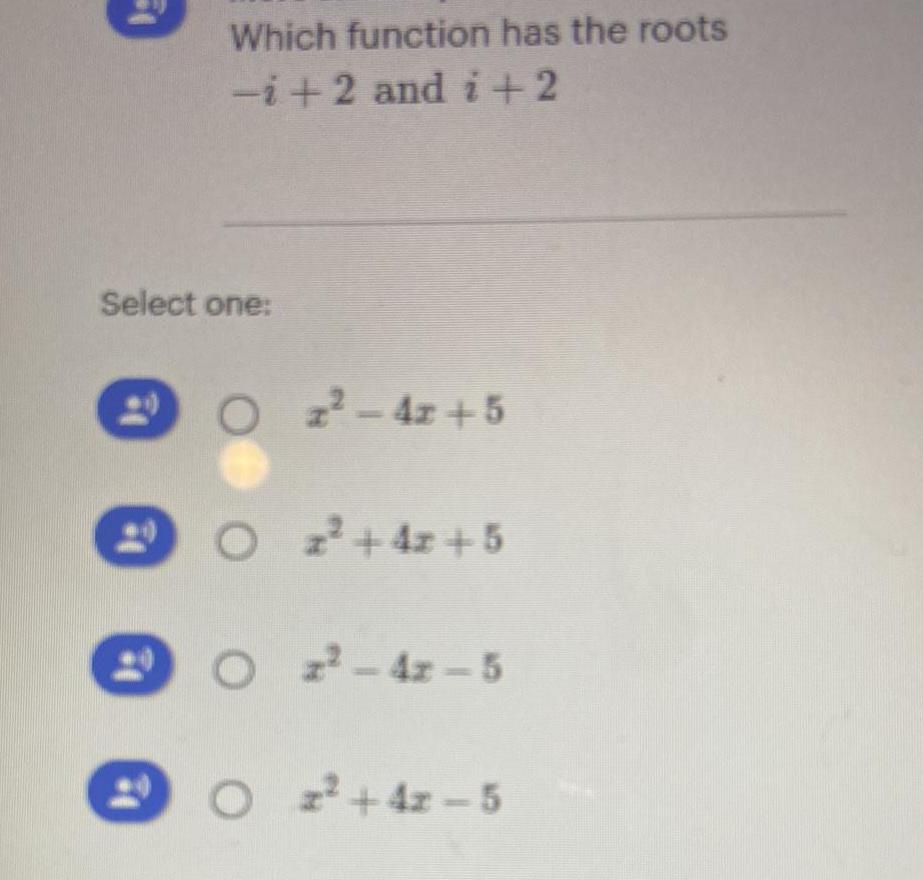
Algebra
Complex numbersWhich function has the roots
-i +2 and i + 2
Select one:
z²-4x+5
z² + 4z +5
z²-42-5
z² +42-5
Algebra
Complex numbersIs it possible for a sixth degree polynomial function with integer coefficients to have no real zeroes?
Choose all that apply:
Yes
No
Algebra
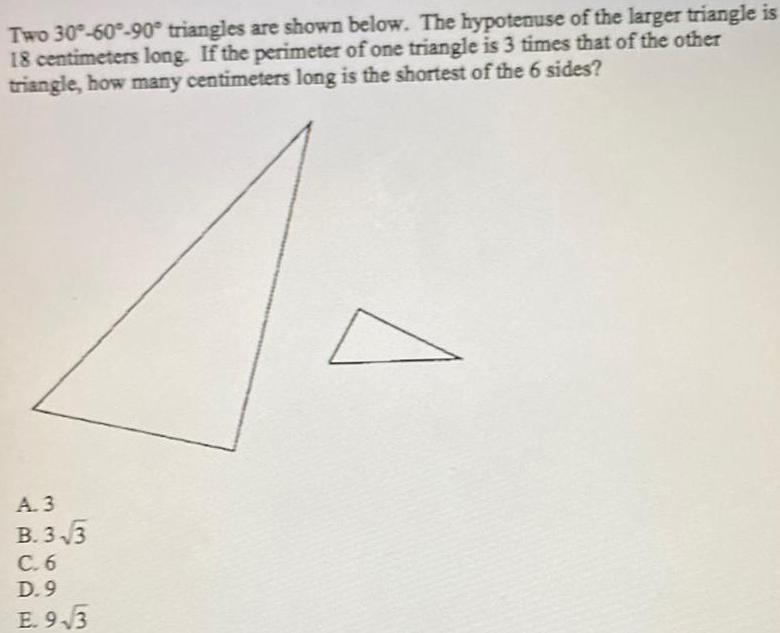
Complex numbersTwo 30°-60°-90° triangles are shown below. The hypotenuse of the larger triangle is 18 centimeters long. If the perimeter of one triangle is 3 times that of the other triangle, how many centimeters long is the shortest of the 6 sides?
A. 3
B.3√3
C. 6
D.9
E. 9-√3

Algebra
Complex numbersThis program find the sum of the
series 1!/1+2!/2+3!/3+4!/4+5!/5 using the function.
S = F(1)/1+F(2)/2 + F(3)/3+F(4)/4+F(5)/5
Algebra
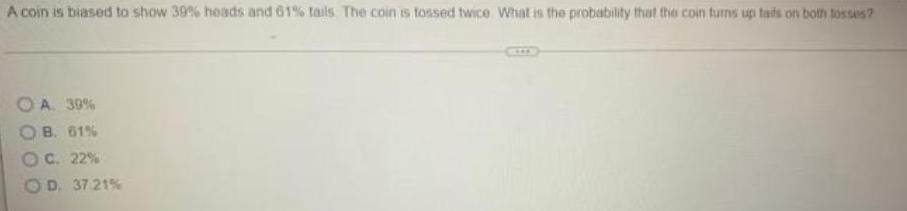
Complex numbersA coin is biased to show 39% heads and 61% tails. The coin is tossed twice. What is the probability that the coin turns up tails on both tosses?
A. 39%
B. 61%
C. 22%
D. 37.21%

Algebra
Complex numbersExperts fear that without conservation efforts, an endangered species could disappear from the wild by 2022. Just one hundred years ago, there were at least 100,000 of this endangered species. By 2010, the estimated world population of this endangered species was 800. The bar graph shows the estimated world population of this endangered species for selected years from 1970 through 2010. Also shown is a polynomial function, with its graph, that models the data. Use this information to complete parts a through c. Click the icon to view the bar graph and the graph of the polynomial function.
a. Find and interpret f(40).
In the year 2010, the polynomial estimates the population of this species to be 844. (Round to the nearest integer as needed.)
Identify this information as a point on the graph of f. (Type an ordered pair. Do not use commas in the individual coordinates.)


Algebra
Complex numbersUse the leading coefficient test to determine the end behavior of the graph of the given polynomial function.
f(x) = 4x⁷ - 2x⁵ + 4x +2
A. Rises left & falls right.
B. Rises left & rises right.
C. Falls left & falls right.
D. Falls left & rises right.
E. None of the above.

Algebra
Complex numbersA ship is sailing east and sight as partially submerged rock at a bearing of 32 degrees 12 minutes. The ship sails for 37 miles and then the rock is at a b earing of 302 degrees 12 minutes. How far was the rock from the ship at the first sighting?

Algebra
Complex numbersThe profit of a company, in dollars, is the difference between the company's revenue and cost. The cost, C(x), and revenue, R(x), are functions for a particular company. The x represents the number of items produced and sold to distributors.
C(x)=2200 + 40x
R(x)=800x-x²
a) Determine the maximum profit of the company.
b) Determine the number of items that must be produced and sold to obtain the maximum profit.

Algebra
Complex numbersThe parallel sides of the trapezoidal lot measure 160 m and 240 m are 40 m apart Find the distance of the dividing line from the 160m line parallel to the 2 sides that will divide the trapezoid into 2 equal parts.
a. 23.45.
B. 25.33
C. 21.98.
D. 22.34.
B. Find the length of this dividing line
a. 203.96.
B.241. 33
C. 221.56.
D. 222.22
Algebra
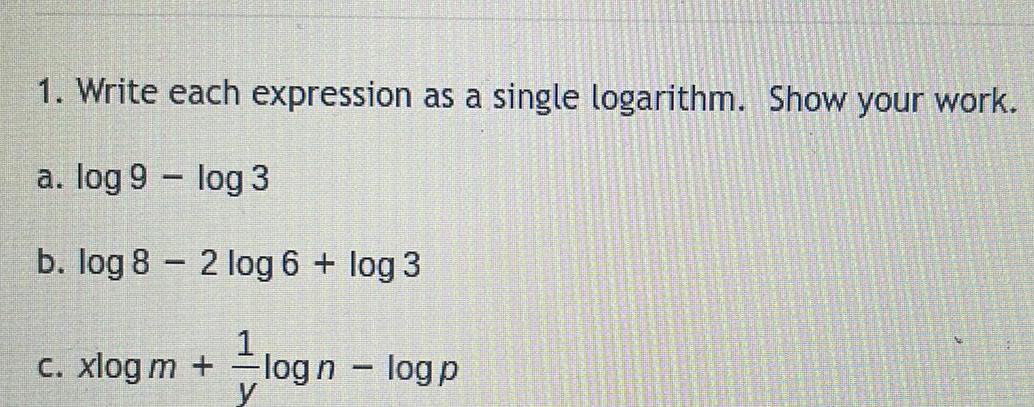
Complex numbers1. Write each expression as a single logarithm. Show your work.
a. log 9 - log 3
b. log 82 log 6 + log 3
c. xlog m +
¹ logn - logp

Algebra
Complex numbersFind all the real square roots of -9/16.
Select one:
a. -3/4 and 3/4
b. no real root
c.-3/4
d. 81/256

Algebra
Complex numbersFind the quotient of the complex numbers. Leave your answer in polar form.
Z2
N
Z₁
21
22
*
2₁ = 6 (cos+ i sin ) 22=7 [cos + i sin
5
5
11
11
11
-
expression T