Matrices & Determinants Questions and Answers

Algebra
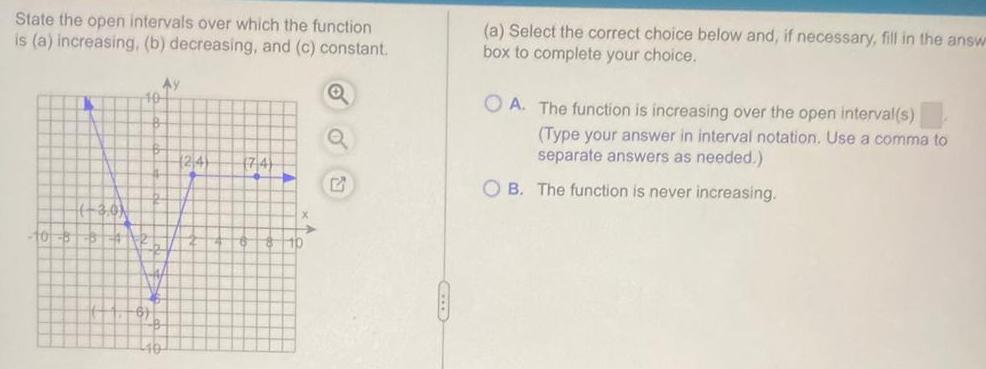
Matrices & DeterminantsState the open intervals over which the function is a increasing b decreasing and c constant Q 10 40 Ay 124 74 E CELLE a Select the correct choice below and if necessary fill in the answ box to complete your choice OA The function is increasing over the open interval s Type your answer in interval notation Use a comma to separate answers as needed OB The function is never increasing
Algebra
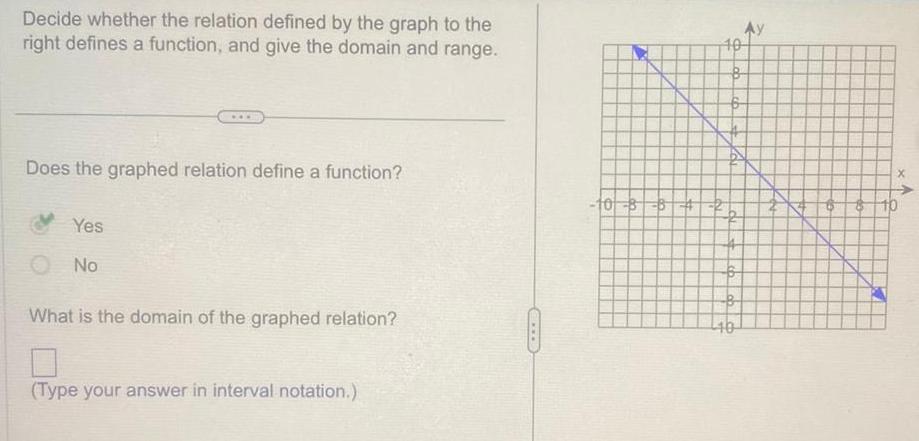
Matrices & DeterminantsDecide whether the relation defined by the graph to the right defines a function and give the domain and range Does the graphed relation define a function Yes No What is the domain of the graphed relation Type your answer in interval notation 10 884 10 B 6 B B 40 2 10 67 X
Algebra
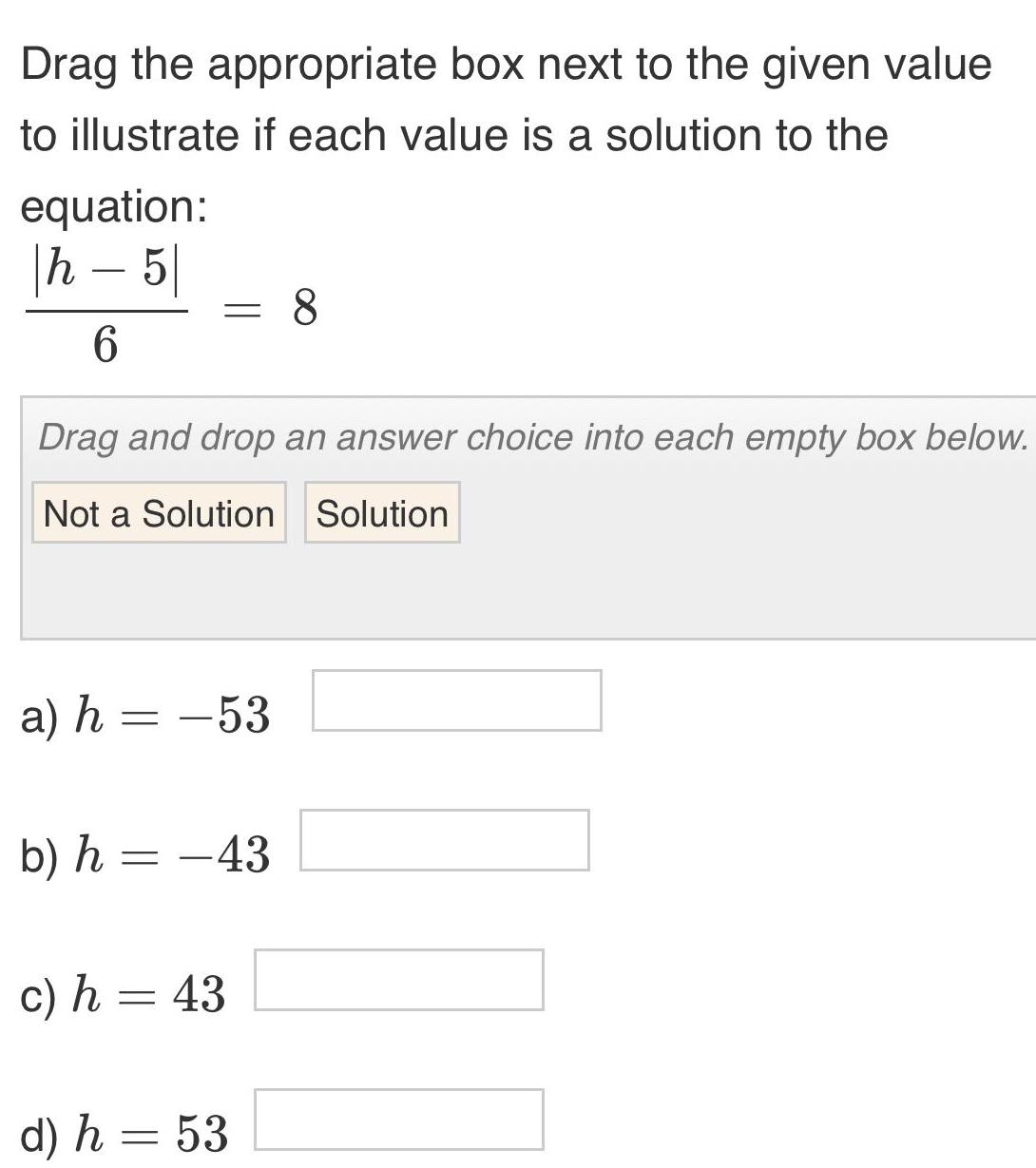
Matrices & DeterminantsDrag the appropriate box next to the given value to illustrate if each value is a solution to the equation h5 6 Drag and drop an answer choice into each empty box below Not a Solution Solution a h 53 b h 43 c h 43 8 d h 53

Algebra
Matrices & DeterminantsAn nth degree polynomial p satisfies the following conditions p is of degree 4 is a root of P 7i is a root of p p 3 2900 Determine an nth degree polynomial that satisfies the aforemention P x

Algebra
Matrices & DeterminantsAn nth degree polynomial p satisfies the following conditions p is of degree 3 1 is a zero with multiplicity 1 of p 5 is a zero with multiplicity 1 of p is a zero with multiplicity 1 of p p 2 84 T Determine an nth degree polynomial that satisfies the aforementioned conditions P T

Algebra
Matrices & DeterminantsAn nth degree polynomial p satisfies the following conditions p is of degree 3 6 is a zero with multiplicity 2 of p 4 is a zero with multiplicity 1 of p p 3 162 Determine an nth degree polynomial that satisfies the aforementioned conditions P x
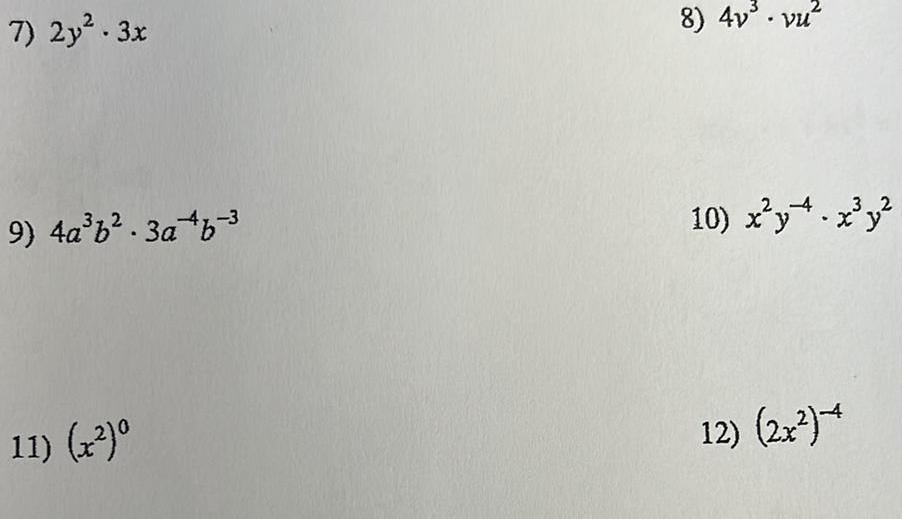


Algebra
Matrices & Determinants6 Which is the inverse function of f x x 9 A B f x x 9 f x x 12 c f x D f x x 9 x 1

Algebra
Matrices & DeterminantsK The game of Scrabble has 100 tiles The diagram shows the number of tiles for each letter and the letter s point value One tile is drawn from Scrabble s 100 tiles Find each probability a Find the probability of selecting a U b Find the probability of not selecting a U Part 1 of 2 a The probability of selecting a U is Type an integer or a simplified fraction HW Score 0 0 of O Points 0 of 1 A F2K1 B 2 G3 L Q V M 6 W2 C 2 H D 4 N S X E 12 JOT Y 6 2 UZ how
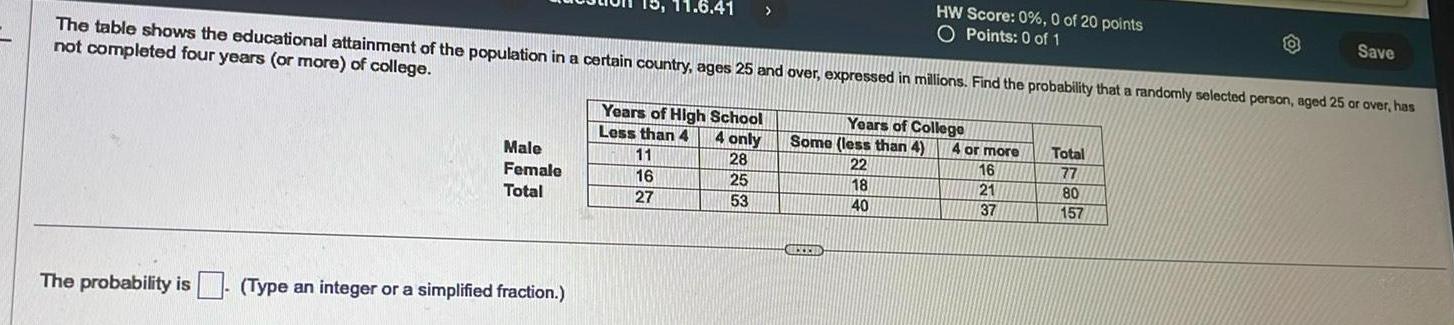
Algebra
Matrices & DeterminantsMale Female Total 11 6 41 The probability is Type an integer or a simplified fraction The table shows the educational attainment of the population in a certain country ages 25 and over expressed in millions Find the probability that a randomly selected person aged 25 or over has not completed four years or more of college Years of High School Less than 4 4 only 11 28 16 25 27 53 HW Score 0 0 of 20 points O Points 0 of 1 Years of College Some less than 4 22 18 40 RECEI 4 or more 16 21 37 Total 77 80 157 Save
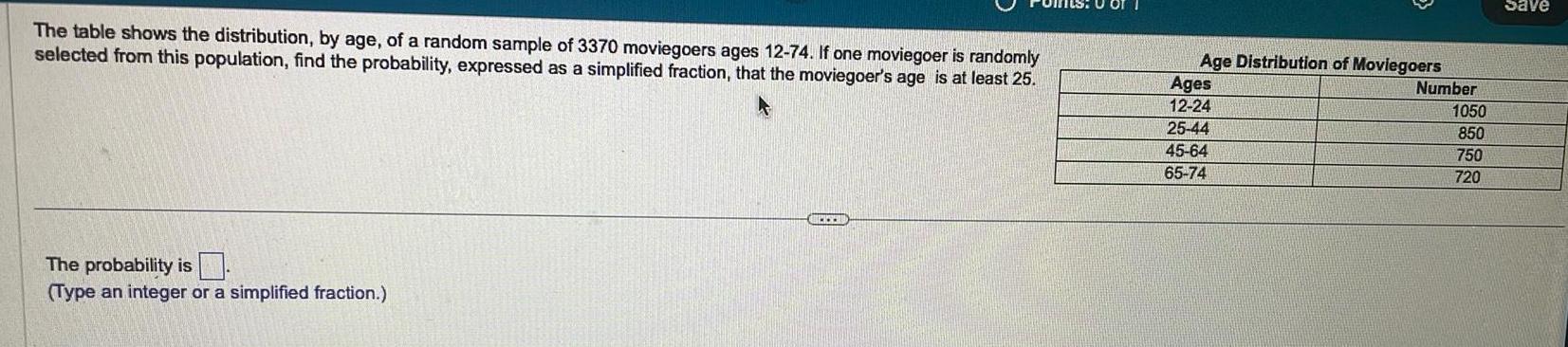
Algebra
Matrices & DeterminantsThe table shows the distribution by age of a random sample of 3370 moviegoers ages 12 74 If one moviegoer is randomly selected from this population find the probability expressed as a simplified fraction that the moviegoer s age is at least 25 The probability is Type an integer or a simplified fraction Age Distribution of Moviegoers Ages 12 24 25 44 45 64 65 74 Number 1050 850 750 720 Save

Algebra
Matrices & DeterminantsQuestion 10 11 4 21 The probability of getting one tail is Type an integer or a simplified fraction Points 0 of 1 A fair coin is tossed three times in succession The set of equally likely outcomes is HHH HHT HTH THH HTT THT TTH TTT Find the probability of getting exactly one tail
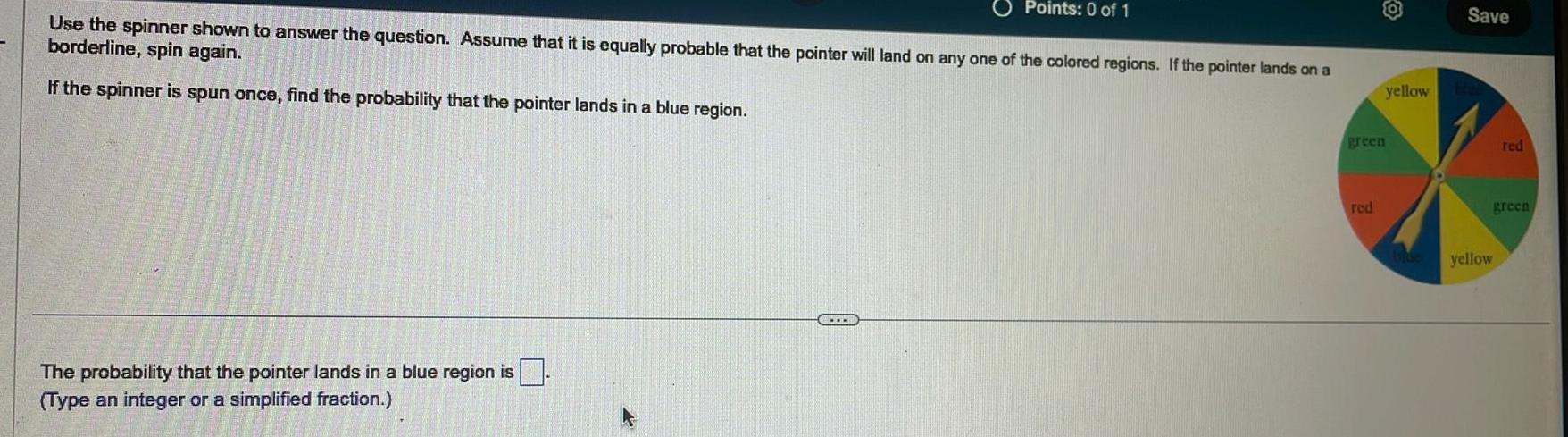
Algebra
Matrices & DeterminantsPoints 0 of 1 Use the spinner shown to answer the question Assume that it is equally probable that the pointer will land on any one of the colored regions If the pointer lands on a borderline spin again If the spinner is spun once find the probability that the pointer lands in a blue region The probability that the pointer lands in a blue region is Type an integer or a simplified fraction green red yellow Save yellow red green
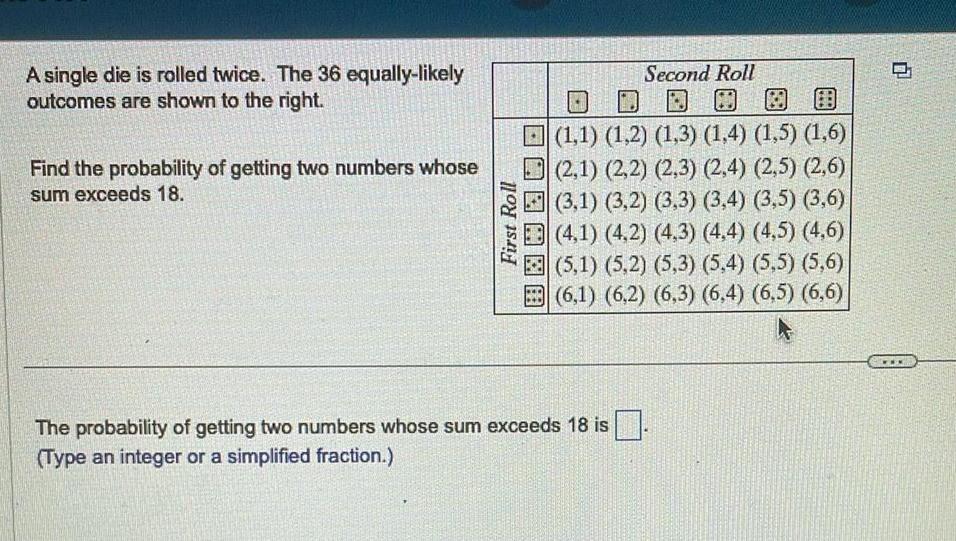
Algebra
Matrices & DeterminantsA single die is rolled twice The 36 equally likely outcomes are shown to the right Find the probability of getting two numbers whose sum exceeds 18 First Roll Second Roll 1 1 1 2 1 3 1 4 1 5 1 6 2 1 2 2 2 3 2 4 2 5 2 6 3 1 3 2 3 3 3 4 3 5 3 6 4 1 4 2 4 3 4 4 4 5 4 6 5 1 5 2 5 3 5 4 5 5 5 6 6 1 6 2 6 3 6 4 6 5 6 6 The probability of getting two numbers whose sum exceeds 18 is Type an integer or a simplified fraction
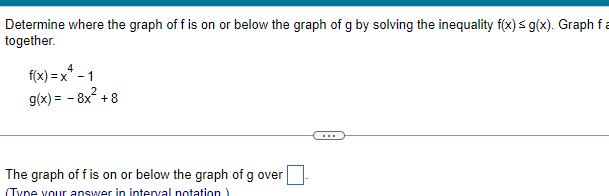
Algebra
Matrices & DeterminantsDetermine where the graph of f is on or below the graph of g by solving the inequality f x g x Graph fa together f x x 1 g x 8x 8 The graph of f is on or below the graph of g over Type your answer in interval notation

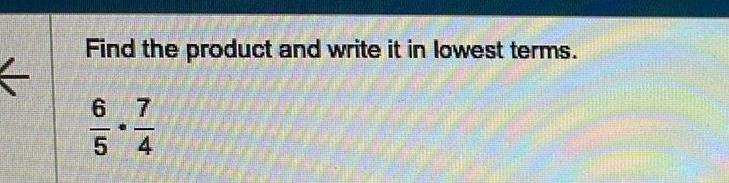
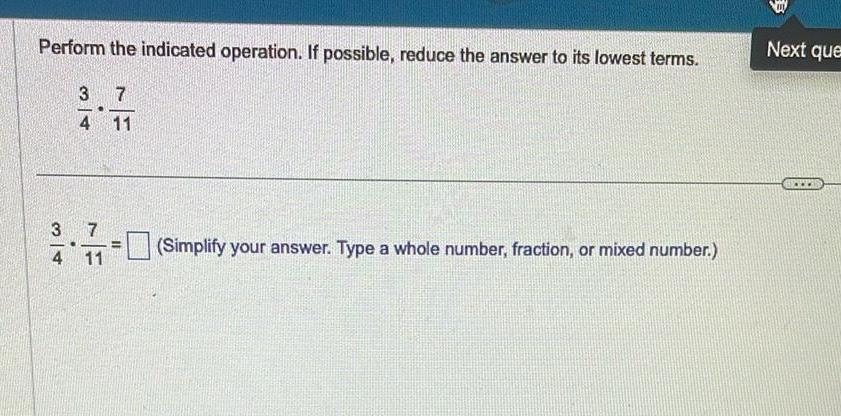
Algebra
Matrices & DeterminantsPerform the indicated operation If possible reduce the answer to its lowest terms 3 7 4 11 3 4 7 11 Simplify your answer Type a whole number fraction or mixed number III Next que
Algebra
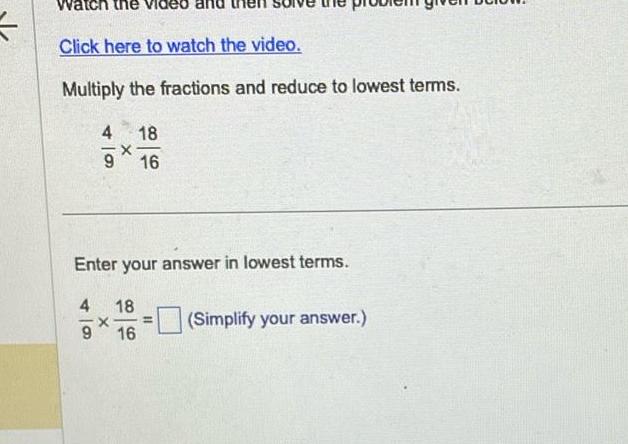
Matrices & DeterminantsClick here to watch the video Multiply the fractions and reduce to lowest terms 4 4 9 9 X Enter your answer in lowest terms 18 16 18 16 Simplify your answer
Algebra
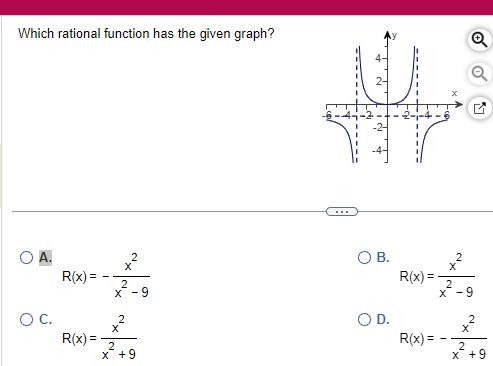
Matrices & DeterminantsWhich rational function has the given graph A O C R x R x x 2 X 2 x 9 x 2 X 2 X 9 NA O B O D R x 2 2 x 9 R x 2 x 2 X 9
Algebra
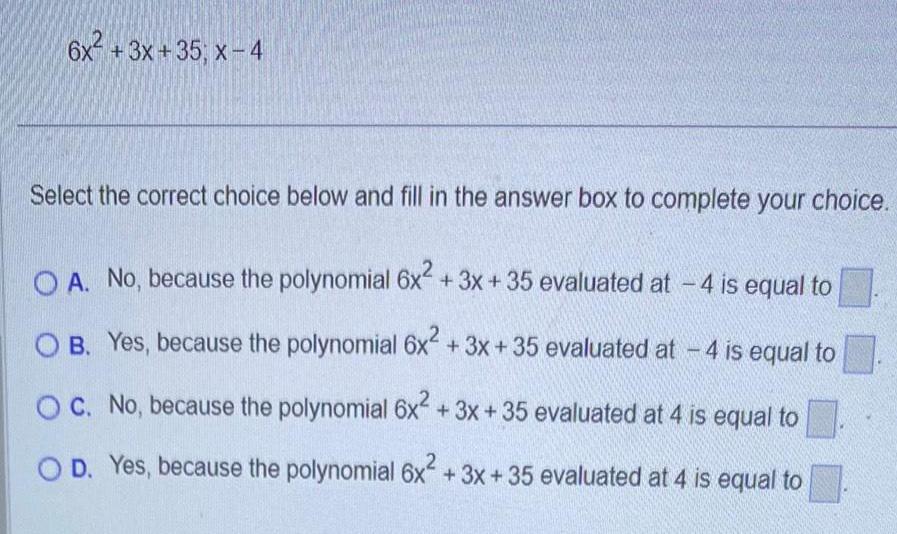
Matrices & Determinants6x 3x 35 x 4 Select the correct choice below and fill in the answer box to complete your choice OA No because the polynomial 6x 3x 35 evaluated at 4 is equal to OB Yes because the polynomial 6x 3x 35 evaluated at 4 is equal to OC No because the polynomial 6x 3x 35 evaluated at 4 is equal to OD Yes because the polynomial 6x 3x 35 evaluated at 4 is equal to

Algebra
Matrices & DeterminantsFind the series interval of convergence and within this interval the sum of the series as a function of x n 0 8 The interval of convergence is Type an exact answer using radicals as needed Type your answer in interval notation Within the interval 8 8 4 S

Algebra
Matrices & Determinantsoblem 9 Consider the following matrix Find a matrix P that diagonalizes A 0 1 A 1 1 1 0 G 0 1 1 1 1 1 0 B 0 0 0 1 01 D 0 0 1 1 E 0 1 1 0

Algebra
Matrices & Determinantsoblem 2 a Find the determinant of the following matrix A 1 2 B 02 3 10 10 Iww 4 1 2 3 3 2 2 NOTM om mo 1 0 1 3 b Find the determinant of the following matrix 0 0 3 3 0 COO 0 0 0 0 0 0 4 0 3 4 2 4 0 2 Hint Do a row operation first

Algebra
Matrices & DeterminantsProblem 8 Consider the following matrix Given that 0 is an eigenvalue of A find a basis for the eigenspace corresponding to 0 00 00 00 00 00 06 D A G AB B
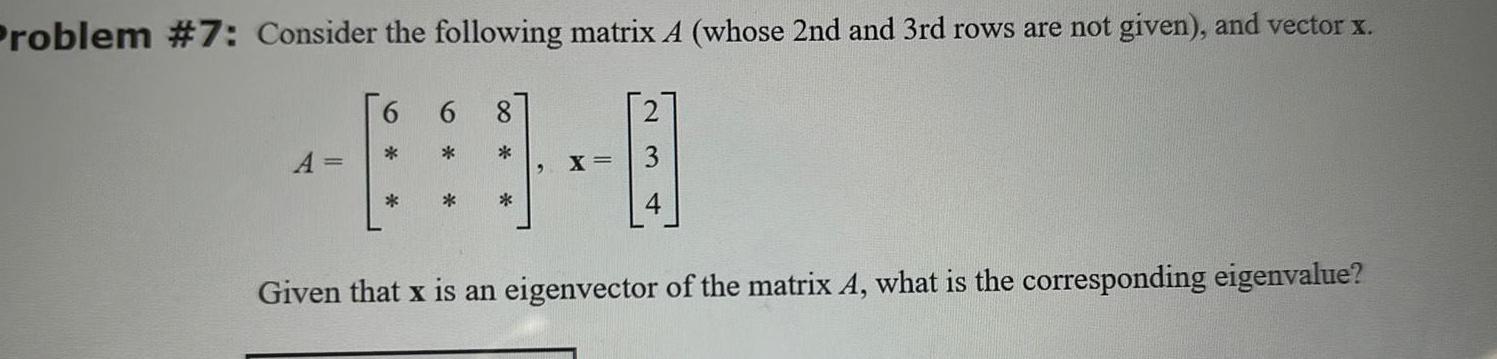
Algebra
Matrices & DeterminantsProblem 7 Consider the following matrix A whose 2nd and 3rd rows are not given and vector x A 6 8 X Given that x is an eigenvector of the matrix A what is the corresponding eigenvalue

Algebra
Matrices & DeterminantsProblem 10 Suppose that a 2 2 matrix A has eigenvalues 1 and 0 with corresponding eigenvectors H respectively Find 4 and
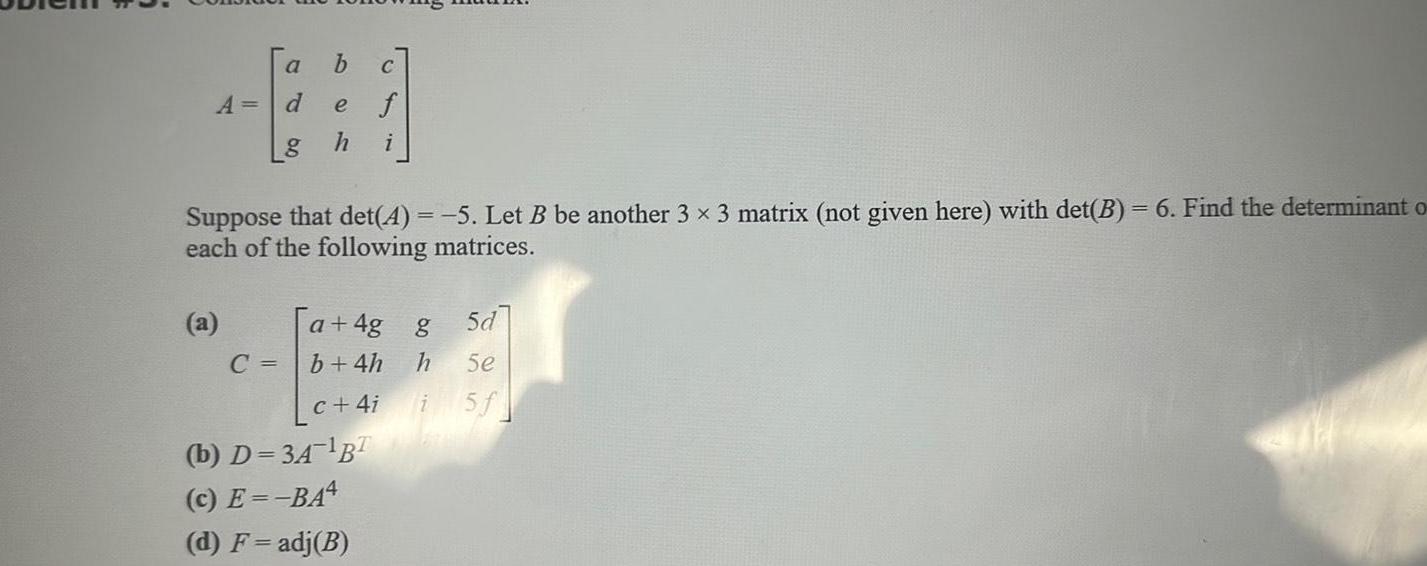
Algebra
Matrices & DeterminantsA a d L8 a b C C e h Suppose that det 4 5 Let B be another 3 x 3 matrix not given here with det B 6 Find the determinant o each of the following matrices f i a 4g b 4h c 4i b D 3A BT c E BA4 d F adj B 5d g h 5e i 5f

Algebra
Matrices & DeterminantsProblem 5 Let A and B be nxn matrices Which of the following statements are always true i If det A det B then det A B 0 ii If A and B are symmetric then the matrix AB is also symmetric iii If A and B are skew symmetric then the matrix AT B is also skew symmetric A ii only B i and iii only C iii only D all of them E i and ii only F none of them G ii and iii only H i only
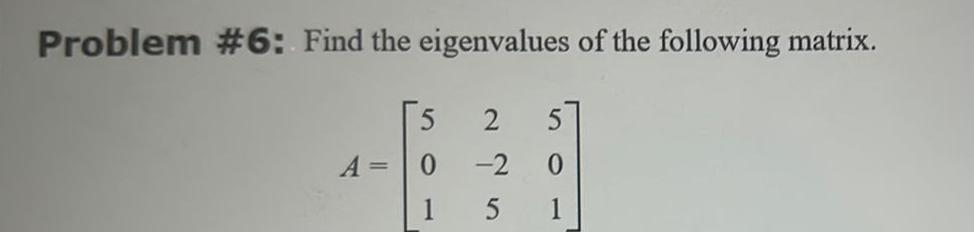
Algebra
Matrices & DeterminantsProblem 6 Find the eigenvalues of the following matrix 5 A 0 1 2 5 2 0 5 1
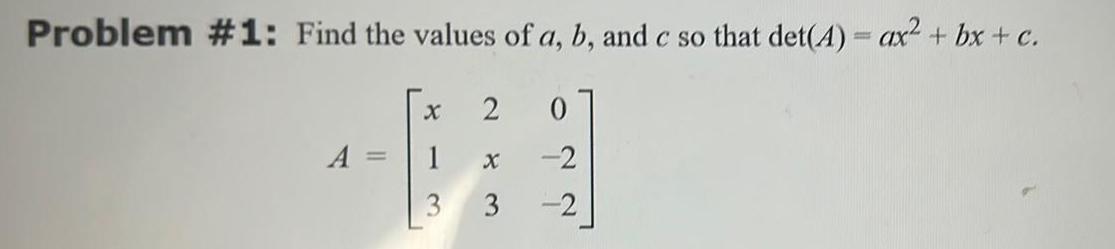
Algebra
Matrices & DeterminantsProblem 1 Find the values of a b and c so that det A ax bx c A 1 3 2 3 0 2 2

Algebra
Matrices & DeterminantsElisha wants to buy book marks to give to her teachers she has a total of 60 to spend Each book mark costs 6 00 and she wants to also buy her mom a cookbook that costs 23 00 Write and solve an inequality to find the greatest number of book marks she can buy Click on show your work to type or write your work The greatest number of bookmarks she can buy is enter number only Tyno a response

Algebra
Matrices & DeterminantsFind all complex zeros of the polynomial function Give exact values List multiple zeros as necessary f x x 14x 44x All complex zeros are Simplify your answer Type an exact answer using radicals and i as needed Use a comma to separate answers as needed


Algebra
Matrices & Determinants6 Sam spent 30 minutes studying for his Math test 15 minutes studying for a Reading test 45 minutes studying for a Science test and 20 minutes studying for an English test What percentage of her study time was spent on Reading

Algebra
Matrices & Determinants1 If 45 of the students in a school are girls and there are 200 students in the school how many are girls

Algebra
Matrices & DeterminantsExercise 8 5 4 Take the 2 x 2 matrix A and consider the matrix A XI where A is a variable scalar and I is the identity matrix Compute det A XI Using the 2 x 2 formula Solve for A when setting this determinant equal to zero Now for each solution solve the equation Ar Ar for x You have just found your first eigen pair We ll talk more about these in a few weeks
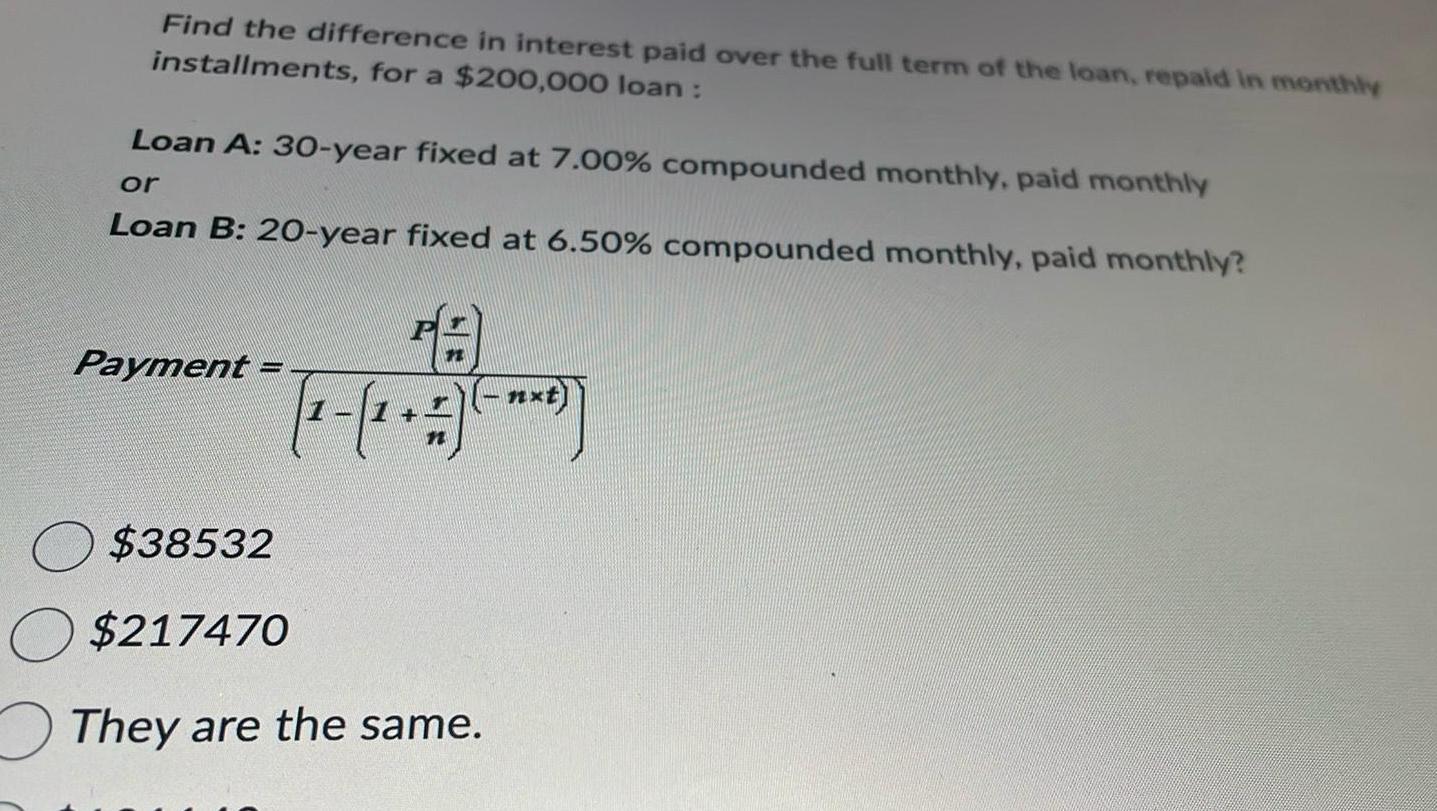
Algebra
Matrices & DeterminantsFind the difference in interest paid over the full term of the loan repaid in monthly installments for a 200 000 loan Loan A 30 year fixed at 7 00 compounded monthly paid monthly or Loan B 20 year fixed at 6 50 compounded monthly paid monthly Payment P 7 1 O 38532 O 217470 They are the same
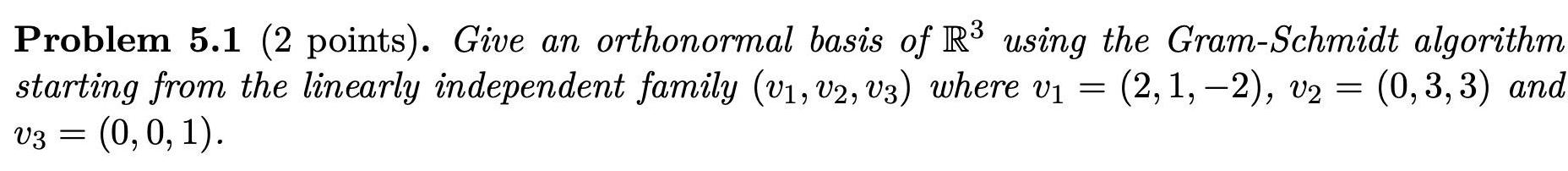
Algebra
Matrices & DeterminantsProblem 5 1 2 points Give an orthonormal basis of R using the Gram Schmidt algorithm starting from the linearly independent family v1 V2 V3 where v 2 1 2 v2 0 3 3 and V3 0 0 1

Algebra
Matrices & DeterminantsGiven use the reduced row echelon form above to solve the system f necessary parametrize your answer using the free variables of the system 1 8 0 0 1 1 1 2 ON 0 0 0 x 2z x y 2z 1 0 2 2 0 1 4 5 00 0 0 0 2
Algebra
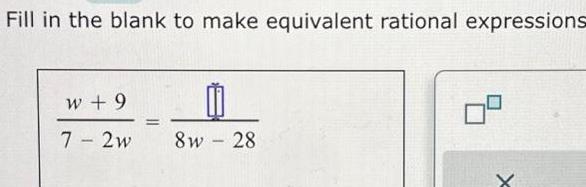
Matrices & DeterminantsFill in the blank to make equivalent rational expressions w 9 7 2w 8w 28
Algebra
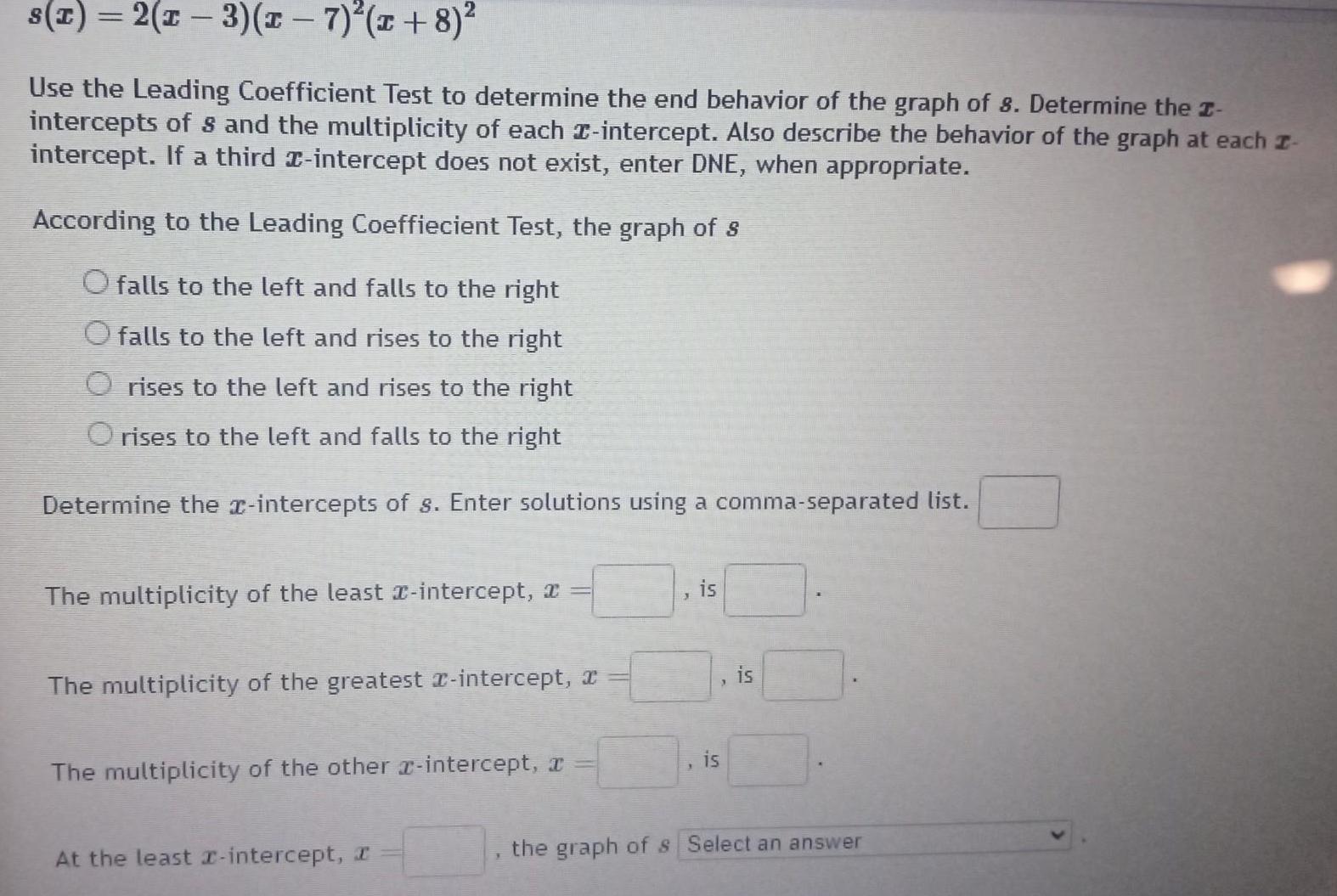
Matrices & Determinantss x 2 x 3 x 7 x 8 Use the Leading Coefficient Test to determine the end behavior of the graph of 8 Determine the I intercepts of 8 and the multiplicity of each intercept Also describe the behavior of the graph at each z intercept If a third x intercept does not exist enter DNE when appropriate According to the Leading Coeffiecient Test the graph of s O falls to the left and falls to the right falls to the left and rises to the right Orises to the left and rises to the right O rises to the left and falls to the right Determine the x intercepts of s Enter solutions using a comma separated list The multiplicity of the least x intercept x The multiplicity of the greatest intercept a The multiplicity of the other intercept x At the least x intercept I is is is the graph of s Select an answer

Algebra
Matrices & DeterminantsIve the following homogeneous system of linear equations x2 x3 3x4 9x5 x2 3x3 9x4 6x5 0 0 x3 3x4 4x5 0 he system has no solution demonstrate this by giving a row echelon form of the augmented matrix for th u can resize a matrix when appropriate by clicking and dragging the bottom right corner of the matrix me system has a unique solution he system has no solution he system has a unique solution he system has infinitely many solutions

Algebra
Matrices & DeterminantsA corporation creates a sinking fund in order to have 510 000 to replace some machinery in 10 years How much should be placed in this account at the end of each week if the annual interest rate is 3 2 compounded weekly Round your answers to the nearest cent How much interest would they earn over the life of the account Determine the value of the fund after 2 4 and 6 years 2 years 4 years 6 years es How much interest was earned during the third week of the 5th year
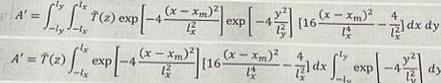
Algebra
Matrices & Determinantsx x A 1 2 xp 4 m exp 42 16 x Xm 1dx dy 1 T 2 exp 4 x 1m 11 4 x xm x xm 16 71dx exp 477 dx dy 1

Algebra
Matrices & DeterminantsEary Logic ve means lements of a set of previousely ements of the Now the following principle tells us that if a statement is proved true then we have simultaneously proved that its dual is true If s is a theorem about a Theorem 2 The principle of duality Boolean algebra then so is its dual s It is because of this principle that the statements in Theorem 1 look so similar Let us now see how to apply Boolean algebra methods to circuit design For this purpose we shall introduce the necessary mathematical terminology and ideas in the following section 3 3 BOOLEAN EXPRESSIONS In Unit 2 you learnt how a compound statement can be formed by combining some propositions P1 P2 Pn say with the help of logical connectives A V and Analogously while expressing circuits mathematically we identify each circuit in terms of some Boolean variables Each of these variables represents either a simple switch or an input to some electronic switch Definition Let B X V A 0 1 be a Boolean algebra A Boolean expression in variables X1 X2 xk say each taking their values in the set X is defined recursively as follows i Each of the variables x x2 xk as well as the elements O and I of the Boolean algebra B are Boolean expressions ii If X and X are previously definecl Boolean expressions then X A X2 X V X2 and X are also Boolean expressions For instance x A x3 is a Boolean expression because so are x and x3 Similarly because x V x2 is a Boolean expression so is x1 V x2 A x AX3 If X is a Boolean expression in n variables x x2 Xn say we write this as X X X X Each variable x and its complement x 1 i k is called a literal For example in the Boolean expression X X1 X2 X3 x1 V x2 x1 X3 there are three literals namely X1 X2 and x3 In the context of designing a circuit or redesigning a circuit with fewer electronic switches we need to consider techniques for minimising Boolean expressions In the process we shall be using the concepts defined below Definition A Boolean expression in k variables x x2 xk is called a minterm if it is of the form y A y2 A Ayki i ii a maxterm if it is of the form y Vy2 V Vyki where each yj is a literal i e it is either an x or an x for 1 i k and Vi y for i j Thus a minterm or a maxterm in k variables is a meet or a join respectively of exactly k distinct variables For example X A x2 and x V x2 is a minterm a maxterm respectively in the two variables X and x2 Definition A Boolean expression involving k variables is in disjunctive

Algebra
Matrices & Determinantslikely to turn around look menacingly at me and say Prove it What she or he really wants is to be convinced of my statement by some evidence In this case it would probably be a big physical push Convincing evidence is also what the world asks for before accepting a scientist s predictions or a historian s claims In the same way if you want a mathematical statement to be accepted as true you would need to provide mathematically acceptable evidence to support it This means that you would need to show that the statement is universally true And this would be done in the form of a logically valid argument Definition An argument in mathematics or logic is a finite sequence of statements P P p such that p A P A A p p Each statement in the sequence except the last one i e pi for i 1 n is called a premise or an assumption or a hypothesis The final statement p is called the conclusion Let s consider an example of an argument that shows that a given statement is true Example 1 Give an argument to show that the mathematical statement For any two sets A and B An BCA is true Solution One argument could be the following Let x be an arbitrary element of AnB Then X E A and x E B by definition of n Therefore x A This is true for every x in An B Therefore AnBC A by definition of C The argument in Example 1 has a peculiar nature The truth of each of tho 4 premises and of its conclusion follows from the truth of the earlier premises in it Of course we start by assuming that the first statement is true Then assuming the definition of intersection the second statement is true Tlic third one is true whenever the second one is true because of the properties of logical implication The fourth statement is truc whenever the first three arc true because of the definition and properties of the term for all And finally the last statement is true whenever all the earlier ones are In this way we have shown that the given statcinent is true In other words we have proved the given statement as the following definitions show Definitions We say that a proposition p follows logically from propositions P P2 and Pn if p must be true whenever P P2 Pn are true i e P AP A AP p Here note the use of the implication arrow For any two propositions r and s rs denotes s is true whenever r is true Note that using the contrapositive this also denotes r is false whenever s is false Thus rs and rs are different except when both r and s are true or both are false A proof of a proposition p is a mathematical argument consisting of a sequence of statements P P2 Pn from which p logically follows So p is the conclusion of this argument The statement that is proved to be true is called a theorem Sometimes as you will see in Sec 2 3 3 instead of showing that a statement p is true we try to prove that it is false i e that p is true Such a proof is