Permutations and Combinations Questions and Answers
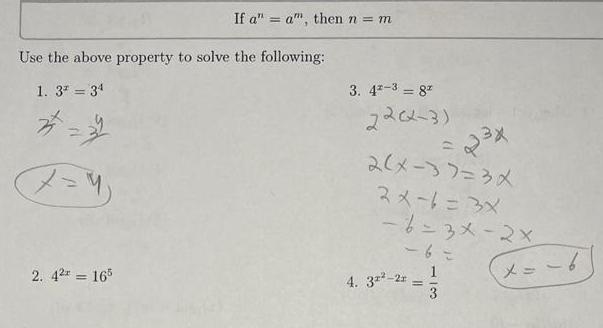
Algebra
Permutations and CombinationsUse the above property to solve the following 1 3 34 2 4 If a a then n m 2 42 165 3 42 3 8 22 2 3 2 x 37 3x 2x 1 3X 6 3x 2x 6 4 32 2x x 3 x 6

Algebra
Permutations and CombinationsFor a vector space V a basis B b b and the coordinate mapping x X show that the coordinate mapping is one to one Hint Suppose u w g for some u and win V and show that u w
Algebra
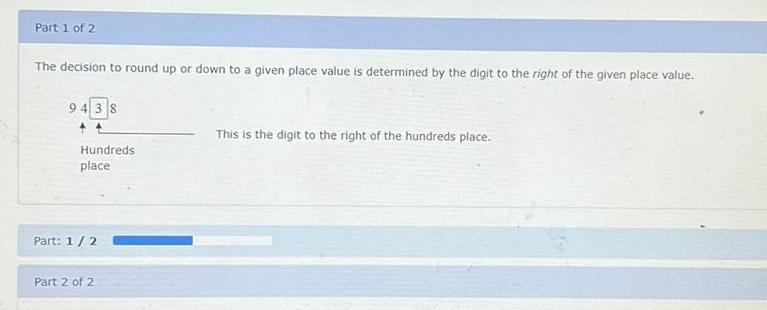
Permutations and CombinationsPart 1 of 2 The decision to round up or down to a given place value is determined by the digit to the right of the given place value 9438 Hundreds place Part 1 2 Part 2 of 2 This is the digit to the right of the hundreds place

Algebra
Permutations and Combinations5 out of 16 students will ride in a car instead of a van.
Combination; 4,368
Permutation; 524,160
Permutation; 3,622
Combination; 1,092

Algebra
Permutations and CombinationsTrue or False: Your finance charge is $6.61 if you have an unpaid balance of $287.45 and the annual
interest rate charge is 2.3% of the unpaid balance.
True
False

Algebra
Permutations and CombinationsYou deposit $400 in an account earning 3% interest compounded annually. How much will you have in the account in 10 years?
Algebra
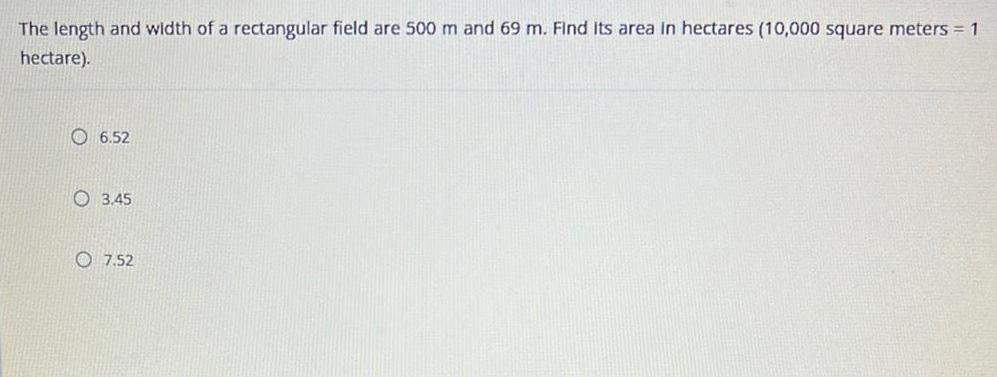
Permutations and CombinationsThe length and width of a rectangular field are 500 m and 69 m. Find Its area in hectares (10,000 square meters = 1
hectare).
6.52
3.45
7.52

Algebra
Permutations and CombinationsThe mean time for a group of runners on the 200 meter dash was 27 seconds with a standard deviation of 1.2. What percent of the runners had time that was less than 25.8 seconds?

Algebra
Permutations and CombinationsJosie is making baked goods for her cheer squad's bake sale. She is selling cookies for $1.50 and brownies for $2.25. She wants to make at least $40 from her baked goods but only has enough batter to make 10 brownies

Algebra
Permutations and CombinationsOn July 1, Mr. Taylor owed $6,000. On the 1st of each of the following months, he repaid
$400. List the amount owed by Mr. Taylor on the 2nd of each month starting with July 2.
Explain why the amount owed each month forms an arithmetic sequence.
Li is developing a fitness program that includes doing push-ups each day. On each day of
the first week he did 20 push-ups. Each subsequent week, he increased his daily push-ups by
5. During which week did he do 60 push-ups a day?
a. Use a formula to find the answer to the question.
b. Write the arithmetic sequence to answer the question.
c. Which method do you think is better? Explain you answer.

Algebra
Permutations and CombinationsSamantha sold 34 bags of popcorn for a fundraiser. If the mean number of bags sold was 38 with a standard deviation of 2.5, find Samantha's z-score.

Algebra
Permutations and CombinationsA survey of 20 colleges found that seniors graduated with an average $28,950 in debt from student loans. The debt was normally distributed with a standard deviation of $3200. Find the probability that a senior graduated owing more than $15,000.

Algebra
Permutations and CombinationsCaroline is going to invest in an account paying an interest rate of 5.2% compounded continuously. How much would Caroline need to invest, to the nearest dollar, for the value of the account to reach $940 in 6 years?

Algebra
Permutations and CombinationsDominic invested $8,600 in an account paying an interest rate of 2.2% compounded daily. Assuming no deposits or withdrawals are made, how long would it take, to the nearest year, for the value of the account to reach $9,600?
![There are 10 applicants for two different jobs (computer programmer and software tester).
This is an example of a [Select]
There are two different jobs of ways to assign these 10 applicants to the](https://media.kunduz.com/media/sug-question/raw/78136253-1660486409.6361442.jpeg?w=256)
Algebra
Permutations and CombinationsThere are 10 applicants for two different jobs (computer programmer and software tester).
This is an example of a [Select]
There are two different jobs of ways to assign these 10 applicants to the
Algebra
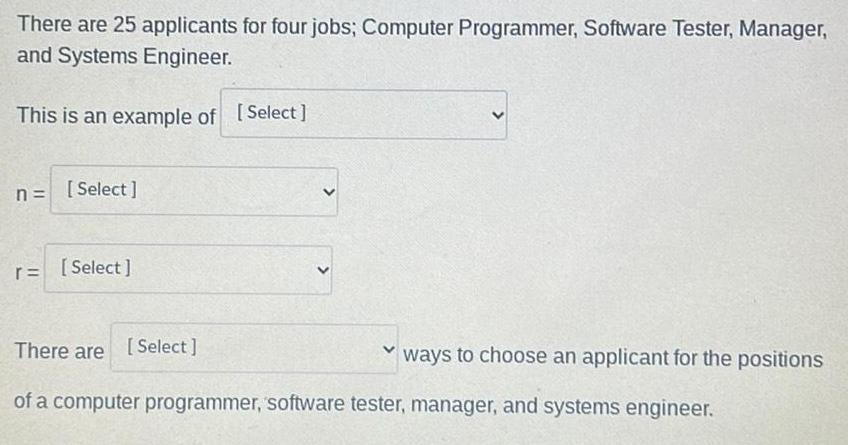
Permutations and CombinationsThere are 25 applicants for four jobs; Computer Programmer, Software Tester, Manager,
and Systems Engineer.
This is an example of
of a computer programmer, software tester, manager, and systems engineer.
ways to choose an applicant for the positions
Algebra
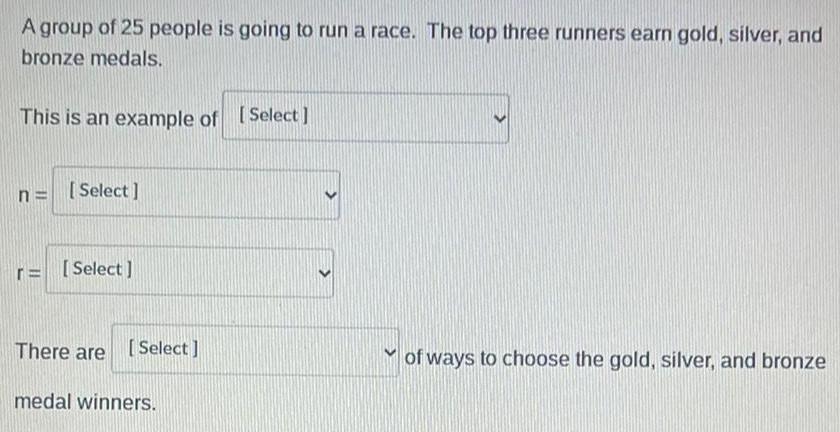
Permutations and CombinationsA group of 25 people is going to run a race. The top three runners earn gold, silver, and
bronze medals.
This is an example of
of ways to choose the gold, silver, and bronze
Algebra
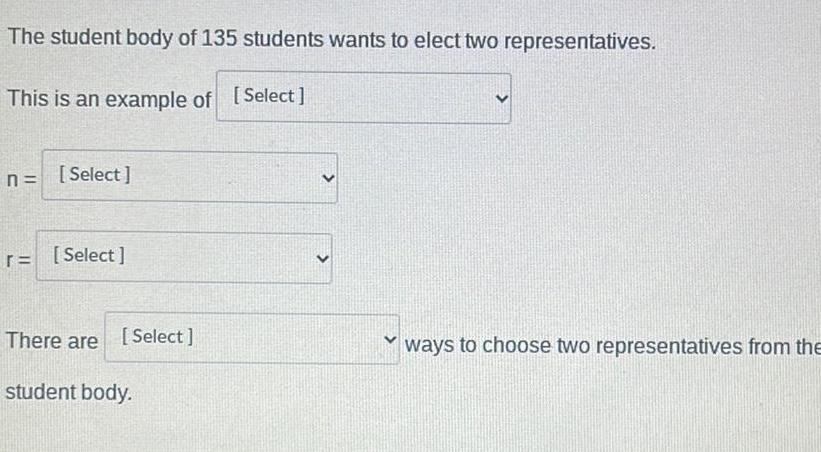
Permutations and CombinationsThe student body of 135 students wants to elect two representatives.

Algebra
Permutations and CombinationsOf the 30 players trying out for the school basketball team, 12 are more than 6 feet tall and 18 have good aim. There are 8 players over 6 feet tall that have good aim Fill in the Venn diagram for the scenario. What is the probability that the coach would randomly pick a player over 6 feet tall or a player with a good aim?

Algebra
Permutations and CombinationsSanji throws an 8-sided solid with faces numbered 1 through 8.
Which of the following statements is true? Select all that apply.
P(number less than 8) = 1
P(factor of 24)
P(the number 9) = 0
P(even number)
P(multiple of 3) = 1
P(odd number)

Algebra
Permutations and CombinationsThere are thirteen songs on your playlist. Seven of them are country and six are pop. With random shuffle and no repetition, you listen to seven songs. What is the probability that you listened to all country songs?
Algebra
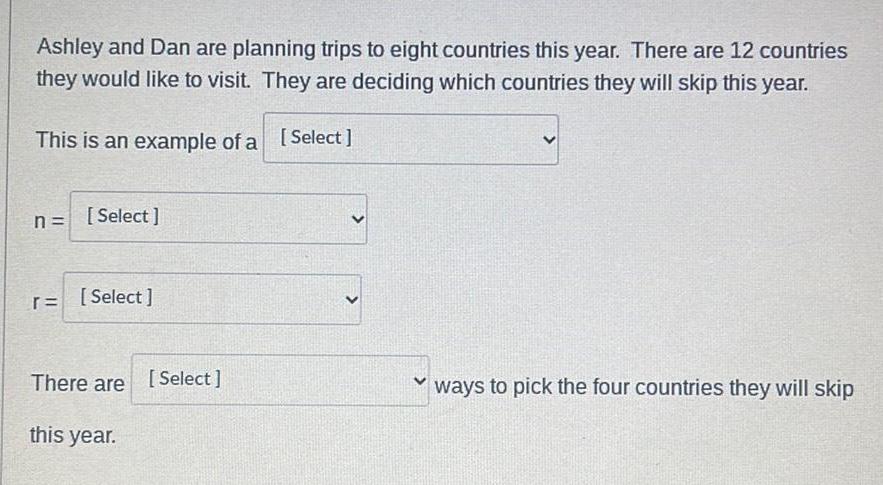
Permutations and CombinationsAshley and Dan are planning trips to eight countries this year. There are 12 countries
they would like to visit. They are deciding which countries they will skip this year.
Algebra
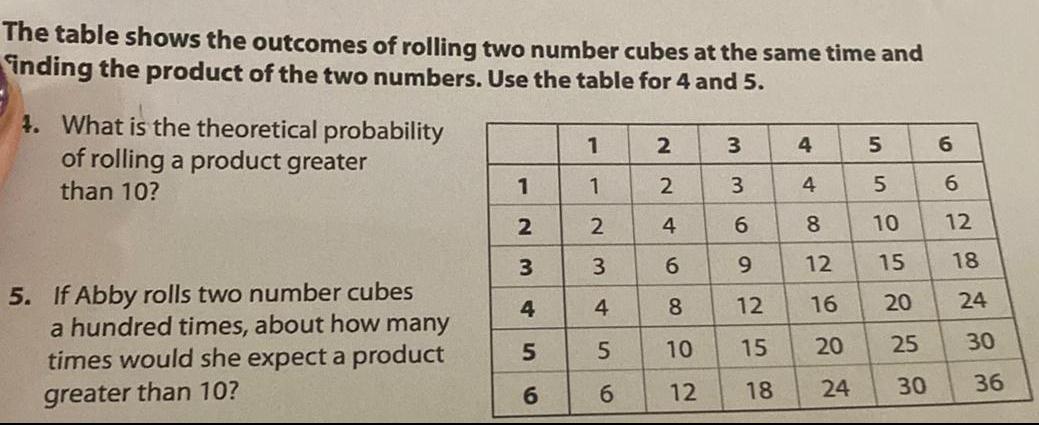
Permutations and CombinationsThe table shows the outcomes of rolling two number cubes at the same time and inding the product of the two numbers. Use the table for 4 and 5. 4. What is the theoretical probability of rolling a product greater than 10? 5. If Abby rolls two number cubes a hundred times, about how many times would she expect a product greater than 10?
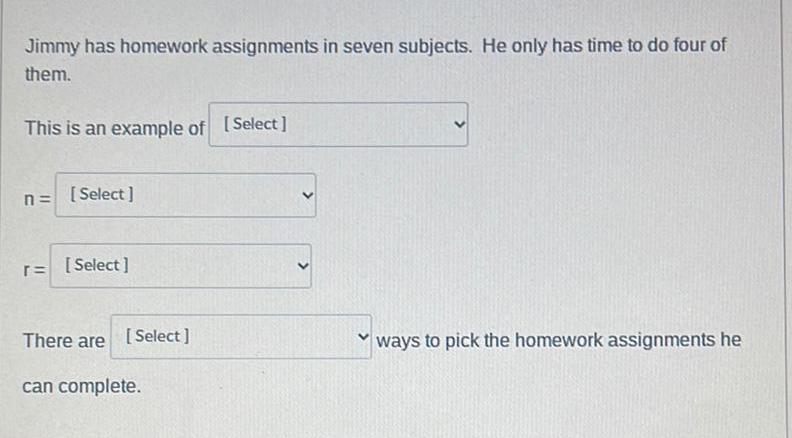
Algebra
Permutations and CombinationsJimmy has homework assignments in seven subjects. He only has time to do four of them. This is an example of
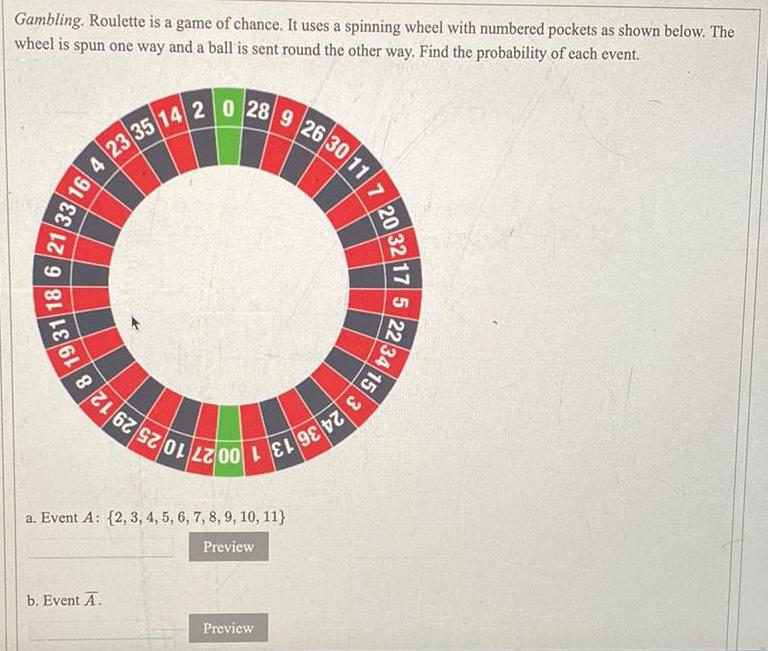
Algebra
Permutations and CombinationsGambling. Roulette is a game of chance. It uses a spinning wheel with numbered pockets as shown below. The wheel is spun one way and a ball is sent round the other way. Find the probability of each event.
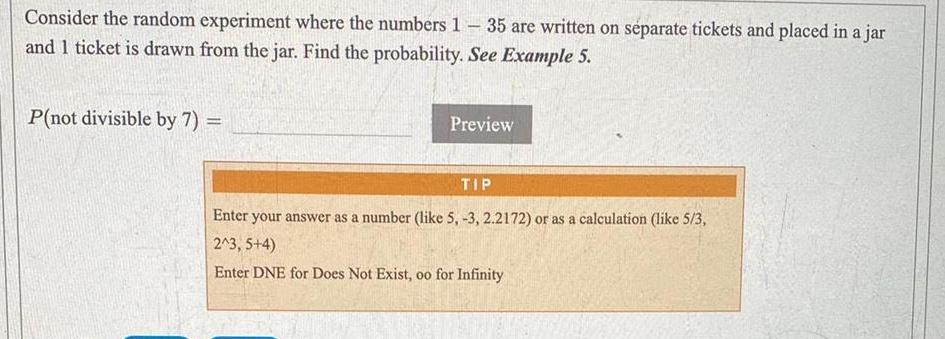
Algebra
Permutations and CombinationsConsider the random experiment where the numbers 1-35 are written on separate tickets and placed in a jar
and 1 ticket is drawn from the jar. Find the probability.
P(not divisible by 7) =
Enter your answer as a number (like 5, -3, 2.2172) or as a calculation (like 5/3,
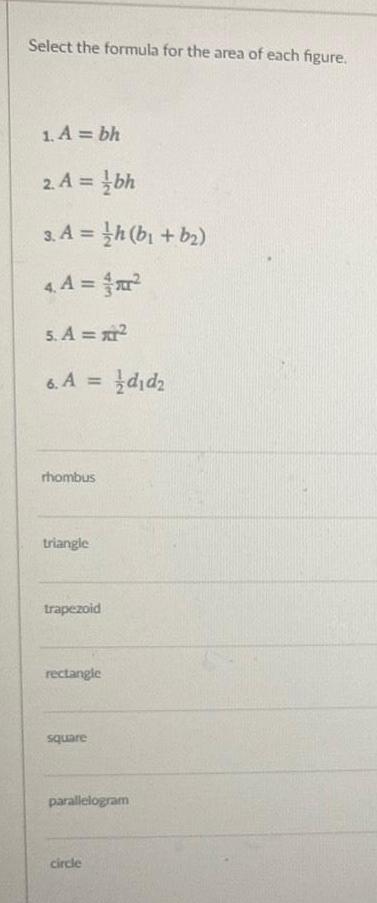
Algebra
Permutations and CombinationsSelect the formula for the area of each figure.
1. A = bh
2. A =
3. A =
rhombus
4. A =
5. A = x²
6. A = 1d₁d₂
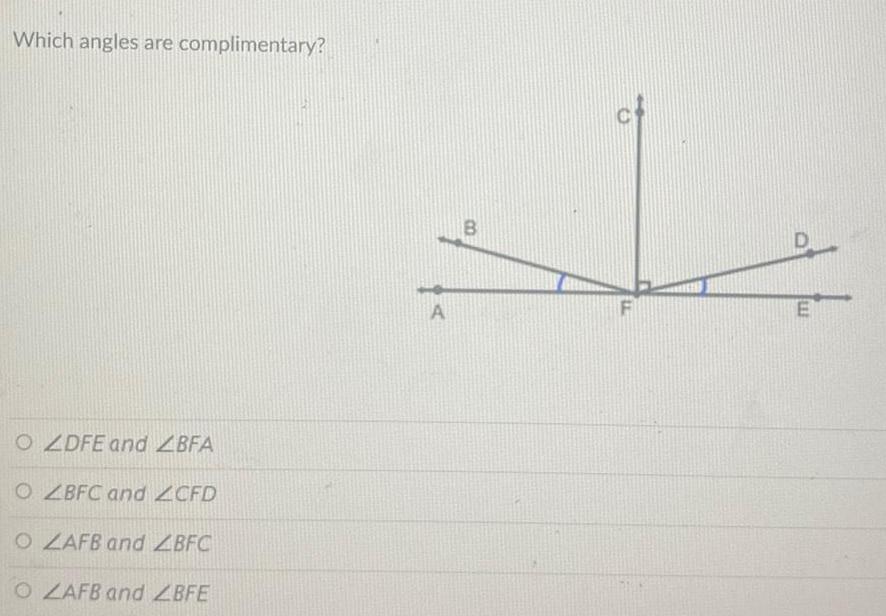
Algebra
Permutations and CombinationsWhich angles are complimentary?
ZDFE and LBFA
ZBFC and CFD
ZAFB and LBFC
ZAFB and ZBFE
Algebra
Permutations and CombinationsLet p represent
Two angles are vertical angles.
Let q represent
The angles are congruent.
What is the symbolic representation of the following statement?
If two angles are congruent, then the angles are vertical angles.

Algebra
Permutations and CombinationsFind the probability for the random experiment of 1 roll of 2 dice. Express the result as a fraction and as a decimal rounded to the nearest thousandth. (The illustration in Section 6.1 Study Set problem 19 may be helpful.) See Example 4.
What is the probability if rolling hard 6 (two 3s) or hard 8 (two 4s)?

Algebra
Permutations and CombinationsGraph the linear equation.
f(x) = -2x+6
Use the graphing tool to graph the linear equation.
Click to
enlarge
graph
-10
R
-64
10
16
AY
10

Algebra
Permutations and CombinationsTrue or false: The chromatic number of a graph is always bigger than the number of vertices of the
graph.
None of these is correct.
True because of Euler's Theorem.
True because of Fermat's Last Theorem.
O True because of Dijkstra's algorithm.
True because of the Euler circuit.
O False because chromatic numbers are a type of prime number and don't have anything to do with graphs.
False because most graphs do not have a chromatic number.
False because the chromatic number of any connected graph is 0.
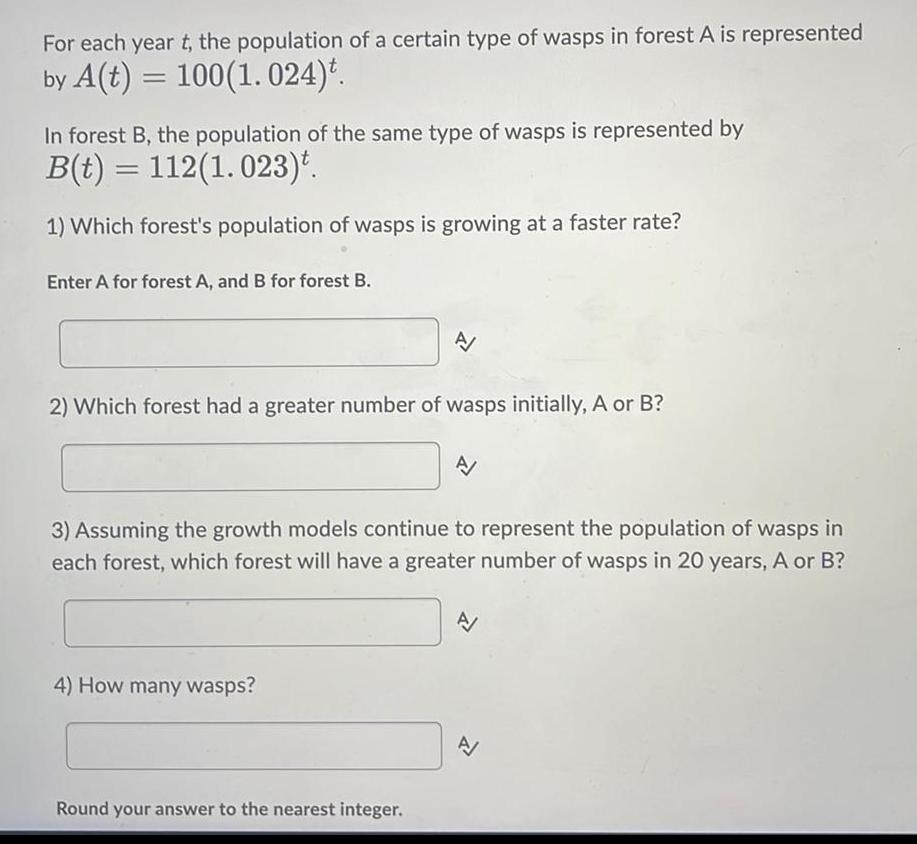
Algebra
Permutations and CombinationsFor each year t, the population of a certain type of wasps in forest A is represented
by A(t) = 100(1.024)t.
In forest B, the population of the same type of wasps is represented by
B(t) = 112(1.023)t.
1) Which forest's population of wasps is growing at a faster rate?
Enter A for forest A, and B for forest B.
2) Which forest had a greater number of wasps initially, A or B?
A
4) How many wasps?
3) Assuming the growth models continue to represent the population of wasps in
each forest, which forest will have a greater number of wasps in 20 years, A or B?
Round your answer to the nearest integer.
A/
A/
A/
Algebra
Permutations and Combinations2. In how many different ways can the letters of the word 'MATHEMATICS' be arranged such
that the vowels must always come together?
A. 9800
B. 120960
C. 100020
D. 140020

Algebra
Permutations and CombinationsDay 9 SB SOL AII.10,12 Exit Ticket
1. A committee of 5 teachers and 2 students is to be formed to judge science projects. If
there are 9 teachers and 5 students to choose from, how many different committees could
be formed?
Class W5
Name Uriah Garland

Algebra
Permutations and CombinationsCaroline is going to invest $66,000 and leave it in an account for 9 years. Assuming
the interest is compounded continuously, what interest rate, to the nearest
hundredth of a percent, would be required in order for Caroline to end up with
$108,000?
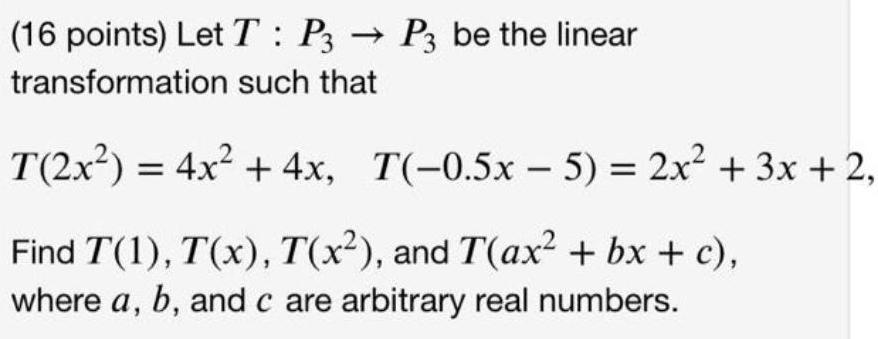
Algebra
Permutations and Combinations(16 points) Let T: P3 → P3 be the linear transformation such that
T(2x²) = 4x² + 4x, T(-0.5x - 5) = 2x² + 3x + 2,
Find T(1), T(x), T(x²), and T(ax² + bx + c),
where a, b, and c are arbitrary real numbers.
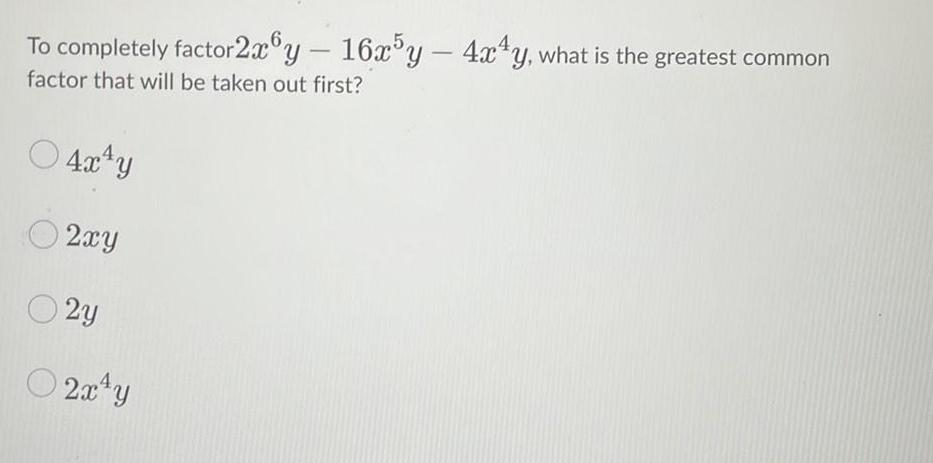
Algebra
Permutations and CombinationsTo completely factor 2x6y - 16x5y - 4x4y, what is the greatest common
factor that will be taken out first?
4x¹y
2xy
02y
2x¹y

Algebra
Permutations and CombinationsWhat is the complete factorization of 8 - 2x4 +1?
(x² − 1)²
© (x² + 1)² (x + 1)² (x − 1)²
(x¹ + 1) (x² − 1)
(x² + 1)² (x² − 1)²

Algebra
Permutations and CombinationsComposing two functions is always the same operation as
Omultiplication
division
addition
Onone of the above

Algebra
Permutations and CombinationsLet f(x) = x² + 1 and g(x) = √3x - 1, find (gof)(x).
4
√3x²+2
18x²-3
√3x²
3x

Algebra
Permutations and CombinationsIf f(x) passes through the point (5, 6n), which of the following points does its
inverse function f¹(x) pass through?
(6n, k)
(-4, -6n)
1
( ² /, /n)
k?
(-6n, -k)
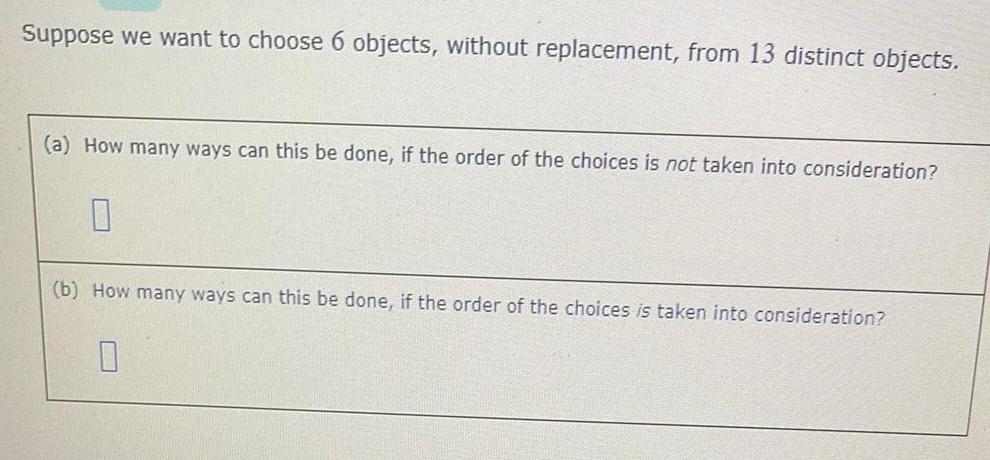
Algebra
Permutations and CombinationsSuppose we want to choose 6 objects, without replacement, from 13 distinct objects.
(a) How many ways can this be done, if the order of the choices is not taken into consideration?
0
(b) How many ways can this be done, if the order of the choices is taken into consideration?
0

Algebra
Permutations and CombinationsIf the following polynomial is written in standard form, what would be the leading
coefficient?
-3x² + 4x² - 2x6 - 2
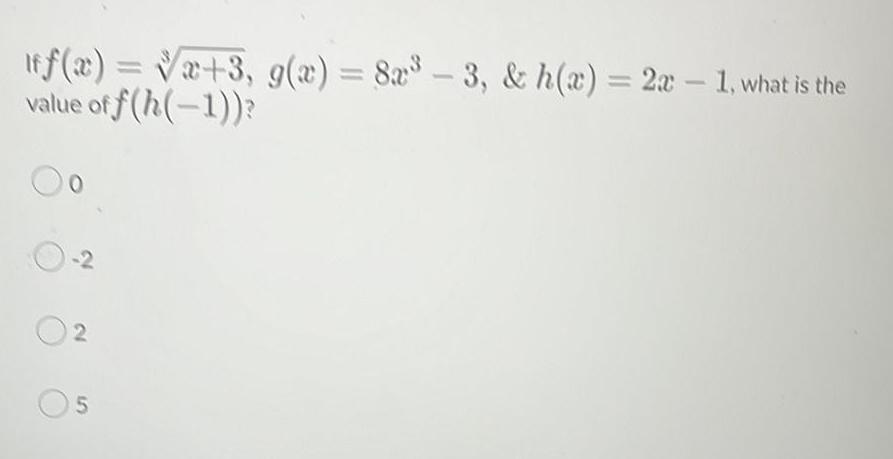
Algebra
Permutations and Combinationsf(x) = √x+3, g(x) = 8x³ - 3, & h(x)=2x-1, what is the
value of f(h(-1))?
-2
2
5

Algebra
Permutations and CombinationsFind the inverse of the function.
x
f(x) = -5
4
4
X
Of(x) = ² + 20
f(x) = 4x + 5
O f(x) = 4x + 20
f(x) = 4x - 20
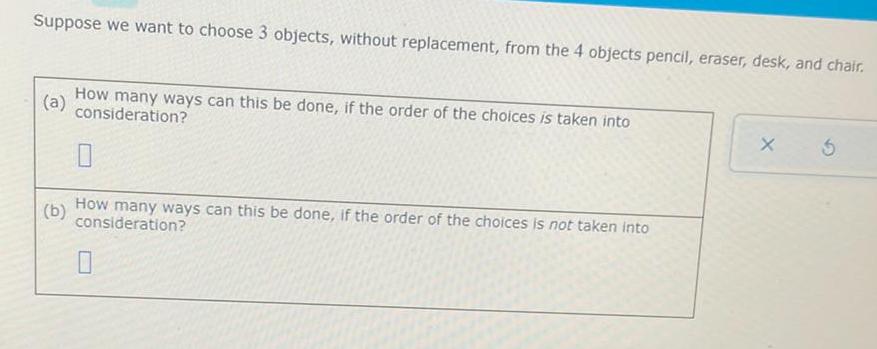
Algebra
Permutations and CombinationsSuppose we want to choose 3 objects, without replacement, from the 4 objects pencil, eraser, desk, and chair.
(a)
How many ways can this be done, if the order of the choices is taken into
consideration?
0
(b)
How many ways can this be done, if the order of the choices is not taken into
consideration?
5

Algebra
Permutations and CombinationsSuppose we want to choose 4 letters, without replacement, from 16 distinct letters.
(a) If the order of the choices is not relevant, how many ways can this be done?
(b) If the order of the choices is relevant, how many ways can this be done?

Algebra
Permutations and CombinationsSuppose we want to choose 7 colors, without replacement, from 11 distinct colors.
(a) How many ways can this be done, if the order of the choices matters?
1
(b) How many ways can this be done, if the order of the choices does not matter?