Permutations and Combinations Questions and Answers
![Find the inverse of g (x) = 1/2(x) + 3/2 .
g-¹ (x) =[?]*x-{?]](https://media.kunduz.com/media/sug-question/raw/80152573-1659868609.253796.jpeg?w=256)
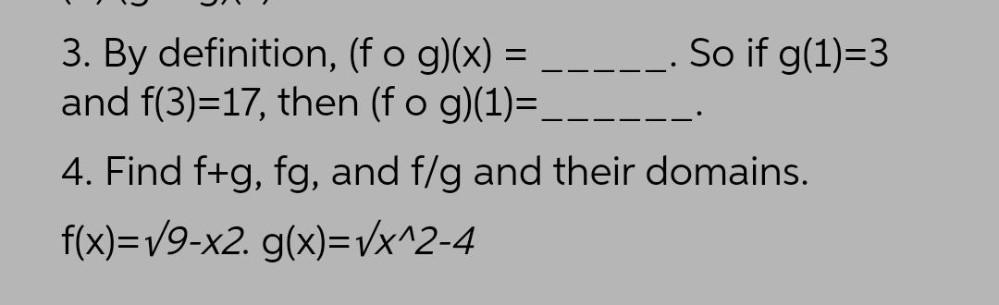
Algebra
Permutations and CombinationsBy definition, (f o g)(x) = So if g(1)=3 and f(3)=17, then (f o g)(1)= 4. Find f+g, fg, and f/g and their domains. f(x)=√9-x2. g(x)=√x^2-4
Algebra
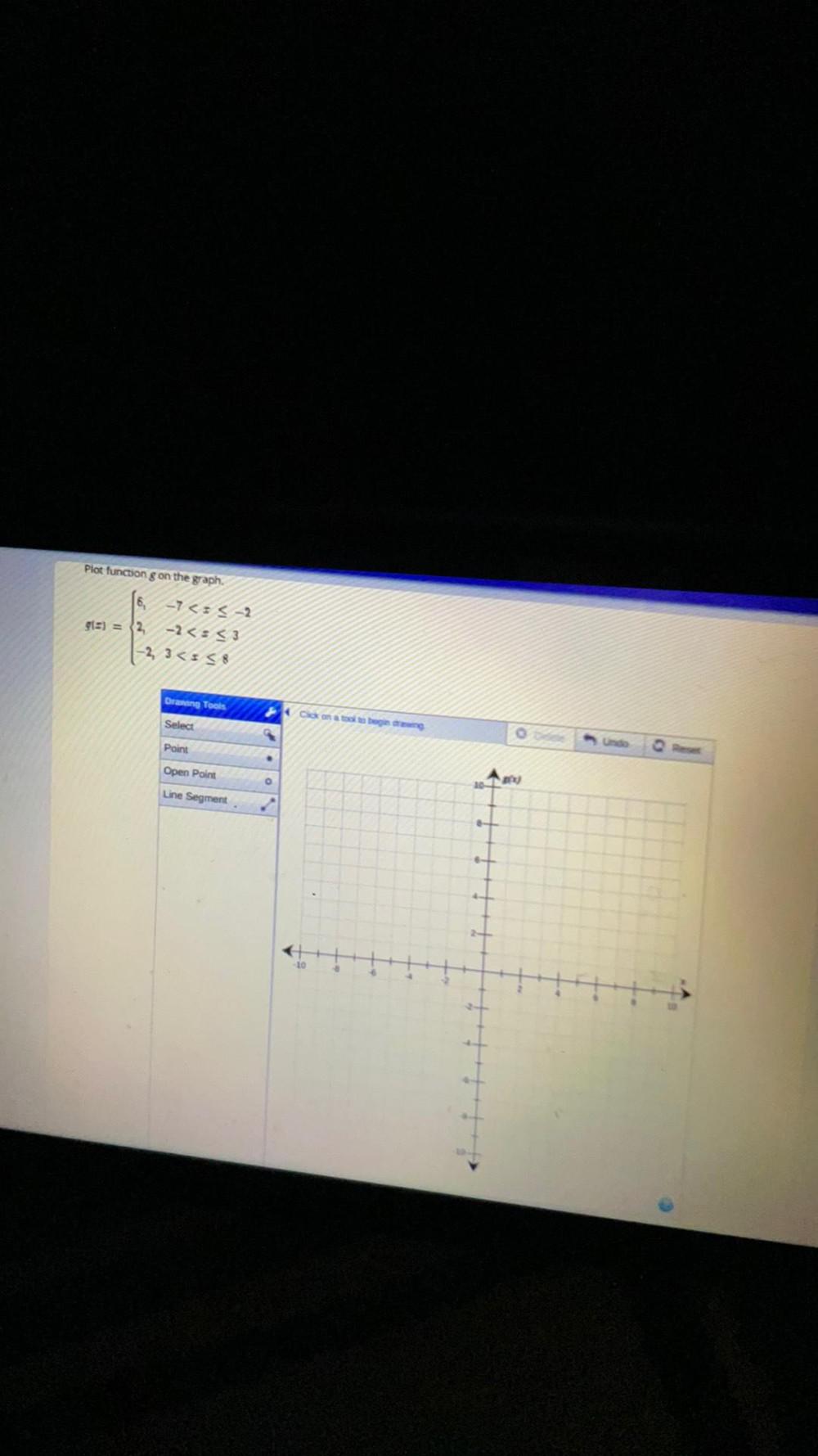
Permutations and CombinationsPlot function g on the graph.
g(x) = -7 <= ≤-2
-2<= <3
-2, 3 <= ≤8
Algebra
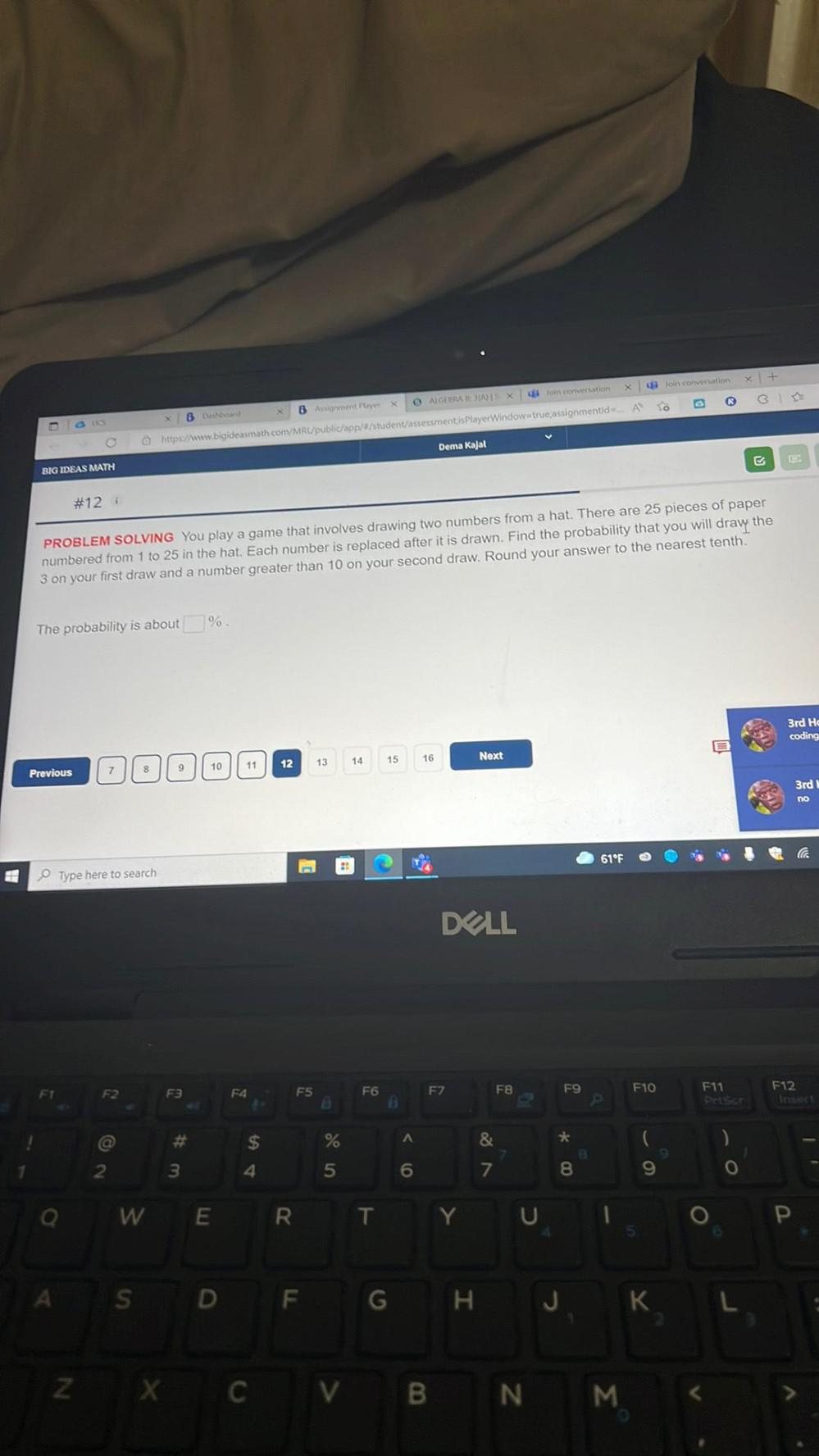
Permutations and CombinationsYou play a game that involves drawing two numbers from a hat. There are 25 pieces of paper numbered from 1 to 25 in the hat. Each number is replaced after it is drawn. Find the probability that you will draw the 3 on your first draw and a number greater than 10 on your second draw. Round your answer to the nearest tenth.
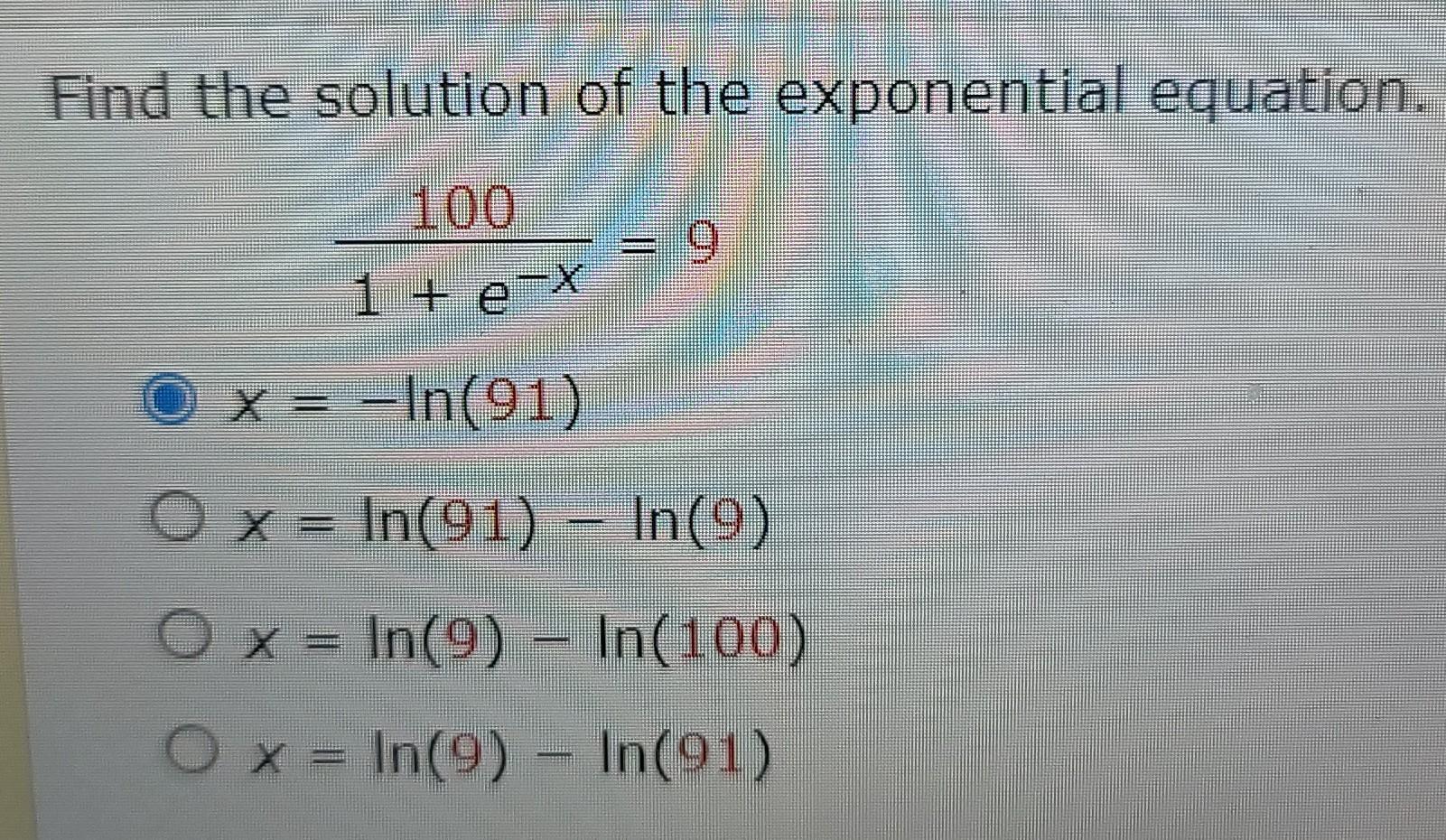
Algebra
Permutations and CombinationsFind the solution of the exponential equation.
100/1 + e^-X
x = -In(91)
x = In(91) - In(9)
x = In(9) - In(100)
x = In(9) - In(91)
Algebra
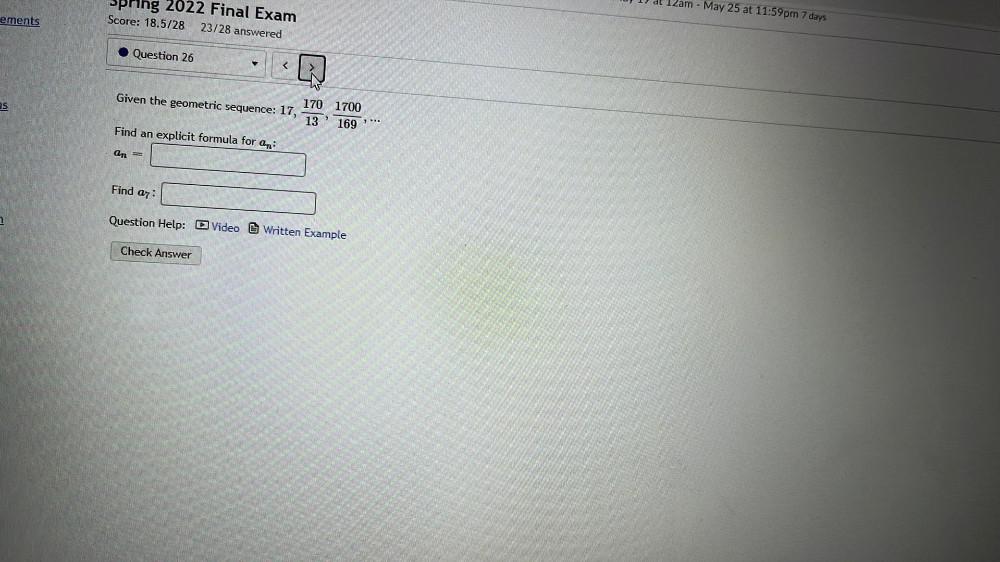
Permutations and CombinationsGiven the geometric sequence: 17,170/3 , 1700/169, ..........
Find an explicit formula for aₙ:
aₙ=
Find a₇:
Algebra
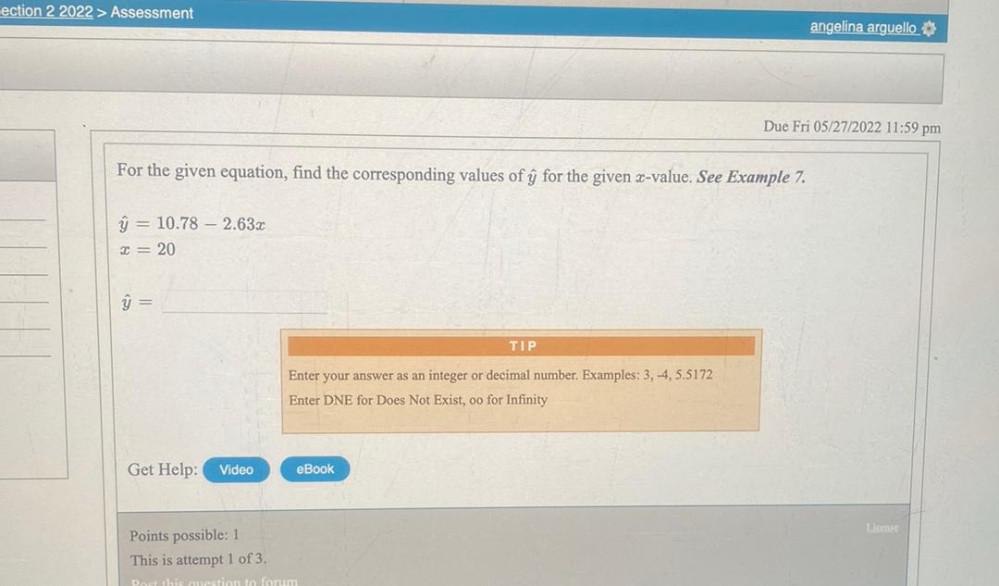
Permutations and CombinationsFor the given equation, find the corresponding values of y for the given x-value. See Example 7.
ŷ 10.78 - 2.63x
x=20
ŷ =
TIP- Enter your answer as an integer or decimal number. Examples: 3, -4, 5.5172
Enter DNE for Does Not Exist, oo for Infinity
Algebra
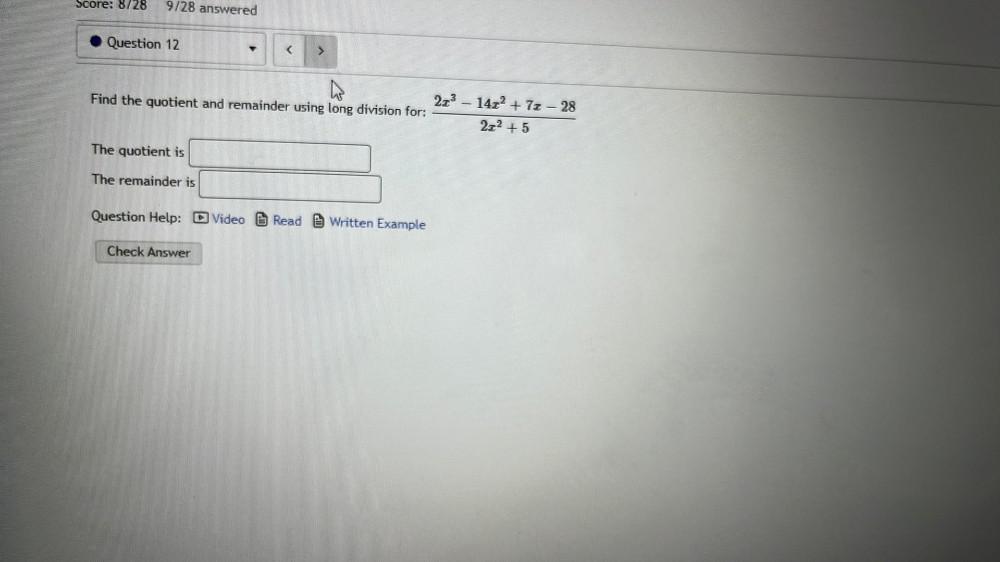
Permutations and CombinationsFind the quotient and remainder using long division for:
2x³ − 14x² + 71 − 28/2x² + 5
a)The quotient is____
b)The remainder is___
Algebra
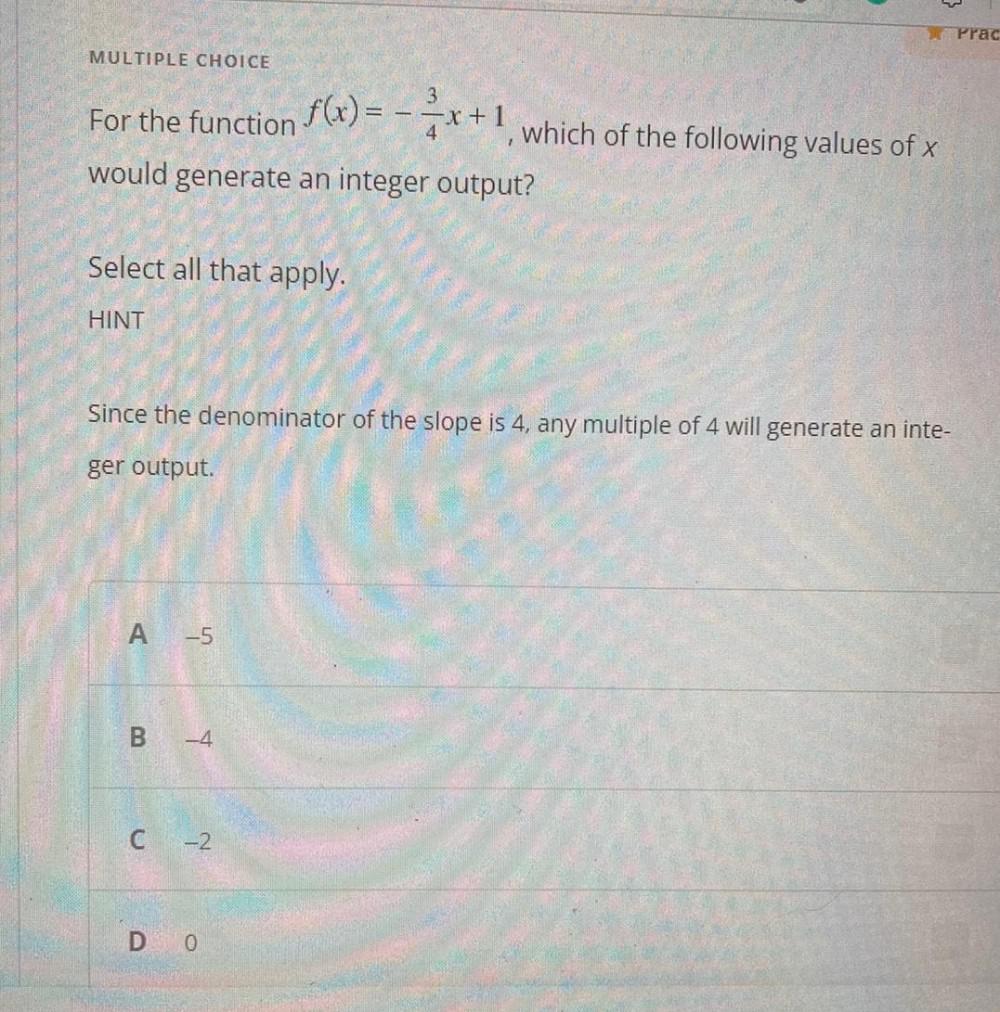
Permutations and CombinationsFor the function f(x) = -(3/4)x+1, which of the following values of x would generate an integer output?
Select all that apply.
Since the denominator of the slope is 4, any multiple of 4 will generate an integer output.
A) -5
B) -4
C) -2
D) O
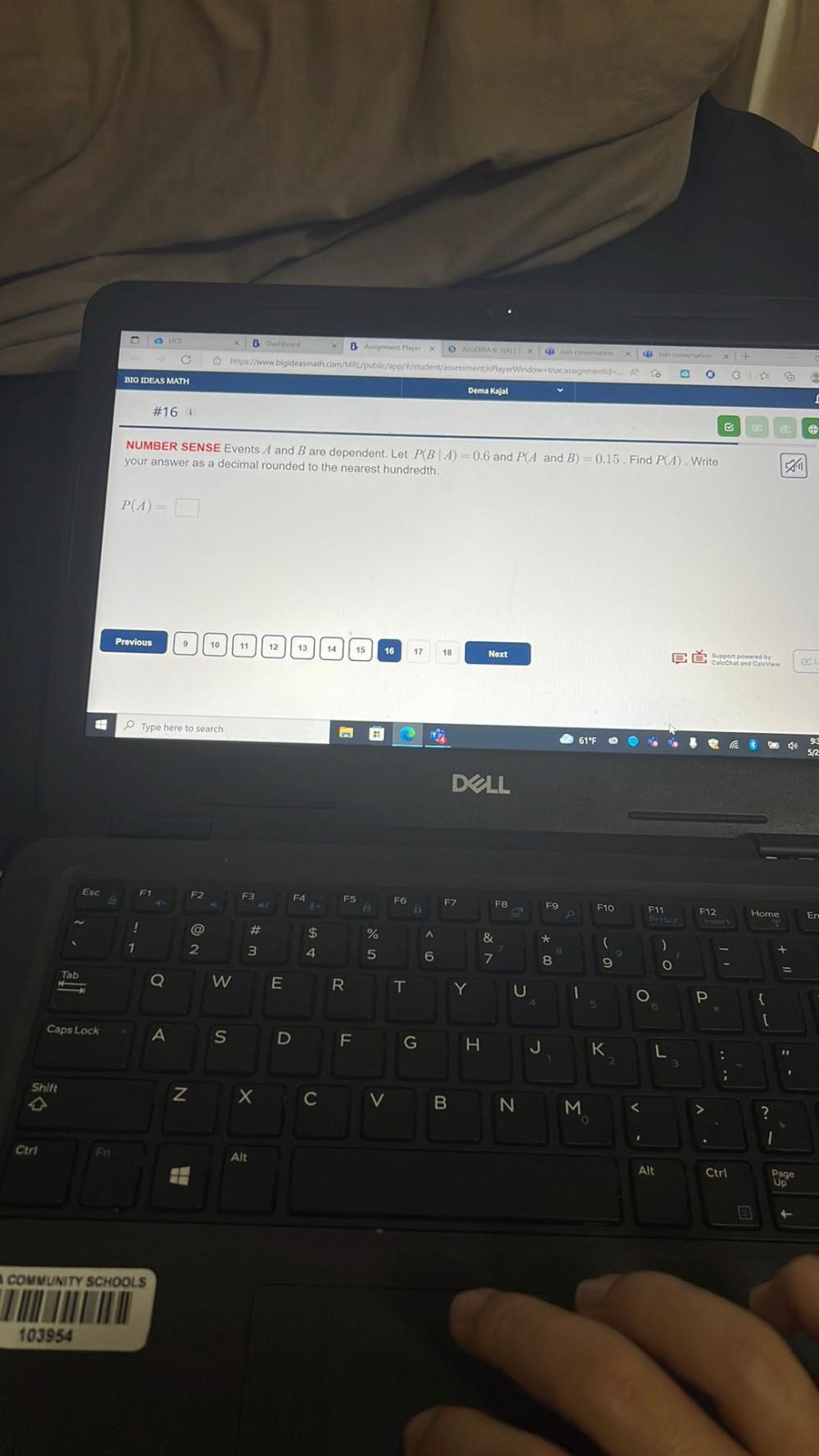
Algebra
Permutations and CombinationsEvents A and B are dependent. Let P(BA)=0.6 and P(A and B) 0.15. Find P(A). Write your answer as a decimal rounded to the nearest hundredth.
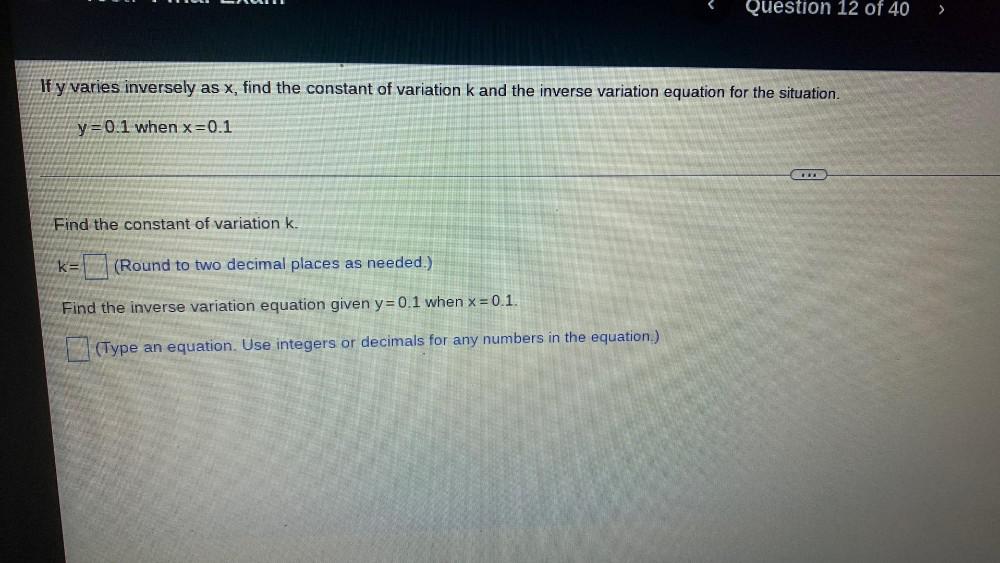
Algebra
Permutations and CombinationsIf y varies inversely as x, find the constant of variation k and the inverse variation equation for the situation. y=0.1 when x = 0.1
Find the constant of variation k.
Find the inverse variation equation given y = 0.1 when x = 0.1.
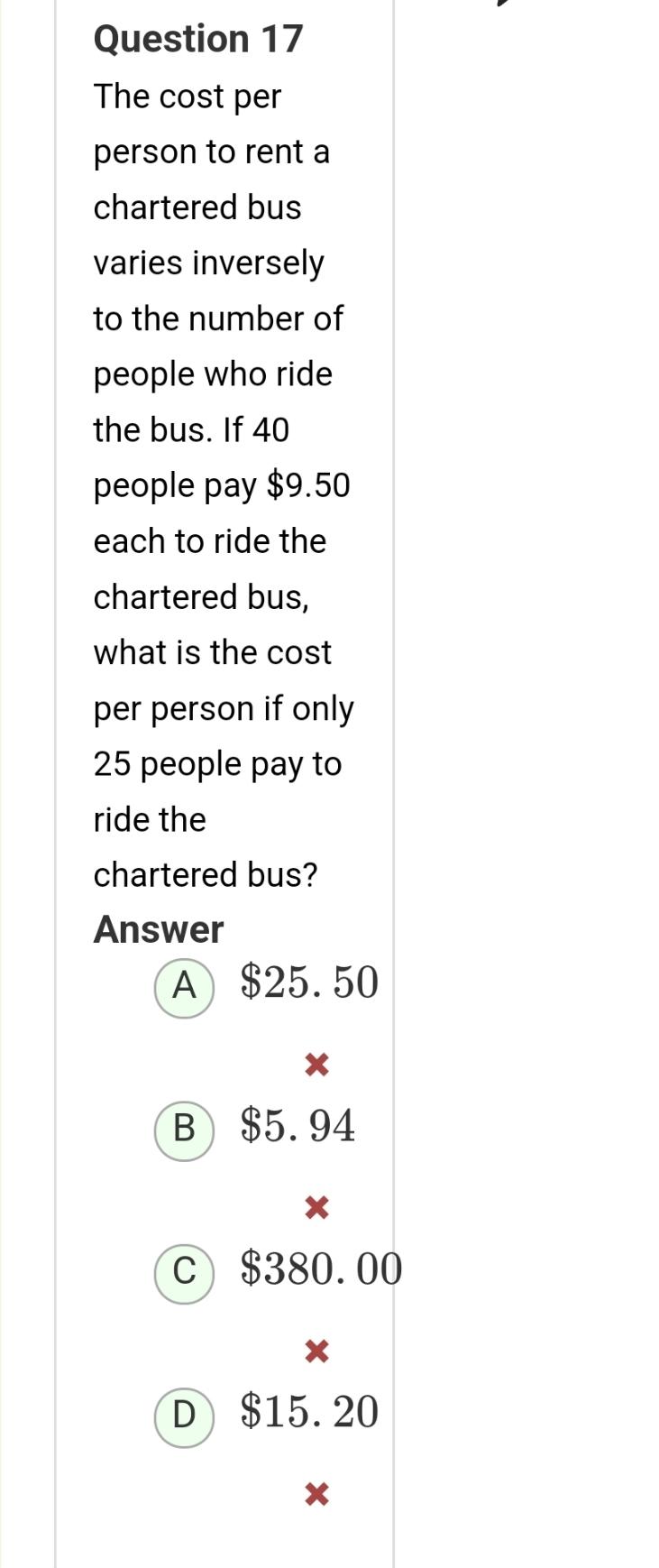
Algebra
Permutations and CombinationsThe cost per person to rent a chartered bus varies inversely to the number of people who ride the bus. If 40 people pay $9.50 each to ride the chartered bus, what is the cost per person if only 25 people pay to ride the chartered bus?
Answer
A) $25.50
B) $5.94
C) $380.00
D) $15.20
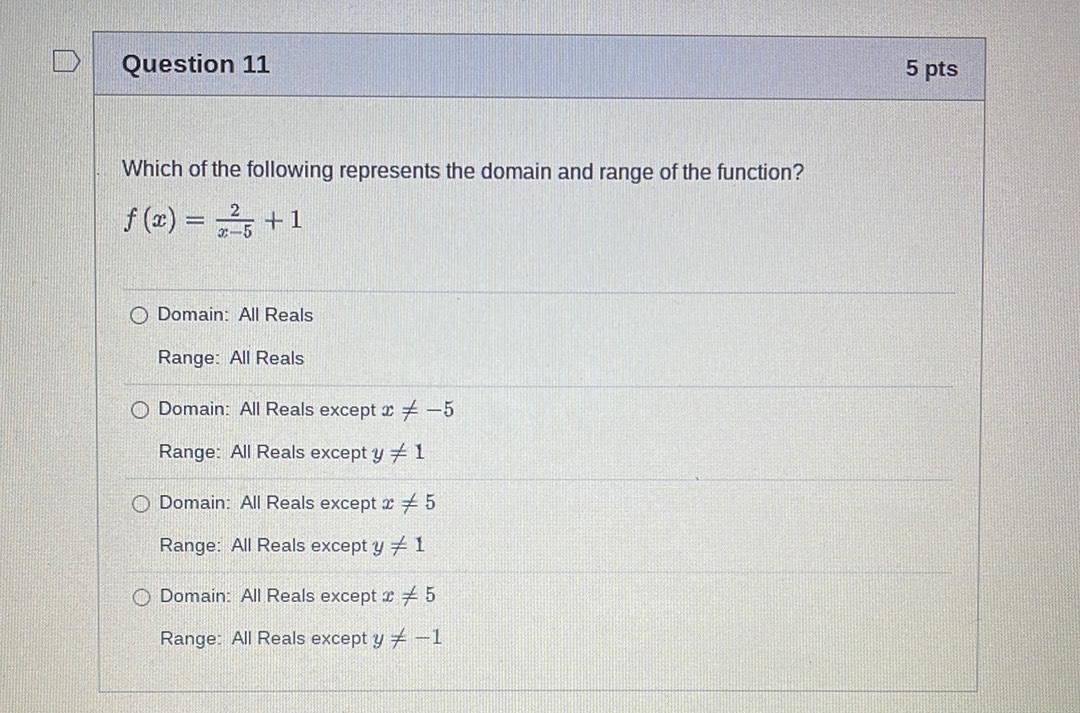
Algebra
Permutations and CombinationsWhich of the following represents the domain and range of the function?
f(x) = 2/(x-5) + 1
A) Domain: All Reals
Range: All Reals
B) Domain: All Reals except x ≠ -5
Range: All Reals except y ≠ 1
C) Domain: All Reals except x ≠ 5
Range: All Reals except y ≠ 1
D) Domain: All Reals except x ≠ 5
Range: All Reals except y ≠ −1
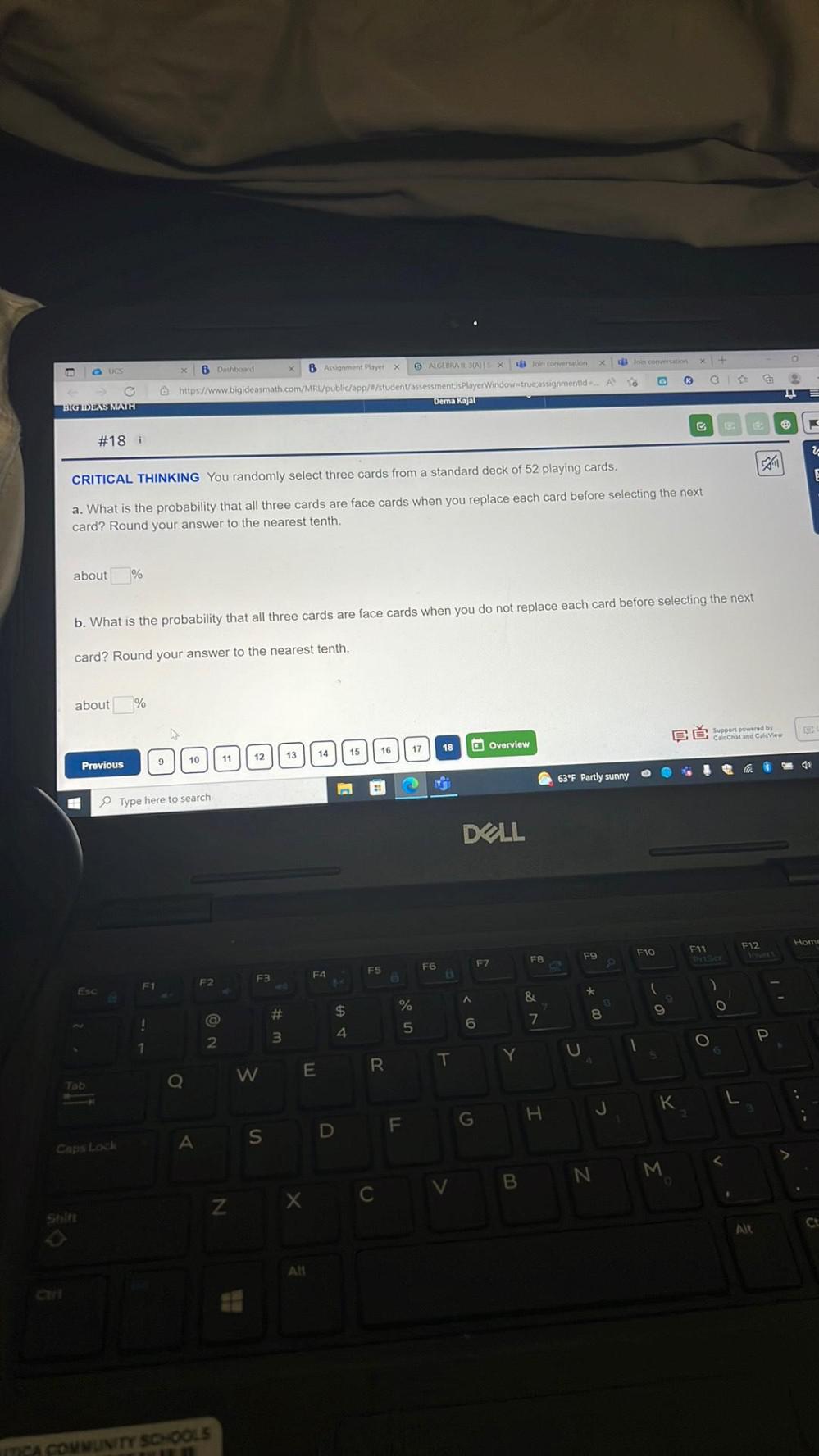
Algebra
Permutations and CombinationsYou randomly select three cards from a standard deck of 52 playing cards.
a. What is the probability that all three cards are face cards when you replace each card before selecting the next card? Round your answer to the nearest tenth.
about _____ %
b. What is the probability that all three cards are face cards when you do not replace each card before selecting the next
card? Round your answer to the nearest tenth.
about ____%

Algebra
Permutations and CombinationsName 2 of the properties that must be true of a normal distribution.

Algebra
Permutations and CombinationsTwo functions are given below.,
f(x) = loge (x)
g(x) = e^x
Which of the following does NOT describe the relationship of f(x) and g(x)?
A) The functions are inverses of each other.
B) The functions have the same domain and range.
C) f(x) has a vertical asymptote at x = 0 and g(x) has a horizontal asymptote at y = 0.
D) f(x) and g(x) are symmetric to each other with respect to the line y = x.

Algebra
Permutations and CombinationsSolve the equations by finding inverse of matrix using MATLAB
x-y + 2z=3
x + 2y + 32 =5
3x - 4y - 5z = -13
Use MATLAB to find the values of unknowns using Cramer's rule.
2x + 3y + 4z = 11
x + 5y + 72 = 15
3x + 11y + 132 = 25
Consider the following set of equations
5x + 2y + z = 12
x + 4y + 2z = 15
x + 2y + 5z = 20
Use MATLAB to solve the syatem. Use x₁° = x₂° = x3° = 0 as initial guesses. Perform first two iterations.

Algebra
Permutations and CombinationsA quadrilateral with all sides congruent and all angles required to be equal to 90° is called a:
A. parallelogram
B. trapezoid
C. rhombus
D. square
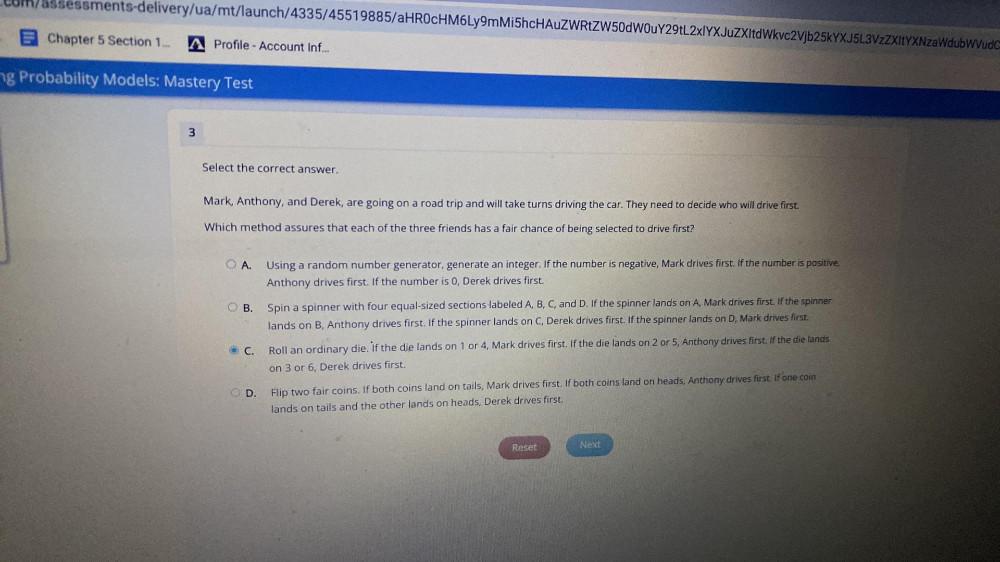
Algebra
Permutations and CombinationsSelect the correct answer.
Mark, Anthony and Derek are going on a road trip and will take turns driving the car. They need to decide who will drive first. Which method assures that each of the three friends has a fair chance of being selected to drive first?
• A.)Using a random number generator, generate an integer. If the number is negative, Mark drives first. If the number is positive,
Anthony drives first. If the number is 0, Derek drives first.
•B.)Spin a spinner with four equal-sized sections labeled A, B, C, and D. If the spinner lands on A, Mark drives first. If the spinner lands on B, Anthony drives first. If the spinner lands on C, Derek drives first. If the spinner lands on D, Mark drives first.
•C.)Roll an ordinary die. If the die lands on 1 or 4, Mark drives first. If the die lands on 2 or 5, Anthony drives first. If the die lands on 3 or 6, Derek drives first.
•D.)Flip two fair coins. If both coins land on tails, Mark drives first. If both coins land on heads, Anthony drives first. If one coin lands on tails and the other lands on heads, Derek drives first.

Algebra
Permutations and CombinationsWhen dealt 5 random cards from a standard deck of playing cards, what is the probability that you are dealt two jacks and 3 sevens?
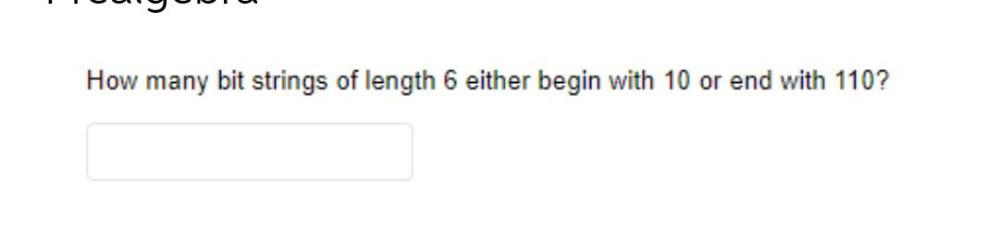
Algebra
Permutations and CombinationsHow many bit strings of length 6 either begin with 10 or end with 110 ?
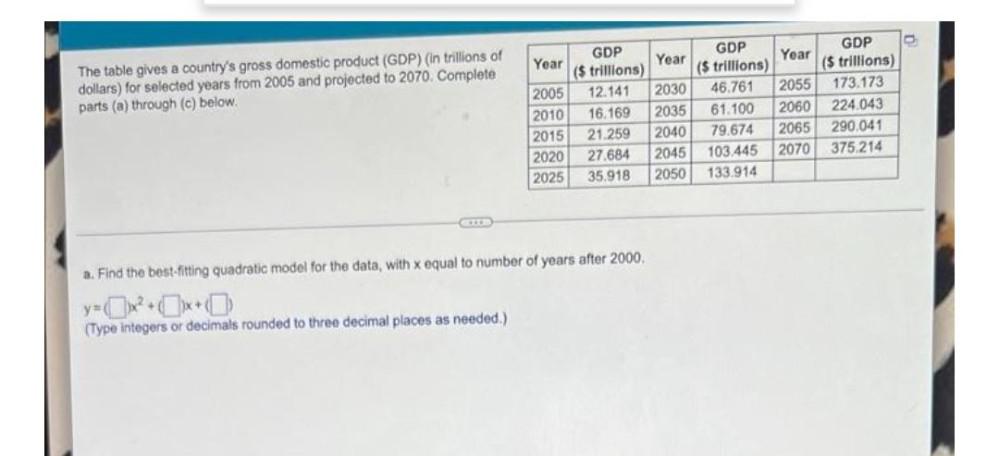
Algebra
Permutations and CombinationsThe table gives a country's gross domestic product (GDP) (in trillions of dollars) for selected years from 2005 and projected to 2070. Complete parts (a) through (c) below.
a. Find the best-fitting quadratic model for the data, with x equal to number of years after 2000.
(Type integers or decimals rounded to three decimal places as needed.)
Algebra
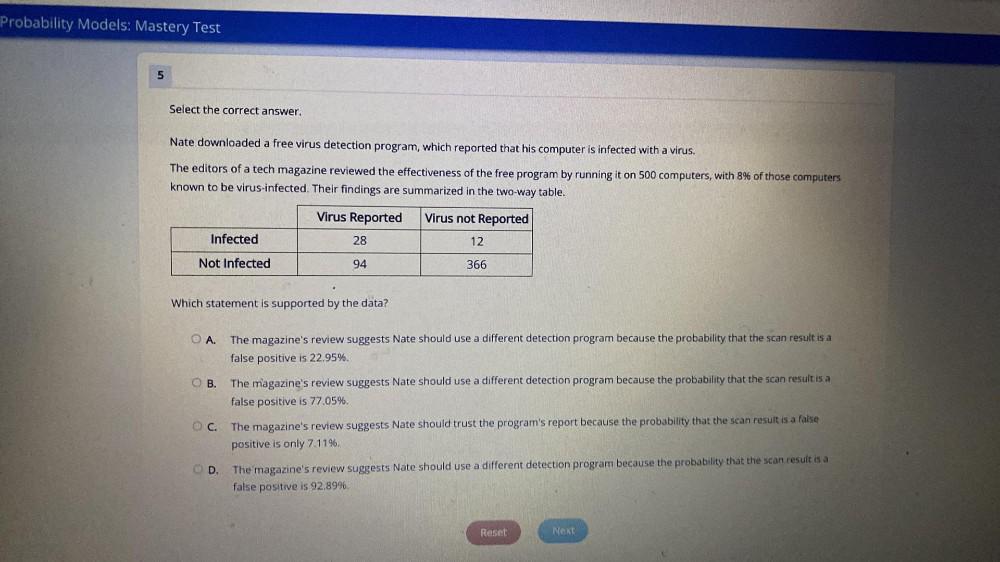
Permutations and CombinationsSelect the correct answer.
Nate downloaded a free virus detection program, which reported that his computer is infected with a virus.
The editors of a tech magazine reviewed the effectiveness of the free program by running it on 500 computers, with 8% of those computers known to be virus-infected. Their findings are summarized in the two way table.
Virus Reported Virus not Reported
Infected 28 12
Not Infected 94 366
Which statement is supported by the data?
A) The magazine's review suggests Nate should use a different detection program because the probability that the scan result is a false positive is 22.95%.
B) The magazine's review suggests Nate should use a different detection program because the probability that the scan result is a false positive is 77.05%.
C) The magazine's review suggests Nate should trust the program's report because the probability that the scan result is a false positive is only 7.11%.
D) The magazine's review suggests Nate should use a different detection program because the probability that the scan result is a false positive is 92.89%,
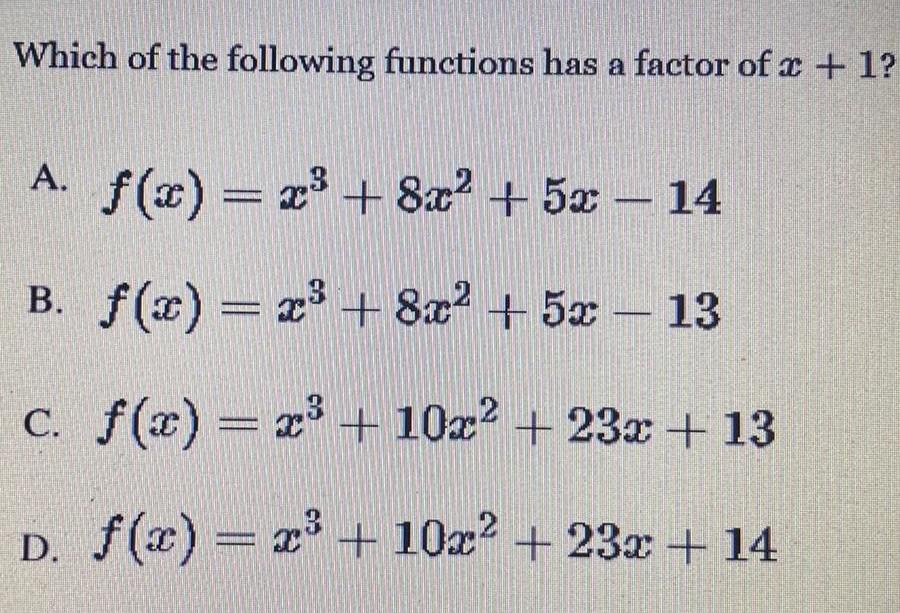
Algebra
Permutations and CombinationsWhich of the following functions has a factor of x + 1?
A). f(x) = x³ + 8x² + 5x - 14
B.)f(x) = x³ + 8x² + 5x - 13
C.)f(x) = x³ + 10x² + 23x + 13
D). f(x) = x³ + 10x² +23x + 14
Algebra
Permutations and CombinationsOut of 55 teenagers enrolled in dance classes, 30 teenagers take either hip hop or jazz classes. There are 13 teenagers who take hip hop classes and 24 teenagers who take jazz classes. What is the probability that a randomly selected teenager takes both hip hop and jazz classes? Express your answer as a fraction in simplest form. The probability that a randomly selected teenager takes both hip hop and jazz classes is

Algebra
Permutations and Combinationsa) The average height of sunflowers in a field is 64 in. with a standard deviation of 3.5 in. On a piece of paper, draw a normal curve for the distribution, including the values on the horizontal axis at one, two, and three standard deviations from the mean. Describe your drawing in as much detail as possible, and explain how you came up with each of your labels. b) If there are 3,000 plants in the field, approximately how many will be taller than 71 in.? Explain how you got your answer.


Algebra
Permutations and CombinationsIn a class of 50 students, 29 are Democrats, 11 are business majors, and 5 of the business majors are Democrats. If one student is randomly selected from the class, find the probability of choosing : (a) Democrat who is not a business major. (b) A student who is neither a Democrat nor a business major.
a. 11/25 b. 4/10
a. 12/25 b. 3/10
a. 9/25 b. 6/10
a. 7/25 b. 5/10
![Of 162 students honored at an academic awards banquet, 48 won awards for mathematics and 78 won awards for English. There are 14 students who won awards for both mathematics and English. A student is selected at random for an interview. What is the probability that the student won an award for English or mathematics? Express your answer as a fraction in simplest form. The probability that the student interviewed won an award for English or mathematics is [?]](https://media.kunduz.com/media/sug-question/raw/80355093-1659818365.757282.jpeg?w=256)
Algebra
Permutations and CombinationsOf 162 students honored at an academic awards banquet, 48 won awards for mathematics and 78 won awards for English. There are 14 students who won awards for both mathematics and English. A student is selected at random for an interview. What is the probability that the student won an award for English or mathematics? Express your answer as a fraction in simplest form. The probability that the student interviewed won an award for English or mathematics is [?]
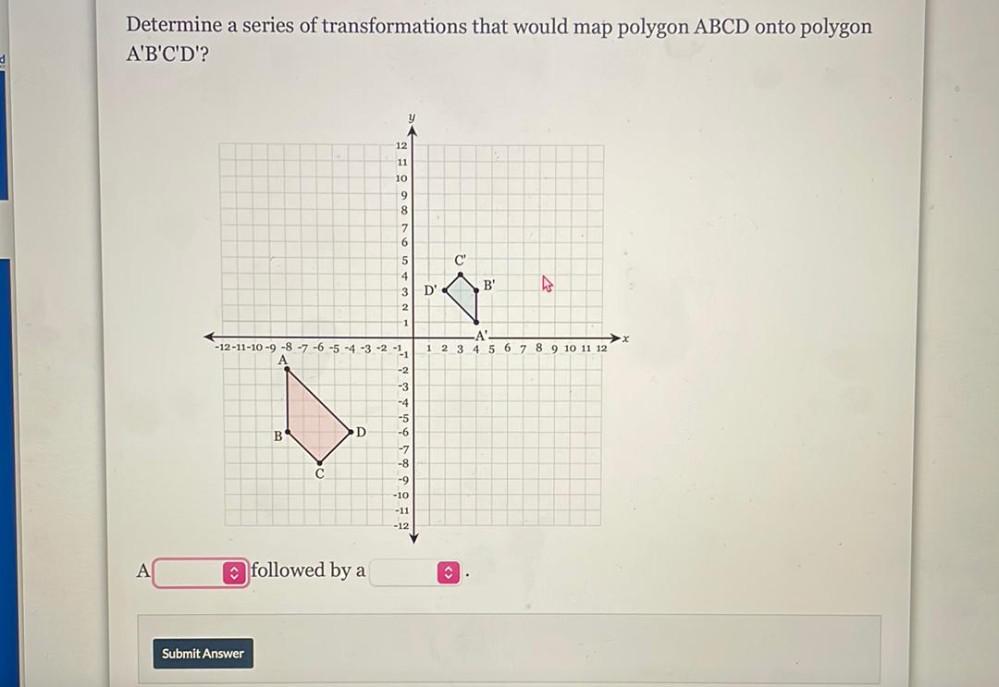
Algebra
Permutations and CombinationsDetermine a series of transformations that would map polygon ABCD onto polygon A'B'C'D'?
Algebra
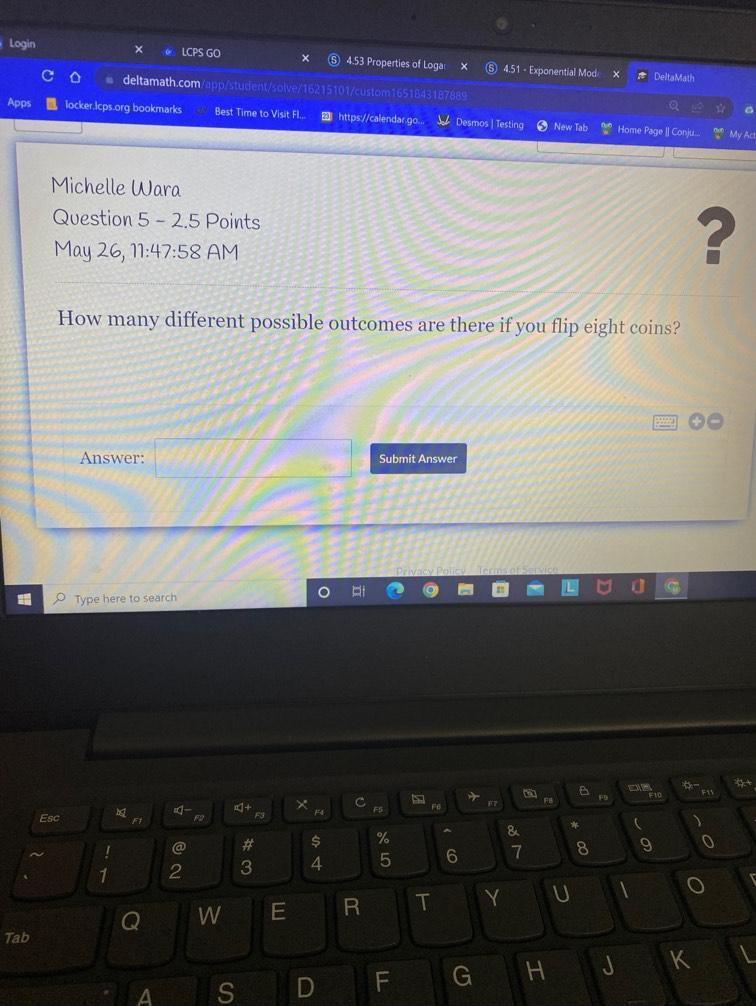
Permutations and CombinationsHow many different possible outcomes are there if you flip eight coins?
Algebra
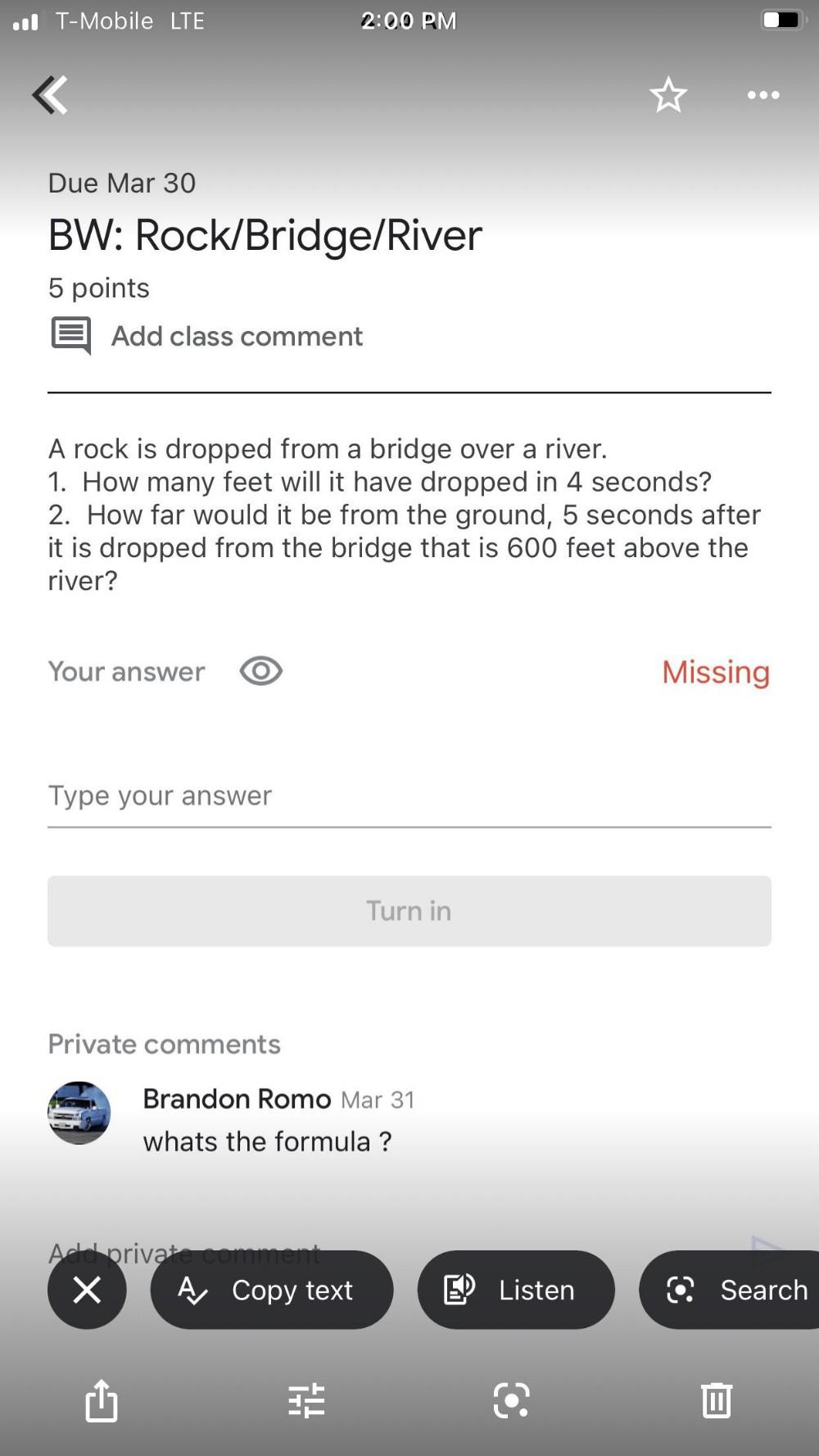
Permutations and CombinationsA rock is dropped from a bridge over a river.
1. How many feet will it have dropped in 4 seconds?
2. How far would it be from the ground, 5 seconds after it is dropped from the bridge that is 600 feet above the river?

Algebra
Permutations and CombinationsIn the game of keno, if eight spots are marked the player wins if five or more of their spots are selected. Complete the chart below:
Outcome
8 winning spots
7 winning spots
6 winning spots
5 winning spots
fewer than 5 winning spots
Algebra
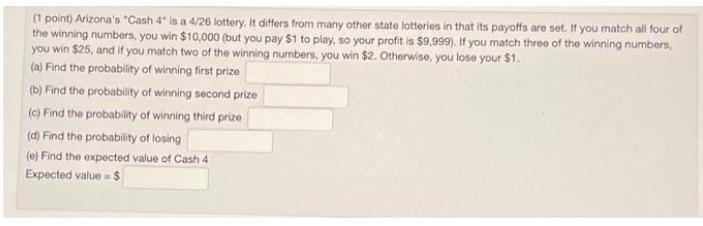
Permutations and CombinationsArizona's "Cash 4" is a 4/26 lottery. It differs from many other state lotteries in that its payoffs are set. If you match all four of the winning numbers, you win $10,000 (but you pay $1 to play, so your profit is $9,999). If you match three of the winning numbers, you win $25, and if you match two of the winning numbers, you win $2. Otherwise, you lose your $1.
(a) Find the probability of winning first prize
(b) Find the probability of winning second prize
(c) Find the probability of winning third prize
(d) Find the probability of losing
(e) Find the expected value of Cash 4
Expected value = $

Algebra
Permutations and CombinationsShow that if a, b, c ∈ Z with c> 0 such that a = b (mod c), then (a, c) = (b, c).
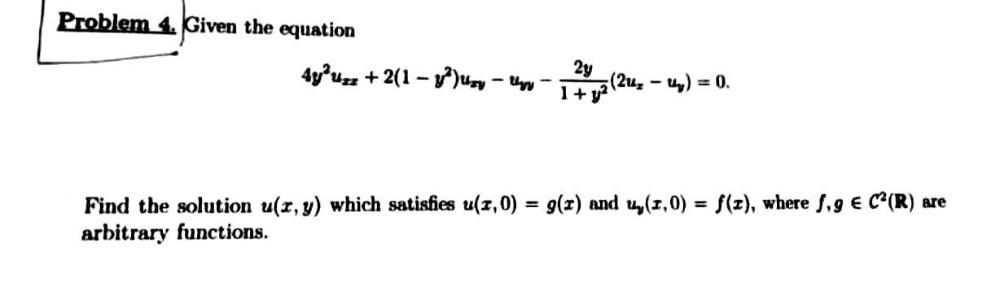
Algebra
Permutations and CombinationsGiven the equation
4y²u𝓏𝓏 + 2(1-y²)u𝓏ᵧ - uᵧᵧ- 2y(2uₓ - uᵧ)/(1+ y²) = 0.
Find the solution u(x, y) which satisfies u(x,0) = g(x) and uᵧ(x,0) = f(x), where f, g ∈ C²(R) are arbitrary functions.

Algebra
Permutations and CombinationsDetermine whether each is dependent or not, based on the rules for independence.
1. P (A) = 1/5, P(B) = 3/10, P(A and B) = 3/100
2. P (A) = 13/20, P(B) = 7/10, P(A and B) = 91/200
3. P (A) = 3/5, P(B) = 2/5, P(A and B) = 6/25


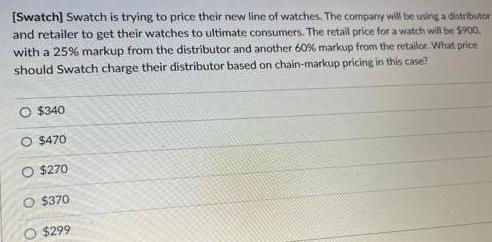
Algebra
Permutations and CombinationsSwatch is trying to price their new line of watches. The company will be using a distributor and retailer to get their watches to ultimate consumers. The retail price for a watch will be $900, with a 25% markup from the distributor and another 60% markup from the retailor. What price should Swatch charge their distributor based on chain-markup pricing in this case?
$340
$470
$270
$370
$299

Algebra
Permutations and CombinationsConsider a mobile moving along the following
path which starts at the point (0, 0). What are
the coordinates of the point of arrival of the
mobile

Algebra
Permutations and CombinationsWrite down the system of linear equations to find the probability that the rat finds the water before dieting. stochastic process.
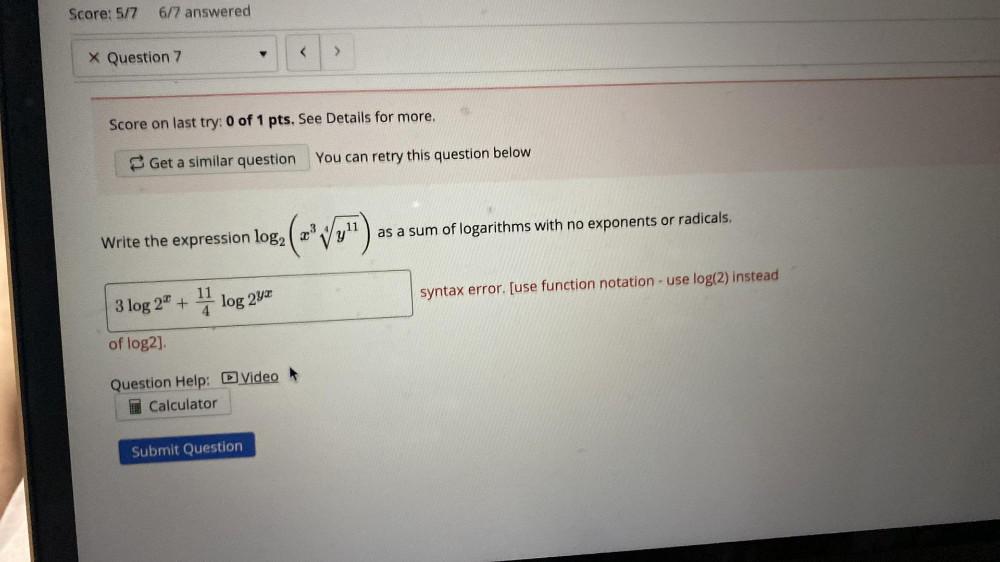
Algebra
Permutations and CombinationsWrite the expression log²(x³ ∜(y¹¹) as a sum of logarithms with no exponents or radicals.
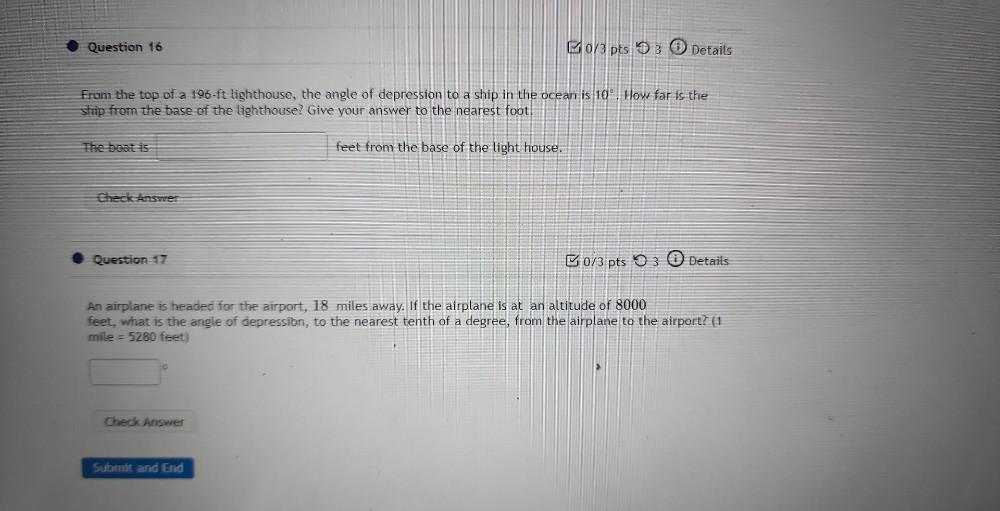
Algebra
Permutations and CombinationsFrom the top of a 196-ft lighthouse, the angle of depression to a ship in the ocean is 10°. How far is the
ship from the base of the lighthouse? Give your answer to the nearest foot. The boat is feet from the base of the light house.
An airplane is headed for the airport, 18 miles away. If the airplane is at an altitude of 8000 feet, what is the angle of depression, to the nearest tenth of a degree, from the airplane to the airport? (1 mile = 5280 feet)

Algebra
Permutations and CombinationsConsider the following homogeneous system of equations,
x-y+u=0
y + 2z-v=0
x+y+u+2v = 0
a) Find the basic solutions of the homogeneous system.
b) Determine the value of the parameters for which
x -1
y -3
m= z = 3
u -2
v 3
is the linear combination of the basic solutions found in a).
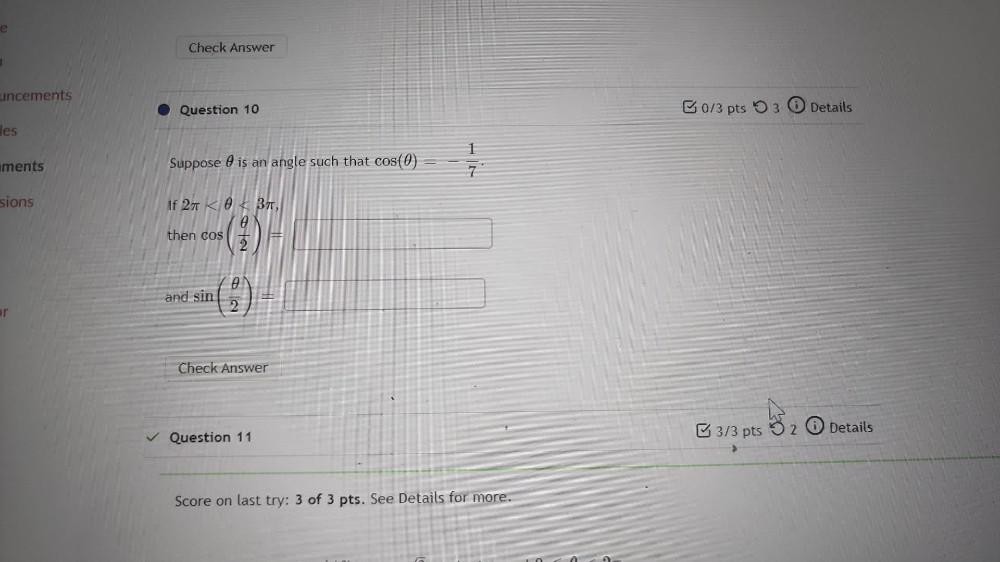
Algebra
Permutations and CombinationsSuppose is an angle such that cos(θ)=-1/7
A)If 2π <θ< 3π,
then cos(θ/2)=__
and sin(θ/2)=__
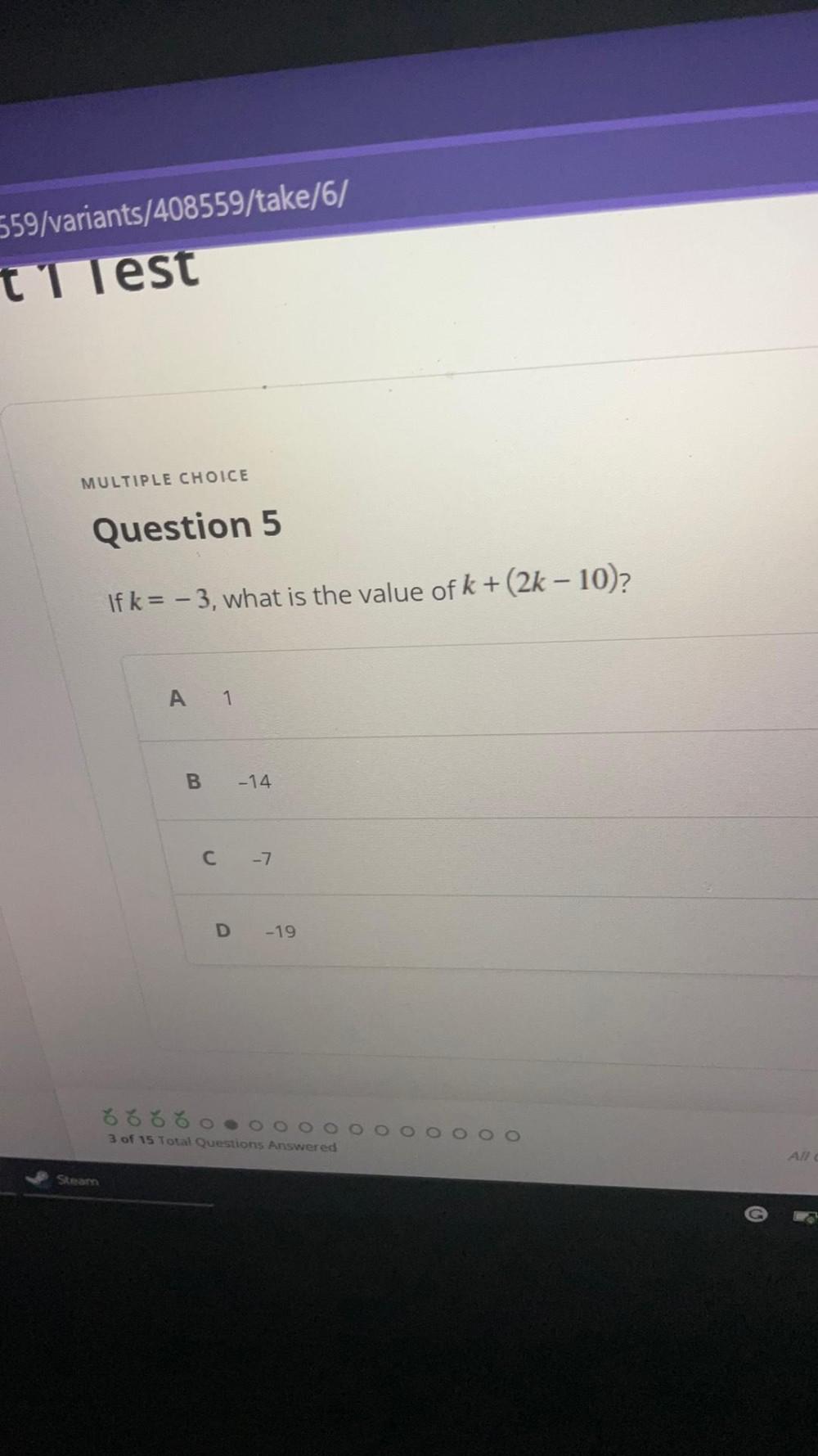
Algebra
Permutations and CombinationsIf k = -3, what is the value of k +(2k-10)?
A )1
B)-14
C) -7
D )-19
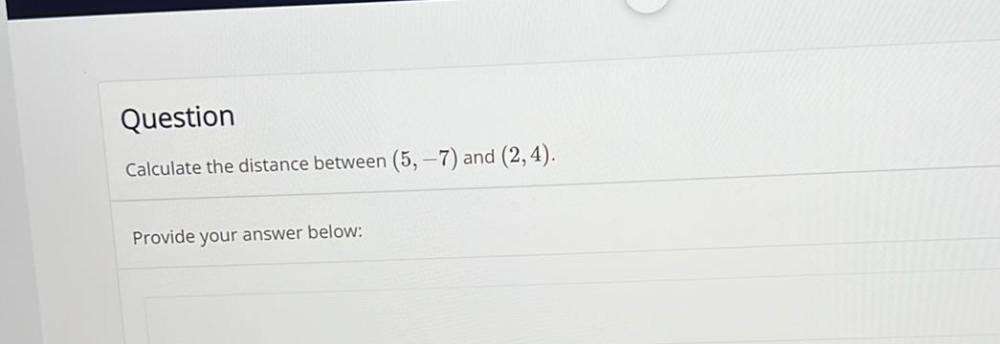
Algebra
Permutations and CombinationsCalculate the distance between (5, -7) and (2,4). Provide your answer below:
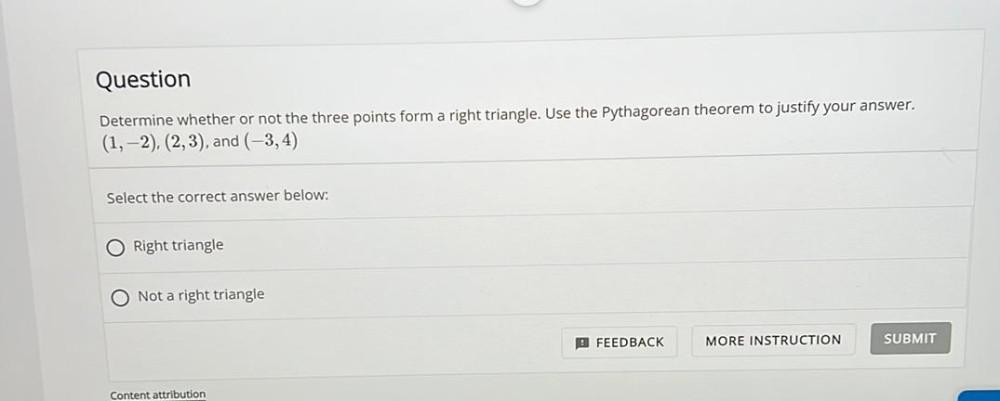
Algebra
Permutations and CombinationsDetermine whether or not the three points form a right triangle. Use the Pythagorean theorem to justify your answer.
(1,-2), (2, 3), and (-3,4)
Select the correct answer below:
(A) Right triangle
(B) Not a right triangle