Permutations and Combinations Questions and Answers

Algebra
Permutations and CombinationsHow many different passwords are possible if each character may be any lowercase letter or digit, and at least one character must be a digit? Enter
your answer in scientific notation with two digits of accuracy after the decimal point.
The possible number of different passwords is

Algebra
Permutations and CombinationsA certain disease has an incidence rate of 1%. It is known that the false negative rate is 10% and the false positive rate is 2%.
Let D be the event that a person has the disease, and let T be the event that a person tests positive. Find P(DT), that is, the probability that someone has the disease, given that he or she has tested positive.
Algebra
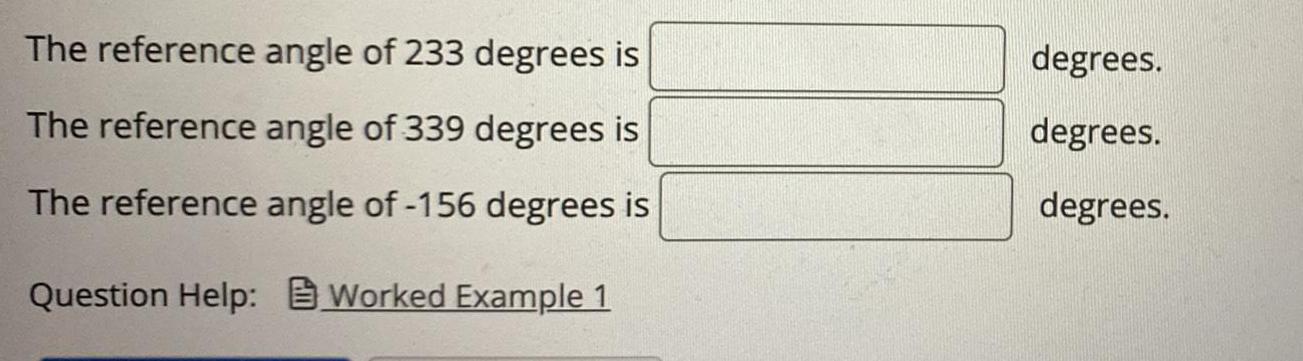
Permutations and CombinationsThe reference angle of 233 degrees is
The reference angle of 339 degrees is
The reference angle of -156 degrees is
Algebra
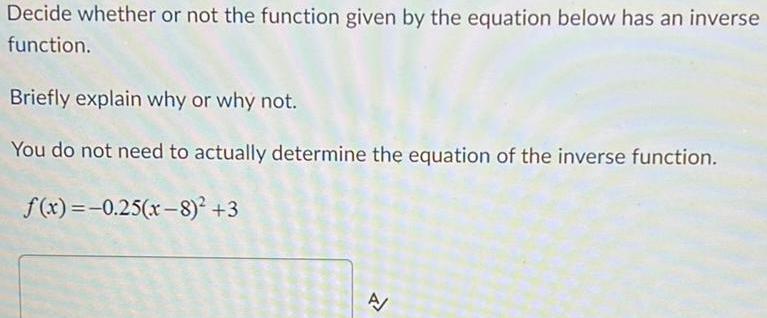
Permutations and CombinationsDecide whether or not the function given by the equation below has an inverse function.
Briefly explain why or why not.
You do not need to actually determine the equation of the inverse function.
f(x)=-0.25(x-8)² +3

Algebra
Permutations and CombinationsA polynomial has a constant term of 6 and a leading coefficient of 4. Which one of the following is a potential rational zero of this polynomial?
A) 3/4
B) 4
c) 2/3
D) 24
E) none of these

Algebra
Permutations and CombinationsA Fermat number is of the form Fn = 2²n + 1.
Find a positive integer k where Fk is not a prime number.
(a) Use Fermat's test to prove that Fk is not a prime number.
(b) Use Miller-Rabin test to prove that Fk is not a prime number.

Algebra
Permutations and CombinationsGiven that 2 is a zero of the polynomial function f(x), find the remaining zeros.
f(x) = x³ - 10x² +41x-50

Algebra
Permutations and CombinationsA 4-person grievance committee is to be selected out of 2 departments, A and B, with 10 and 25 people, respectively. In how many ways can the following committees be selected? Complete parts (A) through (E) below.
(A) 3 from A and 1 from B
(B) 2 from A and 2 from B
(C) All from A
(D) 4 people regardless of department
(E) At least 3 from department A

Algebra
Permutations and CombinationsFind all zeros of the polynomial, (Enter your answers as a comma-separated list. Enter all answers including repetitions.)
P(x)=x4-2x3-7x²- 2x -8

Algebra
Permutations and Combinations3. (Future value) Find the future value of $3600 invested in an account at 5% interest for 10 years if interest is compounded:
a) Annually
b) Continuously

Algebra
Permutations and CombinationsThere are 7 women and 6 men signed up to join a salsa dance class. In how many ways can the instructor choose 4 of the people to join if 1 or fewer must be men?

Algebra
Permutations and CombinationsA catering service offers 3 appetizers, 8 main courses, and 9 desserts. A customer is to select 2 appetizers, 3 main courses, and 4 desserts for a banquet. In how many ways can this be done?

Algebra
Permutations and CombinationsMr T is ready to hit the rod and go on tour. He has a posse consisting of 150 dancers, 90 back-up singers and 150 different musicians and due to union regulations, each performer can only appear once during the tour. A small club tour requires 1 dancer, 1 back-up singer and 2 musicians for each show while a larger arena tours requires 5 dancers, 2 back-up singer and 1 musician for each night. If a club concert nets Mr T $175 a night while an arena shows nets him $400 a night, how many of each show should he schedule so that his income is a maximum and what is his maximum income?
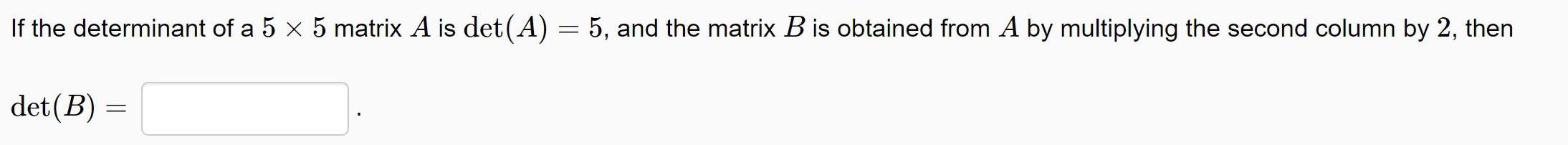
Algebra
Permutations and CombinationsIf the determinant of a 5 × 5 matrix A is det(A)
det (B) =
=
5, and the matrix B is obtained from A by multiplying the second column by 2, then

Algebra
Permutations and CombinationsA pet store has 12 puppies, including 5 poodles, 6 terriers, and 1 retriever. Rebecka and Aaron, in that order, each select one puppy at random without replacement.
Find the probability the
selects a retriever, given Rebecka selects a retriever,
+
Algebra
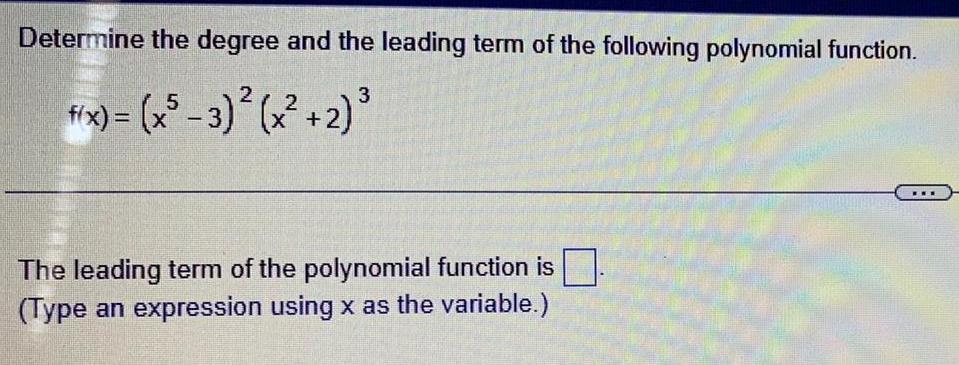
Permutations and CombinationsDetermine the degree and the leading term of the following polynomial function.
3
fix) = (x5-3)²(x²+2) ³
The leading term of the polynomial function is
(Type an expression using x as the variable.)

Algebra
Permutations and CombinationsSantos flipped a coin 300 times. The coin landed heads up 175 times. Find the ratio of heads to total number of coin flips. Express as a simplified ratio.
12 to 7
7 to 12
5 to 12
7 to 5
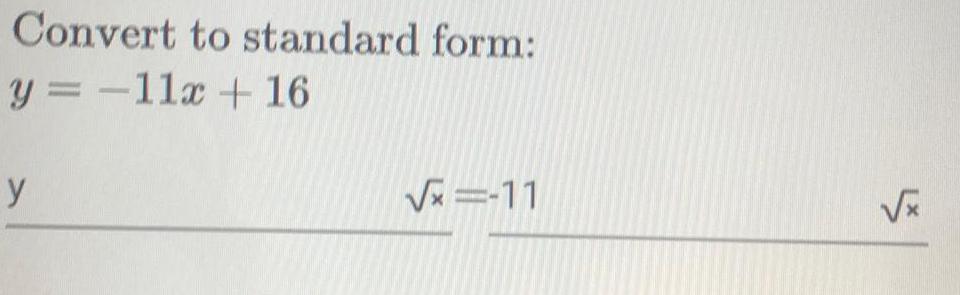

Algebra
Permutations and CombinationsFind the miles per second traveled if one travels 60 miles in 6 hours.
Round to five decimal places if necessary.
√x x miles/second

Algebra
Permutations and CombinationsGiven the set of all of the integers from 15 to 49, what is the probability of choosing a number that is a multiple of 7? If you enter your answer as a decimal, round to the thousandths place. √x

Algebra
Permutations and CombinationsFit a linear function of the form f(t) = co+c₁t to the data points (-8, 27). (0,2). (8, 37), using least squares.
f(t)
Algebra
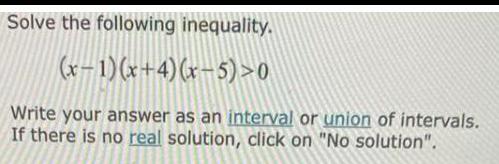
Permutations and CombinationsSolve the following inequality.
(x-1)(x+4)(x-5)>0
Write your answer as an interval or union of intervals.
If there is no real solution, click on "No solution".

Algebra
Permutations and CombinationsConsider the following relation.
-4x8y = 4
Step 2 of 2: Determine if the relation is a function. If it is not, identify two ordered pairs as proof.

Algebra
Permutations and CombinationsHow many ounces of water must be added to 145 oz. of 55% sodium bicarbonate solution to produce a 30% solution? Round your answer to the nearest hundredth. OZ.

Algebra
Permutations and CombinationsWhen the number 1 is written as an exponential expression with a base of 4, what is the exponent?

Algebra
Permutations and CombinationsFind all zeros of the function.
f(x) = x^4 − 9x³ + 13x² + 45x − 50
Entry tip: Enter the zeros separated by commas.
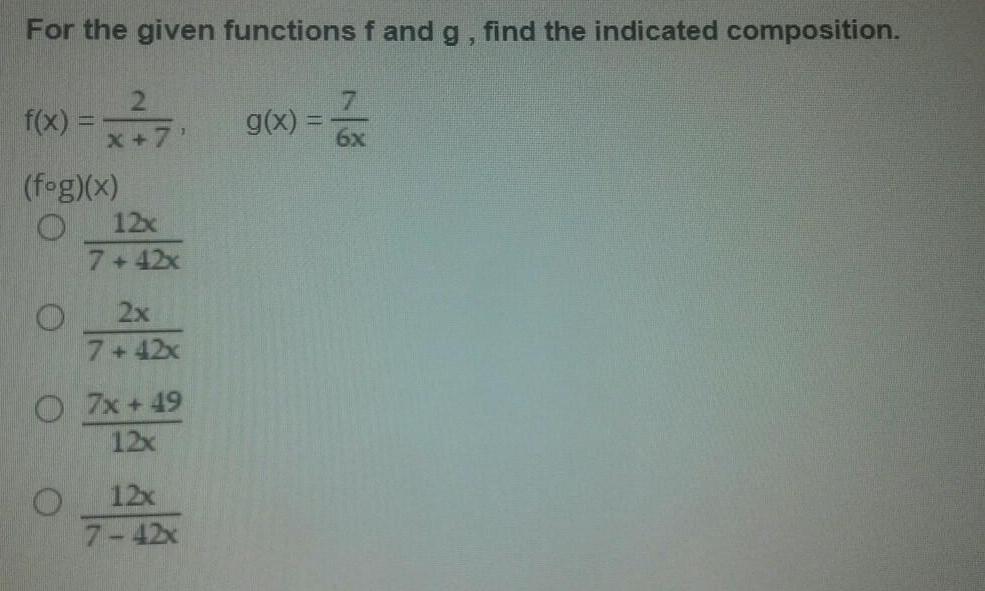
Algebra
Permutations and CombinationsFor the given functions f and g, find the indicated composition.
f(x) =2/ (x+7) g(x)=7/6x
(fog)(x)

Algebra
Permutations and CombinationsGiven functions f and g, perform the indicated operations.
f(x) = 6x² - 7x, g(x) = x² - 2x - 35
Find f/g
(6-x)/35
(6x²-7x)/(x^2-2x-35)
(6x-7)/-2
6x/x+1
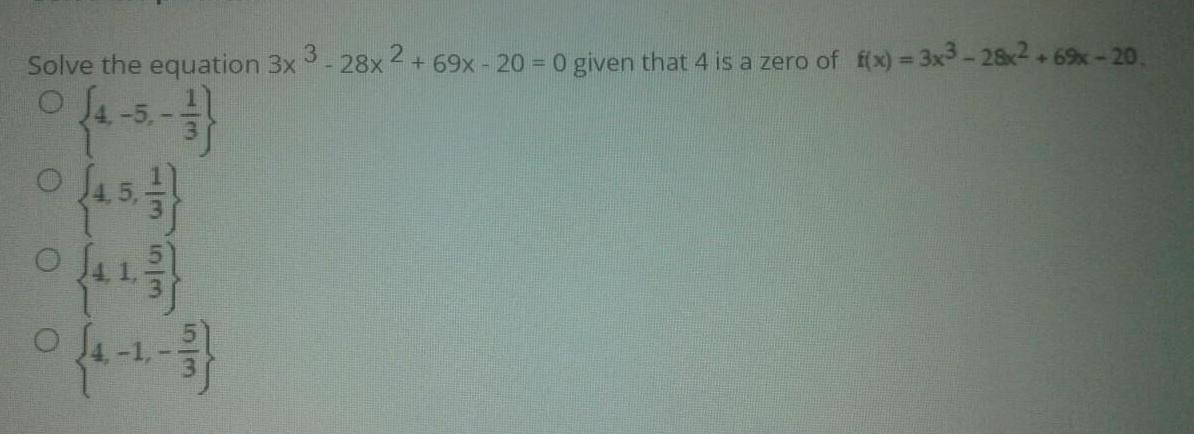
Algebra
Permutations and CombinationsSolve the equation 3x^3-28x^2+69x - 20 = 0 given that 4 is a zero of f(x) = 3x³-28x²+69x-20.

Algebra
Permutations and CombinationsFind the inverse of the one-to-one function.
f(x) = 3x-7/5
f⁻¹(x) =5/3x + 7
f⁻¹(x) =5x+7/3
f⁻¹(x) =5/3x-7
f⁻¹(x) =5x-7/3
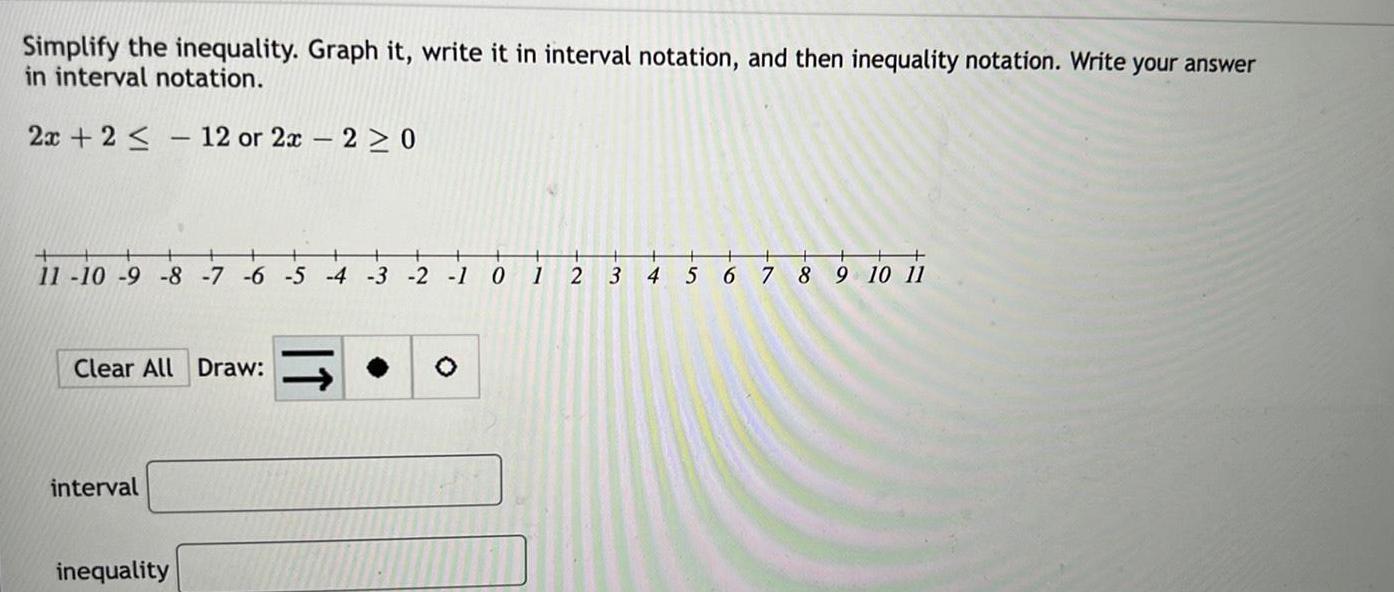
Algebra
Permutations and CombinationsSimplify the inequality. Graph it, write it in interval notation, and then inequality notation. Write your answer in interval notation.
2x+2 ≤12 or 2x - 2≥0

Algebra
Permutations and CombinationsAre the following statements true or false?
1. If the set of vectors U spans a subspace S, then vectors can be added to U to create a basis for S
2. If the set of vectors U spans a subspace S, then vectors can be removed from U to create a basis for
3. If S₁ and S₂ are subspaces of R" of the same dimension, then S₁ = S₂.
4. If the set of vectors U is linearly independent in a subspace S then vectors can be added to U to create a basis for S
5. If the set of vectors U is linearly independent in a subspace S then vectors can be removed from U to create a basis for S.
![To simplify the measurement of the acidity or basicity of a solution, the pH (hydrogen potential) measure was developed. The pH is given by the formula pH = -log [H+], where [H] is the concentration of hydrogen ions in moles per liter in the solution. Find the pH value of a solution for which [H*] =0.0000346.](https://media.kunduz.com/media/sug-question/raw/84477729-1657790166.4236436.jpeg?w=256)
Algebra
Permutations and CombinationsTo simplify the measurement of the acidity or basicity of a solution, the pH (hydrogen potential) measure was developed. The pH is given by the formula pH = -log [H+], where [H] is the concentration of hydrogen ions in moles per liter in the solution. Find the pH value of a solution for which [H*] =0.0000346.
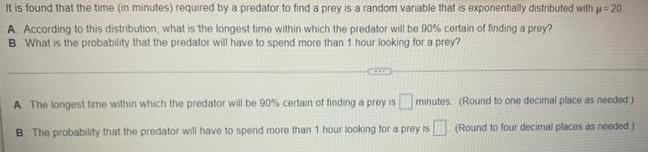
Algebra
Permutations and CombinationsIt is found that the time (in minutes) required by a predator to find a prey is a random variable that is exponentially distributed with μ-20
A According to this distribution, what is the longest time within which the predator will be 90% certain of finding a prey?
B. What is the probability that the predator will have to spend more than 1 hour looking for a prey?
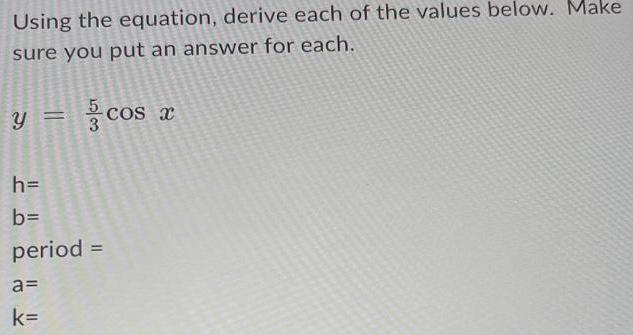
Algebra
Permutations and CombinationsUsing the equation, derive each of the values below. Make
sure you put an answer for each.
y = cos x
h=
b=
period =
a=
k=

Algebra
Permutations and CombinationsA commutative ring with unity element and without zero divisor is called a/an
a. field.
b. subfield.
c. subring.
d. integral domain.

Algebra
Permutations and CombinationsNightclub Management
You have just
opened a new nightclub, Russ' Techno
Pitstop, but are unsure of how high to set the
cover charge (entrance fee). One week you
charged $8 per guest and averaged 240
guests per night. The next week you charged
$10 per guest and averaged 200 guests per
night.
(a)
Find a linear demand equation showing the
number of guests q per night as a function of
the cover charge p.
q(p) =
(b)
Find the nightly revenue R as a function of the
cover charge p.
R(p) =
(c)
The club will provide two free non-alcoholic
drinks for each guest, costing the club $2 per
head. In addition, the nightly overheads (rent,
salaries, dancers, DJ, etc.) amount to $1,000.
Find the cost C as a function of the cover
charge p.
C(p) =
(d)
Now find the profit in terms of the cover
charge p.
P(p) =
Determine the entrance fee you should
charge for a maximum profit (in dollars).
p= $ per guest

Algebra
Permutations and CombinationsFind the general solution of the following equation. Express the solution explicitly as a function of the independent variable.
t^-4 y(t)=7
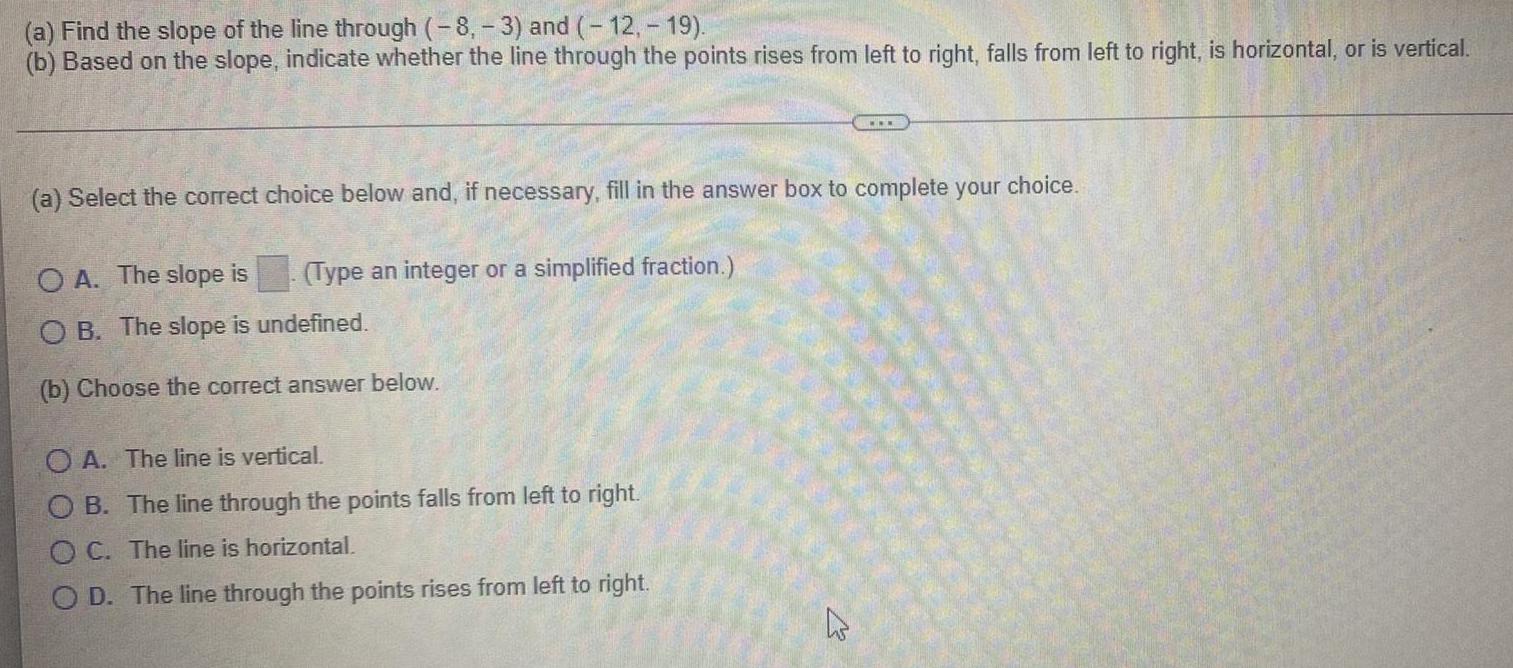
Algebra
Permutations and Combinations(a) Find the slope of the line through (-8, -3) and (-12, -19).
(b) Based on the slope, indicate whether the line through the points rises from left to right, falls from left to right, is horizontal, or is vertical.
(a) Select the correct choice below and, if necessary, fill in the answer box to complete
your choice.
(Type an integer or a simplified fraction.)
A. The slope is
B. The slope is undefined.
(b) Choose the correct answer below.
A. The line is vertical.
B. The line through the points falls from left to right.
C. The line is horizontal.
D. The line through the points rises from left to right.

Algebra
Permutations and CombinationsA standard 52-card deck has four 13-card suits: diamonds, hearts, clubs, and spades. The diamonds and hearts are red, and the clubs and spades are black. Each 13-card suit contains cards numbered from 2 to 10, a jack, a queen, a king, and an ace. An experiment consists of drawing 1 card from the standard deck. Find the probability of drawing a black five of hearts.

Algebra
Permutations and CombinationsHow many four letter passwords are possible if the first letter must be A or U, the second letter must be a vowel and repetition is not allowed?
4416
5520
- 4800
5200
6624

Algebra
Permutations and CombinationsThe notation X~ N(μ, o) is read as follows: X (represents a population distribution) has a normal distribution (represented by M) with mean μ and standard deviation o. This notation is a shorthand way to represent a distribution.
Sampling Distribution and Probability
Q1. If XN(42, 10) and X (represents sampling distribution of the mean) is computed from a random sample of size n 81, what is the distribution of X? In other words, what is X-N(?, ?)?

Algebra
Permutations and CombinationsOn your morning run you pass through a park where the paths are laid in hexagons. You always run left to right. How many possible routes are there through the park.
(A) 8
(B) 12
(C) 16
(D)20
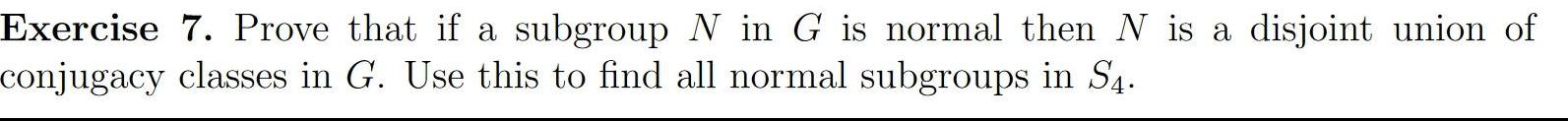
Algebra
Permutations and CombinationsProve that if a subgroup N in G is normal then N is a disjoint union of conjugacy classes in G. Use this to find all normal subgroups in S4.
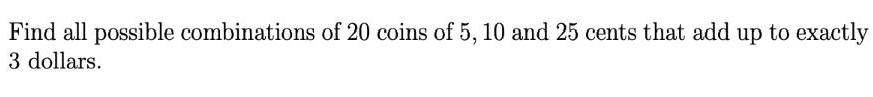
Algebra
Permutations and CombinationsFind all possible combinations of 20 coins of 5, 10 and 25 cents that add up to exactly 3 dollars.
Algebra
Permutations and CombinationsSuppose that $13,095 is invested at an interest rate of 5.2% per year, compounded continuously.
a) Find the exponential function that describes the amount in the account after time t, in years.
b) What is the balance after 1 year? 2 years? 5 years? 10 years?
c) What is the doubling time?
a) The exponential growth function is P(t) =

Algebra
Permutations and CombinationsBilly and Jane are trying to determine how far they can travel in 8 hours if they travel at a rate of 86 km/h. Billy determines they could travel 688 km, while Jane determines they could travel 10.75 km. Who is correct? Use dimensional (unit) analysis to justify your answer.

Algebra
Permutations and CombinationsA rectangular swimming pool is 6 ft deep. One side of the pool is 2.5 times longer than the other. The amount of water needed to fill the swimming pool is 2160 cubic feet. Find the dimensions of the pool.