Sequences & Series Questions and Answers

Algebra
Sequences & SeriesFind the sum of the smallest four-digit positive integer and the greatest three-digit negative integer.

Algebra
Sequences & SeriesAdd and subtract the following terms, if possible.
3√48-√√27 +3√75-√72
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. 3√48-√27 +3√75-√72 =
(Type an exact answer, using radicals as needed.)
B. The radicals cannot be combined.

Algebra
Sequences & SeriesA rock weighing 32.0 g is placed in a graduated cylinder displacing the volume from 12.3 mL to 16.8 mL. What is density of the rock in g/cm3? density = __ g/cm³

Algebra
Sequences & SeriesWhich of the following is the correct way to express 0.0000321 in scientific notation?
A. 32.1 x 106
B. 3.21 x 105
C. 3.21 x 10-5
D. 32.1 x 10-6
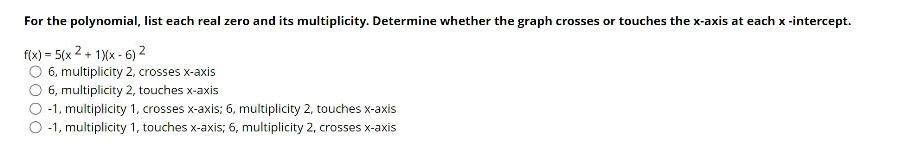
Algebra
Sequences & SeriesFor the polynomial, list each real zero and its multiplicity. Determine whether the graph crosses or touches the x-axis at each x -intercept.
f(x) = 5(x 2 + 1)(x-6) ²
6, multiplicity 2, crosses x-axis
6, multiplicity 2, touches x-axis
-1, multiplicity 1, crosses x-axis; 6, multiplicity 2, touches x-axis
-1, multiplicity 1, touches x-axis; 6, multiplicity 2, crosses x-axis

Algebra
Sequences & SeriesWrite an equation in slope-intercept form for the line with slope - and
--5

Algebra
Sequences & SeriesWhat is the y-intercept of y = a cos(kx) + c?
a) a+c
b) a-c
c) Not possible to find the y-int without the actual values of a, k and c
d) c

Algebra
Sequences & SeriesEvaluate the following statement as true or false:
In f(x) = sin(x) + c, if c < 0, the function f(x) = sin(x) moves down and if c > 0,
f(x) = sin(x) moves up.
a) True
b) False
![Calculate the volume of an object with dimensions measuring:
12 cm x 3 cm x 9 cm
[?] cm³](https://media.kunduz.com/media/sug-question/raw/83443162-1660307726.7693884.jpeg?w=256)
Algebra
Sequences & SeriesCalculate the volume of an object with dimensions measuring:
12 cm x 3 cm x 9 cm
[?] cm³
![A liquid that occupies a volume of 4.7 L has a mass of 5.1 kg. What is the density of the liquid in kg/L?
density = [?] kg/L
Round your answer to the tenths place.
Density (kg/L)](https://media.kunduz.com/media/sug-question/raw/83442992-1660307457.8084366.jpeg?w=256)
Algebra
Sequences & SeriesA liquid that occupies a volume of 4.7 L has a mass of 5.1 kg. What is the density of the liquid in kg/L?
density = [?] kg/L
Round your answer to the tenths place.
Density (kg/L)

Algebra
Sequences & SeriesA trigonometric function of the form f(x) = a sin(x) has a maximum at 4 and a minimum at-4. The function would be:
a) f(x) = sin(x) + 4
b) J(x) = sin(4x)
c) f(x) = 4 sin(x)
d) f(x) = sin(x) - 4

Algebra
Sequences & SeriesThe range for the function f(x) = -3 sin x is:
a) Range:{y|0 ≤ y ≤ 3, y ≤ R}
b) Range: {y-3 ≤ y ≤ 3, y ≤ R}
c) Range: {y2 ≤ y ≤ 3, ye R}
d) Range: {y-2≤ y ≤ 3, ye R}
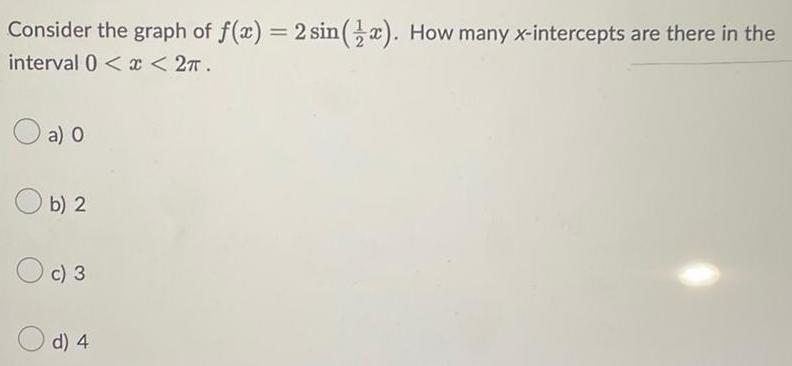
Algebra
Sequences & SeriesConsider the graph of f(x) = 2 sin(x). How many x-intercepts are there in the
interval 0 < x < 2π.
a) 0
b) 2
c) 3
d) 4

Algebra
Sequences & SeriesWhich of the following do we need to be concerned about when determining domain of a real-valued function?
Partial Fractions
Division by Zero
Complex Numbers
Irrational Numbers

Algebra
Sequences & SeriesThe function f(x) = cos x is an example of:
a) a horizontal compression
b) a vertical stretch
c) a horizontal stretch
d) a vertical compression
![This time, include both the coefficient and exponent.
Express 0.00212 in scientific notation.
[? ]×10¹²]
Enter the coefficient in the green box and the](https://media.kunduz.com/media/sug-question/raw/83444099-1660305090.8536544.jpeg?w=256)
Algebra
Sequences & SeriesThis time, include both the coefficient and exponent.
Express 0.00212 in scientific notation.
[? ]×10¹²]
Enter the coefficient in the green box and the


Algebra
Sequences & SeriesSolve the absolute value inequality.
|2x - 2| <6
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set in interval notation is
(Simplify your answer.)
B. The solution set is Ø.
![Convert 100.6 Kelvin to degrees C.
°C = K -273
[?] °C](https://media.kunduz.com/media/sug-question/raw/83434032-1660304429.3979814.jpeg?w=256)
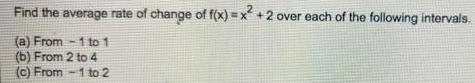
Algebra
Sequences & SeriesFind the average rate of change of f(x)=x²+2 over each of the following intervals.
(a) From-1 to 1
(b) From 2 to 4
(c) From-1 to 2

Algebra
Sequences & SeriesThe function f(x) = sin a can be transformed to a function equivalent to
g(x): = cos a by a phase shift of:
a) units to the left
b) units to the right
c) units to the right
d) units to the left

Algebra
Sequences & SeriesIn f(x) = cos kæ, if k is negative:
a) the function is reflected about both the x and y axes
b) the function is reflected in the x-axis
c) the function's initial value is a minimum
d) the function is reflected in the y-axis
![A piece of copper has a volume of 5.00 cm3. The density of copper is 8.96 g/cm3.
What is the mass of the copper piece?
mass = [?] g](https://media.kunduz.com/media/sug-question/raw/83442699-1660303874.4029067.jpeg?w=256)
Algebra
Sequences & SeriesA piece of copper has a volume of 5.00 cm3. The density of copper is 8.96 g/cm3.
What is the mass of the copper piece?
mass = [?] g

Algebra
Sequences & SeriesFor the function f(x) = -2 cos (3x) -1, the period is:
a) 2
b) 67
c) 1/10
d) -4/3
![The volume of the granite as determined by water displacement is 9.35 mL. What is the volume of the granite in cm3?
Remember: 1 mL = 1 cm3
volume = [?] cm³](https://media.kunduz.com/media/sug-question/raw/83441411-1660303752.8071573.jpeg?w=256)
Algebra
Sequences & SeriesThe volume of the granite as determined by water displacement is 9.35 mL. What is the volume of the granite in cm3?
Remember: 1 mL = 1 cm3
volume = [?] cm³

Algebra
Sequences & SeriesWhich function of the form f(x) = 3 sin(x) + c passes through the point: A(2,5)
a) f(x) = 3 sin(x) +2
b) J(x) = sin(x) - Z
c) f(x) = 3 sin(x) + 4
d) f(x) = 3 sin(x) + 5

Algebra
Sequences & SeriesFind the equation of the line that has y-intercept (0,-7) and slope-4. Write the equation in the form y = mx + b.
y=-7x-4
y = -4x+7
y=-4x-7
y = 4x + 7
Oy=7x-4

Algebra
Sequences & SeriesThe domain of the three basic trigonometric functions is Domain = {x|x € R}. This statement is:
a) true only for the cosine function
b) true for both the sine and cosine functions
c) true for all three basic trigonometric functions
d) true only for the sine function

Algebra
Sequences & SeriesDraw the given rotational angle on the x- y coordinate axis beginning at the positive x-axis. Show all rotation. Then find the EXACT SPECIAL ANGLE VALUE of each
trigonometric function given below. Write your simplified and rationalized answers on the lines provided. DO NOT give
decimal approximations.
cot
sec (-1320)
cos 990°

Algebra
Sequences & SeriesUse the alternative form of the dot product to find u. v.
||u|| = 50, ||v|| = 50, and the angle between u and v is 5π/6.

Algebra
Sequences & SeriesThe trigonometric functions have a period of 27 radians. This statement is:
a) true for all three basic trigonometric functions
b) true only for the cosine function
c) true for both the sine and cosine functions
d) true only for the sine function

Algebra
Sequences & SeriesThe doubling period of a bacterial population is 10 minutes. At time 110 minutes, the bacterial
population was 60000.
What was the initial population at time t=0?
Find the size of the bacterial population after 3 hours.

Algebra
Sequences & SeriesA 60-foot piece of siding is cut into three pieces so that the second piece is four times as long as the first piece and the third piece is five times as long as the first piece. If x represents the length of the first piece, find the lengths of all three pieces.
The length of the first piece of siding is
long, the length of the second piece is
long, and the length of the third piece is long.

Algebra
Sequences & SeriesA ferris wheel at an amusement park completes one revolution every 40 seconds.
The cars can reach the maximum of 5 metres above the ground and a minimum of 1
metre above the ground. The height, h, in meters, above the ground can be modelled
using a sinusodial function. What is the radius of the ferris wheel?
a) 2 meters
b) 4 meters
c) 2.5 meters
d) 5 meters

Algebra
Sequences & SeriesAll asymptotes to the tangent function occur when:
a) cos x = 1
b) sin x = 1
c) sin x = 0
d)
![Find A in degrees.C = 110°
a = 11
b=7
A = [?] degrees](https://media.kunduz.com/media/sug-question/raw/83304309-1660302275.4829245.jpeg?w=256)
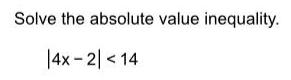
![Find C in degrees.
A = 29°
b= 4
C = 10
C = [?] degrees](https://media.kunduz.com/media/sug-question/raw/83302659-1660301628.894811.jpeg?w=256)
![Find x if the mean of the given data is 7.
x 12 3 4 3 85 11
X= = [?]](https://media.kunduz.com/media/sug-question/raw/85004175-1660301274.6165524.jpeg?w=256)
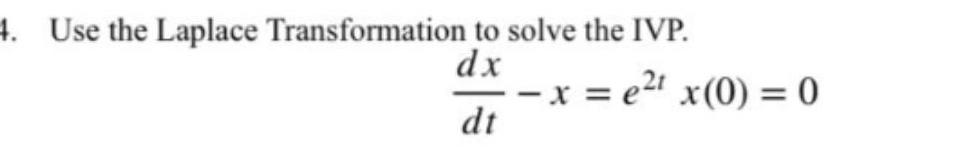

Algebra
Sequences & SeriesUse the formulas for lowering powers to rewrite the expression in terms of the first power of cosine, as in Example 4. sin(x)

Algebra
Sequences & SeriesQuestion 6. Continuous functions
Consider the function
f(x) = -2x, x < 0
0 < x < 1
x-1, x ≥ 1
(a) Sketch f.
(b) At which points of its domain is the function continuous?
(c) At which points of its domain is the function discontinuous? Appeal to the definition of continuity in justifying your answers.

Algebra
Sequences & SeriesMake a list of all possible rational zeros of f(x) = x5
2x² + 4x + 5.
If the answer is not an integer, enter it as a fraction. If there are multiple zeros, separate the answers with commas ().
Rational Zero Candidates:
Algebra
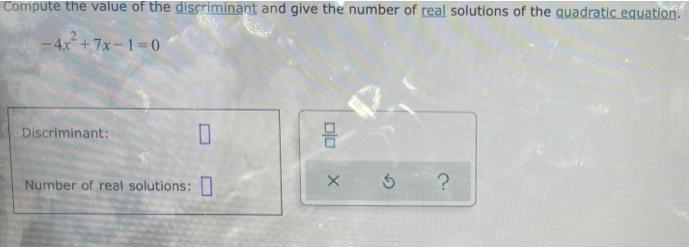
Sequences & SeriesCompute the value of the discriminant and give the number of real solutions of the quadratic equation.
-4x²+7x-1=0
Algebra
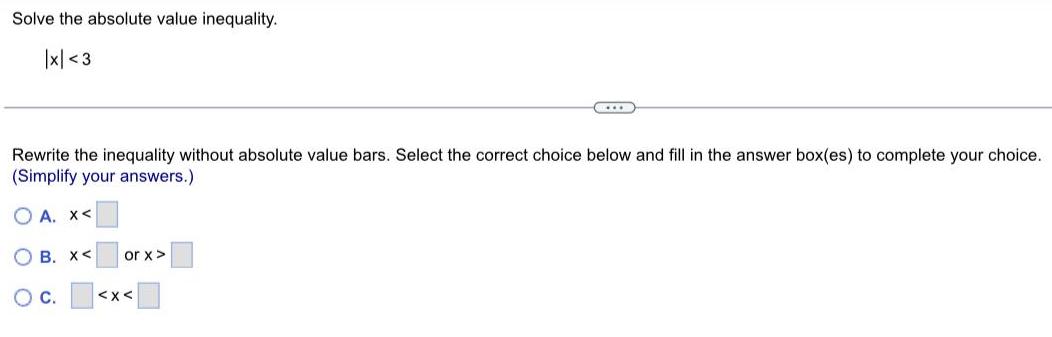
Sequences & SeriesSolve the absolute value inequality.
|x|<3
Rewrite the inequality without absolute value bars. Select the correct choice below and fill in the answer box(es) to complete your choice.
(Simplify your answers.)
A. X<
B. X< or x>
C. <x<

Algebra
Sequences & SeriesOther than a no solution set, use interval notation to express the solution set and then graph the solution set on a number line.
2x+4> 10
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. The solution set is (Type your answer using interval notation.)
B. The solution set is Ø.
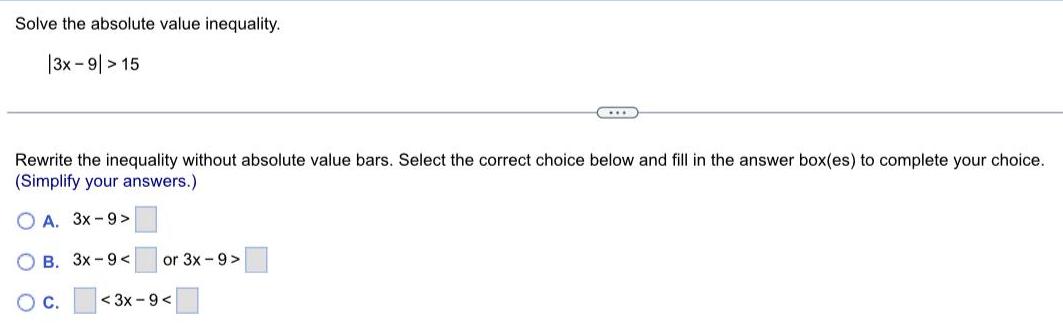
Algebra
Sequences & SeriesSolve the absolute value inequality.
|3x-9| > 15
Rewrite the inequality without absolute value bars. Select the correct choice below and fill in the answer box(es) to complete your choice.
(Simplify your answers.)
A. 3x-9> __
B. 3x-9< __ or 3x-9>__
C. __<3x-9< __

Algebra
Sequences & SeriesIf nominal rate of interest is 4% per annum and interest is compounded quarterly, then find the effective rate of interest.

Algebra
Sequences & SeriesUse the given conditions to find the exact values of sin 2u, cos 2u, and tan 2u using the
double-angle formulas.
cos u = -4/5, π/2<u<π
sin 2u = ________
cos 2u =________