Sequences & Series Questions and Answers

Algebra
Sequences & SeriesLeticia drew a triangle with exactly two sides of equal length. What type of triangle did Leticia draw?
(A) scalene
(B) isosceles
(C)equilateral
(D) equiangular
![Evaluate and simplify the expression when x = 3 and y = 5. 2y + 3(x − y) + x² = [?]](https://media.kunduz.com/media/sug-question/raw/79379808-1659890907.430329.jpeg?w=256)
Algebra
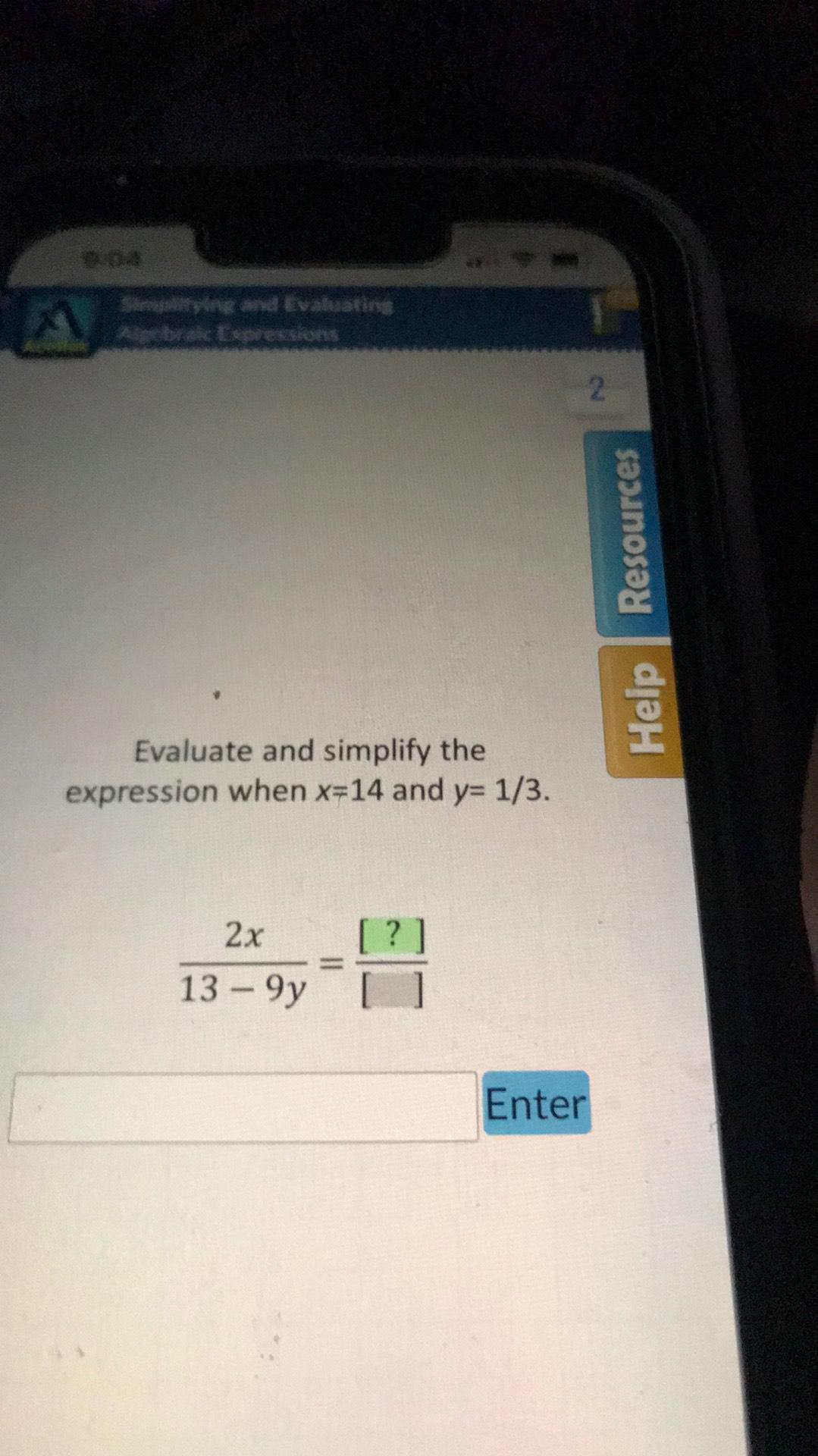
Sequences & SeriesEvaluate and simplify the expression when x = 3 and y = 5. 2y + 3(x − y) + x² = [?]
Algebra
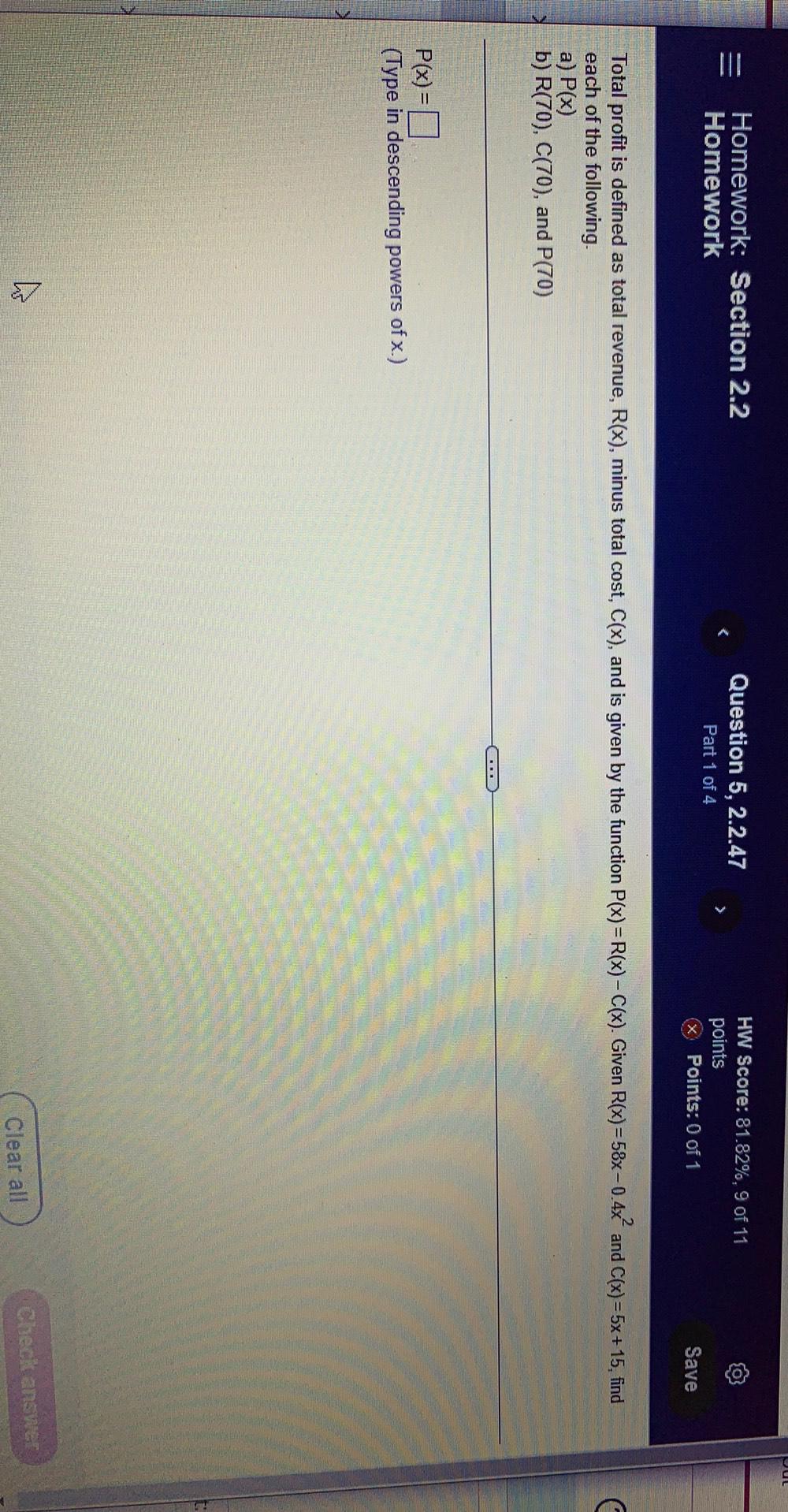
Sequences & SeriesTotal profit is defined as total revenue, R(x), minus total cost, C(x), and is given by the function P(x) = R(x) - C(x). Given R(x)=58x-0.4x² and C(x) = 5x +15, find each of the following.
a) P(x)
b) R(70), C(70), and P(70)
Algebra
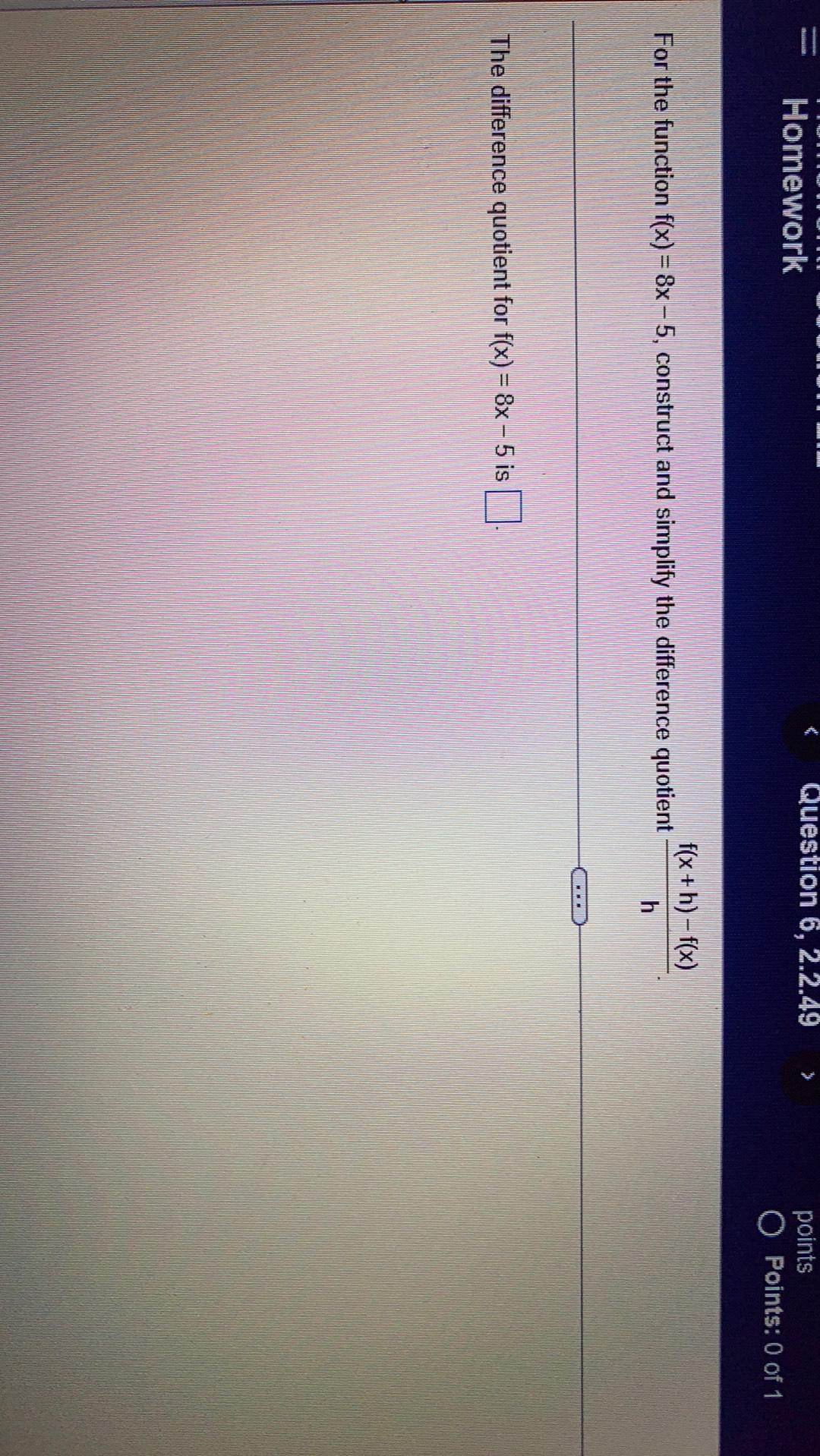
Sequences & SeriesFor the function f(x) = 8x - 5, construct and simplify the difference quotient
{f(x+h)-f(x)}\h
The difference quotient for f(x) = 8x - 5 is
Algebra
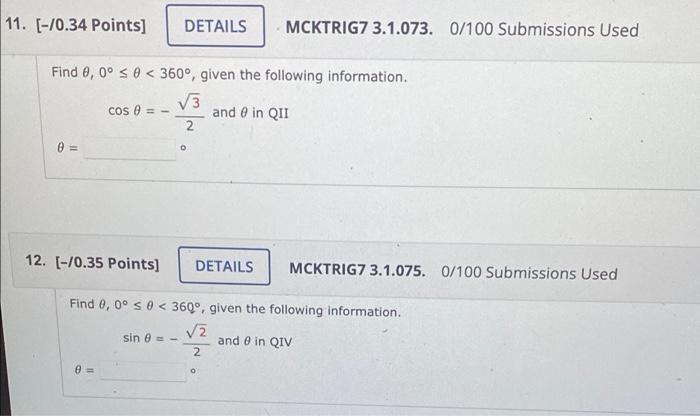
Sequences & SeriesFind θ, 0°≤ θ < 360°, given the following information.
cosθ= -√3/2 and θ in QII
Algebra
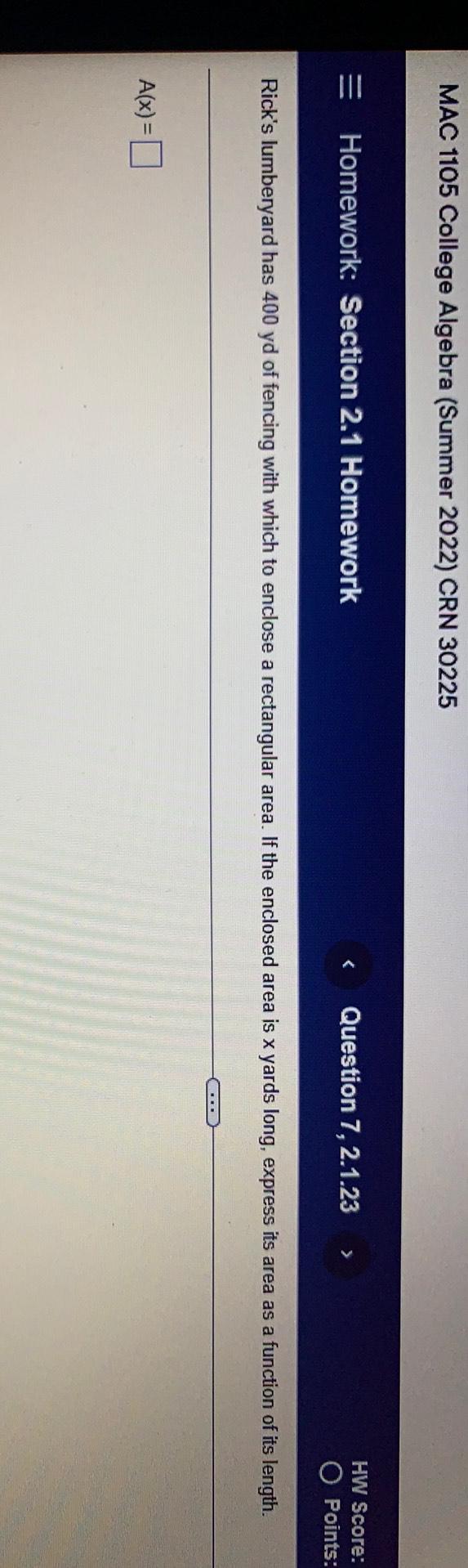
Sequences & SeriesRick's lumberyard has 400 yd of fencing with which to enclose a rectangular area. If the enclosed area is x yards long, express its area as a function of its length.
Algebra
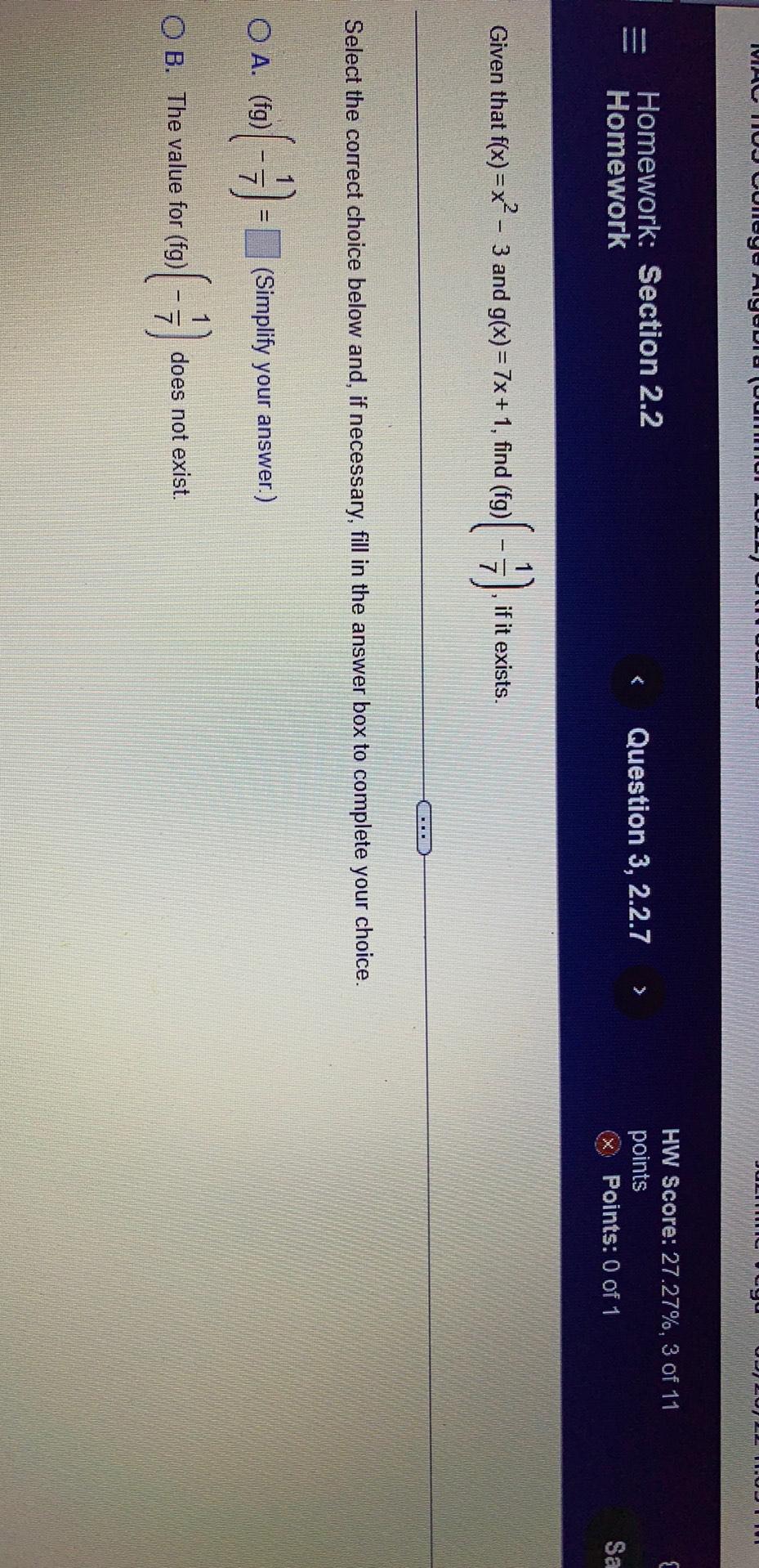
Sequences & SeriesGiven that f(x)=x²- 3 and g(x) = 7x + 1, find (fg) (-1/7) if it exists.
Select the correct choice below and, if necessary, fill in the answer box to complete your choice.
A. (fg)(-1/7)=
B. The value for (fg)(-1/7) does not exist.
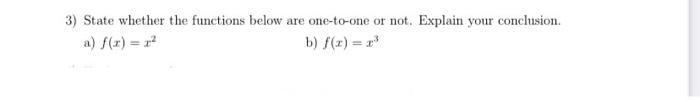
Algebra
Sequences & SeriesState whether the functions below are one-to-one or not. Explain your conclusion.
(a) f(x) = x²
(b) f(x) = x³
Algebra
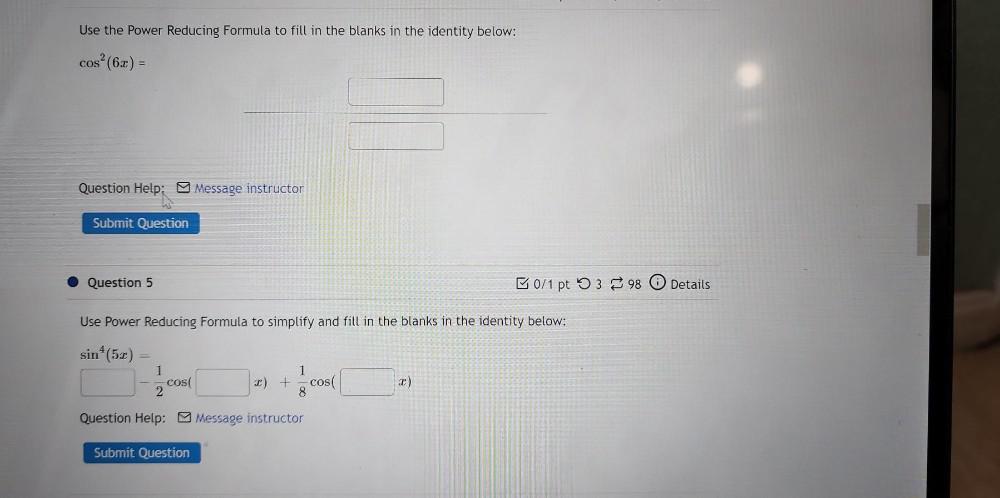
Sequences & SeriesUse the Power Reducing Formula to fill in the blanks in the identity below:
Use Power Reducing Formula to simplify and fill in the blanks in the identity below:
sin^(4)(5x) =
Algebra
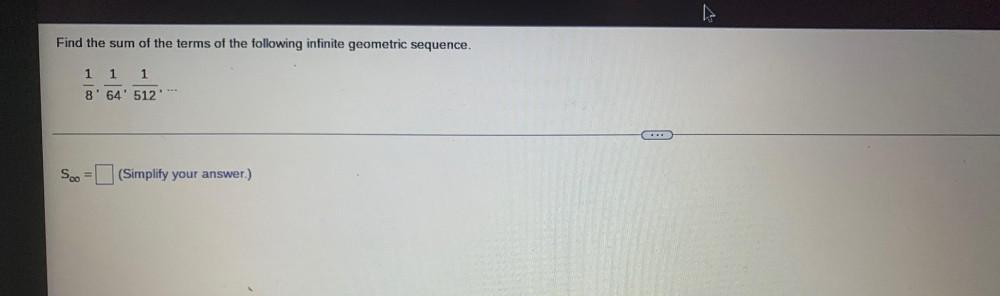
Sequences & SeriesFind the sum of the terms of the following infinite geometric sequence.
1/8, 1/64, 1/512

Algebra
Sequences & SeriesLet X₁ be a closed subspace and X₂ be a finite dimensional subspace of a normed space X. Then X₁ + X₂ is closed in X.
Let X be a normed space such that U(0,1) is totally bounded. Then X is finite dimensional.
Algebra
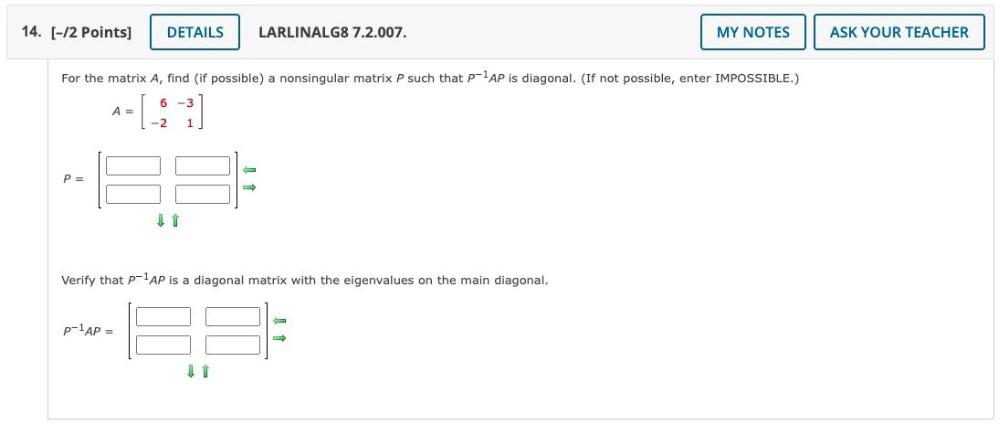
Sequences & SeriesFor the matrix A, find (if possible) a nonsingular matrix P such that P-¹AP is diagonal. (If not possible, enter IMPOSSIBLE.)
Verify that P-¹AP is a diagonal matrix with the eigen values on the main diagonal.
P-¹AP =?
Algebra
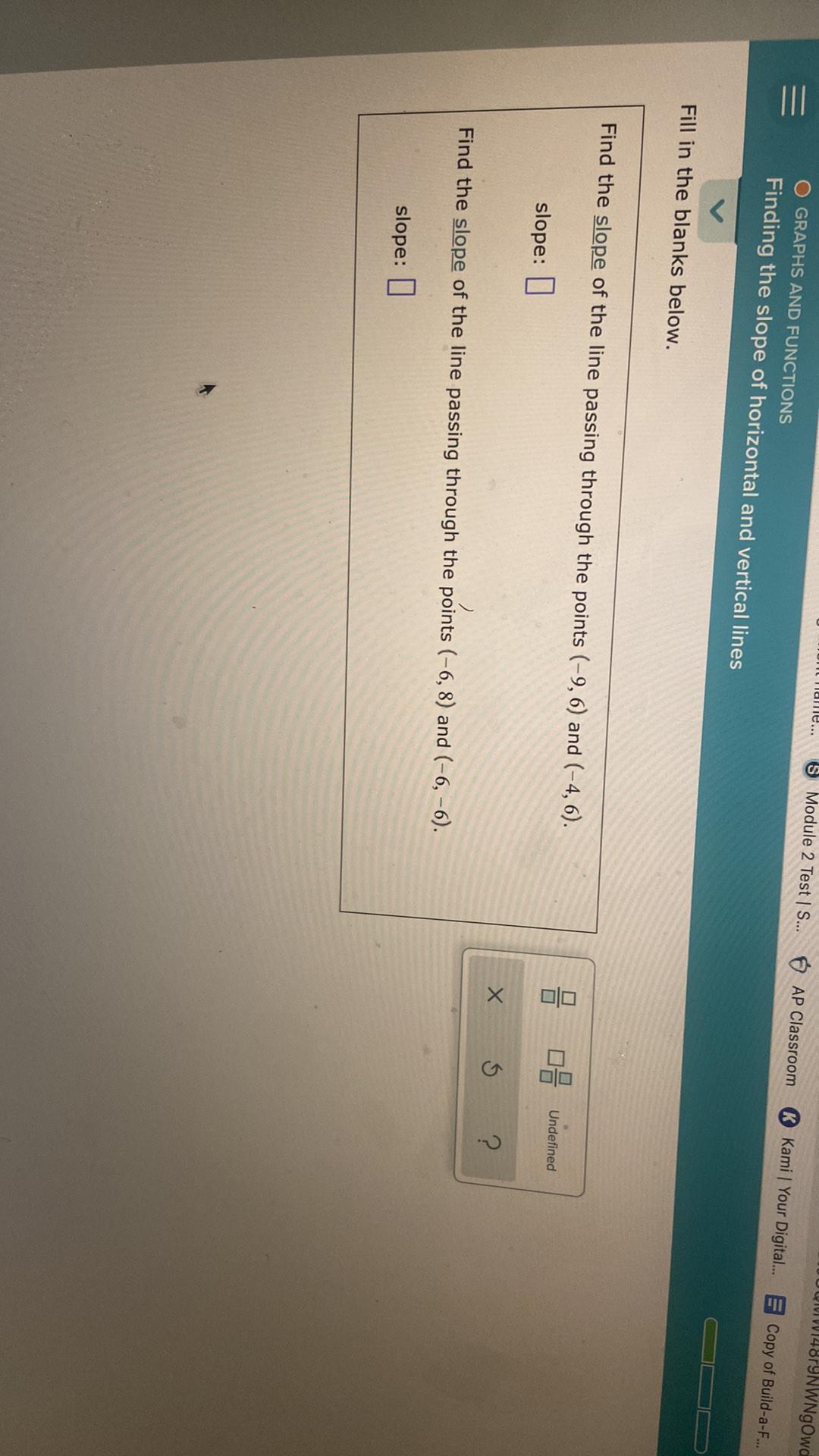
Sequences & SeriesFinding the slope of horizontal and vertical lines
Fill in the blanks below.
Find the slope of the line passing through the points (-9,6) and (-4, 6).
slope:
Find the slope of the line passing through the points (-6, 8) and (-6, -6).
Algebra
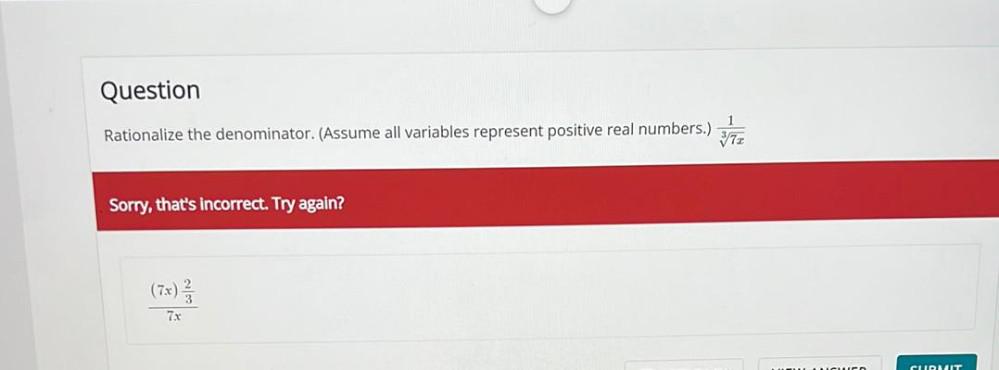
Sequences & SeriesRationalize the denominator. (Assume all variables represent positive real numbers.) 1/∛ 7x

Algebra
Sequences & Seriesdetermine if the general equation of the parabola touches the points (6,0),(11,1) and (3,-1), if its axis coincides with the x axis

Algebra
Sequences & SeriesYou are a game manufacturer. You and your team are trying to find the best pair of dice for a new board game you have made. You are examining the possible results of using one 4-sided die and one 12-sided die and rolling them together. If the random variable is defined as the sum of the two dice when rolled, which of the following values are included in the random variable?
a16
b 1
c 0
d 14
e 17
f 10
g All of the above

Algebra
Sequences & SeriesThe population of the Greenworm neighborhood has been growing steadily since 1982. In 1986, the population was 52200 people. In 1994, it was 66600 people. Find an equation in the form y = mx + b, where x is the number of years past 1982 and y is the population of Greenworm.

Algebra
Sequences & SeriesFactor the GCF out of the following expression:
30x^4y^2 +45x³y +85x²y²
Your answer should take the form A(B+C+D) where A is the GCF of the terms in the expression.

Algebra
Sequences & SeriesFor which values of the parameter a ∈ R the following real quadratic form is positive definite f(x, y, z) = x² + 2xy + 2xy + 2y² + 2ayz +5z²
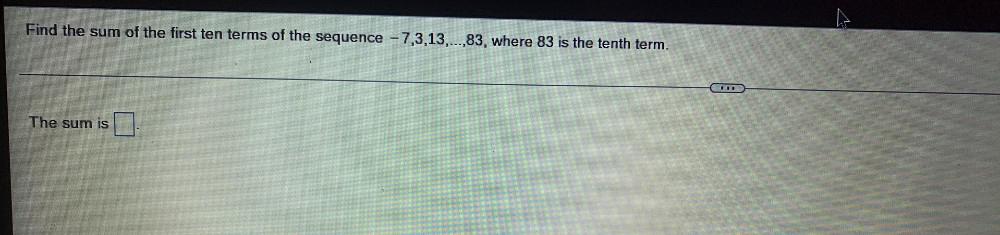
Algebra
Sequences & SeriesFind the sum of the first ten terms of the sequence -7,3,13,...,83, where 83 is the tenth term.

Algebra
Sequences & SeriesThe minimum SOP form of the following function F = (x+ y+ z)' is
(a)xy+xz+x'y'z'
(b)xyz'+xy'z+x'yz+x'y'z'
(c)xyz+xy'z'+xyz'+x'y'z
(d)xz+yz+x'y'z'

Algebra
Sequences & SeriesCompute the angle between p(x) = 2x² − x + 1 and q(x) = x² + 2x, and determine if they are orthogonal where the inner product is the standard.
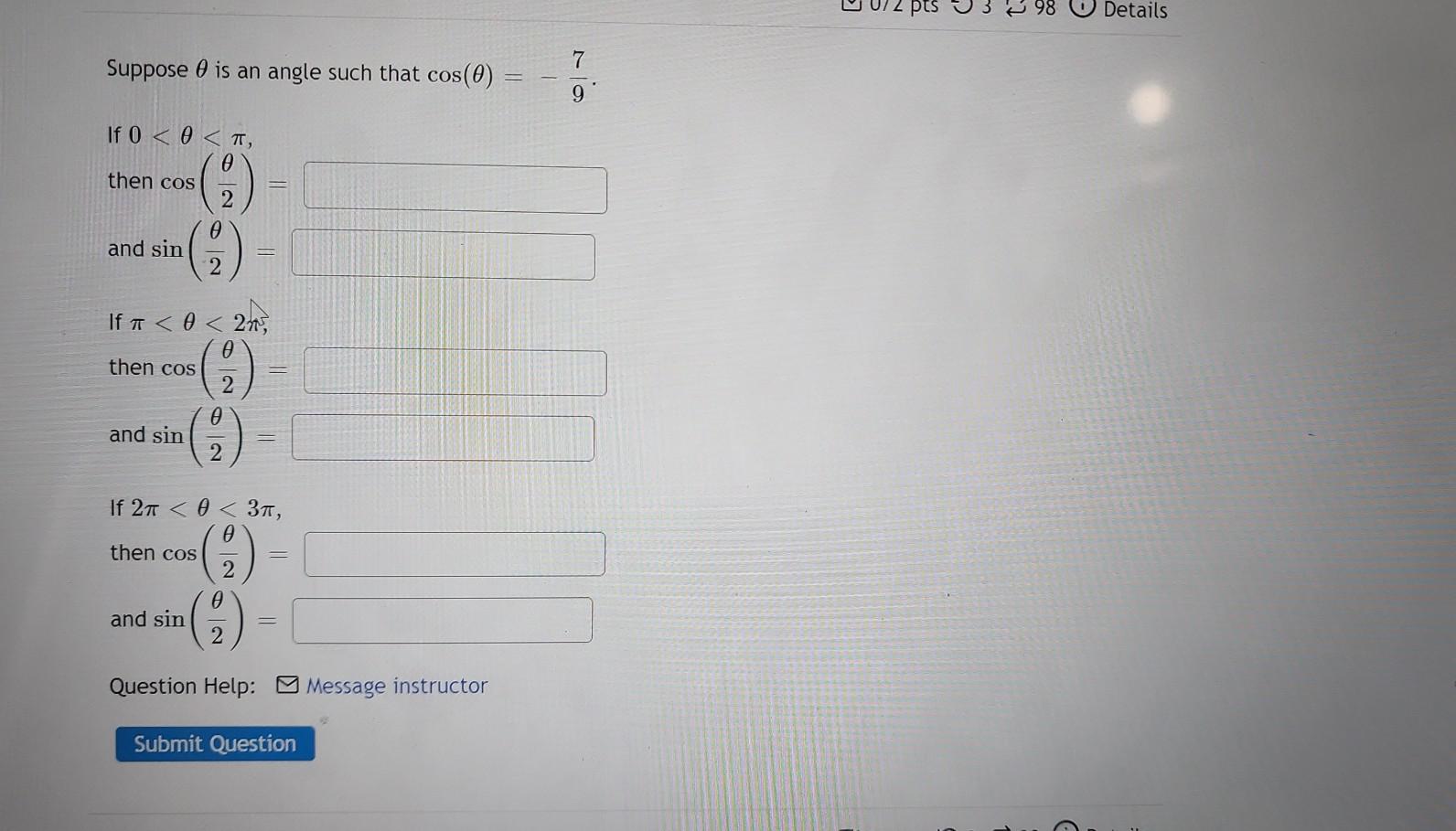
Algebra
Sequences & SeriesSuppose θ is an angle such that cos(θ)= -7/9
If 0 < θ< π,
then cos (θ/2)
and sin (θ/2)
If π<θ<2π
then cos (θ/2)
and sin(θ/2)
If 2π < θ < 3π,
then cos (θ/2)
and sin (θ/2)
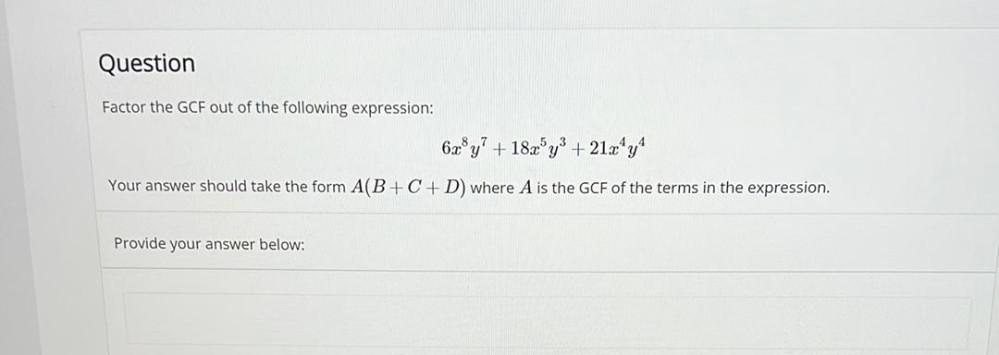
Algebra
Sequences & SeriesFactor the GCF out of the following expression:
6x^8y^7+ 18x^5y³ +21x^4y^4
Your answer should take the form A(B+C+ D) where A is the GCF of the terms in the expression.
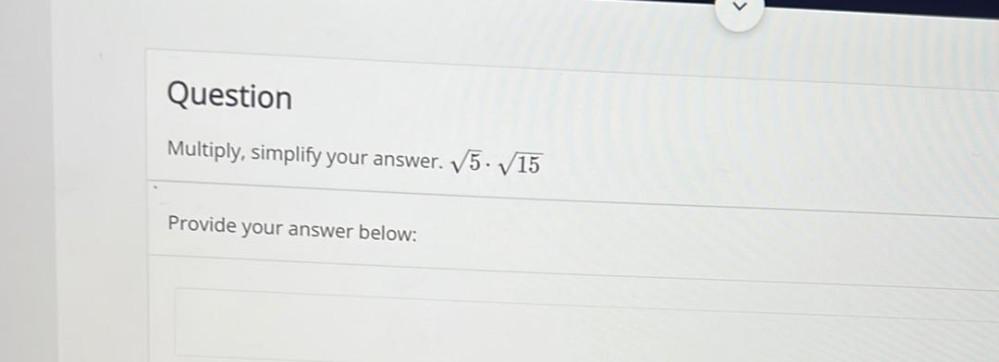

Algebra
Sequences & SeriesConvert the radian measure to degrees. Round to the nearest hundredth if necessary. 4π\9
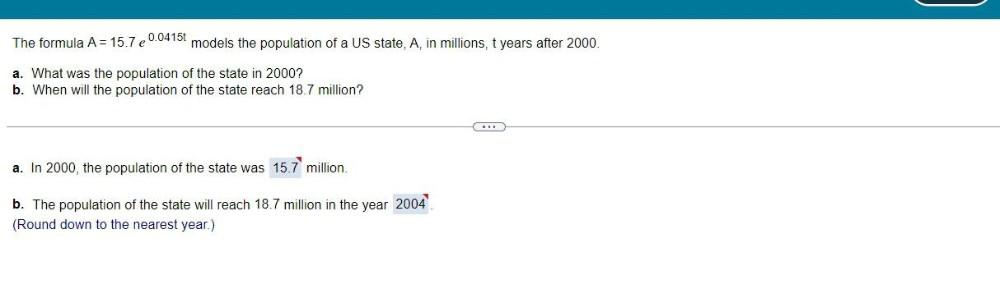
Algebra
Sequences & SeriesThe formula A = 15.7 e⁰.⁰⁴¹⁵ᵗ models the population of a US state, A, in millions, t years after 2000.
(a) What was the population of the state in 2000?
(b) When will the population of the state reach 18.7 million?
(a) In 2000, the population of the state was _____ million.
(b) The population of the state will reach 18.7 million in the year _______.
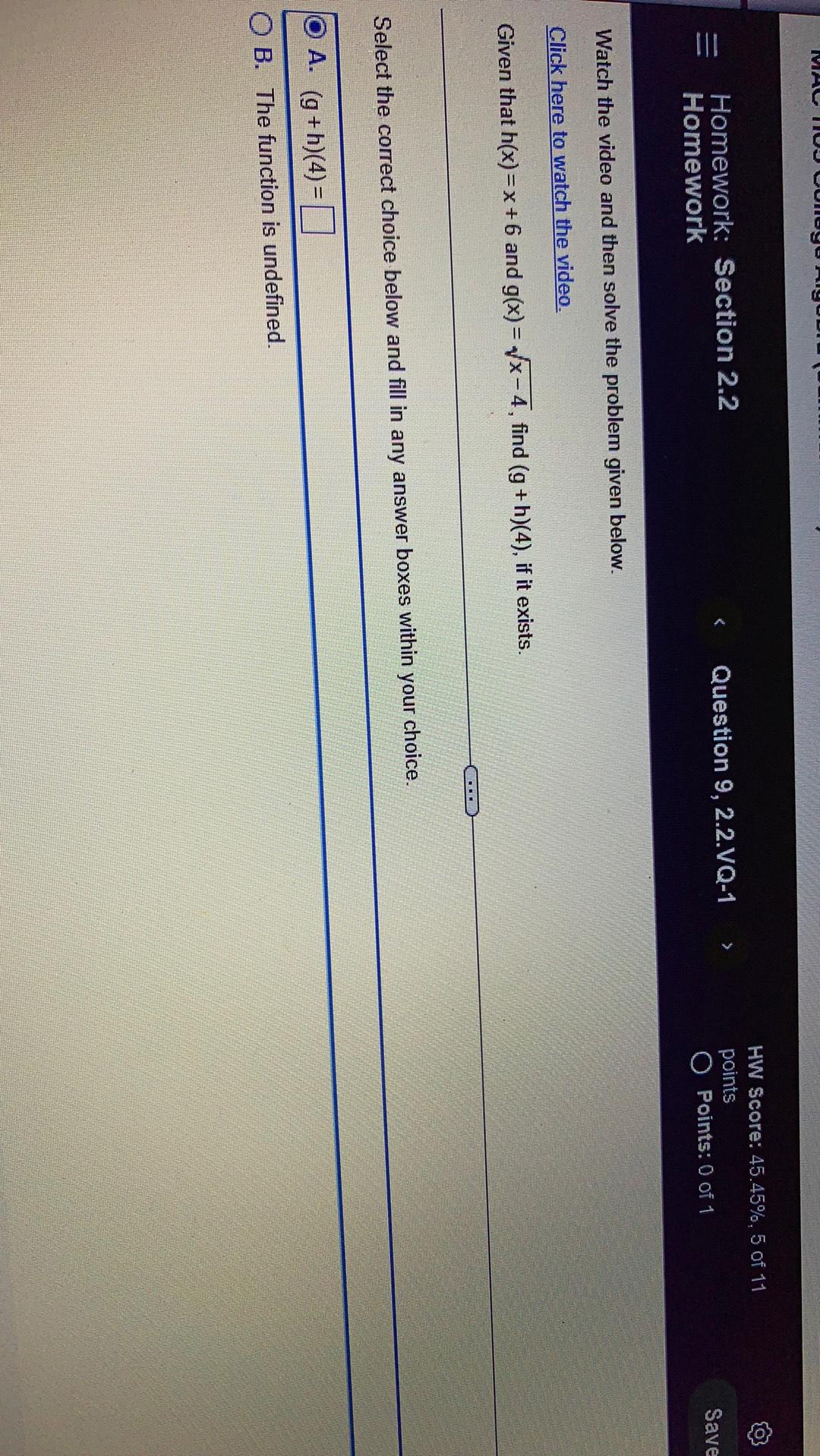
Algebra
Sequences & SeriesGiven that h(x)=x+6 and g(x)=√x-4, find (g+h)(4), if it exists.
Select the correct choice below and fill in any answer boxes within your choice.
A. (g+h)(4) =
B. The function is undefined.
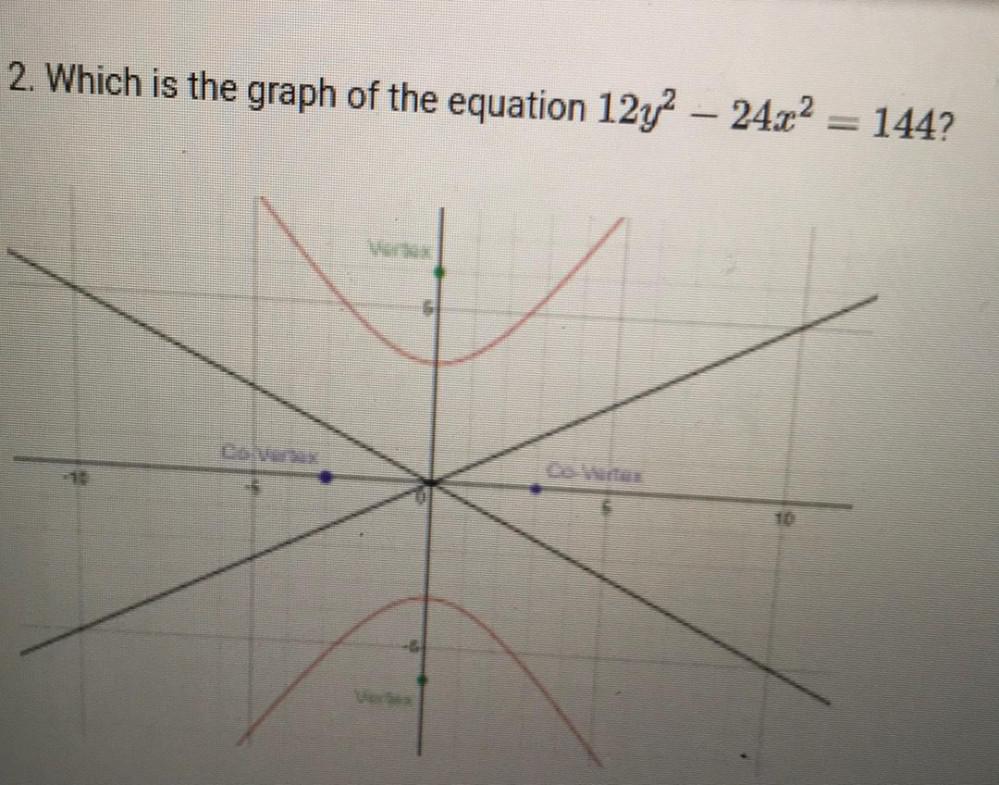

Algebra
Sequences & SeriesWrite an equation for the ellipse centered at the origin with vertices located at (-12, 0) and (12, 0) and foci at (-8,0) and (8,0).
(a) (x²/144)+(y²/80)=1
(b) (x²/144)+(y²/64)=1
(c) (x²/80)+(y²/144)=1
(d) (x²/64)+(y²/144)=1

Algebra
Sequences & SeriesDetermine the area under the following exponential decay curve between 0 and 1 second, as given below.
y = ∫(e-^t)dt
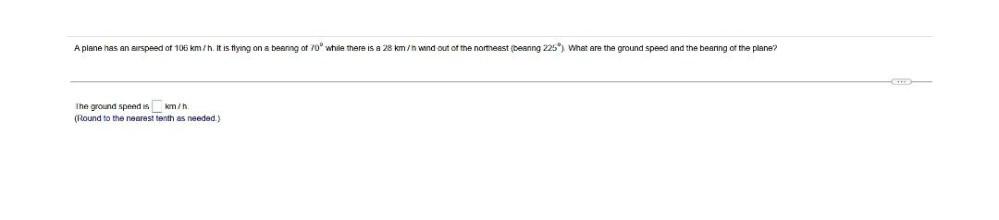
Algebra
Sequences & SeriesA plane has an airspeed of 106 km/h. It is flying on a bearing of 70° while there is a 28 km/h wind out of the northeast (bearing 225°). What are the ground speed and the bearing of the plane?
The ground speed is__km/h

Algebra
Sequences & SeriesOn Melissa's 6th birthday, she gets a $3000 CD that earns 3% interest, compounded quarterly. If the CD matures on her 16th birthday, how much money will be available?
Algebra
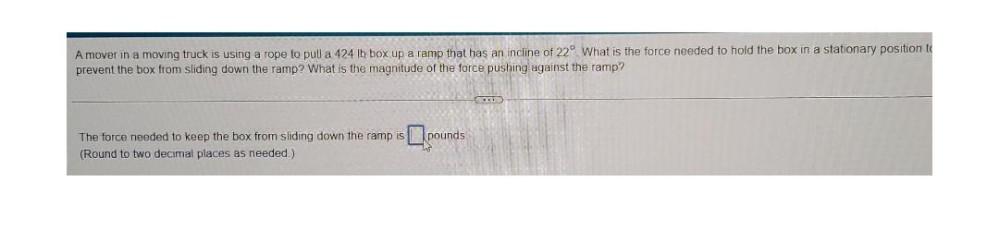
Sequences & SeriesA mover in a moving truck is using a rope to pull a 424 lb box up a ramp that has an incline of 22°. What is the force needed to hold the box in a stationary position to prevent the box from sliding down the ramp? What is the magnitude of the force pushing against the ramp?
The force needed to keep the box from sliding down the ramp is pounds.

Algebra
Sequences & SeriesFind a conformal mapping which maps the region between |z-1|>1 and |z|<2 onto the upper half plane.

Algebra
Sequences & SeriesBody-mass index, or BMI, takes both weight and height into account when assessing whether an individual is underweight or overweight. BMI varies directly as one's weight, in pounds, and inversely as the square of one's height, in
inches. In adults, normal values for the BMI are between 20 and 25, inclusive. Values below 20 indicate that an individual is underweight and values above 25 indicate that an individual is overweight. A person who weighs 180 pounds and is 5 feet, or 60 inches, tall has a BMI of 35.15. Use the four-step procedure for solving variations to determine what the BMI is, to the nearest tenth, for a 175-pound person who is 5 feet 8 inches tall. Is this person underweight, normal, or overweight?
a).What is the BMI of a 175-pound person who is 5 feet 8 inches tall?
(Round to the nearest tenth as needed.)
Algebra
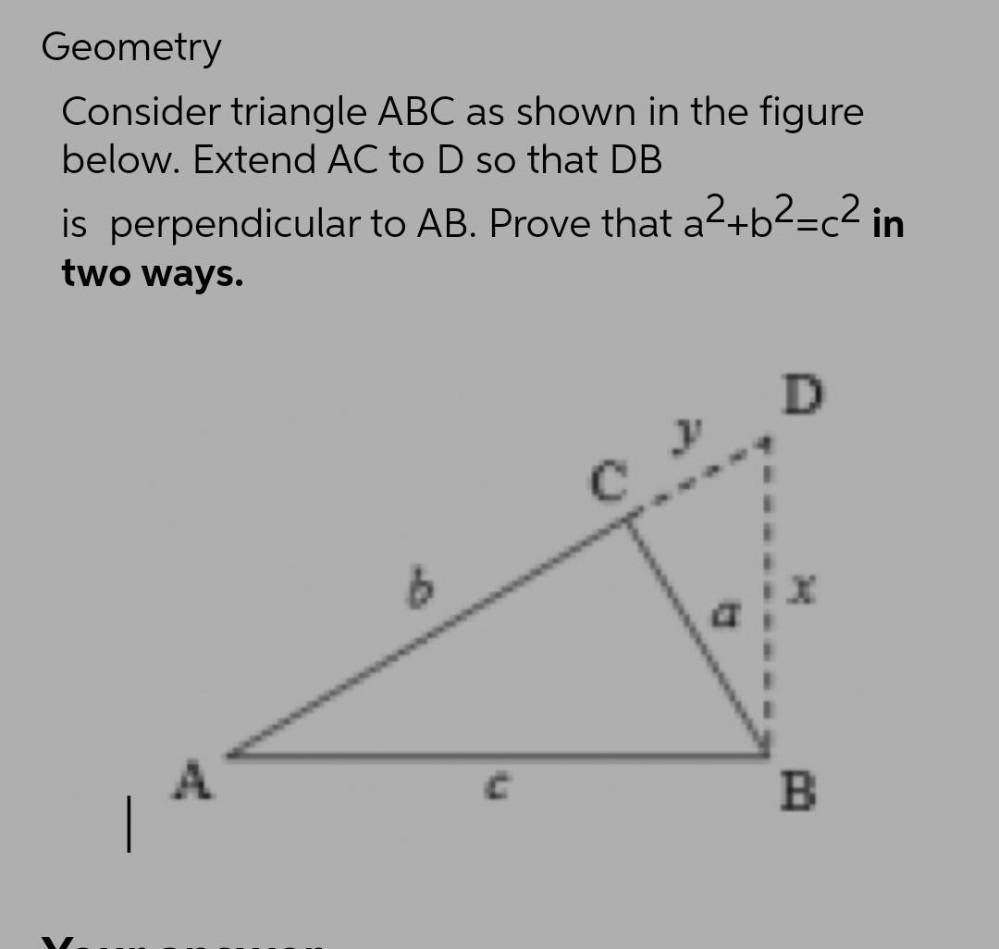
Sequences & SeriesConsider triangle ABC as shown in the figure below. Extend AC to D so that DB
is perpendicular to AB. Prove that a²+b²=c² in two ways.
Algebra
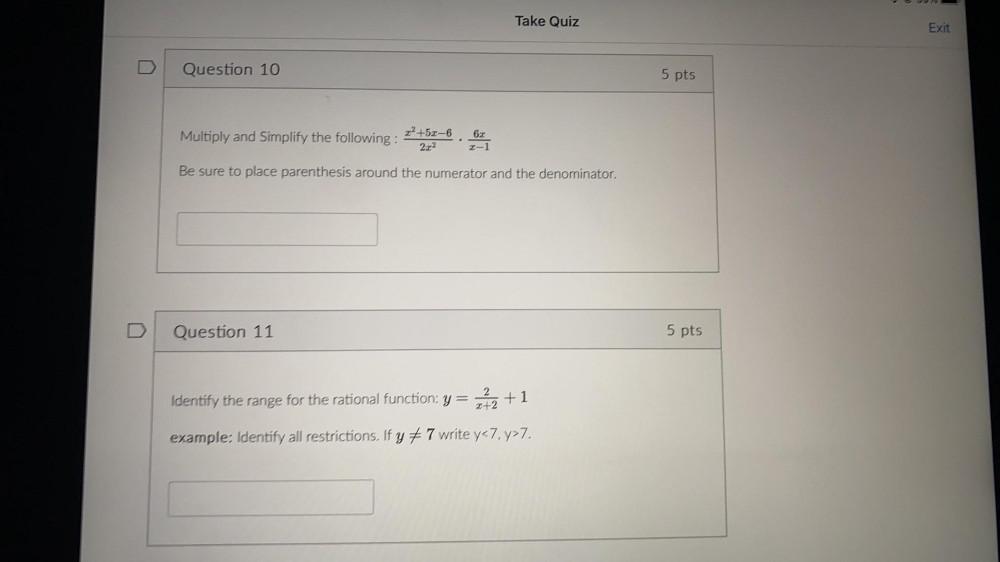
Sequences & SeriesMultiply and Simplify the following:{(x²+5x-6)/2x²}*{6x/(x-1)}
Be sure to place parenthesis around the numerator and the denominator.________
Identify the range for the rational function: y = 2/(x+2) +1
example: Identify all restrictions. If y≠ 7 write y<7, y>7.______

Algebra
Sequences & SeriesFind the first four terms of the recursively defined sequence.
a₁ = 4, a2 = 3, ak+1 = ak+ak-1

Algebra
Sequences & SeriesA pendulum swings a length of 38 inches on its first swing. Each successive swing is 4/5 of the preceding swing. Find the length of the fourth swing and the total length swung during the first four swings.
The length of the fourth swing is _____ in
(Round to the nearest tenth as needed.)
The total length swung during the first four swings is _____ in.
(Do not round until the final answer. Then round to the nearest tenth as needed.)

Algebra
Sequences & SeriesUse algebra to show that in parallelogram ABCD the opposite sides are congruent. Be sure to state whether the sides are congruent or not.
A (-6.7), B (0,10), C (4,2), D (-2-1)
Use algebra to show that in rectangle EFGH the consecutive sides are perpendicular. Be sure to state whether the sides are perpendicular or not. E (-4,0), F (2,8), G (6,5), H (0,-3)

Algebra
Sequences & SeriesLet M be a surface in R² oriented by a unit normal vector field
U = g₁U₁ + g₂U₂ +g₃U₃
Then the Gauss map G: M->Σ of M sends each point p of M to the point (g₁(p), g₂(p), g₃(p)) of the unit sphere Σ. For each of the following surfaces, describe G(M) of the Gauss map in the sphere Σ:
(a) Cylinder, x² + y² = r²
(b) Cone, z = √(x² + y²)
(c) Plane, x+y+z=0
(d) Sphere, (x - 1)² + y² + (x + 2)² = 1
This is a Differential Geometry problem.

Algebra
Sequences & Serieswhat is the percentage of the total variationthst can be explain by the linear relationship between altitude and temperature on the predicted value below
X value =6.327
Pred. Y =47.791211
s.e.(Pred. y) = 47.118038
95% (C. I. for mean) =35.679134,59.9032
95%(P.I. gor new) = 24.3812,72.2012
Algebra
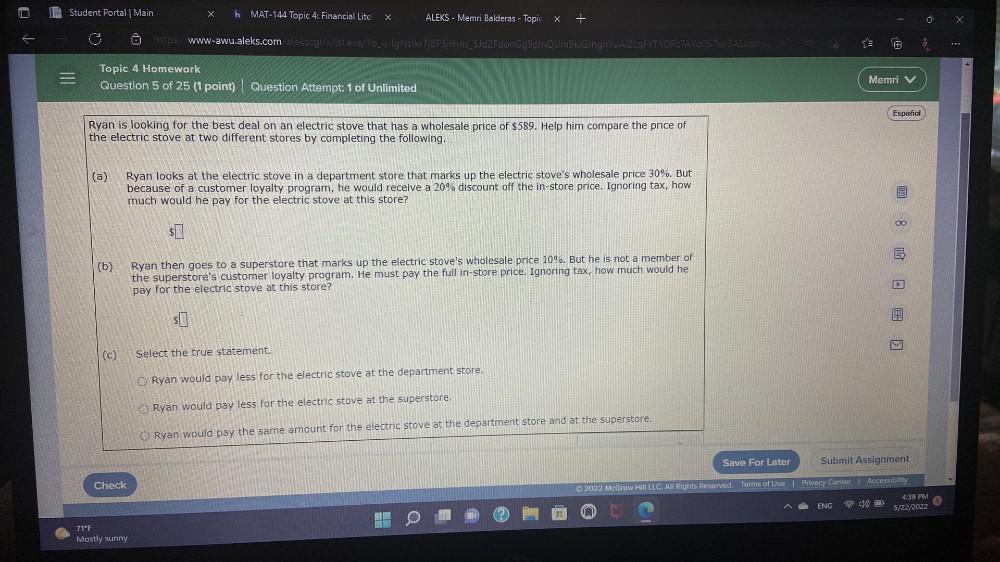
Sequences & SeriesRyan is looking for the best deal on an electric stove that has a wholesale price of $589. Help him compare the price of the electric stove at two different stores by completing the following.
(a) Ryan looks at the electric stove in a department store that marks up the electric stove's wholesale price 30%. But because of a customer loyalty program, he would receive a 20% discount off the in-store price. Ignoring tax, how much would he pay for the electric stove at this store?$________
(b)Ryan then goes to a superstore that marks up the electric stove's wholesale price 10%. But he is not a member of the superstore's customer loyalty program. He must pay the full in-store price. Ignoring tax, how much would he pay for the electric stove at this store?$________
(c) Select the true statement.
i) Ryan would pay less for the electric stove at the department store.
ii)Ryan would pay less for the electric stove at the superstore.
iii) Ryan would pay the same amount for the electric stove at the

Algebra
Sequences & SeriesLet u(x) = sin(x) and v(x) = x³ and f(x)=u(x)/v(x)
u'(x)=....
v'(x)=....
f'=u'v'-uv'/v² =...

Algebra
Sequences & SeriesClassify the sequence as arithmetic or geometric, then write a rule for the nth term. 900 , 450 , 225 ..............

Algebra
Sequences & SeriesFind the derivative of the given equation
f(x)= 1/x²
A) -2x
B) 1/2x
C) 2x
D) -2x^(-3)

Algebra
Sequences & SeriesA certain coil spring having spring constant 10 lb/ft is sus-pended from the ceiling. A 32-lb weight is attached to the lower end of the spring and
comes to rest in its equilibrium position. Beginning at t = 0 an external force given by F (t) = sin t + (1/4) sin 2t + (1/9) sin 3t is applied to the system. The
medium offers a resistance in pounds numerically equal to twice the instantaneous velocity, measured in feet per second. Find the displacement of the weight as a function of the time.

Algebra
Sequences & SeriesGiven are the first three terms of a sequence that is either arithmetic or geometric. If the sequence is arithmetic, find a₁ and d. If a sequence is geometric, find a₁ and r.
s, s +3, s +6..........
What type of sequence is this?
a) Arithmetic
b) Geometric
The value of a₁ is__________(Simplify your answer.)
The value of r/d s__________(Simplify your answer.)