Sequences & Series Questions and Answers
Algebra
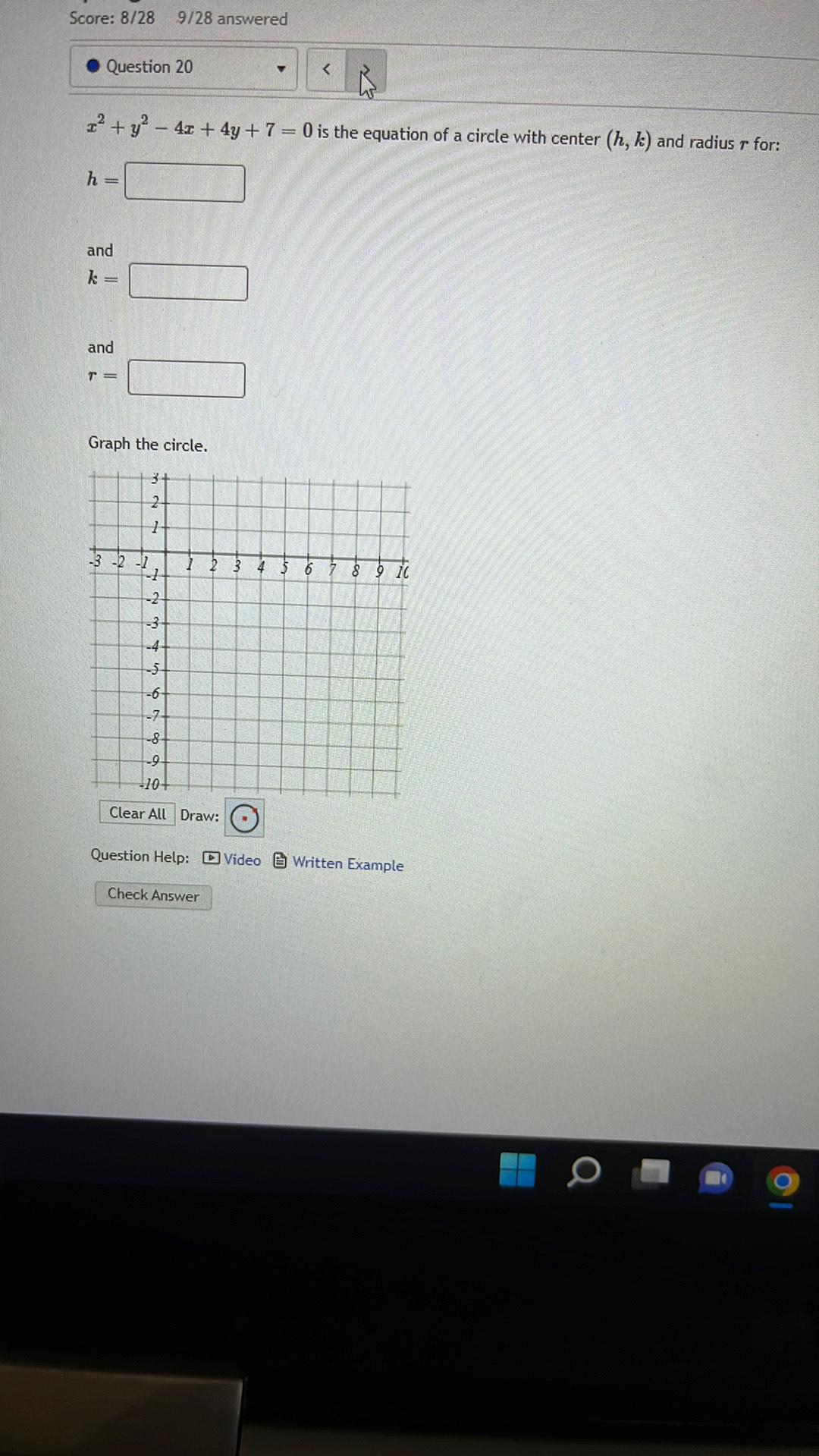
Sequences & Seriesx² + y² - 4x + 4y + 7 = 0 is the equation of a circle with center (h, k) and radius r for:
a)h =
b)k=
c)r=
Graph the circle.

Algebra
Sequences & SeriesAshley, who is currently a high school freshman, is saving money for a big school trip during her senior year. In the first month, she saved $20. She plans to save 2% more each month than the previous month. How much money will she have saved after three years?
A) $540.83
B) $4,692.15
C) $35,720.00
D) $1,039.89
Algebra
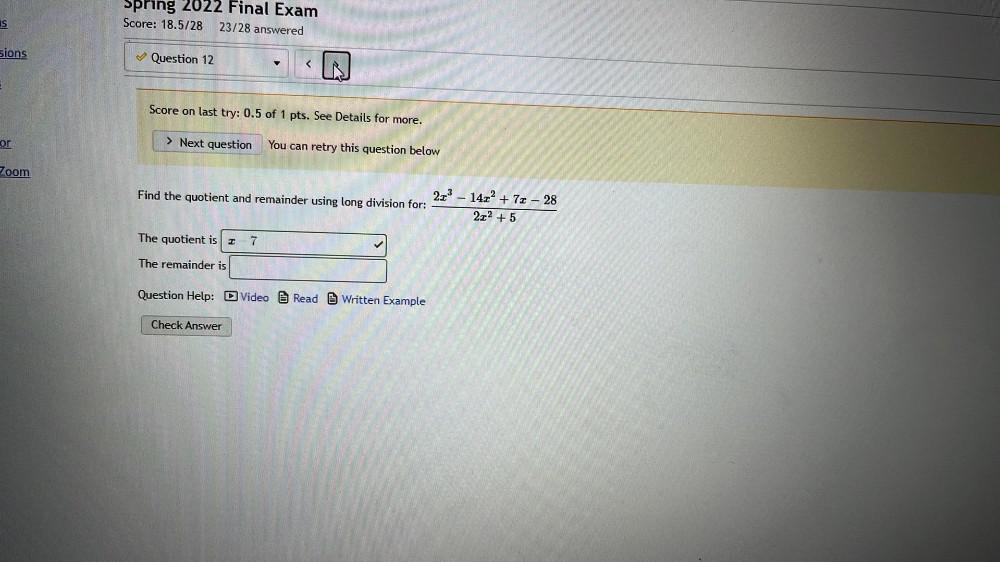
Sequences & SeriesFind the quotient and remainder using long division for:(2x³-14x²+7x-28)/(2x²+5)
The quotient is
The remainder is

Algebra
Sequences & SeriesCalculate the sum:
Σ 1000 (1.01).
(A)1,000,000,000.001
(B)1,000,000.01
(C)100,000,000,000.0001
(D)Does not exist
Algebra
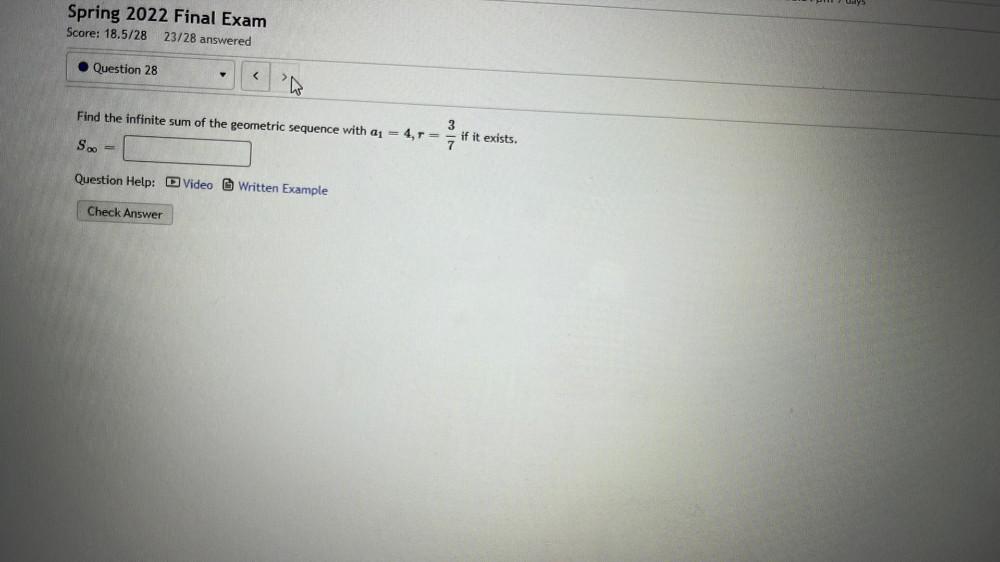
Sequences & SeriesFind the infinite sum of the geometric sequence with a₁ = 4,r= 3/7 if it exists.

Algebra
Sequences & SeriesWhere i is the imaginary unit, the expression (x + 3i)² - (2x -3i)² is equivalent to
(1) -3x²
(2) -3x² - 18
(3) -3x² + 18xi
(4) -3x² - 6xi-18
Algebra
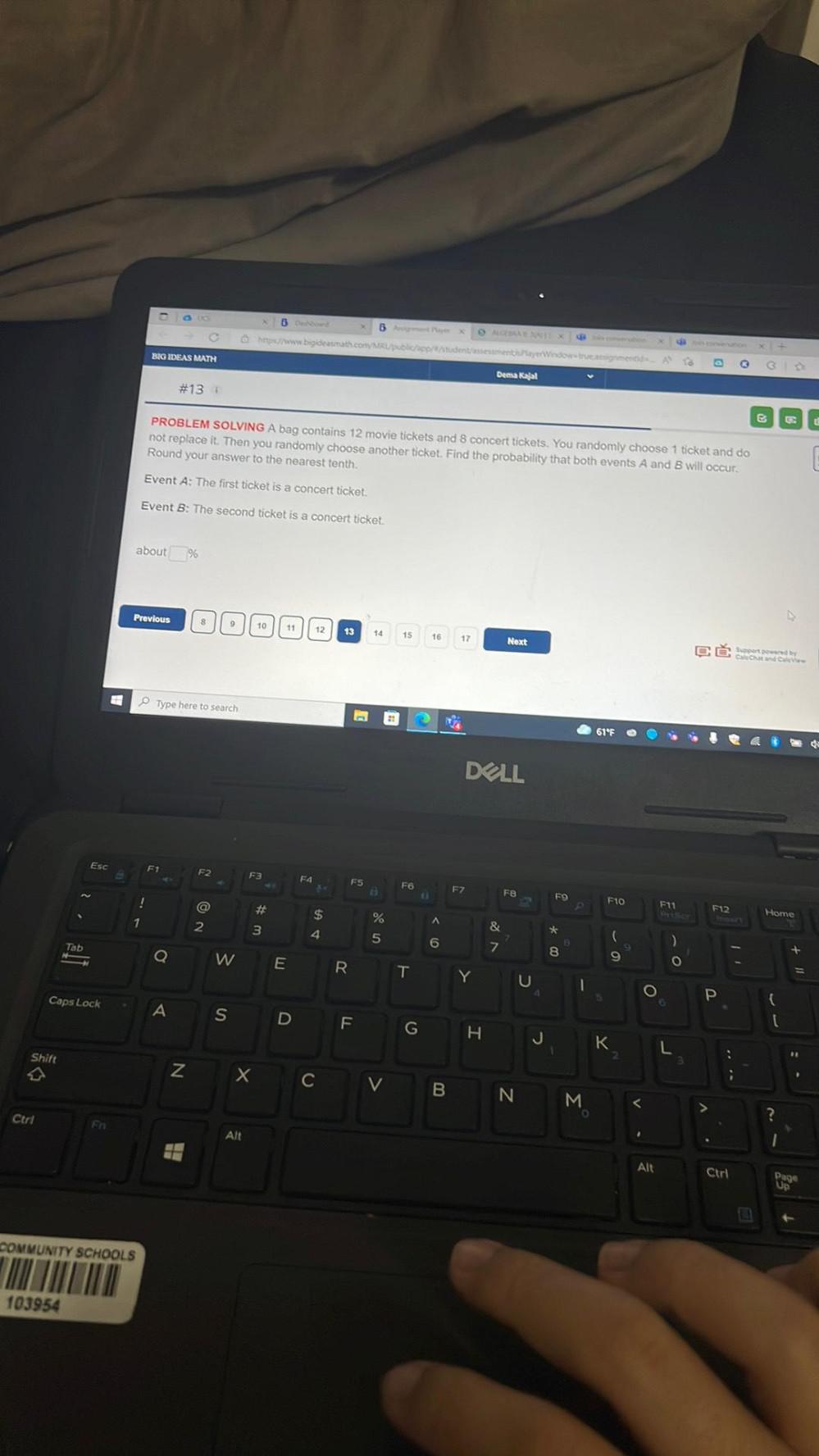
Sequences & SeriesA bag contains 12 movie tickets and 8 concert tickets. You randomly choose 1 ticket and do not replace it. Then you randomly choose another ticket. Find the probability that both events A and B will occur.
Round your answer to the nearest tenth.
Event A: The first ticket is a concert ticket.
Event B: The second ticket is a concert ticket.
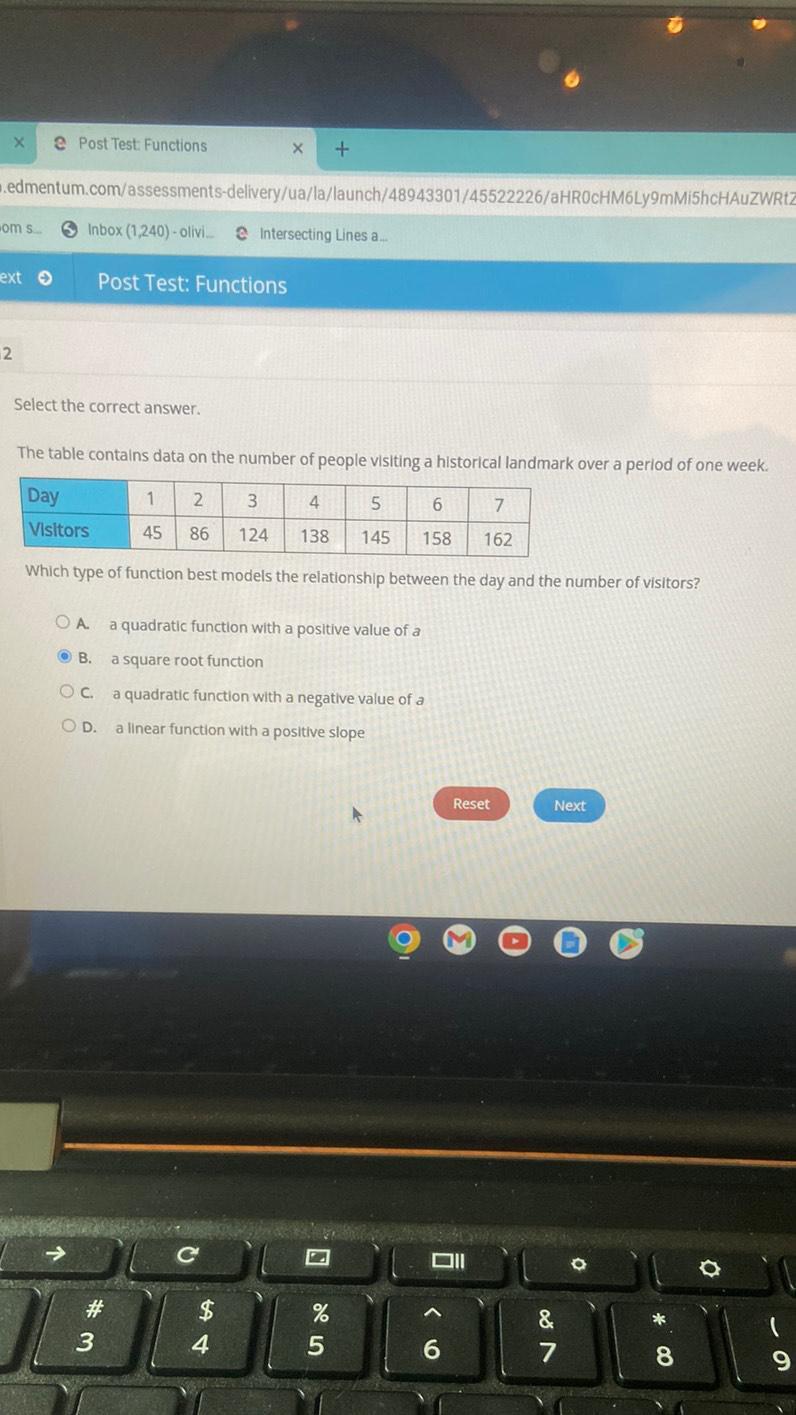
Algebra
Sequences & SeriesThe table contains data on the number of people visiting a historical landmark over a period of one week.
Day 1 2 3 4 5 6 7
Visitors 45 86 124 138 145 158 162
45 86 124 138 145 158 162
Which type of function best models the relationship between the day and the number of visitors?
A a quadratic function with a positive value of a
B. a square root function
C. a quadratic function with a negative value of a
D. a linear function with a positive slope

![For the sequence aₙ = [(-1)ⁿ8]/n²,
its first term is ______ ;
its second term is ____ ;
its third term is ____ ;
its fourth term is ____ ;
its 100th term is ____ ;](https://media.kunduz.com/media/sug-question/raw/80073572-1659865889.8668232.jpeg?w=256)
Algebra
Sequences & SeriesFor the sequence aₙ = [(-1)ⁿ8]/n²,
its first term is ______ ;
its second term is ____ ;
its third term is ____ ;
its fourth term is ____ ;
its 100th term is ____ ;
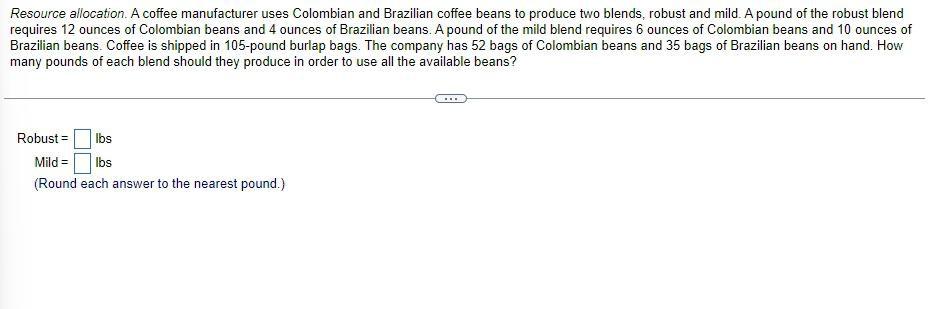
Algebra
Sequences & SeriesResource allocation. A coffee manufacturer uses Colombian and Brazilian coffee beans to produce two blends, robust and mild. A pound of the robust blend requires 12 ounces of Colombian beans and 4 ounces of Brazilian beans. A pound of the mild blend requires 6 ounces of Colombian beans and 10 ounces of Brazilian beans. Coffee is shipped in 105-pound burlap bags. The company has 52 bags of Colombian beans and 35 bags of Brazilian beans on hand. How many pounds of each blend should they produce in order to use all the available beans?

Algebra
Sequences & SeriesFind a scalar equation of the hyperplane with vector equation:
~x = c1 (1, -2, 2, 1) + c2 (-1, 3, -2, 1) + c3 (2,
-3, 5, 4), c1, c2, c3 ∈ R
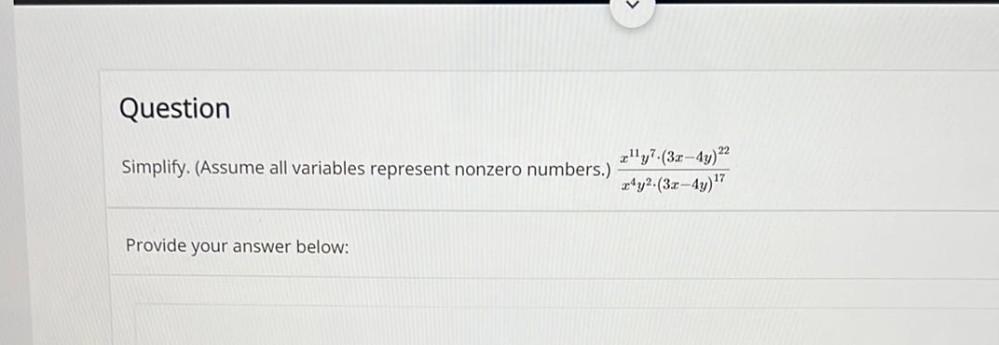
Algebra
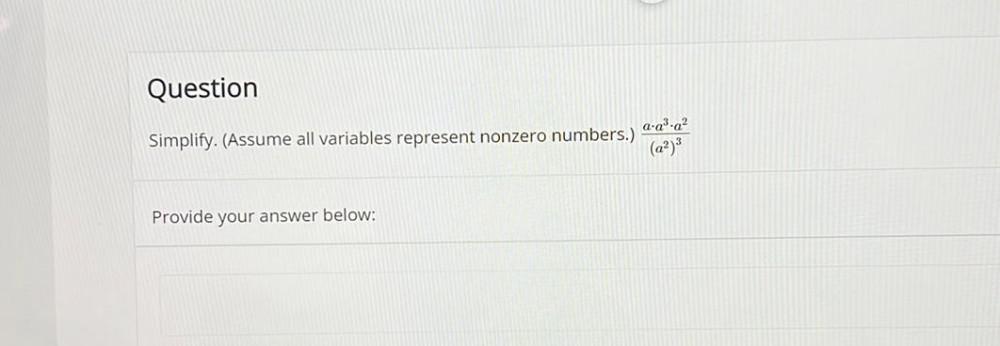
Sequences & SeriesSimplify. (Assume all variables represent nonzero numbers.)
x¹¹y⁷ (3x-4y)²² /(x⁴y²(3x-4y) ¹⁷)
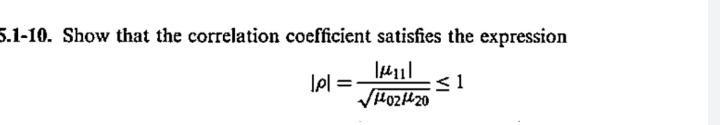
Algebra
Sequences & SeriesShow that the correlation coefficient satisfies the expression
|⍴| = |µ11l / (√(µ02µ20)) ≤1
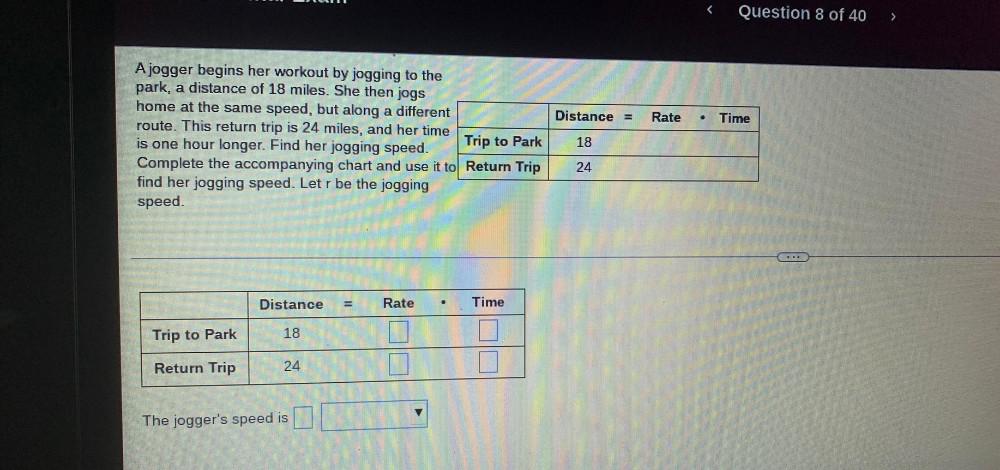
Algebra
Sequences & SeriesA jogger begins her workout by jogging to the park, a distance of 18 miles. She then jogs home at the same speed, but along a different route. This return trip is 24 miles, and her time is one hour longer. Find her jogging speed. Complete the accompanying chart and use it to find her jogging speed. Let r be the jogging speed.
Algebra
Sequences & SeriesAubrey's dinner cost $85. She tips the waitstaff 30% for excellent service. How much does Aubrey tip the waitstaff?
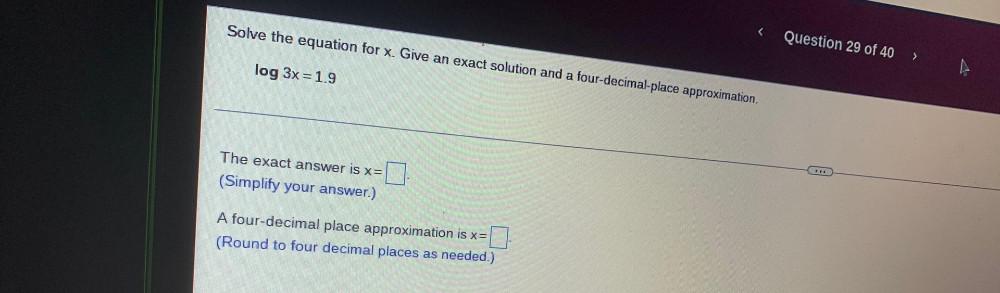
Algebra
Sequences & SeriesSolve the equation for x. Give an exact solution and a four-decimal-place approximation.
log 3x = 1.9
The exact answer is x= A four-decimal place approximation is x= (Round to four decimal places as needed.)

Algebra
Sequences & SeriesFrom a boat, the angle of elevation to the top of a lighthouse is 5". The tower is 50 ft. high. Find the distance from the boat to the lighthouse. Round your answer to the nearest tenth.* Do not include a comma in the answer.
Distance =__ft.
10. From the top of an offshore oil rig that is 199 ft. above sea level, the angle of depression of a passing ship is 15°. Find the distance between the ship and the top of the oil rig. Round your answer to the nearest tenth.
Distance =__ft.
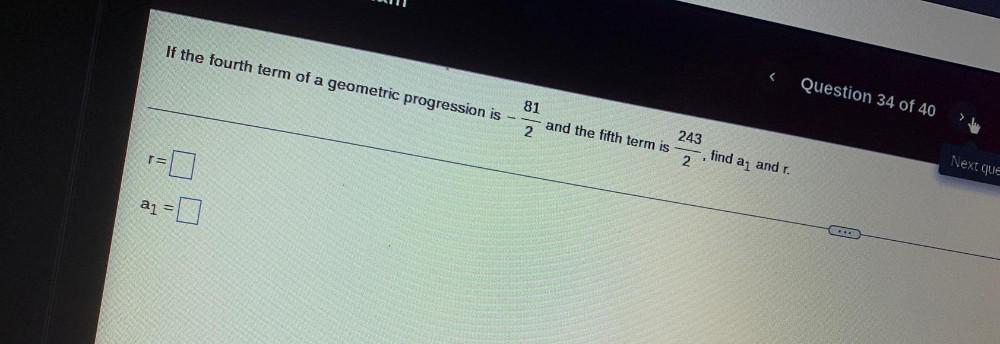
Algebra
Sequences & SeriesIf the fourth term of a geometric progression is -81/2 and the fifth term is 243 / 2 find a₁ and r.
r= __
a₁ =__
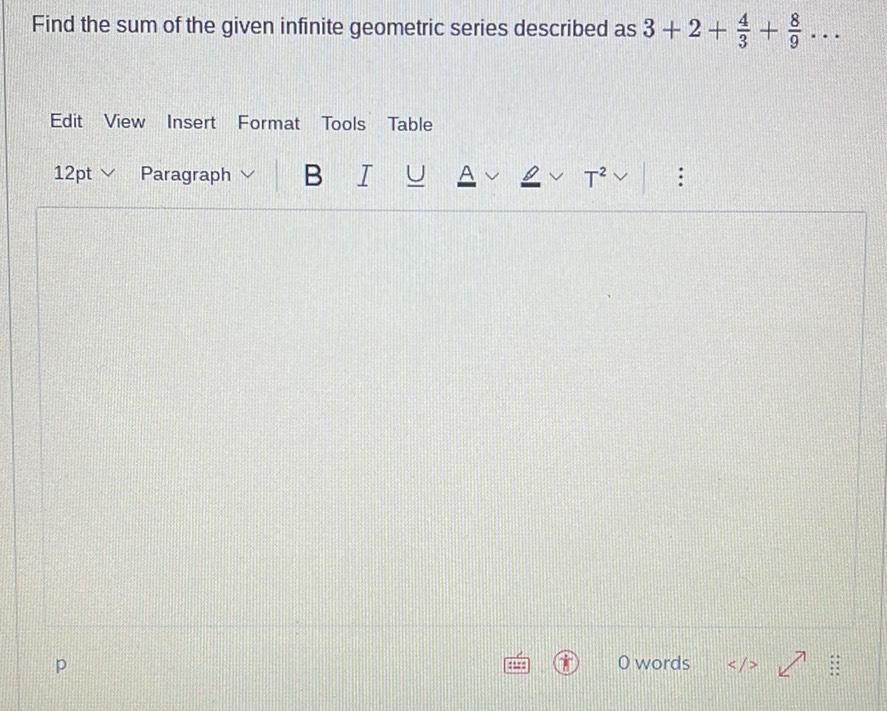
Algebra
Sequences & SeriesFind the sum of the given infinite geometric series described as 3 + 2+ 4/3 + 8/9....
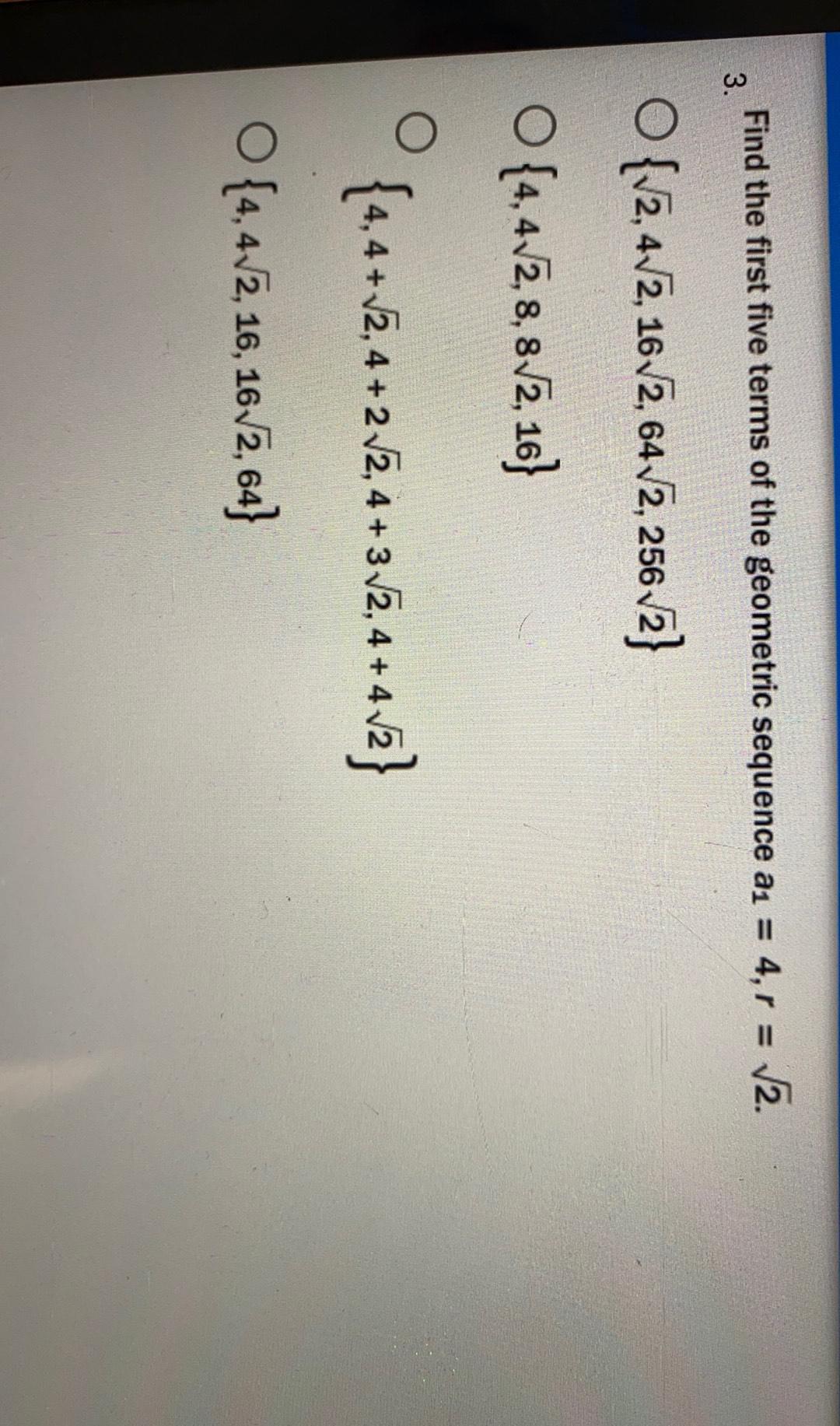
Algebra
Sequences & SeriesFind the first five terms of the geometric sequence a₁ = 4, r = √2.
(a) {√2, 4√2, 16√2, 64√2, 256√2}
(b) [4,4√2, 8, 8√2, 16)
(c) {4,4+ √2, 4+2√2, 4+ 3√2, 4+4√2}
(d) {4, 4√2, 16, 16√2, 64}
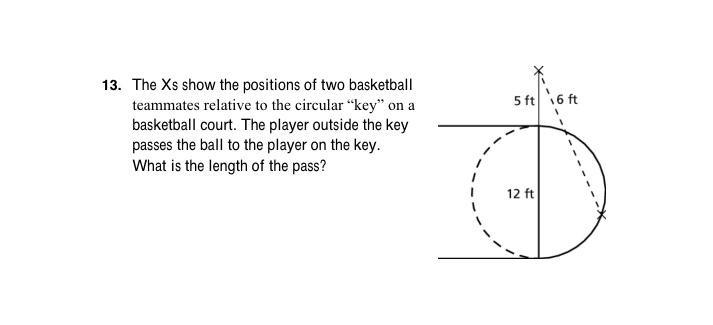
Algebra
Sequences & SeriesThe Xs show the positions of two basketball teammates relative to the circular "key" on a basketball court. The player outside the key passes the ball to the player on the key. What is the length of the pass?
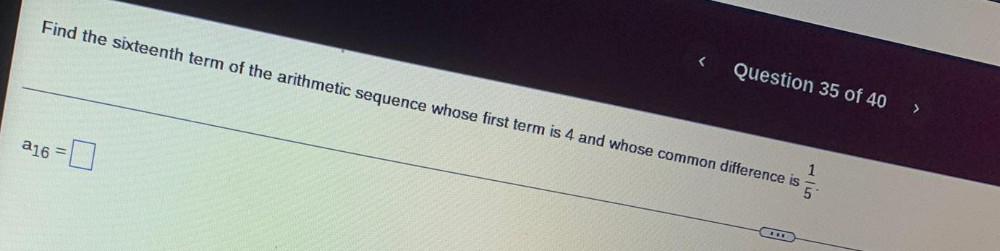
Algebra
Sequences & SeriesFind the sixteenth term of the arithmetic sequence whose first term is 4 and whose common difference is 1/5
a₁₆=?

Algebra
Sequences & SeriesWhat value of x makes the equation log10 x = -1 true over the set of real numbers?
(A) X =5
(B)X =1/10
(C)X =10
(D)X=1/5

Algebra
Sequences & SeriesGiven tan A =7/6 and that angle A is in Quadrant I, find the exact value of sin A in simplest radical form using a rational denominator.
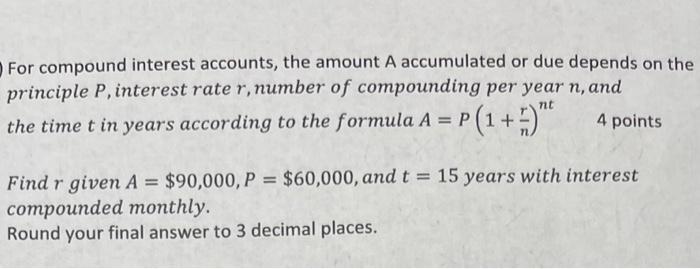
Algebra
Sequences & SeriesFor compound interest accounts, the amount A accumulated or due depends on the principle P, interest rate r, number of compounding per year n, and the time t in years according to the formula A = P(1 + 2) ^n t. Find r given A = $90,000, P = $60,000, and t = 15 years with interest compounded monthly.
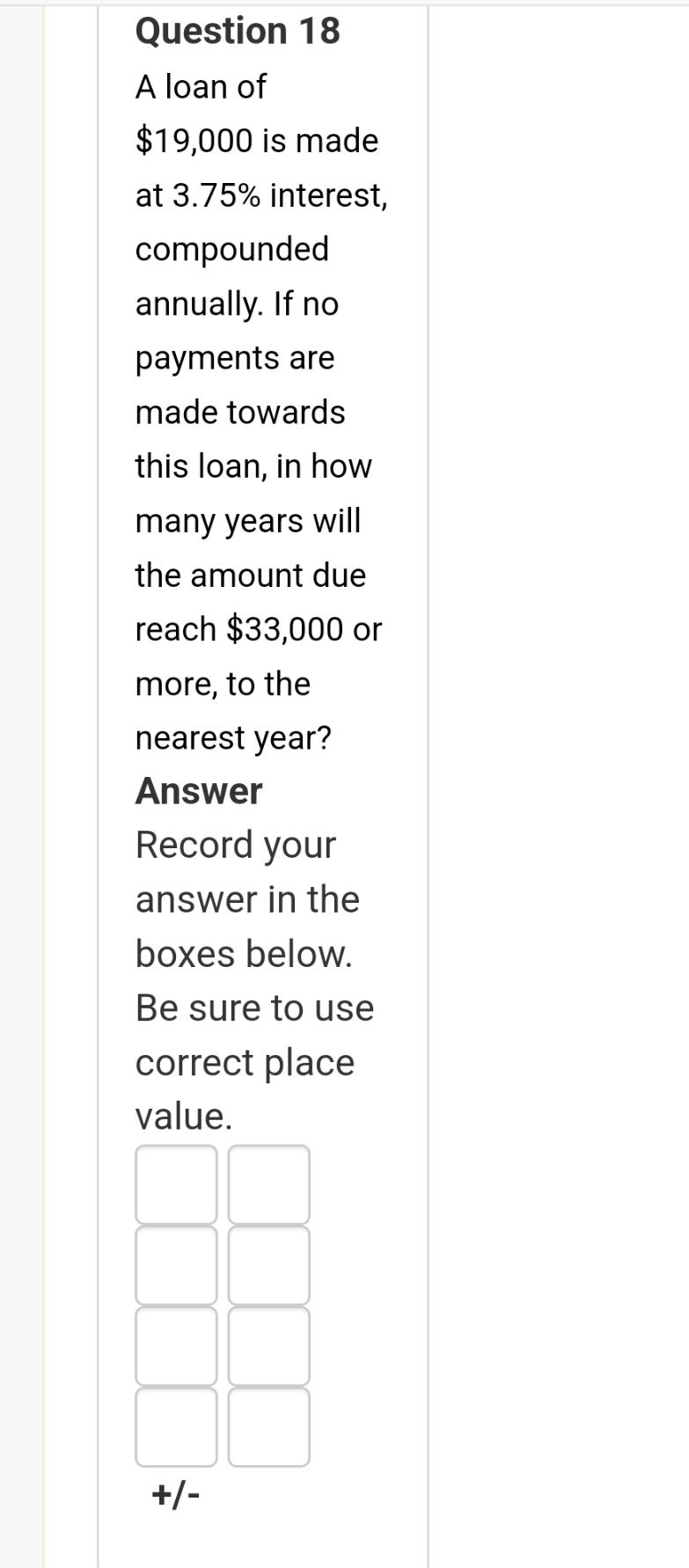
Algebra
Sequences & SeriesA loan of $19,000 is made at 3.75% interest, compounded annually. If no payments are made towards this loan, in how many years will the amount due reach $33,000 or more, to the nearest year?
Answer
Record your answer in the boxes below. Be sure to use correct place value.
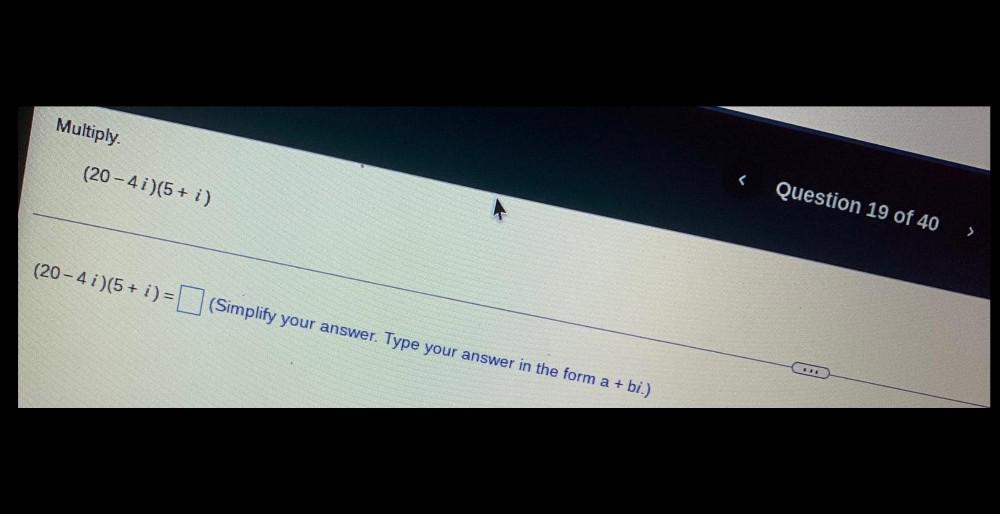
Algebra
Sequences & SeriesMultiply. (20-4 i)(5+ i)
(Simplify your answer. Type your answer in the form a + bi.)
(20-4 i)(5+ i) =

Algebra
Sequences & SeriesUsing a random sample with 100 observations, the regression of Y on X and
W yields an R-squared of 3%.
Then the homoscedasticity-only F-statistic testing the joint significance of X
and W's coefficients is given by ______with a p-value
________________than 5% (use "greater" or "smaller").
This suggests that the coefficients of X and W are jointly_____________ at 5% level. (use "significant" or "insignificant").
Treat the sample size as large when answering the questions.
Critical values for chi-squared(q)/q: when q = 1; 3.84 (5 % level), 6.63 (1% level): when q = 2: 3.00 ( 5 % level), 4.61 ( 1% level): when q = 3; 2.60 (5% level),
3.78 (1% level).

Algebra
Sequences & SeriesSome values for the function f(x) = log x are given in Table 1.
Table 1 Table 2
x f(x) x g(x)
10 1 1 10
100 2 2 100
1,000 3 3 1,000
10,000 4 4 10,000
Which function can generate of the values in Table 2?
Answer
(F) g(x) = x^10
(G) g(x) = 10^x
(H) g(x) = 10x
(J) g(x) = 10/x

Algebra
Sequences & SeriesWhat value of r makes the equation below true?
19/(4r-1)=5
F. 1
G. 1.(1/5)
H. 5
J. 1.(4/5)

Algebra
Sequences & SeriesThe number of cases of a new infectious disease is doubling every year such that the number of cases is modeled by a sequence beginning whose general term is an=75(2)^n-1.where n is the number of the year beginning. Find how many cases there will be at the beginning of the fourth year. Find how many cases there were at the beginning of the first year.
At the beginning of the fourth year, the number of cases will be
At the beginning of the first year, the number of cases was.
![Evaluate cos [tan -¹(1) - cos-¹(-√3/2)].
(1) If cos x = -1/2 with in Qll then find sin(x/2).
(2) Solve for 0 ≤ θ < 2π : 4sinx - 2cscx = 0
(3)Solve for 0° < θ <360° : 2sinx + cotx - cscx =0](https://media.kunduz.com/media/sug-question/raw/80251988-1659864518.5476077.jpeg?w=256)
Algebra
Sequences & SeriesEvaluate cos [tan -¹(1) - cos-¹(-√3/2)].
(1) If cos x = -1/2 with in Qll then find sin(x/2).
(2) Solve for 0 ≤ θ < 2π : 4sinx - 2cscx = 0
(3)Solve for 0° < θ <360° : 2sinx + cotx - cscx =0
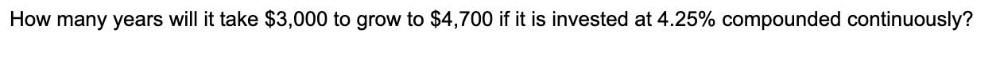
Algebra
Sequences & SeriesHow many years will it take $3,000 to grow to $4,700 if it is invested at 4.25% compounded continuously?
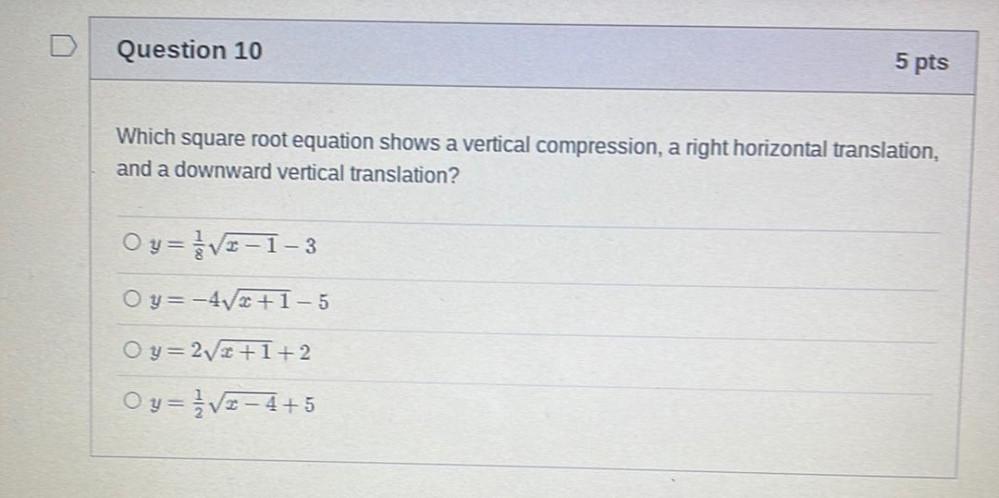
Algebra
Sequences & SeriesWhich square root equation shows a vertical compression, a right horizontal translation, and a downward vertical translation?
y=1/8√x-1-3
y=-4√x+1−5
y= 2√x+1+2
y=√x−4+5
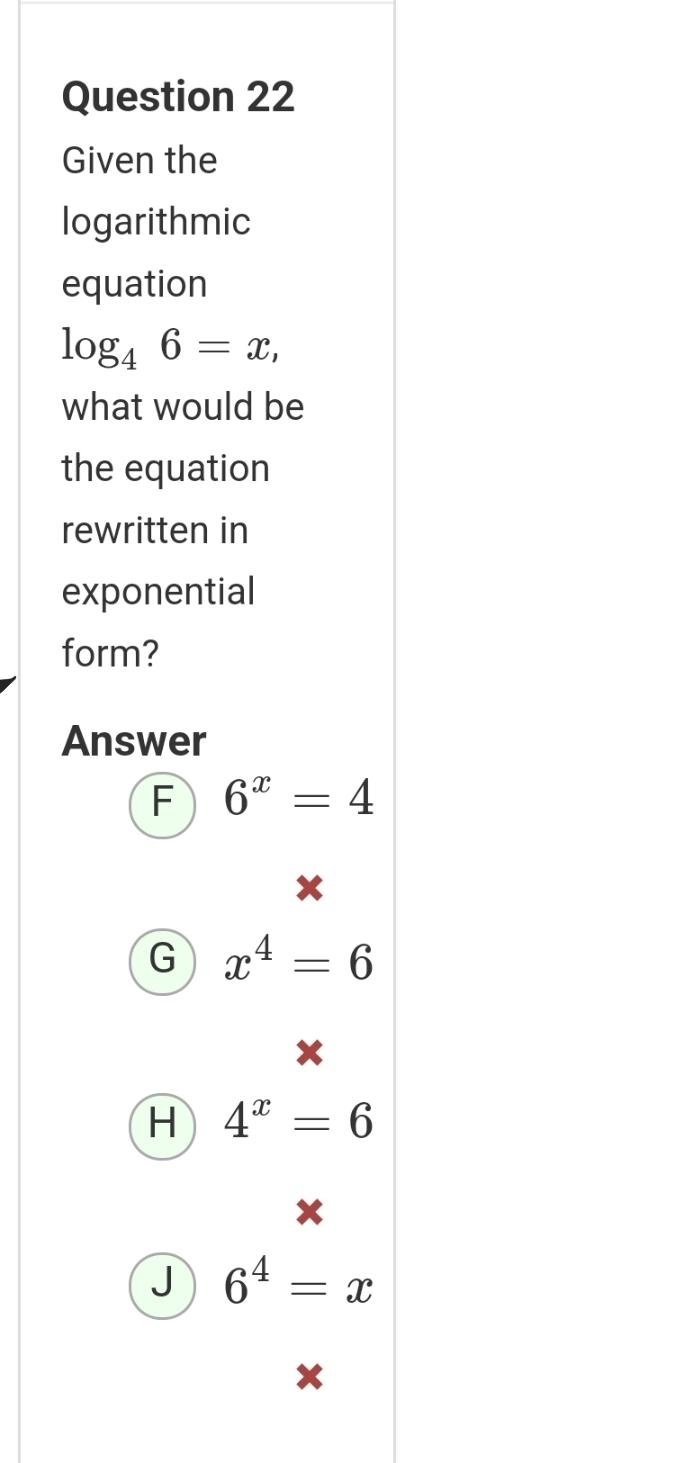
Algebra
Sequences & SeriesGiven the logarithmic equation log4 6 = x, what would be the equation rewritten in exponential form?
F) 6^x = 4
G) x^4 = 6
H 4^x = 6
J) 6^4 = x

Algebra
Sequences & SeriesWhat is the inverse function for the rational function shown below?
ƒ(x)=x/5z-8
5x-8
(a)ƒ-¹ (x)=5x/8x-1
(b)ƒ-¹ (x)=8x/5x+1
(c)ƒ-¹ (x)=8x/5x-1
(d)ƒ-¹ (x)=x/8x-1
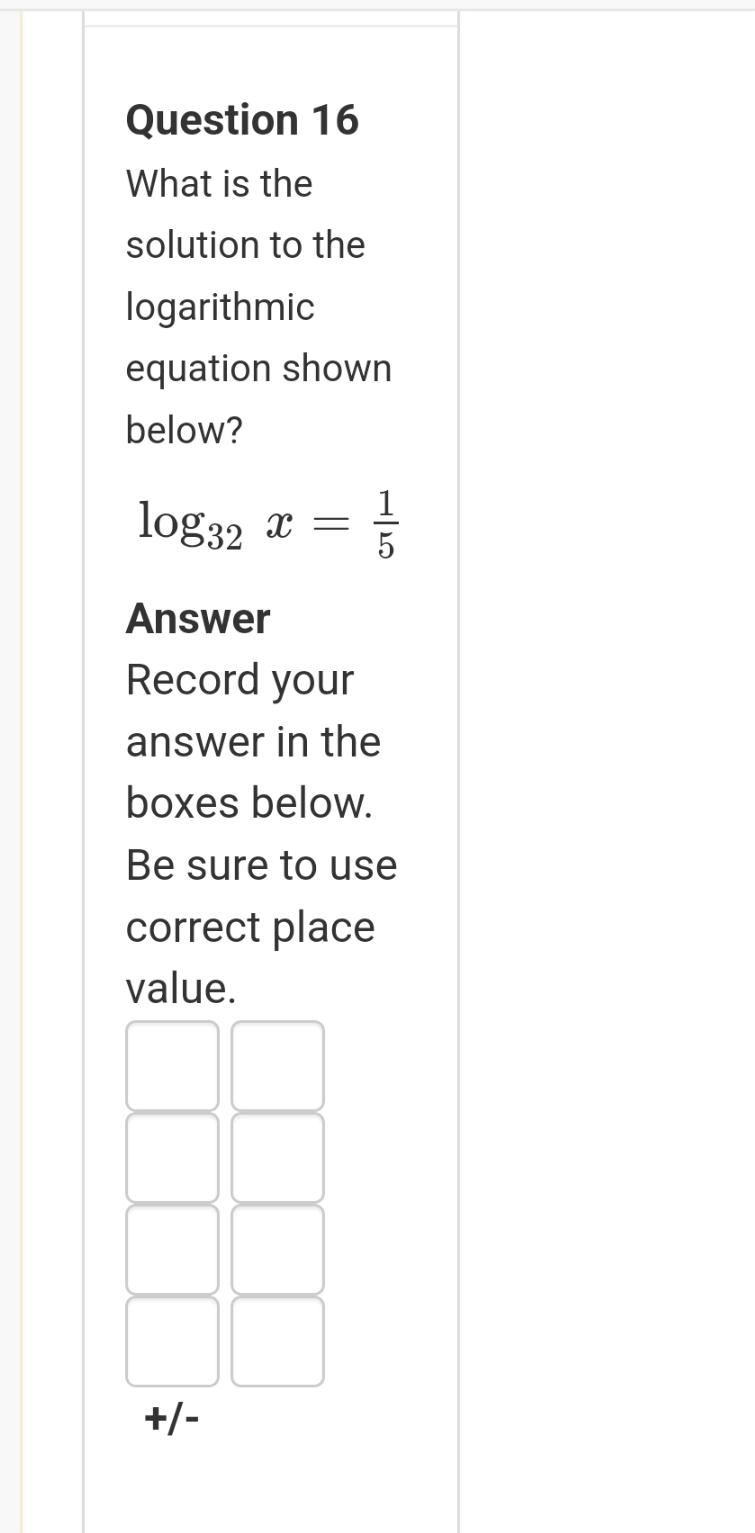
Algebra
Sequences & SeriesWhat is the solution to the logarithmic equation shown below?
log32 x = 1/3
Record your answer in the boxes below. Be sure to use correct place value.

Algebra
Sequences & SeriesSolving Differential Equations:
Solve the following differential equation
y" + 2y' + y = 0
Subject to the initial conditions
y'(0) = 3 & y(0) = 2
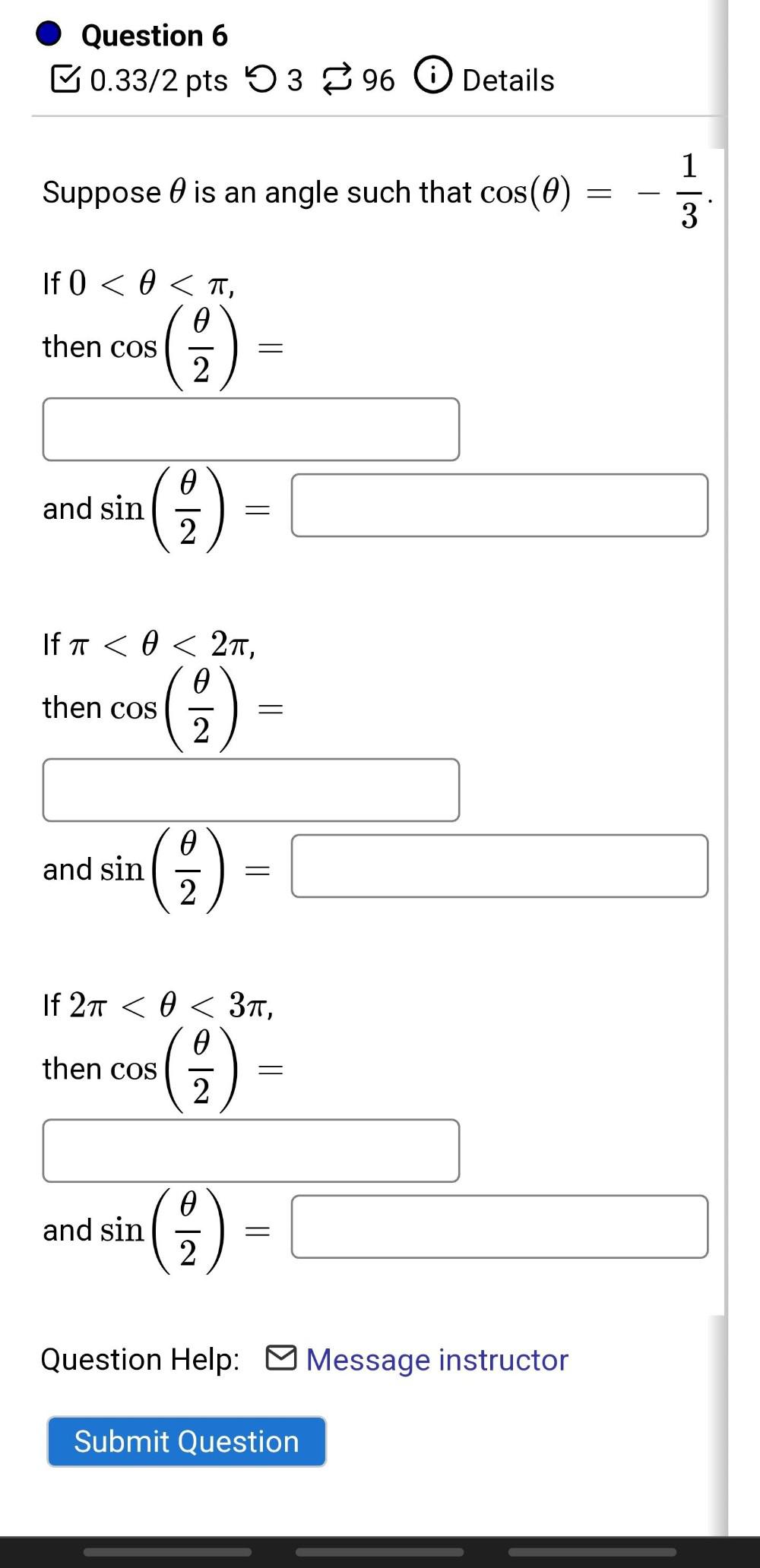
Algebra
Sequences & SeriesSuppose is an angle such that cos(θ)=-1/3
If 0 < θ < π,
then cos(θ/2)=____
and sin(θ/2)=_____
If π < θ < 2π,
then cos(θ/2)=______
and sin(θ/2)=____
If 2π < θ < 3π,
then cos(θ/2)=_____
and sin(θ/2)=______
Algebra
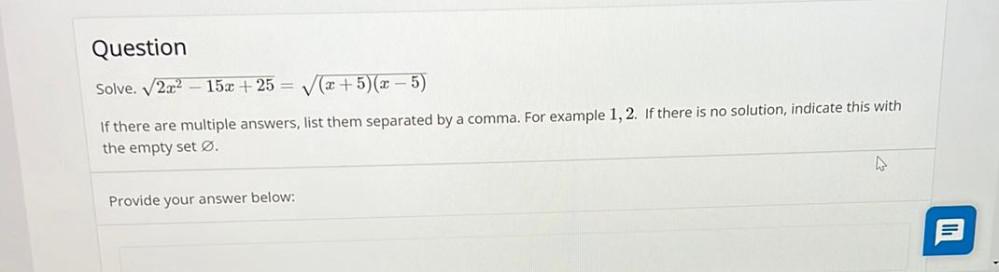
Sequences & SeriesSolve. √(2x²-15x + 25) = √(x+5)(x – 5) If there are multiple answers, list them separated by a comma. For example 1, 2. If there is no solution, indicate this with the empty set Ø. Provide your answer below:
Algebra
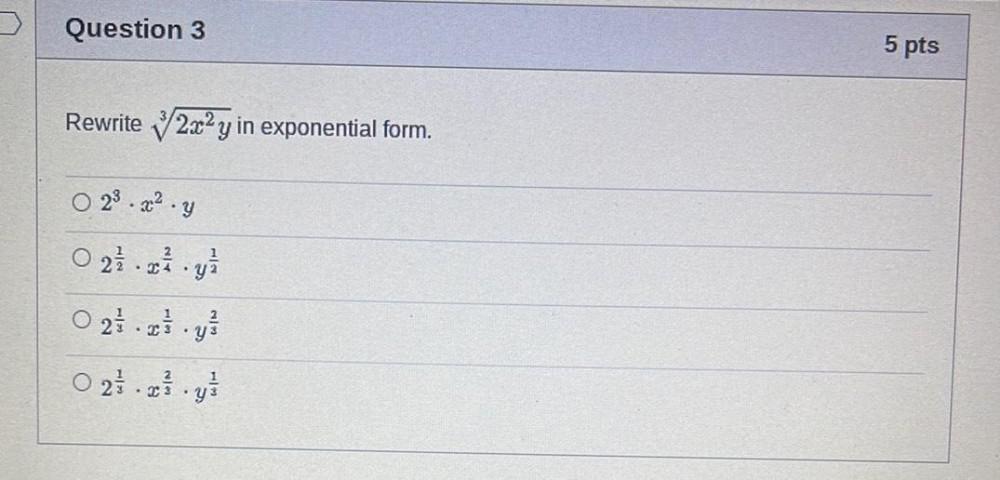
Sequences & SeriesRewrite 2x²y in exponential form.
A) 2³ * x² * y
B) 2^(1/2) * x^(2/4) * y^(1/2)
C) 2^(1/3) * x(1/3) * y(2/3)
D) 2^(1/3) * x^(2/3) * y^(1/3)

Algebra
Sequences & SeriesA mining company is mining silver. The relationship between the mass of the material mined in metric tons and the number of carts required to transport the material is given by the function V(n) = 0.5n. Additionally, the relationship between the amount of silver and the material mined is given by the function G(V)= 0.00001V.
Which function can be used to determine the mass of silver in metric tons as a function of the number of carts required to transport the materials out of the mine?
A) G(V(n))
B) V(G(n))
C) n(G(V))
D) n(V(G))
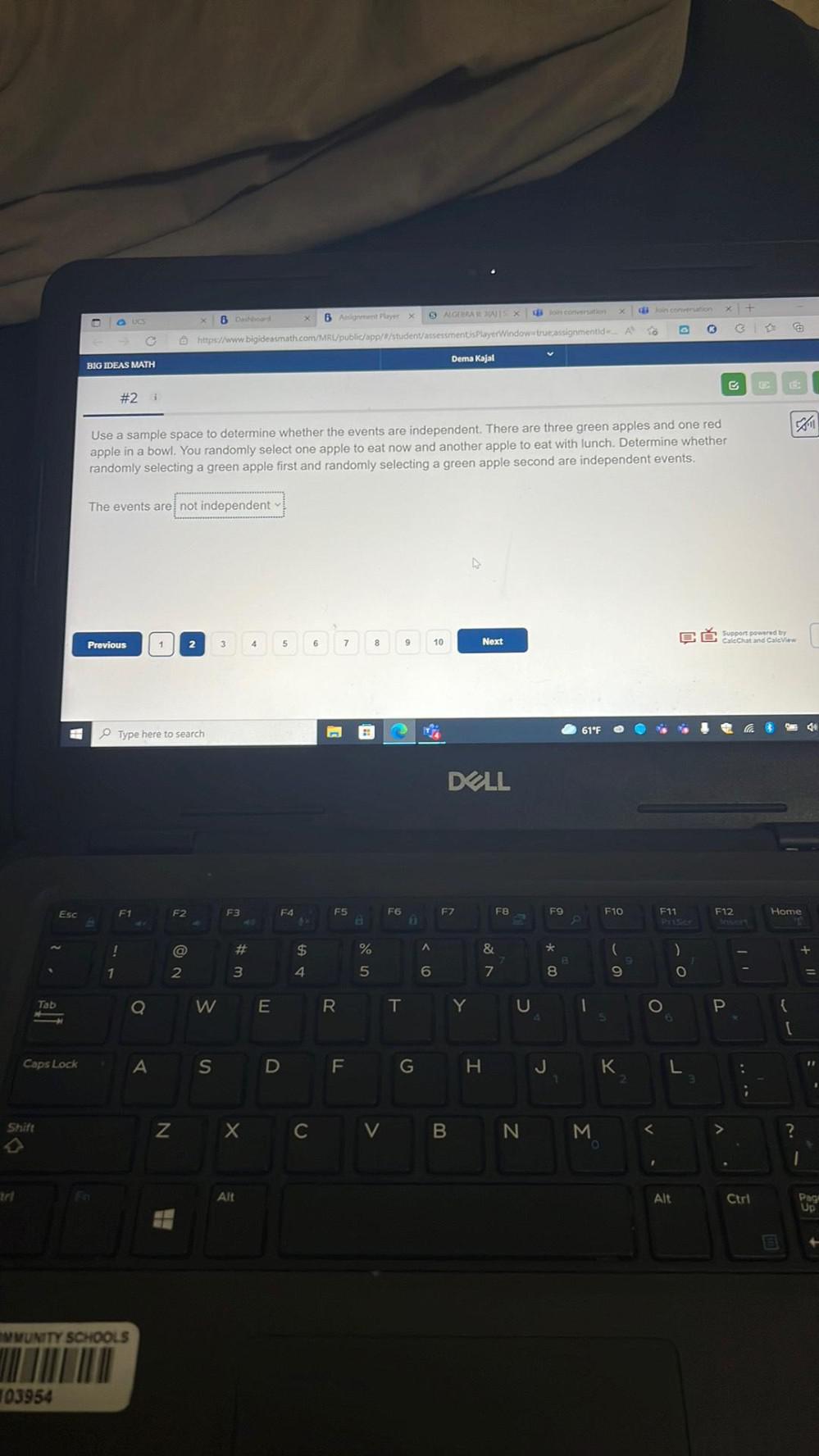
Algebra
Sequences & SeriesUse a sample space to determine whether the events are independent. There are three green apples and one red apple in a bowl. You randomly select one apple to eat now and another apple to eat with lunch. Determine whether randomly selecting a green apple first and randomly selecting a green apple second are independent events. The events are

Algebra
Sequences & SeriesIn the diagram below is P and Q the midpoints of two circles with equations
(x-7)² + (y + 2)² = 49 and x² + y² + 10x - 6y = 30, respectively.
Determine the radius of circle centre Q.
Determine the length of PQ.
Show that the equation of PQ is 5x+12y = 11
Determine the coordinates of A.
Determine the equation of the chord CD.
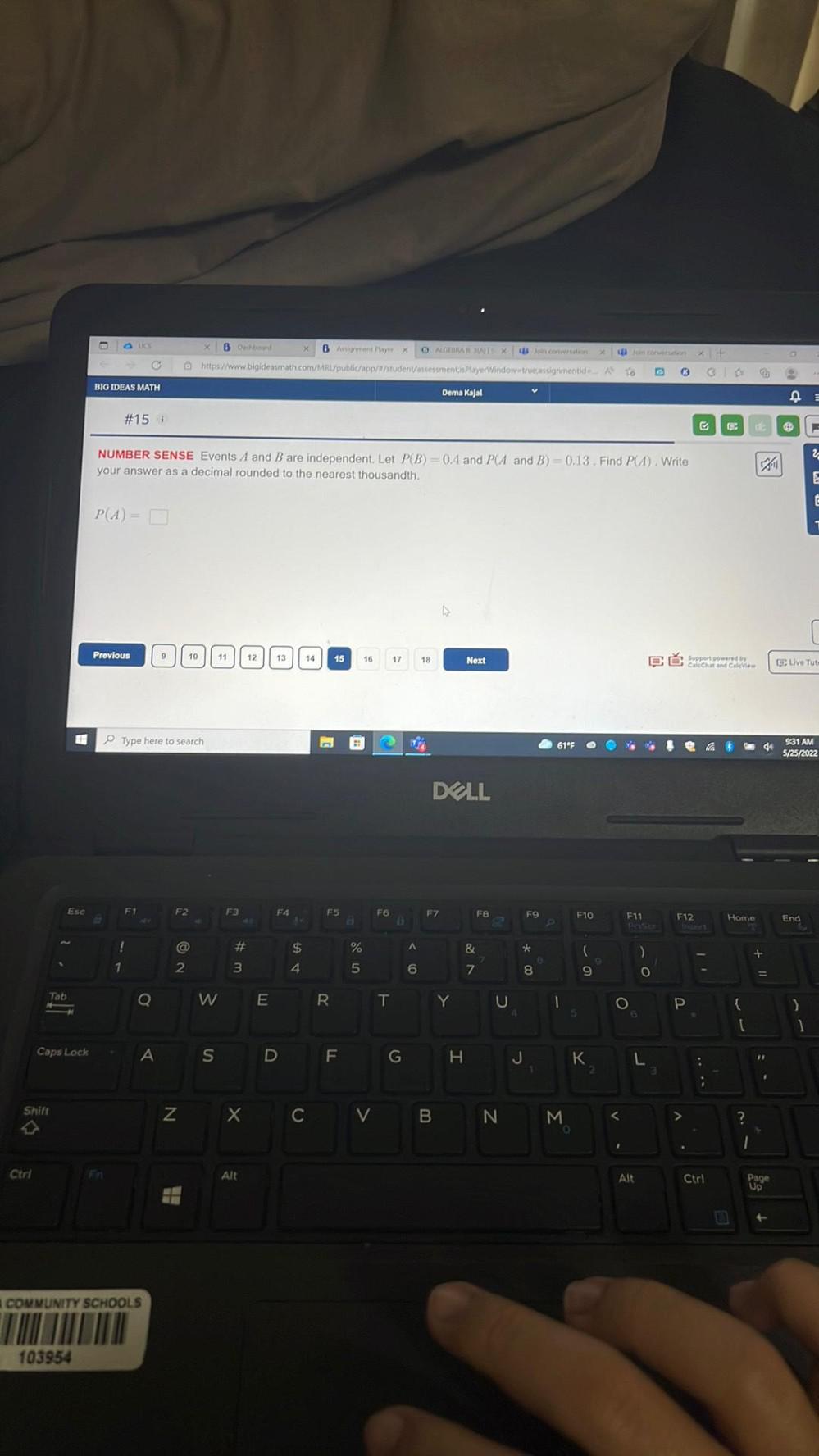
Algebra
Sequences & SeriesEvents A and B are independent. Let P(B) = 0.4 and P(A and B)-0.13. Find P(A). Write your answer as a decimal rounded to the nearest thousandth. P(A) =

Algebra
Sequences & SeriesChoose all of the true statements regarding the graph.
Select all that apply.
The graph passes the vertical line test.
The graph is a function that has an inverse function.
The inverse of the graph is not a function.
The graph is a function.
The graph passes the horizontal line test.
The graph is a one-to-one function.
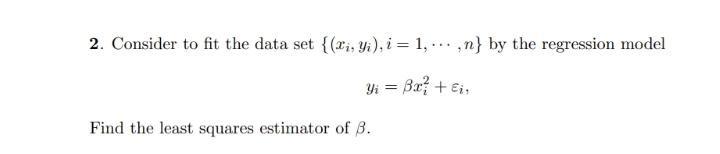
Algebra
Sequences & SeriesConsider to fit the data set {(xi, yi), i = 1,...,n} by the regression model
yi = 3x² + €i,
Find the least squares estimator of β.