Sequences & Series Questions and Answers

Algebra
Sequences & SeriesList the potential rational zeros of the polynomial function Do not attempt to find the zeros 4 3 2 f x 2x 7x x x 1 Choose the answer below that lists the potential rational zeros O A 1 1 11 1 1 2 2 7 7 1 1 11 OB 1 1 2 2 7 7 22 77 1 1 2 2 20 1 1 2 2 O C 1 1
Algebra
Sequences & Series3 Sketch the graph of this line Label at least two points on each line 3 y x 1 A
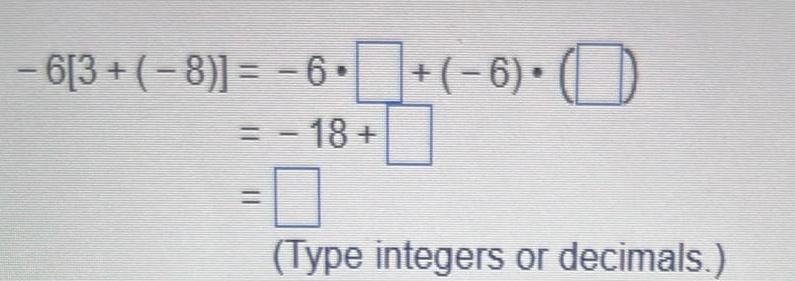

Algebra
Sequences & Series1 Write the recursive formula for the following sequence 3 2 7 12 17 4 Write the explicit equation for the following sequence U 3 U Un 1 2 n22 7 Write the explicit equation for the following sequence 3 2 7 12 17 2 Write the explicit equation that represents the sequence for any whole number n 4 12 36 108 5 Write the explicit equation defined by the following sequence U 800 Un Un 1 0 26 n21 8 Write the recursive routine for the following sequence 4 12 36 108 3 Write a recursive formula represented by the equation y 4x 10 6 Write a recursive formula represented by the equation y 2 5x 9 Write a recursive formula represented by the equation y 3 1 2

Algebra
Sequences & SeriesA grocery store was introducing a new product by setting up a display for people to try the product Between 2 00 pm and 3 00 pm 11 people tried the product Out of those 11 people 1 said they did not like it 5 said they were undec and 5 said that they liked it The store manager said that this survey was biased but the store owner thought that the survey is not biased What is true about the survey O A B D It is not biased because 5 times as many people like the product compared to those who do not It is not biased because the people who tried the product chose to participate in the survey It is biased because only 11 people tried the product It is biased because almost half of the people said that they were undecided about the product
Algebra
Sequences & SeriesExercise 1 24 a Given n E N let Yn be the set of all binary sequences of length n so for example Y1 0 1 and Y2 00 01 10 11 Find and prove a formula for the number of elements in Yn b Let Y be the set of all finite binary sequences that is Y n 1 UYn Decide whether Y is countable or uncountable and prove
Algebra
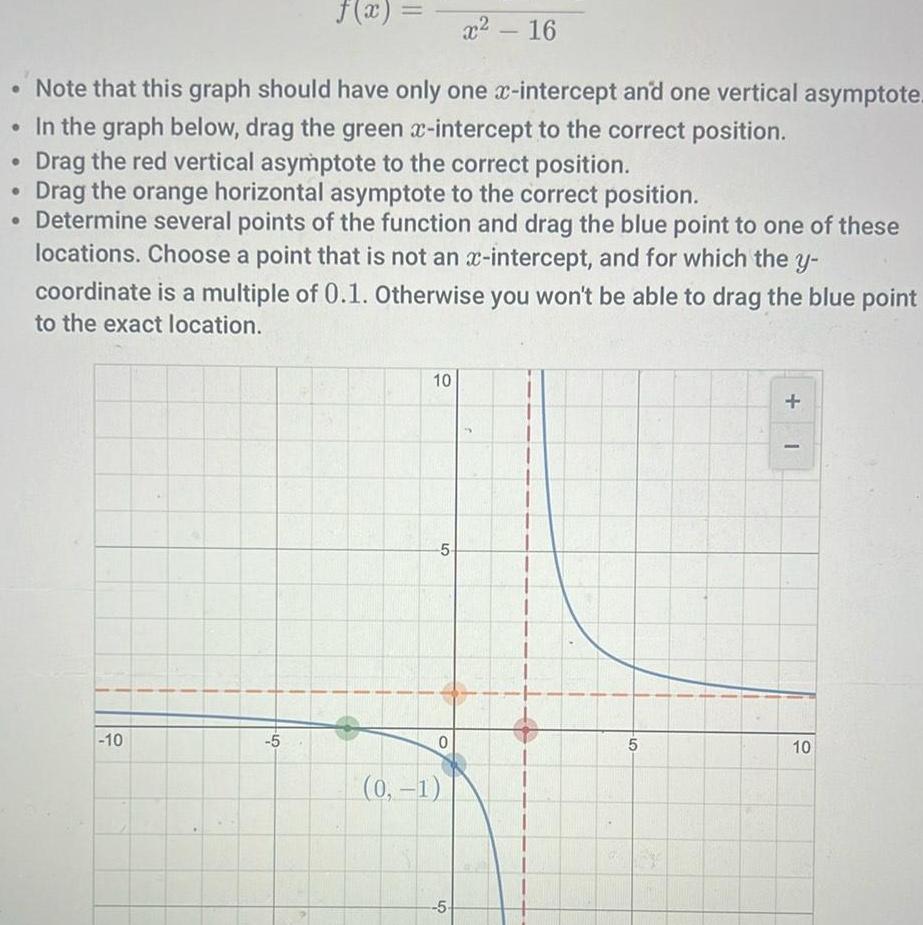
Sequences & Seriesf x x 16 Note that this graph should have only one x intercept and one vertical asymptote In the graph below drag the green x intercept to the correct position Drag the red vertical asymptote to the correct position Drag the orange horizontal asymptote to the correct position Determine several points of the function and drag the blue point to one of these locations Choose a point that is not an x intercept and for which the y coordinate is a multiple of 0 1 Otherwise you won t be able to drag the blue point to the exact location 10 5 10 5 0 0 1 5 6 5 1 10

Algebra
Sequences & Series3 A Contractor is making a different tile patteren using blue and Green tiles In this file Pattern there are blue Filed for every 4 green tiled IF The contractor used ne use 22 5 blue tied how many total thief will he use
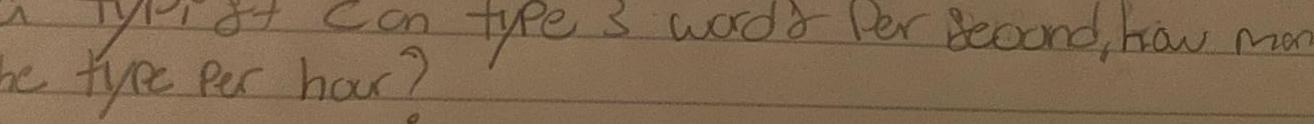
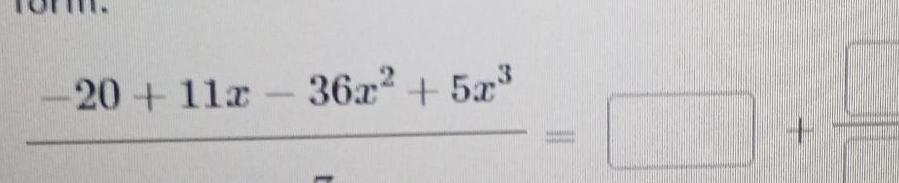

Algebra
Sequences & SeriesJohn rented a truck for one day There was a base fee of 19 99 and there was an additional charge of 71 cents for each mile driven John had to pay 113 when he returned the truck For how many miles did he drive the truck miles X


Algebra
Sequences & SeriesThree is a zero of the equation 4x 3x 18 0 Which factored form is equivalent to the equation O x 2 x 3 x 3 0 x 2 x 3 x 3 0 O x 2 x 3 0 O x 2 x 3 0

Algebra
Sequences & Series8 You have Tegopen solution 0 15 Gm per 5 mL in the medication cart The order reads Tegopen 300 mg po q 12 h How many teaspoons will you give


Algebra
Sequences & SeriesClearly A A a b 1 H H a b 1 1 H H a b A A H H ab G G G G A A H H H H 1 1 Also 0 A A H H 3ab 31 16 17 H 2a b and 22 1 6 1 4 200 3ab a b 1 2b a 2a b 3ab 2b a 2a b 9ab Let P n 25 1 24 n 5735 For n 1 P 1 625 24 5735 6336 24 x 11 which is divisible by 24 Hence P 1 Is true Let P K be the true where K 2 1 25 24 K 5735 24 2 where AEN For n k 1 For x 0 cot x sin P K 1 25 2 24 K 5735 25 25 1 24 K 5735 25 24 K 25 5735 5735 24 K 1 25 24 2 24 K 5735 24 24 25 24 24 K 24 5736 25 24 24 K 24 239 24 2 25 K 230 which is divisible by 24 Hence by the method of mathematical Induction result is true vne N and

Algebra
Sequences & Series1 Use the integral test to determine if the series converge or diverge a 8 0 2 n n 1 b

Algebra
Sequences & SeriesWhat is the remainder when the polynomial 8x2 4x 3 is divided by 2x 1 Enter your answer in the box
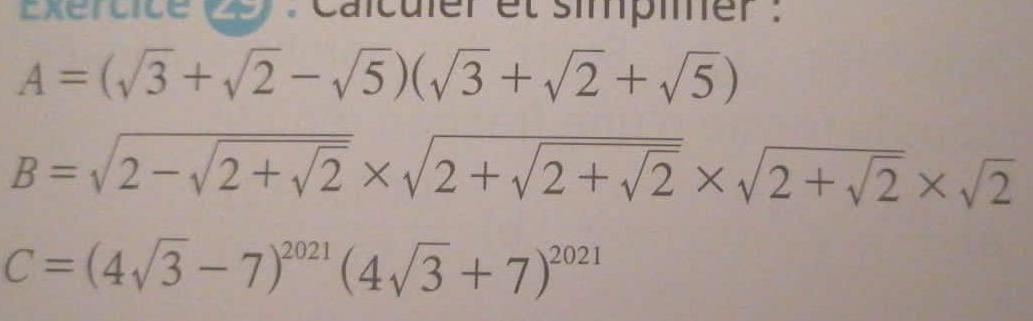

Algebra
Sequences & Series3 Write the equation of the line that passes through the point 4 3 and is PERPENDICULAR to the line y 2x 4

Algebra
Sequences & Series7 4 points Determine whether the following are functions simply answer yes or no 1 2 2 2 3 2 a b

Algebra
Sequences & Series3 4 Across 4 A number that can be written a b where a and b are integers and b is not equal to numbers in decimal form are terminating or repeating zero 5 The numbers 3 2 1 0 1 2 3 consisting of the negative integers zero and positive integers are known as 6 Down 1 numbers start with the number zero ex 0 1 2 3 4 5 numbers are also known as natural numbers ex 1 2 3 4 5 2 all numbers on the number line 3 A number that cannot be written as the quotient of two integers The decimal form number neither terminates nor repeats of an
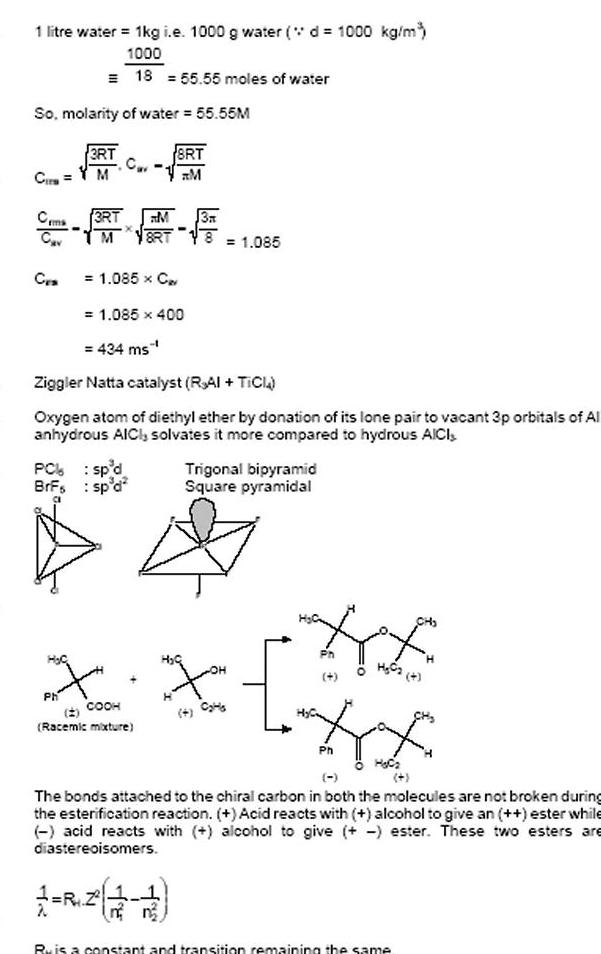
Algebra
Sequences & Series1 litre water 1kg i e 1000 g water d 1000 kg m 1000 18 55 55 moles of water So molarity of water 55 55M Cir Ceme Cav CES PC BrFs H C 3RT M Ph 3RT M M 8RT 1 085 x C 1 085 400 434 ms Ziggler Natta catalyst RAI TICI Oxygen atom of diethyl ether by donation of its lone pair to vacant 3p orbitals of Al anhydrous AICI solvates it more compared to hydrous AICI sp d sp d 8RT M 3A Racemic mixture 1 085 X X COOH Trigonal bipyramid Square pyramidal HE Ph H C2 4 Ph H C The bonds attached to the chiral carbon in both the molecules are not broken during the esterification reaction Acid reacts with alcohol to give an ester while acid reacts with alcohol to give ester These two esters are diastereoisomers Ru is a constant and transition remaining the same
Algebra
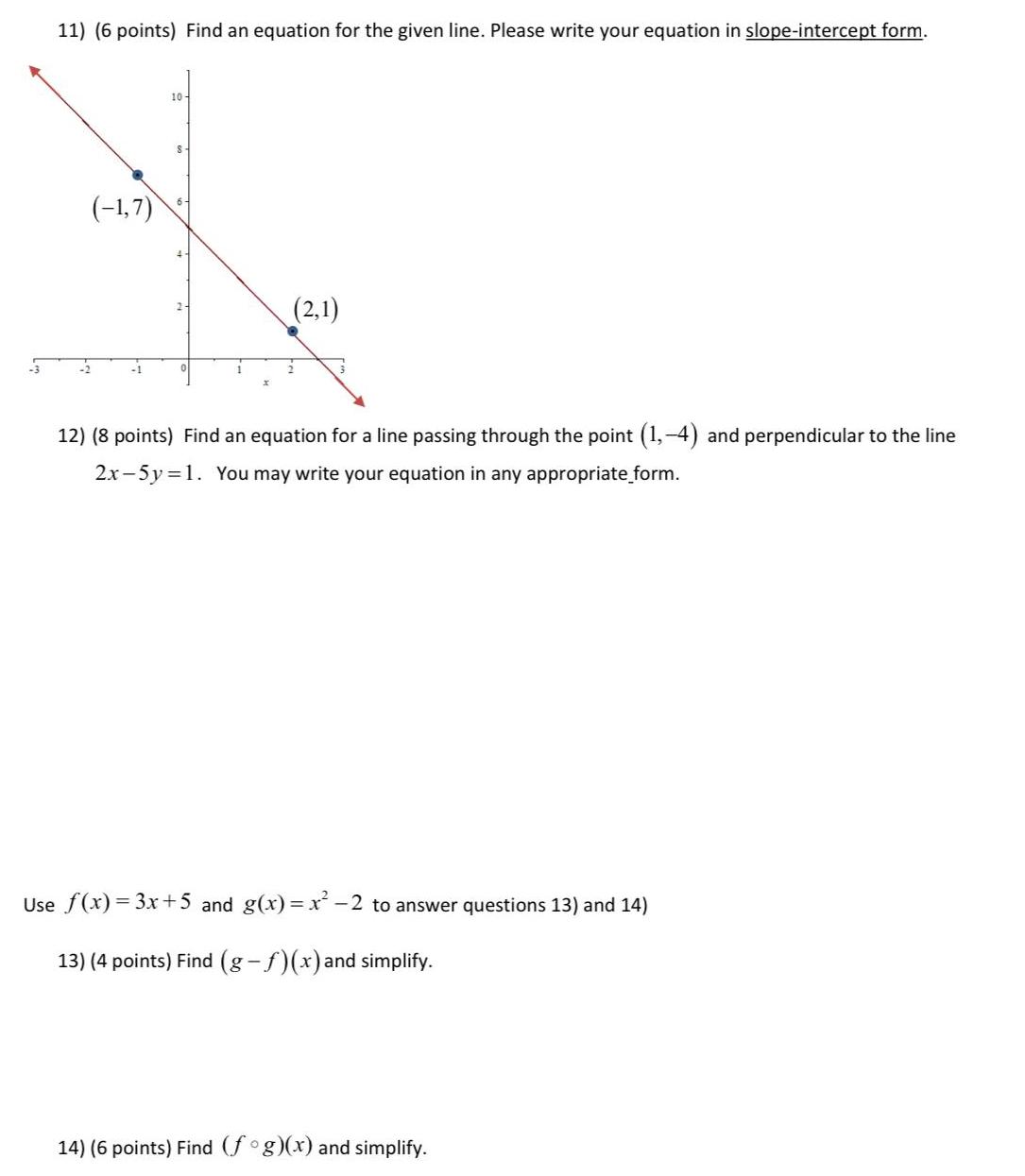
Sequences & Series3 11 6 points Find an equation for the given line Please write your equation in slope intercept form 1 7 10 S 2 1 12 8 points Find an equation for a line passing through the point 1 4 and perpendicular to the line 2x 5y 1 You may write your equation in any appropriate form Use f x 3x 5 and g x x 2 to answer questions 13 and 14 13 4 points Find g f x and simplify 14 6 points Find fog x and simplify
Algebra
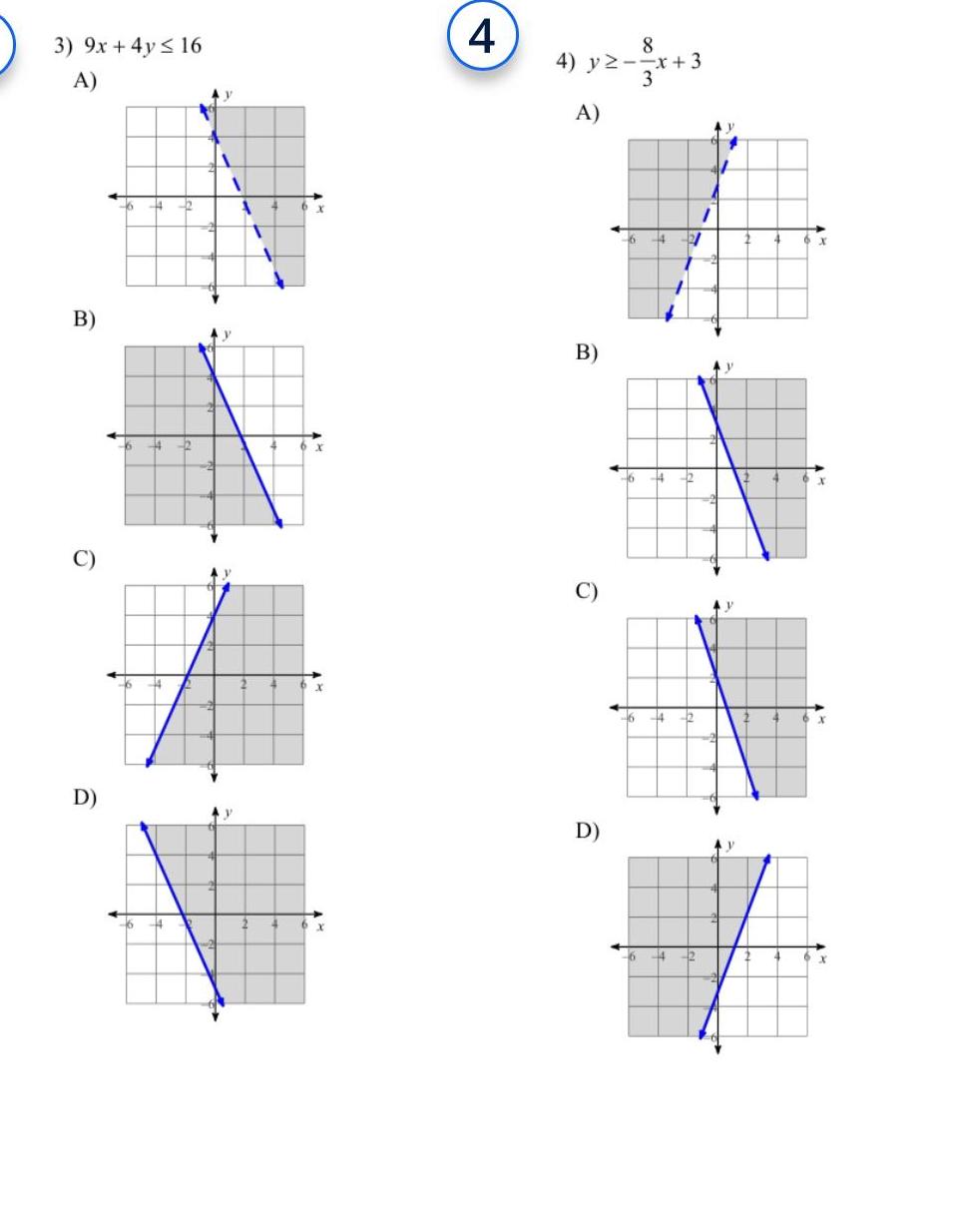
Sequences & Series3 9x 4y 16 A B C D 16 H 2 6 4 16 44 4 22 y 1 y y T 4 4 x 4 8 4 y x 3 3 A B C D 6 4 2 6 6 6 2 2 2 4 12 1 y V y 2 4 4 X X

Algebra
Sequences & SeriesAS SI Tigure below a O 1112 kg is ng along a v 7 00 m s when it encounters a ramp inclined at an angle of 8 23 8 W Net Wa The coefficient of kinetic friction between the ramp and the box is 0 0704 and the box slides a distance d up the ram before coming momentarily to rest a Determine the distance in m the box slides up the ramp before coming momentarily to rest m W frictionless surface b Determine which of the following statements is most correct about the box traveling up the ramp and coming momentarily to rest AKE 1 APEg W Net AE W cons W noncons AKE APE AE all of these rough surface ess sun noncons ce at a speed

Algebra
Sequences & Seriesind the horizontal and vertical asymptotes of the curve You may want to use a graphing calculator or computer to heck your work by graphing the curve and estimating the asymptotes Enter your answers as comma separated list Fan answer does not exist enter DNE f x 6ex ex 5

Algebra
Sequences & Series1 point If a ball is thrown straight up into the air with an initial velocity of 95 ft s it height in feet after t second is given by y 95t 16t2 Find the average velocity for the time period begining when t 2 and lasting 1 0 1 seconds 29 4 ii 0 01 seconds 162 84 iii 0 001 seconds 125 984 Finally based on the above results guess what the instantaneous velocity of the ball is when t 2 125 984
Algebra
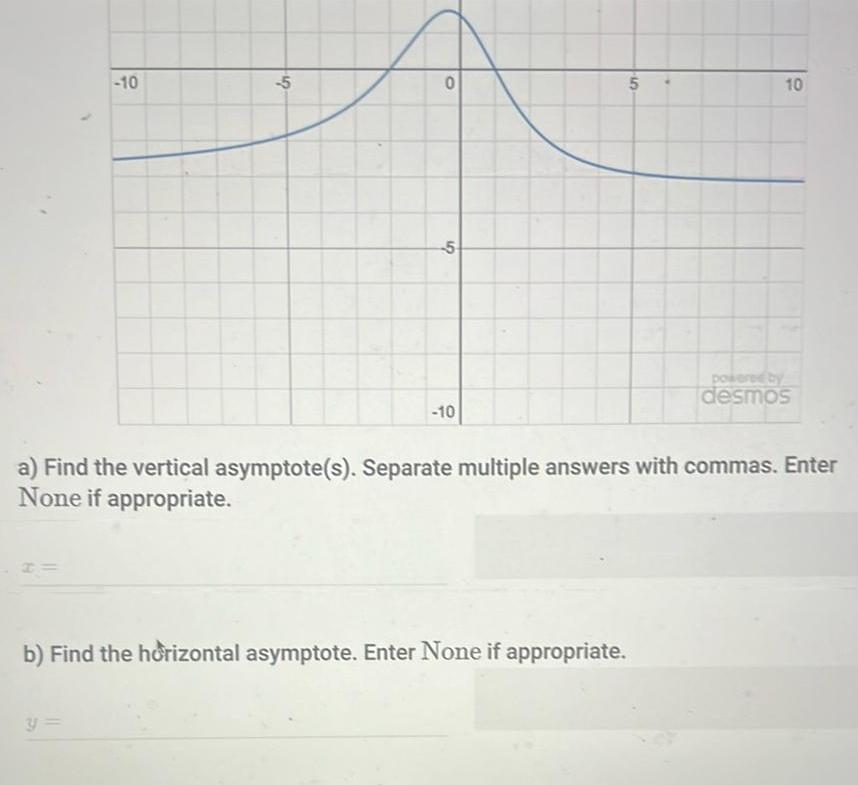
Sequences & Series10 5 0 5 10 5 10 b Find the horizontal asymptote Enter None if appropriate powered by desmos a Find the vertical asymptote s Separate multiple answers with commas Enter None if appropriate
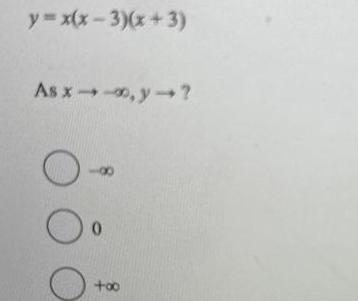


Algebra
Sequences & SeriesUse the nth term test for divergence to show that the series is divergent or state that the test is inconclusive 8 COS n 1 19 n Choose the correct answer below O A The test is inconclusive because lim cos n 19 OB The series diverges because lim cos n nx O c The series diverges because lim cos nix O D The series diverges because lim cos n18 19 n 19 n 19 n o and fails to exist exists and is equal to and fails to exist

Algebra
Sequences & SeriesMalika has 17 00 in quarters dimes and nickels She has 10 more dimes than quarters If Malika has 130 coins in all how many of each type of coin does she have 2 WRITE THE SYSTEM OF EQUATIONS 1 d 11 3 q d n DECLARE YOUR VARIABLES SOLVE THE SYSTEM EQ 19 EQ 2 EQ 3 EXPLAIN YOUR PROCESS Which method did you use to solve the problem Explain your process

Algebra
Sequences & SeriesB IS 52 nk 3 then Cik For example if C The matrix C Ciklmxp is the product of A and B 2 7 1 MATHEMATICS and is given by CD Entry in first row first column Entry in first row second column 0 Entry in second row first column 1 1 0 3 Thus CD AB Example 12 Find AB 1 entry is the sum of the products across some row of C with the corresponding entries down some column of D These four computations are 2 1 4 13 2 17 13 1 2 34 3 1 34 1 0 3 4 a 22k 2 N 4 Rationalised 2023 24 2 and D 1 5 2 1 2 1 5 second column 03 43 lish Entry in second row a 3 D3k 1 5 4 7 1 5 4 2 2 3 1 100 12 63 36 81 0 72 4 21 12 27 0 24 This is a 2 x 2 matrix in which each 1 in 1 2 1 1 2 5 27 13 1 2 4 then the product CD is defined 13 1 7 1 1 260 3 and B 28 79 to be 6 2 9 7 6 6 9 9 6 0 9 8 2 2 3 7 2 6 3 9 2 0 3 8 Solution The matrix A has 2 columns which is equal to the number of rows of B Hence AB is defined Now 2 0 7 3 1 4 4 2 75 117 72 25 39 24
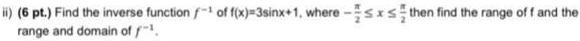
Algebra
Sequences & Seriesii 6 pt Find the inverse function of f x 3sinx 1 where sxs then find the range of f and the range and domain off

Algebra
Sequences & Series2 Let f x x3 6x2 11x 6 1 a Find the Secant formula p k 1 g pk 1 pk b Start with p0 2 5 and p1 3 5 find p2 p3 and p4 c Determine the relative error at each iteration

Algebra
Sequences & Series2 c Clearly by a and b above f is neither increasing nor decreasing in 0 2 Example 10 Find the intervals in which the function f given by f x x 4x 6 is a increasing b decreasing Solution We have or f x x 4x 6 f x 2x 4 156 Therefore f x 0 gives x 2 Now the point x 2 divides the real line into two disjoint intervals namely 2 and 2 Fig 6 3 In t 4 0 interval 2 f x 2x Therefore f is decreasing in this interval Also in the interval 2 f x 0 and so the function f is increasing in this interval Solution We have Example 11 Find the intervals in which the function fgiven by f x 4x 6x 72x 30 is a increasing b decreasing f x 4x 6x 72x 30 12x 12x 72 12 x x 6 12 x 3 x 2 Therefore f x 0 gives x 2 3 The points x 2 and x 3 ides the real line into three disjoint intervals namely 2 2 3 and 3 00 or 80 MATHEMATICS Interval 2 2 3 3 00 8 Rationalised 2023 24 Sign of f x 0 0 0 pun you Fig 6 4 3 In the intervals 2 and 3 f x is positive while in the interval 2 3 f x is negative Consequently the function is increasing in the intervals 2 and 3 0 while the function is decreasing in the interval 2 3 However fis neither increasing nor decreasing in R Example 12 Find intervals in which the function given by f x a increasing b decreasing Nature of function f fis increasing fis decreasing fis increasing o Sin 3x xe 0 1 is

Algebra
Sequences & Seriesprovided this limit exists Derivative of fat c is denoted by f c or dx function defined by wherever the limit exists is defined to be the derivative off The derivative of fis d dy dx dx denoted by f x or f x or if y f x by or y The process of finding derivative of a function is called differentiation We also use the phrase differentiate f x with respect to x to mean find f x The following rules were established as a part of algebra of deriva 1 ut v u v 2 uv u v uv Leibnitz or product rule 3 U lim h 0 120 u v uv its answer If lim h 0 wherever v 0 Quotient rule The following table gives a list of derivatives of rtain standard functions Table 5 3 f x f x tan x sin x sec x Whenever we defined derivative we had put a caution provided the limit exists Now the natural question is what if it doesn t The question is quite pertinent and so is f c h f c h does not exist we say that fis not differentiable at c In other words we say that a function fis differentiable at a point c in its domain if both f c h f c f c h f c h are finite and equal A function is said h to be differentiable in an interval a b if it is differentiable at every point of a b As in case of continuity at the end points a and b we take the right hand limit and left hand limit which are nothing but left hand derivative and right hand derivative of the function at a and b respectively Similarly a function is said to be differentiable in an interval a b if it is differentiable at every point of a b f x lim h 0 MATHEMATICS Therefore But for x c we have nx 1 and lim h 0 f x h f x h lim X C sin x Rationalised 2023 24 COS X f x f c Theorem 3 If a function f is differentiable at a point c then it is also continuous at that point Proof Since fis differentiable at c we have f x f c X C blish lim f x f c lim X C X C COS X f x f c X C f c 5 co J x c The x c f x f c X C 7 x c ed
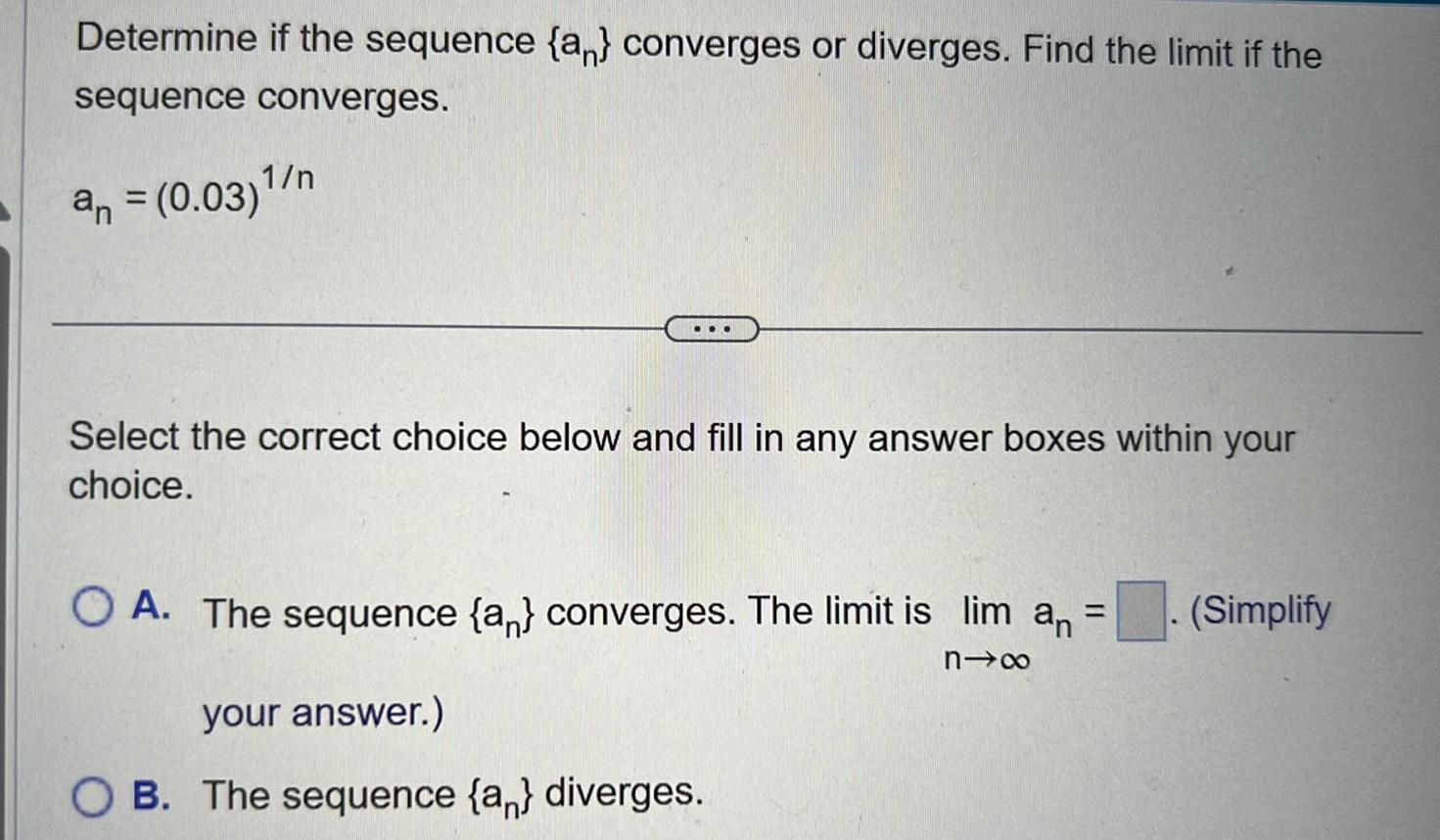
Algebra
Sequences & SeriesDetermine if the sequence a converges or diverges Find the limit if the sequence converges an 0 03 n Select the correct choice below and fill in any answer boxes within your choice O A The sequence a converges The limit is lim an 81x your answer OB The sequence an diverges Simplify
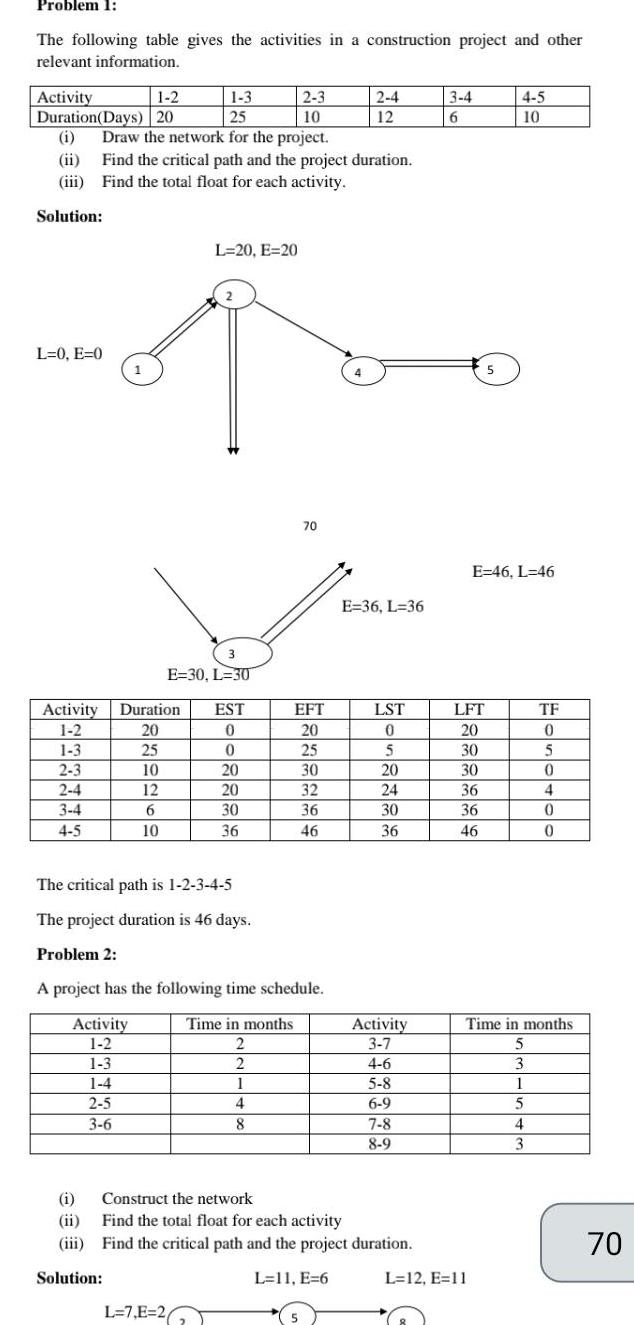
Algebra
Sequences & SeriesProblem 1 The following table gives the activities in a construction project and other relevant information Activity 1 2 1 3 2 3 Duration Days 20 25 10 i Draw the network for the project ii Find the critical path and the project duration iii Find the total float for each activity Solution L 0 E 0 Activity 1 2 1 3 2 3 2 4 3 4 4 5 1 i ii iii Solution 3 E 30 L 30 Duration 20 25 10 12 6 10 L 20 E 20 EST 0 0 L 7 E 26 20 20 30 36 The critical path is 1 2 3 4 5 The project duration is 46 days Problem 2 A project has the following time schedule Time in months Activity 1 2 2 1 3 2 1 4 1 2 5 3 6 4 8 70 EFT 20 25 30 32 36 46 5 2 4 12 E 36 L 36 LST 0 5 20 24 30 36 Activity 3 7 4 6 Construct the network Find the total float for each activity Find the critical path and the project duration L 11 E 6 5 8 6 9 7 8 8 9 3 4 6 LFT 20 30 30 36 36 46 5 E 46 L 46 L 12 E 11 4 5 10 TF 0 5 0 4 0 0 Time in months 5 3 1 5 4 3 70

Algebra
Sequences & SeriesIn this model we assume that the ordering quaintly is received only over a period of time Further is assumed that the production rate is greater than the demand rate otherwise there will be no inventory build up and stock only will occur These two assumptions are made in addition to the assumption of model I Let k be the production rate r be the demand rate otherwise there will be no inventory build up and stock only will occur There two assumptions are made in addition to the consumption of model I Let k be the production rate r be the demand rate Let tbe the length of production run rate r be the demand rate Let t be the length of production run inventory level past of inventory part of inventory when there is no during production production Maximum inventory Total production Q kt t period 1 The average height is half the height of the triangle and the height in determined by the rate of replenishment less the demand over the replimshment G Total cost total Ordering cost Total Carrying cost uC 1 G CA Q cs 1 G CA 2r 0 always CA O Q 2rCs Total minimum cost is given by 59 CA Q rcs k r 1 k r G 2rGK 2 2rGK 2Gr k r GK 2Gr k r GK time The optimum time interval between orders is t The optimum of number of order is

Algebra
Sequences & SeriesSolution The minimum processing time among all the jobs in the 2 machines M and M is 2 which is marked in under lined bold face which correspond to the job J2 on machine M Thus the job J2 is placed sequenced in the first position in the sequence J2 We are now left with 4 jobs and their processing times are given below Machines M M Jobs J J3 J4 Js J2 Jobs J3 10 J4 Js 18 34 6 20 Among jobs the those four minimum processing time between the two machines is 4 which corresponds to the job J1 on machine M Hence the job J is placed in the last position in the sequence shown below The remaining 3 jobs and their processing times are given below Machines M M 18 J 6 20 14 16 6 J 14 16 6 The minimum processing time among these jobs is 6 which corresponds to the job J4 on machine M and job Js on machine M Hence J4 is placed in the first available position in the sequence as shown below Jz J4 J5 Finally the job J3 is placed as shown below J J4 J3 J5 J Thus J2J4J3 J5 J is the optimal sequence of the five jobs on the

Algebra
Sequences & Seriesagus any vi u uw won TAN counter is identical and follows the same exponentioal distribution law The mean service rate per busy service is u Therefore over all service rate when there are n units in the system may be obtained in the following two situations i And If n s all the customers may be served simulataneously There will be no queue s n number of servers may remain idle and then Hn nu n 0 1 2 s ii If n s all the servers are busy maximum number of customers waiting in queue will be n s then nu MODEL IV B MMS NIFCFS In model IV A if the maximum number in the system is limited to N then as in model III s 1 sp 12n 0 n sp Zn 0 n P An 0 H x su Where Pe may be written as sp s 1 p Virtually the same relationships hold between P and Po as in model IV A with infinite capacity Therefore 8 1 P 51 n 1 sp n Po nl foro nss St pt Po s s 0 for n N for 0 n N sp n n nu for 0 nss TUSIN MINU n s for n N 1 p s 1 1 1 p for s n N sp N s 1 p s sp sp s s s SH DUVA for s n N 1 1 This queueing modrl with limited waiting room is valuable because of its relevance to many real situations and the fact that changes may be made to its properties by adjusting the number of servers or the capacity of the waiting room However while poission arrivals are common in practice negative exponential service times are less so and it is the second assumption in the system MIM s that limits its usefulness Example
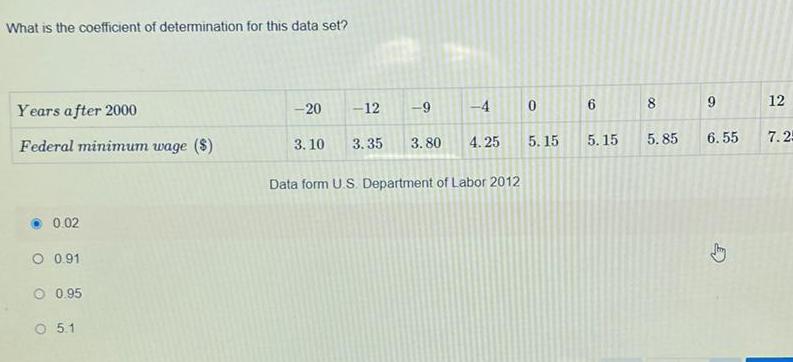
Algebra
Sequences & SeriesWhat is the coefficient of determination for this data set Years after 2000 Federal minimum wage 0 02 O 0 91 0 95 O 5 1 20 3 10 12 3 35 4 3 80 4 25 9 Data form U S Department of Labor 2012 0 5 15 6 5 15 00 8 5 85 9 6 55 Jhy 12 7 25

Algebra
Sequences & Seriesotherwise go to step 4 Step 4 Convert the m machines problem into a two machine problem by introducing two fictious machines H and K such that thi t j t j tk and U tkj 12 t3j tkj Where tj is the processing time of jth job in machine H and tx is the processing time of jth job in machine K Step 5 Determine the optimal sequence for n jobs and 2 machines sequencing problem Problem Find the sequence that minimizes the total elapsed time required to complete the following six jobs on three machines M M and M3 in the order M M M3 Jobs Machines J Jz M 3 12 M 8 M3 13 6 a min ty 2 max t j j 2 5 b min tj 2 max t j j 2 5 M 2 12 14 36 J3 5 M 1 8 4 2 6 Js J6 11 9 3 9 12 8 Solution We are given 6 jobs each of which is to be processed in 3 machines M M2 M3 in the order M M M3 Hence n 6 and m 3 Hence the given problem becomes 6 jobs in 3 machines problem For optimum sequence the required condition is either or both of the following conditions must be true M3 8 14 1 13 Minimum time Maximum time Min t 2 and nt3j 8 Max taj 8 Clearly Min t3 Max t 8 Hence the condition to reduce 3 machines problem to 2 maxhines problem is satisfied Hence the given problem can be converted to an equivalent two machines for six jobs problem Hence we have the processing table for the two machines H and K Jober Let H and K be two fictious machines such that the processing times are got from the following relations H M M z i e H tj tj t j K M 2 M 3 i e K txj tzi t3j Where 1 i 6

Algebra
Sequences & Series2 Least Cost Method The procedure is as follows Step 1 Determine the smallest cost in the cost matrix of the transportation table Let it be Cij Allocate x j min a b in the ij cell Step 2 If x j a cross off ith row of the transportation table and decrease b by a If x b cross off jh column of the transportation table and decrease a by bj If Xij a bj cross off either the first row or the first column but not both Step 4 Repeat steps 1 and 2 for the resulting table Reduce transportation table until all requirements are satisfied Problem Find an initial basic feasible solution to the following TP using Least Cost Method 1 2 3 F 2 Solution Step 1 0 is the minimum element which appears in 1 2 and 3 1 cells For the First allocation in X 2 min 15 15 15 Cross out first row or first column 1 3 4 3 2 3 2 3 2 3 I 2 3 4 10 0 20 11 15 2 12 7 9 20 25 Step 2 Second allocate in 3 1 cell X 1 min 5 5 5 12 3 4 12 7 3 0 14 16 18 5 5 15 15 10 10 0 20 H 12 7 9 20 0 5 15 15 1 Step 3 Third allocate in 2 2 cell X 2 min 25 0 0 2 3 4 2 Solution 14 16 18 5 14 5 0 15 10 Step 4 Fourth allocate in 2 3 cell X23 min 25 15 15 7 9 20 25 14 16 18 0 0 15 10 B 4 3 Step 5 Fifth allocate in 3 4 cell X34 min 0 10 0 4 1 9 20 25 16 18 5 15 10 4 2 20 10 18 10 9 20 25 16 18 5 20 10 Step 6 Sixth allocate in 2 4 cell X24 min 10 10 10 0 The initial basic feasible solution is given by x12 15 X31 5 x22 0 X23 15 X34 0 X24 10 1 3 4 10 1 2 d 3 A A P 50 30 220 1 P 90 45 170 3 P 250 250 50 4 4 2 2 8 1 2 1 10 0 10 5 10 15 12 25 0 14 16 18 Minimum transportation cost 15 9 10 20 Rs 335 Exercise 1 Using Least Cost Method find out the initial basic feasible solution to the following TP 0 3 Vogel s Approximation Method VAM 20 The procedure is as given below Step 1 For each row of the transportation table find the smallest cost and next to it Determine the difference between them for each row Write them within brackets along the side of the table 21 Step 2 For each column do the same step as in step 1 Step 3 Identify the row or column with the largest difference Let the greatest difference correspond to p and let Cij be the smallest cost in the ith row Allocate x min a b in that cell If xa cross off ith row of the transportation table and decrease b by a If x b cross off jth column of the transportation table and decrease a by bj If xa b cross off either the first row or the first column but not both 3 4 2 3 Step 4 Repeat steps 1 2 and 3 for the resulting table Reduce transportation table until all requirements are satisfied 0 Problem Find an initial basic feasible solution to the following TP using Vogel s Approximation Method 2 12 7 9 20 25 2 15 22 0 14 16 18 5 5 15 15 10 11 15 4 0 20 11 15 10 7 20 11 Step 1 Here the maximum difference is 14 which corresponds to third row of the table For the First allocation in X min 5 5 5 Cross out third column or first column 9 20 0 23 15 10 2 12 7 9 20 25 2 3 a 14 16 18 5 14 15 15 1 10 7 7 7 23

Algebra
Sequences & Serieslease convert the following linear optimization problem into the standard form of a linear rogram maximize x 5x x3 3x4 subject to x 3x x4 5 3x x 4 x 3x3 x4 4 x 0 i 1 2 3 4
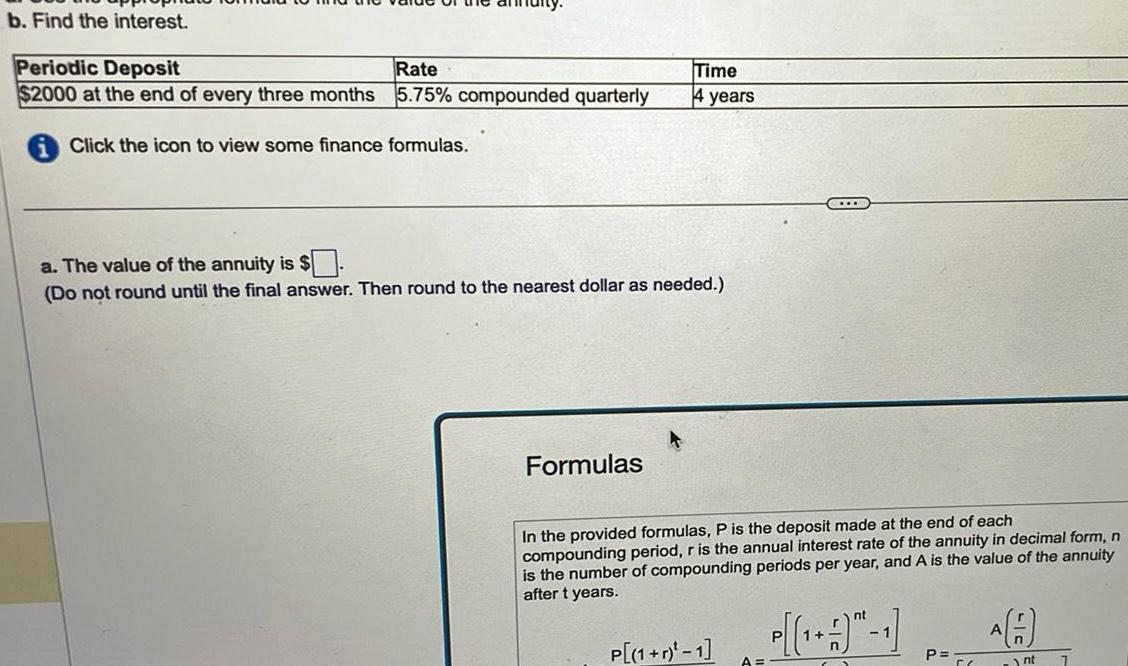
Algebra
Sequences & Seriesb Find the interest Periodic Deposit Rate 2000 at the end of every three months 5 75 compounded quarterly Click the icon to view some finance formulas Time 4 years a The value of the annuity is Do not round until the final answer Then round to the nearest dollar as needed Formulas In the provided formulas P is the deposit made at the end of each compounding period r is the annual interest rate of the annuity in decimal form n is the number of compounding periods per year and A is the value of the annuity after t years P 1 r 1 nt 1 P P A n nt
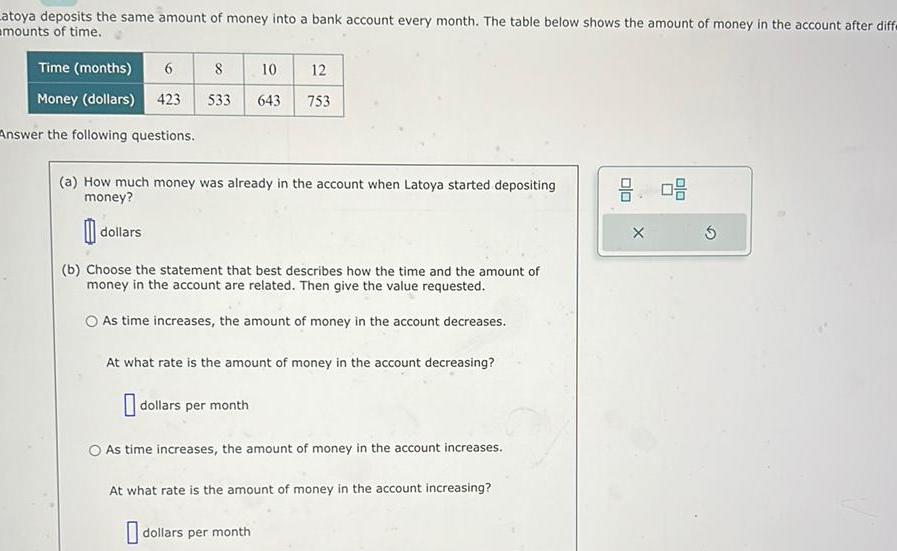
Algebra
Sequences & SeriesLatoya deposits the same amount of money into a bank account every month The table below shows the amount of money in the account after diffe mounts of time Time months 6 Money dollars 423 Answer the following questions 8 10 533 643 dollars a How much money was already in the account when Latoya started depositing money 12 753 b Choose the statement that best describes how the time and the amount of money in the account are related Then give the value requested As time increases the amount of money in the account decreases At what rate is the amount of money in the account decreasing dollars per month O As time increases the amount of money in the account increases At what rate is the amount of money in the account increasing dollars per month 8 08 X 5
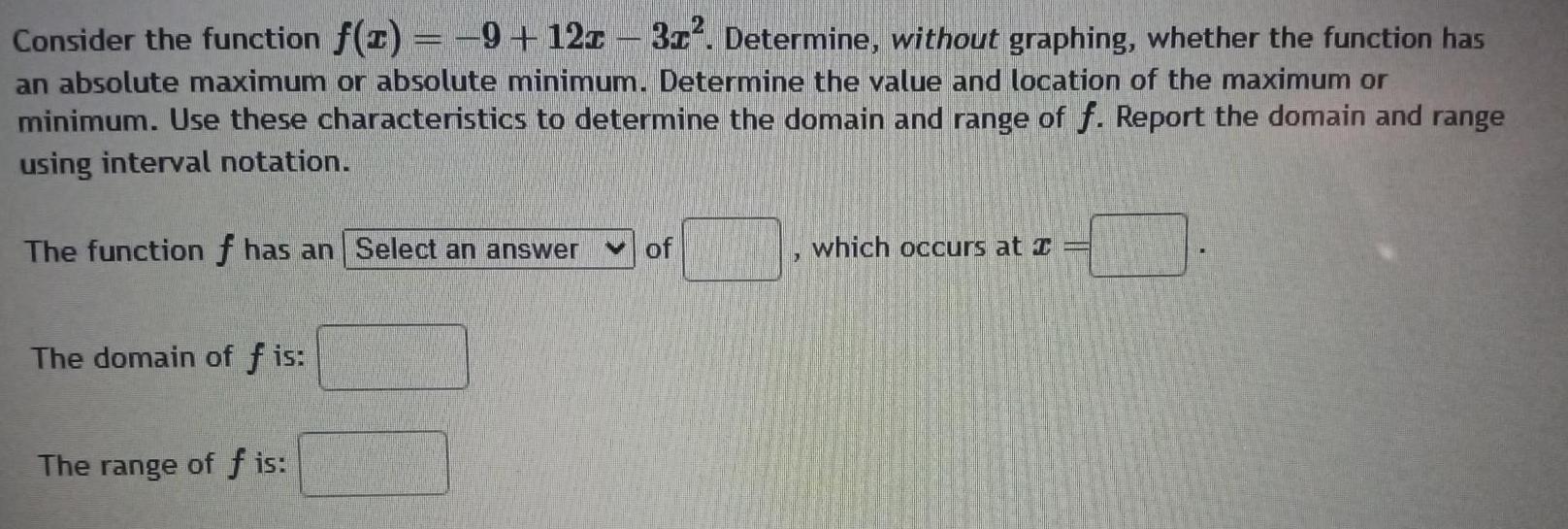
Algebra
Sequences & SeriesConsider the function f z 9 12z 3x Determine without graphing whether the function has an absolute maximum or absolute minimum Determine the value and location of the maximum or minimum Use these characteristics to determine the domain and range of f Report the domain and range using interval notation The function f has an Select an answer of The domain of fis The range of f is which occurs at I