Application of derivatives Questions and Answers

Calculus
Application of derivativesven f x find g x and h x such that f x g h x and neither g x nor h x is solely r wer g x f x 1 4x 3
Calculus
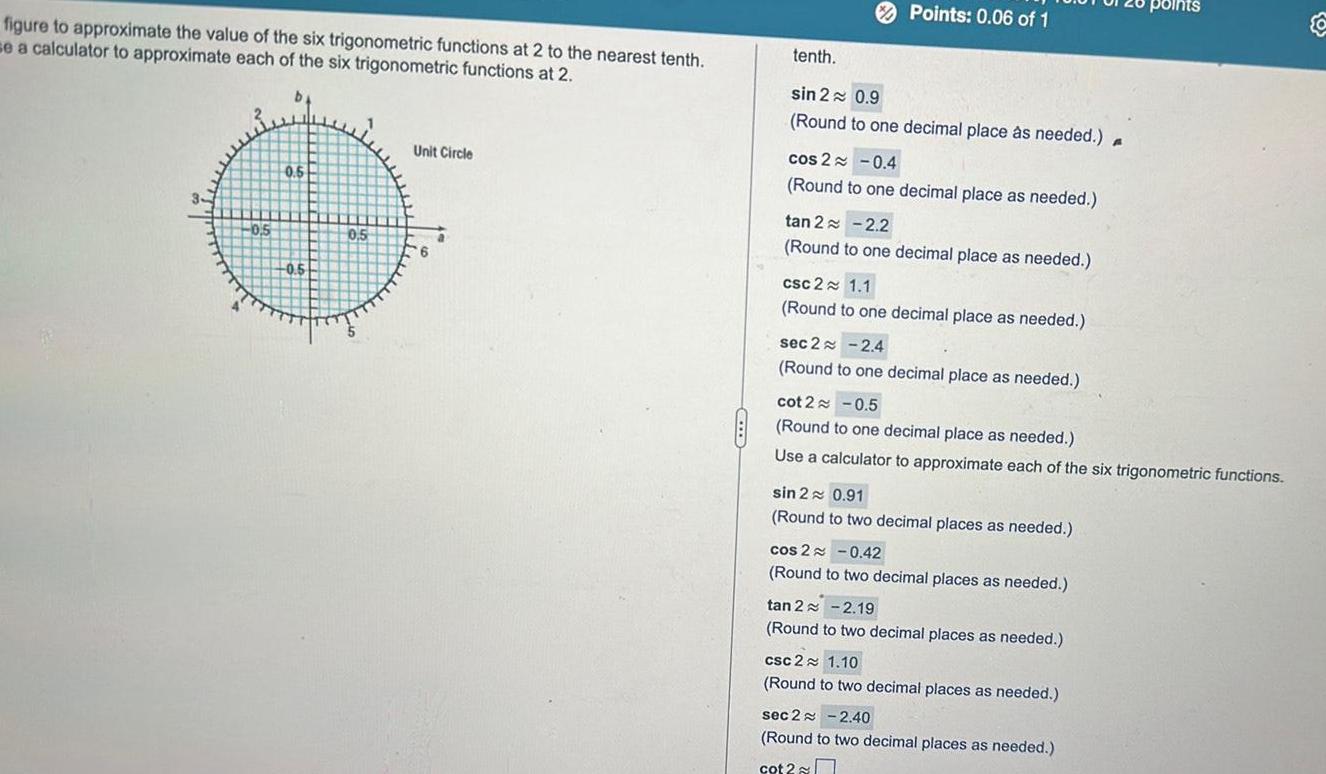
Application of derivativesfigure to approximate the value of the six trigonometric functions at 2 to the nearest tenth se a calculator to approximate each of the six trigonometric functions at 2 0 5 0 5 0 5 0 5 Unit Circle 6 a Points 0 06 of 1 tenth sin 2 0 9 Round to one decimal place as needed A cos 2 0 4 Round to one decimal place as needed tan 2 2 2 Round to one decimal place as needed csc 2 1 1 Round to one decimal place as needed sec 2 2 4 Round to one decimal place as needed cot 2 0 5 Round to one decimal place as needed Use a calculator to approximate each of the six trigonometric functions sin 2 0 91 Round to two decimal places as needed cos 2 0 42 Round to two decimal places as needed tan 2 2 19 Round to two decimal places as needed csc 2 1 10 Round to two decimal places as needed poll sec 2 2 40 Round to two decimal places as needed cot 2

Calculus
Application of derivativesFor the same function f x 5x 2x 3x 1 find all x values where there is a horizontal tangent line
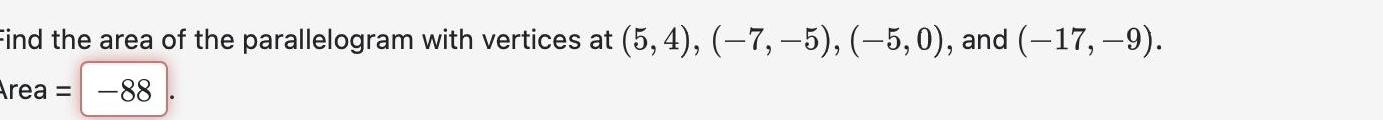
Calculus
Application of derivativesFind the area of the parallelogram with vertices at 5 4 7 5 5 0 and 17 9 Area 88
Calculus
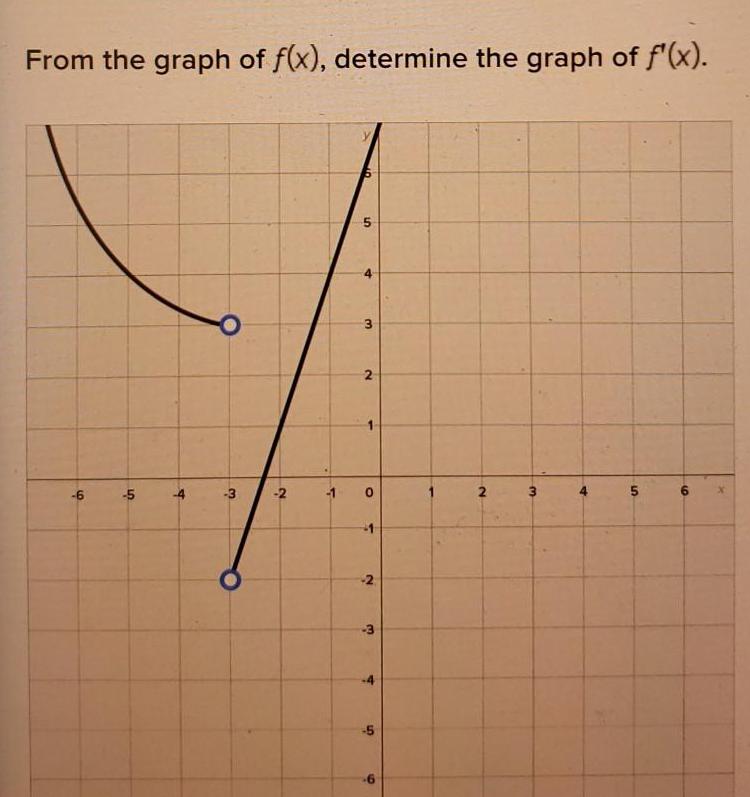
Application of derivativesFrom the graph of f x determine the graph of f x 6 5 4 3 2 1 5 5 4 3 2 0 5 2 3 4 5 2 W 4 5 6

Calculus
Application of derivativesConsider the equation below If an answer does f x 5x e x a Find the interval on which f is increasing Enter your answer using interval notation Find the Interval on which f is decreasing Enter your answer using Interval notation b Find the local minimum and maximum values of f local minimum value local maximum value c Find the Inflection point x y Find the interval on which f is concave up Enter your answer using interval notation Find the Interval on which f is concave down Enter your answer using interval notation

Calculus
Application of derivativesConsider the following functions Step 2 of 4 Find f g 1 Answer How to enter your answer opens in new window f 4 1 1 1 1 3 and g 0 2 1 1 4 2
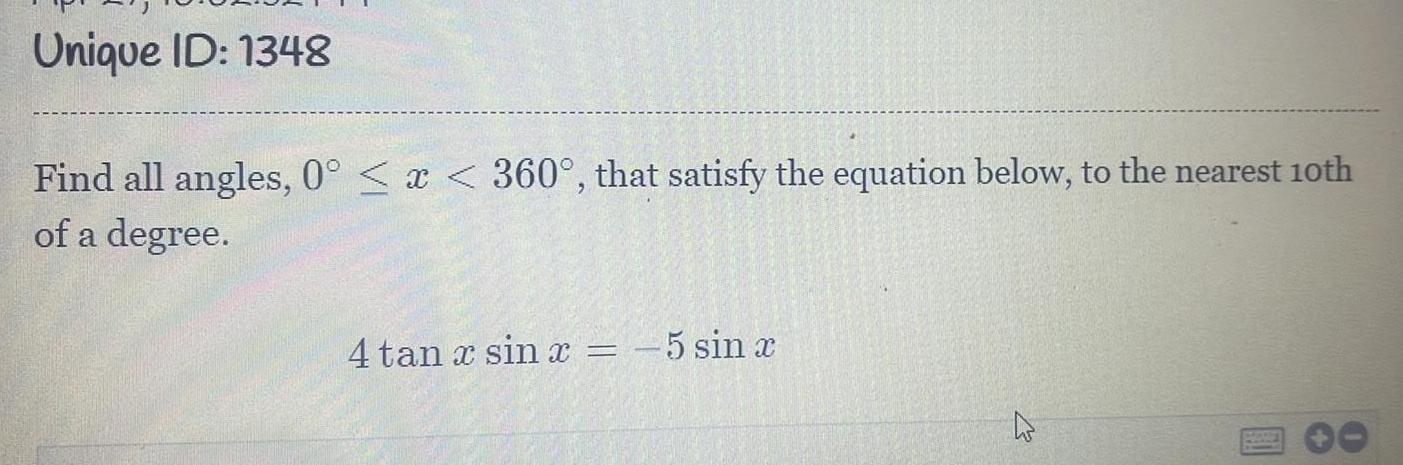
Calculus
Application of derivativesUnique ID 1348 Find all angles 0 x 360 that satisfy the equation below to the nearest 10th of a degree 4tan xsinx 5 sinx Mary

Calculus
Application of derivatives4 For the function f x 5x equation of the tangent line at x 1 2x 3x 1 find the
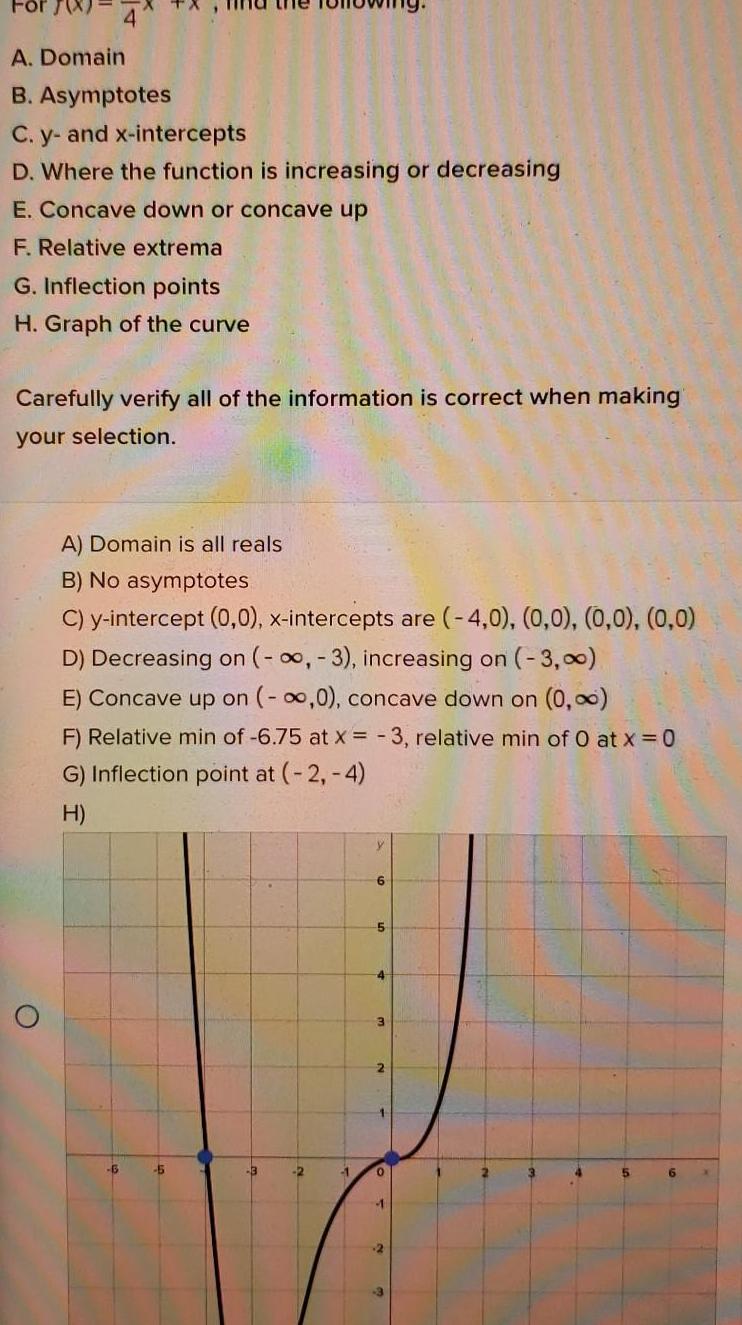
Calculus
Application of derivatives4 A Domain B Asymptotes C y and x intercepts D Where the function is increasing or decreasing E Concave down or concave up F Relative extrema G Inflection points H Graph of the curve Carefully verify all of the information is correct when making your selection A Domain is all reals B No asymptotes C y intercept 0 0 x intercepts are 4 0 0 0 0 0 0 0 D Decreasing on 3 increasing on 3 00 E Concave up on 0 concave down on 0 F Relative min of 6 75 at x 3 relative min of 0 at x 0 G Inflection point at 2 4 H 16 5 3 2 1 5 4 3 2 0 1 2 3 4 5 6

Calculus
Application of derivativesA hole in the ground in the shape of an inverted cone is 17 meters deep and has radius at the top of 14 meters This cone is filled to the top with sawdust The density p of the sawdust in the hole depends upon its depth kg p x 2 1 1 2e 0 12 m3 The total mass of sawdust in the conical hole is kg
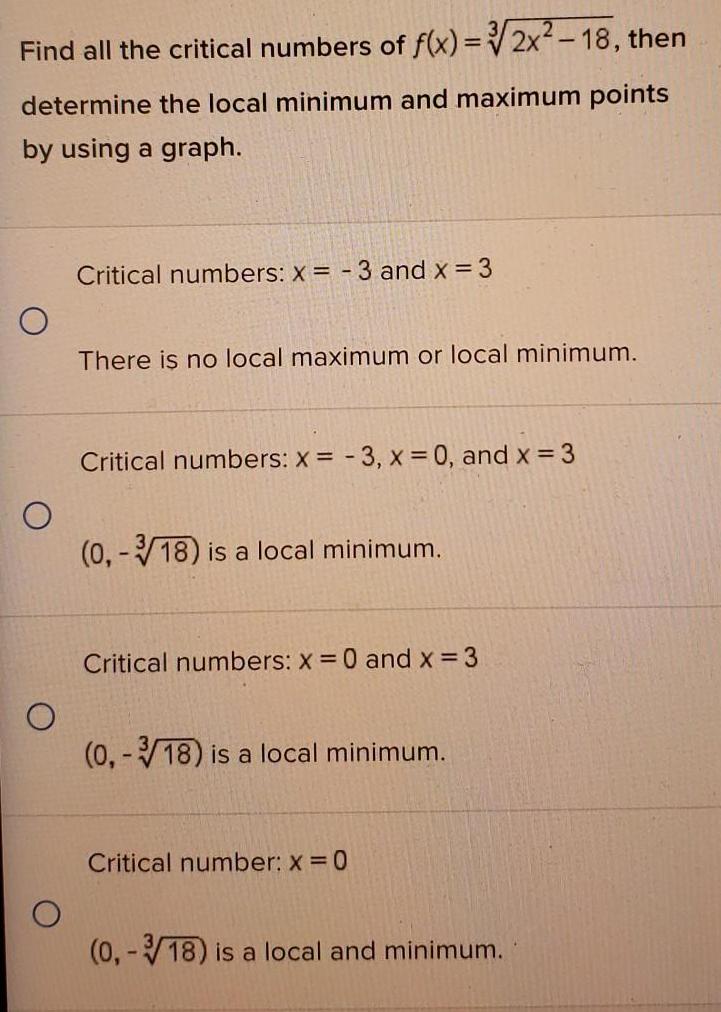
Calculus
Application of derivativesFind all the critical numbers of f x 2x 18 then determine the local minimum and maximum points by using a graph O O O Critical numbers x 3 and x 3 There is no local maximum or local minimum Critical numbers x 3 x 0 and x 3 0 3 18 is a local minimum Critical numbers x 0 and x 3 0 18 is a local minimum Critical number x 0 0 3 18 is a local and minimum

Calculus
Application of derivativesConsider the equation below If an answer does not exist enter DNE f x x4 8x 2 a Find the interval on which f is increasing Enter your answer using interval notation Find the interval on which f is decreasing Enter your answer using interval notation b Find the local maximum and minimum values of f local minimum value local maximum value c Find the inflection points Order your answers from smallest to largest x then from smallest to large x y x y Find the interval on which f is concave up Enter your answer using interval notation 3 Find the interval on which f is concave down Enter your answer using interval notation
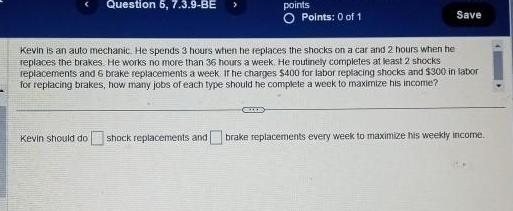
Calculus
Application of derivativesQuestion 5 7 3 9 BE points O Points 0 of 1 GEDERD Save Kevin is an auto mechanic He spends 3 hours when he replaces the shocks on a car and 2 hours when he replaces the brakes He works no more than 36 hours a week He routinely completes at least 2 shocks replacements and 6 brake replacements a week If he charges 400 for labor replacing shocks and 300 in labor for replacing brakes how many jobs of each type should be complete a week to maximize his income Kevin should do shock replacements and brake replacements every week to maximize his weekly income
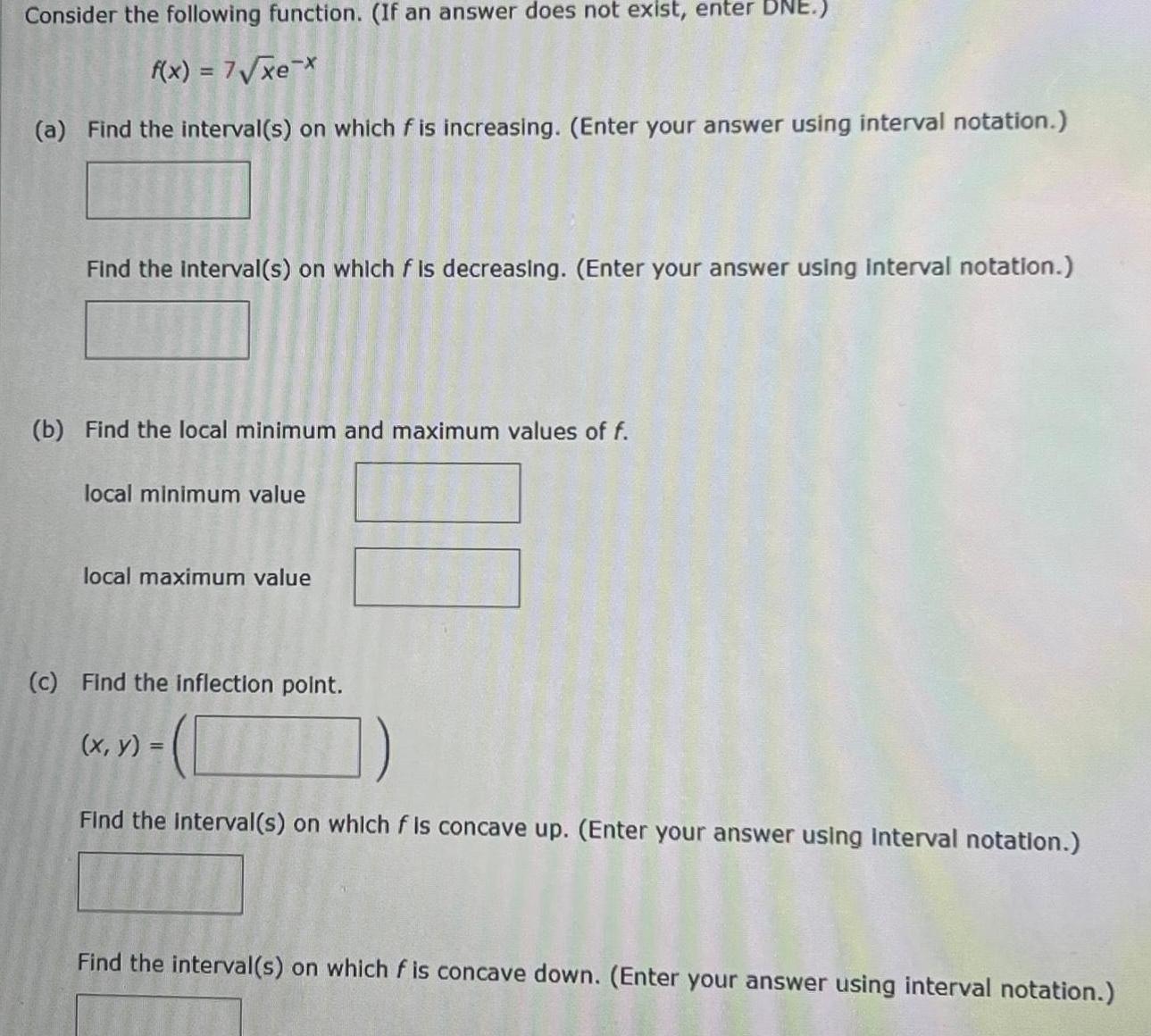
Calculus
Application of derivativesConsider the following function If an answer does not exist enter DNE f x 7 xe x a Find the interval s on which f is increasing Enter your answer using interval notation Find the interval s on which f is decreasing Enter your answer using interval notation b Find the local minimum and maximum values of f local minimum value local maximum value c Find the inflection point x y TIME Find the interval s on which f is concave up Enter your answer using interval notation Find the interval s on which f is concave down Enter your answer using interval notation
Calculus
Application of derivativesDetermine the interval s over which the graph of f x x6 6x5 12x 2 is concave up or concave down O O O O Concave up on 0 U 4 Concave down on 0 4 Concave up on 0 4 Concave down on 0 U 4 Concave up on 4 U 0 Concave down on 4 0 Concave up on 4 0 Concave down on 4 U 0

Calculus
Application of derivativesDetermine if the requirements for the mean value theorem are met by 7 the function f x 7x on the interval 7 1 If so find the X values of cin 7 1 guaranteed by the theorem f x is continuous on 7 1 and f x is differentiable on 7 1 The value guaranteed by the mean value theorem is c 7 O f x is continuous on 7 1 and f x is differentiable on 7 1 The value guaranteed by the mean value theorem is c 7 f x is continuous on 7 1 and f x is differentiable on 7 1 O The value guaranteed by the mean value theorem is c 7 O f x is continuous on 7 1 and f x is NOT differentiable on 7 1 Therefore the mean value theorem does not apply

Calculus
Application of derivativesDetermine the slant or nonlinear asymptote of x 4x 2 f x X 5 O y x 4 O y 5 O y x 1 O y 1
Calculus
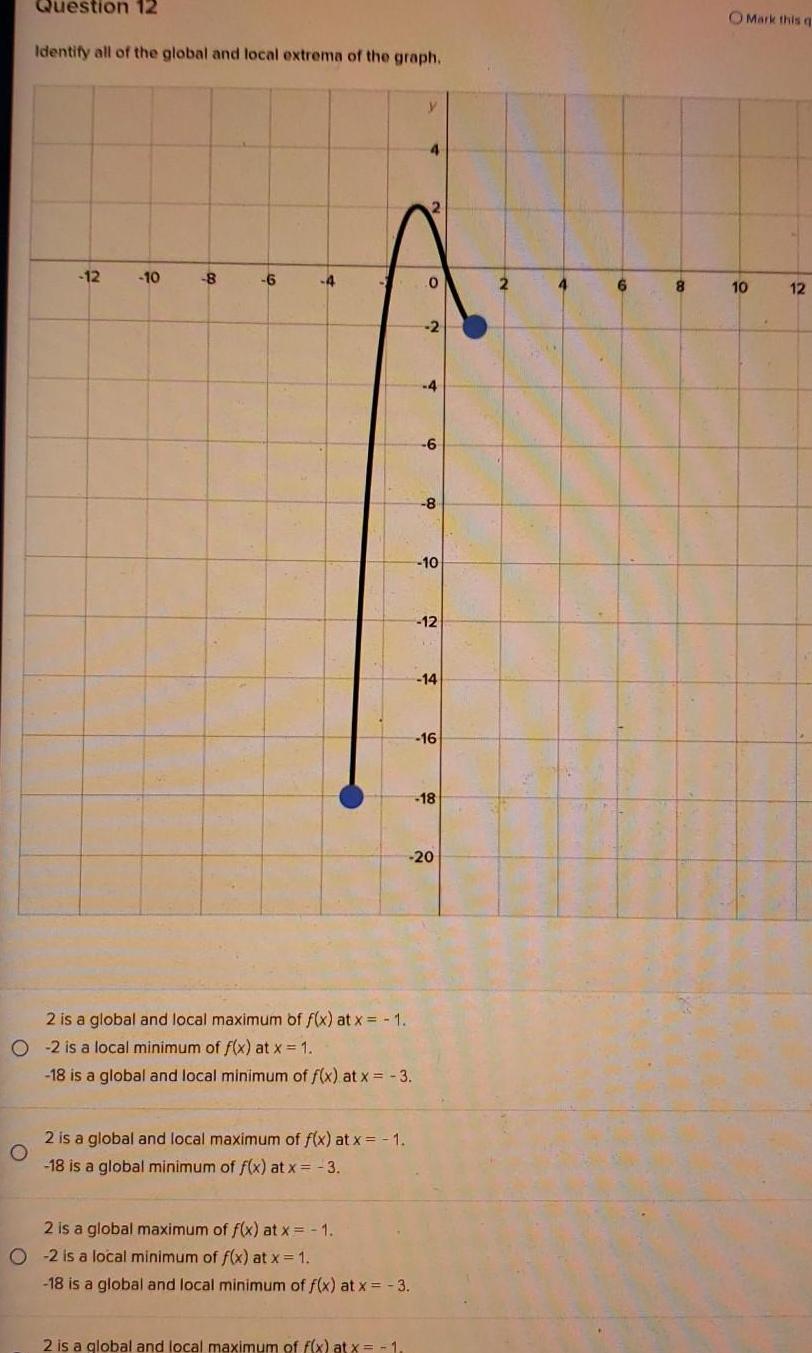
Application of derivativesQuestion 12 Identify all of the global and local extrema of the graph 12 10 8 6 4 2 is a global and local maximum of f x at x 1 18 is a global minimum of f x at x 3 2 is a global and local maximum of f x at x 1 O2 is a local minimum of f x at x 1 18 is a global and local minimum of f x at x 3 2 is a global maximum of f x at x 1 O 2 is a local minimum of f x at x 1 18 is a global and local minimum of f x at x 3 2 is a global and local maximum of f x at x 1 y 0 2 6 8 10 12 14 16 18 00 20 2 4 6 8 OMark this q 10 12
Calculus
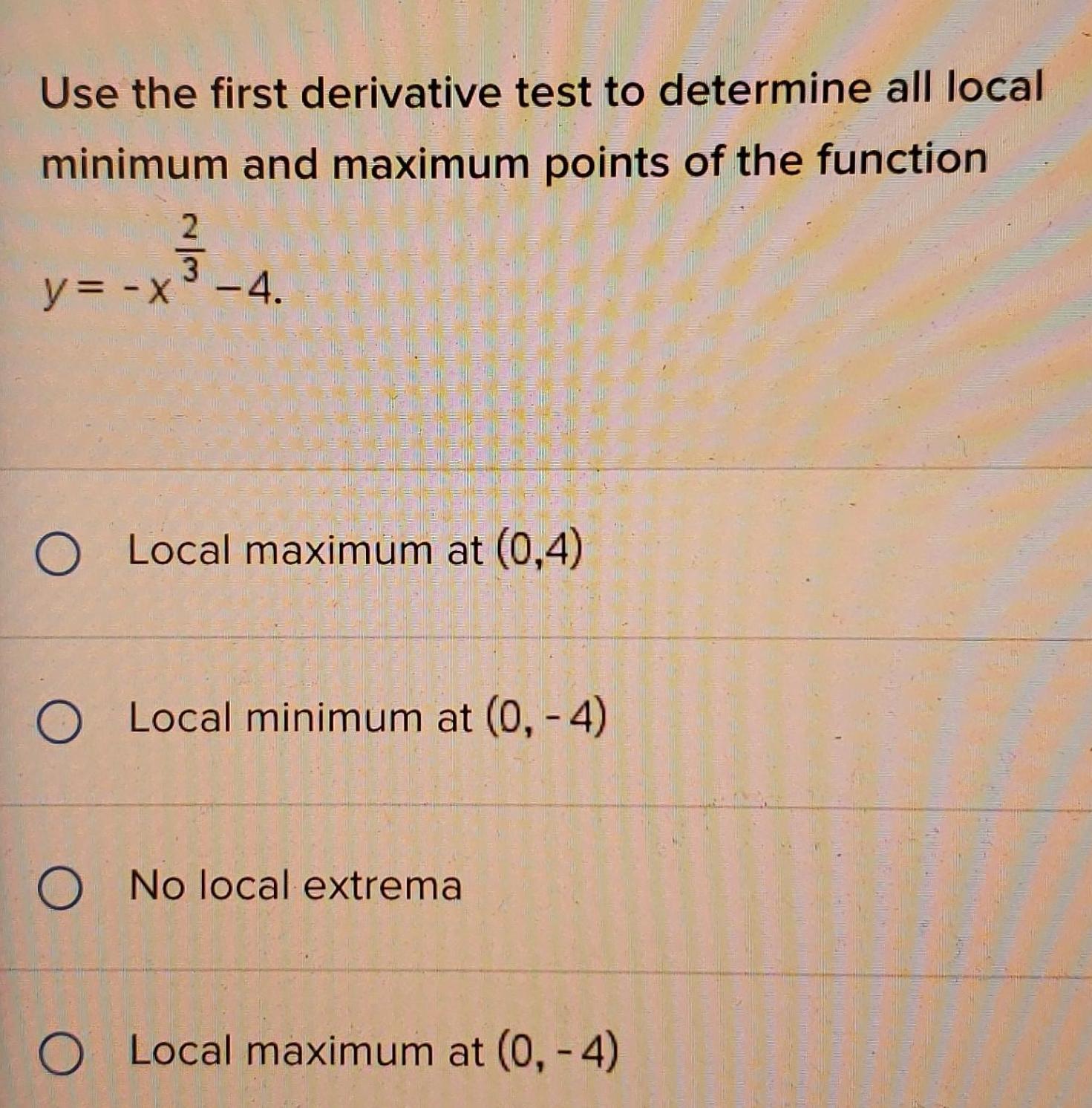
Application of derivativesUse the first derivative test to determine all local minimum and maximum points of the function y x 4 O Local maximum at 0 4 O Local minimum at 0 4 O No local extrema O Local maximum at 0 4
Calculus
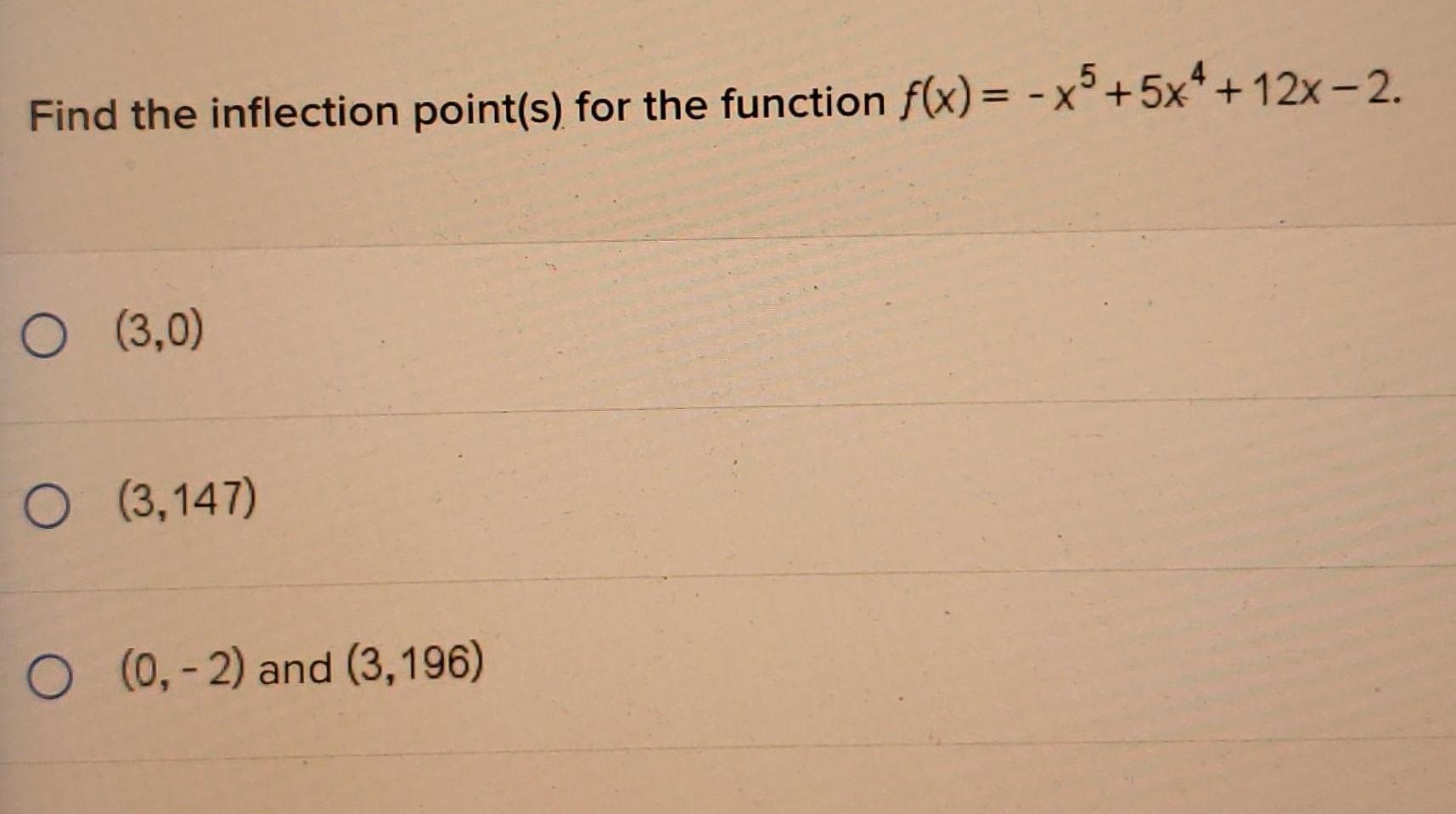
Application of derivativesFind the inflection point s for the function f x x5 5x 12x 2 O 3 0 O 3 147 O 0 2 and 3 196

Calculus
Application of derivativesEvaluate the following limit lim O 6x 17x 3 lim x 5x 14x 3 O 6x 17x 3 x 5x 14x 3 Olim 6x 17x 3 lim 5x 14x 3 X Olim 0 x 5x 14x 3 6x 17x 3 6 6x 17x 3 x 5x 14x 3 1 6 5 6 5
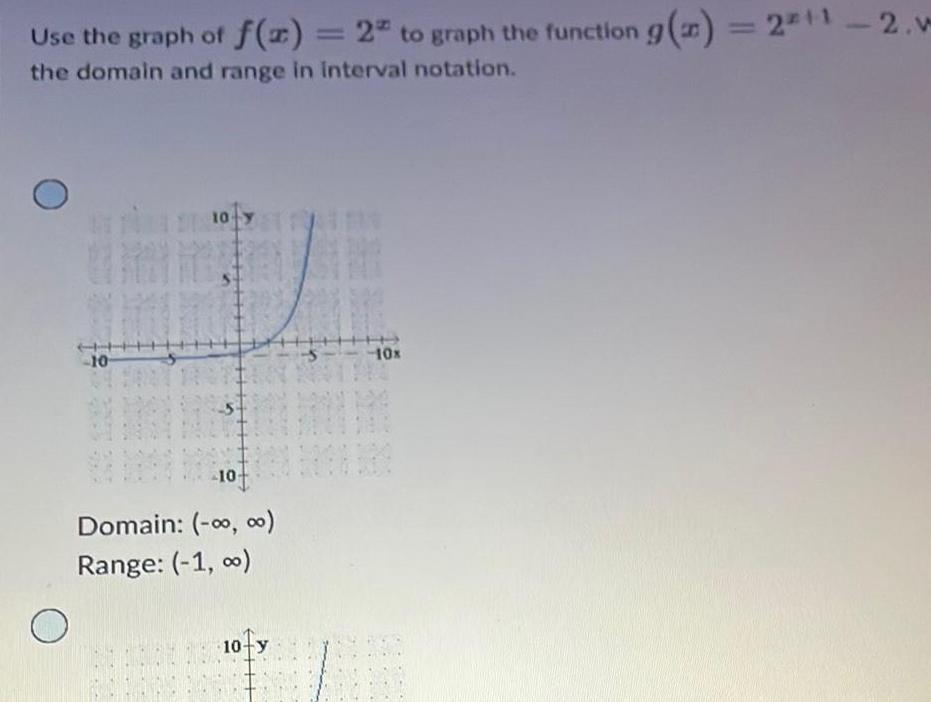
Calculus
Application of derivativesUse the graph of f x 2 to graph the function g x 2 1 2 w the domain and range in interval notation 10 10 y 10 Domain 00 Range 1 10x 10 y TI

Calculus
Application of derivativesPart 1 of 2 O Points 0 of 5 Write a system of inequalities that describes all the given conditions and graph the easible region of the system Joyce is the marketing director for a new company selling a fashion collection for women and she wishes to place ads in two magazines magazine V and magazine Joyce estimates that each one page ad in magazine V will be read by 1 7 million pe and each one page ad in magazine E will be read by 1 1 million people Joyce wants each at least 7 million readers and to place at least 2 ads in each magazine Write a system of inequalities that describes all the given conditions Let x represe number of ads in magazine V and y the number of ads in magazine E Choose the answer below 21 7x 1 3 22 29 Round to two decimal places as needed

Calculus
Application of derivativesProblem 8 10 points Rates of Change Riemann Sum Integrals A car is driving on the road and suddenly notices an obstacle 500 feet away and immediately starts braking The car s velocity in ft s is measured every four seconds and is given in the table below t 0 4 8 12 16 20 v 60 40 20 12 4 0 a Roughly at what time does the car come to a stop Justify your answer b Give an upper and a lower estimate for the distance travelled between t 0 and t seconds Justify your answer 20 c Based on your results which of the following statements can you make Please explain your answer briefly below The car hits the obstacle It does not hit the obstacle We can not tell from just the given data
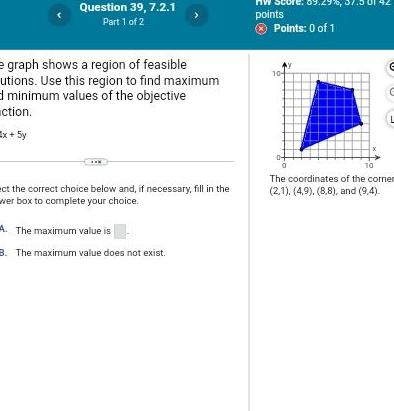
Calculus
Application of derivativesQuestion 39 7 2 1 Part 1 of 2 e graph shows a region of feasible utions Use this region to find maximum d minimum values of the objective ction Ex 5y ect the correct choice below and if necessary fill in the wer box to complete your choice A The maximum value is 8 The maximum value does not exist points Points 0 of 1 10 01 42 C 10 The coordinates of the corner 2 1 4 9 8 8 and 9 4

Calculus
Application of derivativesA manufacture has been selling 2000 television sets a week at 390 each A market survey indicates that for each 30 rebate offered to a buyer the number of sets sold will increase by 300 per week a Find the demand function p x where x is the number of the television sets sold per week 1 10 I p x X b How large rebate should the company offer to a buyer in order to maximize its revenue c If the weekly cost function is 130000 130x how should it set the size of the rebate to maximize its profit

Calculus
Application of derivativesGiven the given cost function C x 5750 530x 1x and the demand function p x 1590 Find the production level that will maximize profit to at least 2 decimal places x
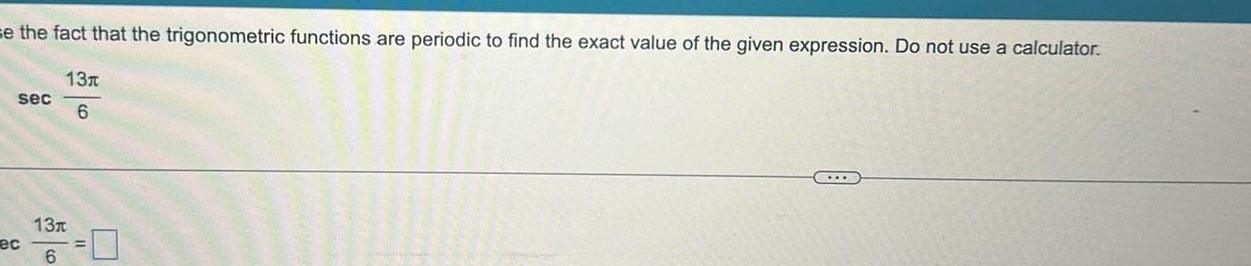
Calculus
Application of derivativesse the fact that the trigonometric functions are periodic to find the exact value of the given expression Do not use a calculator 13 6 sec ec 13T 6

Calculus
Application of derivativespoint P 2 3 on the circle x y 2 is also on the terminal side of an angle 0 in standard position Find sin 0 cos 0 tan 0 csc 0 sec 0 and cot 0 GELOND me Simplify your answer including any radicals Use integers or fractions for any numbers in the expression
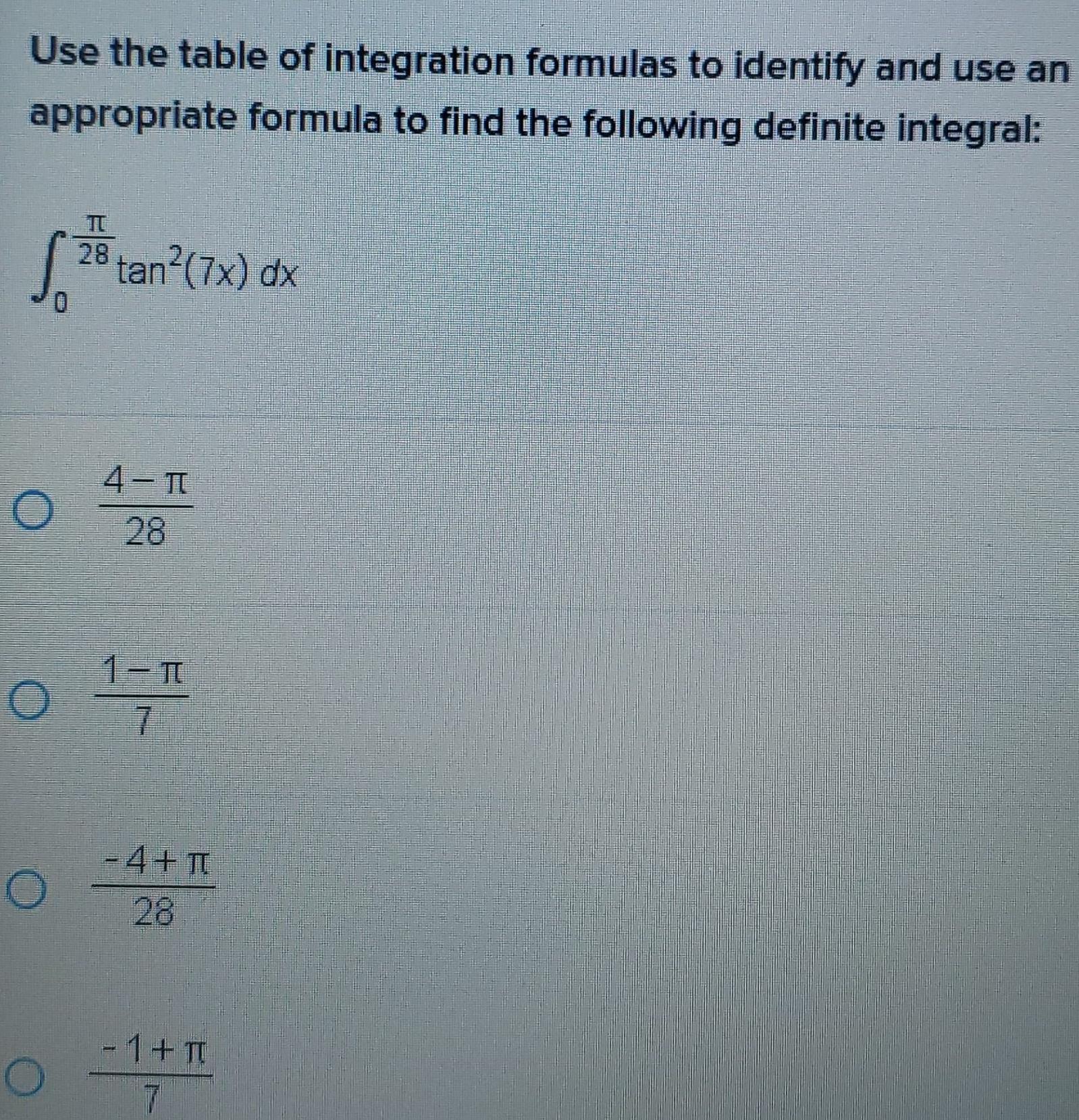
Calculus
Application of derivativesUse the table of integration formulas to identify and use an appropriate formula to find the following definite integral So 4 T 28 0 17 Th O O 28 tan 7x dx O 4 28 1 T 7
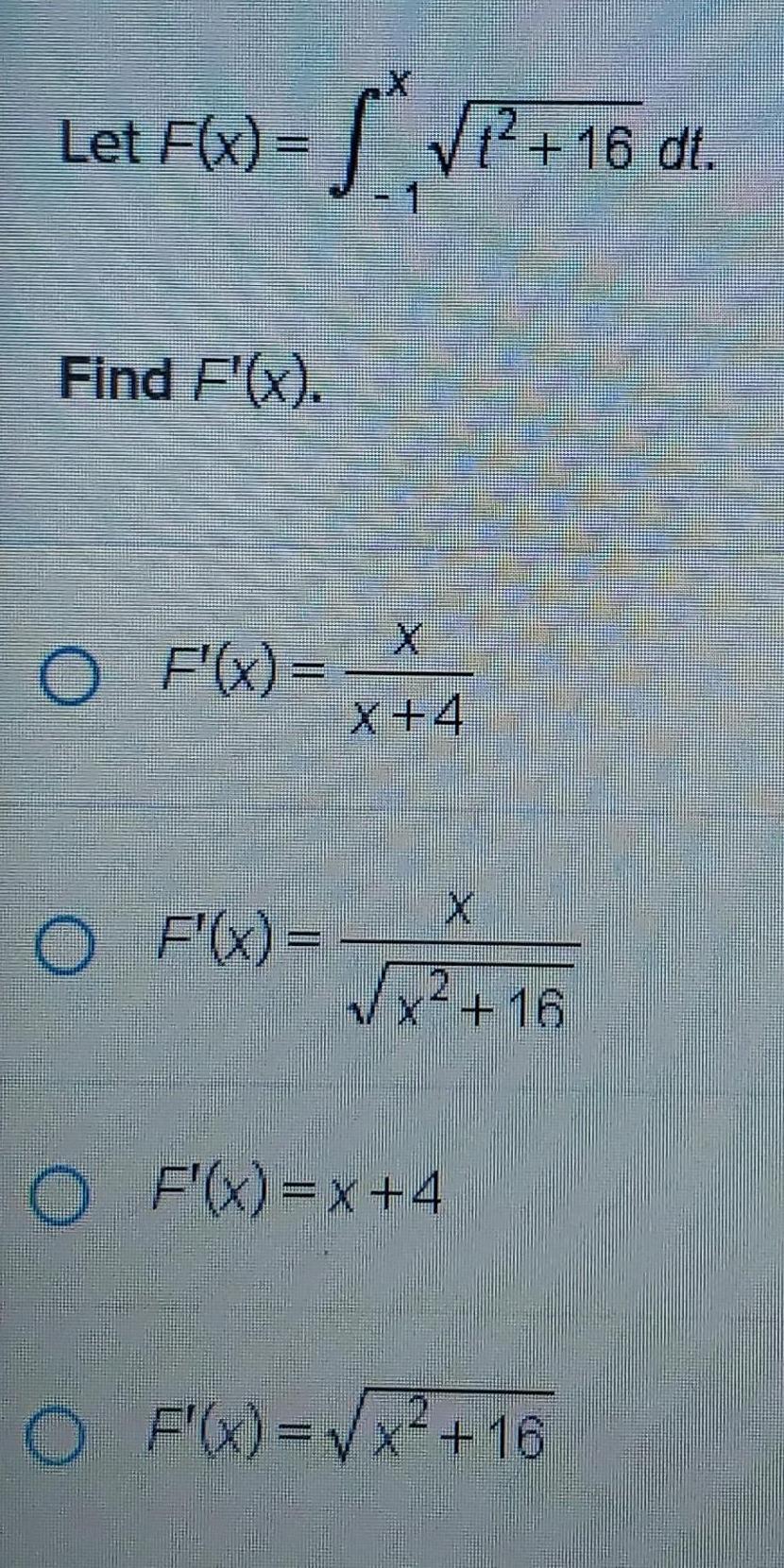
Calculus
Application of derivativesLet F x 16 dl Find F x O F x O F x 1 X 4 x 16 2 O F x x 4 O F x x 16
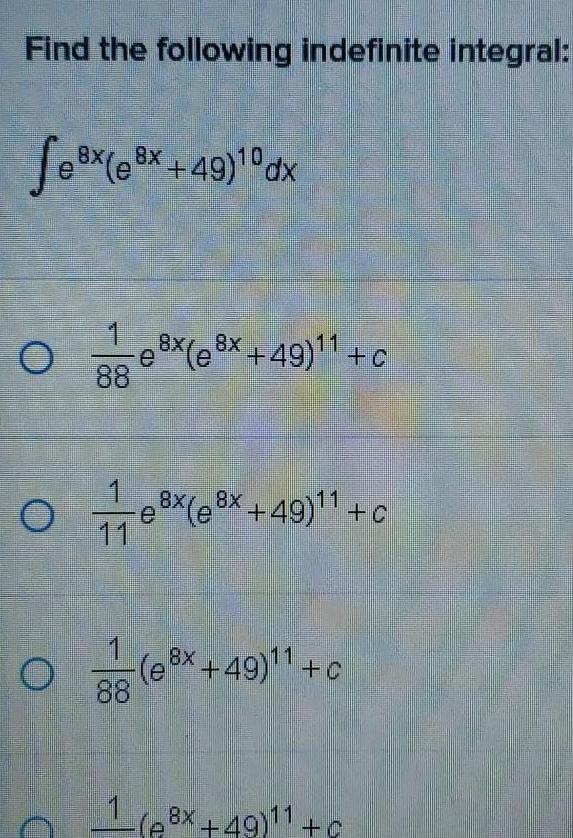
Calculus
Application of derivativesFind the following indefinite integral Sex e 8x 49 0 dx O 0 e 8x e 8x 49 1 C 88 8x 8x Ox x 49 C O D 1 88 1 ex 49 11 8x P 0 11 49 C
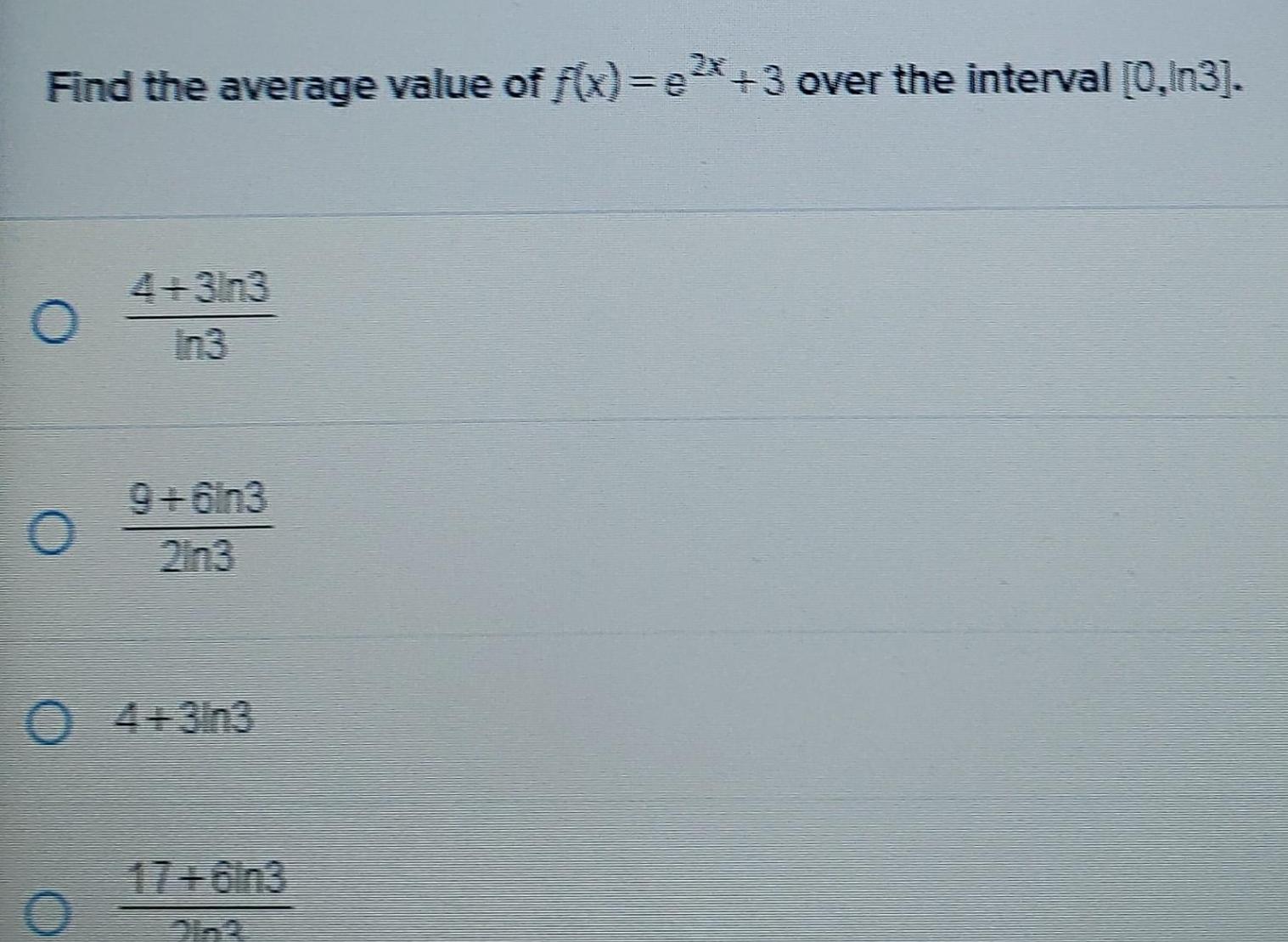
Calculus
Application of derivativesFind the average value of f x x 3 over the interval 0 In3 O O 4 3ln3 In3 9 6ln3 2n3 O4 3n3 17 0n3 Dink
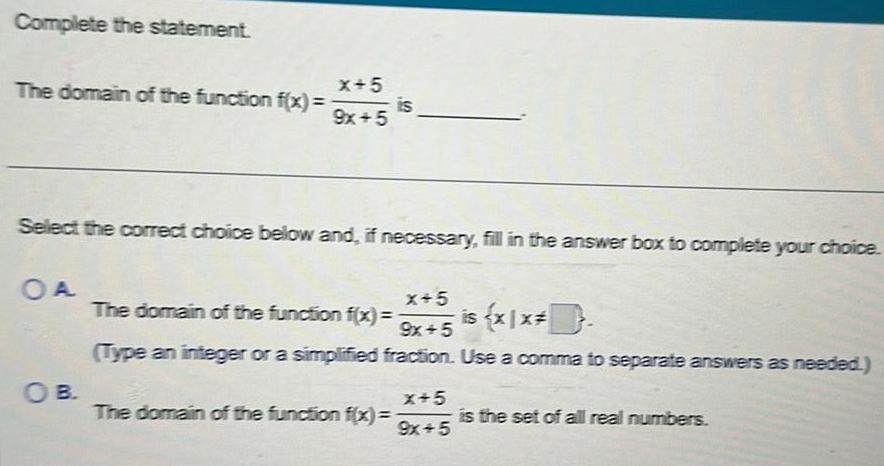
Calculus
Application of derivativesComplete the statement The domain of the function f x OA x 5 9x 5 Select the correct choice below and if necessary fill in the answer box to complete your choice OB is x 5 The domain of the function f x is x1x 9x 5 Type an integer or a simplified fraction Use a comma to separate answers as needed The domain of the function f x x 5 9x 5 is the set of all real numbers
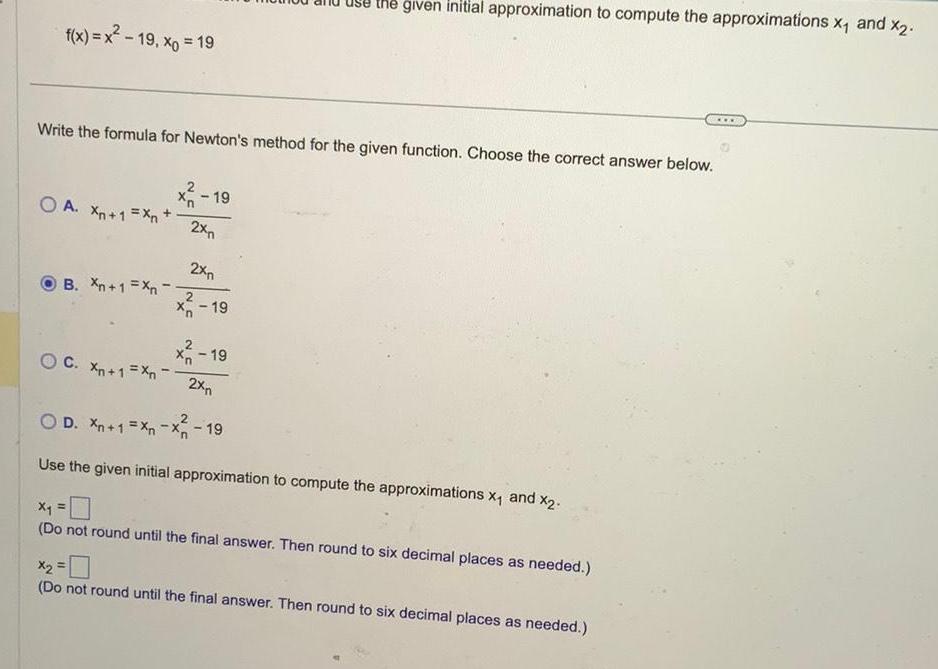
Calculus
Application of derivativesf x x 19 xo 19 Write the formula for Newton s method for the given function Choose the correct answer below OA Xn 1 Xn B Xn 1 Xn OC Xn 1 Xn X Xn 19 2xn 2xn 2 Xn 19 the given initial approximation to compute the approximations X and x 2 xn 19 2xn O D Xn 1 Xn x 19 Use the given initial approximation to compute the approximations x and x Do not round until the final answer Then round to six decimal places as needed x Do not round until the final answer Then round to six decimal places as needed

Calculus
Application of derivativesA piece of cardboard measuring 12 inches by 14 inches is formed into an open top box by cutting squares with side length x from each corner and folding up the sides Find a formula for the volume of the box in terms of a V x Find the value for x that will maximize the volume of the box x A

Calculus
Application of derivativesAnswer the following questions about the cotangent function a Is the cotangent function even odd or neither h is the graph of the cotangent function symmetric With respect to what
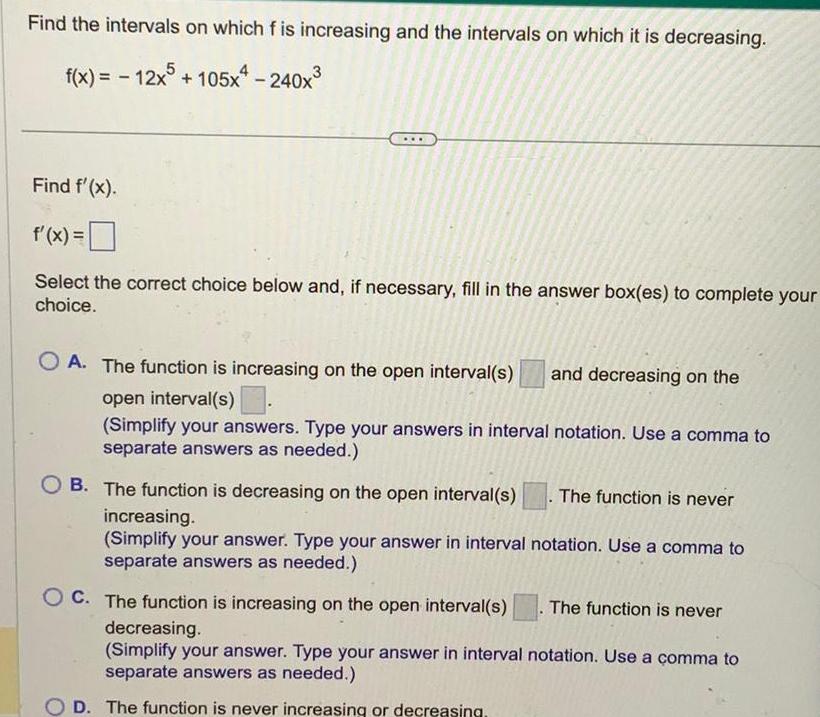
Calculus
Application of derivativesFind the intervals on which f is increasing and the intervals on which it is decreasing f x 12x5 105x4 240x Find f x f x Select the correct choice below and if necessary fill in the answer box es to complete your choice OA The function is increasing on the open interval s and decreasing on the open interval s Simplify your answers Type your answers in interval notation Use a comma to separate answers as needed B The function is decreasing on the open interval s increasing Simplify your answer Type your answer in interval notation Use a comma to separate answers as needed The function is never C The function is increasing on the open interval s The function is never decreasing Simplify your answer Type your answer in interval notation Use a comma to separate answers as needed D The function is never increasing or decreasing

Calculus
Application of derivativesf x sin x and f a find the exact value of the following f a f a f a 2x f a 4x

Calculus
Application of derivativesIs Built with one side against a bam If 1000 m of fencing are used for the other three sides of the pen what dimensions maximize the area of the pen b A rancher plans to make four identical and adjacent rectangular pens against a barn each with an area of 400 m see figure What are the dimensions of each pen that minimize the amount of fence that must be used a To maximize the area of the pen the sides perpendicular to the bar should be m long and the side parallel to the bar should be m long Type exact answers using radicals as needed Barn 400 400 400 400 b To minimize the amount of fence that must be used each of the sides perpendicular to the barn should bem long and each of the sides parallel to the barn should be m long Type exact answers using radicals as needed
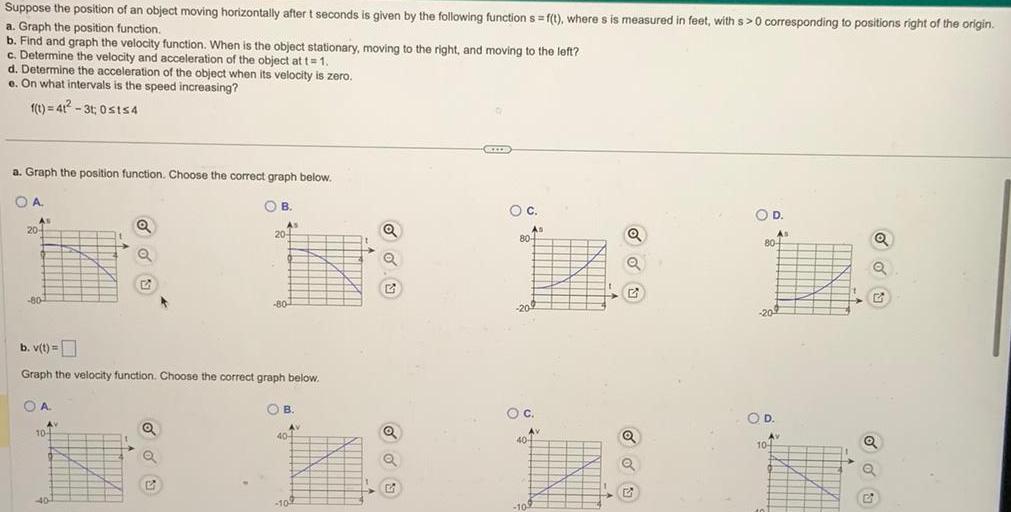
Calculus
Application of derivativesSuppose the position of an object moving horizontally after t seconds is given by the following function s f t where s is measured in feet with s 0 corresponding to positions right of the origin a Graph the position function b Find and graph the velocity function When is the object stationary moving to the right and moving to the left c Determine the velocity and acceleration of the object at t 1 d Determine the acceleration of the object when its velocity is zero e On what intervals is the speed increasing f t 41 3t 0sts4 a Graph the position function Choose the correct graph below OA As 20 80 A AV 104 A Q b v t Graph the velocity function Choose the correct graph below 40 Q B 2 As 20 80 B AV 40 4 109 Q Q DWID O C As 804 O C 10 Av 40 4 G Q O D 80 20 As OD Av 104 Q Q

Calculus
Application of derivativesa Write the equation of the line that represents the linear approximation to the following function at the given point a b Use the linear approximation to estimate the given quantity c Compute the percent error in the approximation 100 f x 15 x at a 1 f 0 9 a L x b Using the linear approximation f 0 9 Type an integer or a decimal c The percent error in the approximation is approximation exact exact where the exact value is given by a calculator

Calculus
Application of derivativesthe Fundamental Theorem of Calculus to evaluate the following definite integral 2 1 0 5 dx 1 x X 2 150 5 dx 2 1 x Type an exact answor 0
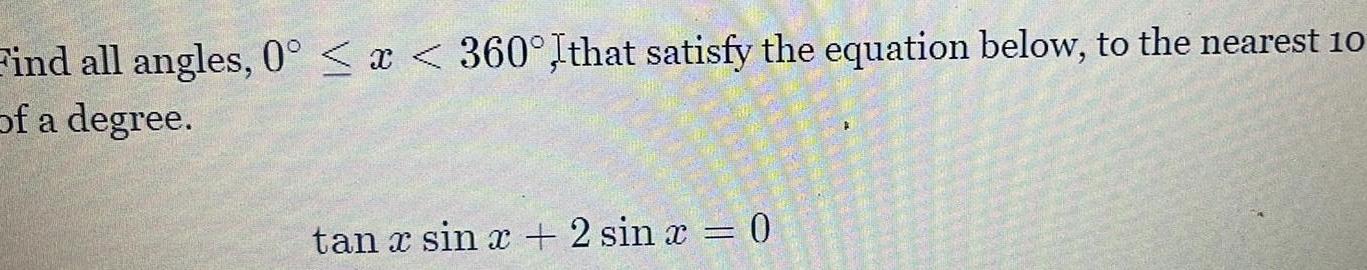
Calculus
Application of derivativesFind all angles 0 x 360 Ithat satisfy the equation below to the nearest 10 of a degree tan x sin x 2 sin x 0

Calculus
Application of derivativesDeandre lilled his gos tank three times last week Here are the amounts of gas he bought fin gr 18 5 35 18 28 What is the total amount of gas Deandre bought last week

Calculus
Application of derivatives8 Solve using ALGEBRA 2sin30 2 0 A General Formula s exact radians B In the interval 0 2 Solve using ALGEBRA 2sin 8 1 A General Formula s exact radians B In the interval 0 2
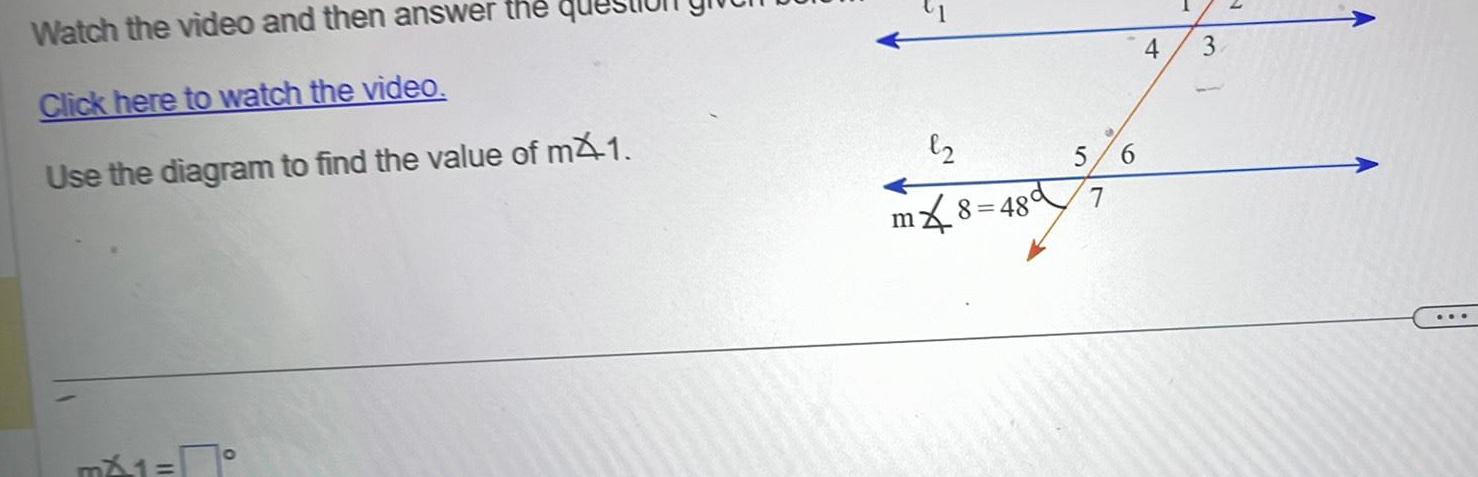
Calculus
Application of derivativesWatch the video and then answer the que Click here to watch the video Use the diagram to find the value of mx1 mX1 8 m8 480 5 6 7 3

Calculus
Application of derivatives6 Find the exact value no calculator cos sin 4 5 Find the exact radian answer in pi form cos 1 cos 2 SO leviedni dr