Application of derivatives Questions and Answers
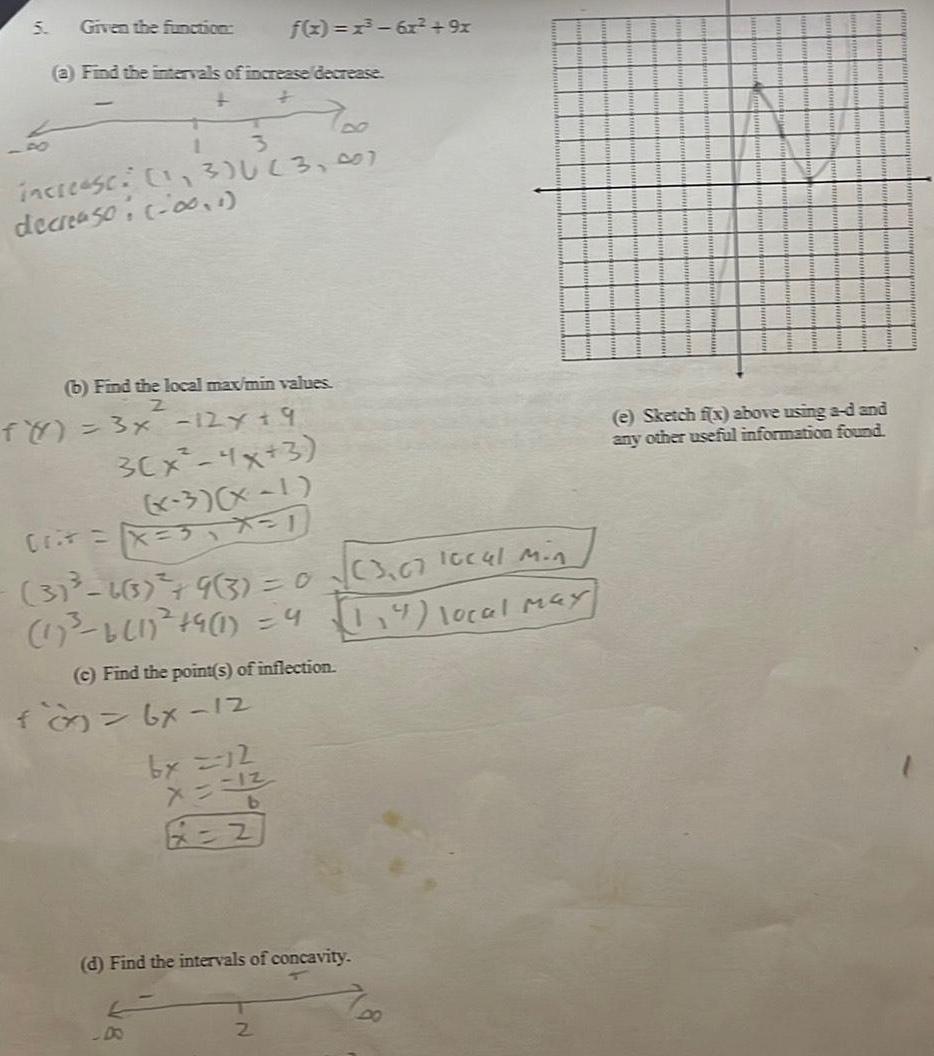
Calculus
Application of derivatives5 Given the function a Find the intervals of increase decrease T 1 3 increase 3 U 3 007 decreaso 0 1 f x x 6x 9x b Find the local max min values 2 f y 3x 12Y 9 3 x 4x 3 x 3 x 1 crit x 3 X 1 31 6 3 9 3 0 3 07 local Min 1 6 1 4 1 4 1 4 local may c Find the point s of inflection fo 6x 12 by 2 12 X 12 b x 2 d Find the intervals of concavity 2 DO e Sketch f x above using a d and any other useful information found
Calculus
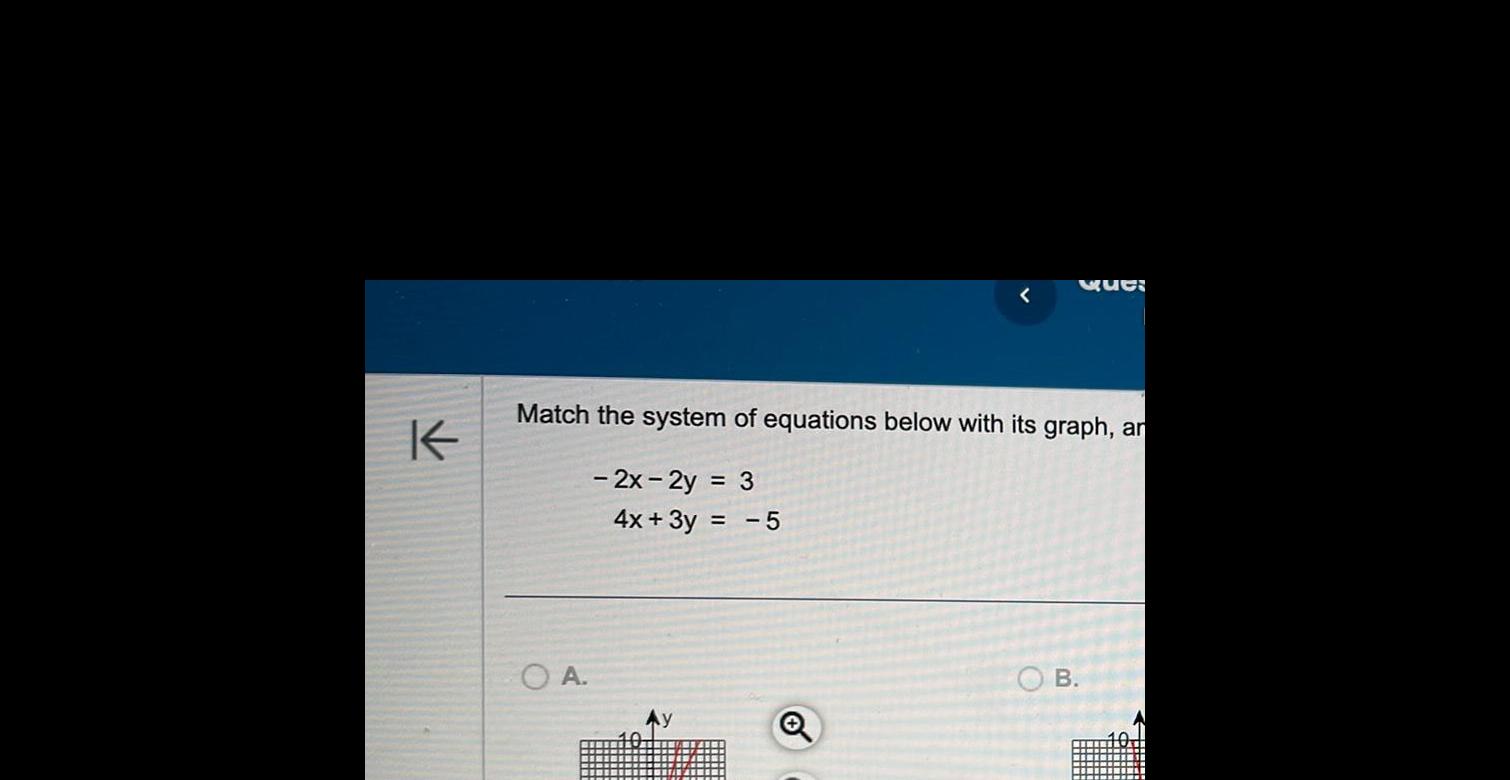
Application of derivativesK Match the system of equations below with its graph an 2x 2y 3 OA 4x 3y 5 Que OB
Calculus
Application of derivativesve the system of equations by graphing y 5 2y 10 se the graphing tool to graph the two equa Click to enlarge graph

Calculus
Application of derivativesa 3 Given the function 3Y F fat 241 9 a Find all critical points b Find all horizontal and vertical asymptotes c Find all local max and local mins d Find the intervals of increase and decrease on f st fa g 3x 3 0 3 f x IL 3x x 1 11 3 3x 2x x 1 X 1 0 3 ST VA non c 7 zo ha
Calculus
Application of derivativesmics Spring 2023 ck Questi pany markets exercise DVDs that sell for 24 9 materials shipping etc are 6 45 per DVD d the cost equation and the revenue equation w many DVDs must be sold each month for th aph the cost and revenue equations in the sam of the break even point
Calculus
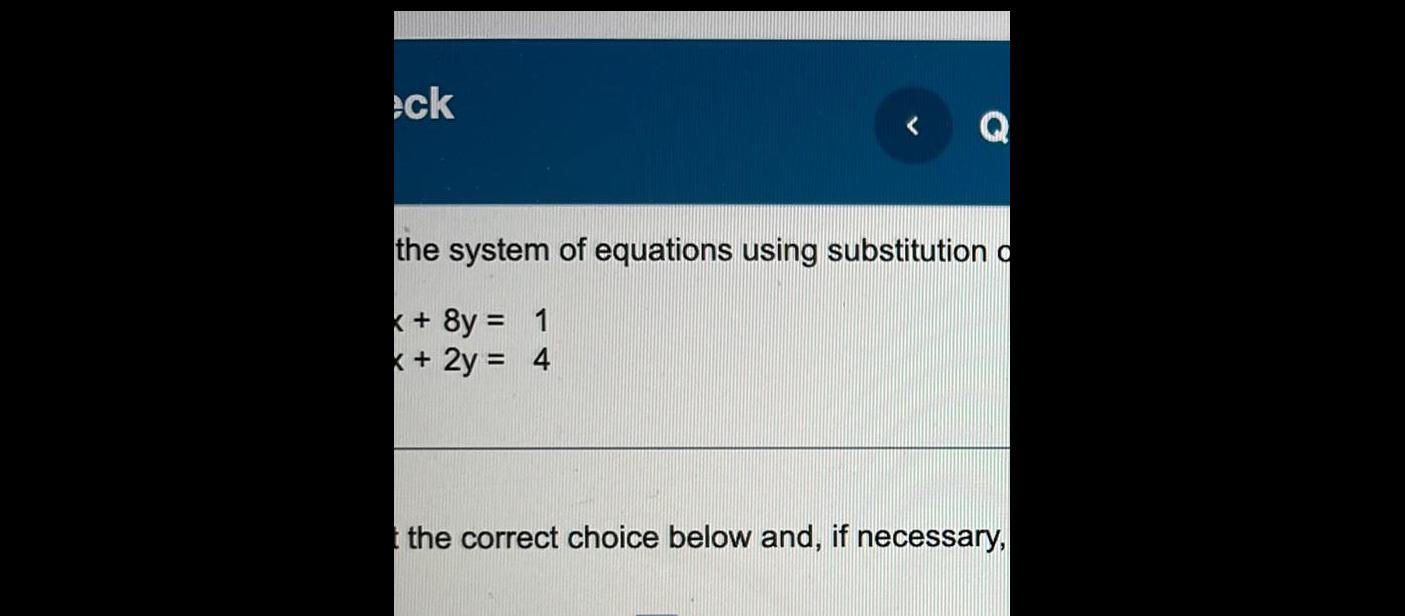
Application of derivativeseck Q the system of equations using substitution o k 8y 1 x 2y 4 the correct choice below and if necessary
Calculus
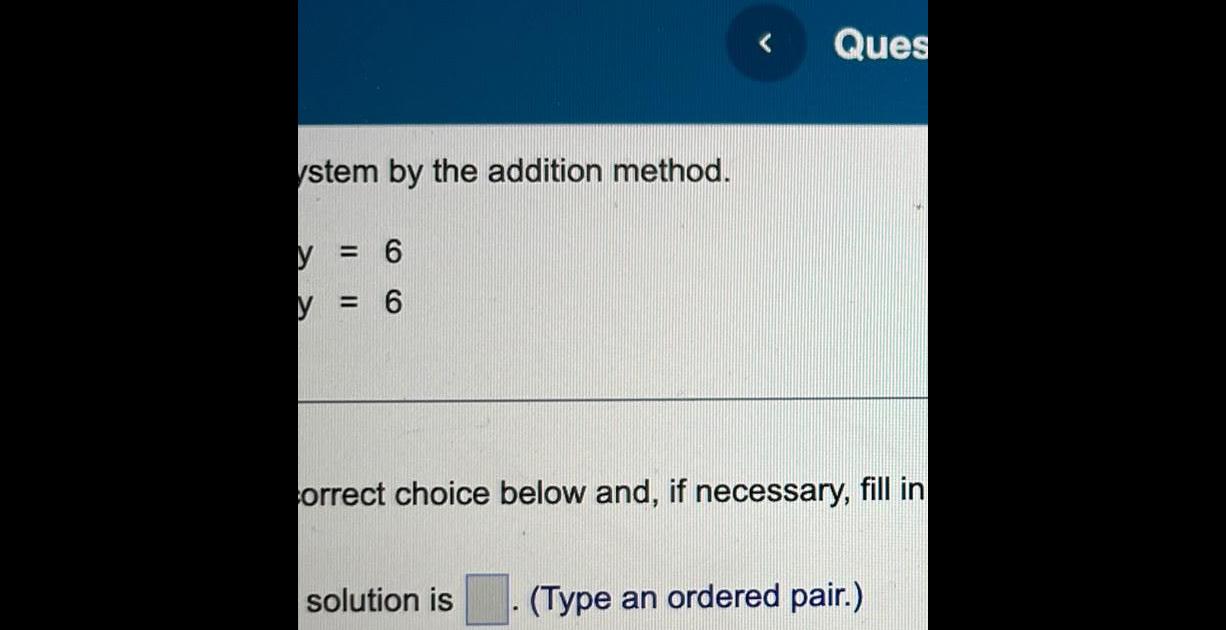
Application of derivativesystem by the addition method y 6 6 y Ques correct choice below and if necessary fill in solution is Type an ordered pair
Calculus
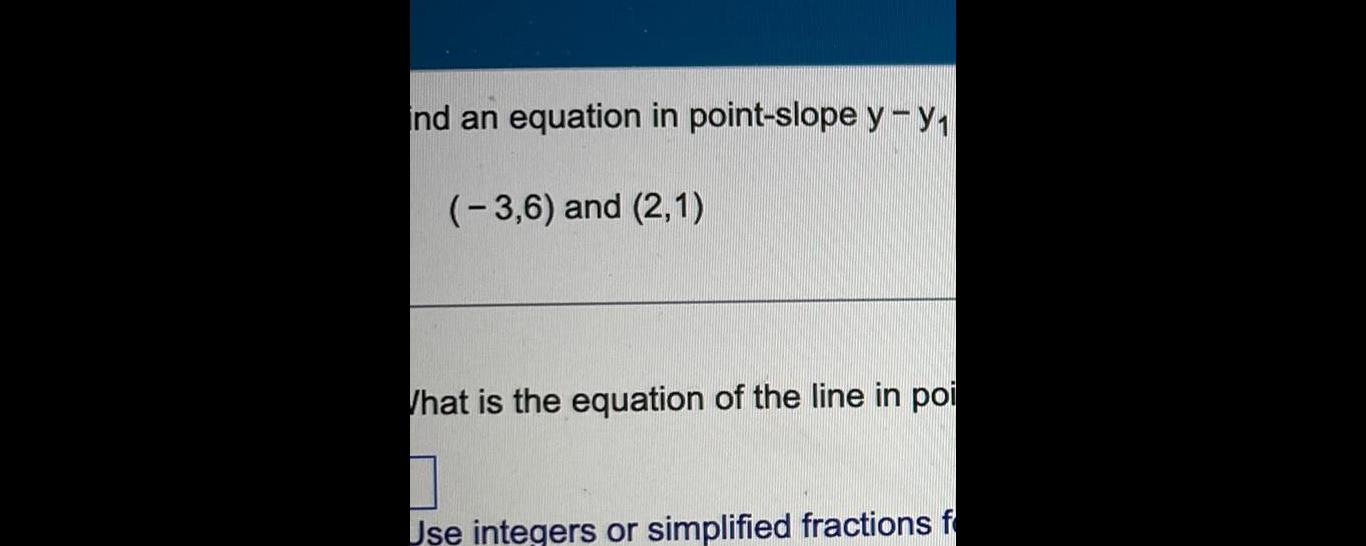
Application of derivativesnd an equation in point slope y y 3 6 and 2 1 What is the equation of the line in poi 0 Use integers or simplified fractions f

Calculus
Application of derivativesFind an equation for an exponential function that passes through the points 1 22 3 20 125 and has a horizontal asymptote at y 20
Calculus
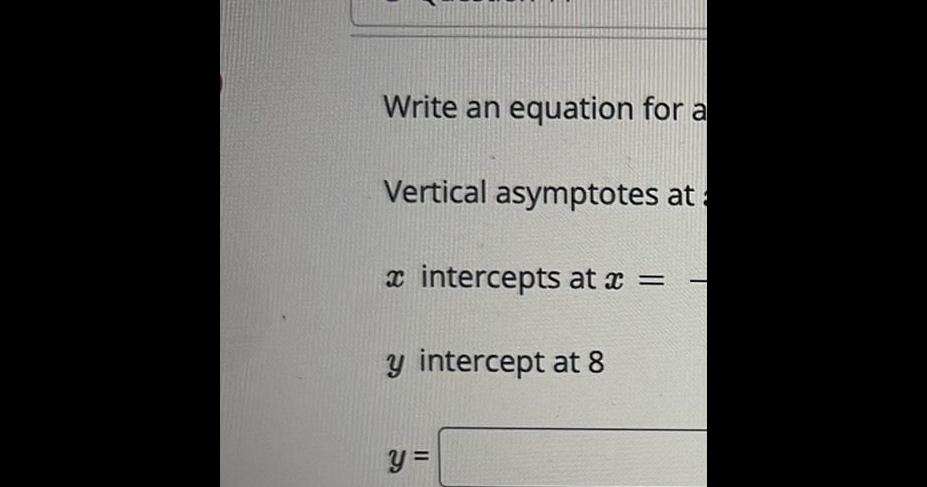
Application of derivativesJ Write an equation for a Vertical asymptotes at a intercepts at x y intercept at 8 y
Calculus
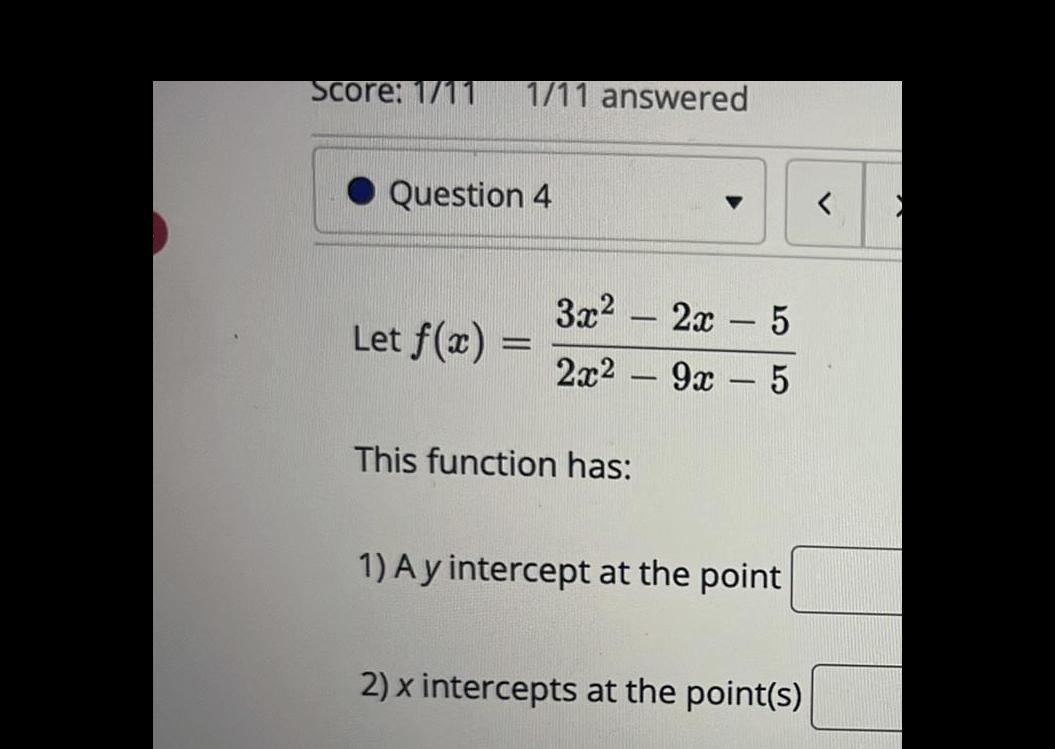
Application of derivativesScore 1 11 1 11 answered Question 4 Let f x 3x 2x This function has 2x 5 9x 5 1 A y intercept at the point 2 x intercepts at the point s

Calculus
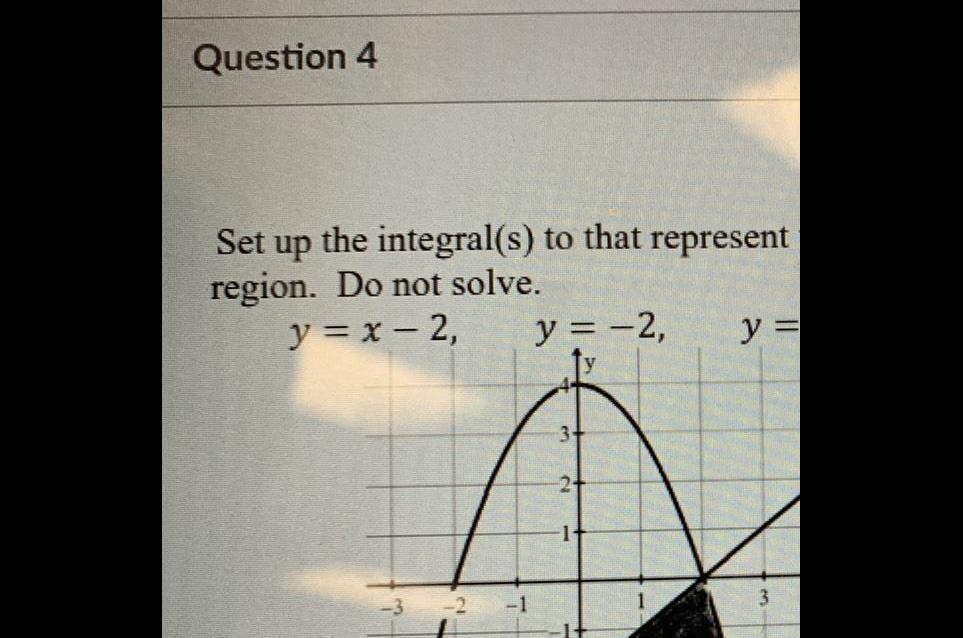
Application of derivativesQuestion 4 Set up the integral s to that represent region Do not solve y x 2 y 2 3 14 y 3

Calculus
Application of derivatives22 Similar to Q1 c consider the DE dy 2y t dt a Write down the general solution of this DE and use Desmos or MATLAB to plo of them for different values of your unknown constant and for 0 t 5

Calculus
Application of derivativesConsider the function f x whose second derivative is f x 4x 2 sin x If f 0 4 and f 0 4 what is f 2

Calculus
Application of derivativesA ball is shot from the ground straight up into the air with initial velocity of 47 ft sec Assuming that the air resistance can be ignored how high does it go Hint Th
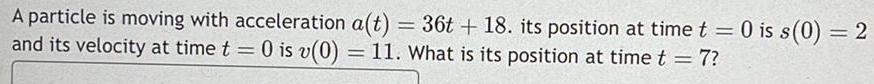
Calculus
Application of derivativesA particle is moving with acceleration a t 36t 18 its position at time t 0 is s 0 2 and its velocity at time t 0 is v 0 11 What is its position at time t 7
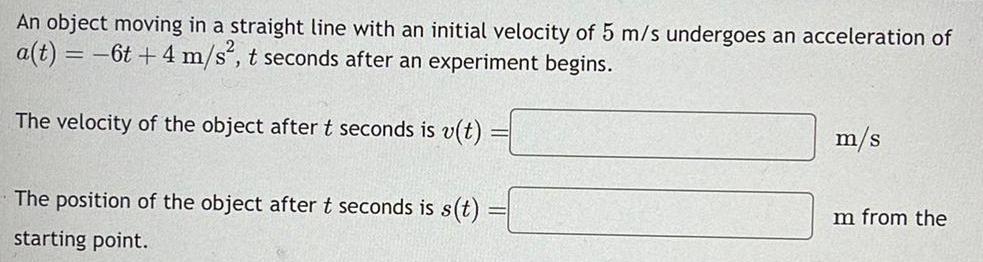
Calculus
Application of derivativesAn object moving in a straight line with an initial velocity of 5 m s undergoes an acceleration of a t 6t 4 m s t seconds after an experiment begins The velocity of the object after t seconds is v t The position of the object after t seconds is s t starting point m s Im from the
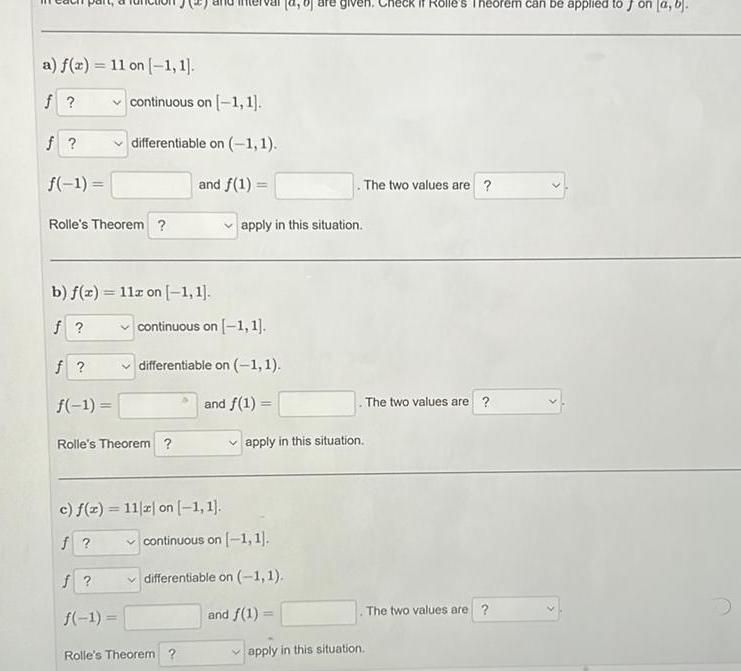
Calculus
Application of derivativesa f x 11 on 1 1 f f f 1 Rolle s Theorem b f x 11z on 1 1 f f f 1 continuous on 1 1 differentiable on 1 1 and f 1 Rolle s Theorem c f x 11 z on 1 1 f f 1 continuous on 1 1 differentiable on 1 1 and f 1 apply in this situation Rolle s Theorem given Check if Rolle s Theorem can be applied to J on a b continuous on 1 1 differentiable on 1 1 and f 1 apply in this situation The two values are apply in this situation The two values are The two values are
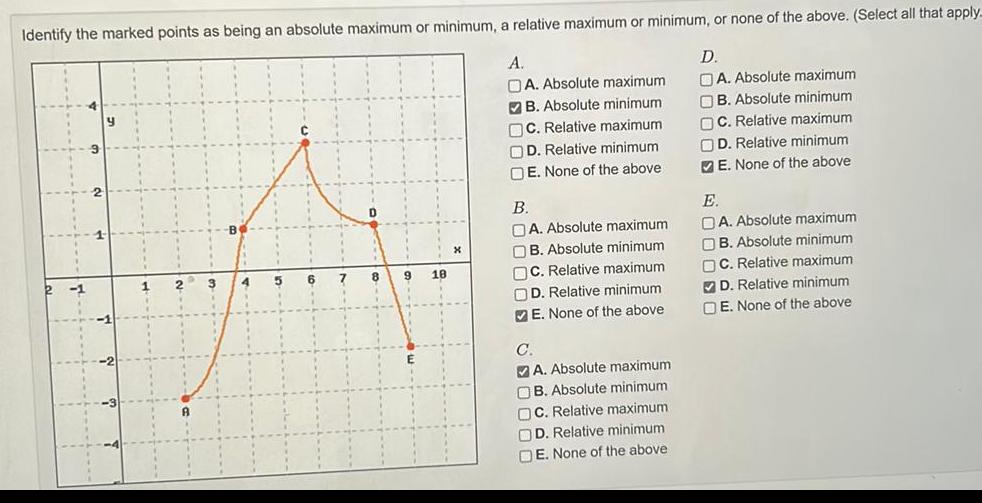
Calculus
Application of derivativesIdentify the marked points as being an absolute maximum or minimum a relative maximum or minimum or none of the above Select all that apply D A Absolute maximum B Absolute minimum C Relative maximum OD Relative minimum E None of the above 7 8 9 18 A DA Absolute maximum B Absolute minimum DC Relative maximum D Relative minimum DE None of the above B OA Absolute maximum OB Absolute minimum OC Relative maximum OD Relative minimum E None of the above C A Absolute maximum OB Absolute minimum OC Relative maximum OD Relative minimum DE None of the above E DA Absolute maximum OB Absolute minimum OC Relative maximum D Relative minimum DE None of the above

Calculus
Application of derivatives1 2 4 3 1 2 Graph of f e graph of the function fabove consists of three line segments 2 0 3 2 82 20 T 0 6 Let g be the function given by g x f t dt For each of g 1 g 1 and g 1 find the value or state that it does not exist Lin For the function g defined in part a find the x coordinate of each point of inflection of the graph of g on the open interval 4 x 3 Explain your reasoning 1 5 1 og bill in ovsus od Let h be the function given by h z f t dt Find all values of x in the closed interval 45x53 for which it odt parte do tog ewt od to anilnico h x 0 niele Og je imannetje ict For the function h defined in part c find all intervals on which h is decreasing Explain your reasoning


Calculus
Application of derivatives5 A GRAPHING CALCULATOR IS REQUIRED FOR THIS QUESTION You are permitted to use your calculator to solve an equation find the derivative of a function at a point or calculate the value of a definite integral However you must clearly indicate the setup of your question namely the equation function or integral you are using If you use other built in features or programs you must show the mathematical steps necessary to produce your results Your work must be expressed in standard mathematical notation rather than calculator syntax Show all of your work even though the question may not explicitly remind you to do so Clearly label any functions graphs tables or other objects that you use Justifications require that you give mathematical reasons and that you verify the needed conditions under which relevant theorems properties definitions or tests are applied Your work will be scored on the correctness and completeness of your methods as well as your answers Answers without supporting work will usually not receive credit Unless otherwise specified answers numeric or algebraic need not be simplified If your answer is given as a decimal approximation it should be correct to three places after the decimal point Unless otherwise specified the domain of a function f is assumed to be the set of all real numbers for which f x is a real number t hours vp t meters per hour 0 0 3 1 7 2 8 4 0 55 29 55 48 The velocity of a particle P moving along the x axis is given by the differentiable function up where up t is measured in meters per hour and t is measured in hours Selected values of up t Particle P is at the origin at time t 0 are shown in the table above of A a Justify why there must be at least one time t for 0 3 t 2 8 at which up t the acceleration of particle P equals 0 meters per hour per hour b Use a trapezoidal sum with the three subintervals 0 0 3 0 3 1 7 and 1 7 2 8 to approximate the value 2 8 6 vp t dt c A second particle Q also moves along the x axis so that its velocity for 0 t 4 is given by vo t 45 t cos 0 063t meters per hour Find the time interval during which the velocity of particle is at least 60 meters per hour Find the distance traveled by particle Q during the interval when the velocity of particle is at least 60 meters per hour d At time t 0 particle is at position 90 Using the result from part b and the function vo from part c approximate the distance between particles P and Q at time t 2 8

Calculus
Application of derivativesSuppose f x and g x have the following values lim f x and lim f x 8 x 818 x48 lim g x and lim g x 8 818 x48 Assume all functions are continuous Find the following lim X18 f x 2 f x 3 a r 1
Calculus
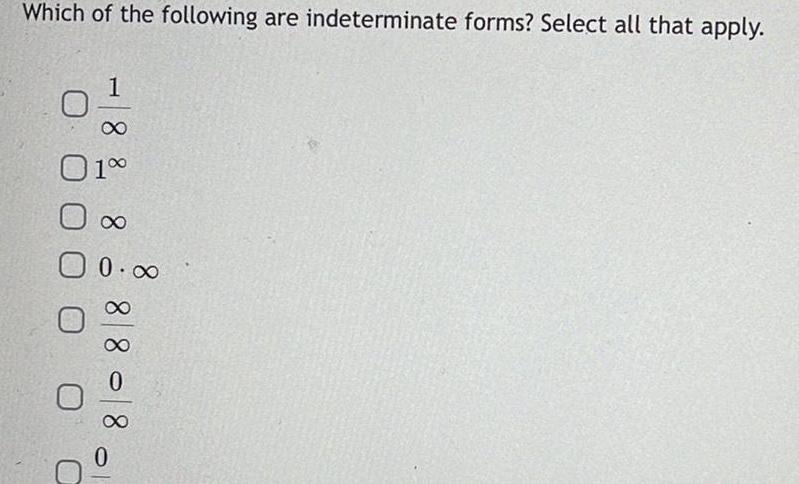
Application of derivativesWhich of the following are indeterminate forms Select all that apply 1 01 0 0 0 0 0 108088
Calculus
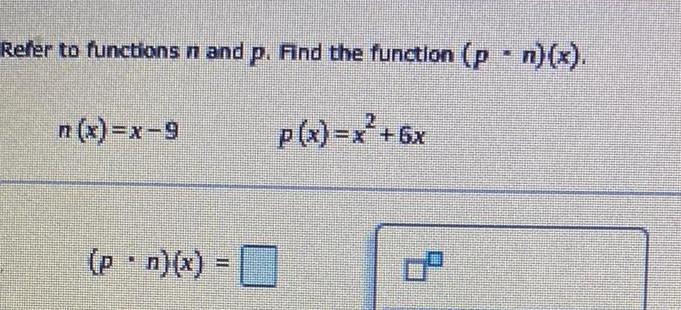
Application of derivativesRefer to functions n and p Find the function p n x p x x 6x n x x 9 p n x
Calculus
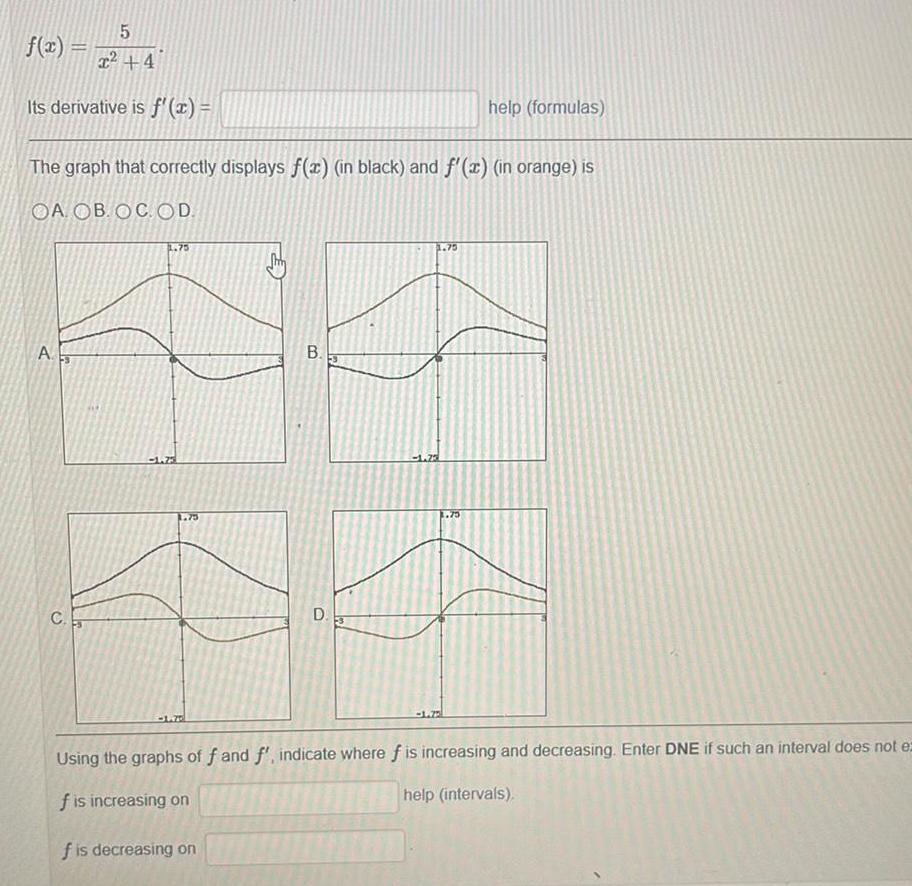
Application of derivativesf 2 2254 Its derivative is f x The graph that correctly displays f x in black and f x in orange is OA OB OC OD A C 1 75 B D 1 73 help formulas 75 Using the graphs of f and f indicate where f is increasing and decreasing Enter DNE if such an interval does not ez f is increasing on help intervals f is decreasing on
Calculus
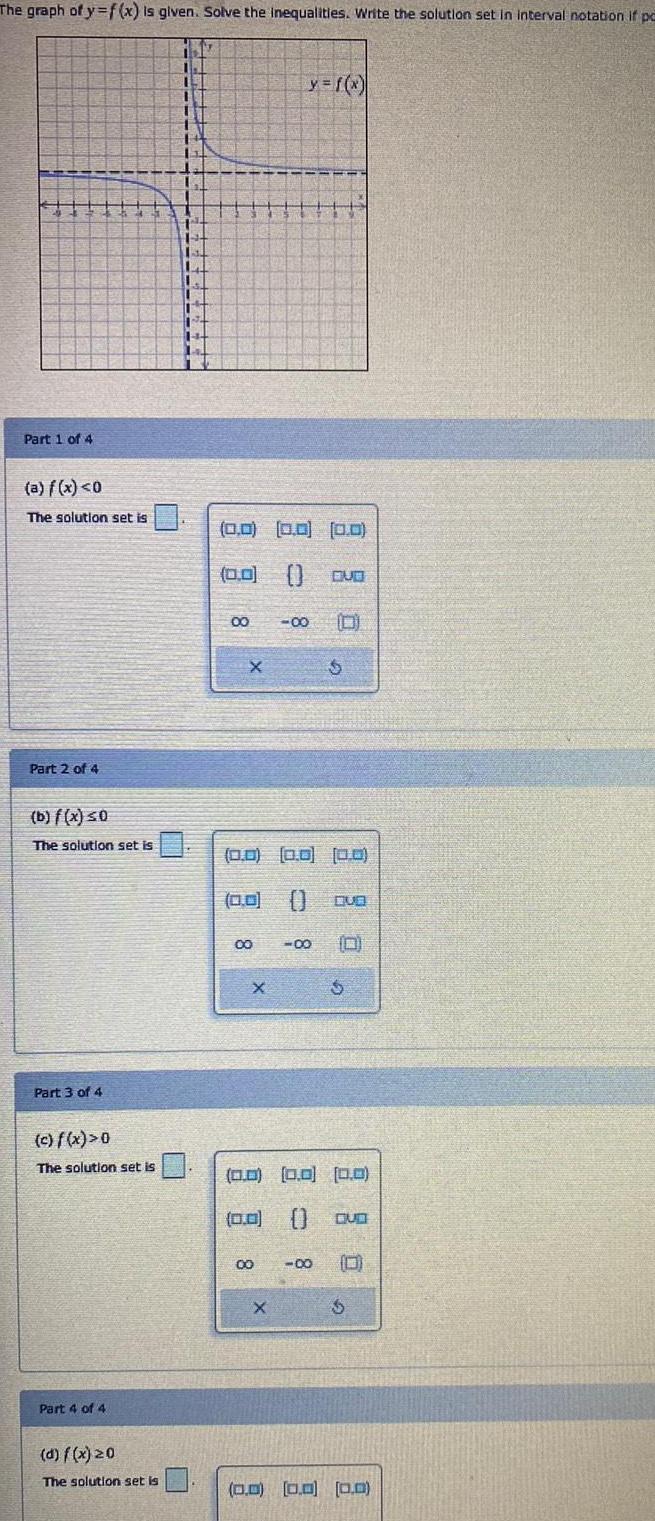
Application of derivativesThe graph of y f x is given Solve the inequalities Write the solution set in interval notation if pe Part 1 of 4 a f x 0 The solution set is Part 2 of 4 b f x 0 The solution set is Part 3 of 4 c f x 0 The solution set is Part 4 of 4 d f x 20 The solution set is 1 1 11 1 1 1 23 11 JE TE 11 11 11 11 HI 1 La 00 0 0 0 0 0 0 0 0 X 8 00 X 0 0 0 0 0 0 0 0 0 y f x 8 00 X 8 30 00 S 8 0 0 0 0 0 0 0 0 0 GUD QUO 6 S 0 0 0 0 0 0
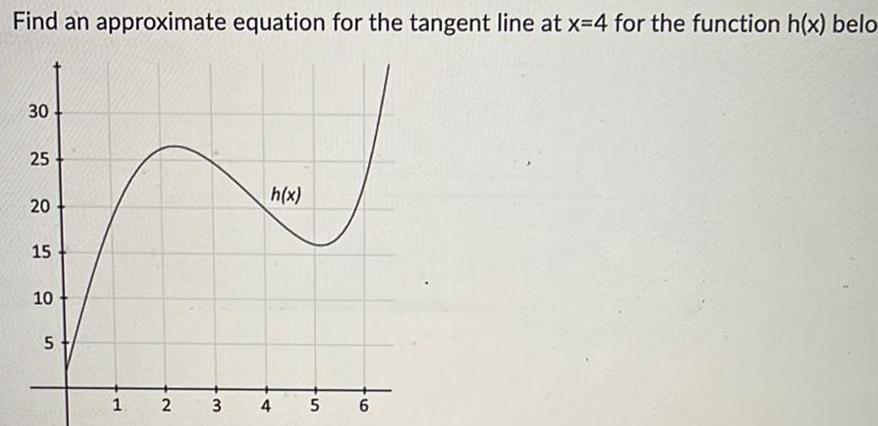
Calculus
Application of derivativesFind an approximate equation for the tangent line at x 4 for the function h x belo 30 25 20 15 10 5 1 2 3 h x 4 5 6
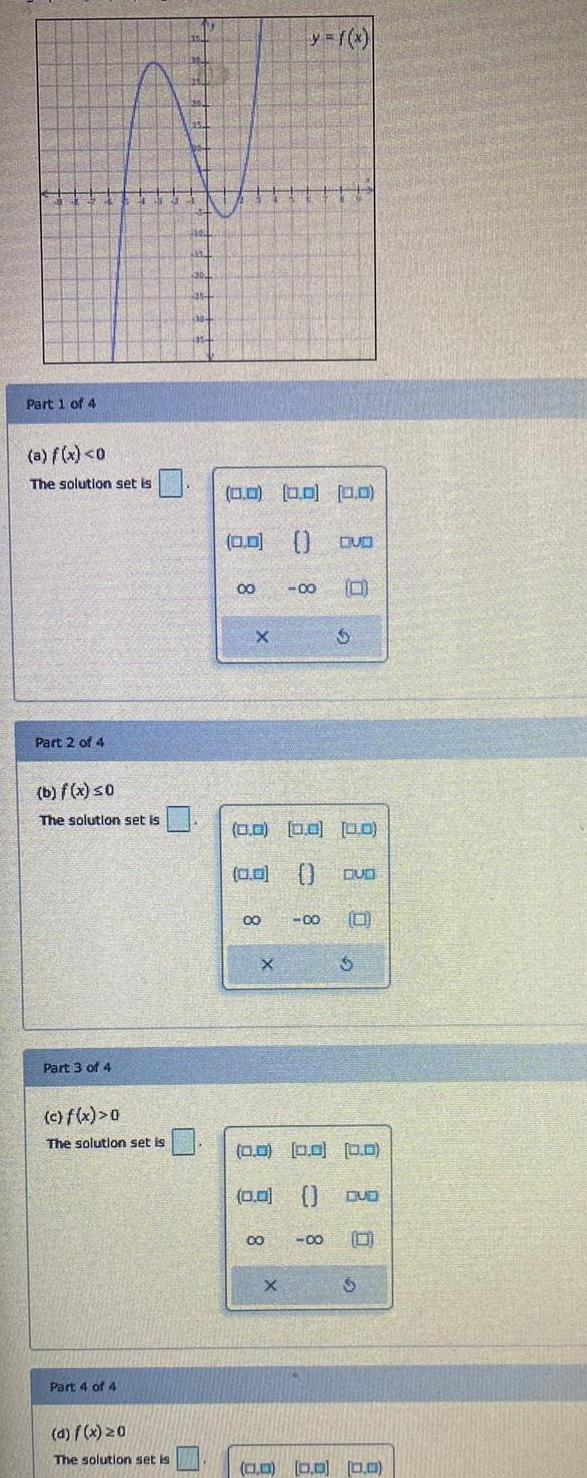
Calculus
Application of derivativesPart 1 of 4 a f x 0 The solution set is Part 2 of 4 b f x 0 The solution set is Part 3 of 4 c f x 0 The solution set is Part 4 of 4 d f x 20 The solution set is 0 0 0 0 0 0 0 0 00 X 00 X 00 0 0 0 0 0 0 0 0 GUD 00 0 00 X OVO 0 8 S 0 0 0 0 0 0 0 0 QUD S S 0 0 0 0 0 0
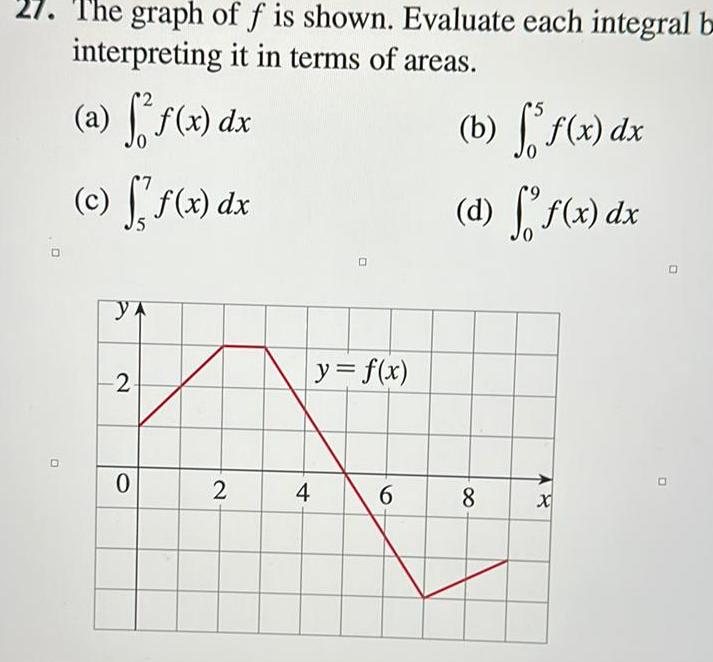
Calculus
Application of derivativesD O The graph of f is shown Evaluate each integral b interpreting it in terms of areas a ff f x dx c ff x dx YA 2 0 2 4 y f x 6 b f f x dx d f f x dx 8 48 D


Calculus
Application of derivativesShow that the derivative of the function g t 3t t 5 g t 6t 1 using the limit definition of the derivative Demonstrate that the definition was used and use proper notation throughout Th means do not use differentiation shortcuts

Calculus
Application of derivativesThis is a Part 2 question Please show all work and upload that here either as a picture PDF or as typed work A cup of coffee has its temperature F in degrees Fahrenheit at time t given by the function F t 75 110e 0 05t where time is measured in minutes 1 Using the rules of differentiation find F 10 and show all work 2 What are the units of F 10 that you computed above What is the practical meaing of the value of F 10 3 What would be the units of F t
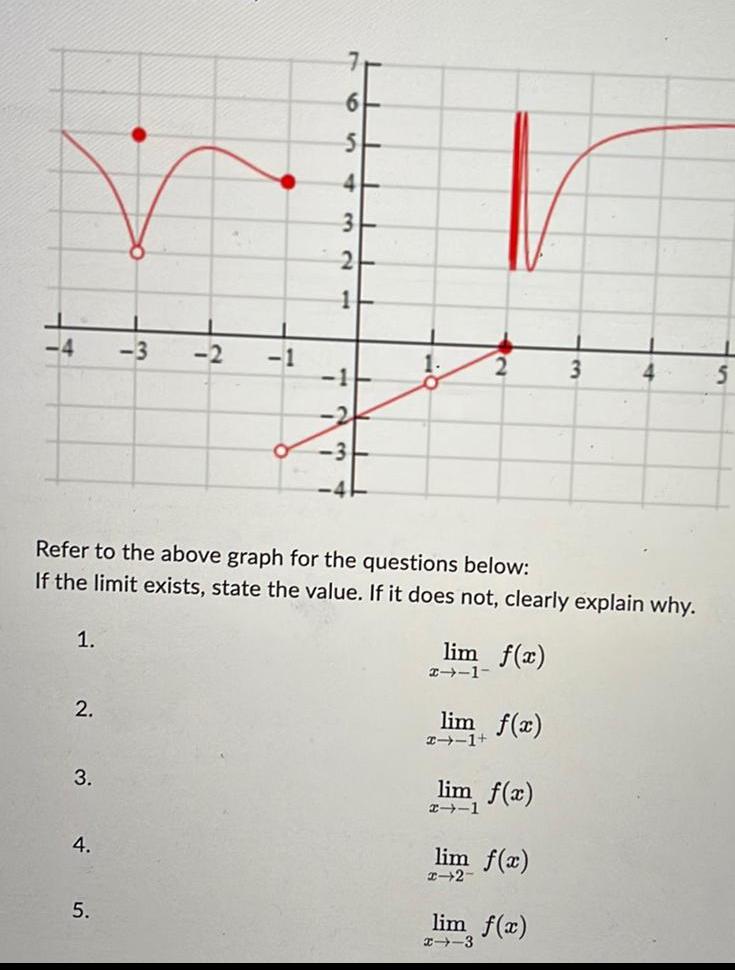
Calculus
Application of derivatives1 2 3 4 5 3 2 1 7 S V 4 Refer to the above graph for the questions below If the limit exists state the value If it does not clearly explain why 3 2 1 2 lim f x 1 12 lim f x x 1 lim f x 1 3 lim f x lim f x 3 4 5
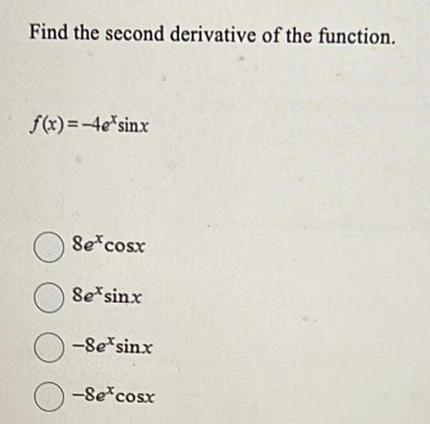
Calculus
Application of derivativesFind the second derivative of the function f x 4e sin x O O O Se cost Se sinx 8e sinx Se cost
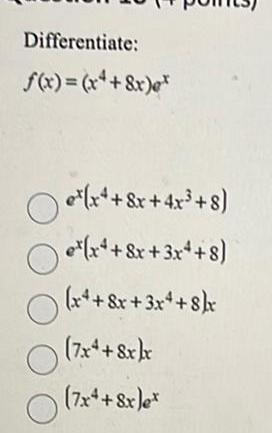
Calculus
Application of derivativesDifferentiate f x x 8x DOO e x 8x 4x 8 e x x 3x 8 x 8x 3x 8 x 7x 8x kx 7x 8x ex
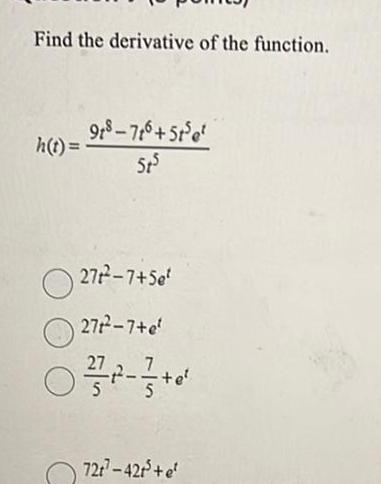
Calculus
Application of derivativesFind the derivative of the function h t 918 716 5t5e 5t5 27t 7 Set 27t 7 e 02 1 17 0 O 72t 42t e

Calculus
Application of derivativesSuppose the distance s in feet covered by a car moving along a straight road after t sec is given by the function s f t 21 20r Calculate the instantaneous velocity of the car when t 34 a 2992 ft sec b 22 ft sec c 748 ft sec d 156 ft sec
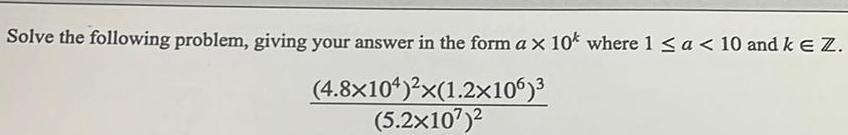
Calculus
Application of derivativesSolve the following problem giving your answer in the form ax 10k where 1 a 10 and k E Z 4 8x104 x 1 2x106 5 2x10
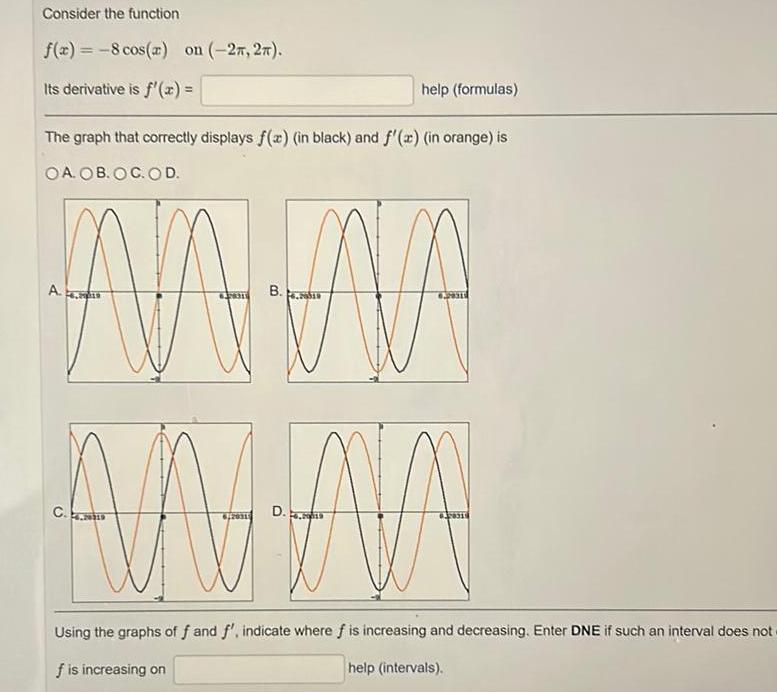
Calculus
Application of derivativesConsider the function f x 8 cos x on 27 27 Its derivative is f x help formulas The graph that correctly displays f x in black and f x in orange is OA OB OC OD A B NA NA AA WAR D 6 20315 4 2013 Using the graphs of f and f indicate where f is increasing and decreasing Enter DNE if such an interval does not f is increasing on help intervals C 2019
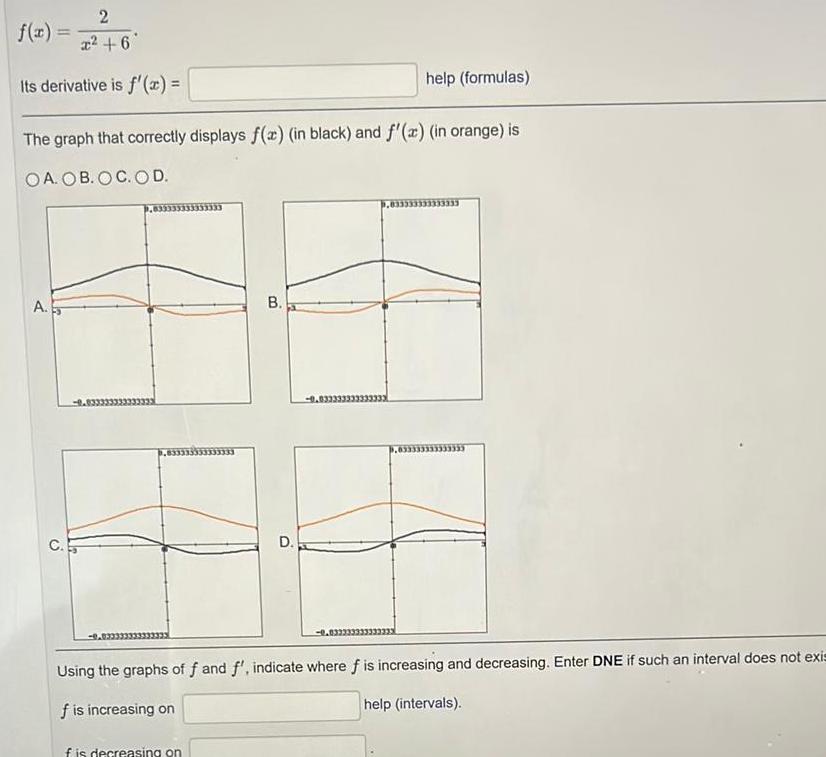
Calculus
Application of derivatives2 x 6 Its derivative is f x f x The graph that correctly displays f x in black and f x in orange is OA OB OC OD A B f is decreasing on D help formulas 0 033333333333 33333333 Using the graphs of f and f indicate where f is increasing and decreasing Enter DNE if such an interval does not exis f is increasing on help intervals
Calculus
Application of derivativesFind the extreme values of the function f x x 2 x on the interval 0 5 6 If an extreme value does not exist enter DNE help numbers Absolute minimum value Absolute maximum value
Calculus
Application of derivativesa a la W sin COS R TU tan 7 4 1 0 8 5 2 9 6 3 ans 1 X I a b x A radio tower is located 275 feet from a building From a window in the building a person determines that the angle of elevation to the top of the tower is 31 and that the angle of
Calculus
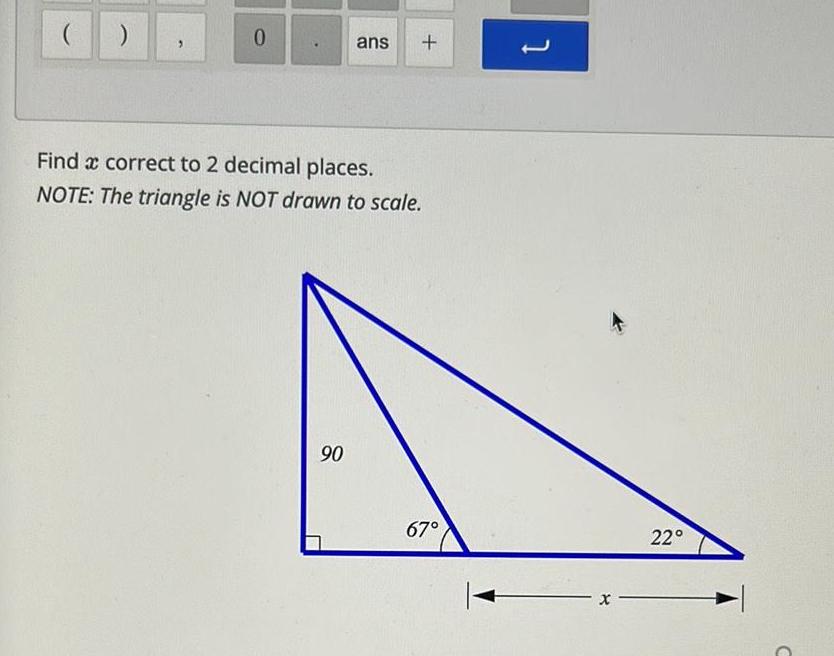
Application of derivatives0 ans Find a correct to 2 decimal places NOTE The triangle is NOT drawn to scale 90 67 J X 22 C
Calculus
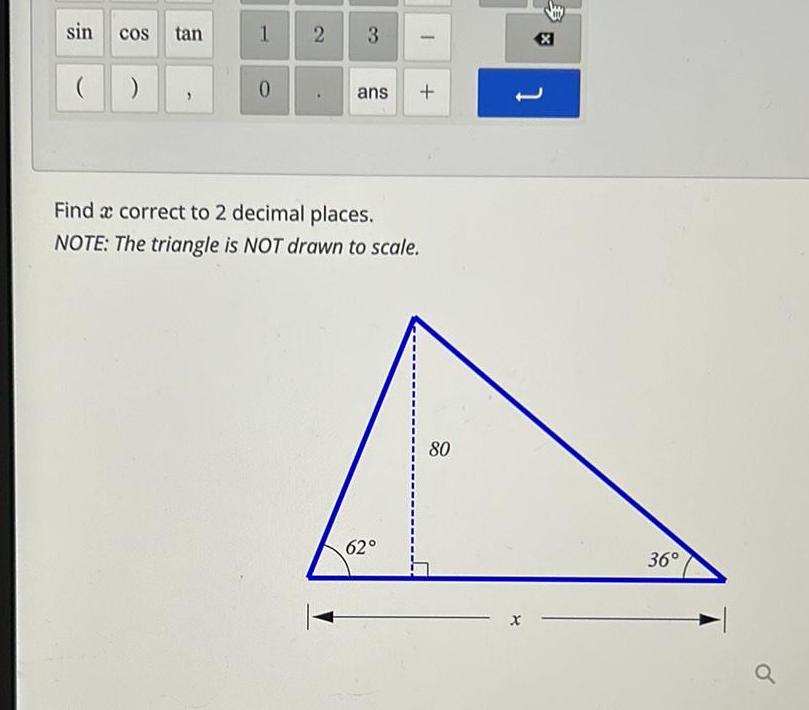
Application of derivativessin COS tan 1 0 2 3 ans I 62 Find a correct to 2 decimal places NOTE The triangle is NOT drawn to scale 80 x 1 36
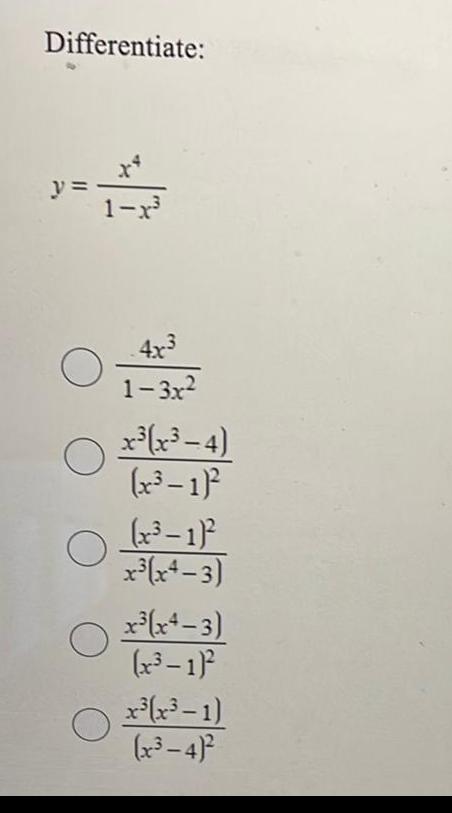
Calculus
Application of derivativesDifferentiate y 1 x O 4x 1 3x x x 4 x 1 x 1 x x4 3 x x4 3 x 1 x x 1 x 4

Calculus
Application of derivativesSuppose 7 4 7 4 and 7 6 6 and let g x f x cosx Find g 6 6 080 2 54 02 3 3 0 5 10 O 0 3 2 2 3 3 bo 7 6 g 6