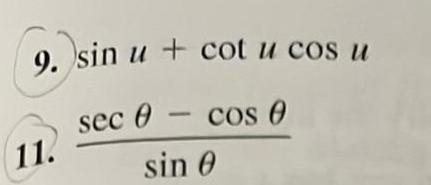Application of derivatives Questions and Answers

Calculus
Application of derivativesConsider the function f x 3x 7x For this function there are four important intervals A A B B C and C o where A and C are the critical numbers and the function is not defined at B Find A and B and C For each of the following open intervals tell whether f x is increasing or decreasing A Select an answer A B Select an answer B C Select an answer C 0 Select an answer Note that this function has no inflection points but we can still consider its concavity For each of the following intervals tell whether f x is concave up or concave down B Select an answer Box Select an answer

Calculus
Application of derivatives2x 4 Consider the function f x 52 2 A where the function is not defined at A Find A For this function there are two important intervals A and For each of the following intervals tell whether f x is increasing or decreasing A Select an answer A 0 Select an answer Note that this function has no inflection points but we can still consider its concavity For each of the following intervals tell whether f x is concave up or concave down 0 A Select an answer A 0 Select an answer
Calculus
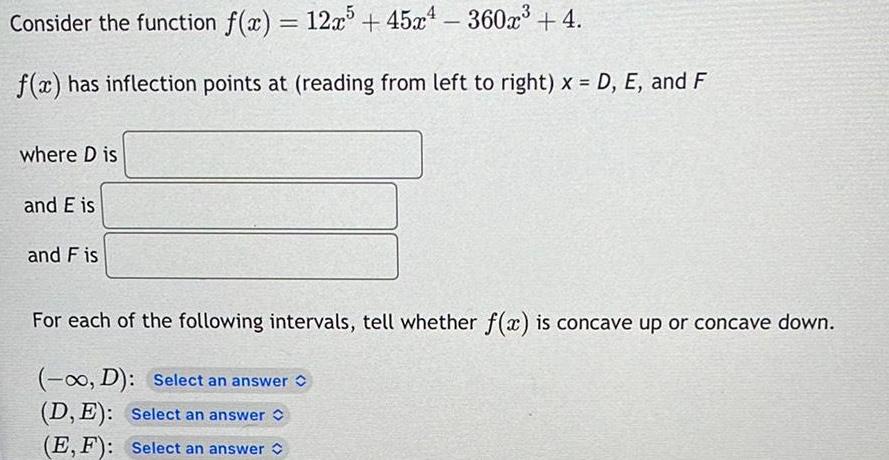
Application of derivativesConsider the function f x 12x5 45x 360x 4 f x has inflection points at reading from left to right x D E and F where D is and E is and F is For each of the following intervals tell whether f x is concave up or concave down D Select an answer D E Select an answer C E F Select an answer

Calculus
Application of derivativesA solid is formed by rotating the region in the first quadrant of the xy plane bounded by the curves 2 0 y 1 and x y about the line y 1 The volume of this solid is

Calculus
Application of derivativesIf the partial fraction expansion of 6x 39 x 5 x 6 then A B A x 5 6x 39 x 5 x 6 B x 6 is

Calculus
Application of derivativesAnswer the following questions for the function f x x x 4 defined on the interval 7 x 4 f x is concave down on the interval x f x is concave up on the interval x The inflection point for this function is at x The minimum for this function occurs at x The maximum for this function occurs at to x to x
Calculus
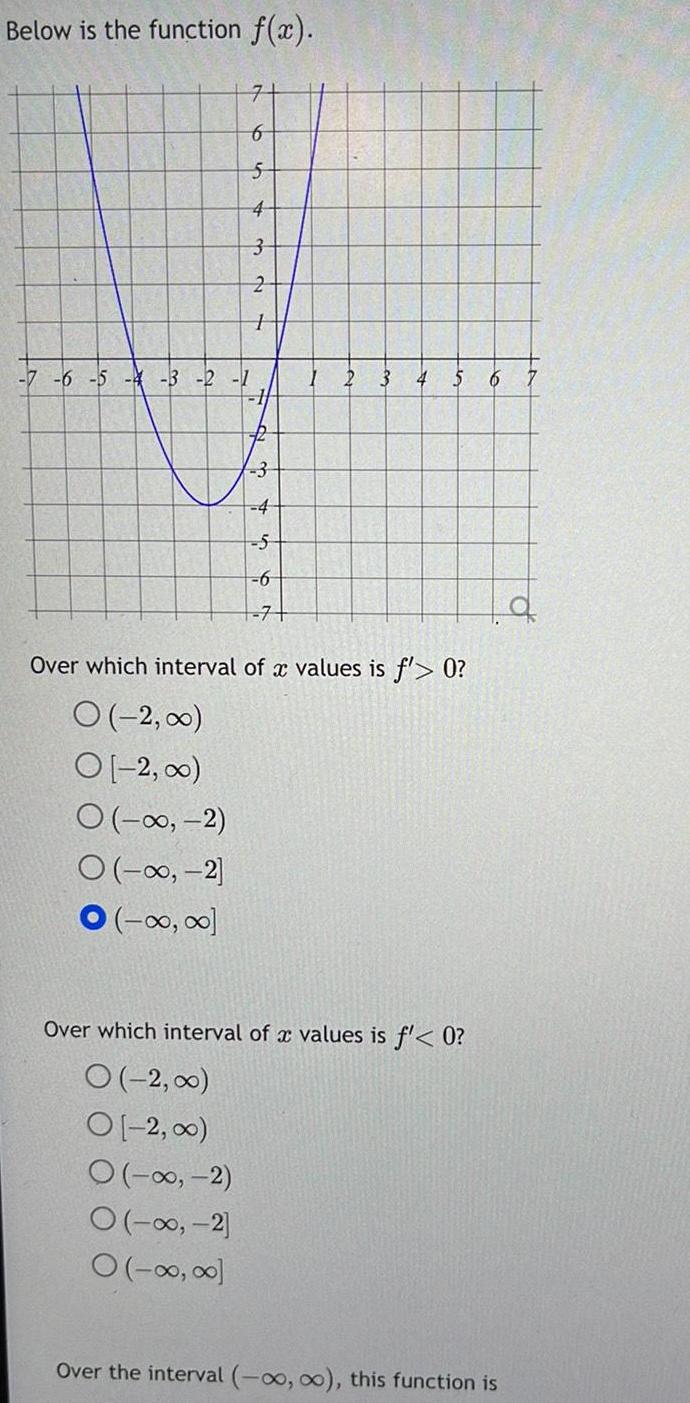
Application of derivativesBelow is the function f x 7 6 5 7 6 5 4 O 2 O 2 3 2 3 2 1 74 3 4 5 6 7 6 2 3 4 5 Over which interval of x values is f 0 0 2 00 O 2 00 Over which interval of a values is f 0 O 2 00 O 2 00 O 2 O 2 O 0 00 6 Over the interval 0 o this function is q
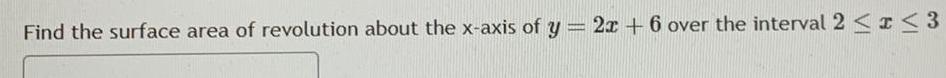
Calculus
Application of derivativesFind the surface area of revolution about the x axis of y 2x 6 over the interval 2 x 3

Calculus
Application of derivativess were asked to simplify the same trig expression but they eacl sec 2 x csc 2 x csc 2 x csc 2 x sec 2 x 1 simplification steps to show how Natalie simplified the expressio

Calculus
Application of derivativesFind the surface area of revolution about the x axis of y 4 sin 6x over the interval 0 x 70 6
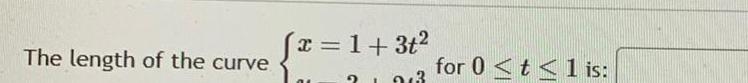

Calculus
Application of derivativesfind the stectionary points of the equation bolow x 2 y 2 15 at 1 4
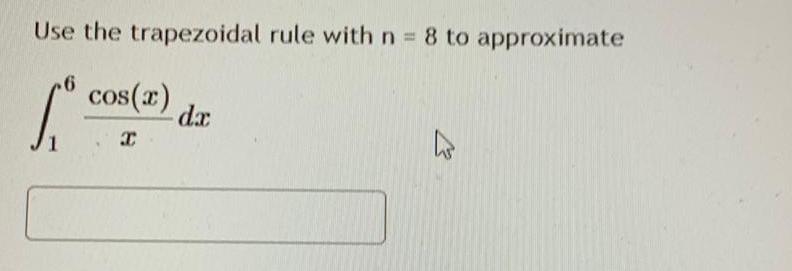
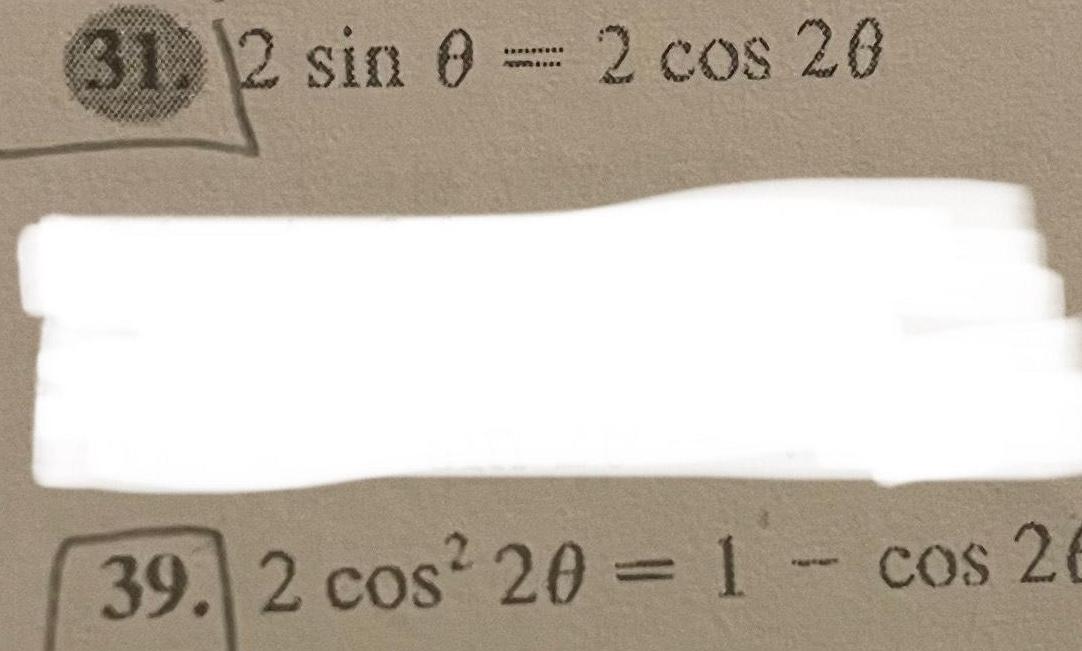

Calculus
Application of derivativesD D O Give the genus of the object If the object has a gen A fly swatter
Calculus
Application of derivativesfrom the Metric System erritory shares a 1 2 kilometer border with a country The territory c ometers and a famous rock in the territory has a maximum height of Determine the length of the border in miles Determine the area of the territory in square miles Determine the height of the rock in feet

Calculus
Application of derivativesb Find the area of the walkway The area of the region covered by Round to the nearest whole numbe

Calculus
Application of derivativesHow large should n be to guarantee that the Trapezoidal Rule approximation to 13 0 n x 0x 54x 5x 4 dx is accurate to within 0 001 How large should n be to guarantee that the Simpsons Rule approximation to 3 2 0r 542 5x 4 da is accurate to within 0 001 n 19 Hint Remember your answers should be a whole numbers and Simpson s Rule requires even values fc Question Help Video 1 Video 2 Post to forum
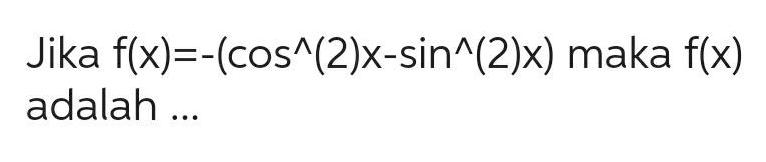

Calculus
Application of derivatives1 Given the polynomial function f x x 1 x 2 x 4 find the following a End Behavior Model behaviors here b What are the x intercepts 3 points c What is the y intercept 1 point d Determine the zeros of the function their multiplicity and whether the graph will Bounce Touch Wiggle cross or simply Cross the x axis 6 points Zeros Multiplicity B W C 10 10 5 5 0 5 Draw a sketch of those end 2 points 5 10
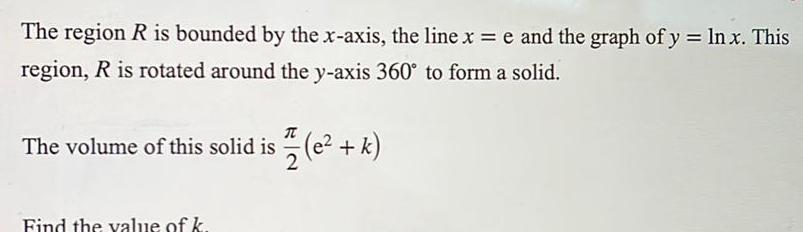
Calculus
Application of derivativesThe region R is bounded by the x axis the line x e and the graph of y ln x This region R is rotated around the y axis 360 to form a solid T The volume of this solid is e k Find the value of k

Calculus
Application of derivatives4 Let V be the vector space of real polynomials with inner product 1 f g f x g x da dx where f g V Find the cosine of the angle between f x 2 and g x x OA 1 20 OB 3 OC 0 OD 1 OE 2 2 2
Calculus
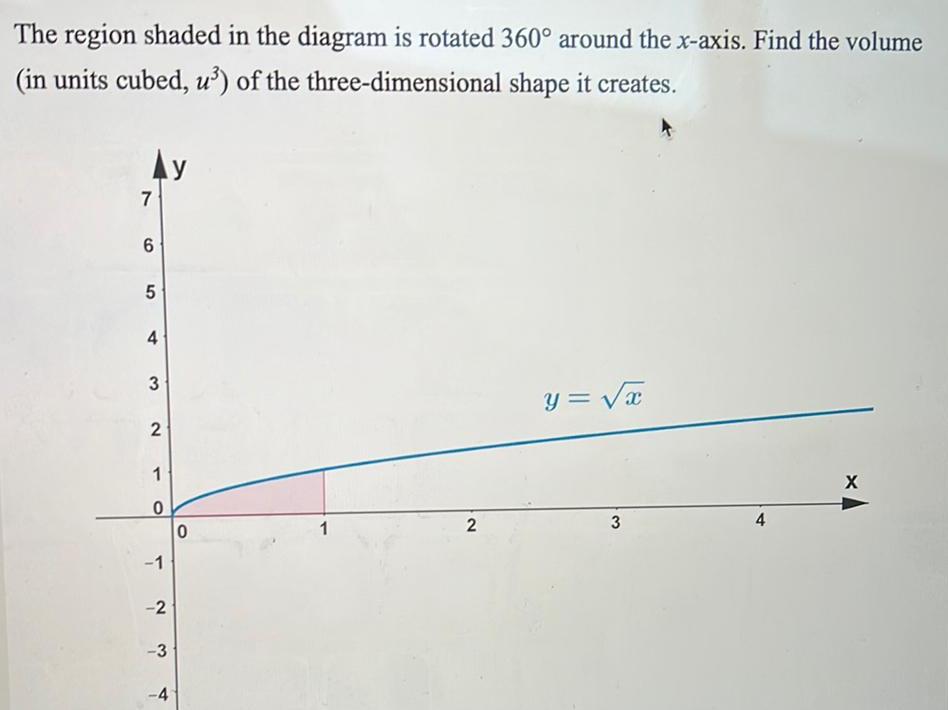
Application of derivativesThe region shaded in the diagram is rotated 360 around the x axis Find the volume in units cubed u of the three dimensional shape it creates 7 6 5 4 3 2 1 0 1 2 3 4 y 0 1 2 y x 3 4 X
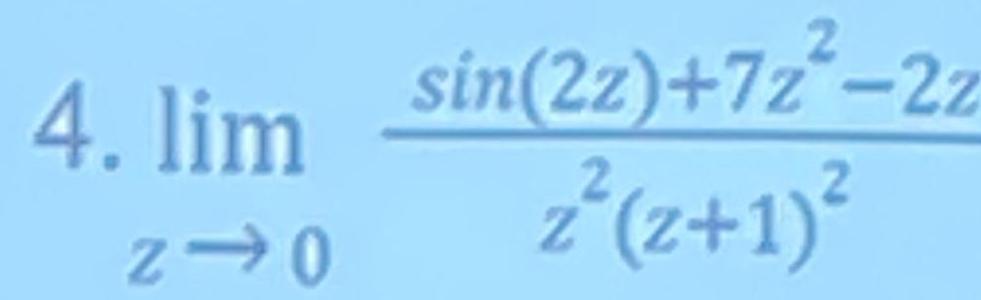
Calculus
Application of derivativesProve that for every prime p and for all natural numbers a a ged p a p iff p divides a b ged p a 1 iff p does not divide a

Calculus
Application of derivatives5 The members of a youth football program are required to sell tickets to chicken dinners for the program s fundraiser They can sell adult tickets for 10 and child tickets for 5 Each athlete must bring in at least 350 from the ticket sales Write an expression to represent the total amount of money an athlete makes from ticket sales Let x represent the number of adult tickets sold and let y represent the number of child tickets sold Write an inequality in two variables to represent the amount an athlete must make Graph the inequality from part b Use the graph to determine whether an athlete will bring in at least 350 when they sell 10 adult tickets and 30 child tickets Explain your reasoning
Calculus
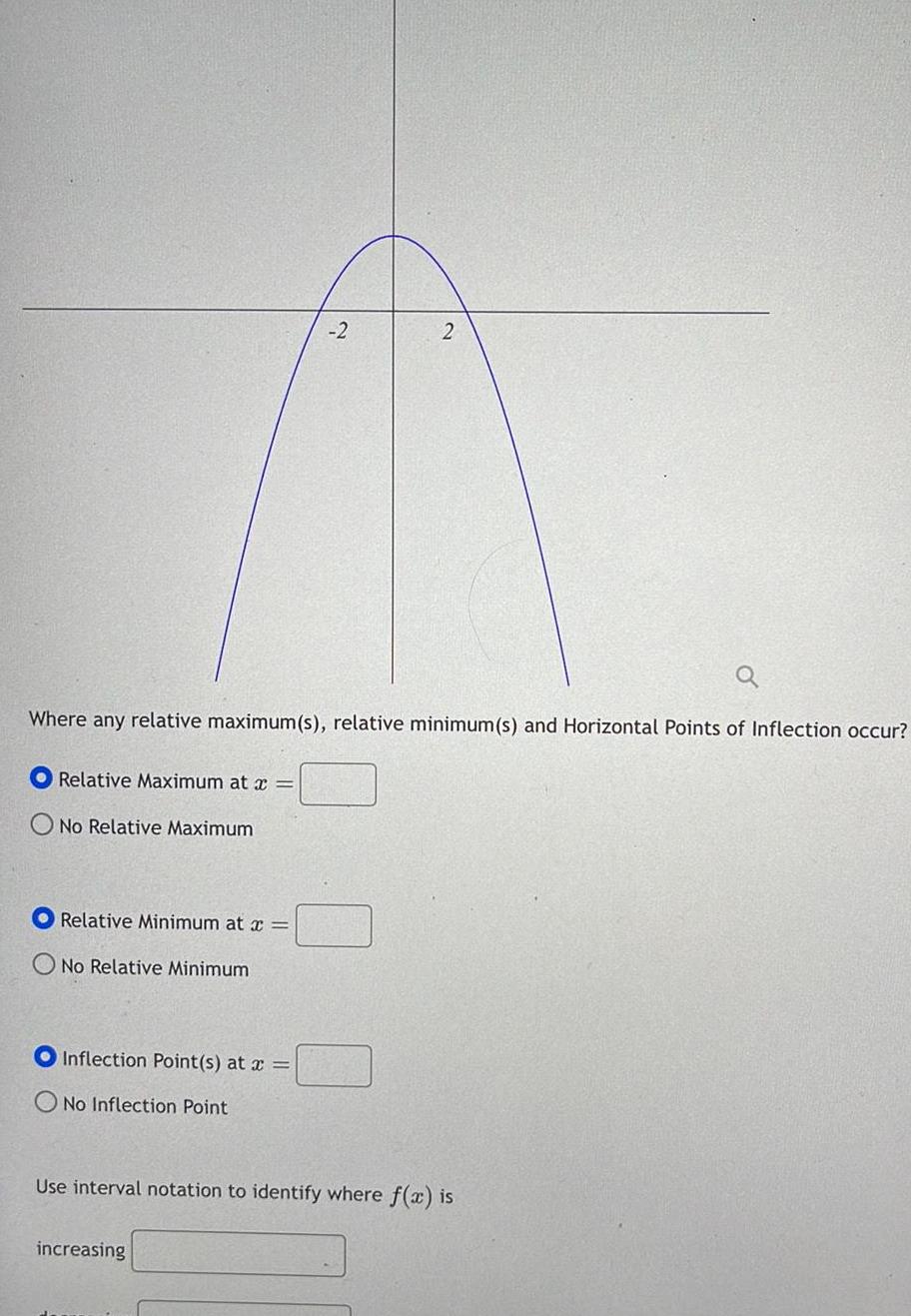
Application of derivativesRelative Maximum at x Where any relative maximum s relative minimum s and Horizontal Points of Inflection occur No Relative Maximum Relative Minimum at x O No Relative Minimum Inflection Point s at x No Inflection Point 2 2 increasing Use interval notation to identify where f x is
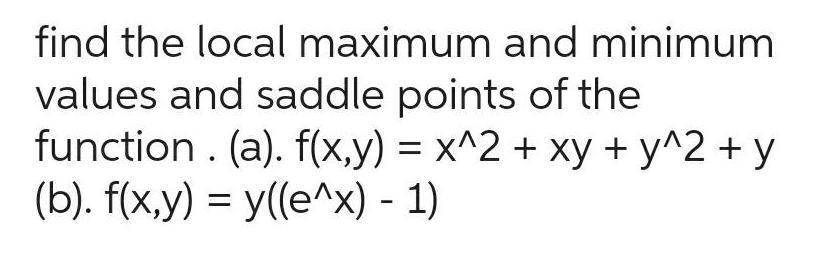
Calculus
Application of derivativesfind the local maximum and minimum values and saddle points of the function a f x y x 2 xy y 2 y b f x y y e x 1
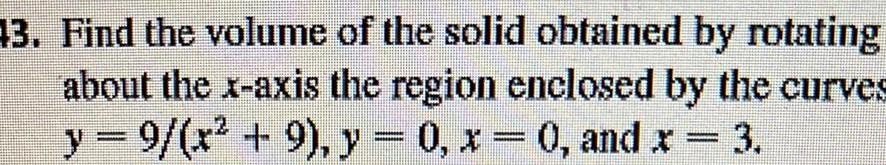
Calculus
Application of derivatives13 Find the volume of the solid obtained by rotating about the x axis the region enclosed by the curves y 9 x 9 y 0 x 0 and x 3

Calculus
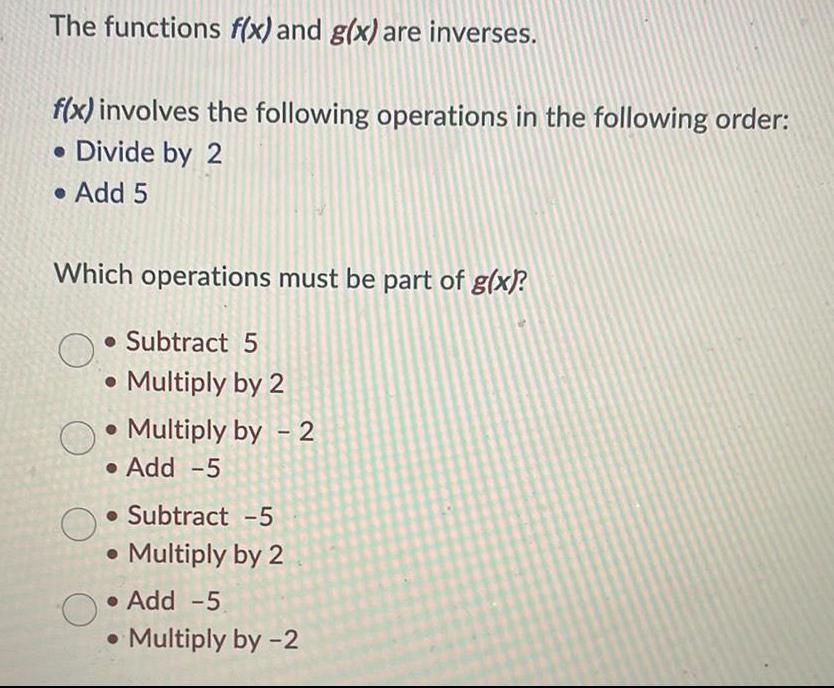
Application of derivativesThe functions f x and g x are inverses f x involves the following operations in the following order Divide by 2 Add 5 Which operations must be part of g x Subtract 5 Multiply by 2 Multiply by 2 Add 5 Subtract 5 Multiply by 2 Add 5 Multiply by 2
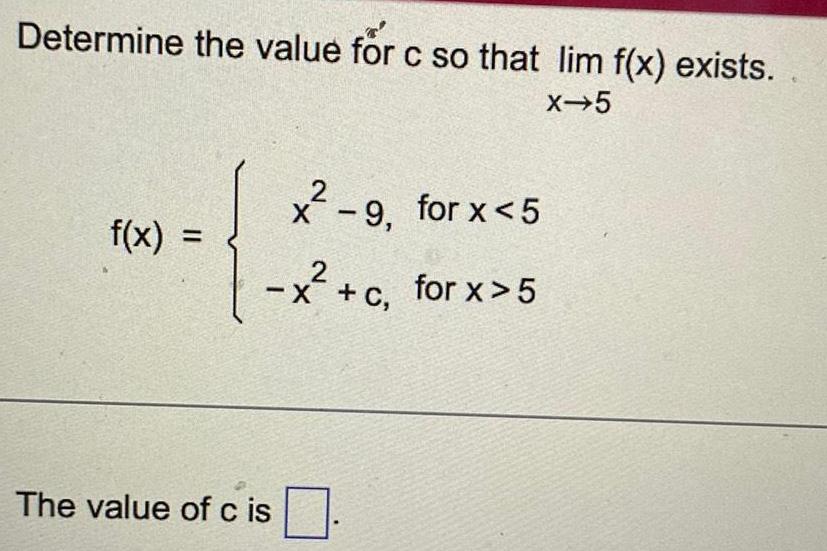
Calculus
Application of derivativesDetermine the value for c so that lim f x exists x 5 f x 2 x 9 for x 5 2 x c for x 5 The value of cis
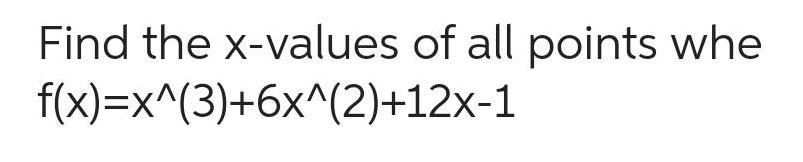
Calculus
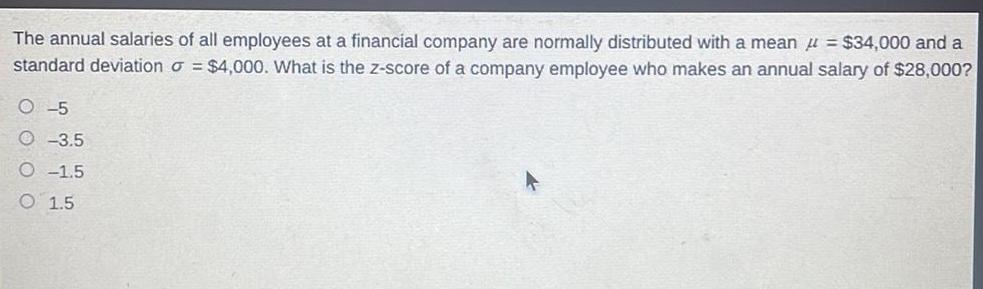
Application of derivativesThe annual salaries of all employees at a financial company are normally distributed with a mean 34 000 and a standard deviation 4 000 What is the z score of a company employee who makes an annual salary of 28 000 O 5 3 5 O 1 5 O 1 5

Calculus
Application of derivativesExercise 14 7 4 Let f x y x 2xy 3xy Find the change rate of f if the point is moving from 0 0 to 1 1 with unit speed
Calculus
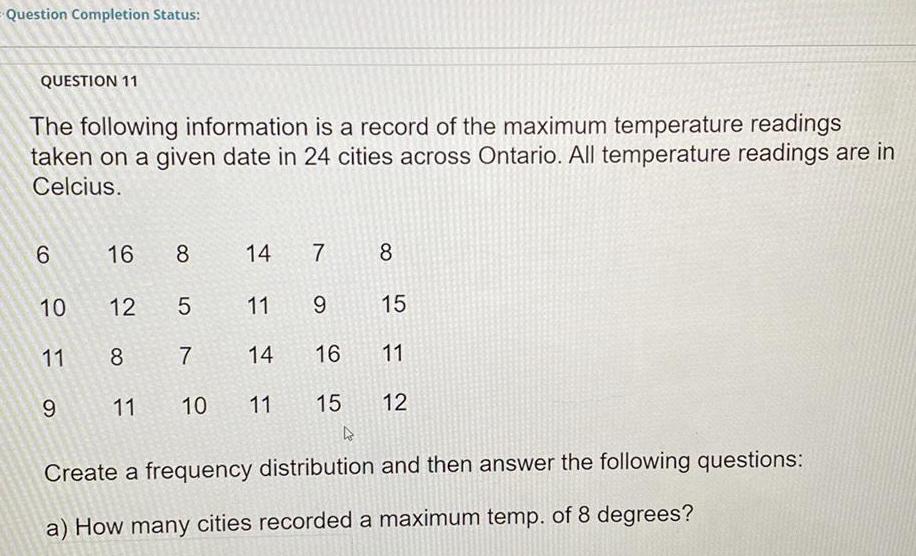
Application of derivativesQuestion Completion Status QUESTION 11 The following information is a record of the maximum temperature readings taken on a given date in 24 cities across Ontario All temperature readings are in Celcius 6 10 11 9 16 8 12 5 11 8 7 14 10 11 15 14 7 8 9 15 11 12 11 16 4 Create a frequency distribution and then answer the following questions a How many cities recorded a maximum temp of 8 degrees

Calculus
Application of derivativesIn a class of 47 students scores on a test ranged from a low of 28 to a high of 94 Determine the midrange of the marks

Calculus
Application of derivativesThe number of students attending English 101 varied throughout the week On Monday there were 15 students on Tuesday 12 students Wednesday 21 students on Thursday 15 students and on Friday 17 students Please state the midrange from this data

Calculus
Application of derivatives4 Explain why each integral is improper then determine if the integral is convergent or divergent Hint use comparison theorems if needed a x3 x x 1 b dx In x dx
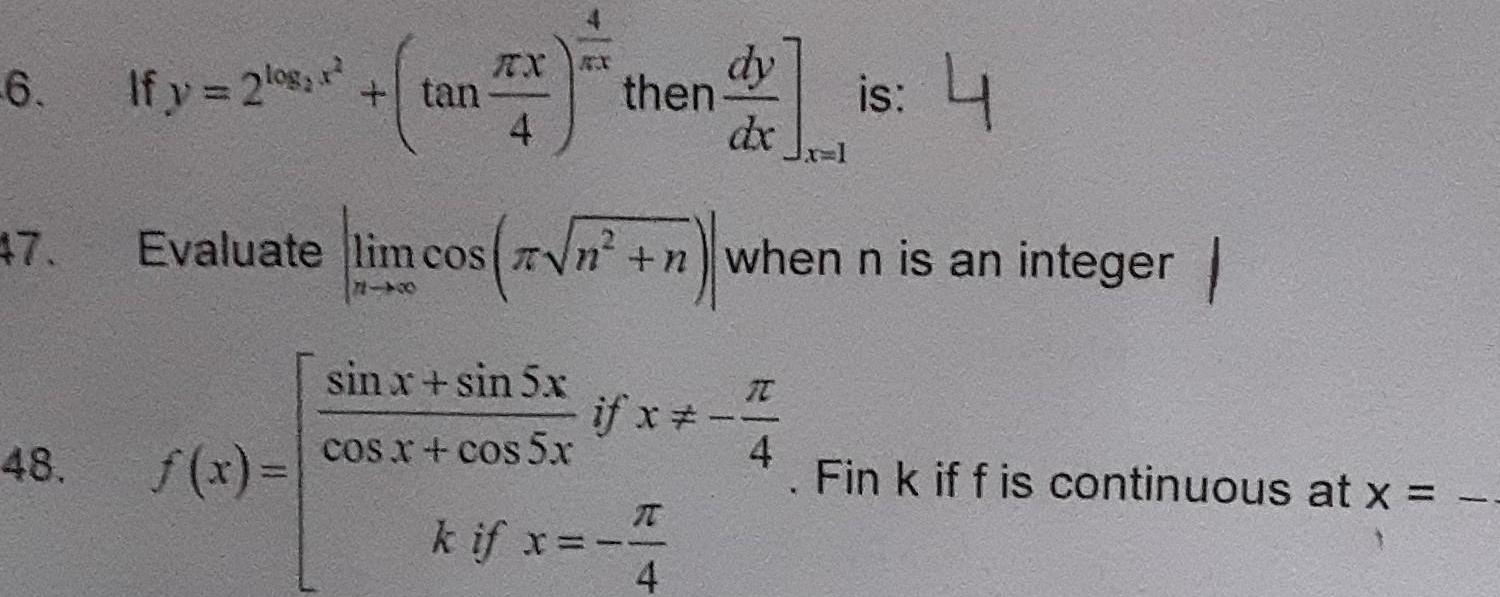
Calculus
Application of derivatives6 47 48 If y 2log r tan RX 4 then is 4 dy dx Evaluate lim cos x n n wi Evaluate lim cos n n when n is an integer sin x sin 5x f x cos x cos 5x I if x T k if x 4 4 Fin k if f is continuous at x
Calculus
Application of derivatives1 Find the taylor expansion for f x e about a 0 and find nth order Taylor polynomial t r and give an estimate for the remainder if r 0 1 Then find n so that lez t z is less than 0006

Calculus
Application of derivatives89 94 Trigonometric Substitution Make the indicated trigonometric substitution in the given algebraic expression and simplify see Example 7 Assume that 0 0 TT 2 90 V1 x x tan 0 89 X x sin 0 V1 x 91 Vx 1 x sec 0 93 V9 x x 3 sin 0 92 94 1 x 4 x x 25 2 X x 2 tan 0 x 5 sec 0
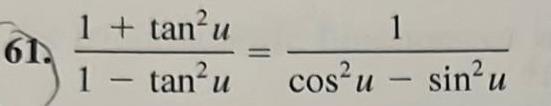
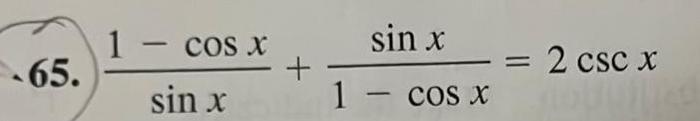

Calculus
Application of derivatives31 88 Proving Identities Verify the identity sin 0 tan 0 31 33 cos u sec u tan u tan y 35 cos 0 csc y cot u 1 1 cos y sec y 32 tan x 36 sec x 34 cot x sec x CSC X sin x cos v sin v 37 cos x sin x cos x sin x 38 cot a cos a sin a csc a 39 tan 0 cot sec 0 csc 0 40 sin x cos x 1 2 sin x cos x 1 CSC D sin L
Calculus
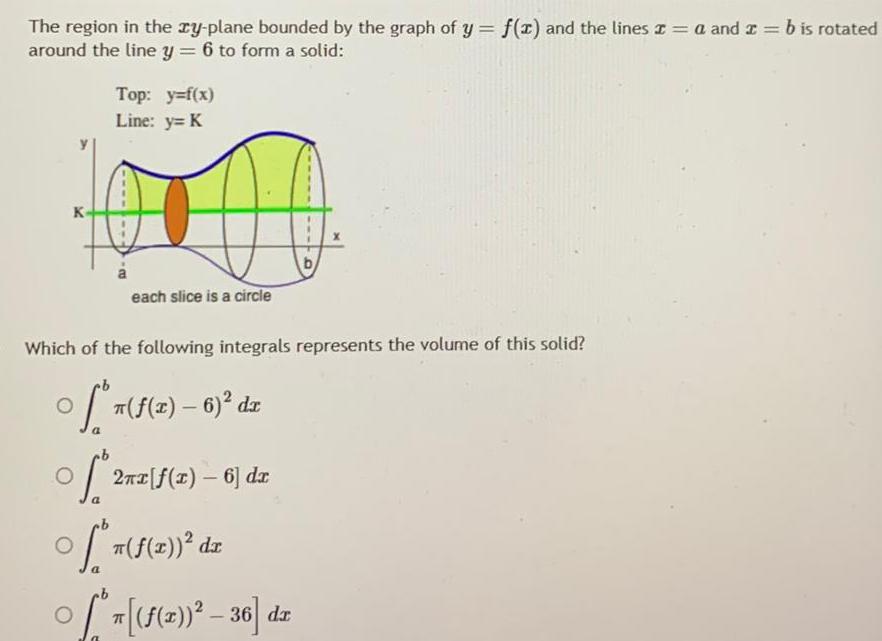
Application of derivativesThe region in the xy plane bounded by the graph of y f x and the lines I a and x b is rotated around the line y 6 to form a solid K O Top y f x Line y K each slice is a circle Which of the following integrals represents the volume of this solid O x 6 dx a 2 x f x 6 dx O f n 2 dz b f x 36 dr

Calculus
Application of derivativesFind the surface area of the ellipsoid formed by 3 2 y 9 4 rotated around the X 1