Application of derivatives Questions and Answers

Calculus
Application of derivativesConsider the function defined by f x a Find f x In x Using the substitution u X for x 0 b There is a local maximum and minimum point on the graph off Find both of these points In x or otherwise find f x dx
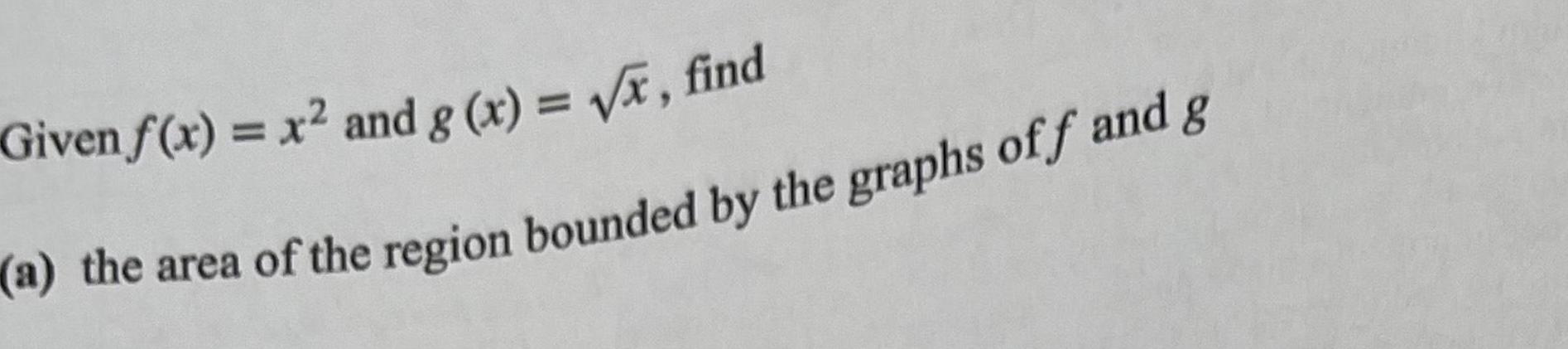
Calculus
Application of derivativesGiven f x x and g x x find a the area of the region bounded by the graphs off and g
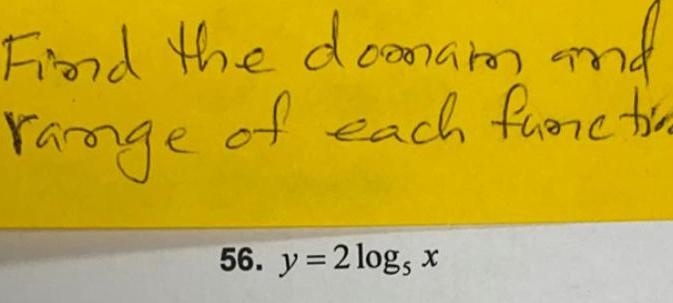
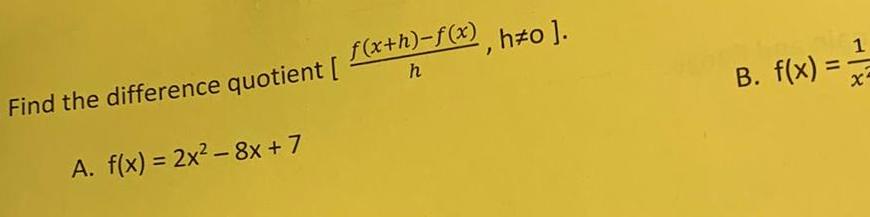
Calculus
Application of derivativesFind the difference quotient f x h f x h o h A f x 2x 8x 7 B f x 1 X

Calculus
Application of derivativesFor questions 9 and 10 find the absolute maximum and minimum values of f if the domain is the indicated region R 9 f x y x 2xy 3y R x y 2 x 4 1 y 3 Hint To determine boundary extrema consider the following functions of one variable f x 1 f x 3 f 2 and f 4 y 0 f x y x 3xy y 2y 6x R the triangular region with vertices 1 2 1 2 and 1 2

Calculus
Application of derivativesThis real world information can be modeled by the expression 15c 5d c represents how many hours he works at the caf 15c represents how much money he makes at the caf d represents how many hours he walks dogs 5d represents how much money he makes walking dogs 15c 5d represents the total amount of money Kurt makes working both jobs Write an expression or equation representing the real world information below You can use one or two variables and it can be written as an expression without an equal sign or as an equation with an equal sign 1 Gene has a pocket full of quarters and dimes that amount to 2 45 2 Rita s start up cost for opening an online Etsy jewelry store is 300 and she has to pay an additional 70 per month to keep it running successfully

Calculus
Application of derivativesIn Section 5 4 of our textbook example 3 calculates the work needed to drink a soda If the cola glass shape is inverted from the one given in example 3 would the amount of work be the same You need to explain your answer in a few sentences below
Calculus
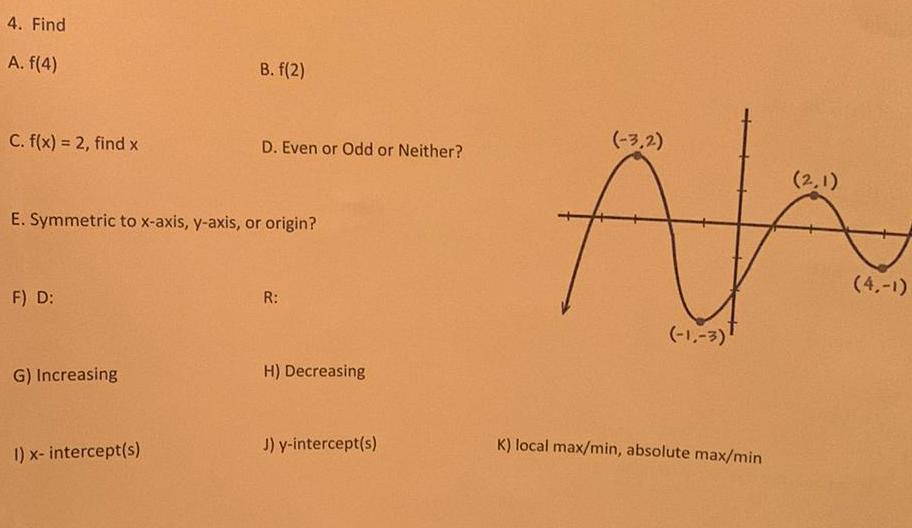
Application of derivatives4 Find A f 4 C f x 2 find x F D E Symmetric to x axis y axis or origin G Increasing B f 2 1 x intercept s D Even or Odd or Neither R H Decreasing J y intercept s 3 2 1 3 K local max min absolute max min 2 1 4 1

Calculus
Application of derivativesA ball of radius 16 has a round hole of radius 7 drilled through its center Find the volume of the resulting solid

Calculus
Application of derivativesSuppose that R is the finite region bounded by y x y x 5 x 0 and x 3 Find the exact value of the volume of the object we obtain when rotating R about the z axis Y

Calculus
Application of derivatives10 a Find the critical points and draw the phase portrait for the autonomous DE dv 320 0 5v Sketch typical solution curves for each region of the tv plane dt determined by the critical points 2

Calculus
Application of derivativesCalculate the derivative of the function h t 5 t 6 F t Express numbers in exact form Use symbolic notation and fractions where needed 5 h 1 h 2 2

Calculus
Application of derivativesLet f x 43 if x 3 I 3 2x 9 if x 3 Calculate the following limits Enter DNE if the limit does not exist or oo or oo for the behavior if appropriate lim f x 2 3 lim f x 3 lim f x

Calculus
Application of derivativesCalculate the difference quotient for f x 2x2 at a 1 Express numbers in exact form Use symbolic notation and fractions where needed f 1 h f 1 h Calculate f 1 by finding the following limit f 1 h f 1 h lim h 0 Give an exact answer Use symbolic notation and fractions where needed f 1 Find an equation of the tangent line to f at a 1 Express numbers in exact form Use symbolic notation and fractions where needed
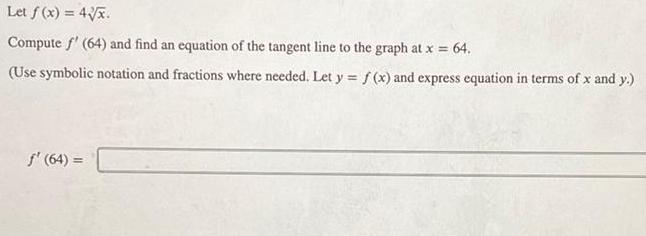
Calculus
Application of derivativesLet f x 4 x Compute f 64 and find an equation of the tangent line to the graph at x 64 Use symbolic notation and fractions where needed Let y f x and express equation in terms of x and y 64

Calculus
Application of derivativesCompute f and find an equation of the tangent line to the graph at x a f x 11x a 5 Use symbolic notation and fractions where needed Let y f x and express equation in terms of x and y f x

Calculus
Application of derivativesA circular swimming pool has a diameter of 20 m the sides are 4 m high and the depth of the water is 3 m How much work in Joules is required to pump all of the water over the side The acceleration due to m gravity is 9 8 and the density of water is 1000 kg 82 m

Calculus
Application of derivativesFind the points on the graph of f x 12x x where the tangent line is horizontal Use symbolic notation and fractions where needed Give your answer as a comma separated list or ordered pairs in the form x y

Calculus
Application of derivativesCalculate the derivative of the function 6 t Express numbers in exact form Use symbolic notation and fractions where needed h t 5 t
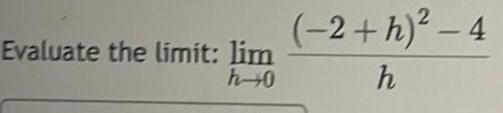

Calculus
Application of derivativesLet f x Calculate f x f 5 f 5 h f 5 x x 5 h Express numbers in exact form Use symbolic notation and fractions where needed f x f 5 x 5 f 5 h f 5 h 5x and Take the appropriate limit to find f 5 Give an exact answer Use symbolic notation and fractions where needed

Calculus
Application of derivativesFind f 4 and f 4 assuming that the tangent line to y f x at a 4 is y 8x 2 Give exact answers Use symbolic notation and fractions where needed f 4 4

Calculus
Application of derivativesFind the horizontal asymptotes of f 71 3 641 8 1 6 f 1 Let y f t and give your answer as a comma separated list of equations in terms of the given variables Express numbe exact form Use symbolic notation and fractions where needed horizontal asymptote s
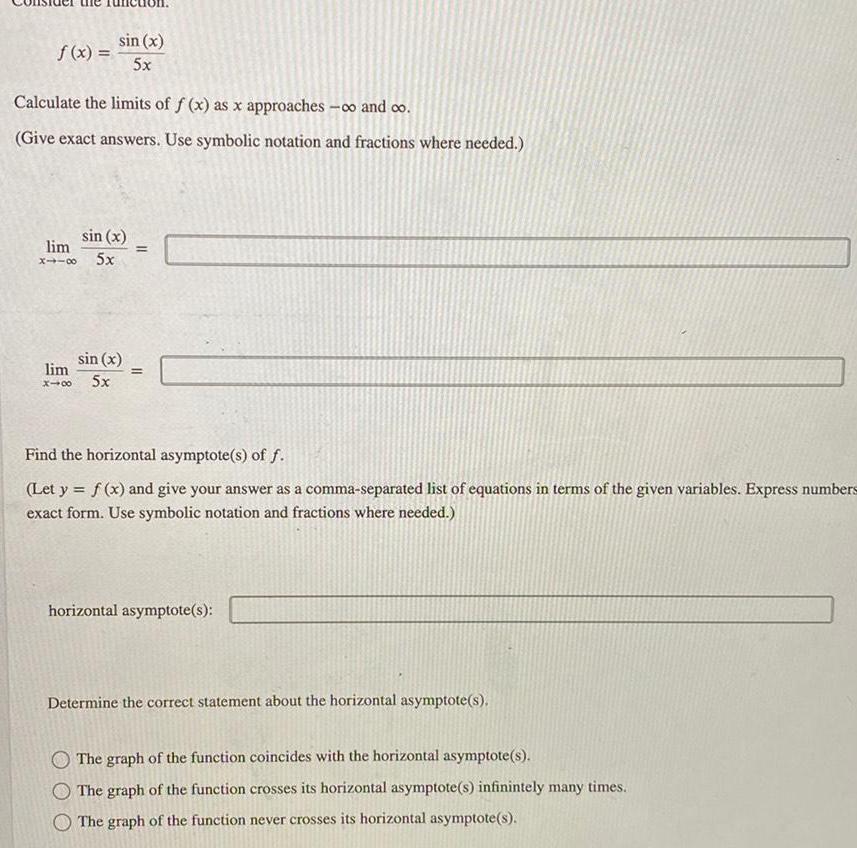
Calculus
Application of derivativesf x sin x 5x Calculate the limits of f x as x approaches and co Give exact answers Use symbolic notation and fractions where needed sin x lim X118 5x sin x lim X48 5x 11 Find the horizontal asymptote s of f Let y f x and give your answer as a comma separated list of equations in terms of the given variables Express numbers exact form Use symbolic notation and fractions where needed horizontal asymptote s Determine the correct statement about the horizontal asymptote s The graph of the function coincides with the horizontal asymptote s O The graph of the function crosses its horizontal asymptote s infinintely many times The graph of the function never crosses its horizontal asymptote s

Calculus
Application of derivativesIn physics one can examine the kinematic properties of an object accelerating at a constant rate based on its initial position and initial velocity The formula for distance traveled s is shown S So Vot 1 at In this equation so is the initial distance away from the starting point vo is the initial velocity of an object t is the time elapsed since the motion began and a is the constant acceleration of the object The derivative of the distance traveled with respect to time in Leibniz notation is dt ds dt Find the formula for the object s instantaneous velocity ds when so 40 units vo 16 units s and a 10 units s Round all coefficients to one decimal place units s
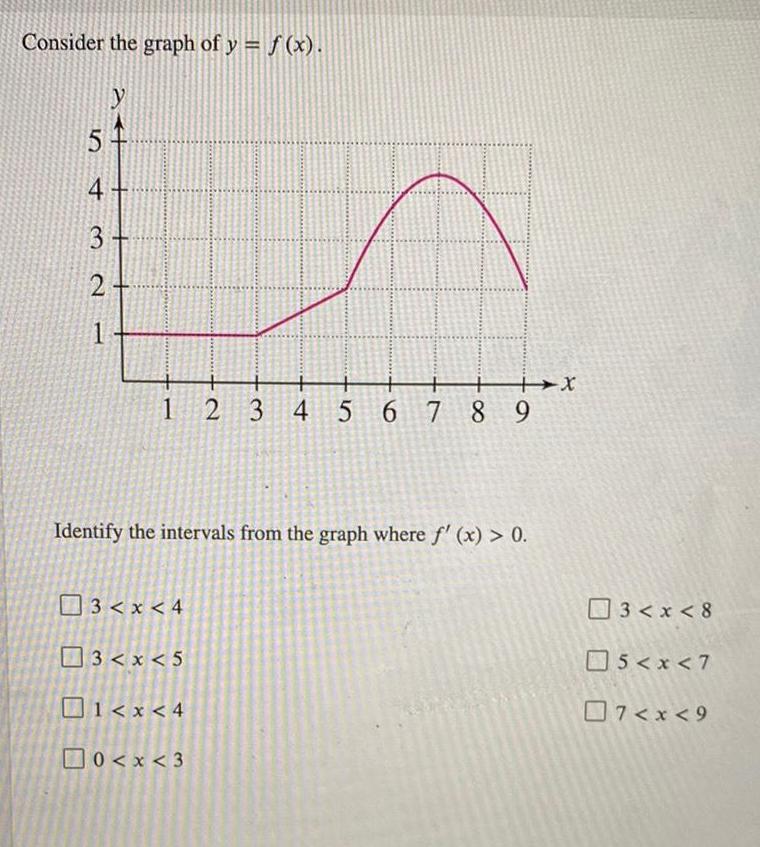
Calculus
Application of derivativesConsider the graph of y f x y 5 4 3 2 1 3 x 4 Identify the intervals from the graph where f x 0 3 x 5 1 x 4 X 0 x 3 2 3 4 5 6 7 8 9 3 x 8 5 x 7 7 x 9
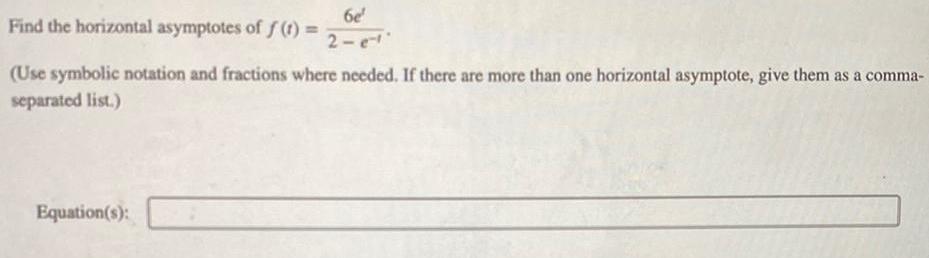
Calculus
Application of derivatives6e 2 e Find the horizontal asymptotes of f t Use symbolic notation and fractions where needed If there are more than one horizontal asymptote give them as a comma separated list Equation s

Calculus
Application of derivativesFind the equation of the tangent line at 1 f 1 when f 1 4 and f 1 2 Use symbolic notation and fractions where needed equation

Calculus
Application of derivativesthe rectangular equation y 4x to polar form and sketch its graph 2 1 pt Convert the polar equation r 6 cos 0 to rectangular form and sketch its graph 3 2 pts Sketch the curve r 3 2 cos 0 by first sketching the graph of r as a function of 0 in Cartesian coordinates

Calculus
Application of derivativesA bucket begins holding 30 kgs of sand The bucket is to be lifted to the top of a 15 meter tall building by a rope of negligible weight However the bucket has a hole in it and leaks 0 3 kgs of sand each meter it is lifted Find the work done lifting the bucket to the top of the building Joules

Calculus
Application of derivativesConsider the region in the first quadrant that is enclosed by y 1 and y f x x Rotate this region around a horizontal line y ke where the shape of the slice is a washer a What is a possible value of k that will result in this washer shape Note There is more than one possible answer b Set up the integral but do not evaluate that gives the volume of this solid In your work list values of important quantities i e r and or R Edit Insert Formats B 7 MEE III Edit Insert Formats B 1 T S I U X X Next rotate this region around a horizontal line y k where the shape of the slice is a disc a What is the value of k that will result in this disc shape b Set up the integral but do not evaluate that gives the volume of this solid In your work list values of important quantities i e r and or R U X 00 5 A N A N A A C A A Finally rotate this region around a vertical line z c that results in the shape of the slice being a washer
Calculus
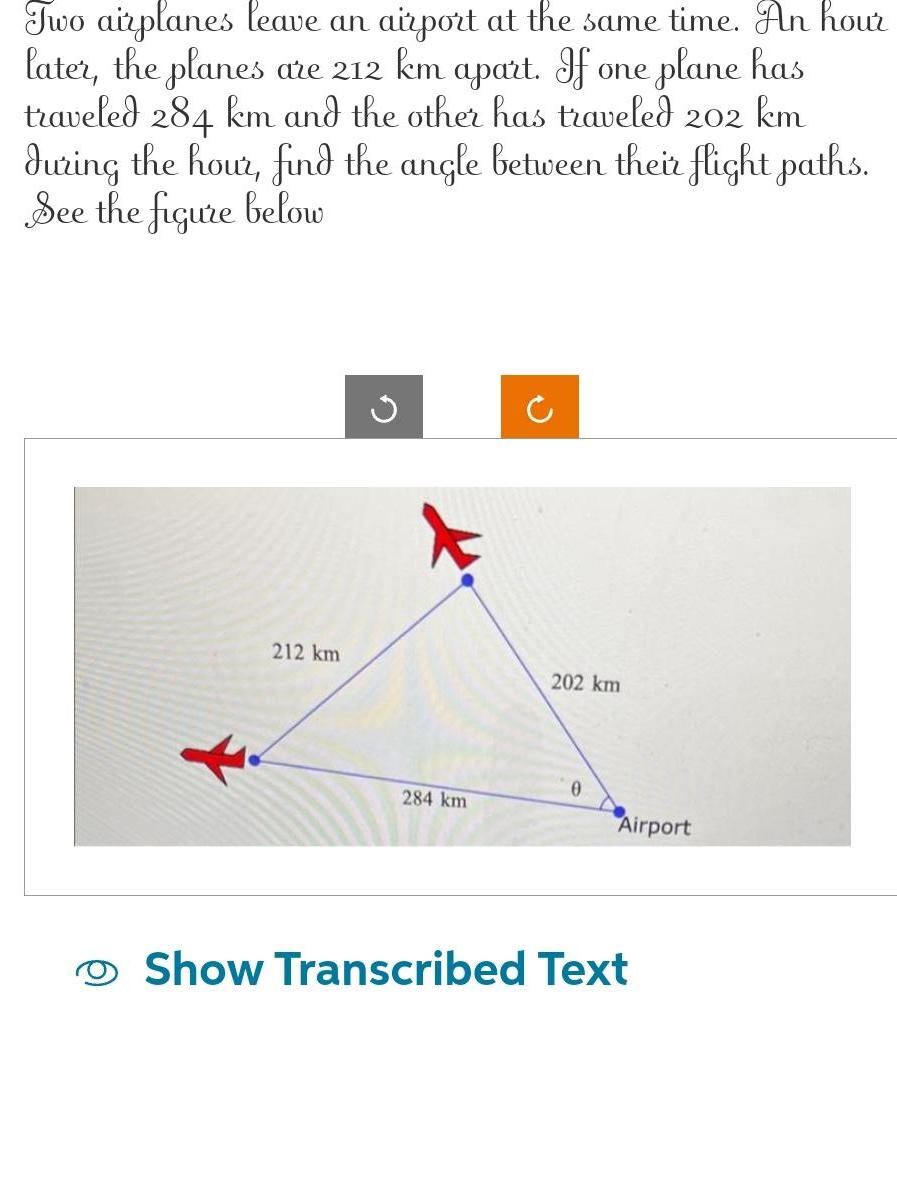
Application of derivativesTwo airplanes leave an airport at the same time An hour later the planes are 212 km apart If one plane has traveled 284 km and the other has traveled 202 km during the hour find the angle between their flight paths See the figure below 212 km G 284 km 202 km Airport Show Transcribed Text
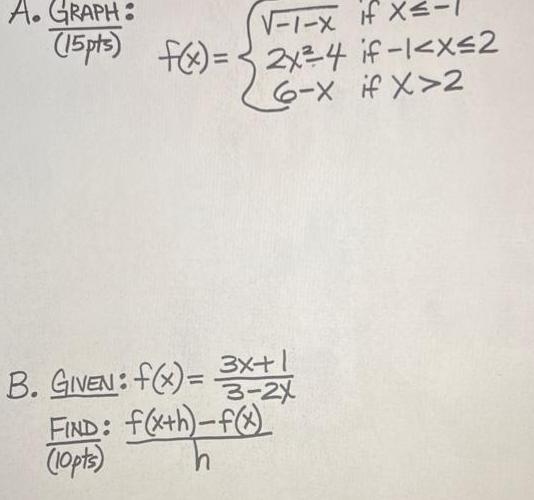
Calculus
Application of derivativesA GRAPH 1 X if X 15 pts f x 2x 4 if 1 x 2 6 X if X 2 B GIVEN f x 3x 1 3 2X f x h f x f x h FIND 10pts h
Calculus
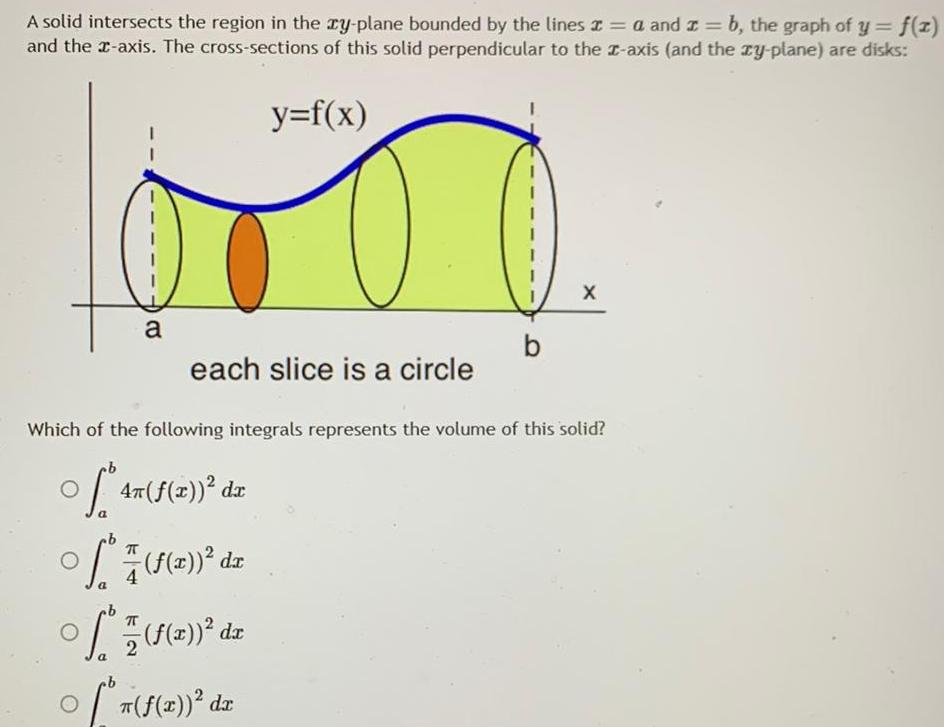
Application of derivativesA solid intersects the region in the rzy plane bounded by the lines a and x b the graph of y f z and the x axis The cross sections of this solid perpendicular to the z axis and the zy plane are disks y f x a each slice is a circle b 7 f x d O Which of the following integrals represents the volume of this solid f 4m f 2 dz O a 7 1 2 dz f x dr b X

Calculus
Application of derivativesThe side lengths The height of the triangle is h and CD x Complete the steps below to prove the Law of Cosines When filling in the blanks you may use the letters a b c x and h C D A I 41 1 h n B Part 1 Use the Pythagorean Theorem to find Od b x Od x h Oa c x h Oa b c Part 2 Use the Pythagorean Theorem to find c 02 2 b a 02 b x Oc a x h Oc b x h Part 3 Use the answer from Part 2 to fill in the blanks 2 2 0 0 Part 4 Use the answers from Parts 1 and 3 to fill in the blanks 2 2 0 0 Part 5 Use trigonometry to fill in the blank x cos C C Part 6 Use the answers from Parts 4 and 5 to fill in the blanks 2 200cos C
Calculus
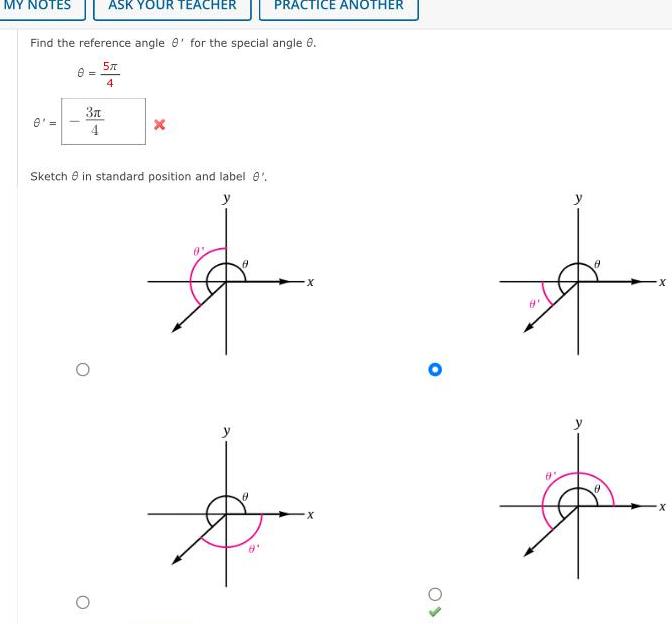
Application of derivativesASK YOUR TEACHER Find the reference angle 8 for the special angle 8 5 4 MY NOTES 0 8 3 4 Sketch in standard position and label 8 y O y 8 PRACTICE ANOTHER X 09 8

Calculus
Application of derivatives10 Given the function f x x x 5 X 3 a Find the domain of fin interval notation b Find the asymptotes of f x as well as any holes c Find the intercepts of f d Locate at least one point on each side near the vertical asymptote e Sketch the graph of f Label the intercepts asymptotes and any holes
Calculus
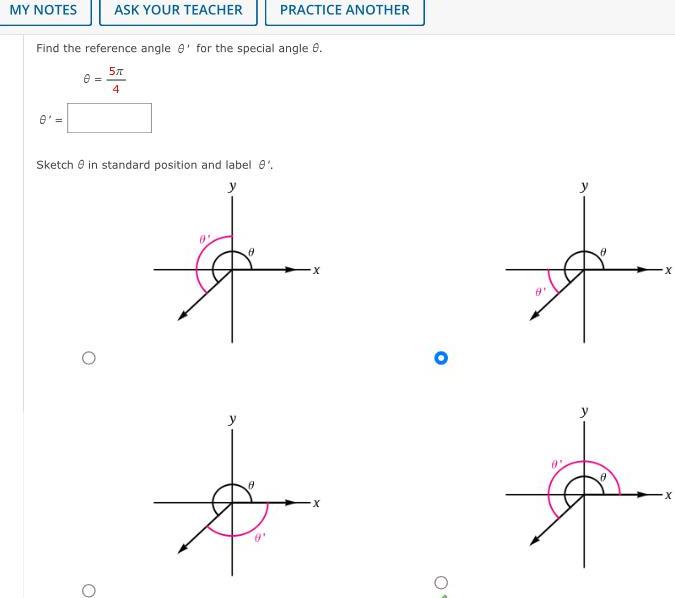
Application of derivativesMY NOTES 0 Find the reference angle for the special angle 8 5x 4 0 ASK YOUR TEACHER Sketch in standard position and label 9 y O 0 PRACTICE ANOTHER 0 A X 8 0 X X

Calculus
Application of derivativesFind the area of the region bounded by the graph of f x xsin x and the x axis between x 0 and x The area bounded by the region is Simplify your answer unit s
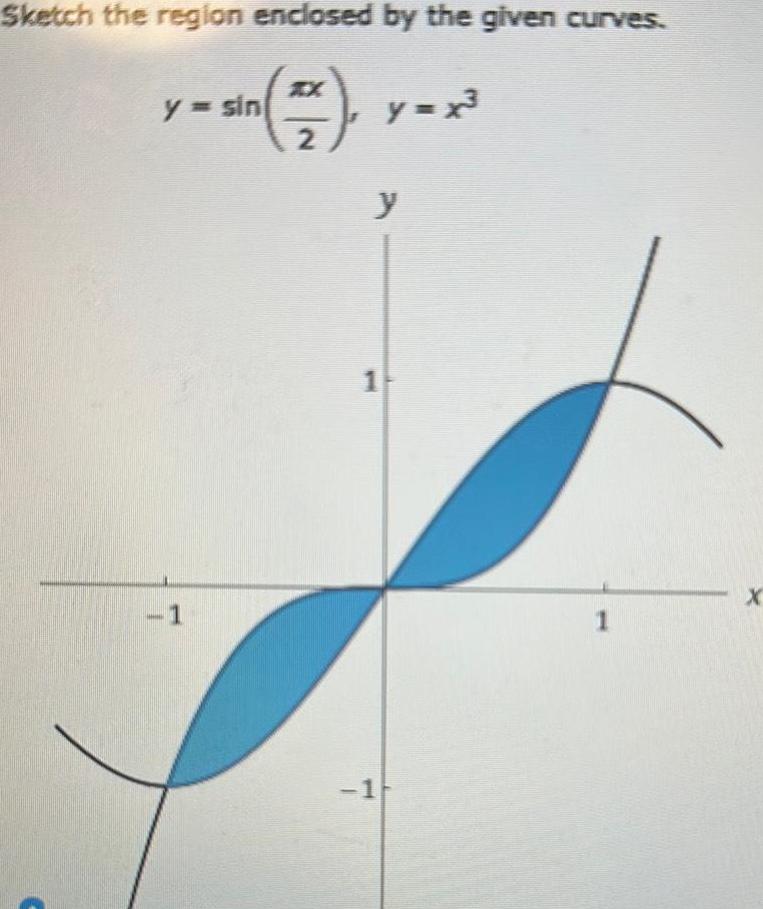
Calculus
Application of derivativesSketch the region enclosed by the given curves y sin 1 THANE 2 y 1 y x 1 1 X
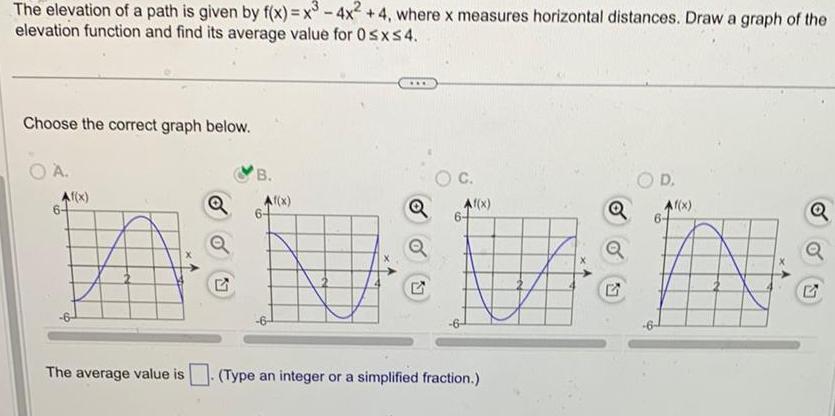
Calculus
Application of derivativesThe elevation of a path is given by f x x3 4x 4 where x measures horizontal distances Draw a graph of the elevation function and find its average value for 0 x 4 Choose the correct graph below O A Af x The average value is G B Af x 6 C Af x Type an integer or a simplified fraction Q D Af x Q Q 5
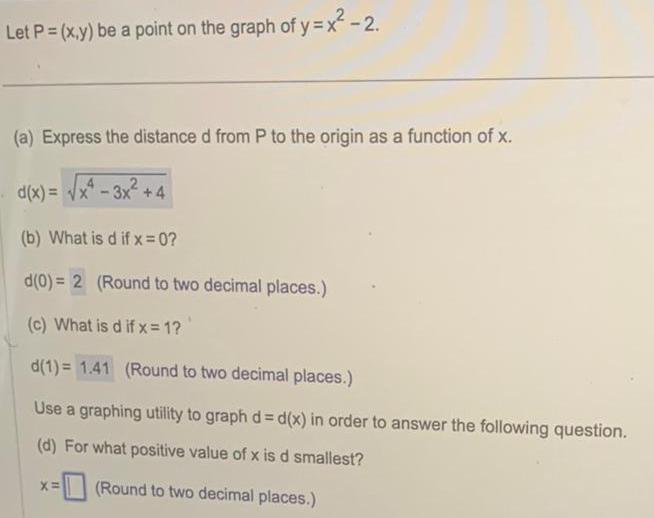
Calculus
Application of derivativesLet P x y be a point on the graph of y x 2 a Express the distance d from P to the origin as a function of x d x x 3x 4 b What is d if x 0 d 0 2 Round to two decimal places c What is d if x 1 d 1 1 41 Round to two decimal places Use a graphing utility to graph d d x in order to answer the following question d For what positive value of x is d smallest Round to two decimal places X

Calculus
Application of derivatives19 A furnace manufacturer wants to know how much of the metal surface area is giving off heat in this design The metal box is cube shaped all sides equal with sides measuring 40 in The circular metal vent is 30 in tall with a diameter of 8 in Calculate the surface area giving off heat excluding the cube s base and the bottom and top of the vent tube Hint You must also subtract the area of the circle where the vent connects to the cube 5 marks

Calculus
Application of derivativesIf the range of the linear function in Item 3 is 8 y 68 what is the domain
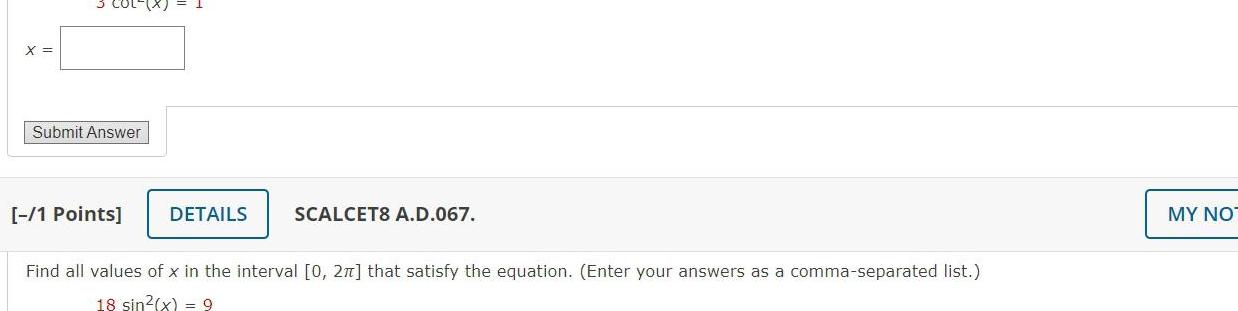
Calculus
Application of derivativesX Submit Answer 1 Points DETAILS SCALCET8 A D 067 Find all values of x in the interval 0 2 that satisfy the equation Enter your answers as a comma separated list 18 sin x 9 MY NO

Calculus
Application of derivativesPart B Jose predicts that the value of his car will decrease exponentially by 25 over the next 4 years If Jose s prediction is correct about how much will his car be valued at to the nearest thousand dollars after 4 more years
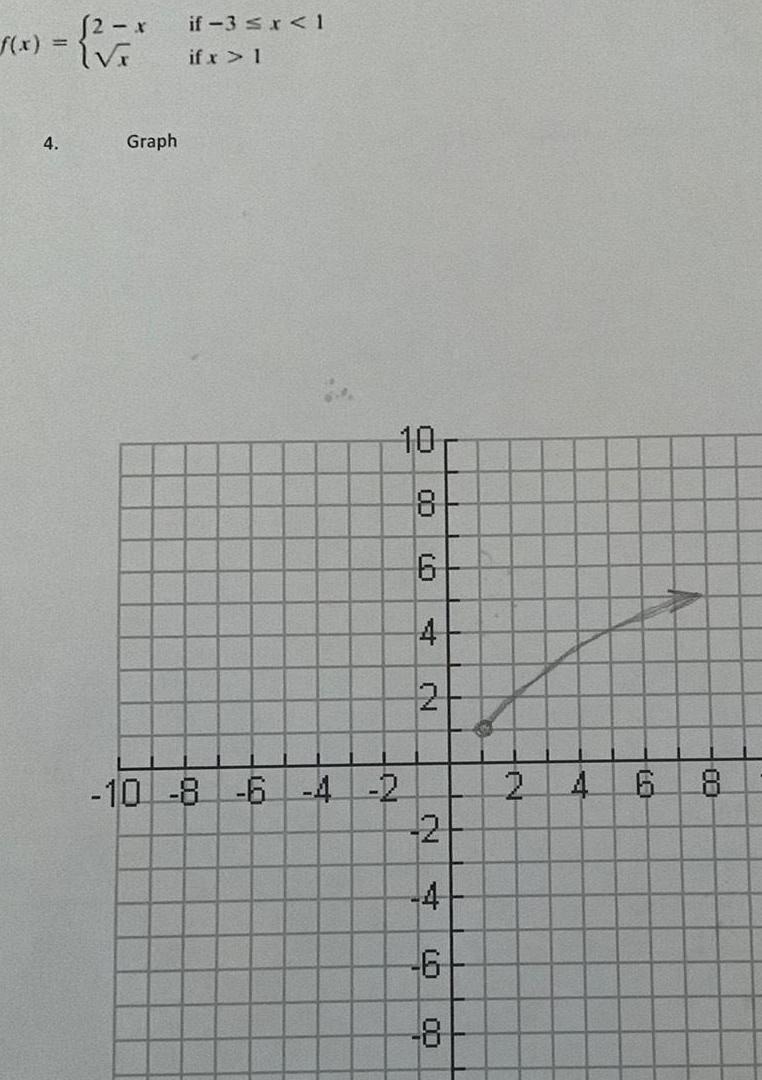
Calculus
Application of derivatives2 x f x x 4 Graph if 3 x 1 if x 1 10 8 6 4 2 10 00 8 6 4 2 2 4 61 8 O 2 A 6 8 00
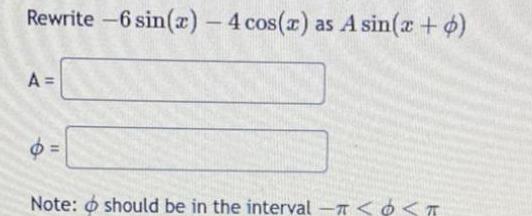
Calculus
Application of derivativesRewrite 6 sin x 4 cos x as A sin x 4 A e 11 Note should be in the interval T