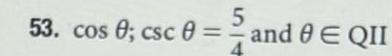Application of derivatives Questions and Answers
Calculus
Application of derivativesA graphing calculator is recommended An object with weight W is dragged along a horizontal plane by a force acting along a rope attached to the object If the rope makes an angle with the plane then the magnitude of the force is HW sin 0 cos 0 where is a constant called the coefficient of friction a Find the rate of change of F with respect to 8 dF de Fo b When is this rate of change equal to 07 m c If W 50 lb and 0 7 draw the graph of F as a function of 6 35 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 Use the graph to locate the value of 0 for which dF de 9M Is the value consistent with your answer to part b 1 8 O 35 35 2 35 2 35 0 0 1 0 2 0 3 04 03 0 6 0 7 0 8 0 9 1 0 Round your answer to two decimal places F 70 35 35 70 8 0 1 0 2 0 3 04 03 0 6 0 7 0 8 0 9 1 35 2 N 2 8 0 1 0 2 0 3 0 4 0 5 0 6 0 7 0 8 0 9 1


Calculus
Application of derivatives1 Four points and their coordiates are shwon on the unit circle Which value a b c d e f g or h is equal to a sin 3 2 b cos 360 C COS e f c d 0 g h a b

Calculus
Application of derivatives5 Which angles on the unit circle have a reference angle of Give your answers in radians
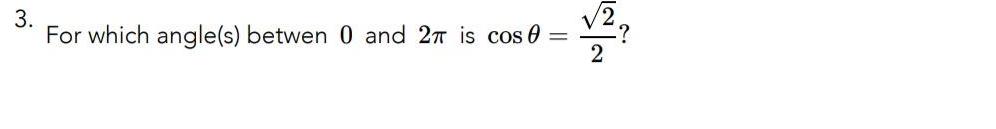
Calculus
Application of derivativesFind an equation of the tangent line to the curve at the given point f x 6x x 1 5 y Illustrate by graphing the curve and the tangent line on the same screen y 0 2 30 20 10 Submit Answer 2 y N N V 4 2 4 2 2 6 O 6 2 0 2
Calculus
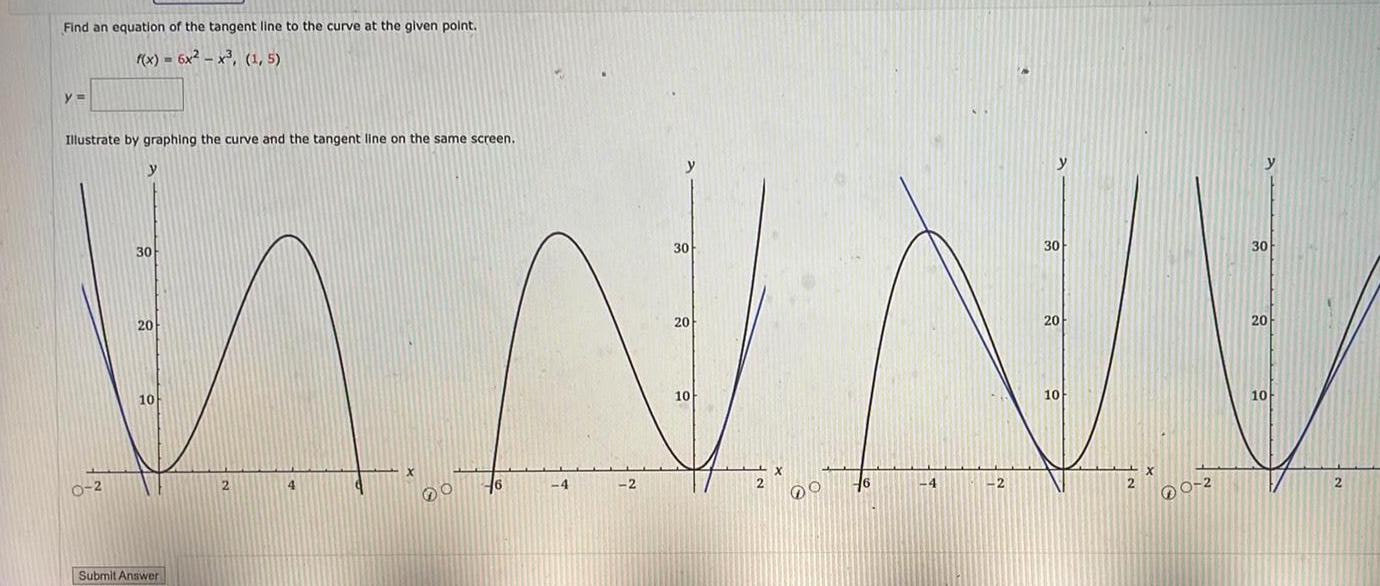
Application of derivativesWhere does the normal line to the parabola y x 1 at the point 1 0 intersect the parabola a second time If an answer does not exist enter DNE x y Illustrate with a sketch 4 3 2 Submit Answer 1 y 4 3 2 1 2 3 1 2 3 4 X 4 3 2 y 4 3 2 1 2 3 1 2 3 4 X 4 3 2 41 y 2 2 3 1 2 3 4 X 4 3 2 1 3 2 2 3 1 2 3

Calculus
Application of derivativesIn this problem consider the curve y f x x2 3x 1 a For any real number a the formula for f a b The equation of the tangent line to the curve y f x at the point P a f a is x y c There are two tangent lines to the curve y f x with x intercept 8 The x coordinates of these two points of tangency listed left to right are and

Calculus
Application of derivativesA car travels up a hill at a constant speed of 41 km h and returns down the hill at a constant speed of 60 km h Calculate the average speed for the round trip Number i 98 7 Units km h
Calculus
Application of derivativesFind the area of the surface generated when the given curve is revolved about the x axis 2 for x 2 The area of the surface is square units Type an exact answer using as needed

Calculus
Application of derivativesWrite the integral that gives the area of the surface generated when the curve is revolved about the given axis b Use a calculator or software to approximate the surface area y tan x for sxs about the x axis K a Choose the correct answer below x 4 OA 2xx 1 s x 6 x 4 OB 2x tanxV 1 secxdx x 6 x 4 OC 2x XV17 S C X X 2x tanx 1 1 sec xdx x 6 x 4 OD Stan x 6 tan xV 1 sec xdx

Calculus
Application of derivativesFind the area of the surface generated when the given curve is revolved about the given a 3 7 9 9 y 4 16 x between the points 4 4 and The surface area is square units Type an exact answer using as needed 2 2 about the y axis

Calculus
Application of derivativesProspect Realty Co pays weekly salaries of 18 030 on Monday for a six day workweek ending the preceding Saturday Journalize the necessary adjusting entry at the end of the accounting period assuming that the period ends on Friday Refer to the Chart of Accounts for exac wording of account titles Round your answer to the nearest dollar

Calculus
Application of derivativesA stone is dropped into a lake creating a circular ripple that travels outward at a speed of 40 cm s a Express the radius r of this circle as a function of the time t in seconds r t b If A is the area of this circle as a function of the radius find A o r Aor t Interpret the answer found in part b O This formula gives the radius of the rippled area in cm at any time t This formula gives the circumference of the rippled area in cm at any time t O This formula gives the extent of the rippled area in cm at any time t

Calculus
Application of derivativesThe tangent line to the curve y x 2x 5x 3 is parallel to the line 10x 5y 2 at two points on the curve Find the two points The two points are Type an ordered pair Use a comma to separate answers as needed

Calculus
Application of derivativesScotland the price of gasoline averages around 1 55 per liter sing unit analysis calculate the cost of gasoline in Scotland in dollars per gallon 1 55 1 L X 1000 mL rag and drop your selection from the following list to complete the answer 1 gal gal 128 fl oz 3 79 L 29 6 mL

Calculus
Application of derivativesWrite each of the following numbers to 3 significant figures in exponential or scientific notation Write each number with only one non zero digit before the decimal point 254 0 00711 74500 0 00221

Calculus
Application of derivativesHow many significant figures are there in each of the following numbers 57 30 0 07084 0 9923 821 65
Calculus
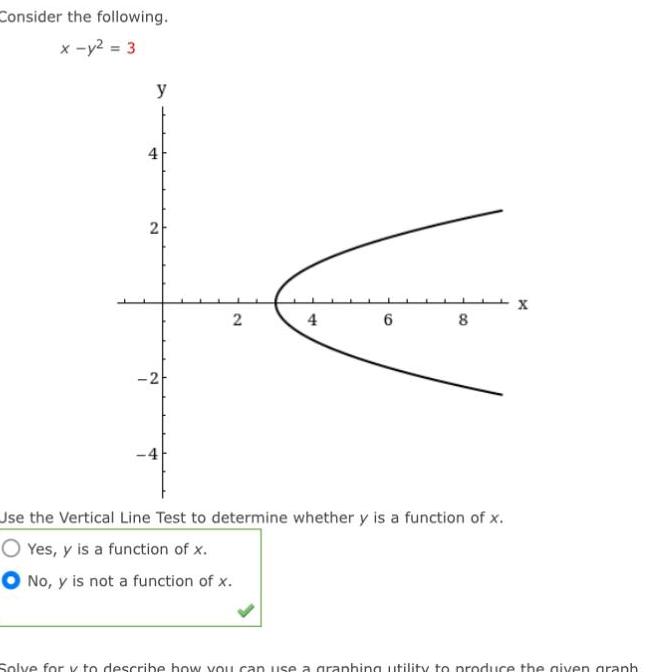
Application of derivativesConsider the following x y 3 y 4 2 2 2 4 6 8 Use the Vertical Line Test to determine whether y is a function of x Yes y is a function of x No y is not a function of x X Solve for y to describe how you can use a graphing utility to produce the given graph
Calculus
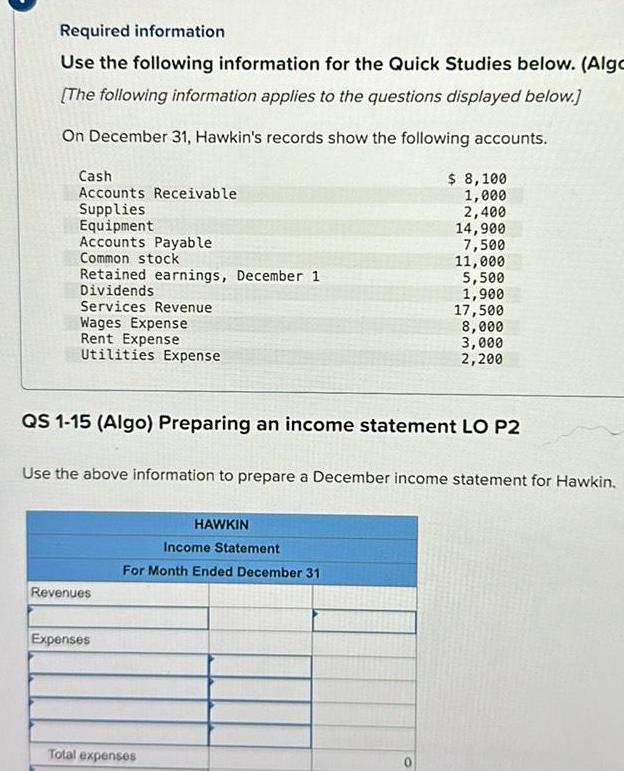
Application of derivativesRequired information Use the following information for the Quick Studies below Algo The following information applies to the questions displayed below On December 31 Hawkin s records show the following accounts Cash Accounts Receivable Supplies Equipment Accounts Payable Common stock Retained earnings December 1 Dividends Services Revenue Wages Expense Rent Expense Utilities Expense QS 1 15 Algo Preparing an income statement LO P2 Revenues Use the above information to prepare a December income statement for Hawkin Expenses 8 100 1 000 2 400 14 900 HAWKIN Income Statement For Month Ended December 31 Total expenses 7 500 11 000 5 500 1 900 17 500 8 000 3 000 2 200

Calculus
Application of derivativesUse a calculator to find each of the following Round all answers to four places past the decimal point 33 sin 27 2 36 sin 42 34 cos 82 9 37 tan 87 32 35 cos 18 38 tan 81 43

Calculus
Application of derivativesConvert each of the following to degrees and minutes 15 35 4 16 63 2 17 16 25 18 18 75

Calculus
Application of derivativesAdd and subtract as indica 1 37 45 26 24 3 51 55 37 45 5 61 33 45 16 7 90 34 12 9 180 120 17

Calculus
Application of derivativesFind exact values for each of the following 43 sec 30 45 csc 60 47 cot 45 49 sec 45 44 csc 30 46 sec 60 48 cot 30 50 csc 45
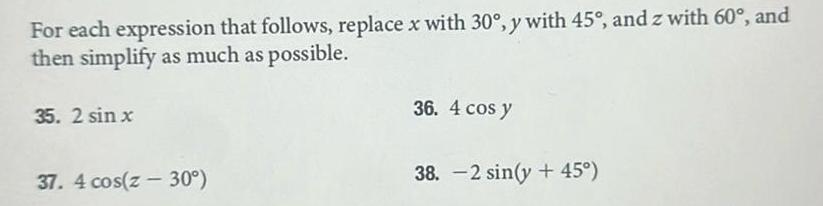
Calculus
Application of derivativesFor each expression that follows replace x with 30 y with 45 and z with 60 and then simplify as much as possible 35 2 sin x 37 4 cos z 30 36 4 cos y 38 2 sin y 45

Calculus
Application of derivativesSimplify each expression by first substituting values from the table of exact value and then simplifying the resulting expression 23 4 sin 30 25 2 cos 30 24 5 sin 30 26 sin 30

Calculus
Application of derivativesUse the Cofunction Theorem to fill in the blanks so each expression becomes a true statement 13 sin 10 cos 15 tan 8 cot 17 sec 73 csc 19 sin x cos 21 tan 90 x cot 14 cos 40 sin 16 cot 12 tan 18 csc 63 sec 20 sin y cos 22 tan 90 y cot

Calculus
Application of derivativesUse the Cofunction Theorem to fill in the blanks so each expression becomes a true statement 13 sin 10 cos 14 cos 40 sin

Calculus
Application of derivativesFind the area of the surface generated when the given curve is revolved about the given axis y 22 x for 4 x 15 about the x axis The area of the surface is square units Type an exact answer using as needed
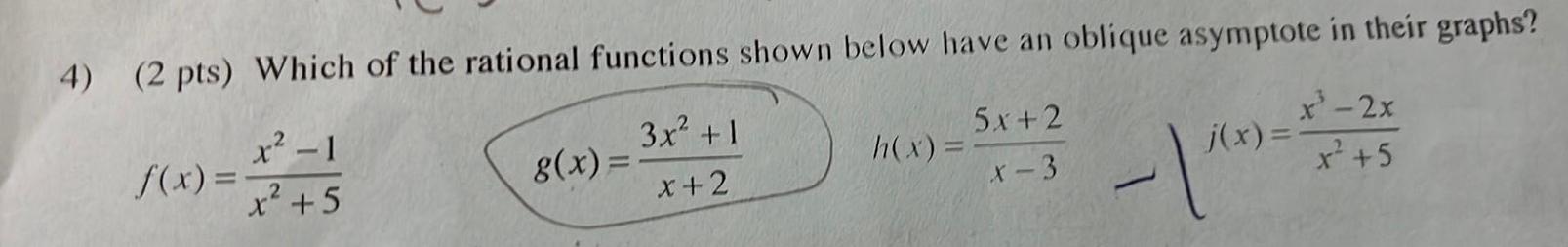
Calculus
Application of derivatives4 2 pts Which of the rational functions shown below have an oblique asymptote in their graphs x 1 2 3x 1 x 2 x 2x x 5 f x x 5 g x h x 5x 2 X 3 j x 1

Calculus
Application of derivativespts Find the quotient and remainder using polynomial long division 4x 9x 1 x 2
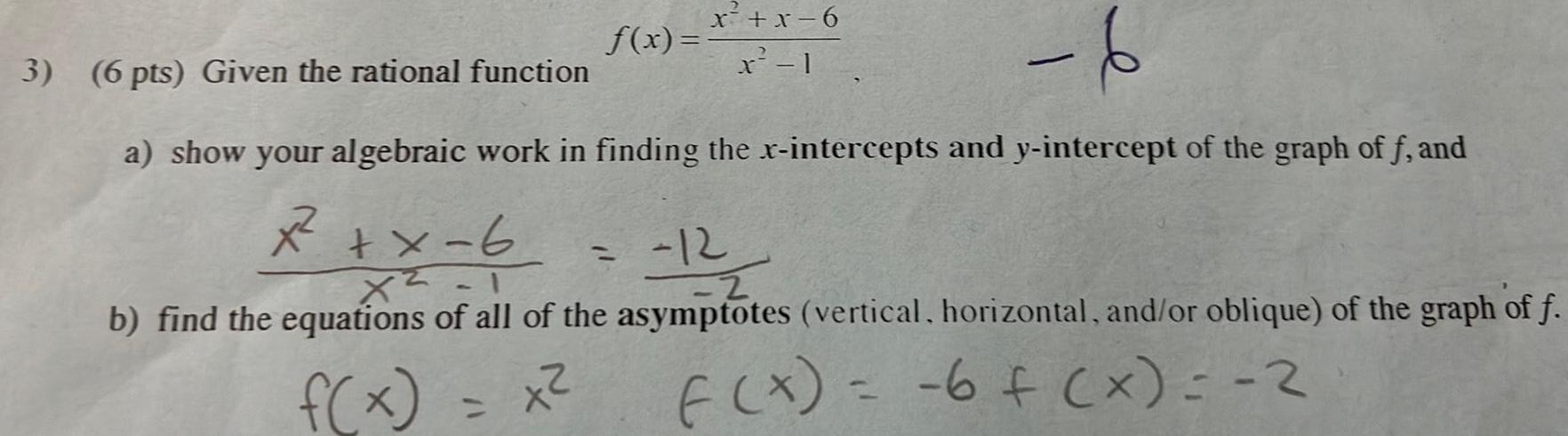
Calculus
Application of derivativesf x x x 6 x 1 3 6 pts Given the rational function 6 a show your algebraic work in finding the x intercepts and y intercept of the graph of f and x 2 x 6 12 X b find the equations of all of the asymptotes vertical horizontal and or oblique of the graph of f f x x f x 6 x 2
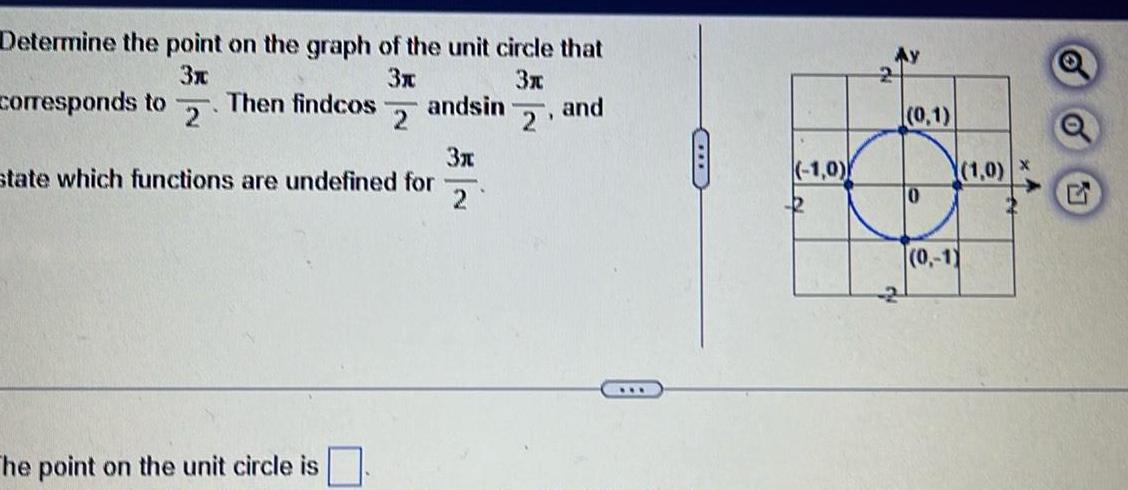
Calculus
Application of derivativesDetermine the point on the graph of the unit circle that 3x 3x 3x andsin 2 2 corresponds to Then findcoS 2 V 3x state which functions are undefined for 2 The point on the unit circle is and C 1 0 Lo 12 Ay 1 0 1 0 0 1 1 0 5

Calculus
Application of derivatives3 T Let f x cos x The Mean Value Theorem guarantees the existence of a value c 1 c 3 What is this value A 0 765 B 1 817 C 2 270 D 2 817
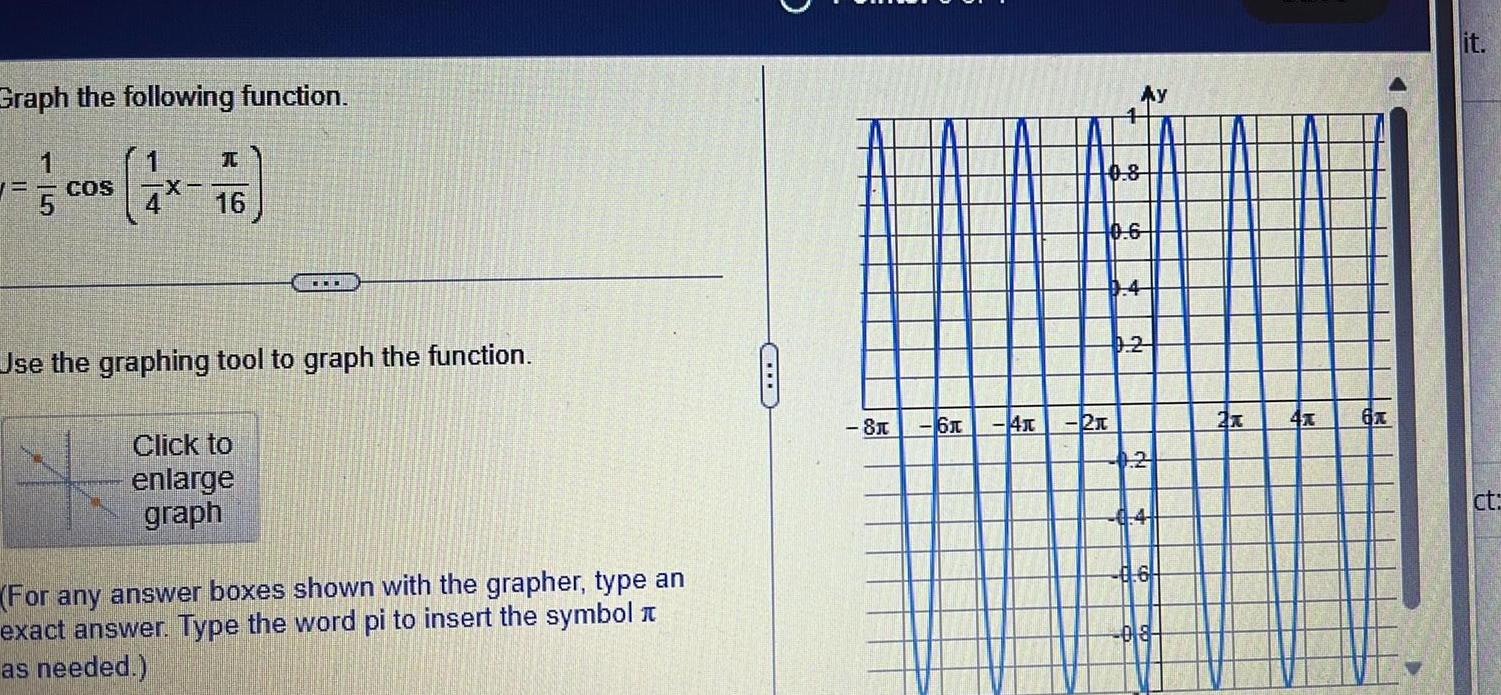
Calculus
Application of derivativesGraph the following function COS X 4 16 Use the graphing tool to graph the function Click to enlarge graph For any answer boxes shown with the grapher type an exact answer Type the word pi to insert the symbol as needed 81 6x 4x Ay 4 0 8 10 6 2x 9 4 0 2 0 2 6 08 H 2x 4x 6x 2 it ct

Calculus
Application of derivativesK Find the a amplitude b period c phase shift if any d vertical translation if any and e range of the following function Then graph the function over at least one period y cos 1 2 T a The amplitude is
Calculus
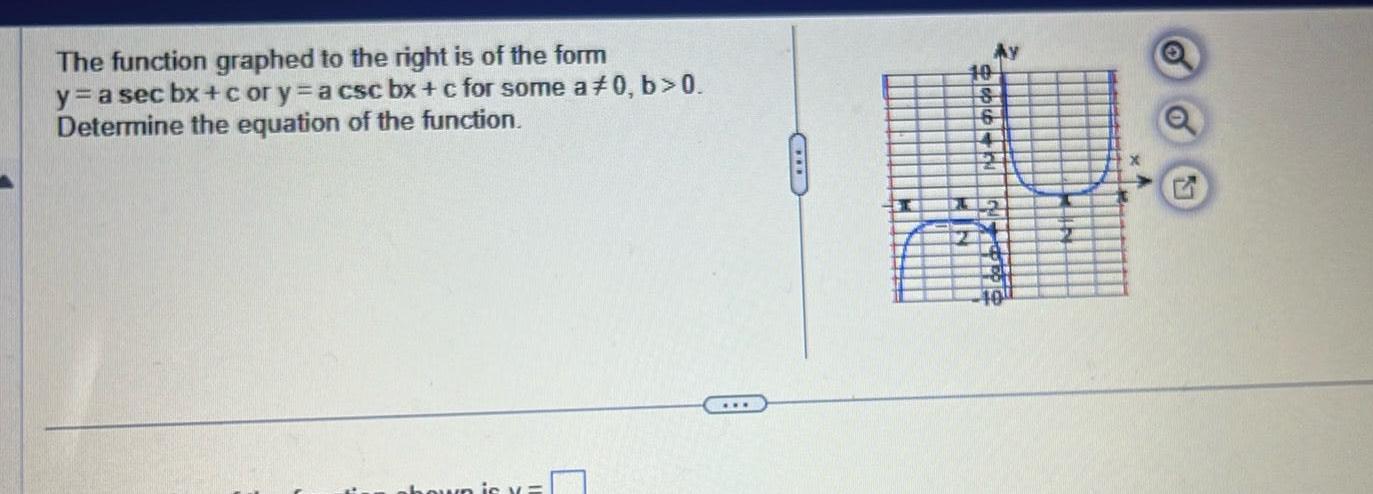
Application of derivativesThe function graphed to the right is of the form y a sec bx c or y a csc bx c for some a 0 b 0 Determine the equation of the function Ay 10 18 6 14
Calculus
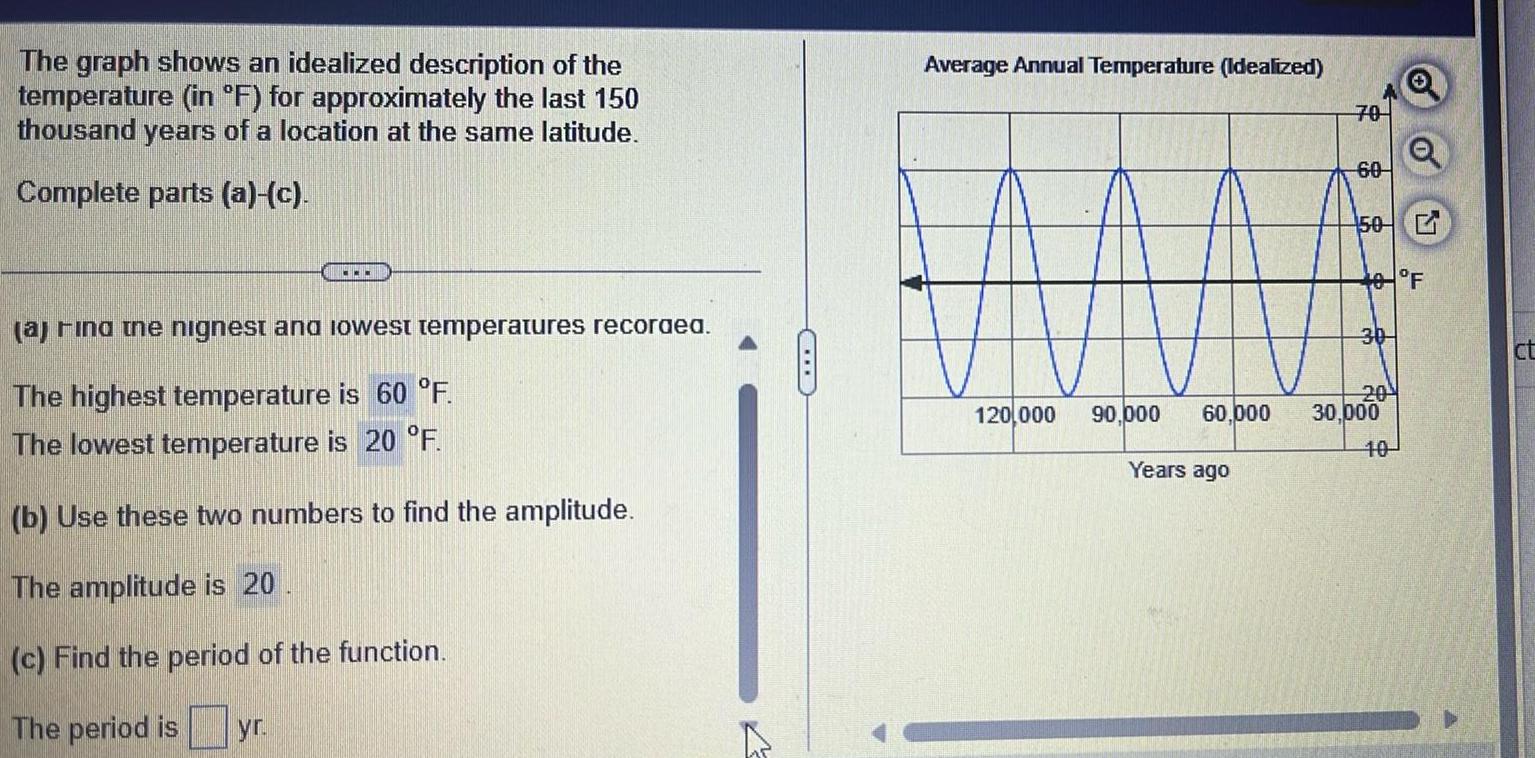
Application of derivativesThe graph shows an idealized description of the temperature in F for approximately the last 150 thousand years of a location at the same latitude Complete parts a c a ring the nignest and lowest temperatures recordea The highest temperature is 60 F The lowest temperature is 20 F b Use these two numbers to find the amplitude The amplitude is 20 c Find the period of the function The period is yr 4 C Average Annual Temperature Idealized 120 000 90 000 60 000 Years ago 70 60 50 40 F 30 20 30 000 Q 10

Calculus
Application of derivativesShow that each of the following statements is an identity by transforming the left side of each one into the right side 43 cos tan 0 sin 0 45 sin 8 sec 0 cot 0 1 47 csc 8 49 cot 8 sec 8 sec 8 csc 8 51 sin tan 0 cos 0 sec 0 tan 8 53 tan 0 cot 0 sec 0 csc 0 cos 0 sin 0 55 csc sin 0 57 1 sin 0 cos 0 44 sin cot cos 0 46 cos csc tan 0 1 sec 0 48 50 tan 8 csc 8 csc 0 cot 0 sec 0 52 cos cot sin 0 csc 0 54 tan 0 1 sec 0 56 sec cos 0 si sin 0 cos 8 58 1 cos 0 sin 0

Calculus
Application of derivatives13 In year 2015 the population of a town was an annual 12000 and it was growing at rate of 3 2 Use this information for following Questions a write an exponential function of form pct town ab P Population of the and Number of years to b use your function from part a find algebraically the year the population reach 20000

Calculus
Application of derivativesC 0 045 The function A 72e modies The decay of a sample of radio active material as a function of time In years In this modle A is the amount of radio active material remaining in grams at time t a How much radio active material Is preasent after 8 years round to tenth necrest The b Algebraically determine half life of this material show steps round to nearest tenth
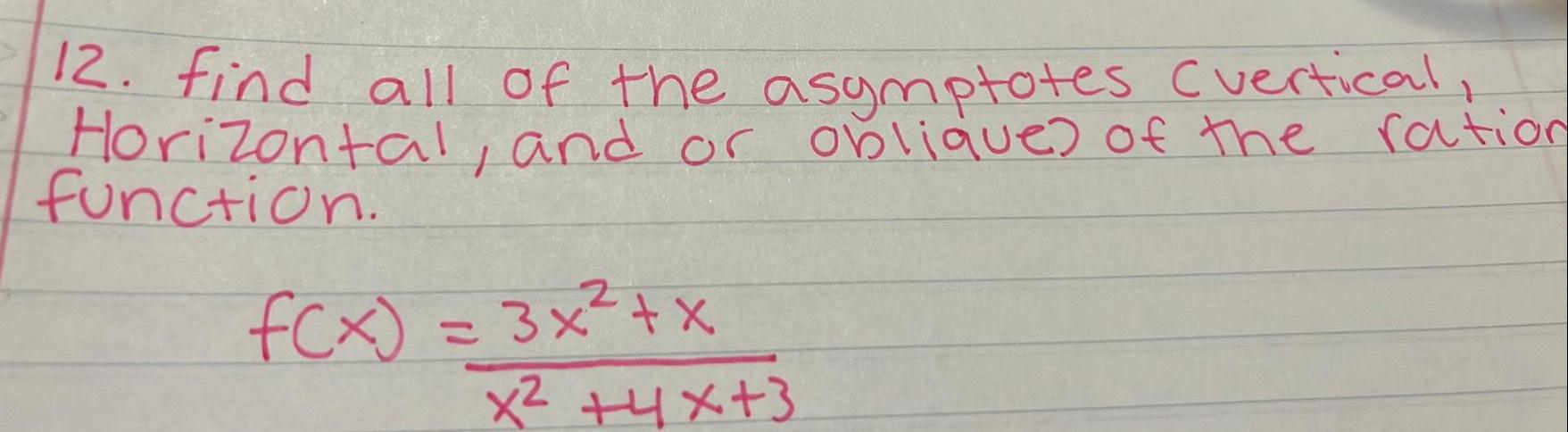
Calculus
Application of derivatives12 find all of the asymptotes vertical Horizontal and or oblique of the ration function f x 3x x x 4x 3

Calculus
Application of derivatives6 Find a curve that passes through the point 1 2 and has an arc length on the interval 2 6 given by 2 What is one such curve y 0 1 400x 6

Calculus
Application of derivatives60 Find tan if is the angle formed by the line y mx and the positive x axis B 1 m
Calculus
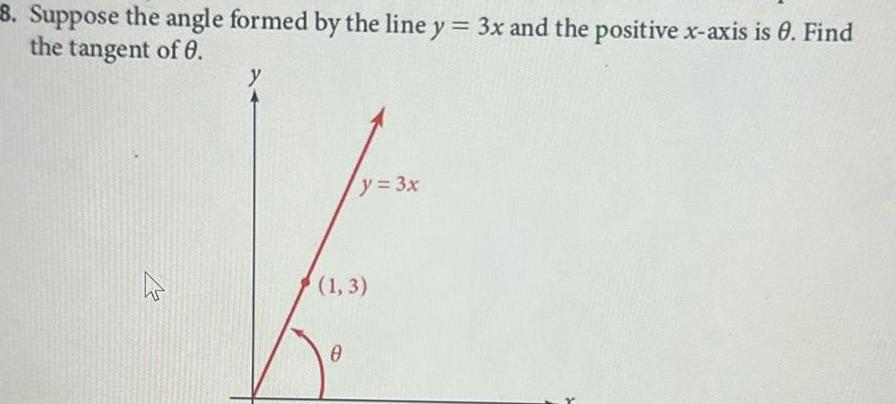
Application of derivatives8 Suppose the angle formed by the line y 3x and the positive x axis is 8 Find the tangent of 0 y y 3x 1 3 0

Calculus
Application of derivativesThe function defined by years and x 0 corresponds to 1960 325 b When do the seasonal maximum and minimum carbon dioxide levels occur 3 7 11 2 2 2 OA Maximums x 0 OB Maximums X 15 2 2 3 7 11 2 22 159 OC Maximums X 51515 2 2 2 OD Maximums X Minimums x 222 Minimums x 0 Minimums x 5 www Minimums x 2 2 2 2 2 159 325