Application of derivatives Questions and Answers
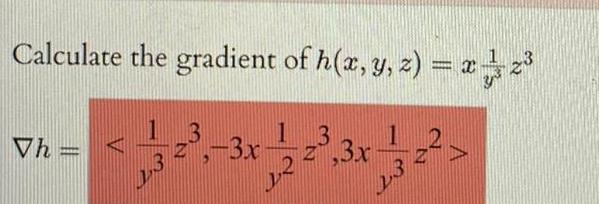
Calculus
Application of derivativesCalculate the gradient of h x y z x 2 23 Vh A B 5 3 Z 3x x 122 1 2 3x2 23

Calculus
Application of derivativesEvaluate the following Find the arc length of the graph of y on the interval 1 2 To enter your answer click on the three vertical dots on the right of the task bar then click on the symbol This will bring up the equation editor Use the symbols to write the mathematical sentence Work will be graded separately Your Answer 11 S T
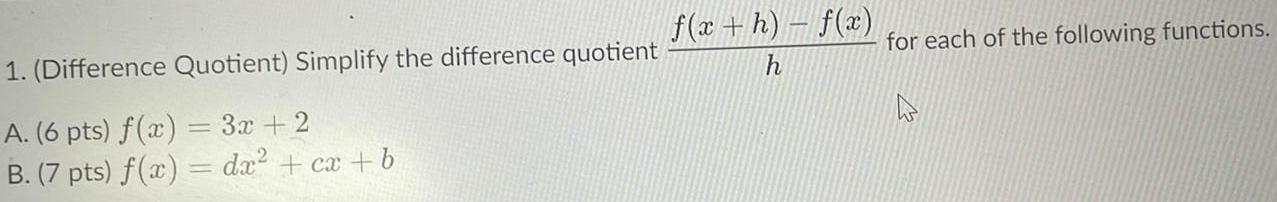
Calculus
Application of derivatives1 Difference Quotient Simplify the difference quotient A 6 pts f x 3x 2 B 7 pts f x dx cx b f x h f x h for each of the following functions

Calculus
Application of derivatives7 Instantaneous velocity Consider the position function s t 1612 128t Exercise 13 Complete the following table with the appropriate average velocities Then make a conjecture about the value of the instantaneous velocity at t 1 1 2 1 1 5 1 1 1 1 1 01 1 1 001 Time interval Average velocity
Calculus
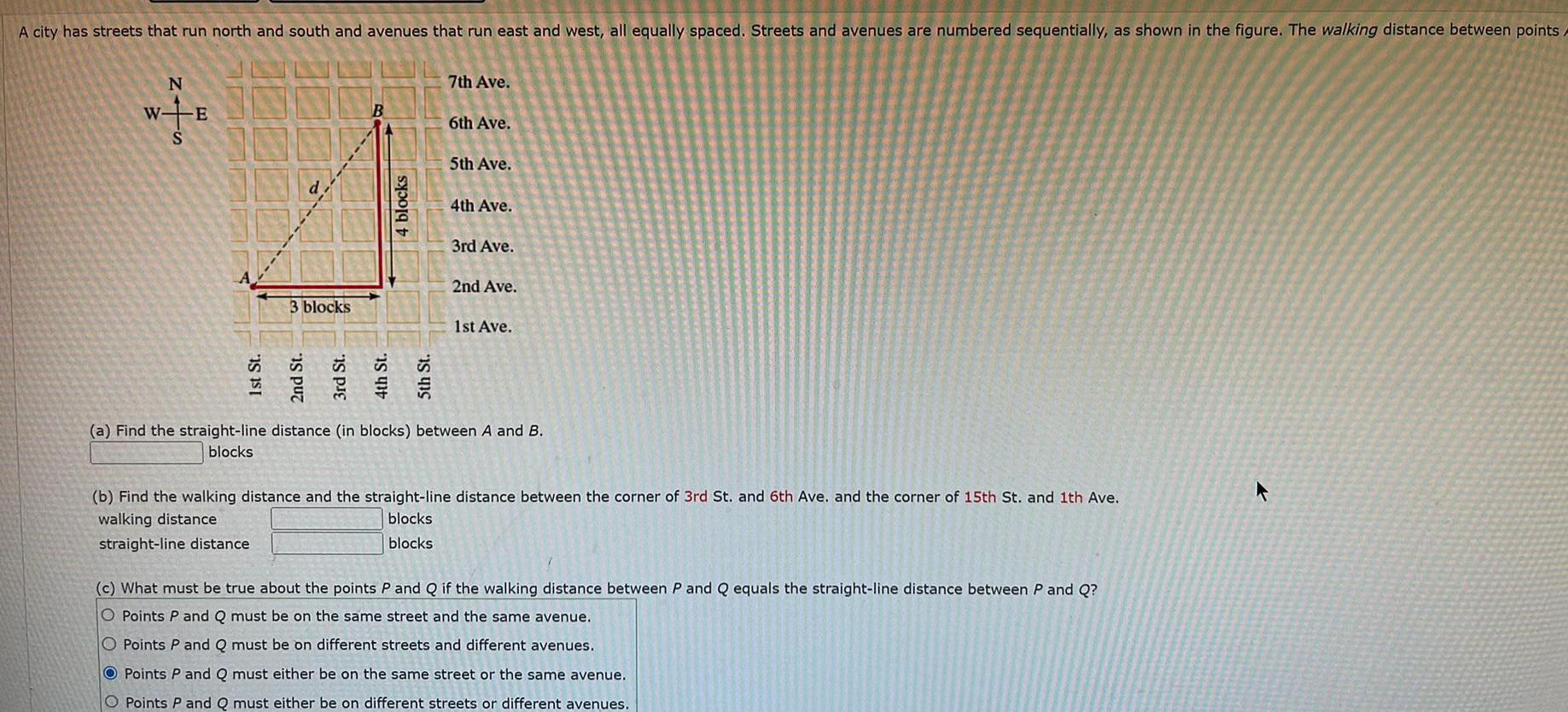
Application of derivativesA city has streets that run north and south and avenues that run east and west all equally spaced Streets and avenues are numbered sequentially as shown in the figure The walking distance between points N W E 1st St 3 blocks 2nd St 4 blocks 5th St 7th Ave 6th Ave 5th Ave 4th Ave 3rd Ave 2nd Ave 1st Ave a Find the straight line distance in blocks between A and B blocks b Find the walking distance and the straight line distance between the corner of 3rd St and 6th Ave and the corner of 15th St and 1th Ave walking distance blocks straight line distance blocks c What must be true about the points P and Q if the walking distance between P and Q equals the straight line distance between P and Q O Points P and Q must be on the same street and the same avenue O Points P and Q must be on different streets and different avenues OPoints P and Q must either be on the same street or the same avenue O Points P and Q must either be on different streets or different avenues

Calculus
Application of derivativesLet f x y xey and P 5 25 a Calculate Vfp l b Find the rate of change of f in the direction Vfp c Find the rate of change of f in the direction of a vector making an angle of 45 with Vfp Answers b c CAR P AMD


Calculus
Application of derivativesThe function f has continuous second derivatives and a critical point at 10 1 Suppose faz 10 1 2 f 10 1 1 f 10 1 4 Then the point 10 1 O A is a saddle point OB cannot be determined OC is a local maximum OD is a local minimum OE None of the above

Calculus
Application of derivativesDetermine the global extreme values of the function on the given set without using calculus f x y 2e 2 8y z 8y 1 fmin
Calculus
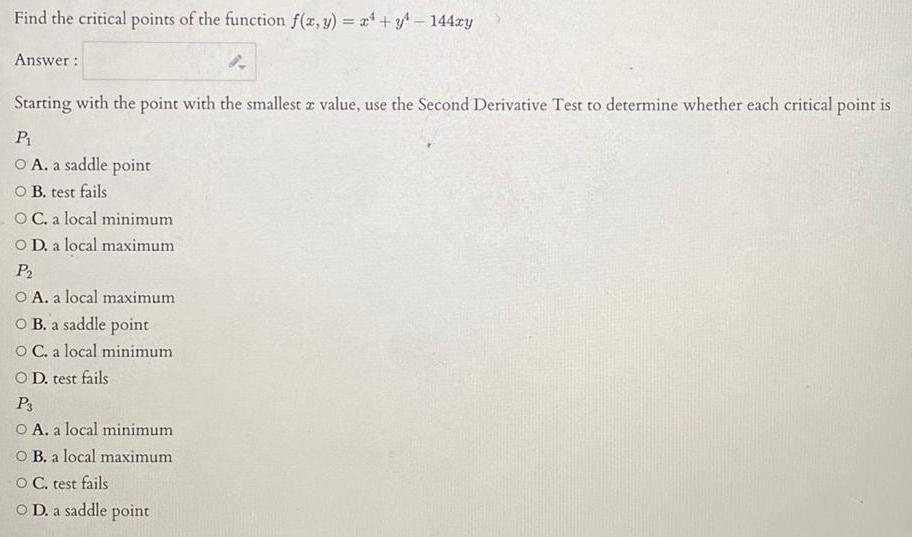
Application of derivativesFind the critical points of the function f x y x y 144xy Answer 8 Starting with the point with the smallest z value use the Second Derivative Test to determine whether each critical point is P O A a saddle point O B test fails OC a local minimum O D a local maximum P O A a local maximum OB a saddle point O C a local minimum OD test fails P3 O A a local minimum O B a local maximum O C test fails O D a saddle point

Calculus
Application of derivativesLet f x y x y and c t t 2t a Calculate Vf c t B b Use the Chain Rule for Paths to evaluate f c t at t 1 f c 1

Calculus
Application of derivativesFind an equation of the circle that satisfies the given conditions Center at the origin passes through 5 8

Calculus
Application of derivativesA spherical balloon with radius r inches has volume V r r Find a function that represents the amount of air required to inflate the balloon from a radius of r inches to a radius of r 1 inches
Calculus
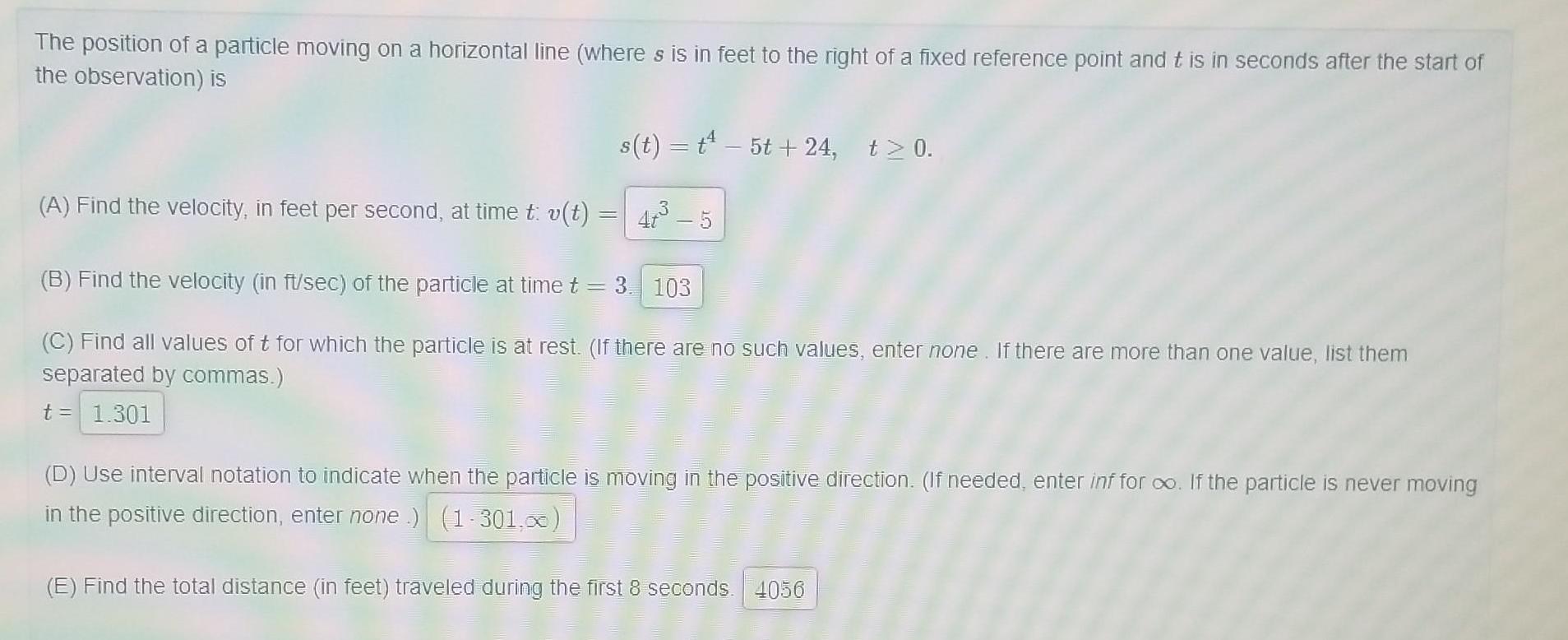
Application of derivativesThe position of a particle moving on a horizontal line where s is in feet to the right of a fixed reference point and t is in seconds after the start of the observation is s t t 5t 24 t 0 3 A Find the velocity in feet per second at time t v t 4 5 B Find the velocity in ft sec of the particle at time t 3 103 C Find all values of t for which the particle is at rest If there are no such values enter none If there are more than one value list them separated by commas t 1 301 D Use interval notation to indicate when the particle is moving in the positive direction If needed enter inf for oo If the particle is never moving in the positive direction enter none 1 301 00 E Find the total distance in feet traveled during the first 8 seconds 4056
Calculus
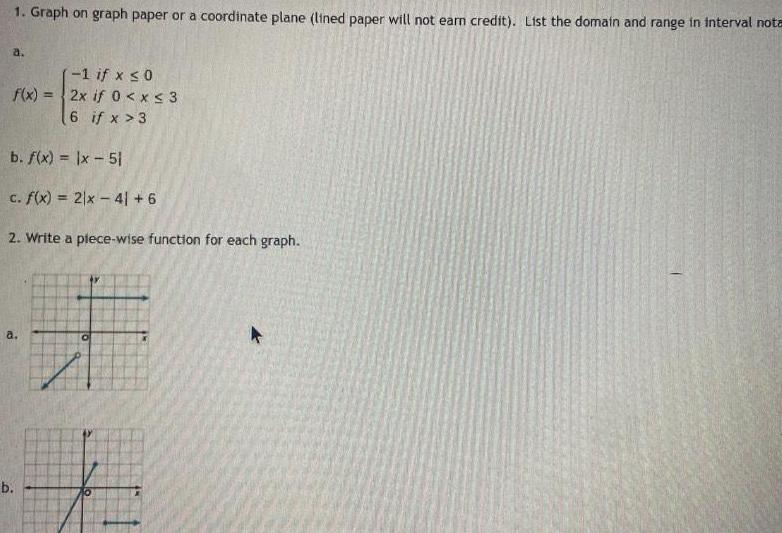
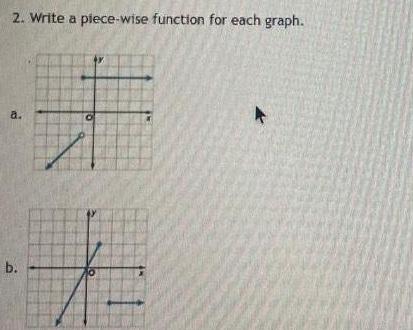
Application of derivatives1 Graph on graph paper or coordinate plane lined paper will not earn credit List the domain and range in interval nota a f x b f x x 51 c f x 2x 41 6 2 Write a plece wise function for each graph a b 1 if x 0 2x if 0 x 3 6 if x 3 0
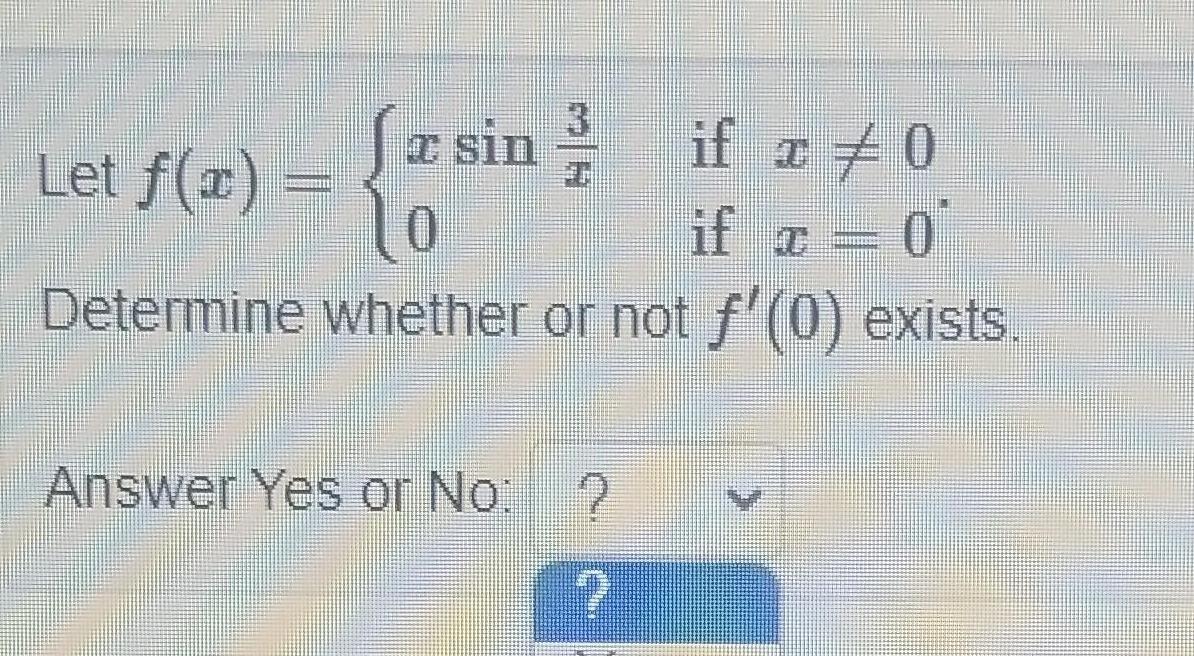
Calculus
Application of derivatives3 Jasin if x 0 z sin if x 0 Determine whether or not f 0 exists Let f 1 Answer Yes or No

Calculus
Application of derivativesIf a ball is thrown vertically upward from the roof of 32 foot building with a velocity of 48 ft sec its height after t seconds is s t 32 48t 16t a What is the maximum height the ball reaches Answer 80ft b What is the velocity of the ball when it hits the ground height 0 Answer 48

Calculus
Application of derivativesLet h x 7 2x Use this to find the equation of the tangent line to the curve y 7 2 at the point 1 5 and write your answer in the form y mx b where m is the slope and b is the y intercept h 1

Calculus
Application of derivativesFor the following exercises find the domain of each function expressing answers using Interval notation 3 4 5 2 3x 2 x 3 f x 4x 12 x 4

Calculus
Application of derivativesConsider the following matrix A and it s inverse A 1 2 1 1 2 1 2 By hand calculate the condition number of A using the infinity norm 1 5 2 3 2 1 2
Calculus
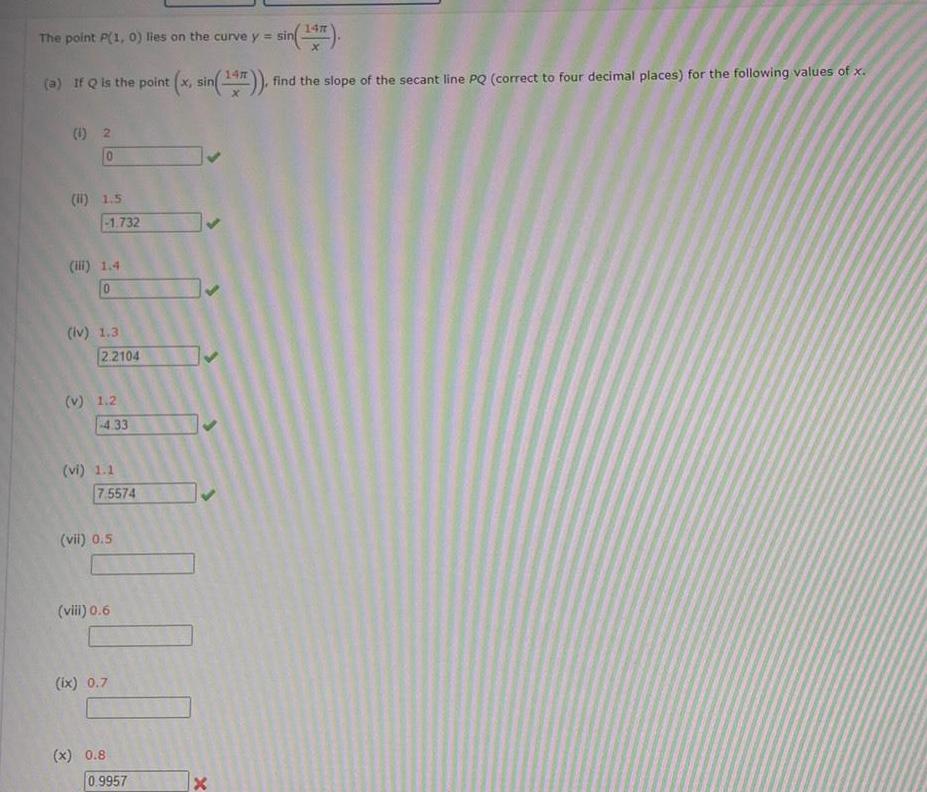
Application of derivativeslies on the curve y sin 147 a If Q is the point x sin 147 find the slope of the secant line PQ correct to four decimal places for the following values of x The point P 1 0 1 2 0 1 1 5 1 732 1 4 0 iv 1 3 2 2104 v 1 2 4 33 vi 1 1 7 5574 vii 0 5 viii 0 6 ix 0 7 x 0 8 0 9957 x
Calculus
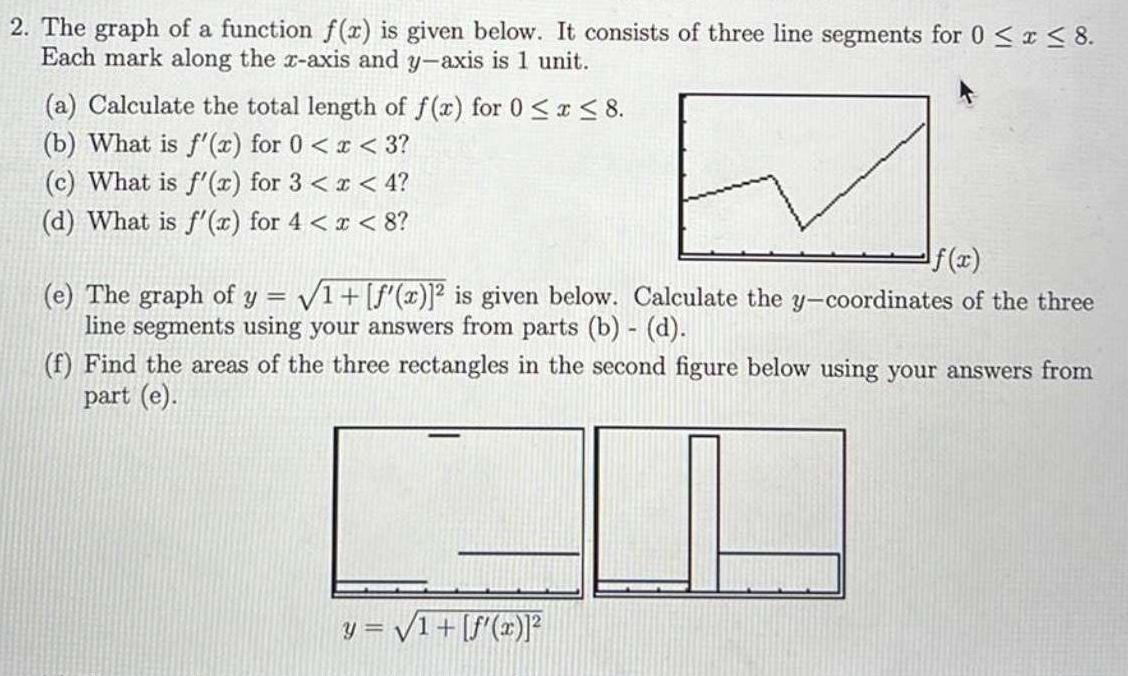
Application of derivatives2 The graph of a function f x is given below It consists of three line segments for 0 x 8 Each mark along the x axis and y axis is 1 unit a Calculate the total length of f x for 0 x 8 b What is f x for 0 x 3 c What is f x for 3 x 4 d What is f x for 4 x 8 f x e The graph of y 1 f x 2 is given below Calculate the y coordinates of the three line segments using your answers from parts b d f Find the areas of the three rectangles in the second figure below using your answers from part e y 1 f x

Calculus
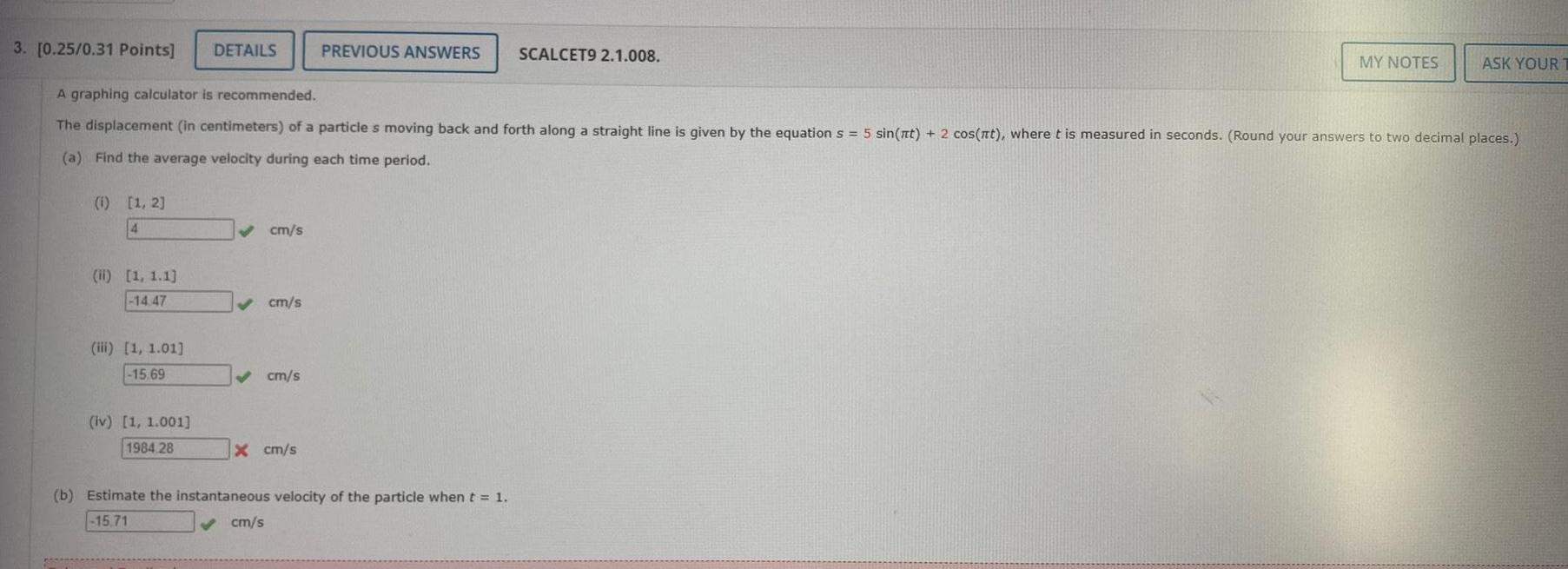
Application of derivatives3 0 25 0 31 Points DETAILS 1 1 2 4 A graphing calculator is recommended The displacement in centimeters of a particle s moving back and forth along a straight line is given by the equation s 5 sin nt 2 cos nt where t is measured in seconds Round your answers to two decimal places a Find the average velocity during each time period ii 1 1 1 14 47 iii 1 1 01 15 69 iv 1 1 001 1984 28 cm s cm s cm s x cm s PREVIOUS ANSWERS SCALCET9 2 1 008 cm s b Estimate the instantaneous velocity of the particle when t 1 15 71 MY NOTES ASK YOUR
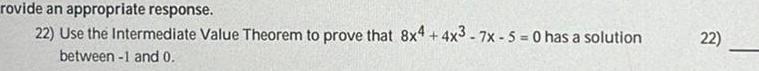
Calculus
Application of derivativesrovide an appropriate response 22 Use the Intermediate Value Theorem to prove that 8x4 4x3 7x 5 0 has a solution between 1 and 0 22

Calculus
Application of derivativesCalculate the derivative of the function by using the formula f x Lim h 0 26 g x 3x2 4x A g x 6x 27 f x 8 X 8 A f x x2 B g x 6x 4 B f x 8 f x h f x h C g x 2x 4 C f x 8x2 D g x 3x 4 D f x 8 x2

Calculus
Application of derivativesFind a function whose graph is a parabola with vertex 1 5 and that passes through the point 5 11


Calculus
Application of derivativesUse the laws of exponents to simplify 3 4 3 3 3 8 3 3 8 3 Simplify your answer Type exponential notation with posit

Calculus
Application of derivativesRewrite with positive exponents 7x 1 8 1 7x Type exponential notation with positive exponents Use integers any numbers in the expression


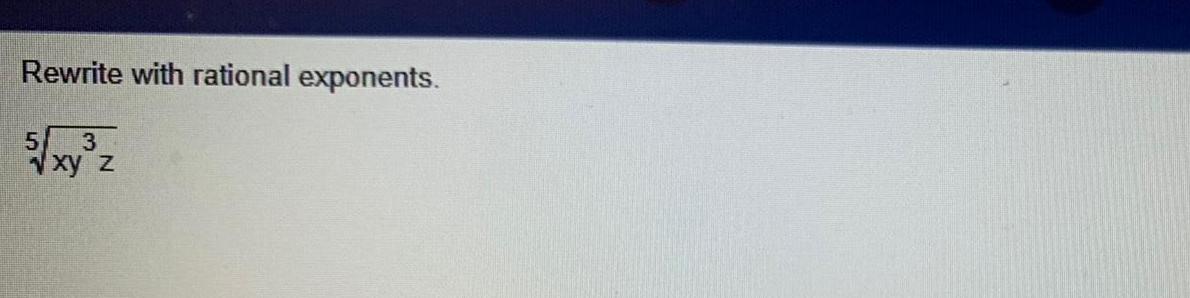
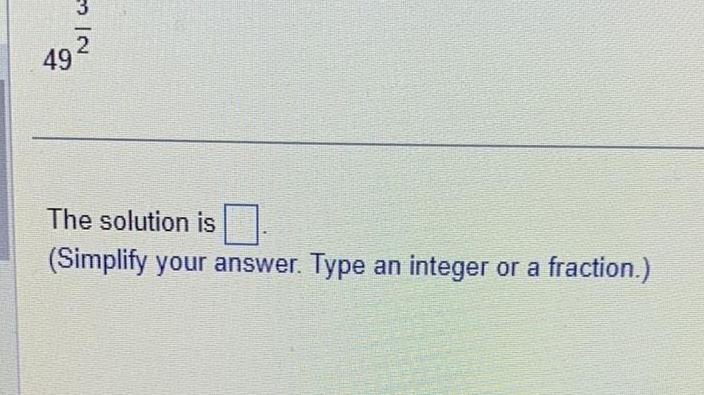
Calculus
Application of derivatives49 The solution is Simplify your answer Type an integer or a fraction
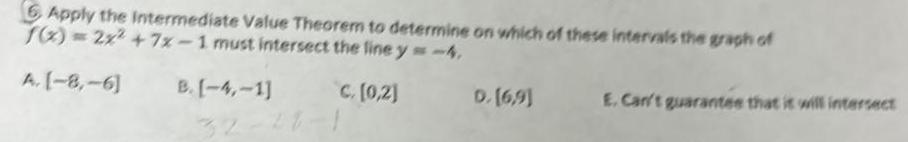
Calculus
Application of derivatives6 Apply the Intermediate Value Theorem to determine on which of these intervals the graph of f x 2x 7x 1 must intersect the line y 4 A 8 6 B 4 1 C 0 2 D 6 9 E Can t guarantee that it will intersect
Calculus
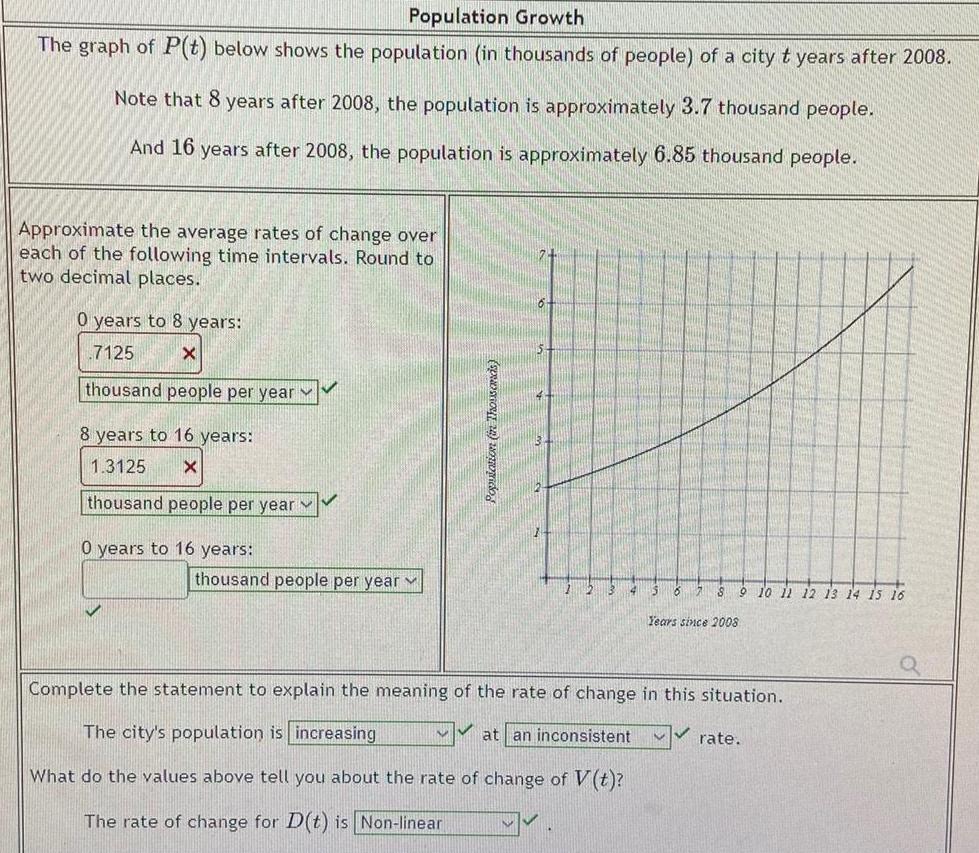
Application of derivativesPopulation Growth The graph of P t below shows the population in thousands of people of a city t years after 2008 Note that 8 years after 2008 the population is approximately 3 7 thousand people And 16 years after 2008 the population is approximately 6 85 thousand people Approximate the average rates of change over each of the following time intervals Round to two decimal places 0 years to 8 years 7125 X thousand people per year 8 years to 16 years 1 3125 X thousand people per year 0 years to 16 years thousand people per year set 2 wido 2 13 12 7 8 9 10 11 12 13 14 15 16 Years since 2008 Complete the statement to explain the meaning the rate of change in this situation The city s population is increasing at an inconsistent What do the values above tell you about the rate of change of V t The rate of change for D t is Non linear rate
Calculus
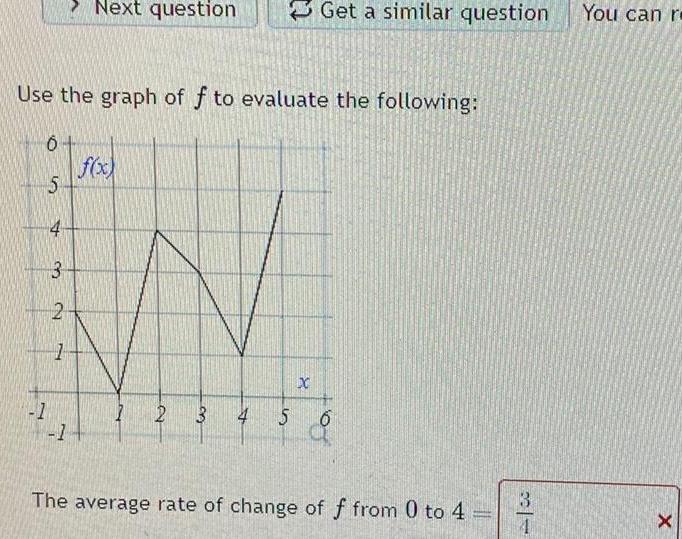
Application of derivativesUse the graph of f to evaluate the following 6 5 1 4 3 Next question 2 1 14 Get a similar question 8 1 2 3 4 5 6 The average rate of change of f from 0 to 4 Zeman 3 4 You can re X
Calculus
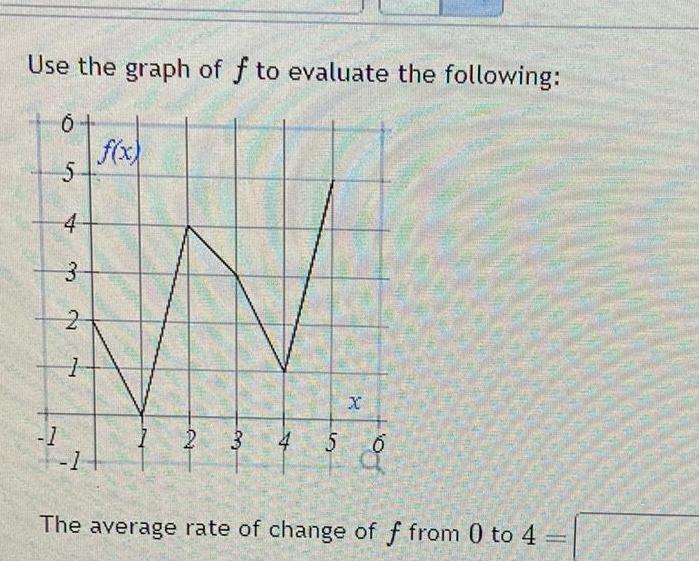
Application of derivativesUse the graph of f to evaluate the following 1 6 5 4 3 2 1 1 f x 2 3 4 5 X of The average rate of change of f from 0 to 4
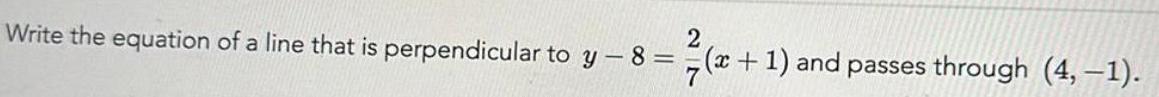
Calculus
Application of derivatives2 Write the equation of a line that is perpendicular to y 8 x 1 and passes through 4 1
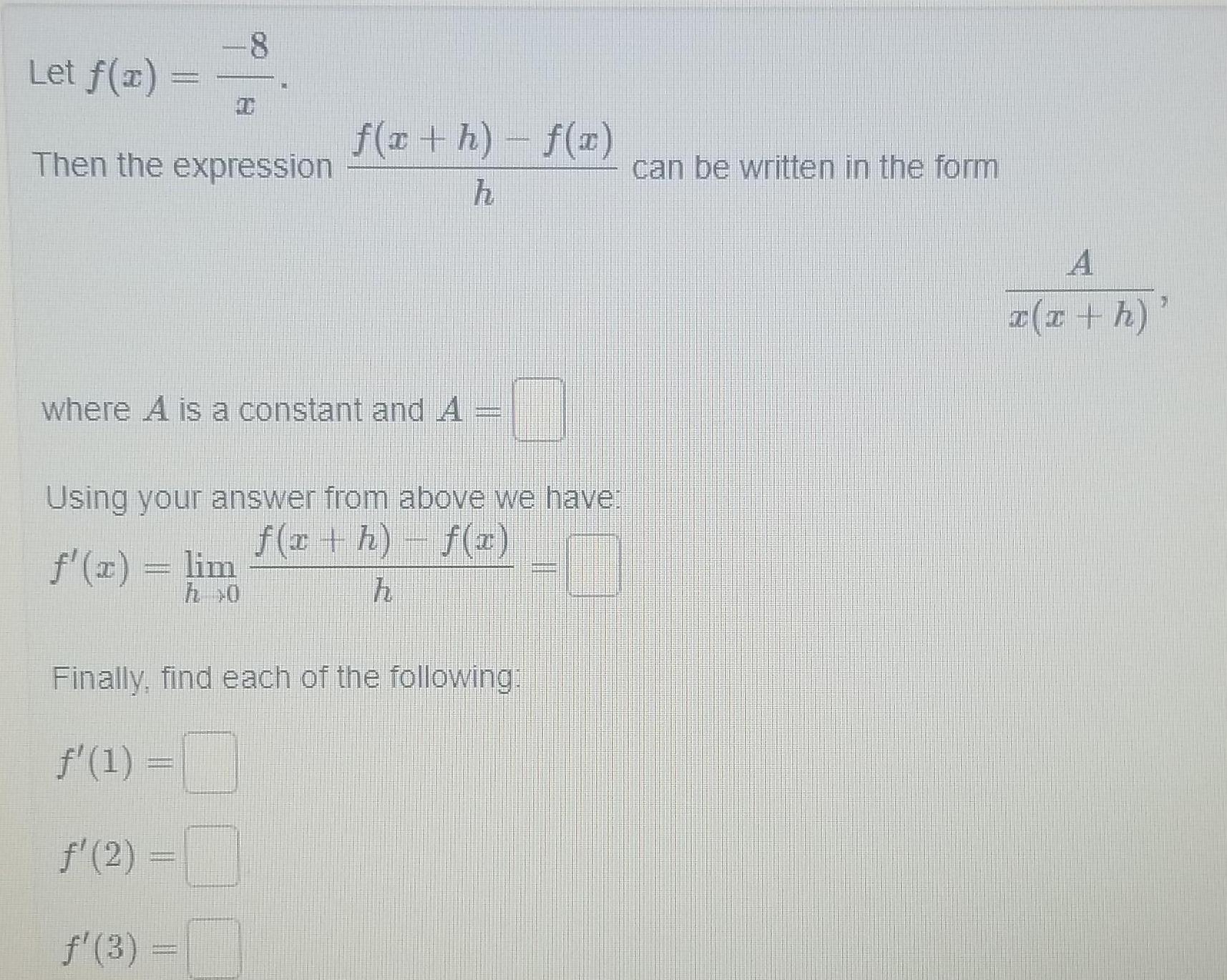
Calculus
Application of derivativesLet f x 8 Then the expression f x h f x h where A is a constant and A I Using your answer from above we have f x h f x f x lim h Finally find each of the following 1 m 2 3 can be written in the form A x x h
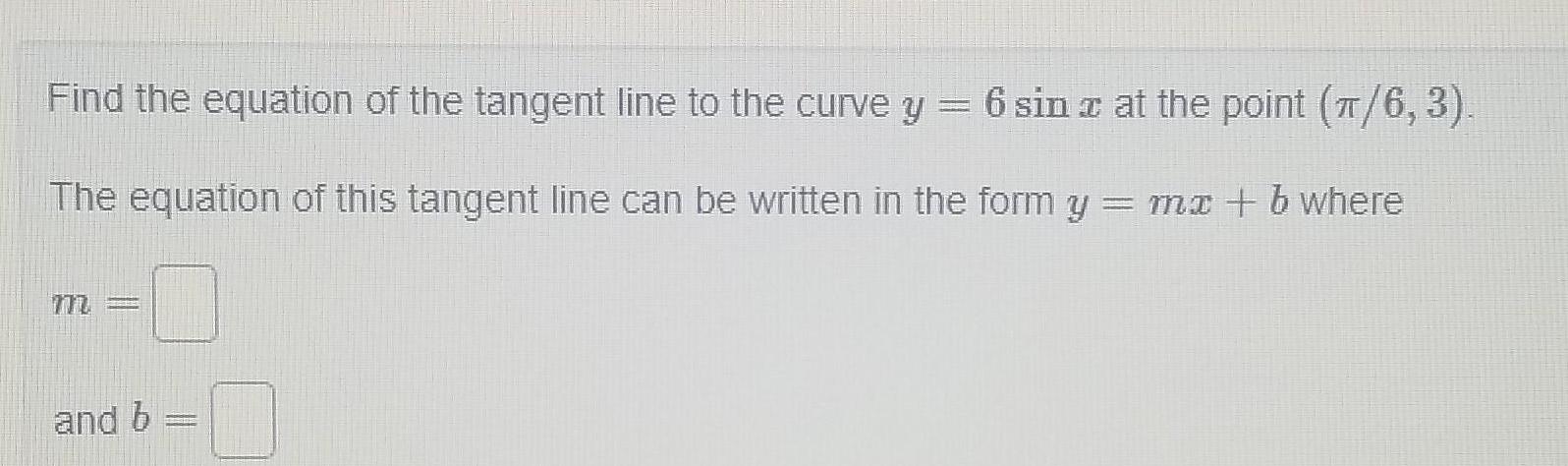
Calculus
Application of derivativesFind the equation of the tangent line to the curve y 6 sin x at the point 6 3 z The equation of this tangent line can be written in the form y mx b where and b
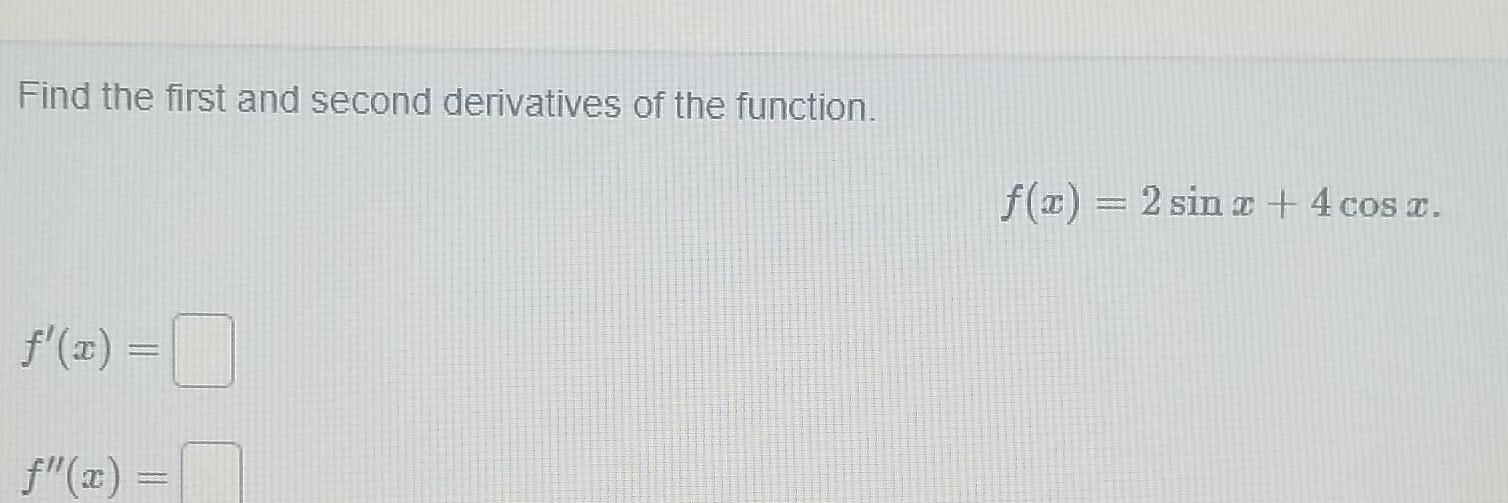
Calculus
Application of derivativesFind the first and second derivatives of the function f x x FORRE f z 2sin2 4cost
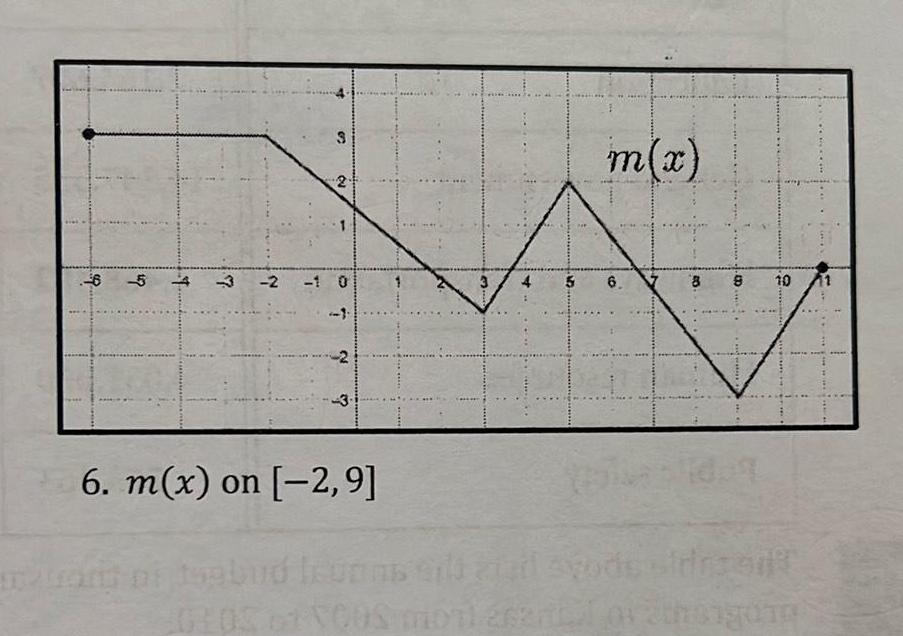
Calculus
Application of derivatives65 3 2 1 0 N 3 6 m x on 2 9 3 m x 4 5 6 ns sild zizil sode GLOS VOOS moral 8 9 10 OTH
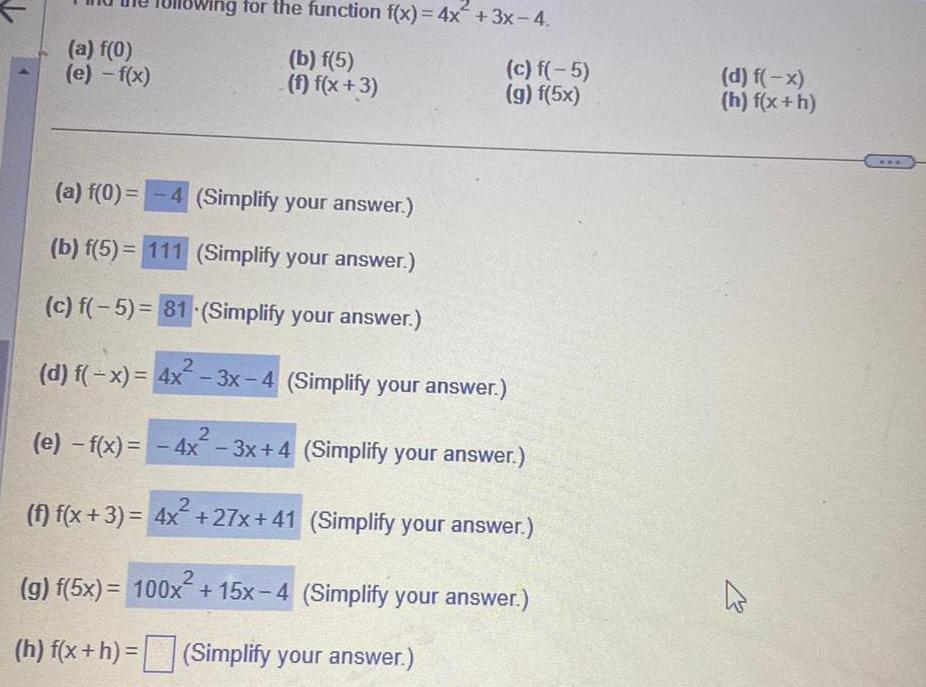
Calculus
Application of derivativesa f 0 e f x Wing for the function f x 4x 3x 4 b f 5 f f x 3 a f 0 4 Simplify your answer b f 5 111 Simplify your answer c f 5 81 Simplify your answer c f 5 g f 5x 2 d f x 4x 3x 4 Simplify your answer e f x 4x 3x 4 Simplify your answer f f x 3 4x 27x 41 Simplify your answer 2 g f 5x 100x 15x 4 Simplify your answer h f x h Simplify your answer d f x h f x h K
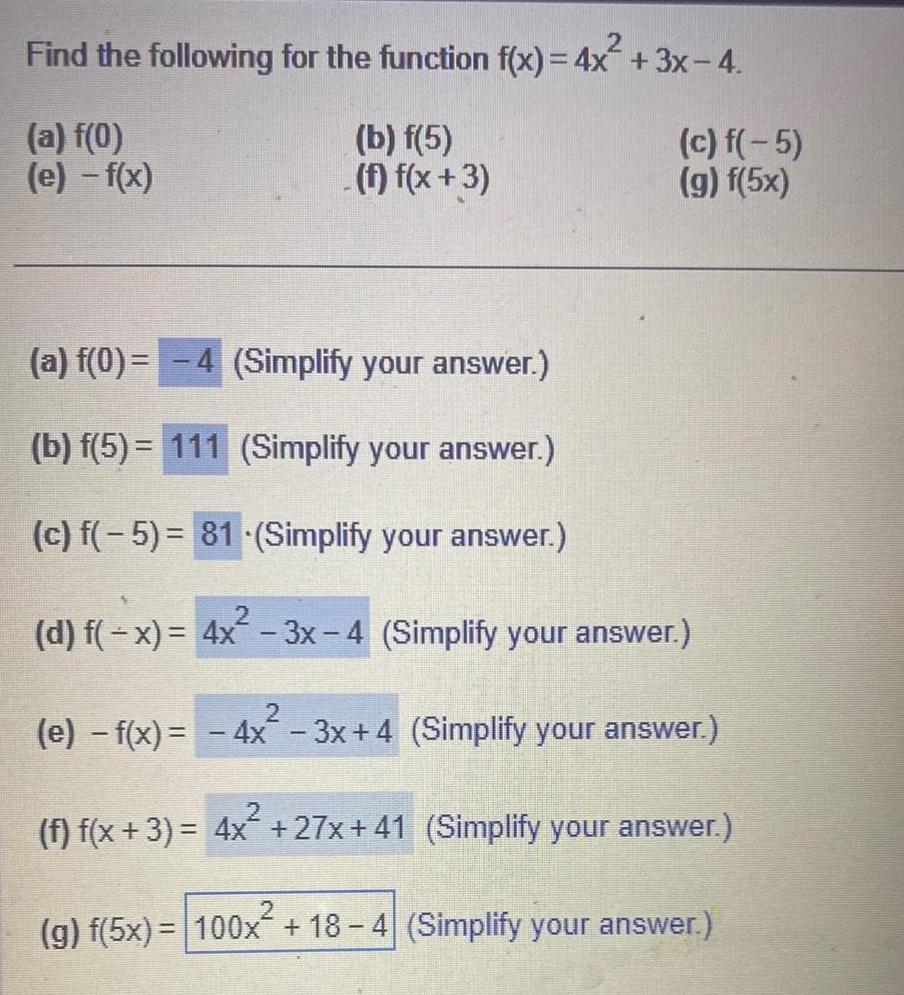
Calculus
Application of derivativesFind the following for the function f x 4x 3x 4 b f 5 a f 0 e f x c f 5 g f 5x f f x 3 a f 0 4 Simplify your answer b f 5 111 Simplify your answer c f 5 81 Simplify your answer 2 d f x 4x 3x 4 Simplify your answer 2 e f x 4x 3x 4 Simplify your answer f f x 3 4x 27x 41 Simplify your answer 2 g f 5x 100x 18 4 Simplify your answer

Calculus
Application of derivativesa f 0 e f x b f 3 f f x 3 c f 3 g f 7x a f 0 14 Simplify your answer Type an integer or a fraction b f 3 17 Simplify your answer Type an integer or a fraction c f 3 Simplify your answer Type an integer or a fraction d f x h f x h

Calculus
Application of derivativesSylvanite is a mineral that contains 28 0 gold by mass How much sylvanite would you need to dig Express your answer with the appropriate units View Available Hint s Value Submit Part C 1220 Units If an athlete weighs 141 lb and has 15 0 body fat by weight how many pounds of fat does the athlete s body contain Express your answer with the appropriate units View Available Hint s
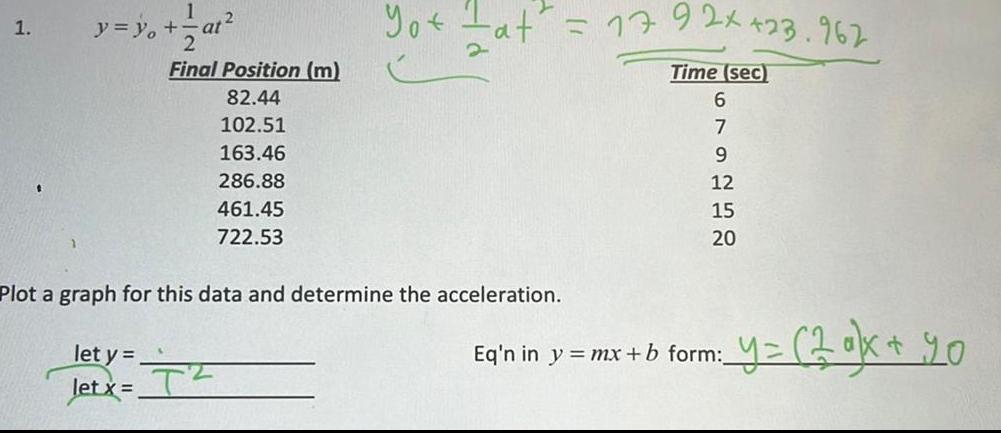
Calculus
Application of derivatives1 1 y y at Final Position m 82 44 102 51 163 46 286 88 461 45 722 53 let y letx T Yotat 17 92x 23 962 Plot a graph for this data and determine the acceleration Time sec 6 7 9 12 15 20 Y 2 o x yo Eq n in y mx b form