Application of derivatives Questions and Answers

Calculus
Application of derivativesa Find the point on the curve y x where the tangent line is parallel to the line y 10 X X b On the same axes plot the curve y x the line y and the tangent line to y x that is parallel to y 10 10 3 X a The point on the curve y x where the tangent line is parallel to the line y 10 is Type an ordered pair
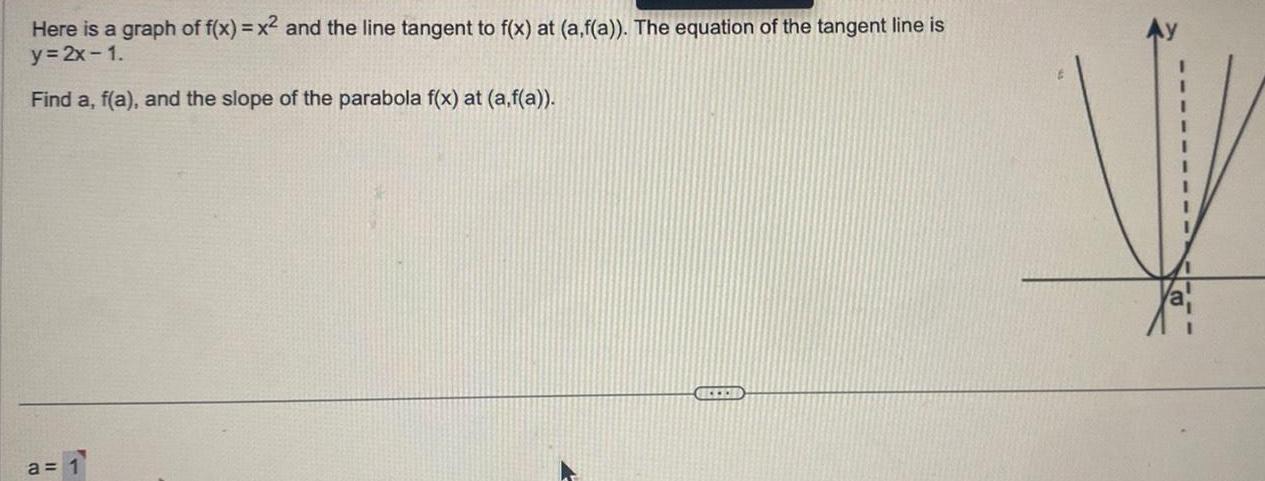
Calculus
Application of derivativesHere is a graph of f x x and the line tangent to f x at a f a The equation of the tangent line is y 2x 1 Find a f a and the slope of the parabola f x at a f a a 1 GESED

Calculus
Application of derivativesrt the following degree measure to radian measure 33 radians Type an integer or a decimal nearest hundredth
Calculus
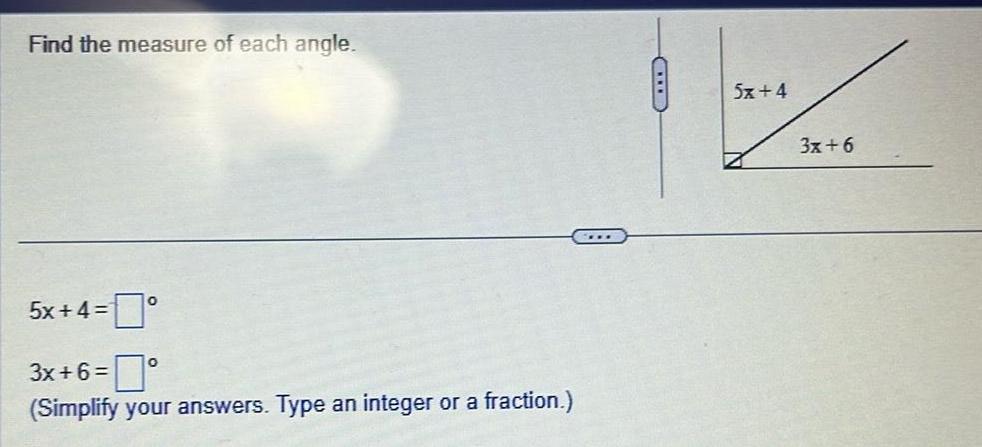
Application of derivativesFind the measure of each angle 5x 4 3x 6 Simplify your answers Type an integer or a fraction 5x 4 3x 6

Calculus
Application of derivativesThe rotation of the smaller wheel in the figure causes the larger wheel to rotate Through how many degrees will the larger wheel rotate if the smaller one rotates through 270 3 The larger wheel rotates through approximately Do not round until the final answer Then round to the nearest integer as needed 7 2 cm
Calculus
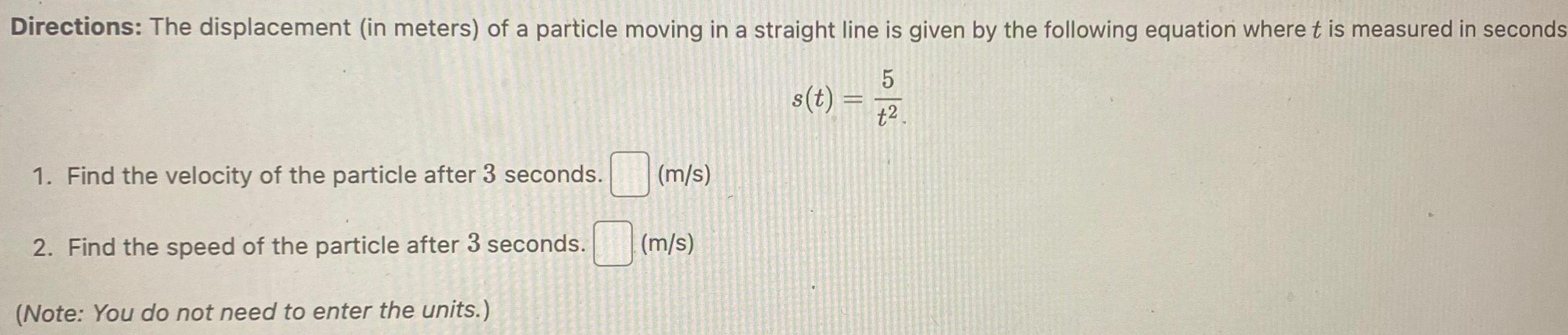
Application of derivativesDirections The displacement in meters of a particle moving in a straight line is given by the following equation where t is measured in seconds 1 Find the velocity of the particle after 3 seconds 2 Find the speed of the particle after 3 seconds Note You do not need to enter the units m s m s s t 52 t2

Calculus
Application of derivativesA population of cattle is increasing at a rate of 600 80 t per year where t is measured in years By how much does the population increase between the 6 th and the 9 th years Total Increase 240


Calculus
Application of derivativesHere is a graph of f x x2 and the line tangent to f x at a f a The equation of the tangent line is y 2x 1 Find a f a and the slope of the parabola f x at a f a X

Calculus
Application of derivativesFind the point s on the graph to the right where the slope is equal to 6 11 The point s on the given graph at which the slope is equal to F is are Type an ordered pair Type an exact answer for each coordinate using radicals as needed Use s y x3 y x y X Slope is 3x2
Calculus
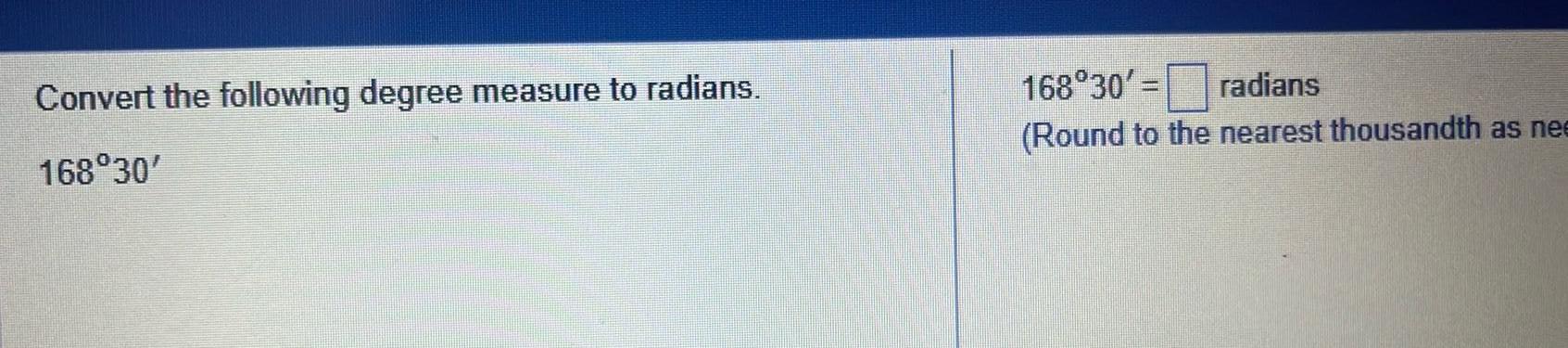
Application of derivativesConvert the following degree measure to radians 168 30 168 30 radians Round to the nearest thousandth as nee

Calculus
Application of derivativesConvert the following degree measure to radian measure 65 15 65 15 radians Type an integer or a decimal Round to the nearest thousandth as needed

Calculus
Application of derivativesFind the slope of the line tangent to the curve y x at the point The slope is Tyne an integer or a simplified fraction 9 81 4 16 and then find the corresponding equation of the tangent line
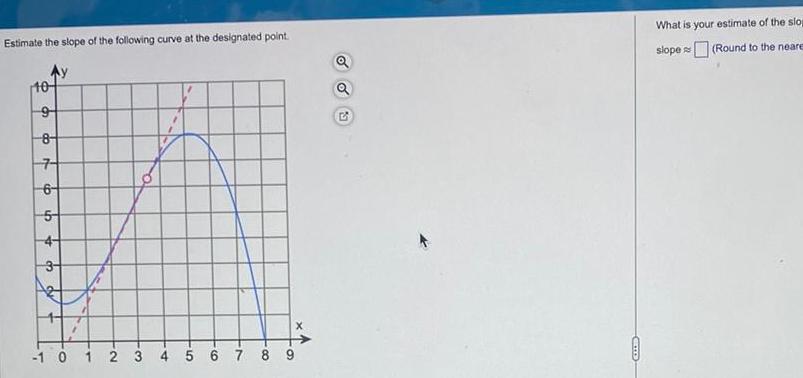
Calculus
Application of derivativesEstimate the slope of the following curve at the designated point 10 8 7 6 5 4 1 0 1 2 3 A 5 6 7 8 9 X Q COLED What is your estimate of the slop slope Round to the neare

Calculus
Application of derivatives1 A tank holds 1000 gallons of water which drains from the bottom of the tank in half an hour The values in the table show the volume V of water remaining in the tank in gallons after t minutes t min V gal 5 694 444 250 111 10 15 20 25 28 30 0 a If P is the point 15 250 on the graph of V find the slopes of the secant lines PQ when Q is the point on the graph with t 5 10 20 25 and 30 b Estimate the slope of the tangent line at P by averaging the slopes of two secant lines c Use a graph of V to estimate the slope of the tangent line at P This slope represents the rate at which the water is flowing from the tank after 15 minutes
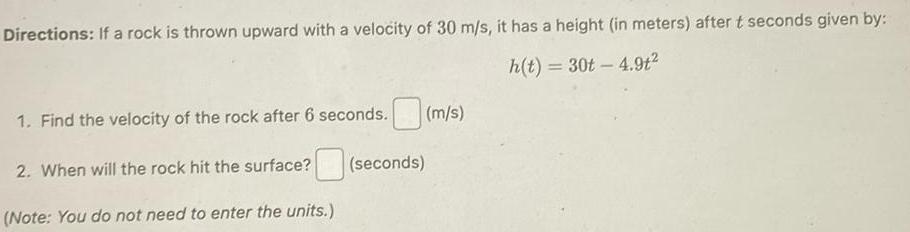
Calculus
Application of derivativesDirections If a rock is thrown upward with a velocity of 30 m s it has a height in meters after t seconds given by h t 30t 4 9t 1 Find the velocity of the rock after 6 seconds 2 When will the rock hit the surface Note You do not need to enter the units seconds m s
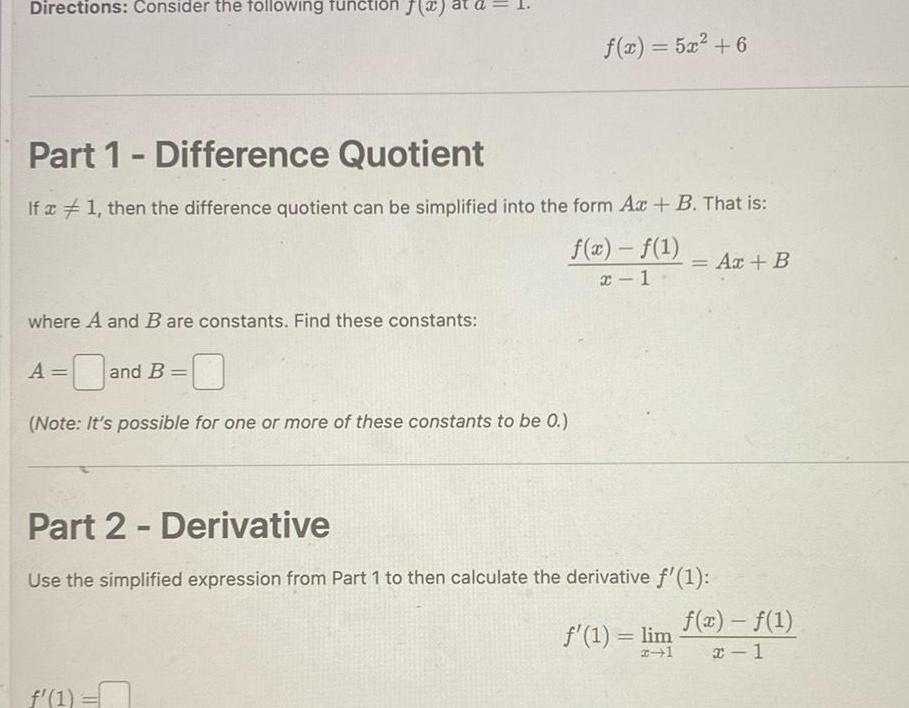
Calculus
Application of derivativesDirections Consider the following function where A and B are constants Find these constants A and Part 1 Difference Quotient If x 1 then the difference quotient can be simplified into the form Ax B That is f x f 1 x 1 and B IL Note It s possible for one or more of these constants to be 0 f x 5x 6 f 1 n Part 2 Derivative Use the simplified expression from Part 1 to then calculate the derivative f 1 Ax B f 1 lim f x f 1 x 1

Calculus
Application of derivativesFind an equation of the tangent line to the given curve at the point 1 0 Tangent Line y y x 1 x x 1

Calculus
Application of derivativesIf a 1 2 6 6 and b 3 2 7 find a b Your Answer Answer Which statement best describes the result of the cross product a It gives the magnitude of the projection of one vector onto another b It defines a vector perpendicular to both given vectors c The cross product gives a vector parallel to both given vectors d It is the division of one vector by another If A 3 2 9 and B 4 7 2 are two points in 3 space then find the vector AB a AB 7 5 7 b AB 1 9 11 c AB 12 14 18 d AB 7 5 71 The dot product represents a The magnitude of the projection of one vector onto another b A vector perpendicular to both given vectors Oc A vector parallel to both given vectors d The division of one vector by another What is 0 0 1 x 0 1 0 a 0 1 0 b 0 0 1 c 1 0 0 d 1 0 0
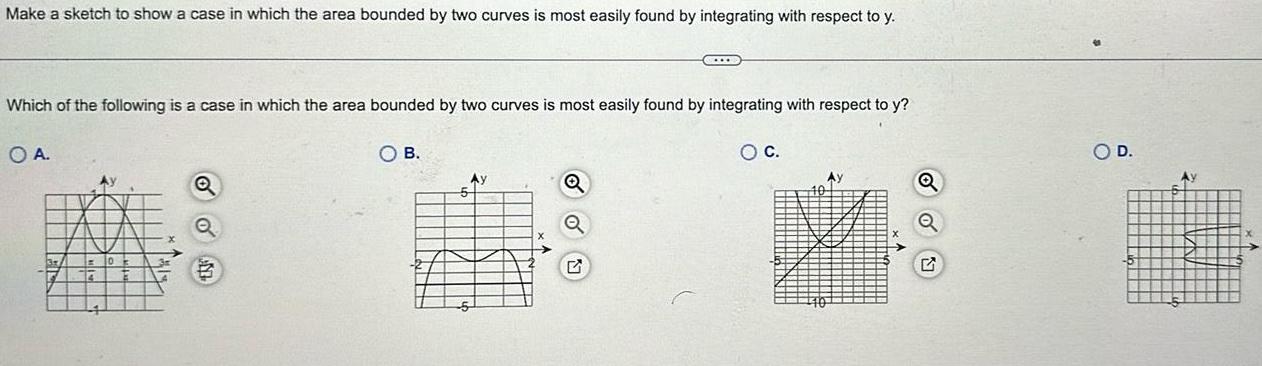
Calculus
Application of derivativesMake a sketch to show a case in which the area bounded by two curves is most easily found by integrating with respect to y Which of the following is a case in which the area bounded by two curves is most easily found by integrating with respect to y OA OB 5 Ay COL G O C Q O D Ay
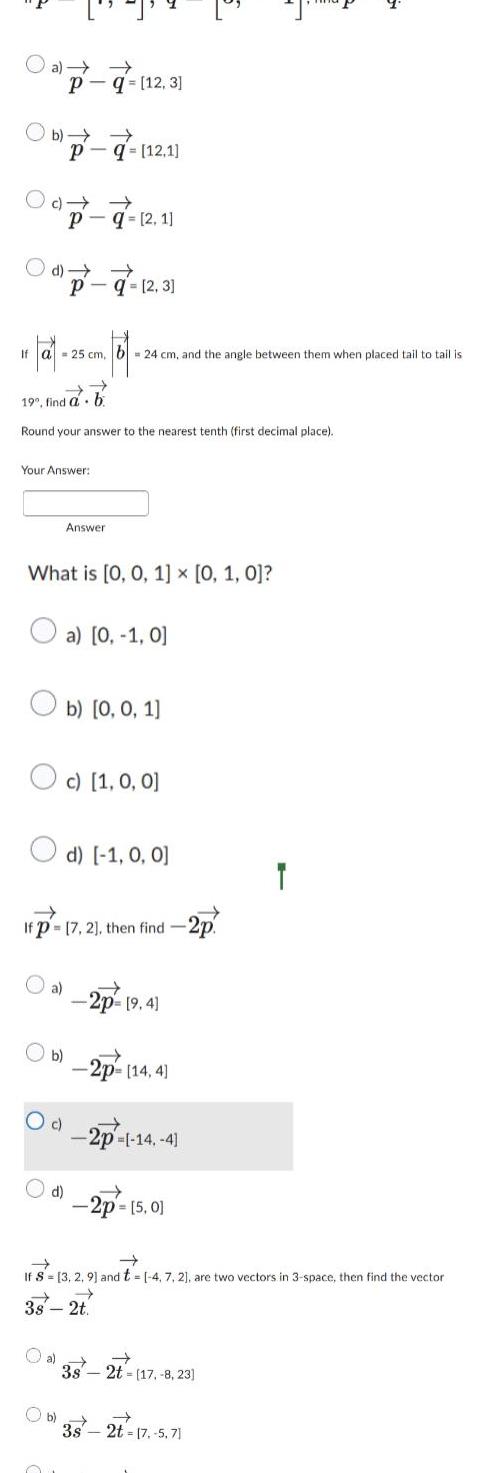
Calculus
Application of derivativesa Pq 12 3 Ob Pq 12 1 PO d P q 2 3 10 101 102 101 101 If a 25 cm b 24 cm and the angle between them when placed tail to tail is Pq 2 1 19 find a Round your answer to the nearest tenth first decimal place Your Answer b a What is 0 0 1 0 1 0 Ob O c Answer Oc 1 0 0 d a 0 1 0 If p 17 2 then find 2p b 0 0 1 d 1 0 0 2p 9 4 b 2p 14 4 2p 14 4 2p 5 0 If S 3 2 9 and t 4 7 2 are two vectors in 3 space then find the vector 3s 2t 3s 2t 17 8 23 Ob 3s 2t 17 5 71
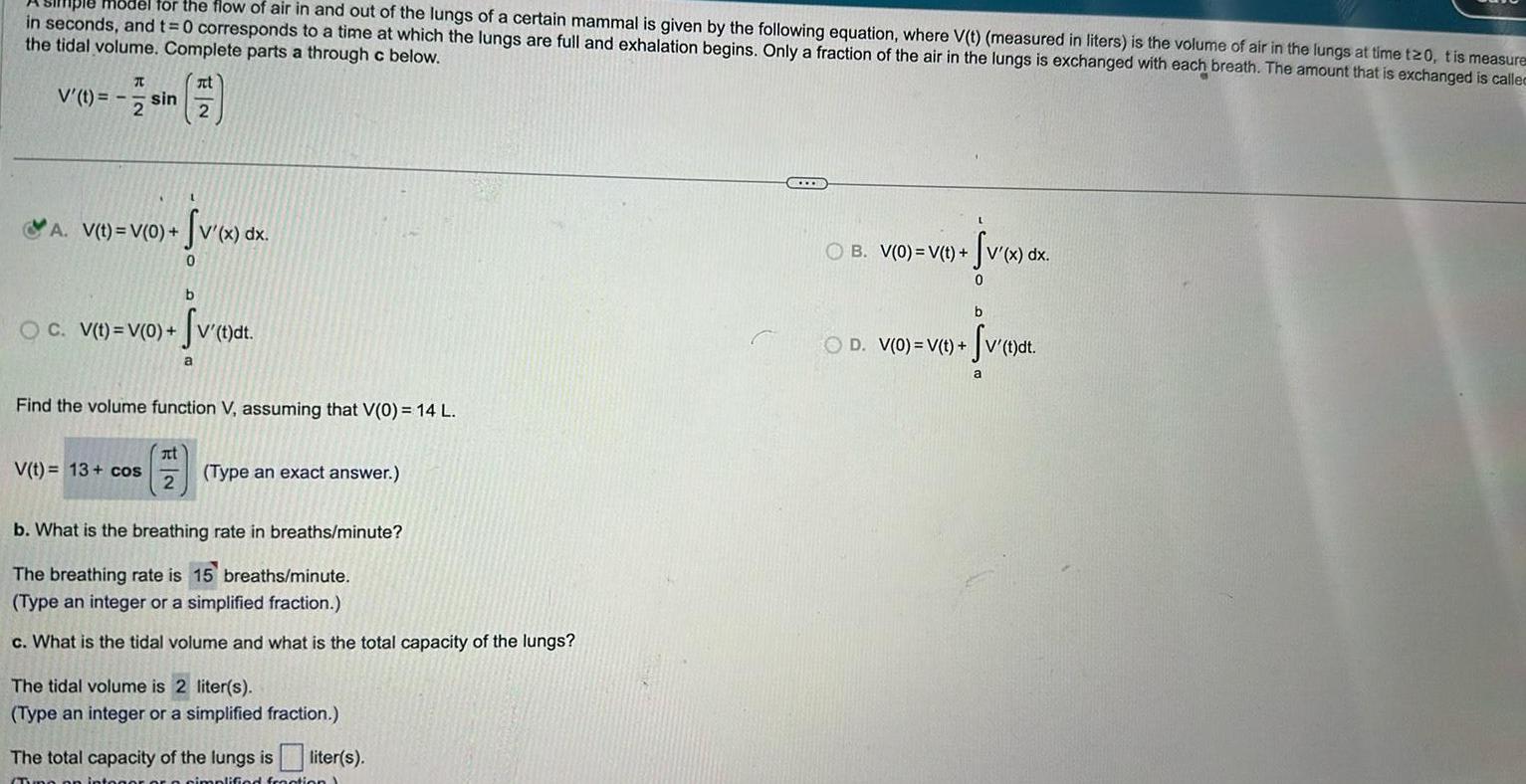
Calculus
Application of derivativesHiple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time t20 tis measures in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is called the tidal volume Complete parts a through c below It V sin 7 2 2 A V t V 0 b OC V t V 0 V t dt Svet a v x dx 0 Find the volume function V assuming that V 0 14 L V t 13 cos at 2 Type an exact answer b What is the breathing rate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs The tidal volume is 2 liter s Type an integer or a simplified fraction The total capacity of the lungs is liter s o simplified fraction Sv x dx 0 OB V 0 V t b Sv t dt OD V 0 V t a
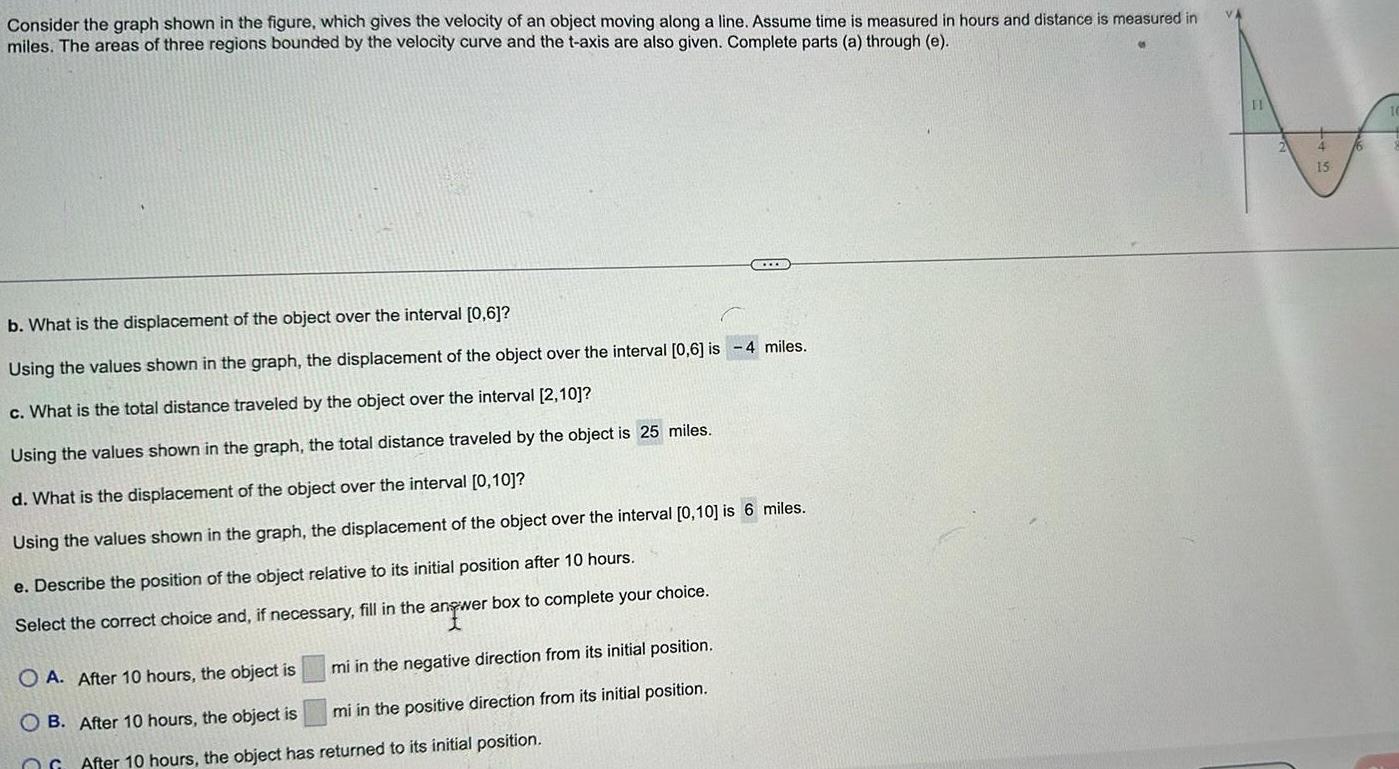
Calculus
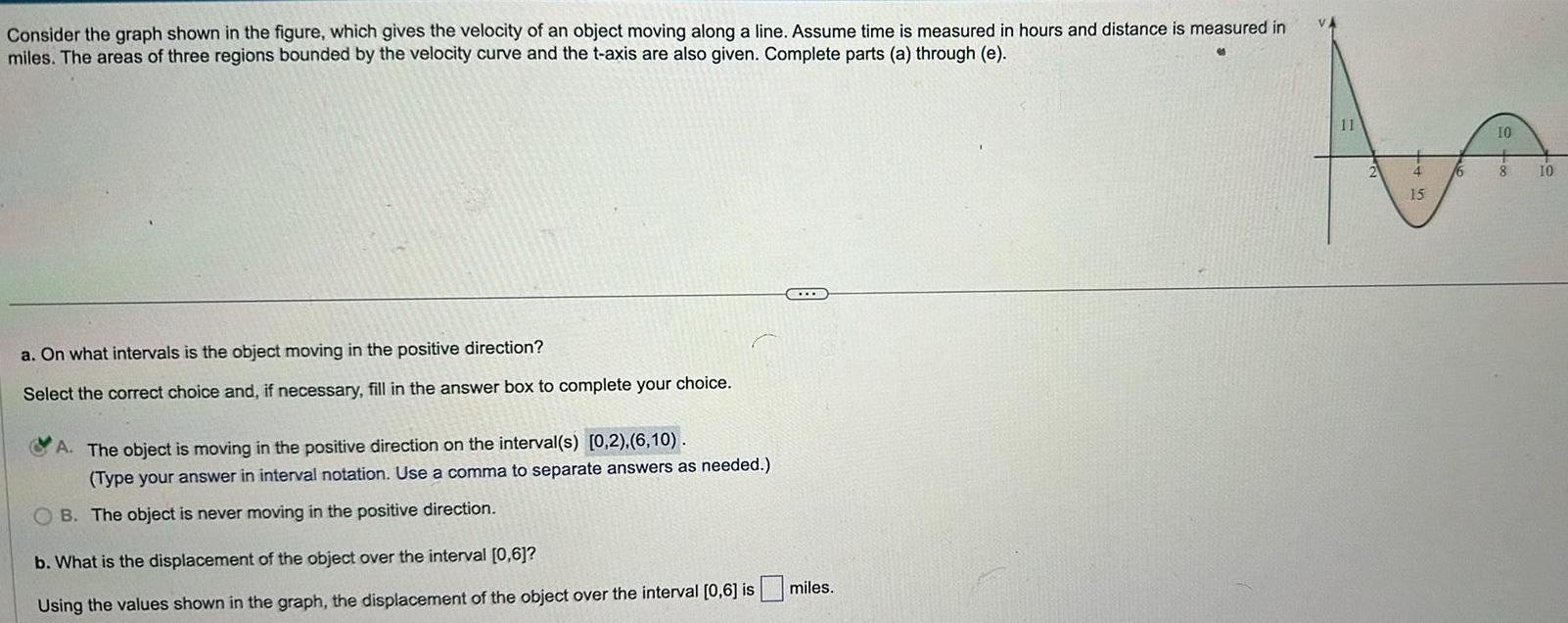
Application of derivativesConsider the graph shown in the figure which gives the velocity of an object moving along a line Assume time is measured in hours and distance is measured in miles The areas of three regions bounded by the velocity curve and the t axis are also given Complete parts a through e b What is the displacement of the object over the interval 0 6 Using the values shown in the graph the displacement of the object over the interval 0 6 is 4 miles c What is the total distance traveled by the object over the interval 2 10 Using the values shown in the graph the total distance traveled by the object is 25 miles d What is the displacement of the object over the interval 0 10 Using the values shown in the graph the displacement of the object over the interval 0 10 is 6 miles e Describe the position of the object relative to its initial position after 10 hours Select the correct choice and if necessary fill in the answer box to complete your choice angwe mi in the negative direction from its initial position mi in the positive direction from its initial position CCXXX O A After 10 hours the object is OB After 10 hours the object is After 10 hours the object has returned to its initial position 11 15
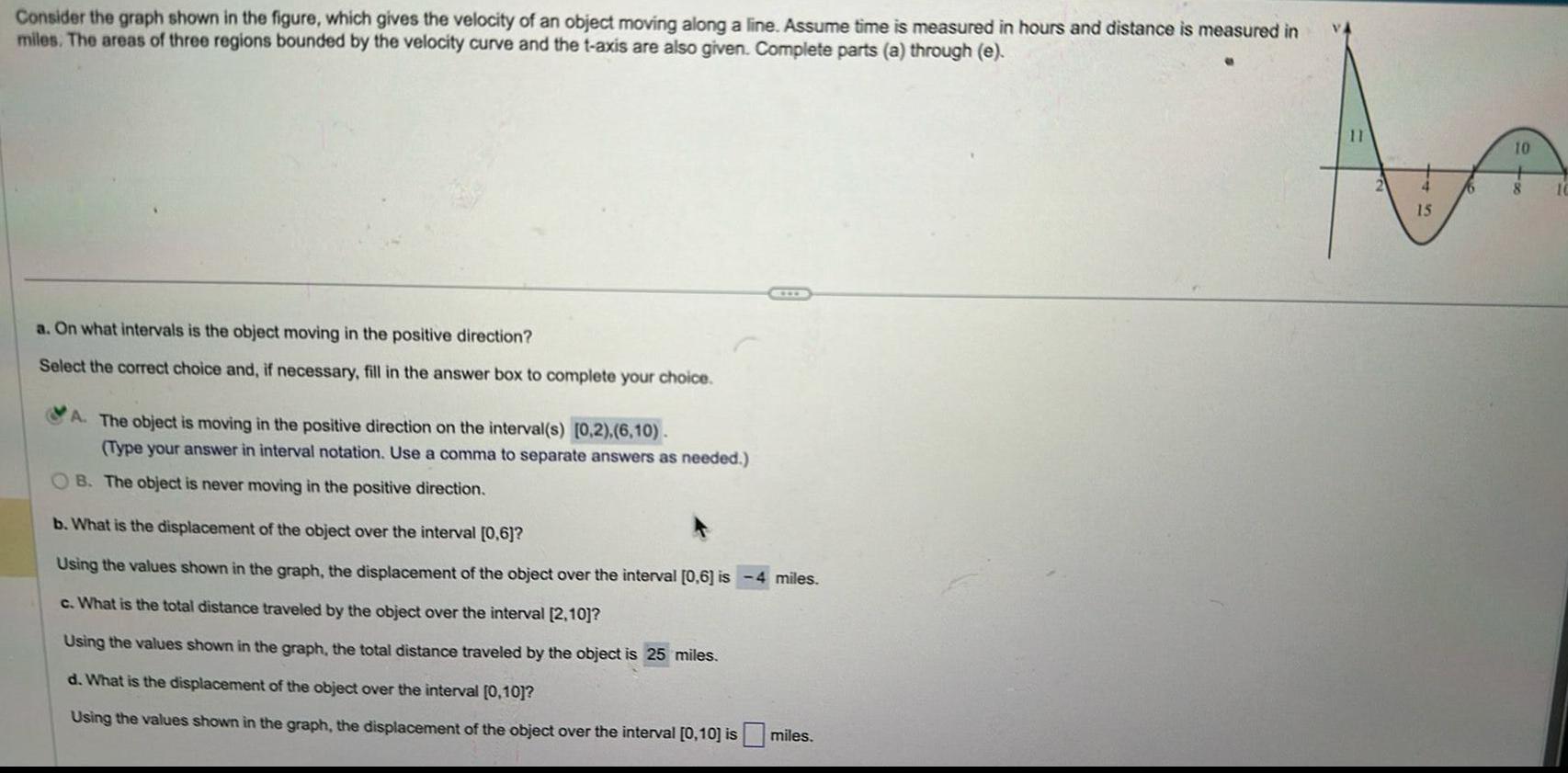
Calculus
Application of derivativesConsider the graph shown in the figure which gives the velocity of an object moving along a line Assume time is measured in hours and distance is measured in miles The areas of three regions bounded by the velocity curve and the t axis are also given Complete parts a through e a On what intervals is the object moving in the positive direction Select the correct choice and if necessary fill in the answer box to complete your choice A The object is moving in the positive direction on the interval s 0 2 6 10 Type your answer in interval notation Use a comma to separate answers as needed B The object is never moving in the positive direction b What is the displacement of the object over the interval 0 6 Using the values shown in the graph the displacement of the object over the interval 0 6 is 4 miles c What is the total distance traveled by the object over the interval 2 10 Using the values shown in the graph the total distance traveled by the object is 25 miles d What is the displacement of the object over the interval 0 10 Using the values shown in the graph the displacement of the object over the interval 0 10 is miles 11 15 16 10 8 10
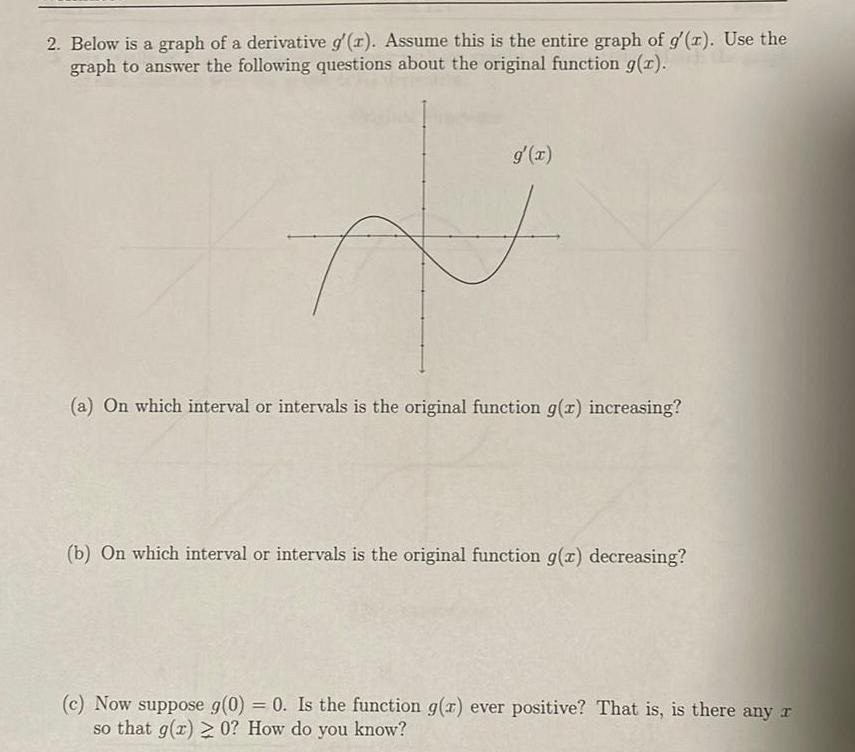
Calculus
Application of derivatives2 Below is a graph of a derivative g r Assume this is the entire graph of g z Use the graph to answer the following questions about the original function g x g x F a On which interval or intervals is the original function g z increasing b On which interval or intervals is the original function g x decreasing c Now suppose g 0 0 Is the function g z ever positive That is is there any r so that g x 0 How do you know

Calculus
Application of derivativesA company makes two types of biscuits Jumbo and Regular The oven can cook at most 200 biscuits per day Each jumbo biscuit requires 2 oz of flour each regular biscuit requires 1 oz of flour and there is 300 oz of flour available The income from each jumbo biscuit is 0 08 and from each regular biscuit is 0 09 How many of each size biscuit should be made to maximize income What is the maximum income The company should make Type whole numbers jumbo and regular biscuits

Calculus
Application of derivativesTo find the numbers for which f is discontinuous we look for x values for which the function is not defined or the left and right limits do not match Starting from the left and moving right the first x value for which f x is discontinuous is x At this point f x is not defined Therefore at this point f is which of the following O continuous from the right O continuous from the left O neither
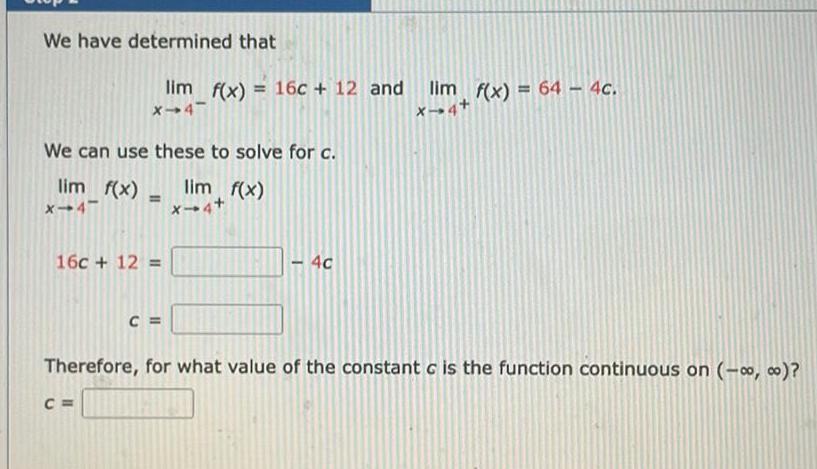
Calculus
Application of derivativesWe have determined that lim f x 16c 12 and X 4 We can use these to solve for c lim f x x 4 16c 12 C C lim f x X 4 4c lim f x 64 4c X 4 Therefore for what value of the constant c is the function continuous on 0 o
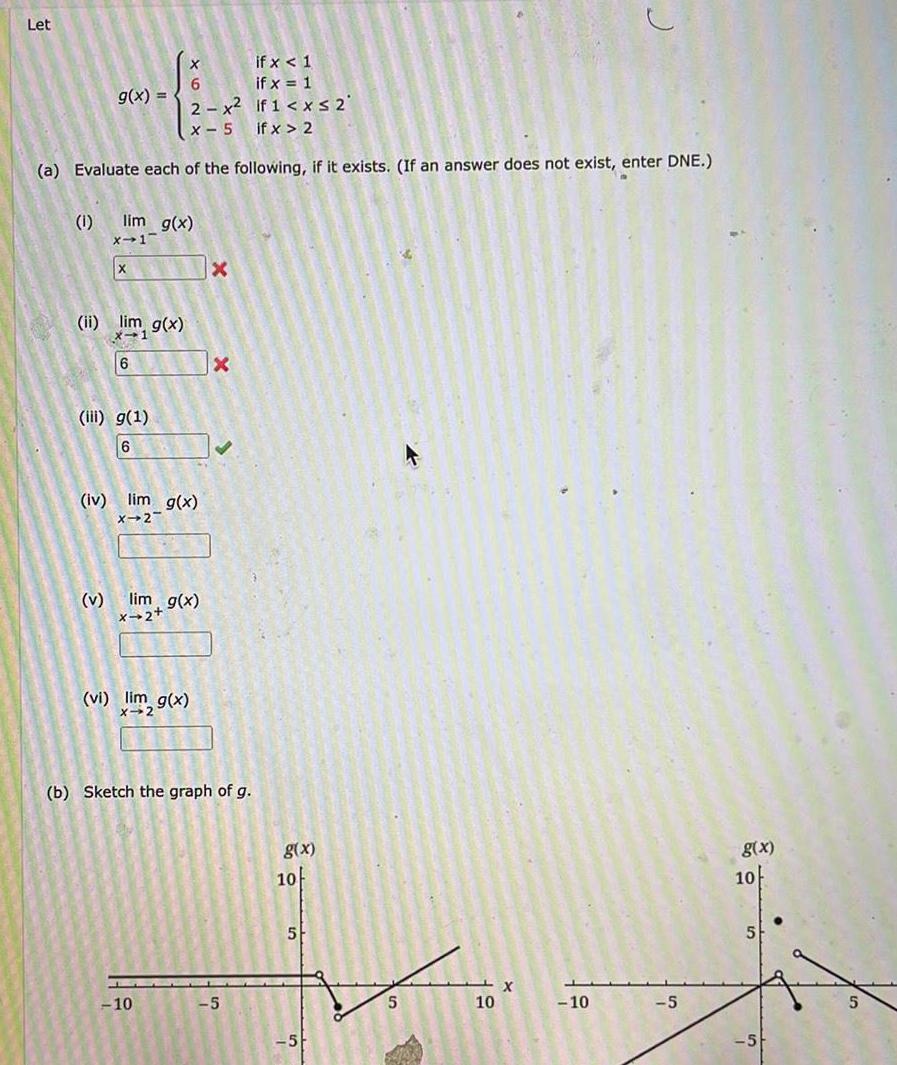
Calculus
Application of derivativesLet if x 1 6 if x 1 2 x if 1 x 2 x 5 if x 2 a Evaluate each of the following if it exists If an answer does not exist enter DNE 1 g x lim g x x 1 v X ii lim g x x 1 6 iii g 1 6 iv lim g x X 2 lim g x x 2 vi lim g x X 10 Xx b Sketch the graph of g 5 g x 10 5 5 5 X 10 61 C 10 5 g x 10 5 5
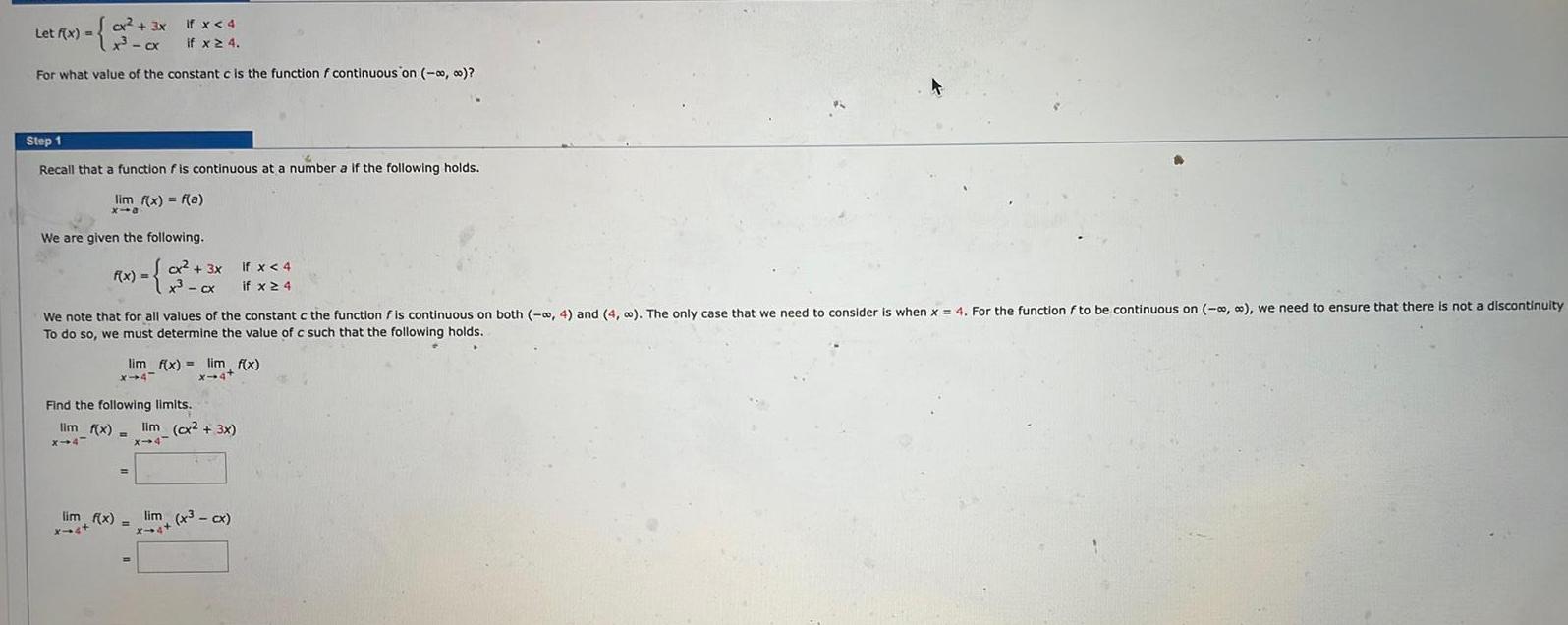
Calculus
Application of derivativesLet f x cx if x 4 For what value of the constant c is the function f continuous on 0 Step 1 Recall that function is continuous at a number a if the following holds lim f x f a x10 We are given the following F x 2x Cx 3x If x 4 x cx if x 4 We note that for all values of the constant c the function f is continuous on both 4 and 4 The only case that we need to consider is when x 4 For the function f to be continuous on we need to ensure that there is not a discontinuity To do so we must determine the value of c such that the following holds lim f x lim f x X 44 x 4 Find the following limits lim f x lim cx 3x x 4 X 4 lim f x lim x cx x st x 4

Calculus
Application of derivativesA simple model for the flow of air in and out of the lungs of a certain mammal is given by the following equation where V t measured in liters is the volume of air in the lungs at time t20 t is measured in seconds and t 0 corresponds to a time at which the lungs are full and exhalation begins Only a fraction of the air in the lungs is exchanged with each breath The amount that is exchanged is called the tidal volume Complete parts a through c below I V t sin 2 A V t V 0 zt 2 t Sv x dx 0 b OC V t V 0 v t dt a V t 13 cos Find the volume function V assuming that V 0 14 L at 2 Type an exact answer b What is the breathingrate in breaths minute The breathing rate is 15 breaths minute Type an integer or a simplified fraction c What is the tidal volume and what is the total capacity of the lungs The tidal volume is liter s SOCCE t Sv x dx 0 OB V 0 V t b OD V 0 V t SV t dt a

Calculus
Application of derivativesFor this question you should type which formula you should use simple compound annuity payout annuity loan You should also tell me which variable you will be solving for and you should type your final answer to two decimal places ALL OTHER WORK MUST BE ON PAPER YOU SEND TO ME so I can see you substituted into the equation properly and the steps you took to solve You deposit 2 500 in an account earning 3 25 interest compounded quarterly a How much will you have in 15 years b How much of that is interest Formulas

Calculus
Application of derivativesSet up a sum of two integrals that equals the area of the shaded region bounded by the graphs of the functions f and g on a c in the figure Assume the curves intersect at x b Choose the correct answer below b OB OA S x 9 C f x g x dx g x f x dx S g x f b b C f x 9 f x g x dx f x g x dx x S x a b b O C Sg x 1 x dx S x 9 b b g x dx BELLS y f x y g x
Calculus
Application of derivativesConsider the graph shown in the figure which gives the velocity of an object moving along a line Assume time is measured in hours and distance is measured in miles The areas of three regions bounded by the velocity curve and the t axis are also given Complete parts a through e a On what intervals is the object moving in the positive direction Select the correct choice and if necessary fill in the answer box to complete your choice A The object is moving in the positive direction on the interval s 0 2 6 10 Type your answer in interval notation Use a comma to separate answers as needed B The object is never moving in the positive direction STOR b What is the displacement of the object over the interval 0 6 Using the values shown in the graph the displacement of the object over the interval 0 6 is miles 11 2 4 15 16 10 8 10
Calculus
Application of derivatives2 Consider a circle O with radius r How many arcs of length rare equal to the length of the following arcs a a semicircle of circle O b an arc that is three quarters of circle O
Calculus
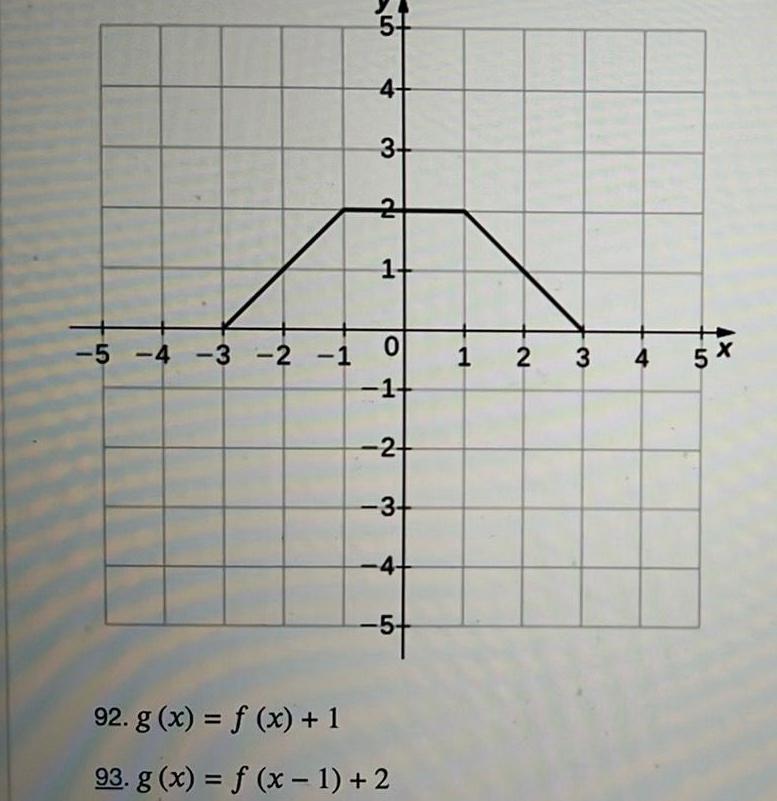
Application of derivatives5 4 3 2 1 5 4 3 2 1 0 14 2 3 4 5 92 g x f x 1 93 g x f x 1 2 1 2 3 4 5
Calculus
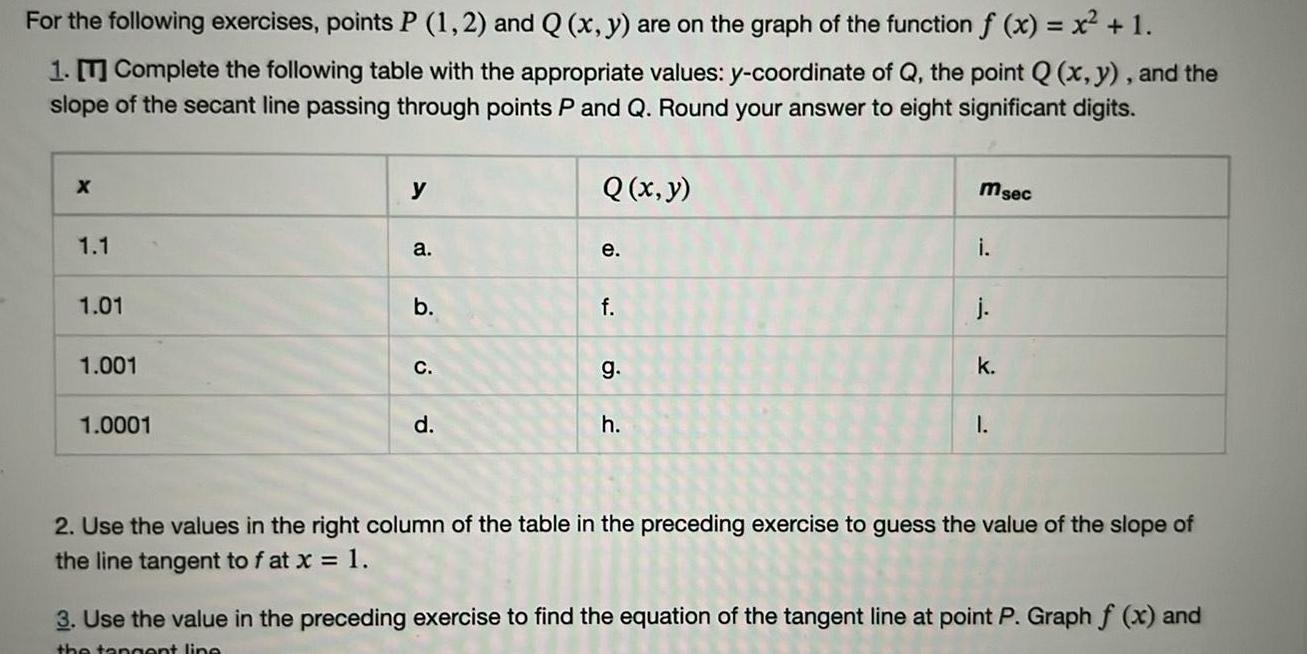
Application of derivativesFor the following exercises points P 1 2 and Q x y are on the graph of the function f x x 1 1 T Complete the following table with the appropriate values y coordinate of Q the point Q x y and the slope of the secant line passing through points P and Q Round your answer to eight significant digits X 1 1 1 01 1 001 1 0001 y a b C d Q x y e f g h Msec i j k I 2 Use the values in the right column of the table in the preceding exercise to guess the value of the slope of the line tangent to f at x 1 3 Use the value in the preceding exercise to find the equation of the tangent line at point P Graph f x and the tangent line
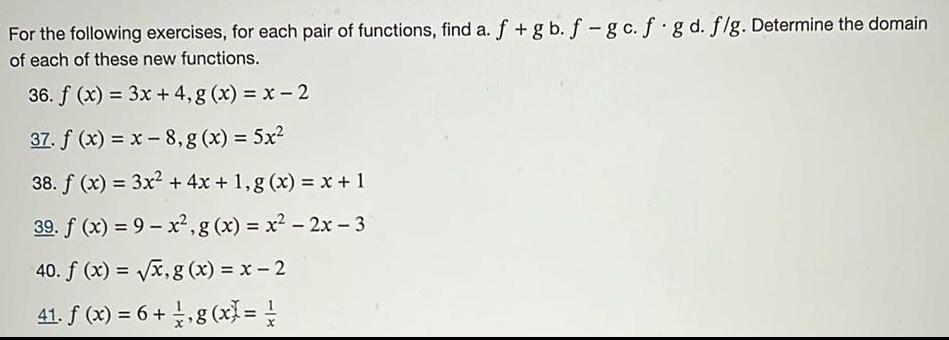
Calculus
Application of derivativesFor the following exercises for each pair of functions find a f gb f gc f g d f g Determine the domain of each of these new functions 36 f x 3x 4 g x x 2 37 f x x 8 g x 5x 38 f x 3x 4x 1 g x x 1 39 f x 9 x g x x 2x 3 40 f x x g x x 2 41 f x 6 g x

Calculus
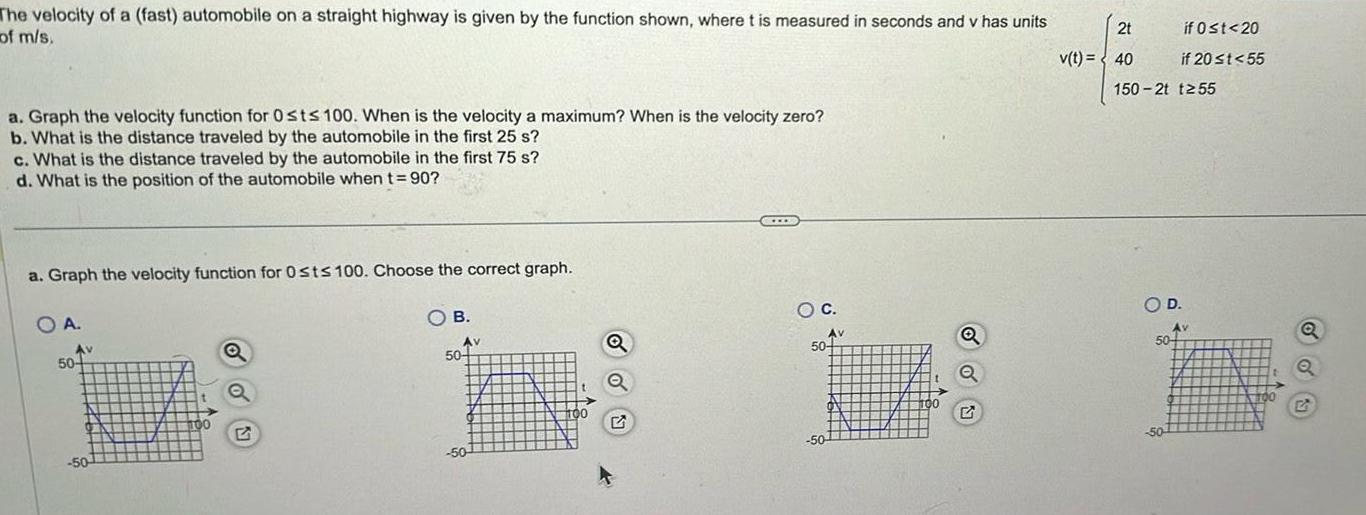
Application of derivativesThe velocity of a fast automobile on a straight highway is given by the function shown where t is measured in seconds and v has units of m s a Graph the velocity function for Osts 100 When is the velocity a maximum When is the velocity zero b What is the distance traveled by the automobile in the first 25 s c What is the distance traveled by the automobile in the first 75 s d What is the position of the automobile whent 90 OA AV 50 50 00 OB Av On 50 50 100 G OA At the specific time s t Use a comma to separate answers as needed OC 50 When is the velocity a maximum Select the correct choice and fill in the answer box to complete your choice 50 100 OA At the specific time s t Use a comma to separate answers as needed B At all values of t in the interval s 20 55 Type your answer in interval notation Use a comma to separate answers as needed When is the velocity zero Select the correct choice and fill in the answer box to complete your choice 21 v t 40 unur oft in the interval s Type your answer in interval notation Use a comma to separate answers as needed if 0 t 20 if 20 t 55 150 2t t255 D 50 50
Calculus
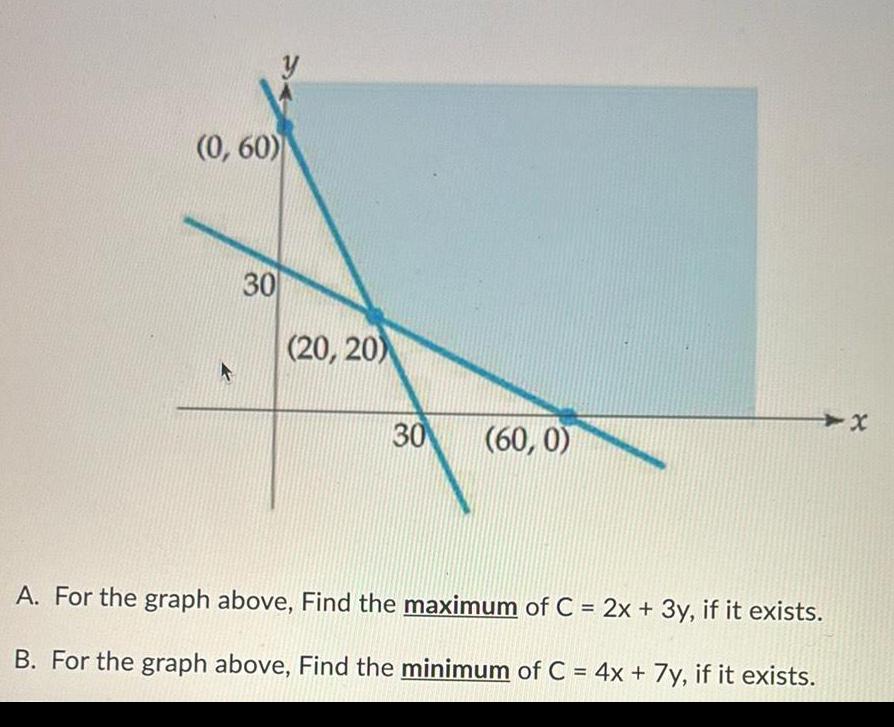
Application of derivatives0 60 k 30 20 20 30 60 0 A For the graph above Find the maximum of C 2x 3y if it exists B For the graph above Find the minimum of C 4x 7y if it exists

Calculus
Application of derivativest Starting with an initial value of P 0 50 the population of a prairie dog community grows at a rate of P t 40 in units of prairie dogs month for 0 t 200 5 a What is the population 11 months later b Find the population P t for Ost 200
Calculus
Application of derivativesThe velocity of a fast automobile on a straight highway is given by the function shown where t is measured in seconds and v has units of m s a Graph the velocity function for Osts 100 When is the velocity a maximum When is the velocity zero b What is the distance traveled by the automobile in the first 25 s c What is the distance traveled by the automobile in the first 75 s d What is the position of the automobile when t 90 a Graph the velocity function for Osts 100 Choose the correct graph O B OA Av 50 50 Q Av 50 50 100 Q O C Av 50 50 00 Q Q 2t v t 40 150 2t t255 if 0 t 20 if 20 t 55 O D 50 50 Av TOO Q

Calculus
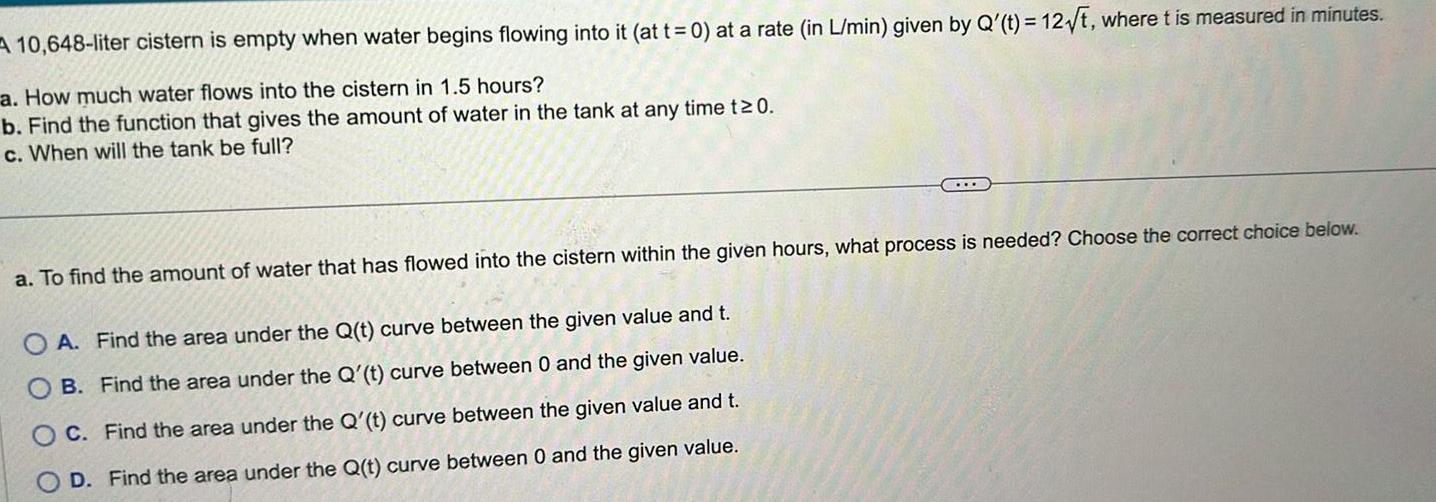
Application of derivatives10 648 liter cistern is empty when water begins flowing into it at t 0 at a rate in L min given by Q t 12 t where t is measured in minutes a How much water flows into the cistern in 1 5 hours b Find the function that gives the amount of water in the tank at any time t 0 c When will the tank be full a To find the amount of water that has flowed into the cistern within the given hours what process is needed Choose the correct choice below OA Find the area under the Q t curve between the given value and t B Find the area under the Q t curve between 0 and the given value C Find the area under the Q t curve between the given value and t D Find the area under the Q t curve between 0 and the given value

Calculus
Application of derivativesA population of cattle is increasing at a rate of 600 80t per year where t is measured in years By how much does the population increase between the 6 th and the 9 th years Total Increase
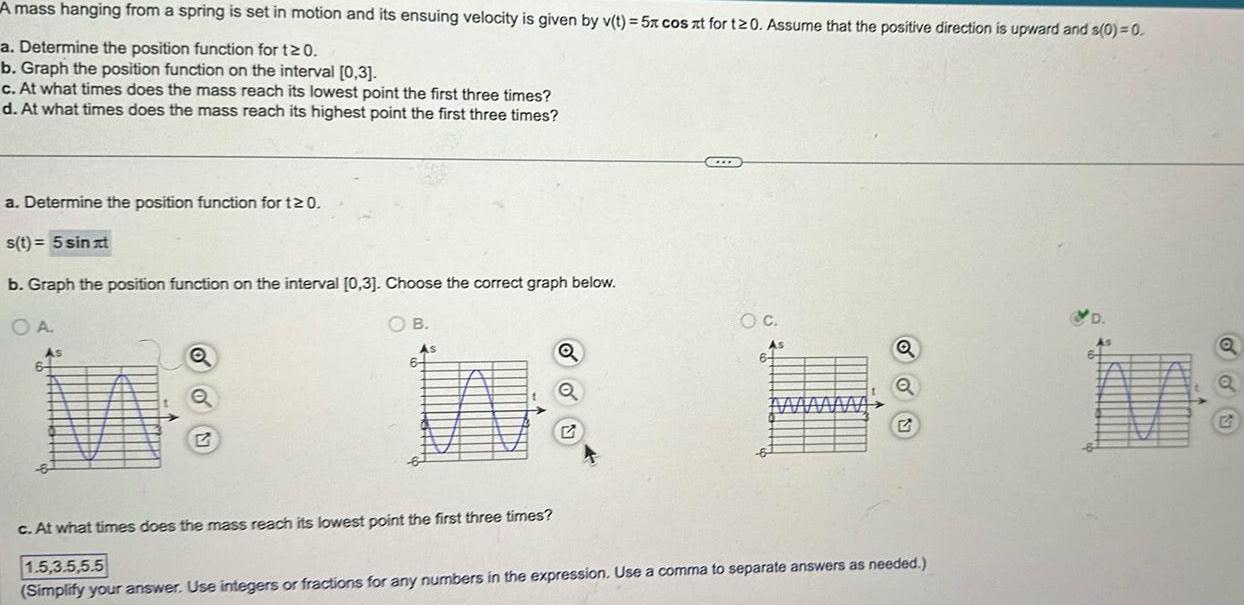
Calculus
Application of derivativesA mass hanging from a spring is set in motion and its ensuing velocity is given by v t 5x cos xt for t20 Assume that the positive direction is upward and s 0 0 a Determine the position function for t20 b Graph the position function on the interval 0 3 c At what times does the mass reach its lowest point the first three times d At what times does the mass reach its highest point the first three times a Determine the position function for 120 s t 5 sinat b Graph the position function on the interval 0 3 Choose the correct graph below OA As 6 Q B As 6 Q C O C As MAMA Q Q c At what times does the mass reach its lowest point the first three times 1 5 3 5 5 5 Simplify your answer Use integers or fractions for any numbers in the expression Use a comma to separate answers as needed D in Q

Calculus
Application of derivativesPower and energy are often used interchangeably but they are quite different Energy is measured in units of joules J or Calories Cal where 1 Cal 4184 J On the other hand power is the rate at which energy is used and is measured in watts W 1 W 1 J s Other useful units of power are kilowatts kW and megawatts 1 MW 106 W If energy is used at a rate of 1 kW for 1 hr the total amount of energy used is 1 kilowatt hour kWh which is 3 6x 106 J Suppose the power function of a large city over a 24 hr period is given by P t E t 255 170 sin t 12 where P is measured in MW and t 0 corresponds to 6 00 p m see accompanying figure Complete parts a through d below Click the icon to view the graph of P t E t 255 170 sin t 12 C a How much energy is consumed by this city in a typical 24 hr period Express the answer in MWh and in J The energy consumed in a typical 24 hour period in MWh is 6120 MWh Simplify your answer 13 The energy consumed in a typical 24 hour period in J is 2 2032 10 J Simplify your answer Use scientific notation b Burning 1 kg of coal produces about 450 kWh of energy How many kg of coal are required to meet the energy needs of the city for 1 day For 1 yr The amount of coal needed in a day is kg

Calculus
Application of derivativesPower and energy are often used interchangeably but they are quite different Energy is measured in units of joules J or Calories Cal where 1 Cal 4184 J On the other hand power is the rate at which energy is used and is measured in watts W 1 W 1 J s Other useful units of power are kilowatts kW and megawatts 1 MW 106 W If energy is used at a rate of 1 kW for 1 hr the total amount of energy used is 1 kilowatt hour kWh which is 3 6 x 106 J Suppose the power function of a large city over a 24 hr period is given by P t E t 255 170 sin t 12 where P is measured in MW and t 0 corresponds to 6 00 p m see accompanying figure Complete parts a through d below Click the icon to view the graph of P t E t 255 170 sin t 12 a How much energy is consumed by this city in a typical 24 hr period Express the answer in MWh and in J The energy consumed in a typical 24 hour period in MWh is MWh Simplify your answer
Calculus
Application of derivativesa Determine whether the Mean Value Theorem applies to the function f x 7 x on the interval 1 2 b If so find the point s that are guaranteed to exist by the Mean Value Theorem a Choose the correct answer below OA No because the function is continuous on the interval 1 2 but is not differentiable on the interval 1 2 OB No because the function is differentiable on the interval 1 2 but is not continuous on the interval 1 2 OC No because the function is not continuous on the interval 1 2 and is not differentiable on the interval 1 2 D Yes because the function is continuous on the interval 1 2 and differentiable on the interval 1 2 b Select the correct choice below and if necessary fill in the answer box to complete your choice OA The point s is are x www Simplify your answer Use a comma to separate answers as needed B The Mean Value Theorem does not apply in this case
Calculus
Application of derivativesder an object moving along a line with the following velocity and initial position v t 6 3t on 0 4 s 0 0 Determine the position function for t20 using both the antiderivative method and the Fundamental Theorem of Calculus Check for agreement between the two methods To determine the position function for t20 using the antiderivative method first determine how the velocity function and the position function are related Choose the correct answer below A The position function is the antiderivative of the velocity function OB The position function is the absolute value of the antiderivative of the velocity function OC The position function is the derivative of the velocity function OD The velocity function is the antiderivative of the absolute value of the position function Which equation below will correctly give the position function according to the Fundamental Theorem of Calculus A s t s 0 t Sv x dx 0 MIN b C s t s 0 Sv t dt b B s t v t dt t OD s 0 s t v x d Sv x dx Determine the position function for t20 using both methods Select the correct choice below and fill in the answer box es to complete your choice OA The same function is obtained using each method The position function is s t OB Different functions are obtained using each method The position function obtained using the antiderivative method is s t of Calculus is s t 0 and the position function obtained using the Fundamental Th