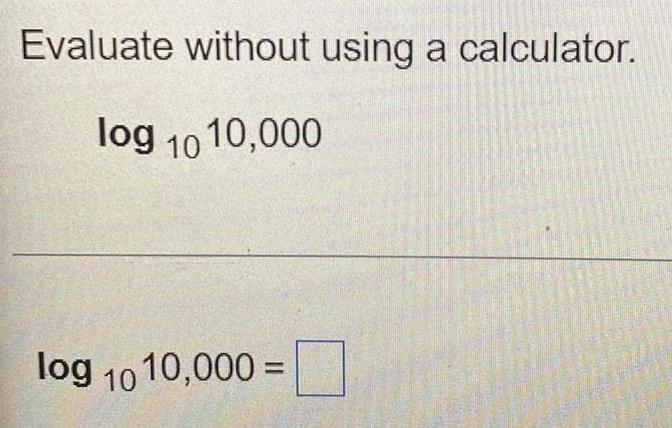
Application of derivatives Questions and Answers
Calculus
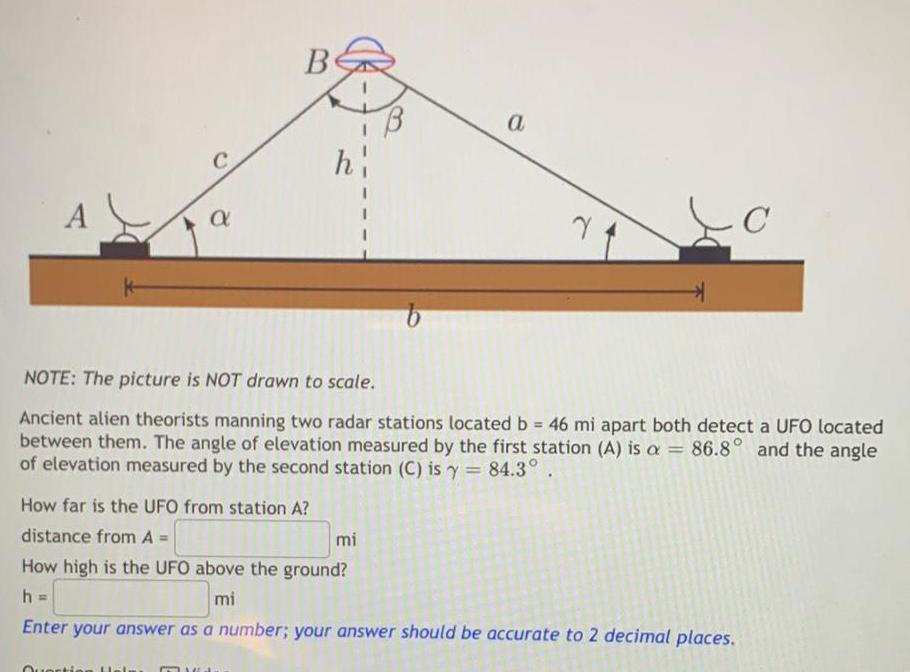
Application of derivativesA a Be How far is the UFO from station A distance from A Question Hel h I I B NOTE The picture is NOT drawn to scale Ancient alien theorists manning two radar stations located b 46 mi apart both detect a UFO located between them The angle of elevation measured by the first station A is a 86 8 and the angle of elevation measured by the second station C is y 84 3 mi a Y How high is the UFO above the ground h mi Enter your answer as a number your answer should be accurate to 2 decimal places

Calculus
Application of derivativesYou have learned how to apply the chain rule and to solve problems involving rates of change In this task you will solve a problem involving a combination of these ideas Hypothesis The rate of change of the volume of a sphere is proportional to its surface area Experiment a Obtain a spherical lollipop on a stick Assume that it is a perfect sphere Measure and record the initial radius of this sphere Hint Remember the relationship between radius and circumference b Place the lollipop in your mouth and carefully consume it uniformly for 30 s Measure and record the new radius in a table similar to the one here Repeat until you have at least ten measurements Time s Radius of Lollipop cm 0 30 60 90 120 150 180 210 240 270 300 c Use your data to determine the rate of change of radius with respect to time Write an equation to model the radius as a function of time Justify your choice of models d Write the formula to model the volume as a function of the radius Use your equation from part c to model the volume as a function of time e Use your model from part c to calculate the rate of change of volume with respect to time when the radius has reached half its original value f Explain why you should not expect the rate of change of volume with respect to time to be constant in this situation g Use your model to estimate how much time is required to completely consume the lollipop h Does this experiment confirm the hypothesis Explain i How would the time to consume the lollipop change if the initial radius were multiplied by a constant k Justify your response

Calculus
Application of derivativesUse the trapezoidal rule with 4 trapezoids to find an approximation for O O O O x3 2 dx A A A A 5 2 2 3 3 32 9 2 2 3 3 64 9 2 2 3 3 32 17 4 2 9 3 320
Calculus
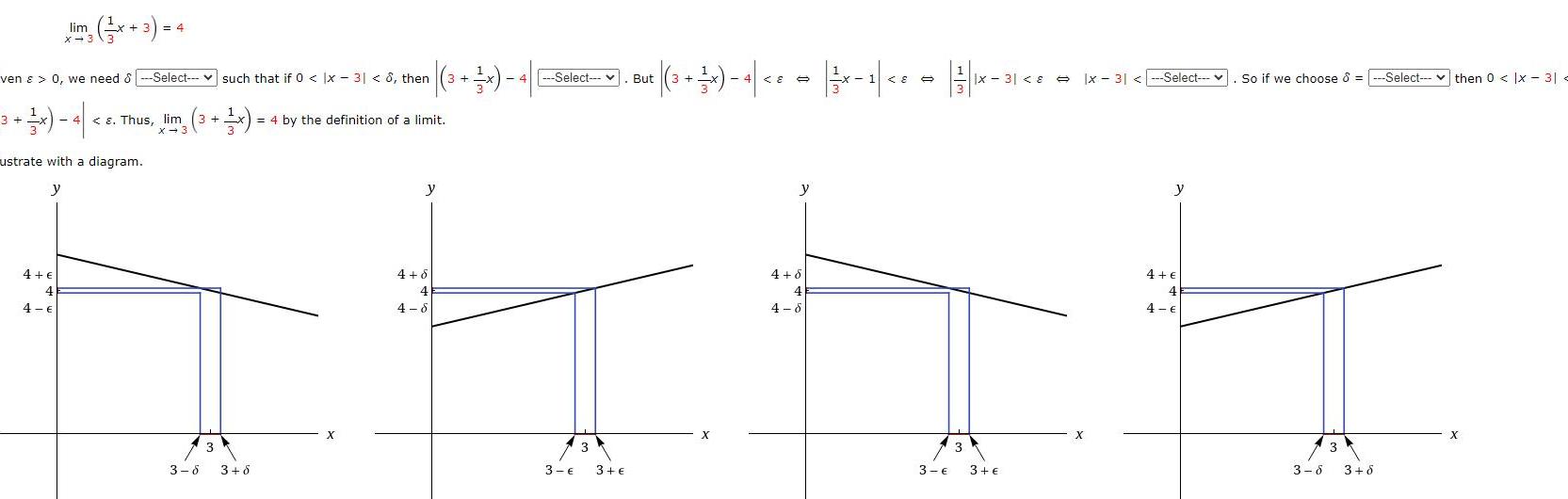
Application of derivativeslim 3 1 4 3 x 3 x 3 ven 0 we need 8 Select such that if 0 x 31 8 then 1 1 lim 3 x 4 4 4 E 4 ustrate with a diagram y Thus lim 3 3 6 3 6 4 by the definition of a limit X y 4 6 4 4 6 4 Select But 3 E 3 3 E 3 x 4 8 X y 4 6 4 4 6 8 11 3 x3 8 x 31 Select 3 3 X y 4 4 4 So if we choose Select then 0 x 3 3 3 6 3 6 X

Calculus
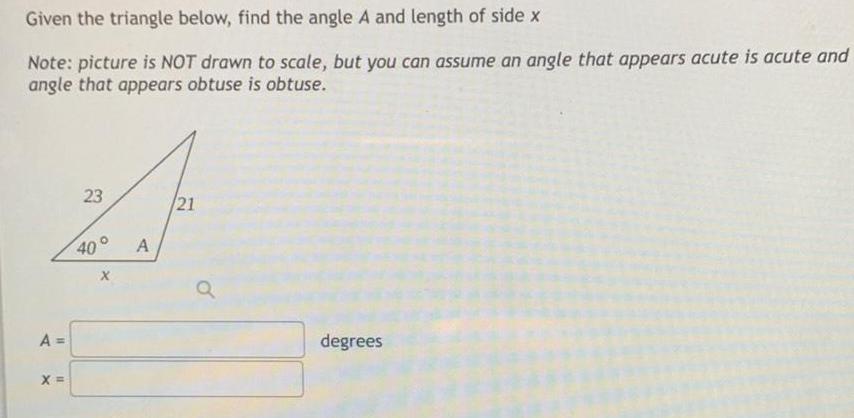
Application of derivativesGiven the triangle below find the angle A and length of side x Note picture is NOT drawn to scale but you can assume an angle that appears acute is acute and angle that appears obtuse is obtuse A X 23 A 21 Q degrees
Calculus
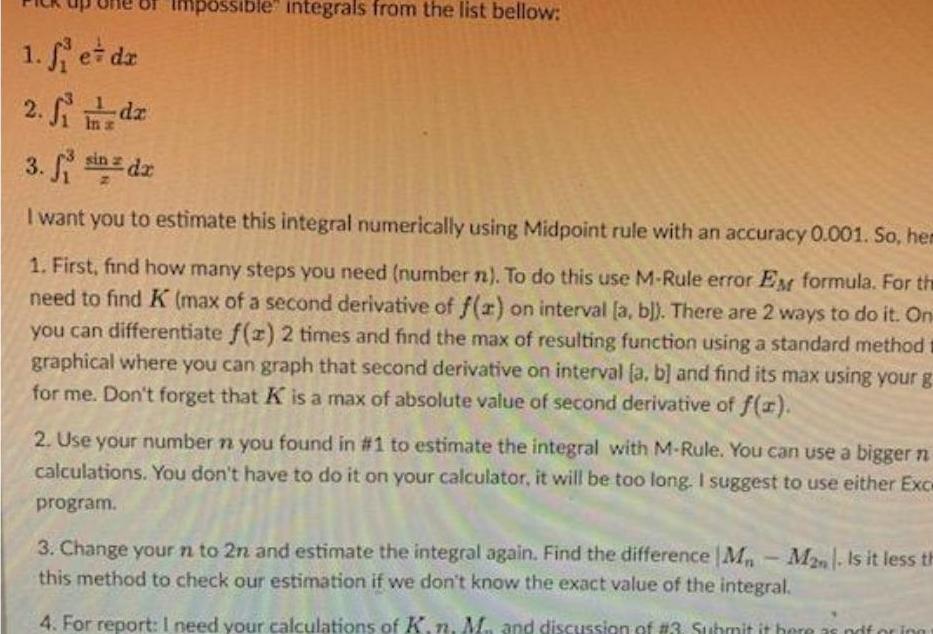
Application of derivatives1 et dz 2 Si dz In s Impossible integrals from the list bellow 3 fi in dr I want you to estimate this integral numerically using Midpoint rule with an accuracy 0 001 So hem 1 First find how many steps you need number n To do this use M Rule error EM formula For the need to find K max of a second derivative of f x on interval a b There are 2 ways to do it On you can differentiate f z 2 times and find the max of resulting function using a standard method graphical where you can graph that second derivative on interval a b and find its max using your g for me Don t forget that K is a max of absolute value of second derivative of f x 2 Use your number n you found in 1 to estimate the integral with M Rule You can use a bigger n calculations You don t have to do it on your calculator it will be too long I suggest to use either Exce program 3 Change your n to 2n and estimate the integral again Find the difference M M2n Is it less th this method to check our estimation if we don t know the exact value of the integral 4 For report I need your calculations of K n M and discussion of 3 Submit it here as noforing
Calculus
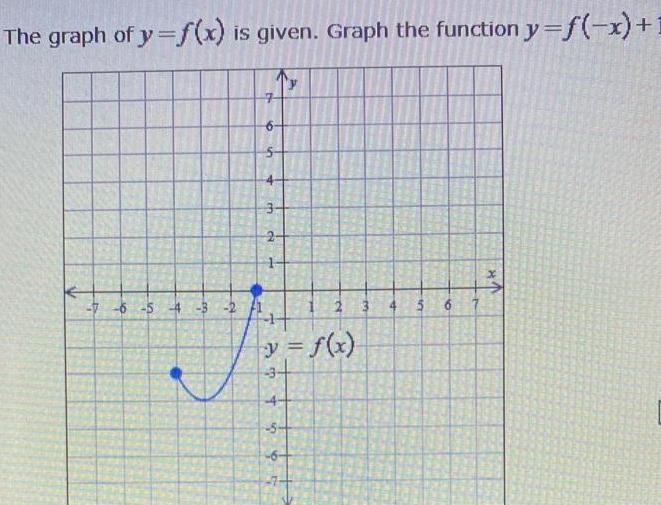
Application of derivativesThe graph of y f x is given Graph the function y f x 7 6 5 4 3 2 H 3 2 y f x 3 6 4 5 41

Calculus
Application of derivatives0 Which of the following functions is not differentiable at x A f x ex B f x x C f x tan x D f x arcsin x

Calculus
Application of derivativesFind the interval s on which the function f x x4 4x is concave down A 0 2 B 0 3 C 0 2 D 0 3
Calculus
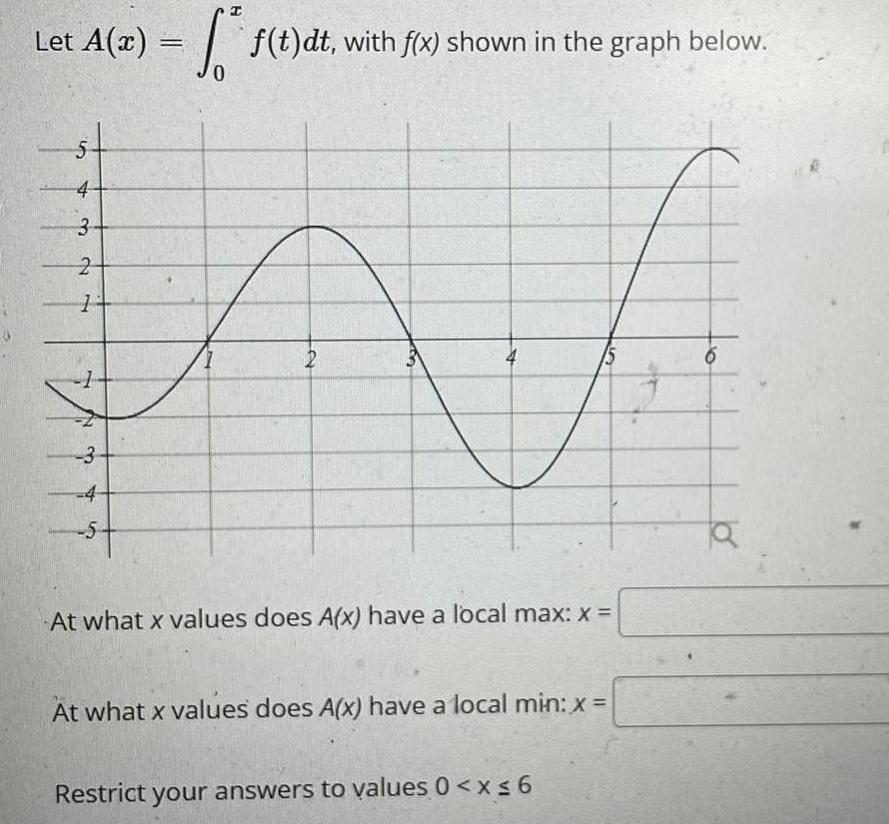
Application of derivativesLet A x f t dt with fix shown in the graph below st 4 3 2 1 1 N 3 4 st 2 At what x values does A x have a local max x At what x values does A x have a local min x Restrict your answers to values 0 x 6 6 o
Calculus
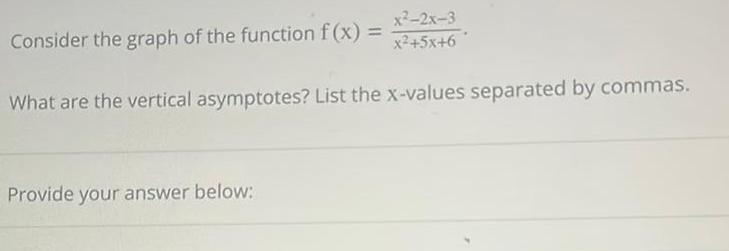
Application of derivativesx 2x 3 Consider the graph of the function f x X 5076 What are the vertical asymptotes List the x values separated by commas Provide your answer below
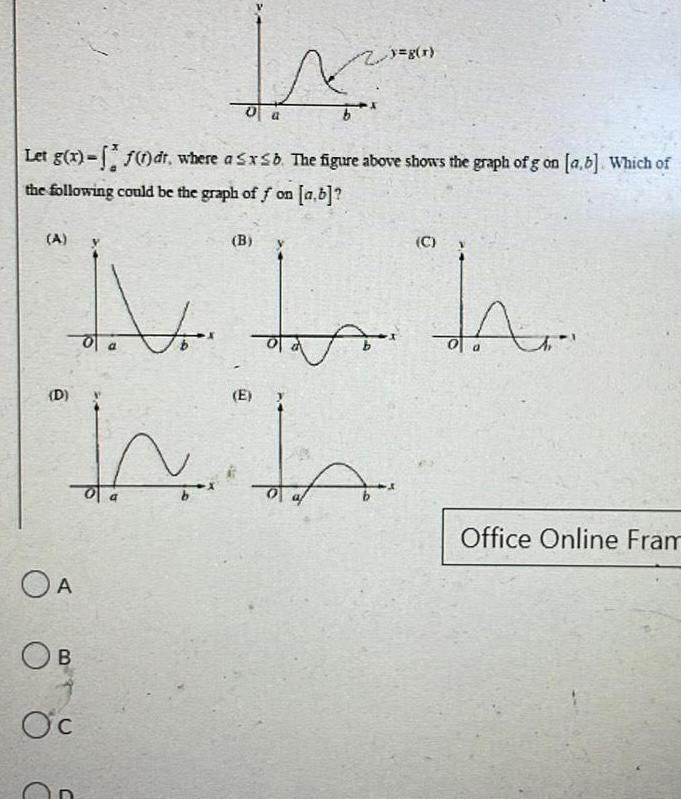
Calculus
Application of derivativesA to a Let g x f 1 dt where a x b The figure above shows the graph of g on a b Which of the following could be the graph of f on a b D 0 a OA OB Oc B M E y g r In th be he C Office Online Fram
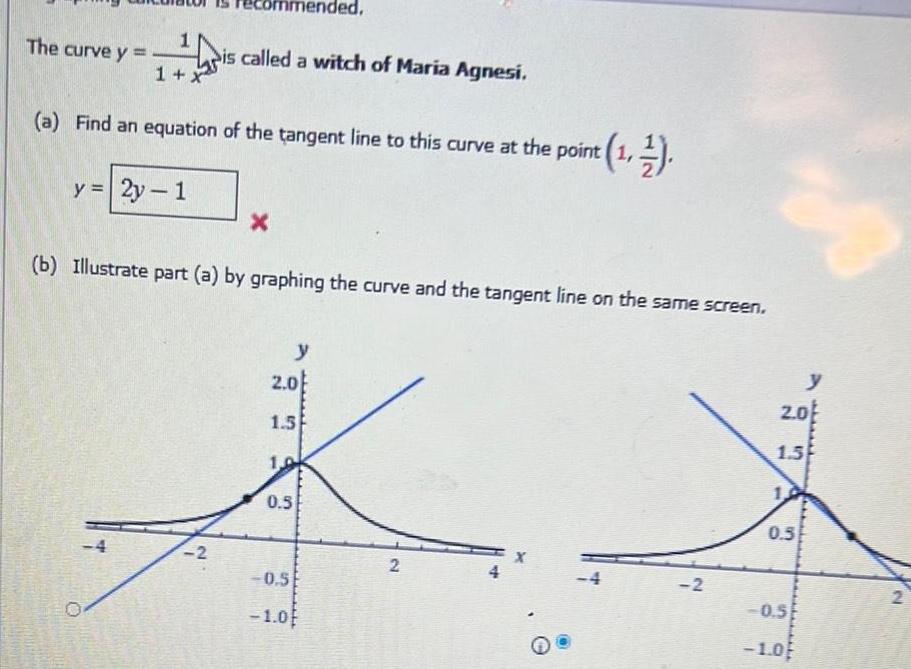
Calculus
Application of derivativesThe curve y is called a witch of Maria Agnesi 1 a Find an equation of the tangent line to this curve at the point 1 y 2y 1 2 X b Illustrate part a by graphing the curve and the tangent line on the same screen 2 0 1 5 y 1 0 0 5 0 5 1 0 2 4 2 A 2 0 y 1 5 0 5 0 5 1 0 2
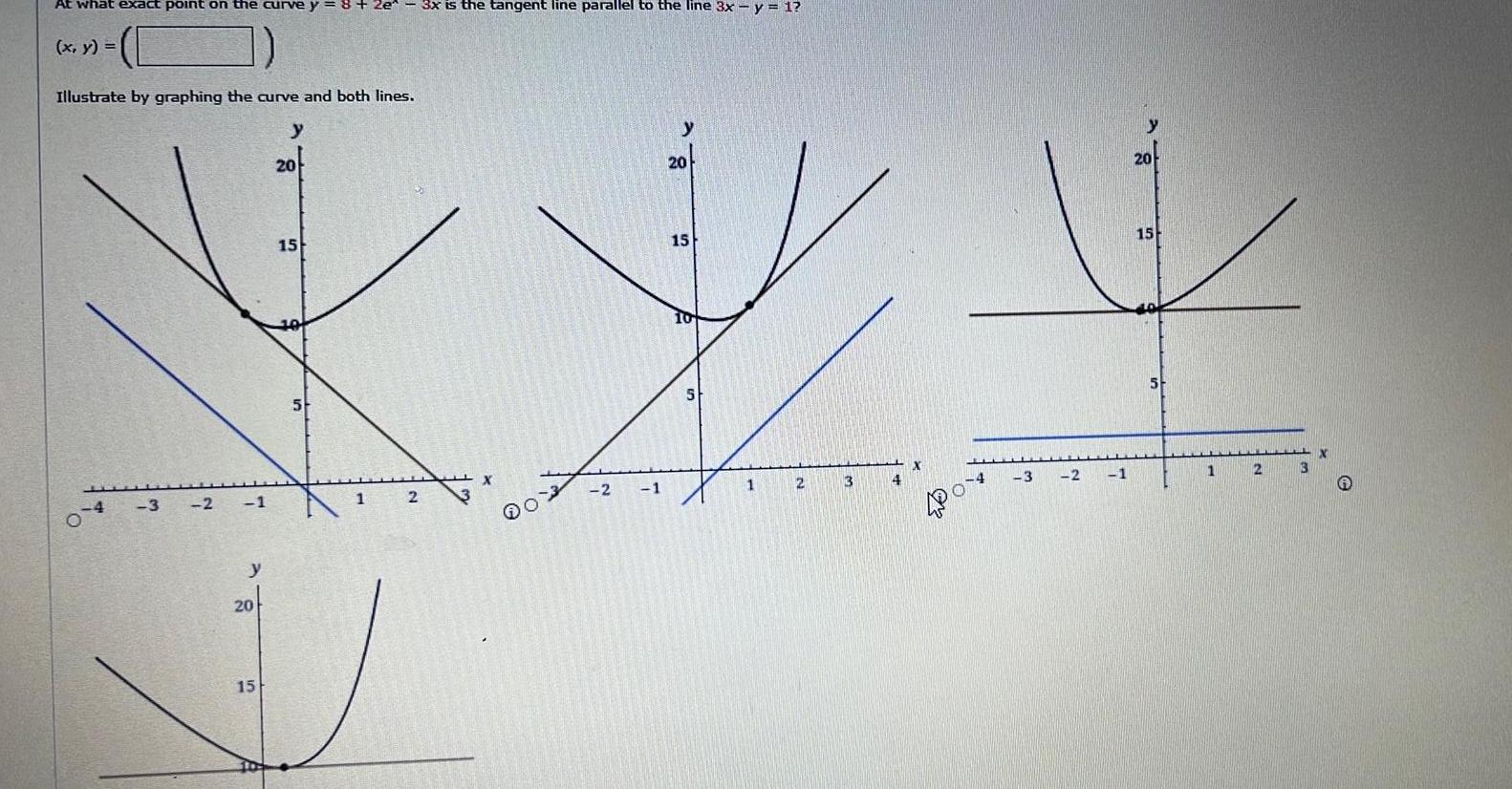
Calculus
Application of derivativesAt what exact point on the curve y 8 2e x y Illustrate by graphing the curve and both lines 4 3 2 1 y 20 15 y 20 15 5 1 2 3x is the tangent line parallel to the line 3x y 1 3 X 103 2 1 y 20 15 10 5 1 2 3 4 X 04 3 2 1 20 15 5 1 2 3 X
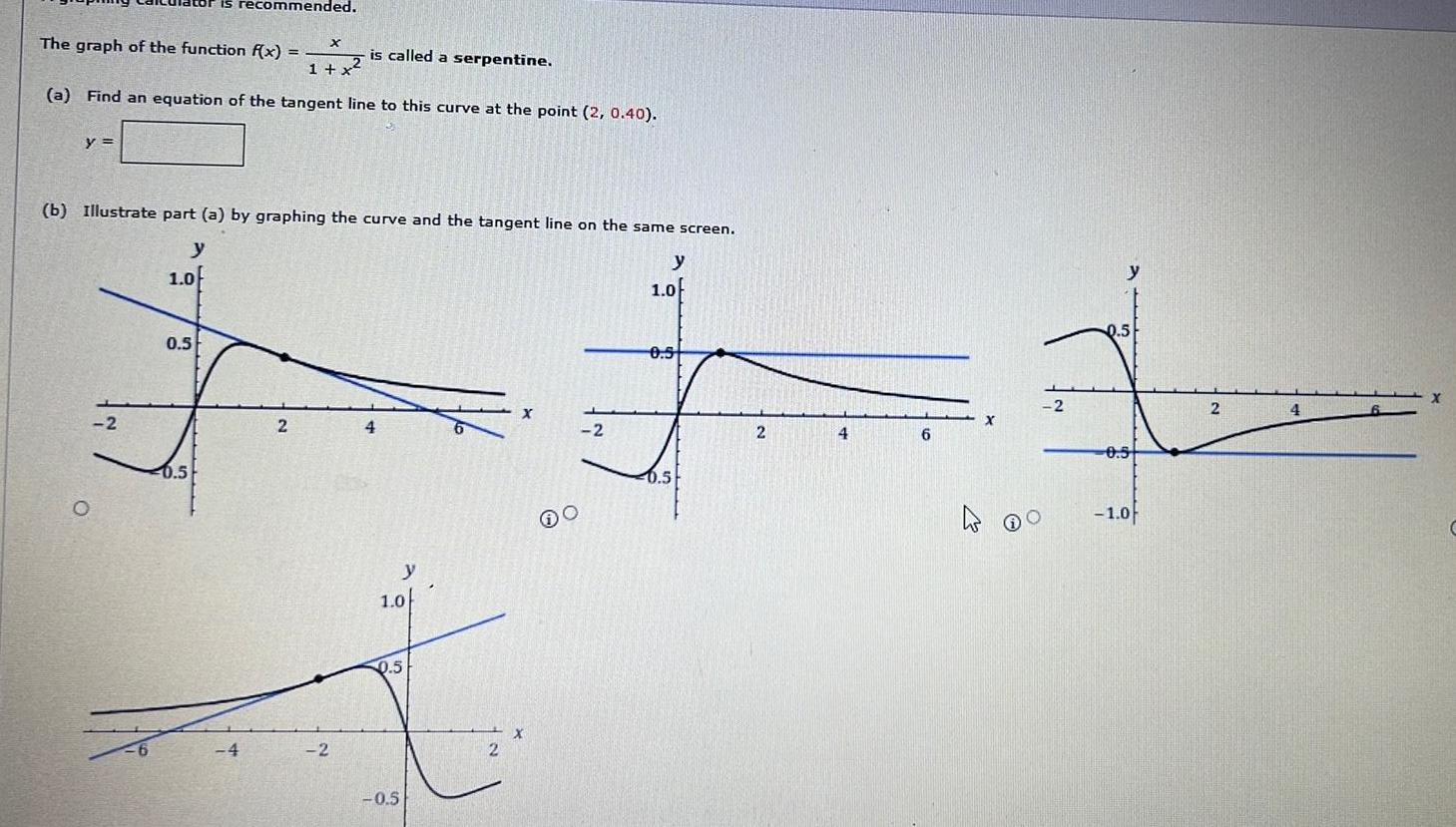
Calculus
Application of derivativesThe graph of the function f x is called a serpentine 1 x a Find an equation of the tangent line to this curve at the point 2 0 40 y O b Illustrate part a by graphing the curve and the tangent line on the same screen y 2 is recommended 1 0 0 5 0 5 X 4 2 2 4 y 1 0 0 5 0 5 2 X X O 2 y 1 0f 0 5 0 5 2 4 6 2 O 0 5 0 5 1 0 2 4 X
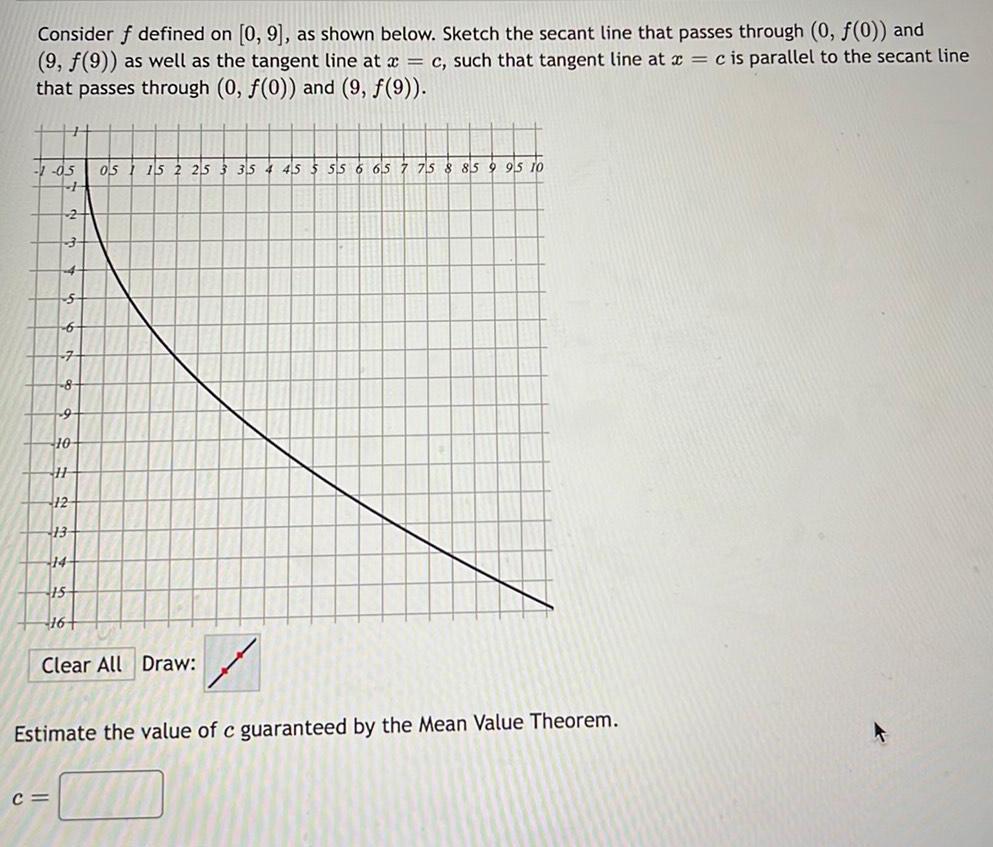
Calculus
Application of derivativesConsider f defined on 0 9 as shown below Sketch the secant line that passes through 0 f 0 and 9 f 9 as well as the tangent line at x c such that tangent line at x c is parallel to the secant line that passes through 0 f 0 and 9 9 1 05 05 15 2 253 354 455 55 6 65 7 75 8 859 95 10 2 4 C 7 8 9 10 H 12 13 14 15 16 7 Estimate the value of c guaranteed by the Mean Value Theorem Clear All Draw
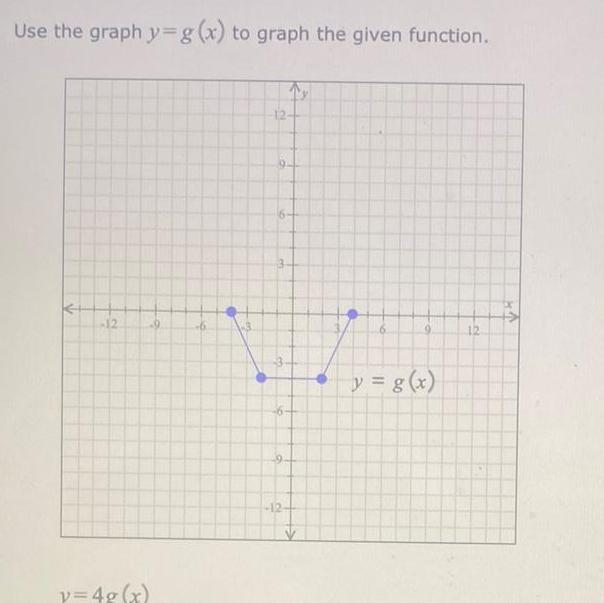
Calculus
Application of derivativesUse the graph y g x to graph the given function 12 9 y 4g x 6 2 12 12 0 P y g x S vx

Calculus
Application of derivativesynthia works at a factory where they make desks t the beginning of the day as Cynthia greets other orkers and gathers her materials she gets little done At id of the day as she gets fatigued and as she cleans up he ork station her production drops off The number of de ynthia makes each hour can be modeled by the equation 10t 1 25t where b is the number of desks and t is e number of hours since she begins her shift raph this situation on your calculator or on a sheet of pa That is a reasonable domain and a reasonable range for t D 0 t 8 R 0 b 20 D b 20 R t 8 D t 8 R b 20 R 0 b 20 R 0 t 8

Calculus
Application of derivativesA company will need 50 000 in 6 years for a new addition To meet this goal the company deposits money in an account today that pays 9 annual interest compounded quarterly Find the amount that should be invested to total 50 000 in 6 years The company should invest Do not round until the final answer Then round to the nearest dollar as needed GILD
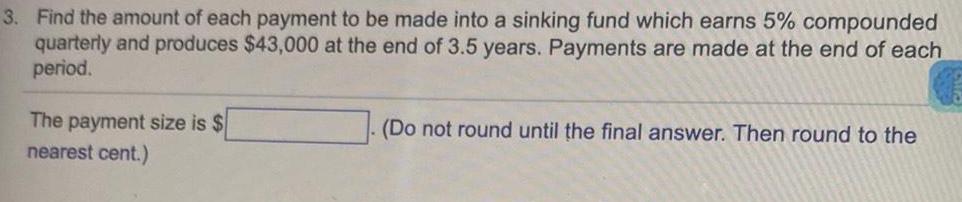
Calculus
Application of derivatives3 Find the amount of each payment to be made into a sinking fund which earns 5 compounded quarterly and produces 43 000 at the end of 3 5 years Payments are made at the end of each period The payment size is nearest cent Do not round until the final answer Then round to the
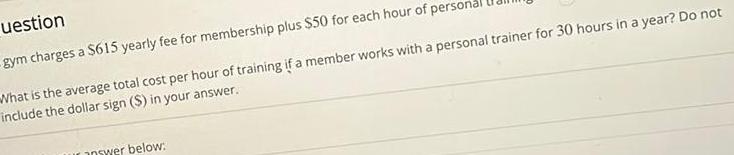
Calculus
Application of derivativesuestion gym charges a 615 yearly fee for membership plus 50 for each hour of perso What is the average total cost per hour of training if a member works with a personal trainer for 30 hours in a year Do not include the dollar sign in your answer answer below

Calculus
Application of derivativesThe pie chart below depicts the beverage size customers choose while at a fast food restaurant Complete parts a through c Most popular beverage sizes at a restaurant Small 22 Medium 16 Large 52 XL 10 a What is the most popular size What percentage of customers choose this siz O A XL 10 OB Large 52 C Small 22 OD Medium 16

Calculus
Application of derivatives2 10 4 of the population is 65 or older Find the probability that the following number of persons selected at random from 50 people are 65 or older The probability that at most 2 are 65 or older is Round to three decimal places as needed

Calculus
Application of derivativesA study determined that 8 of children under 18 years of age live with their father only Find the probability that at most 2 persons selected at random from 10 children under 18 years of age live with their father only The probability that at most 2 children live with their father only is Do not round until the final answer Then round to the nearest thousandth as needed
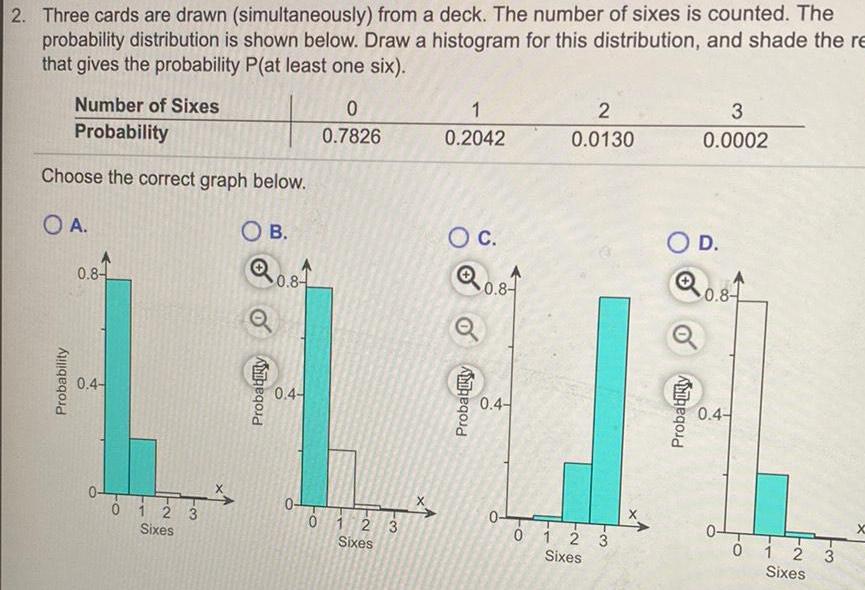
Calculus
Application of derivatives2 Three cards are drawn simultaneously from a deck The number of sixes is counted The probability distribution is shown below Draw a histogram for this distribution and shade the re that gives the probability P at least one six Number of Sixes Probability Choose the correct graph below OA Probability 0 8 0 4 0 1 2 3 Sixes X OB Probability 0 8 0 4 0 0 7826 0 1 2 3 Sixes 1 0 2042 O C Probability 0 8 0 4 0 0 2 0 0130 1 2 Sixes w3 3 0 0002 O D 0 8 Probabiky 0 4 0 1 2 Sixes 3 X

Calculus
Application of derivatives10 Fill in the missing value to make a valid probability distribution 15 0 19 X P x What is the missing probability Type an integer or a decimal 25 35 0 21 45 0 37
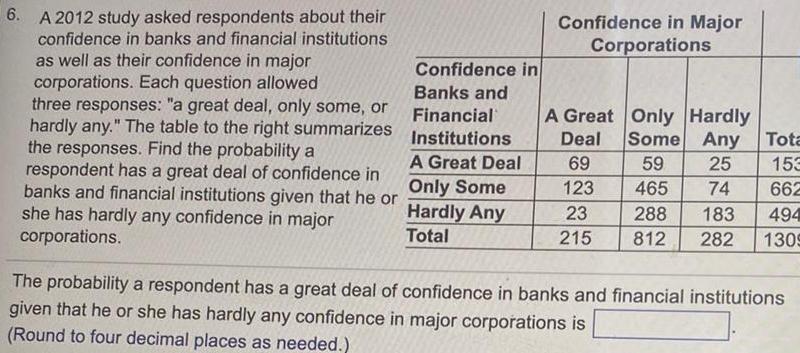
Calculus
Application of derivatives6 A 2012 study asked respondents about their confidence in banks and financial institutions as well as their confidence in major corporations Each question allowed three responses a great deal only some or hardly any The table to the right summarizes the responses Find the probability a respondent has a great deal of confidence in banks and financial institutions given that he or she has hardly any confidence in major corporations Confidence in Banks and Financial Institutions A Great Deal Only Some Hardly Any Total Confidence in Major Corporations A Great Only Hardly Deal Some Any 69 59 25 123 465 74 288 183 812 282 23 215 Tota 153 662 494 1309 The probability a respondent has a great deal of confidence in banks and financial institutions given that he or she has hardly any confidence in major corporations is Round to four decimal places as needed

Calculus
Application of derivatives10 The table below cross classifies the price of 487 stocks in a particular stock exchange with whether the earnings per share ratio was positive or not Use the data in the table to find the probability that the price of the stock is less than 50 ar the eamings per share ratio is negative or 0 Price of Stock 0 49 99 26 APE 457 BP E OC P E 50 00 99 99 100 00 or higher Set up an equation to find the probability of the event occurring Choose the correct answer below Oo P E Negative or C 26 26 14 7 26 126 Earnings per Share 26 126 487 26 14 7 Positive 126 184 130 The probability that the price of the stock is less than 50 and the eamings per share ratio is negative or 0 is Round in In

Calculus
Application of derivatives5 Tami goes shopping and sees three kinds of shoes flats 2 in heels and 3 in heels The shoes come in two shades of beige light and dark and black If each option has an equal chance of being selected find the probability that the shoes Tami buys have less than a 3 in heel and are beige The probability that the shoes Tami buys have less than a 3 in heel and are beige is Type the ratio as a simplified fraction

Calculus
Application of derivativesA manufacturing company performs a quality control analysis on the ceramic tile it produces Suppose a batch of 20 tiles has 6 defective tiles If 5 tiles are sampled at random what is the probability that exactly 1 of the sampled tiles is defective How many ways can 5 tiles be selected from 20 tiles 15504 ways Type a whole number The probability that exactly 1 of the sampled tiles is defective is Round to four decimal places as needed
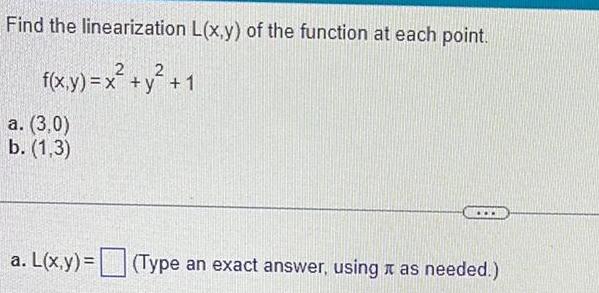
Calculus
Application of derivativesFind the linearization L x y of the function at each point 2 f x y x y 1 a 3 0 b 1 3 a L x y Type an exact answer using it as needed
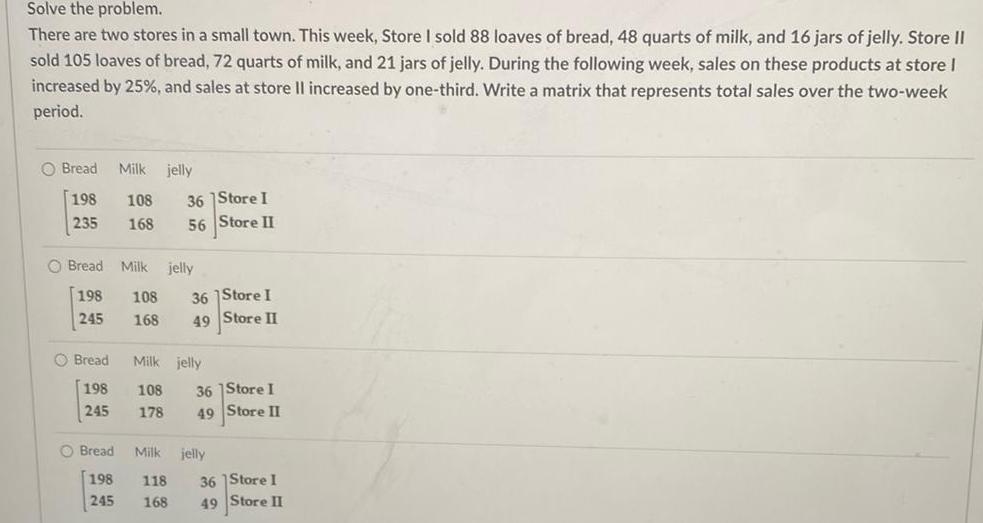
Calculus
Application of derivativesSolve the problem There are two stores in a small town This week Store I sold 88 loaves of bread 48 quarts of milk and 16 jars of jelly Store II sold 105 loaves of bread 72 quarts of milk and 21 jars of jelly During the following week sales on these products at store I increased by 25 and sales at store Il increased by one third Write a matrix that represents total sales over the two week period O Bread Milk jelly 198 108 235 168 O Bread Milk jelly 198 245 O Bread 198 245 Bread 198 245 108 168 36 Store I 56 Store II 36 Store I 49 Store II Milk jelly 108 178 118 168 36 Store I 49 Store II Milk jelly 36 Store I 49 Store II
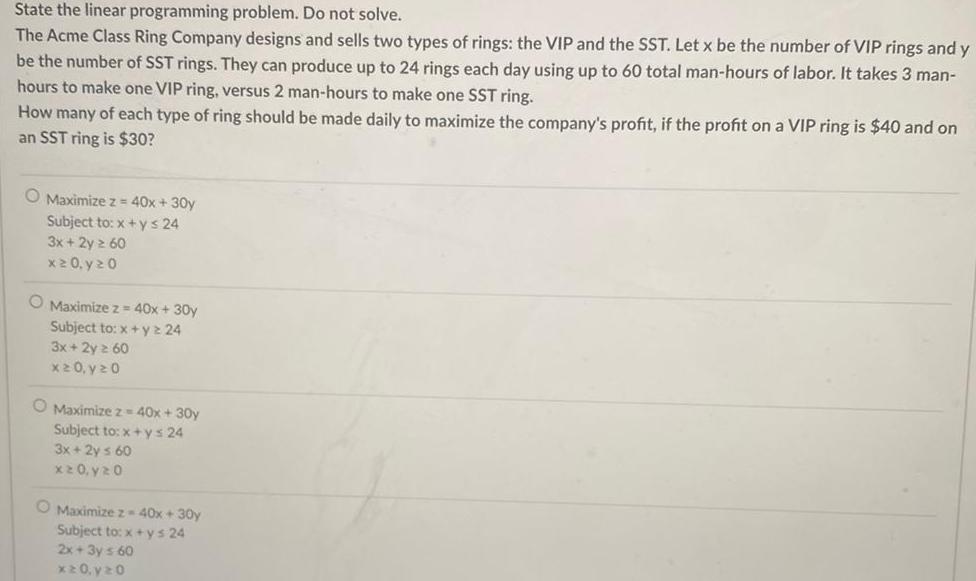
Calculus
Application of derivativesState the linear programming problem Do not solve The Acme Class Ring Company designs and sells two types of rings the VIP and the SST Let x be the number of VIP rings and y be the number of SST rings They can produce up to 24 rings each day using up to 60 total man hours of labor It takes 3 man hours to make one VIP ring versus 2 man hours to make one SST ring How many of each type of ring should be made daily to maximize the company s profit if the profit on a VIP ring is 40 and on an SST ring is 30 O Maximize z 40x 30y Subject to x y 24 3x 2y 60 x 20 y 20 O Maximize z 40x 30y Subject to x y2 24 3x 2y 60 x 20 y 20 O Maximize z 40x 30y Subject to x ys 24 3x 2y s 60 x20 y 20 O Maximize z 40x 30y Subject to x ys 24 2x 3y 60 x 20 y 20
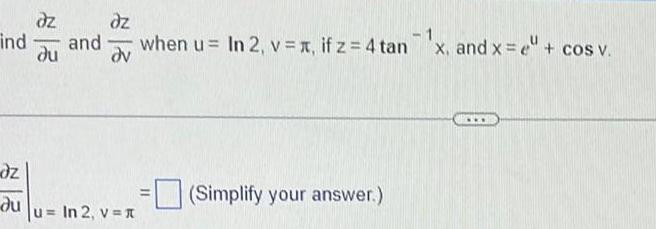
Calculus
Application of derivativesdz dz ind and when u ln 2 v x if z 4 tan x and x cos v du dv dz du u In 2 v Simplify your answer

Calculus
Application of derivativesFind the derivative of the function at Po in the direction of A f x y 2xy 6y Po 8 6 A 6i 8j Find the gradient off at Po Vfp Di Di Type exact answers using radicals as needed
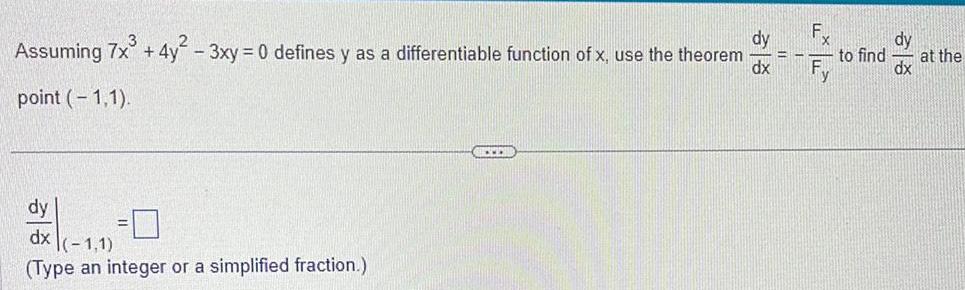
Calculus
Application of derivativesAssuming 7x 4y2 point 1 1 3xy 0 defines y as a differentiable function of x use the theorem dy dx 1 1 Type an integer or a simplified fraction dy dx dy to find at the dx
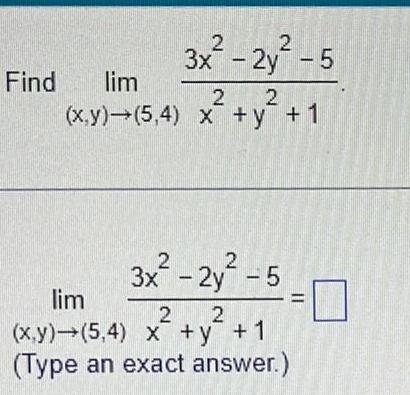
Calculus
Application of derivatives3x 2y 5 2 2 x y 5 4 x y 1 Find lim 2 3x 2y 5 lim 2 2 x y 5 4 x y 1 Type an exact answer

Calculus
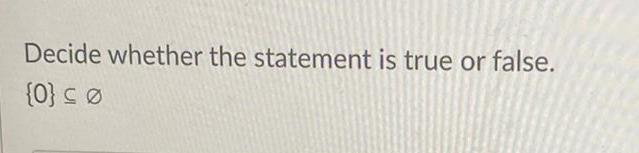
Application of derivativesDecide whether the statement is true or false 1 2 3 u 1 2 3 Edit Insert Format Table

Calculus
Application of derivativesWrite the initial simplex table for the problem Do not solve Maximize z 2x 5x2 subject to 5x 10x 123 10x 15x2 131 X 0 X 0 O X1 X2 1 2 Z 5 10 2 Ox1 5 10 2 10 1 0 0 15 0 1 0 5 0 0 1 x2 1 2 Z 10 10 0 15 0 1 0 5 0 0 1 x1 x2 1 2 Z 5 10 2 10 1 0 0 15 0 1 0 5 0 0 1 O x1 x2 1 2 Z 5 10 1 0 0 10 15 0 0 2 5 0 1 131 123 0 131 123 0 123 131 0 123 1 131

Calculus
Application of derivativesFind the number of subsets of the set A x x is a letter in the word honor



Calculus
Application of derivativesFind the number of subsets of the set A x x is a whole number less than 5 O 32 08 O 12 O 64 16

Calculus
Application of derivativesLet U 0 1 2 3 4 5 6 7 8 A 1 2 3 B 2 3 4 and C 3 5 7 List the members of the indicated set using set braces An B O 0 3 O 1 O 1 2 0181

Calculus
Application of derivativesx 5 x 12 Consider the graph of the function f x x 3 x 2 x 5 What is the y intercept Write your answer in the form x y and use fractions if necess power below

Calculus
Application of derivativesx 5 x 12 x 3 x 2 x 5 Consider the graph of the function f x What are the x intercepts Write your answer as ordered pairs separated by a comma if necessary For example if the intercepts were at x 2 and x 5 you would enter your answer as 2 0 5 0
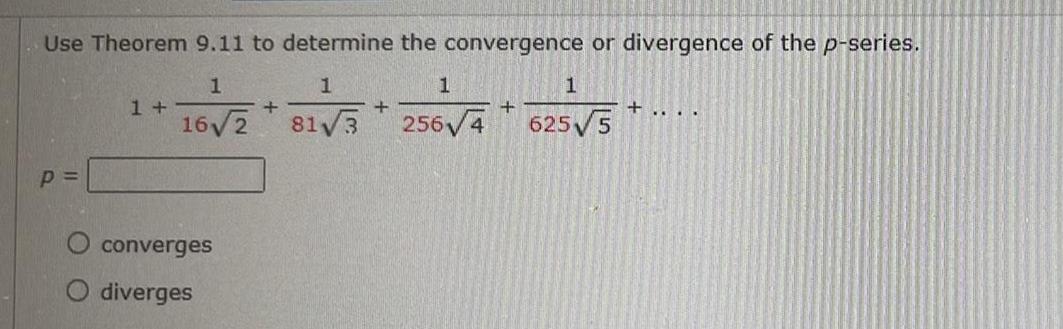
Calculus
Application of derivativesUse Theorem 9 11 to determine the convergence or divergence of the p series 1 16 2 p 1 converges diverges 1 81 3 1 256 4 1 625 5