Definite Integrals Questions and Answers

Calculus
Definite IntegralsX Let A be a vector with magnitude A and components A and Ay In terms of components we can write A A Ay Consider the following specific case A 18 0 km 11 0 km What is the direction of A Note Express your answer as an angle measured clockwise from the Provide your answer below direction
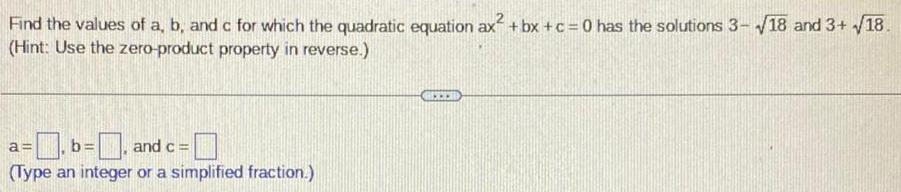
Calculus
Definite IntegralsFind the values of a b and c for which the quadratic equation ax bx c 0 has the solutions 3 18 and 3 18 Hint Use the zero product property in reverse a b and c Type an integer or a simplified fraction

Calculus
Definite IntegralsExample 1 Find the area enclosed by the circle x y a Solution From Fig 8 5 the whole area enclosed by the given circle 4 area of the region AOBA bounded by the curve x axis and the ordinates x 0 and x a as the circle is symmetrical about both x axis and y axis 45 ydx taking vertical strips 4 a x dx Since x y a gives As the region AOBA lies in the first quadrant y is taken as positive Integrating we get the whole area enclosed by the given circle a y 22 to be republish a x a v tu a x 0 sin 1 2 1x x0 sin 1 2 1 a sin y sin Alternatively considering horizontal strips as shown in Fig 8 6 the whole area of the region enclosed by circle X B 0 a 45 xdy 4 y dy Rationalised 2023 24 0 Why Fig 8 5 X APPLICATION OF INTEGRALS b dx A a 0 X dy O Fig 8 6 295 A a 0 ied Example 2 Find the area enclosed by the ellipse Solution From Fig 8 7 the area of the region ABA B A bounded by the ellipse area of the region AOBA in the first quadrant bounded 4 by the curve x axis and the ordinates x 0 x a as the ellipse is symmetrical about both x axis and y axis

Calculus
Definite Integrals440 MATHEMATICS 8 12 17 20 24 29 1 2 C 9 x x 1 C x 4 x 8 C 32 log x 1 m log e e C 22 tan 7 4x C 2e 1 26 2sin x C 39 B C x 1 22 C 15 log19 4x C 16 log 2sin x 3 cos x C log sin x C 18 C x 1 28 14 2 tanx C 35 cos tan x C sin 4x 10 C NCERT 10 2log x 1 C I 13 18 2 3x 30 log 1 cosx C31 1 log x C Rationalised 2023 24 19 log e EXERCISE 7 3 sin 12x x sin 8x sin 4x 25 n2x C 28 2 1 sin x C otto e republished tan 2x 3 x C 33 1 sin x C 1 1 tan x 1 1 cosx C x 1 2 2 38 D C log cos x sin x C 36 x log x C ANSWERS 441

Calculus
Definite Integralsthe Derivation of cartesian form from vector form Let the coordinates of the given point A be x y z and the direction ratios of the line be a b c Consider the coordinates of any point P be x y z Then 7 xi y zk a x i j z k and b al bj ck Substituting these values in 1 and equating the coefficients of i and k we get x x a y y b z z kc 2 These are parametric equations of the line Eliminating the parameter from 2 we get x X 2 4 b This is the Cartesian equation of the line Note If 1 m n are the direction cosines of the line the equation of the line is 2 4 11 m Example 6 Find the vector and the Cartesian equations of the line through the point 5 2 4 and which is parallel to the vector 3 2j 8k Solution We have a Si 2 4k and b 3i 2j 8k cos 8 Rationalised 2023 24 Therefore the vector equation of the line is F 57 23 4k 37 27 8k Now F is the position vector of any point P x y z on the line Therefore xi yj zk 5i 2j 4k 3 2j 8k Eliminating we get 5 3 2 2X j 4 8 k 5y 2 4 8 THREE DIMENSIONAL GEOMETRY 383 which is the equation of the line in Cartesian form 11 4 Angle between Two Lines Let L and L be two lines passing through the origin and with direction ratios a b c and a b c respectively Let P be a point on L and Q be a point on L Consider the directed lines OP and OQ as given in Fig 11 6 Let 8 be the acute angle between OP and OQ Now recall that the directed line segments OP and OQ are vectors with components a b c and a b c respectively Therefore angle 8 between them is given by aa bb cc a b c b c The angle between the lines in terms of sin 8 is given by sin 0 1 cos 0 3 a bb 56 Fig 11 4 resublished Q L
Calculus
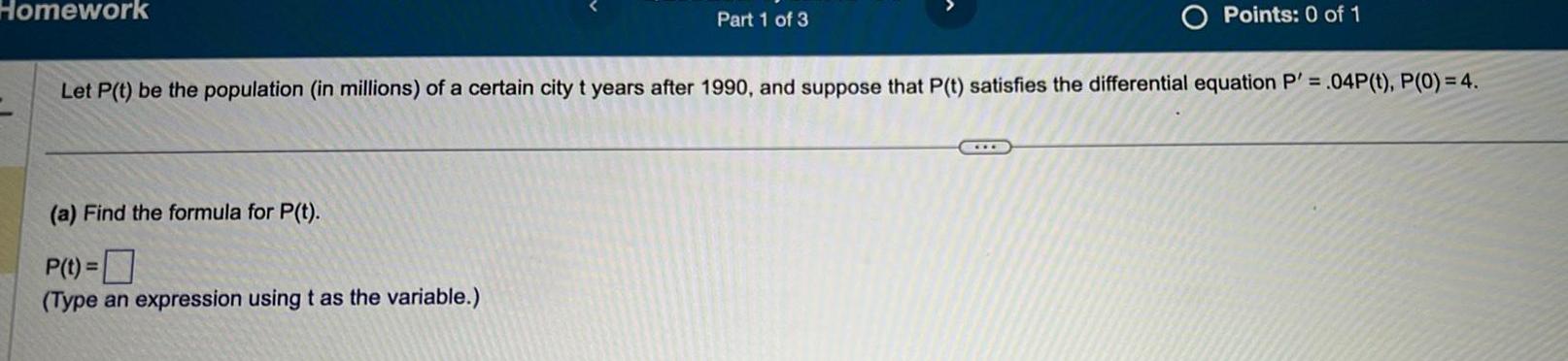
Definite IntegralsHomework Part 1 of 3 a Find the formula for P t P t Type an expression using t as the variable Points 0 of 1 Let P t be the population in millions of a certain city t years after 1990 and suppose that P t satisfies the differential equation P 04P t P 0 4

Calculus
Definite IntegralsAns 115 Civil Lines Ajmer 25 July 20 The Principal Dayanand Senior Secondary School Ajmer Subject To Issue Transfer Certificate Sir I am a student of class XI C of your school My father is a clerk in the State Bank of India Ajmer But now he has been transferred to Suratgarh I have to secure admission to a school at Suratgarh You are therefore requested to issue me my T C No dues certificate is attached herewith Regards Yours obediently Nand Lal S o Mr Hira Lal S R No 326 20 19 A Letter for Railway Concession

Calculus
Definite Integralsfoculista doctor who examines and treats people s eyes 12 A Letter to Teach through Project Utkarsh ne that you are Balvir Bairagi a student of class XI of Gout Senior Secondary Scho letter to the principal of your school requesting him to teach your class through Shanti Sadan Baseri 23 October 20 The Principal Govt Senior Secondary School Baseri of scholarsh to know unt I questes bmitt best reg obedie Verm Yesterday I got myself registered as a student and found that it would be very helpful for us in improving our division and the result of our school if we were taught through it I hope that you will personally look into the matter and make necessary arrangement for it With best regards Yours obediently Balvir Bairagi 13 Non deposit of Scholarshin XC ter Ne A Lett et cho Subject Teaching through project Utkarsh Sir With due respect I wish to state that I am a student of class XI B Almost all the teachers of Rom our school are highly talented and qualified There is no doubt that they teach us excellently They are truly devoted to us They are keen in solving our problems But no teacher teaches us through Project Utkarsh instgar Octob The Prin vt Se abject

Calculus
Definite IntegralsThe area of the region bounded by the curve y x the lines x 1 and x 4 and the x axis is the area ABCD Class XII Chapter 8 Application of Integrals Maths Area of ABCD ydx xdx 11 14 3 units

Calculus
Definite IntegralsAnswer The area of the region bounded by the curve x 4y y 2 and y 4 and the y axis is the area ABCD Class XII Chapter 8 Application of Integrals Maths Area of ABCD xdy 2 ydy 2 ydy 1 Page 4 of 53
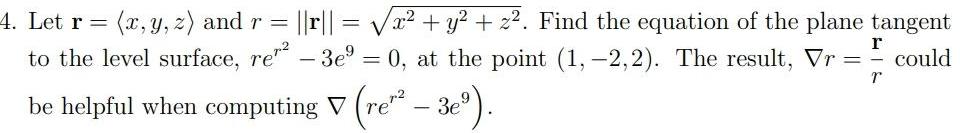
Calculus
Definite Integrals4 Let r x y z and r r x y z Find the equation of the plane tangent to the level surface re 3e 0 at the point 1 2 2 The result Vr r could be helpful when computing V re2 3e r

Calculus
Definite Integralsa unique perspective of investme Forex Trading Platform JE 34 H 10 30 314 313 fafrius 3Thise th Fions 3 al da fa d az H 100 Safe and Secure Platform Best Opportunity in India fund com
Calculus
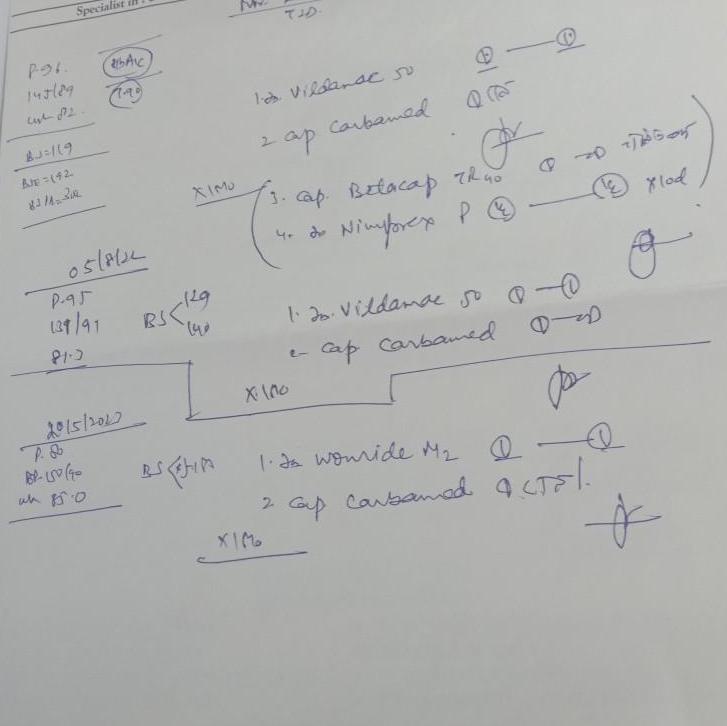
Definite IntegralsPOT 145 89 list 82 83 119 BJ 42 Specialist 05 8 12 P95 139 91 81 2 2015 2012 AC wh 85 0 RS XIMU 129 BS ANIMA 1 Vildande so 2 ap 3 cap Belacap Thuo 4 de Nimforex P Carbamed x 100 XIM 1 2 Vildamae 50 000 cap carbamed p 1 Is wounide M 2 cup carbamed actrl Don plod o

Calculus
Definite IntegralsKaniska Joshi Register No 23 Class XI A 6 Spelling Mistake on the Shaala Darpan Portal Imagine that you are Rabindra Khurana a student of class XI You come to know that there is mistake in the spelling of your name on the portal of Shaala Darpan Write a letter to the principal of your school to update the spelling of your name Ans Ram Mandir Road Matalwas 30 December 20 The Principal Govt Senior Secondary School Matalwas Subject Error in the entry on the Portal of Shaala Darpan Sir Respectfully I am a student of class XI A of your school Yesterday I visited the portal of Shaala Darpan and found out that there was mistake in the spelling of my name It is a kind of clerical error It is as under What is uploaded Ravindra Kurana What must be uploaded Rabindra Khurana I am enclosing my birth certificate and Aadhaar Card for your perusal It will be very kind if you please update it and do the needful With best regards Yours obediently Rabindra Khurana ject For incor spectfully I an at our class has de whole set of the detail of the Hornbill Snapsho fat fet Physics Chemi Biolog We made req tests are at h to us as earl With best re Yours obedi Shantanu S Monitor Class XI A 11 8 Cleanin Imagine th not been cl to clean th
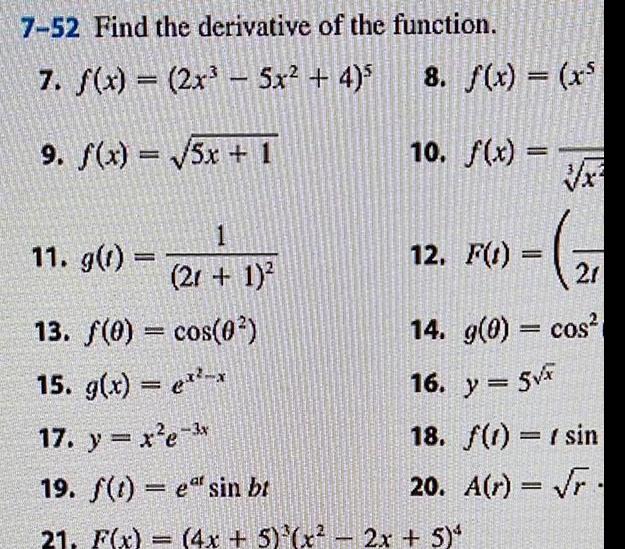
Calculus
Definite Integrals7 52 Find the derivative of the function 7 f x 2x 5x 4 9 f x 5x 1 11 g t 8 f x x5 10 f x 1 21 1 13 f 0 cos 0 15 g x e 17 y x e 3x 19 f t e sin bt 21 F x 4x 5 x 2x 5 12 F t 21 14 g 0 cos 16 y 5 x 18 f 1 sin 20 A r r

Calculus
Definite Integrals8 The Taylor Series of 1 x x2 x3 x4 for 1 x 1 1 x Knowing that 0 51dx 0 693147180 1 x a Truncate the series to the first 4 terms then calculate the definite integral based on these four terms b What is the absolute error c What is the relative error d Determine the accuracy of the approximation obtained the number

Calculus
Definite Integralsf x x Let x be any arbitrary element of R then Right hand limit at x x lim f x lim f x h X X Institute of Lifelong Learning University of Delhi lim x h 40 lim x h 2xh 0 0 lim f x x X X Left hand limit at x x lim f x lim f x h lim x h 60 lim x h 2x h x 0 0 lim f x x x x Hence lim f x x 2 Au Since lim f x lim f x x2 X 195 Continuity of Functions Now the value of the function at x x is SITY f x x from equation 1 and 2 we have lim f x f x x X 30 f x f x Thus f x x is continuous at x x Since is an arbitrary element of R Therefore f x is continuous at each point of R Hence f x is continuous on R Example 4 Show that the function f x defined by if x 0 X 0 if x 0 is continuous on R Solution Given function is DELHI xsin if x 0 1 2
Calculus
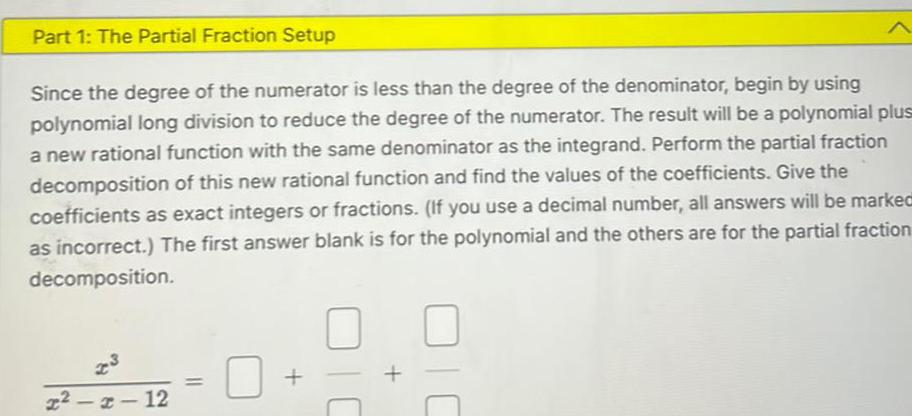
Definite IntegralsPart 1 The Partial Fraction Setup Since the degree of the numerator is less than the degree of the denominator begin by using polynomial long division to reduce the degree of the numerator The result will be a polynomial plus a new rational function with the same denominator as the integrand Perform the partial fraction decomposition of this new rational function and find the values of the coefficients Give the coefficients as exact integers or fractions If you use a decimal number all answers will be marked as incorrect The first answer blank is for the polynomial and the others are for the partial fraction decomposition x x 12

Calculus
Definite IntegralsLet V 1 2 3 n Let X i j i je V and are relatively prime The resulting graph V X is denoted by G Draw G4 and G5 Solution For G V 1 2 3 4 and X 1 2 1 3 1 4 2 3 3 4 For G V 1 2 3 4 5 and X 1 2 1 3 1 4 1 5 2 3 2 5 3 4 3 5 4 5 3 2 4 Graph of G Fig 1 11 1 2 DEGREES Graph of Gs Fig 1 12 Definition The degree of a point v in graph G is the number of lines incident with v It is denoted by d v or deg v or d G vi

Calculus
Definite IntegralsSo the appropriate domain for this situation is all non negative real numbers or in interval notation 0 00 b The range of a function refers to the set of all possible output values that the function can produce In this case the function H t represents the temperature of the hot chocolate Looking at the equation H t 70 100 0 819 t The first term 70 is a constant that represents the base temperature The second term 100 0 819 t represents the increase in temperature due to the exponentiation of 0 819 to the power of t Since 0 819 is between 0 and 1 raising it to larger and larger powers will cause it to approach zero resulting in diminishing temperature increases This means that the temperature of the hot chocolate will increase over time but will asymptotically approach a maximum value which is the base temperature plus the initial increase As time goes to infinity the exponential term will approach zero so the temperature will approach the constant value of 70 However it will never quite reach 70 ift is finite and positive

Calculus
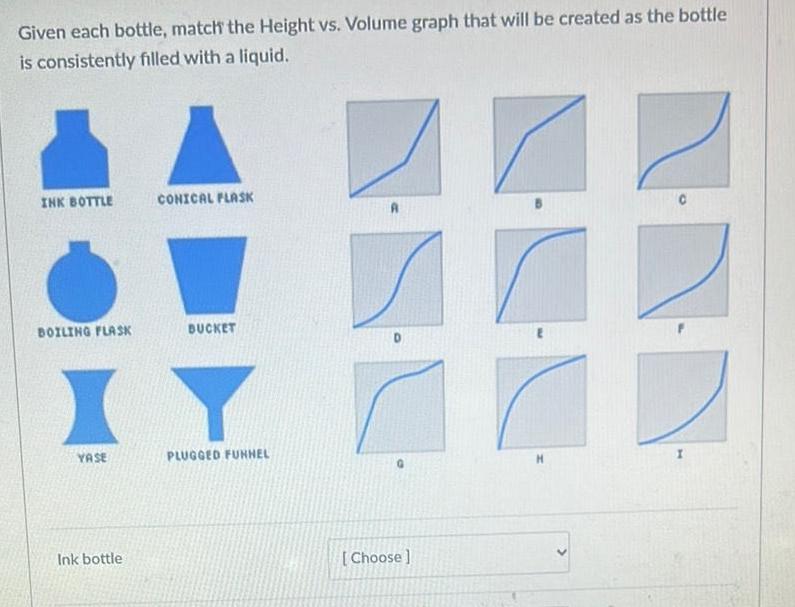
Definite IntegralsGiven each bottle match the Height vs Volume graph that will be created as the bottle is consistently filled with a liquid INK BOTTLE BOILING FLASK YASE Ink bottle CONICAL FLASK BUCKET PLUGGED FUNNEL Choose


Calculus
Definite IntegralsProblem 6 Find a formula for the inverse of the following function Set 7e 4 f x A y G y 7et 4et 5 7e 4 Set B y In H y 4x 7x 5 7e 4 Set 5ln x C y7lnx 4 D y 7lnx 4 5in x In Fy In 7 4x

Calculus
Definite Integrals7 10 points Consider the contour map below of the popular hiking area known with the famous potato chip rock Suppose that f x y is the function that gives the vertical height in feet of the mountain over a point x y 008 a 2 points Assume the lines are level curves that are equally spaced What is the elevation at the point P Answer b 3 points Draw a vector at Q in the direction of Vf Q 000 i f c 0 1600 ii At t 1 f c t 0 iii At t 2 f c t 0 iv At t 3 f c t 0 v ALSO at t 3 f c t P c 5 points Draw ONE curve c t for 0 t 4 on the graph with ALL of the following properties Label time stamps for t 0 t 1 t 2 t 3 for your curve

Calculus
Definite Integrals1 10 points Find the volume of the solid region under the surface z x y e and over the rectangle 0 1 x 1 3 in the x y plane
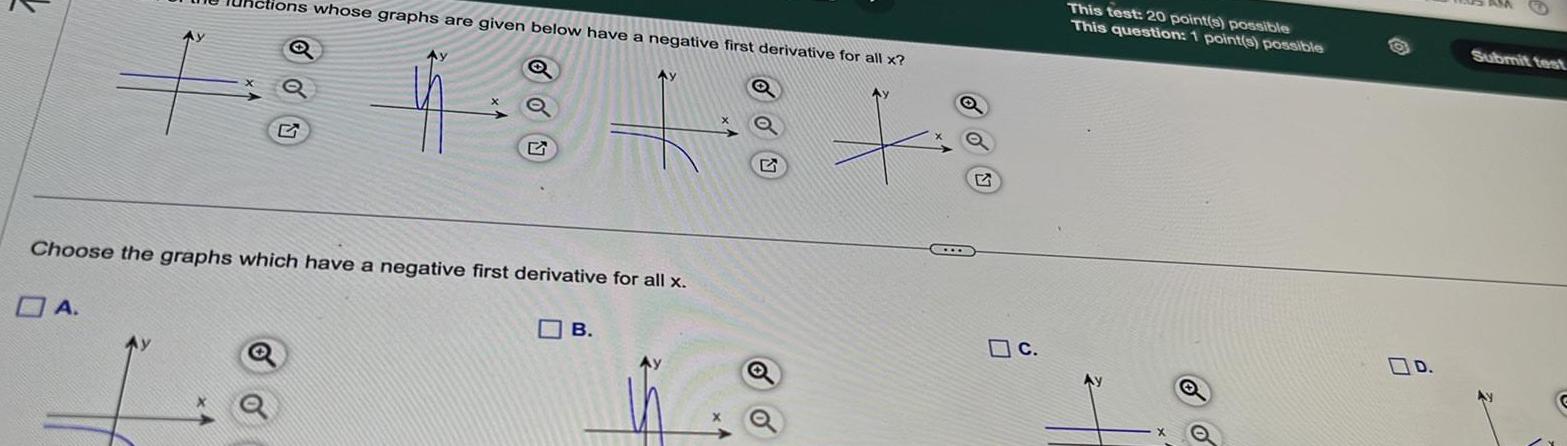
Calculus
Definite Integralstions whose graphs are given below have a negative first derivative for all x Q 4 Choose the graphs which have a negative first derivative for all x A B Q c This test 20 point s possible This question 1 point s possible o D Submit test
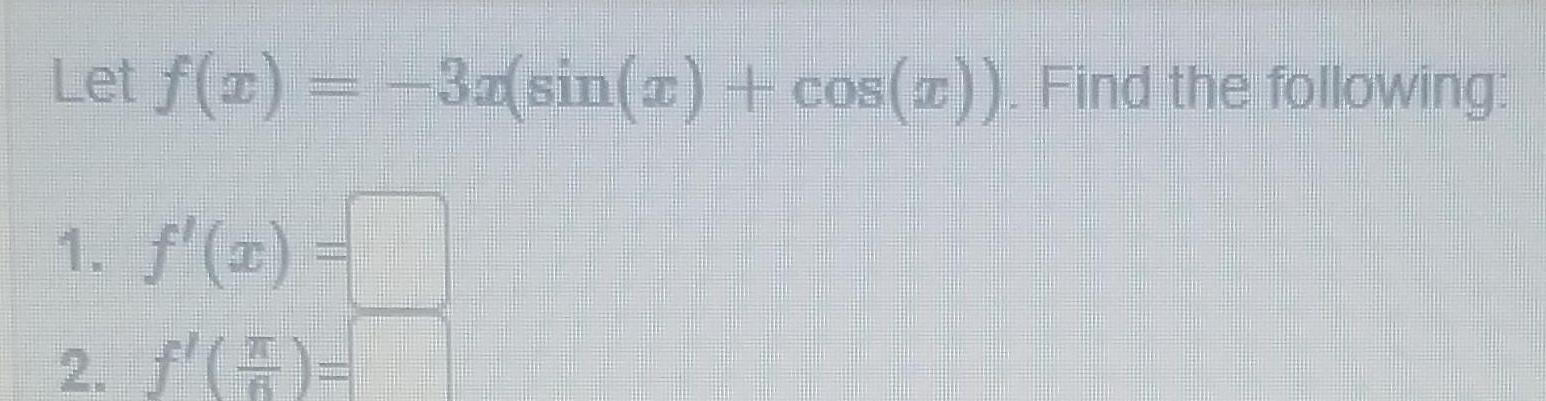
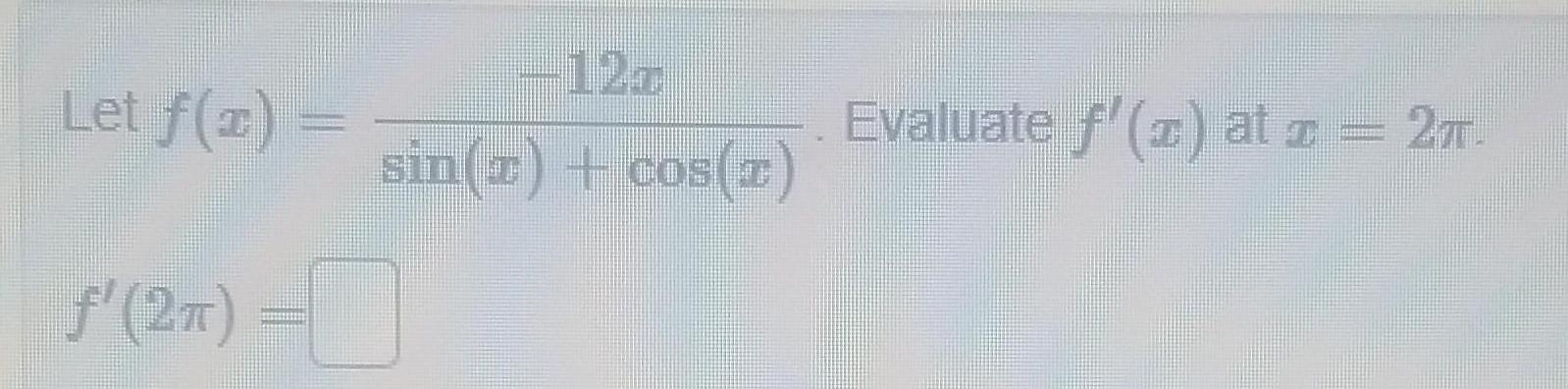
Calculus
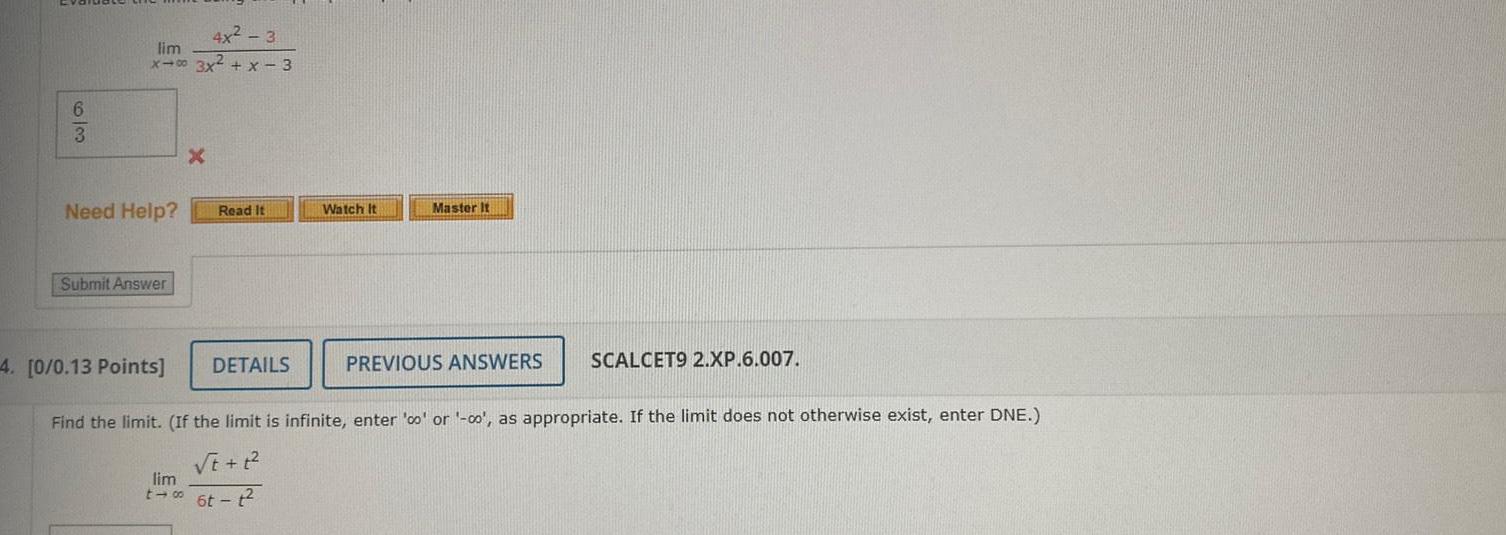
Definite Integrals6 3 4x 3 lim x 00 3x x 3 Need Help Submit Answer 4 0 0 13 Points X Read It DETAILS Watch It Master It PREVIOUS ANSWERS SCALCET9 2 XP 6 007 Find the limit If the limit is infinite enter co or co as appropriate If the limit does not otherwise exist enter DNE t t lim t 6t t

Calculus
Definite IntegralsValues of f x y are shown in the table below x 32 3 32 3 6 y 4 8 y 4 5 10 13 10 12 16 V 5 12 14 7 Let R be the rectangle 3 3 6 4 y 5 Find the values of Riemann sums which are reasonable over and under estimates for f f x y dA with Ar 0 3 and Ay 0 over estimate 5 85 under estimate 6

Calculus
Definite IntegralsEvaluate the integral Answer 484x 5y Answers A Answer S e42 5y dA R 0 6 x 0 8 5y d
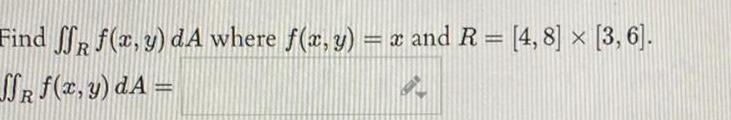
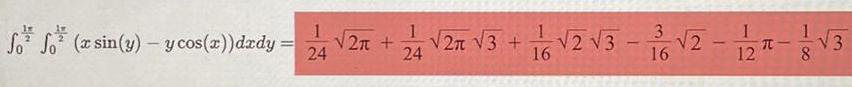
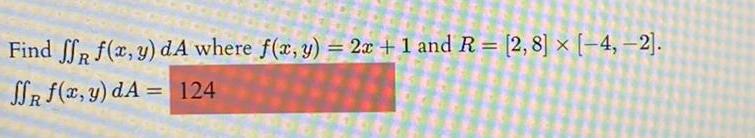

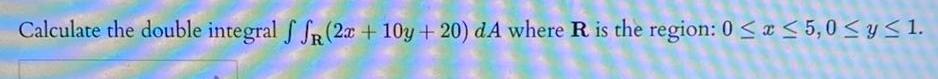
Calculus
Definite IntegralsCalculate the double integral f SR 2x 10y 20 dA where R is the region 0 x 5 0 y 1
Calculus
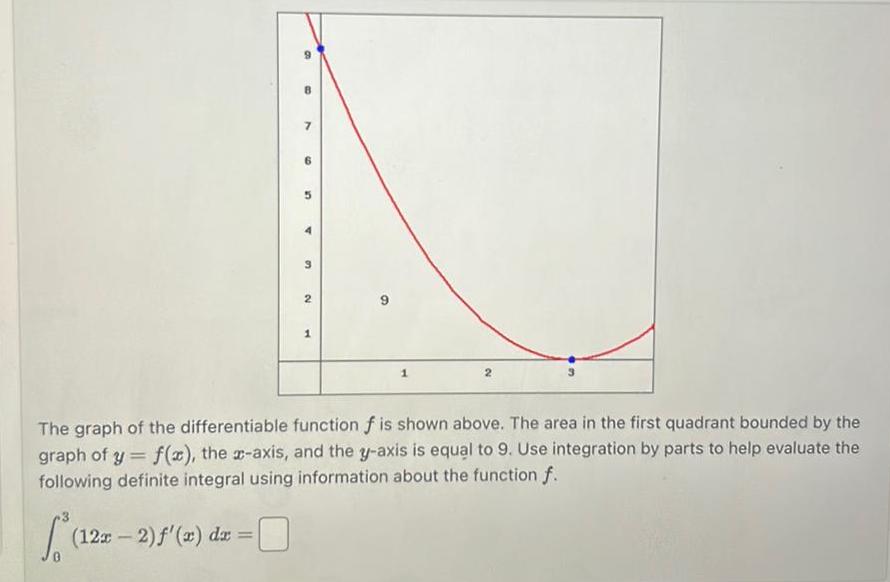
Definite Integrals8 122 12r 2 f x dx 7 6 5 3 2 1 6 1 The graph of the differentiable function f is shown above The area in the first quadrant bounded by the graph of y f x the x axis and the y axis is equal to 9 Use integration by parts to help evaluate the following definite integral using information about the function f

Calculus
Definite Integralss 4x4 5 1 dx In the following we will evaluate the integral using two Consider the integral methods A First rewrite the integral by multiplying out the integrand 40 4x x 1 dx Then evaluate the resulting integral term by term 4x 4 x x5 1 dx da B Next rewrite the integral using the substitution w x5 1 42 10dw 4x x5 1 dx Evaluate this integral and back substitute for w to find the value of the original integral 14 4x4 x5 1 dx C How are your expressions from parts A and B different What is the difference between the two Ignore the constant of integration answer from B answer from A

Calculus
Definite IntegralsUsing the method of u substitution 4 S 6x 8 dx 2 where U du a b f u S f f u du enter a function of x dx enter a function of x enter a number enter a number enter a function of u The value of the original integral is


Calculus
Definite IntegralsSuppose that the graph of a function f is known Then the graph of y f x 2 may be obtained by a f the graph of f a distance of 2 units vertical
Calculus
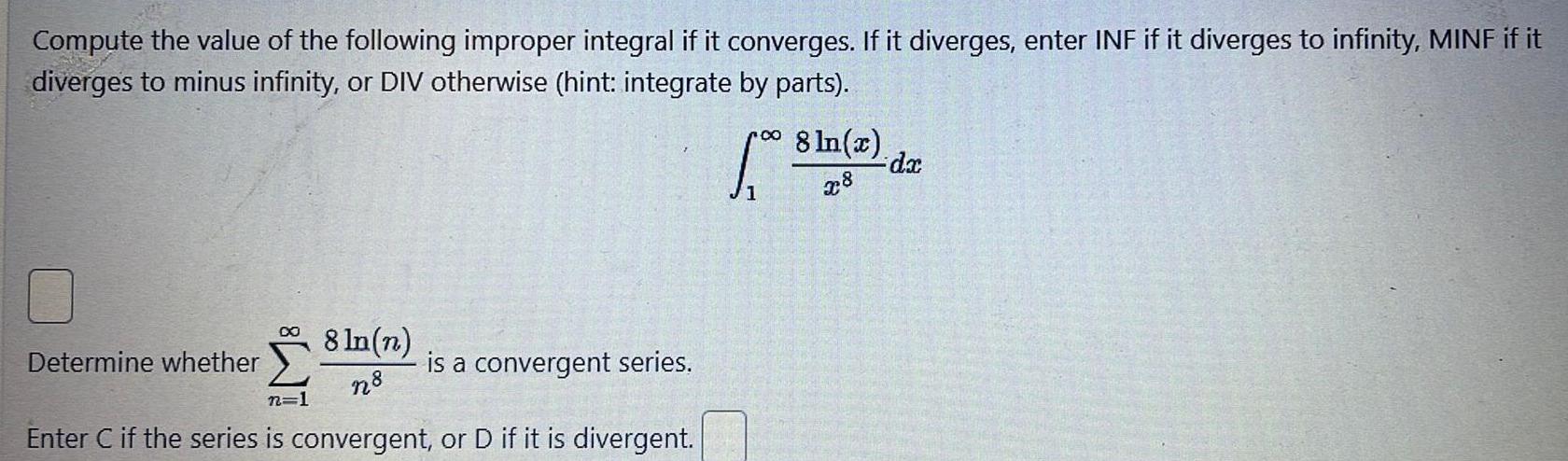
Definite IntegralsCompute the value of the following improper integral if it converges If it diverges enter INF if it diverges to infinity MINF if it diverges to minus infinity or DIV otherwise hint integrate by parts 8 ln n n8 n 1 Enter C if the series is convergent or D if it is divergent Determine whether is a convergent series 1 8 ln x x8 dx
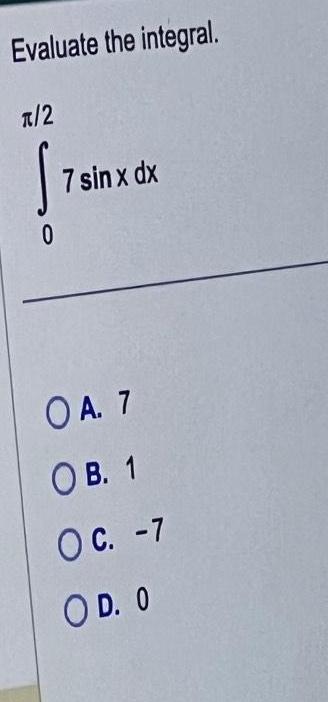
Calculus
Definite IntegralsA force of 1 N will stretch a rubber band 5 cm Assuming Hooke s law applies how much work is done on the rubber band by a 3 A 0 075 J OB 2 250 J C 0 225 J D 0 025 J

Calculus
Definite IntegralsA water tank in the shape of a hemispherical bowl of radius 6 m is filled with water to a depth of 3 m rm dm How much work is required to pump all the water over the top of the tank The density of water is 1000 kg m Use symbolic notation and fractions where needed

Calculus
Definite IntegralsMultiply and simplify Assume that all expressions under the radicals represent nonnegative numbers 9 n Type an exact answer using radicals as needed